MODUL PRAKTIKUM Perkuliahan Astrofisika (FI567)
|
|
|
- Sudirman Lie
- 9 tahun lalu
- Tontonan:
Transkripsi
1 MODUL PRAKTIKUM Perkuliahan Astrofisika (FI567) Disusun oleh: Judhistira Aria Utama, M.Si. Laboratorium Bumi dan Antariksa Jurusan Pendidikan Fisika Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam Universitas Pendidikan Indonesia 2012
2 MODUL 1 Orbit Planet Tujuan Dalam aktivitas laboratorium ini mahasiswa berlatih membangun dan menginterpretasi grafik berdasarkan data posisi planet untuk memperoleh bentuk dan nilai sejumlah parameter orbit Perlengkapan Komputer yang dilengkapi perangkat lunak pengolah data Microsoft Excel dan perangkat lunak planetarium CyberSky A. Deskripsi Bagaimanakah Johannes Kepler ( ) memperoleh hukum-hukum tentang bentuk orbit dan gerak planet-planet di Tata Surya? Pekerjaan Kepler yang fenomenal adalah ketika berhasil memperoleh bentuk orbit planet Mars, tidak saja karena memakan waktu yang lama (8 tahun lamanya dari persangkaan awal yang hanya 8 minggu!) namun juga menunjukkan kelengkapan data observasi yang telah diperoleh sebelumnya oleh astronom Denmark Tycho Brahe ( ) di mana Kepler bekerja sebagai asistennya. Dalam aktivitas laboratorium ini, menggunakan gagasan yang sama dengan apa yang telah dilakukan Kepler, Anda diminta merekonstruksi bentuk orbit planet Merkurius berdasarkan data posisi planet ini saat memiliki jarak sudut (elongasi) terjauh dari Matahari menurut pengamat di permukaan Bumi. Memanfaatkan perangkat lunak planetarium CyberSky yang disediakan, Anda akan mengumpulkan data observasi berupa nilai jarak sudut Merkurius dari Matahari selama kurun waktu lima tahun ( ). Selanjutnya, Anda diminta untuk melakukan curve fitting (pencocokan kurva) dengan bantuan perangkat lunak pengolah data Microsoft Excel, di mana Anda memodelkan suatu persamaan matematis yang cocok dengan profil orbit Merkurius yang telah Anda peroleh. Setelah Anda berhasil mendapatkan nilai-nilai terbaik untuk persamaan yang cocok dengan profil orbit Merkurius, Anda diminta untuk memperoleh beberapa parameter orbit, seperti setengah sumbu panjang (a), eksentrisitas (e), dan periode orbit (baik periode sideris maupun periode sinodis). B. Prosedur Menggunakan perangkat lunak Microsoft Excel, lakukan langkah-langkah berikut ini: 1. Isikan secara berturut-turut, dimulai dari sel A1 hingga sel K1, header berikut: Hari, Bulan, Tahun, Nomor Urut Hari, Tahun Kabisat, Julian 1
3 Day, Elongasi, Jarak dari Matahari (AU), Bujur Ekliptika ( 0 ), x (AU), dan y (AU). 2. Di dalam sel I34 berikan header Matahari. 3. Isikan tanggal ke dalam sel A2 hingga A33, bulan ke dalam sel B2 hingga B33 (Januari = 1, Februari = 2, dst), dan tahun (dua digit terakhir) ke dalam sel C2 hingga C Tuliskan ke dalam sel D2: =INT(275*(B2/9)) 2*INT((B2+9)/12) + A2 30 Lanjutkan mengisi hingga baris D Tuliskan ke dalam sel E2: =INT((C2 1)/4) Lanjutkan mengisi hingga baris E Tuliskan ke dalam sel F2: = *(C2) + D2 + E2 0.5 Lanjutkan mengisi hingga baris F Tuliskan ke dalam sel G2 hingga G33 nilai elongasi yang diperoleh dari perangkat lunak CyberSky. Bila posisi Merkurius berada lebih timur daripada Matahari, nilai elongasi bertanda negatif (-) dan sebaliknya, nilai elongasi bertanda positif (+) saat posisi Merkurius berada lebih barat daripada Matahari. 8. Tuliskan ke dalam sel H2: =SIN(ABS(G2*PI()/180)) Lanjutkan mengisi hingga baris H Tuliskan ke dalam sel I2 hingga I33 nilai bujur ekliptika Merkurius (dalam satuan derajat) yang disajikan dalam tabel. 10. Tuliskan ke dalam sel J2: =H2*COS(I2*PI()/180) Lanjutkan mengisi hingga baris J Tuliskan ke dalam sel K2: =H2*SIN(I2*PI()/180) Lanjutkan mengisi hingga baris K Tuliskan ke dalam sel J34: 0 dan sel K34: Rajahlah (plot) orbit Merkurius dan posisi Matahari menggunakan Chart Wizard Tool menggunakan tipe Scatter (tanpa garis penghubung). Setelah berhasil memperoleh profil orbit Merkurius, di lembar kerja berbeda lakukan langkah-langkah berikut ini: 1. Isikan secara berturut-turut, dimulai dari sel A1 hingga sel D1, header berikut: Bujur Model q ( 0 ), Jarak Model r (AU), x (AU), y (AU), untuk sel E1 dan F1 (merge cells): (x - h) 2 + (y - k) 2 = a 2, dan sel G1: Satuan. 2. Tuliskan ke dalam sel A2: 0 dan sel A3: =A2+10. Lanjutkan mengisi hingga baris A Tuliskan ke dalam sel B2: =($F$2*COS(A2*PI()/180) + $F$3*SIN(A2*PI()/180)) + SQRT(($F$2*COS(A2*PI()/180) + $F$3*SIN(A2*PI()/180))^2 $F$2^2- $F$3^2+$F$4^2) Lanjutkan mengisi hingga baris B Tuliskan ke dalam sel C2: =B2*COS(A2*PI()/180) Lanjutkan mengisi hingga baris C Tuliskan ke dalam sel D2: =B2*SIN(A2*PI()/180) Lanjutkan mengisi hingga baris D Tuliskan ke dalam sel E2: h=, sel E3: k=, sel E4: a=, sel E5: Posisi, dan sel E6: Pusat. 7. Tuliskan ke dalam sel F2, F3, dan F4 masing-masing 0, sel F5: x, dan sel F6: 0. 2
4 8. Tuliskan ke dalam sel G2, G3, dan G4 masing-masing AU, sel G5: y, dan sel G6: Lakukan pencocokan kurva dengan cara mensuperposisikan grafik orbit Merkurius yang telah diperoleh sebelumnya menggunakan model yang dibangun ini, yaitu dengan cara mengganti-ganti nilai-nilai h, k, dan a hingga diperoleh kurva model yang cocok dengan grafik orbit Merkurius. Sebagai panduan bagi Anda: -1,0 < h < 0,0 ; 0,0 < k < 1,0 dan 0,0 < a < 1,0. C. Data Anda diberikan data berupa waktu dan koordinat planet Merkurius pada saat planet ini memiliki jarak sudut (elongasi) terjauh dari Matahari sebagaimana teramati dari Bumi. Data tersebut ditabelkan di bawah ini. NO. TANGGAL PUKUL (WIB) BUJUR EKLIPTIKA 1 9 Januari : Maret 08: Mei 02: Juli 12: September 13: November 15: Desember 10: Maret : April 00: Juli 09: Agustus 19: Oktober 05: Desember 05: Februari : April 04: Juni 23: Juli 15: Oktober 17: November 09: Januari : Maret 13: Mei 14: Juli 01: September 05: November 19: Januari : Februari 23: Mei 11: Juni 00: September 17: Oktober 10: Desember 10:
5 D. Pertanyaan Setelah menyelesaikan seluruh prosedur di atas, jawablah pertanyaan-pertanyaan di bawah ini. 1. Apakah bentuk orbit planet Merkurius yang Anda dapatkan? 2. Berdasarkan grafik orbit planet yang telah Anda peroleh, berapakah setengah sumbu panjang (a) orbit Merkurius? 3. Berdasarkan grafik orbit planet yang telah Anda peroleh, berapakah periode sideris (Psid) dan periode sinodis (Psin) orbit Merkurius? 4. Apakah nilai setengah sumbu panjang (a) dan periode sideris (Psid) Merkurius yang telah Anda peroleh memenuhi Hukum III Kepler? 5. Berapakah nilai eksentrisitas (e) orbit Merkurius? 6. Dapatkah Anda menggunakan prosedur yang sama untuk menentukan bentuk orbit planet dengan ukuran orbit yang lebih besar daripada orbit Bumi? Paparkan argumen Anda. 7. Apakah yang dapat Anda simpulkan dari aktivitas ini? 4
6 MODUL 2 Periode Rotasi Matahari Tujuan Dalam aktivitas laboratorium astronomi ini, mahasiswa menentukan periode rotasi Matahari berdasarkan perubahan posisi harian bintik hitam (sunspot) yang terekam dalam sejumlah citra Matahari Perlengkapan Komputer yang dilengkapi perangkat lunak pengolah data Microsoft Excel, perangkat lunak pengolah citra AstroArt dan sejumlah citra digital Matahari A. Deskripsi Pengamatan Matahari telah dilakukan manusia sejak ribuan tahun lalu. Gerak bolak-balik Matahari di bola langit yang pada saat tertentu membuatnya terlihat berada di belahan utara langit, saat lainnya di khatulistiwa langit, dan ada kalanya di belahan selatan langit dan akhirnya kembali berada di belahan utara langit, telah mengilhami manusia untuk memanfaatkan keteraturan yang teramati ini dalam menyusun sistem penanggalan atau kalender. Matahari merupakan bintang yang dinamis. Salah satu aktivitas Matahari ditandai dengan kemunculan sunspot atau bintik hitam yang merupakan daerah dengan medan magnet kuat meskipun memiliki temperatur yang lebih rendah daripada daerah di sekitarnya. Itulah yang membuat sunspot terlihat lebih gelap. Pencatatan pengamatan sunspot telah dilakukan oleh para pengamat langit bangsa Cina lebih dari 2000 tahun silam. Dalam sejarah dunia barat, pengamatan sunspot untuk pertama kalinya dilakukan oleh Christoph Scheiner walaupun publik lebih mengenal Galileo Galileilah orangnya ketika astronom Italia ini mengarahkan teleskop buatannya ke langit. Perubahan posisi harian sunspot di permukaan Matahari dapat memberikan informasi tentang gerak rotasi bintang induk di Tata Surya ini. Periode gerak rotasi tersebut dapat ditentukan dengan menganalisis besarnya pergeseran yang dialami sunspot tersebut. Dalam aktivitas laboratorium astronomi ini, Anda diberi sejumlah citra digital Matahari. Menggunakan bantuan perangkat lunak pengolah citra AstroArt Anda akan mencatat posisi dalam arah x dan y masing-masing sunspot di lintang yang berbeda. Setelah melakukan transformasi koordinat bidang datar (x, y) ke dalam koordinat di permukaan lengkung (φ, θ) dan mengetahui banyaknya piksel (pixel: picture element) yang dirangkum dalam garis tengah Matahari, dengan melakukan perhitungan sederhana Anda dapat memperoleh nilai periode rotasi Matahari dari perpindahan sunspot di berbagai lintang. 5
7 B. Prosedur Lakukan langkah-langkah berikut ini: 1. Menggunakan perangkat lunak pengolah data Microsoft Excel siapkan tabel seperti di bawah ini: NAMA CITRA SUNSPOT KE TANGGAL WAKTU (UT) KOORDINAT X KOORDINAT Y 2. Informasi Nama citra, Tanggal observasi, dan Waktu observasi dapat Anda peroleh dari image header dengan cara membuka masing-masing file citra Matahari dengan perangkat lunak AstroArt. 3. Pilihlah 3 buah sunspot yang terletak di lintang berbeda (satu buah di dekat khatulistiwa Matahari, satu buah agak jauh dari khatulistiwa (baik di utara maupun selatan khatulistiwa), dan satu buah lagi paling jauh dari khatulistiwa (baik di utara maupun selatan khatulistiwa). Usahakan ketiga buah sunspot yang telah dipilih tersebut semuanya berada di sisi kiri piringan Matahari. Menggunakan pointer dalam perangkat lunak AstroArt tentukan koordinat pusat masing-masing sunspot yang telah dipilih di atas. Informasi (x, y) terlihat di jendela bawah perangkat lunak tersebut. 4. Lakukan pencatatan koordinat pusat (x,y) ketiga buah sunspot yang telah dipilih dalam citra digital Matahari lainnya. Yang harus Anda ingat adalah, bahwa Anda hanya mencatat koordinat pusat sunspot yang sama. Tentunya posisi ketiga buah sunspot yang sama tersebut relatif berubah antara citra digital yang satu dibandingkan dengan citra digital lainnya. 5. Setelah melengkapi tabel untuk seluruh citra digital Matahari, lakukan transformasi koordinat untuk memperoleh posisi pusat masing-masing sunspot di permukaan Matahari yang sebenarnya melengkung: 1 x φ = tan R x y 1 y θ = cos r r = R y 2 2 Dalam persamaan di atas, r merupakan proyeksi jari-jari Matahari R di bidang X Z. Nilai jari-jari Matahari R yang dinyatakan dalam satuan piksel dapat diperoleh 6
8 menggunakan bantuan perangkat lunak AstroArt. Sementara itu sudut φ merupakan pergeseran sunspot dalam arah mendatar (timur ke barat) dan sudut θ pergeseran dalam arah vertikal (utara ke selatan). 6. Perolehlah rata-rata nilai perubahan sudut φ dari hari ke hari, kemudian tentukan besarnya periode rotasi Matahari melalui persamaan: P = rotasi φ C. Data Anda diberikan data berupa citra digital Matahari yang dipotret pada waktu berbeda. Untuk memperoleh data ini dan perangkat lunak AstroArt, Anda dapat menghubungi dosen pengampu mata kuliah. D. Pertanyaan Setelah menyelesaikan seluruh prosedur di atas, jawablah pertanyaan-pertanyaan di bawah ini. 1. Berapakah periode rotasi Matahari yang Anda peroleh dari sejumlah sunspot yang terletak di lintang berbeda? 2. Sunspot yang terletak di manakah yang memberikan nilai periode rotasi terbesar? Periode rotasi terkecil? 3. Apa yang dapat Anda simpulkan dari aktivitas yang telah dilakukan? 7
9 MODUL 3 Efek Revolusi Bumi Tujuan Dalam aktivitas laboratorium astronomi ini, mahasiswa menentukan pengaruh yang ditimbulkan oleh gerak edar Bumi mengitari Matahari Perlengkapan Komputer yang dilengkapi perangkat lunak planetarium SkyGazer dan perangkat lunak pengolah data Microsoft Excel A. Deskripsi Selain gerak semu harian akibat rotasi Bumi, Matahari pun memiliki gerak semu tahunan sebagai efek dari revolusi Bumi; kadang Matahari terlihat berada di belahan utara, lain waktu di belahan selatan, dan bahkan ada kalanya berada tepat di khatulistiwa. Beruntunglah kita yang secara geografis tinggal di dekat khatulistiwa (kepulauan Indonesia membentang dari 6 derajat LS 11 derajat LU), sebab bukan hal yang sulit untuk dapat mengesani gerak bolak-balik Matahari di belahan utara dan selatan sampai di kedua garis baliknya (utara dan selatan). Kesempatan untuk bisa menikmati fenomena ini akan semakin kecil dengan bertambah jauhnya posisi kita (makin ke utara ataupun selatan) dari khatulistiwa. Oleh karena bidang khatulistiwa langit (perluasan khatulistiwa Bumi) dan ekliptika (bidang orbit Bumi mengitari Matahari) masing-masing berputar dengan arah yang berlawanan, kedua titik potong (titik-titik equinox) dari kedua bidang di atas tidak selalu berada di tempat yang sama di bidang ekliptika setiap tahunnya. Pergeseran equinox ke arah barat sepanjang ekliptika ini disebut presesi, dan akan kembali ke posisi semula setelah menyelesaikan satu putaran dalam kurun waktu tahun! Pengaruh dari presesi ini harus diperhitungkan untuk dapat menyajikan koordinat benda langit yang sesungguhnya untuk waktu tertentu yang dikehendaki. Karena pengaruh presesi inilah, titik vernal equinox yang ribuan tahun lalu berada di zodiak Aries sekarang telah bergeser ke arah zodiak Pisces. Dari pengamatan atas gerak Matahari di bola langit ini, yang merupakan refleksi dari gerak edar Bumi mengelilingi Matahari dengan sumbu rotasi yang miring, manusia telah dapat merumuskan dan memodelkannya dalam bentuk sistem penanggalan untuk kebutuhan praktis sehari-hari, seperti untuk keperluan transaksi, penentuan musim tanam atau panen dan ritual keagamaan, yang kita kenal sebagai kalender Matahari (solar calendar, kalender syamsiyah). 8
10 B. Prosedur Lakukan langkah-langkah berikut ini: 1. Jalankan perangkat lunak SkyGazer dengan cara mengeklik ganda (double click) ikon yang ada di desktop. 2. Pilih Cancel untuk permintaan registrasi. 3. Klik panah atas-bawah di jendela panel Location yang menampilkan nama kota, dan pilih Set Location. 4. Pilihlah East Asia di jendela nama negara kemudian pilihlah kota Bandung dari daftar nama kota yang muncul di bawahnya. Klik OK untuk menyatakan persetujuan. 5. Tutuplah panel Display, Time, dan Location dengan cara mengeklik tanda silang (x). 6. Klik menu Chart dan pilihlah submenu Set Date and Time. 7. Isikan tanggal, bulan, dan tahun pengamatan Matahari akan dilakukan (misalnya: 1 Januari 2011) serta waktunya (misalnya: WIB). Jangan lupa untuk meniadakan tanda centang ( ) dari Automatic Daylight Savings Time. Klik OK untuk memulai pengamatan Matahari. 8. Sekarang di jendela utama akan muncul pemandangan sebuah taman yang merepresentasikan kota Bandung pada tanggal dan waktu yang telah diisikan sebelumnya. 9. Tekan anak panah ke atas hingga menemukan Matahari. Klik kanan di titik yang menyimbolkan Matahari dan pilih menu Show Info for Sun. 10. Dari panel Info yang ada, catatlah di dalam sebuah tabel: tanggal pengamatan, koordinat Matahari (R.A. dalam jam:menit:detik dan DEC. dalam derajat:menit busur:detik busur), waktu transit (dalam jam:menit:detik), serta ketinggian Matahari saat transit tersebut (dalam derajat). Petunjuk: 1 derajat = 60 menit busur & 1 menit busur = 60 detik busur 11. Lakukan langkah di nomor 10 untuk hari-hari lainnya dalam satu tahun. Cukup gunakan 3 hari dalam setiap bulannya (misalnya awal bulan, tengah bulan, dan akhir bulan), sehingga selama pengamatan satu tahun diperoleh data koordinat, waktu transit, dan ketinggian Matahari, masing-masing sebanyak (3 hari/bulan x 12 bulan) 36 buah data. 12. Lengkapilah tugas dan pertanyaan di bawah ini berdasarkan data yang telah diperoleh. 9
11 C. Tugas dan Pertanyaan Tugas 1 Buatlah grafik menggunakan Microsoft Excel atau Microcal Origin antara DEC. (dalam derajat) sebagai sumbu Y dan waktu transit (dalam jam:menit:detik) sebagai sumbu X! Problem 1 (i) Bentuk/profil apakah yang Anda peroleh dari grafik DEC. vs Waktu Transit? Bentuk tersebut disebut analemma, yang mendeskripsikan gerak semu tahunan Matahari di bola langit. Sebenarnya, Bumilah yang bergerak mengelilingi Matahari (revolusi) dan menyelesaikan satu putaran dalam waktu satu tahun. (ii) Pukul berapakah Matahari paling cepat mencapai titik tertinggi (kulminasi atas) dalam gerak semu hariannya? Pukul berapakah Matahari paling lambat mencapai titik tersebut? (iii)dapatkah Anda mengaitkan fenomena yang Anda peroleh dalam (ii) dengan jadwal waktu ibadah umat Islam, yaitu waktu salat dzuhur? Tugas 2 Buatlah grafik antara DEC. (dalam derajat) sebagai sumbu Y dan tanggal (dalam tanggal:bulan:tahun) sebagai sumbu X! Problem 2 (i) Berdasarkan grafik dalam Tugas 2, perkirakan pada tanggal berapa Matahari mencapai posisi paling utara di bola langit (DEC. bernilai paling positif)! Pada tanggal berapa Matahari mencapai posisi paling selatan di bola langit (DEC. bernilai paling negatif)? (ii) Berdasarkan hasil yang Anda peroleh dalam Problem 1 (ii), perkirakan pada tanggal berapakah Matahari paling cepat mencapai titik tertinggi? Pada tanggal berapakah Matahari paling lambat mencapai titik tertinggi? 10
12 Tugas 3 Buatlah grafik antara ketinggian Matahari saat kulminasi atas (dalam derajat) sebagai sumbu Y dan DEC. (dalam derajat) sebagai sumbu X! Problem 3 (i) Berdasarkan grafik dalam Tugas 3, berapakah ketinggian maksimum yang dapat dicapai Matahari dari horison? (ii) Perkirakan deklinasi Matahari saat mencapai ketinggian maksimum tersebut! (iii)klik menu Chart dan pilih submenu Set Location. Dapatkan informasi lintang geografis (latitude) kota Bandung, kemudian bandingkan nilai ini dengan nilai deklinasi Matahari saat mencapai ketinggian maksimum tersebut. Apakah yang dapat Anda simpulkan? 11
TATA KOORDINAT BENDA LANGIT. Kelompok 6 : 1. Siti Nur Khotimah ( ) 2. Winda Yulia Sari ( ) 3. Yoga Pratama ( )
 TATA KOORDINAT BENDA LANGIT Kelompok 6 : 1. Siti Nur Khotimah (4201412051) 2. Winda Yulia Sari (4201412094) 3. Yoga Pratama (42014120) 1 bintang-bintang nampak beredar dilangit karena bumi berotasi. Jika
TATA KOORDINAT BENDA LANGIT Kelompok 6 : 1. Siti Nur Khotimah (4201412051) 2. Winda Yulia Sari (4201412094) 3. Yoga Pratama (42014120) 1 bintang-bintang nampak beredar dilangit karena bumi berotasi. Jika
Wilfried Suhr Gambar 1. Waktu-waktu kontak dalam peristiwa transit Venus.
 TUGAS I ASTROFISIKA (FI 567) BESARAN MENDASAR DALAM ASTRONOMI & ASTROFISIKA: Penentuan 1 AU SEMESTER GANJIL 2014 2015 DOSEN: JUDHISTIRA ARIA UTAMA, M.SI. (KODE: 2582) Dalam aktivitas laboratorium astronomi
TUGAS I ASTROFISIKA (FI 567) BESARAN MENDASAR DALAM ASTRONOMI & ASTROFISIKA: Penentuan 1 AU SEMESTER GANJIL 2014 2015 DOSEN: JUDHISTIRA ARIA UTAMA, M.SI. (KODE: 2582) Dalam aktivitas laboratorium astronomi
MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB
 MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB A. Gerak Semu Benda Langit Bumi kita berputar seperti gasing. Ketika Bumi berputar pada sumbu putarnya maka hal ini dinamakan
MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB A. Gerak Semu Benda Langit Bumi kita berputar seperti gasing. Ketika Bumi berputar pada sumbu putarnya maka hal ini dinamakan
JAWABAN DAN PEMBAHASAN
 JAWABAN DAN PEMBAHASAN 1. Dalam perjalanan menuju Bulan seorang astronot mengamati diameter Bulan yang besarnya 3.500 kilometer dalam cakupan sudut 6 0. Berapakah jarak Bulan saat itu? A. 23.392 km B.
JAWABAN DAN PEMBAHASAN 1. Dalam perjalanan menuju Bulan seorang astronot mengamati diameter Bulan yang besarnya 3.500 kilometer dalam cakupan sudut 6 0. Berapakah jarak Bulan saat itu? A. 23.392 km B.
SAINS BUMI DAN ANTARIKSA
 SAINS BUMI DAN ANTARIKSA NAMA NIM : 15034038 FISIKA B 2015 : PUTI AULIA MARDIAH GERAK SEMU TAHUNAN MATAHRI A. Latar Belakang di beberapa kasus pada belahan bumi, terjadi perbedaan musim dan perbedaan lama
SAINS BUMI DAN ANTARIKSA NAMA NIM : 15034038 FISIKA B 2015 : PUTI AULIA MARDIAH GERAK SEMU TAHUNAN MATAHRI A. Latar Belakang di beberapa kasus pada belahan bumi, terjadi perbedaan musim dan perbedaan lama
Cladius Ptolemaus (abad 2) Geosentris
 ROTASI DAN REVOLUSI BUMI Cladius Ptolemaus (abad 2) Geosentris Bumi sebagai pusat tata surya Planet-planet (termasuk Mth.) berputar mengelilingi bumi Sambil mengelilingi Bumi, planet-planet bergerak melingkar
ROTASI DAN REVOLUSI BUMI Cladius Ptolemaus (abad 2) Geosentris Bumi sebagai pusat tata surya Planet-planet (termasuk Mth.) berputar mengelilingi bumi Sambil mengelilingi Bumi, planet-planet bergerak melingkar
Astronomi Sabar Nurohman, M.Pd
 Astronomi Sabar Nurohman, M.Pd Sabar Nurohman Dafatar Isi Bumi dalam Bola Langit Tata Surya Sistem Bumi-Bulan Gerak Planet dan Satelit Fisika Bintang Evolusi Bintang Galaksi Struktur Jagad Raya Bumi dan
Astronomi Sabar Nurohman, M.Pd Sabar Nurohman Dafatar Isi Bumi dalam Bola Langit Tata Surya Sistem Bumi-Bulan Gerak Planet dan Satelit Fisika Bintang Evolusi Bintang Galaksi Struktur Jagad Raya Bumi dan
Sabar Nurohman Prodi Pendidikan IPA FMIPA UNY
 Sabar Nurohman Prodi Pendidikan IPA FMIPA UNY Dafatar Isi Bumi dalam Bola Langit Tata Surya Sistem Bumi-Bulan Gerak Planet dan Satelit Fisika Bintang Evolusi Bintang Galaksi Struktur Jagad Raya Bumi dan
Sabar Nurohman Prodi Pendidikan IPA FMIPA UNY Dafatar Isi Bumi dalam Bola Langit Tata Surya Sistem Bumi-Bulan Gerak Planet dan Satelit Fisika Bintang Evolusi Bintang Galaksi Struktur Jagad Raya Bumi dan
Oleh : Kunjaya TPOA, Kunjaya 2014
 Oleh : Kunjaya Kompetensi Dasar X.3.5 Menganalisis besaran fisis pada gerak melingkar dengan laju konstan dan penerapannya dalam teknologi X.4.5 Menyajikan ide / gagasan terkait gerak melingkar Pengertian
Oleh : Kunjaya Kompetensi Dasar X.3.5 Menganalisis besaran fisis pada gerak melingkar dengan laju konstan dan penerapannya dalam teknologi X.4.5 Menyajikan ide / gagasan terkait gerak melingkar Pengertian
DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PENDIDIKAN MENENGAH UMUM
 DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PENDIDIKAN MENENGAH UMUM Tes Seleksi Olimpiade Astronomi Tingkat Provinsi 2004 Materi Uji : ASTRONOMI Waktu :
DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PENDIDIKAN MENENGAH UMUM Tes Seleksi Olimpiade Astronomi Tingkat Provinsi 2004 Materi Uji : ASTRONOMI Waktu :
SMA/MA IPS kelas 10 - GEOGRAFI IPS BAB 3. Mengenal Planet Bumilatihan soal 3.2
 SMA/MA IPS kelas 10 - GEOGRAFI IPS BAB 3. Mengenal Planet Bumilatihan soal 3.2 1. Pergerakan bumi sebagai benda angkasa yang menempuh waktu 365 hari disebut. gerak presesi gerak rotasi gerak revolusi gerak
SMA/MA IPS kelas 10 - GEOGRAFI IPS BAB 3. Mengenal Planet Bumilatihan soal 3.2 1. Pergerakan bumi sebagai benda angkasa yang menempuh waktu 365 hari disebut. gerak presesi gerak rotasi gerak revolusi gerak
Meridian Greenwich. Bujur
 5. TATA KOORDINAT Dalam astronomi, amatlah penting untuk memetakan posisi bintang atau benda langit lainnya, dan menerapkan system koordinat untuk membakukan posisi tersebut. Prinsip dasarnya sama dengan
5. TATA KOORDINAT Dalam astronomi, amatlah penting untuk memetakan posisi bintang atau benda langit lainnya, dan menerapkan system koordinat untuk membakukan posisi tersebut. Prinsip dasarnya sama dengan
KUMPULAN SOAL & PEMBAHASAN OSK OSP OSN DLL KOORDINAT BENDA LANGIT (By. Mariano N.)
 KUMPULAN SOAL & PEMBAHASAN OSK OSP OSN DLL KOORDINAT BENDA LANGIT (By. Mariano N.) 1. Seorang pengamat di lintang 0 0 akan mengamati sebuah bintang yang koordinatnya (α,δ) = (16h14m, 0 0 ) pada tanggal
KUMPULAN SOAL & PEMBAHASAN OSK OSP OSN DLL KOORDINAT BENDA LANGIT (By. Mariano N.) 1. Seorang pengamat di lintang 0 0 akan mengamati sebuah bintang yang koordinatnya (α,δ) = (16h14m, 0 0 ) pada tanggal
5. BOLA LANGIT 5.1. KONSEP DASAR SEGITIGA BOLA
 5. BOLA LANGIT 5.1. KONSEP DASAR SEGITIGA BOLA Tata koordinat yang kita kenal umumnya adalah jenis Kartesian (Cartesius) yang memakai sumbu X dan Y. Namun dalam astronomi, koordinat ini tidak sesuai dengan
5. BOLA LANGIT 5.1. KONSEP DASAR SEGITIGA BOLA Tata koordinat yang kita kenal umumnya adalah jenis Kartesian (Cartesius) yang memakai sumbu X dan Y. Namun dalam astronomi, koordinat ini tidak sesuai dengan
KEMENTERIAN PENDIDIKAN NASIONAL DITJEN MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA
 KEMENTERIAN PENDIDIKAN NASIONAL DITJEN MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA Soal Test Olimpiade Sains Nasional 2010 Bidang : ASTRONOMI Materi : Teori (Pilihan Berganda) Tanggal
KEMENTERIAN PENDIDIKAN NASIONAL DITJEN MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA Soal Test Olimpiade Sains Nasional 2010 Bidang : ASTRONOMI Materi : Teori (Pilihan Berganda) Tanggal
ROTASI BENDA LANGIT. Chatief Kunjaya. KK Atronomi, ITB. Oleh : TPOA, Kunjaya 2014
 ROTASI BENDA LANGIT Oleh : Chatief Kunjaya KK Atronomi, ITB KOMPETENSI DASAR XI.3.6 Menerapkan konsep torsi, momen inersia, titik berat dan momentum sudut pada benda tegar (statis dan dinamis) dalam kehidupan
ROTASI BENDA LANGIT Oleh : Chatief Kunjaya KK Atronomi, ITB KOMPETENSI DASAR XI.3.6 Menerapkan konsep torsi, momen inersia, titik berat dan momentum sudut pada benda tegar (statis dan dinamis) dalam kehidupan
DAFTAR ISI DAFTAR GAMBAR DAFTAR TABEL DAFTAR LAMPIRAN DAFTAR LAMBANG DAN SINGKATAN
 DAFTAR ISI PRAKATA DAFTAR ISI DAFTAR GAMBAR DAFTAR TABEL DAFTAR LAMPIRAN DAFTAR LAMBANG DAN SINGKATAN INTISARI ABSTRACT vii x xii xiii xv xvii xviii xix BAB I PENDAHULUAN 1 1.1 Latar Belakang dan Permasalahan
DAFTAR ISI PRAKATA DAFTAR ISI DAFTAR GAMBAR DAFTAR TABEL DAFTAR LAMPIRAN DAFTAR LAMBANG DAN SINGKATAN INTISARI ABSTRACT vii x xii xiii xv xvii xviii xix BAB I PENDAHULUAN 1 1.1 Latar Belakang dan Permasalahan
KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN
 SOAL OLIMPIADE SAINS NASIONAL ASTRONOMI Ronde : Analisis Data Waktu : 240 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS
SOAL OLIMPIADE SAINS NASIONAL ASTRONOMI Ronde : Analisis Data Waktu : 240 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS
BAB I PENDAHULUAN. beraktifitas pada malam hari. Terdapat perbedaan yang menonjol antara siang
 1 BAB I PENDAHULUAN A. Latar Belakang Setiap hari manusia disibukkan dengan rutinitas pekerjaan ataupun aktifitas lainya, ada yang beraktifitas pada siang hari dan ada pula yang beraktifitas pada malam
1 BAB I PENDAHULUAN A. Latar Belakang Setiap hari manusia disibukkan dengan rutinitas pekerjaan ataupun aktifitas lainya, ada yang beraktifitas pada siang hari dan ada pula yang beraktifitas pada malam
PROGRAM PERSIAPAN OLIMPIADE SAINS BIDANG ASTRONOMI 2014 SMA 2 CIBINONG TES 20 MEI 2014
 PROGRAM PERSIAPAN OLIMPIADE SAINS BIDANG ASTRONOMI 2014 SMA 2 CIBINONG TES 20 MEI 2014 NAMA PROVINSI TANGGAL LAHIR ASAL SEKOLAH KABUPATEN/ KOTA TANDA TANGAN 1. Dilihat dari Bumi, bintang-bintang tampak
PROGRAM PERSIAPAN OLIMPIADE SAINS BIDANG ASTRONOMI 2014 SMA 2 CIBINONG TES 20 MEI 2014 NAMA PROVINSI TANGGAL LAHIR ASAL SEKOLAH KABUPATEN/ KOTA TANDA TANGAN 1. Dilihat dari Bumi, bintang-bintang tampak
AS Astronomi Bola. Suhardja D. Wiramihardja Endang Soegiartini Yayan Sugianto Program Studi Astronomi FMIPA Institut Teknologi Bandung
 AS 2201 - Astronomi Bola Suhardja D. Wiramihardja Endang Soegiartini Yayan Sugianto Program Studi Astronomi FMIPA Institut Teknologi Bandung PENDAHULUAN Menjelaskan posisi benda langit pada bola langit.
AS 2201 - Astronomi Bola Suhardja D. Wiramihardja Endang Soegiartini Yayan Sugianto Program Studi Astronomi FMIPA Institut Teknologi Bandung PENDAHULUAN Menjelaskan posisi benda langit pada bola langit.
Macam-macam Waktu. Universal Time dan Dynamical Time
 Macam-macam Waktu Waktu (time) sangat penting bagi kehidupan kita. Allah SWT berfirman dengan bersumpah wal ashri. Barangsiapa yang pandai menggunakan waktu dengan benar, ia akan beruntung. Waktu terus
Macam-macam Waktu Waktu (time) sangat penting bagi kehidupan kita. Allah SWT berfirman dengan bersumpah wal ashri. Barangsiapa yang pandai menggunakan waktu dengan benar, ia akan beruntung. Waktu terus
SOAL PILIHAN GANDA ASTRONOMI 2008/2009 Bobot nilai masing-masing soal : 1
 SOAL PILIHAN GANDA ASTRONOMI 2008/2009 Bobot nilai masing-masing soal : 1 1. [SDW] Tata Surya adalah... A. susunan Matahari, Bumi, Bulan dan bintang B. planet-planet dan satelit-satelitnya C. kumpulan
SOAL PILIHAN GANDA ASTRONOMI 2008/2009 Bobot nilai masing-masing soal : 1 1. [SDW] Tata Surya adalah... A. susunan Matahari, Bumi, Bulan dan bintang B. planet-planet dan satelit-satelitnya C. kumpulan
1. Fenomena Alam Akibat Perubahan Kedudukan Bumi, Bulan, terhadap Matahari. Gerhana Matahari
 1. Fenomena Alam Akibat Perubahan Kedudukan Bumi, Bulan, terhadap Matahari Gerhana Matahari Peristiwa gerhana matahari cincin (GMC) terlihat jelas di wilayah Bandar Lampung, Lampung, pada letak 05.21 derajat
1. Fenomena Alam Akibat Perubahan Kedudukan Bumi, Bulan, terhadap Matahari Gerhana Matahari Peristiwa gerhana matahari cincin (GMC) terlihat jelas di wilayah Bandar Lampung, Lampung, pada letak 05.21 derajat
KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN
 SOAL OLIMPIADE SAINS NASIONAL ASTRONOMI Ronde : Teori Waktu : 240 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS TAHUN 2014
SOAL OLIMPIADE SAINS NASIONAL ASTRONOMI Ronde : Teori Waktu : 240 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS TAHUN 2014
BAB IV ANALISIS PERHITUNGAN ARAH KIBLAT DENGAN MENGGUNAKAN AZIMUT PLANET. A. Algoritma Penentuan Arah Kiblat dengan Metode Azimut Planet
 BAB IV ANALISIS PERHITUNGAN ARAH KIBLAT DENGAN MENGGUNAKAN AZIMUT PLANET A. Algoritma Penentuan Arah Kiblat dengan Metode Azimut Planet Pada dasarnya azimut planet adalah busur yang diukur dari titik Utara
BAB IV ANALISIS PERHITUNGAN ARAH KIBLAT DENGAN MENGGUNAKAN AZIMUT PLANET A. Algoritma Penentuan Arah Kiblat dengan Metode Azimut Planet Pada dasarnya azimut planet adalah busur yang diukur dari titik Utara
GERAK BUMI DAN BULAN
 MATERI ESENSIAL IPA SEKOLAH DASAR (Pengayaan Materi Guru) KONSEP ILMU PENGETAHUAN BUMI DAN ANTARIKSA GERAK BUMI DAN BULAN Agus Fany Chandra Wijaya DIGITAL LEARNING LESSON STUDY JAYAPURA 2010 GERAK BUMI
MATERI ESENSIAL IPA SEKOLAH DASAR (Pengayaan Materi Guru) KONSEP ILMU PENGETAHUAN BUMI DAN ANTARIKSA GERAK BUMI DAN BULAN Agus Fany Chandra Wijaya DIGITAL LEARNING LESSON STUDY JAYAPURA 2010 GERAK BUMI
BAB IV UJI AKURASI AWAL WAKTU SHALAT SHUBUH DENGAN SKY QUALITY METER. 4.1 Hisab Awal Waktu Shalat Shubuh dengan Sky Quality Meter : Analisis
 63 BAB IV UJI AKURASI AWAL WAKTU SHALAT SHUBUH DENGAN SKY QUALITY METER 4.1 Hisab Awal Waktu Shalat Shubuh dengan Sky Quality Meter : Analisis dan Interpretasi Data Pengamatan kecerlangan langit menggunakan
63 BAB IV UJI AKURASI AWAL WAKTU SHALAT SHUBUH DENGAN SKY QUALITY METER 4.1 Hisab Awal Waktu Shalat Shubuh dengan Sky Quality Meter : Analisis dan Interpretasi Data Pengamatan kecerlangan langit menggunakan
Sabar Nurohman, M.Pd
 Sabar Nurohman, M.Pd Bulan merupakan benda langit kedua, setelah matahari, yang kenampakannyapaling menonjol di langit. Di lihat dari luar angkasa, sistem bumi-bulan nampak sebagai suatu sistem planet
Sabar Nurohman, M.Pd Bulan merupakan benda langit kedua, setelah matahari, yang kenampakannyapaling menonjol di langit. Di lihat dari luar angkasa, sistem bumi-bulan nampak sebagai suatu sistem planet
DEPARTEMEN PENDIDIKAN NASIONAL
 Dapatkan soal-soal lainnya di http://forum.pelatihan-osn.com DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA Tes Seleksi Olimpiade Astronomi Tingkat
Dapatkan soal-soal lainnya di http://forum.pelatihan-osn.com DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA Tes Seleksi Olimpiade Astronomi Tingkat
KEMENTERIAN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA. Soal Tes Olimpiade Sains Nasional 2011
 KEMENTERIAN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA Soal Tes Olimpiade Sains Nasional 2011 Bidang : ASTRONOMI Materi : Teori Tanggal : 14 September 2011 Soal
KEMENTERIAN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA Soal Tes Olimpiade Sains Nasional 2011 Bidang : ASTRONOMI Materi : Teori Tanggal : 14 September 2011 Soal
PETA KONSEP. Revolu si. Rotasi. Mataha ri TATA SURYA. satelit buata n. satelit. alami. satelit. Bulan. palapa. Kalender Masehi. Revolu si.
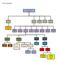 PETA KONSEP TATA SURYA Matahar i Planet Asteroi d Komet Meteor id Pusat Tata Surya Merkuri us Venus Bumi Mars Jupiter Saturnus Uranus Neptunu s Rotasi Revolu si satelit buata n satelit alami Pembagi an
PETA KONSEP TATA SURYA Matahar i Planet Asteroi d Komet Meteor id Pusat Tata Surya Merkuri us Venus Bumi Mars Jupiter Saturnus Uranus Neptunu s Rotasi Revolu si satelit buata n satelit alami Pembagi an
MODEL MATERI PENGETAHUAN SUDUT DALAM PERKULIAHAN IPBA BAGI MAHASISWA FISIKA DAN APLIKASINYA DALAM MEMAHAMI JARAK ANTARBENDA-LANGIT (CELESTIAL BODIES)
 Prosiding Seminar Nasional Penelitian, Pendidikan dan Penerapan MIPA, Fakultas MIPA, Universitas Negeri Yogyakarta, 14 Mei 2011 MODEL MATERI PENGETAHUAN SUDUT DALAM PERKULIAHAN IPBA BAGI MAHASISWA FISIKA
Prosiding Seminar Nasional Penelitian, Pendidikan dan Penerapan MIPA, Fakultas MIPA, Universitas Negeri Yogyakarta, 14 Mei 2011 MODEL MATERI PENGETAHUAN SUDUT DALAM PERKULIAHAN IPBA BAGI MAHASISWA FISIKA
indahbersamakimia.blogspot.com
 Tes Seleksi Olimpiade Astronomi Tingkat Provinsi 2007 Materi Uji : Astronomi Waktu : 150 menit Tidak diperkenankan menggunakan alat hitung (kalkultor). Di bagian akhir soal diberikan daftar konstanta yang
Tes Seleksi Olimpiade Astronomi Tingkat Provinsi 2007 Materi Uji : Astronomi Waktu : 150 menit Tidak diperkenankan menggunakan alat hitung (kalkultor). Di bagian akhir soal diberikan daftar konstanta yang
Kumpulan Soal Astronomi dan Jawabannya
 Kumpulan Soal Astronomi dan Jawabannya 1. Sebutkan ciri ciri galaksi spiral! - Diberi tanda huruf S - Inti pusat dikelilingi oleh piringan yang pipih - Piringan pipih mengandung bintang, gas, dan debu
Kumpulan Soal Astronomi dan Jawabannya 1. Sebutkan ciri ciri galaksi spiral! - Diberi tanda huruf S - Inti pusat dikelilingi oleh piringan yang pipih - Piringan pipih mengandung bintang, gas, dan debu
- - TATA SURYA - - sbl5surya
 - - TATA SURYA - - Modul ini singkron dengan Aplikasi Android, Download melalui Play Store di HP Kamu, ketik di pencarian sbl5surya Jika Kamu kesulitan, Tanyakan ke tentor bagaimana cara downloadnya. Aplikasi
- - TATA SURYA - - Modul ini singkron dengan Aplikasi Android, Download melalui Play Store di HP Kamu, ketik di pencarian sbl5surya Jika Kamu kesulitan, Tanyakan ke tentor bagaimana cara downloadnya. Aplikasi
PEKERJAAN RUMAH SAS PERTEMUAN-1 DAN PERTEMUAN-2 A.Pilihan Ganda
 PEKERJAAN RUMAH SAS PERTEMUAN-1 DAN PERTEMUAN-2 A.Pilihan Ganda 1. Tinggi bintang dari bidang ekuator disebut a. altitude b. latitude c. longitude d. deklinasi e. azimut 2. Titik pertama Aries, didefinisikan
PEKERJAAN RUMAH SAS PERTEMUAN-1 DAN PERTEMUAN-2 A.Pilihan Ganda 1. Tinggi bintang dari bidang ekuator disebut a. altitude b. latitude c. longitude d. deklinasi e. azimut 2. Titik pertama Aries, didefinisikan
Daftar Isi. Tata Surya. Matahari. Gerak edar bumi dan bulan. Lithosfer. Atmosfer.
 Tata Surya L/O/G/O Daftar Isi 1 2 3 4 5 Tata Surya Matahari Gerak edar bumi dan bulan Lithosfer Atmosfer Tujuan Belajar Siswa mampu mendeskripsikan maahari sebagai bintang dan bumi sebagai salah satu planet
Tata Surya L/O/G/O Daftar Isi 1 2 3 4 5 Tata Surya Matahari Gerak edar bumi dan bulan Lithosfer Atmosfer Tujuan Belajar Siswa mampu mendeskripsikan maahari sebagai bintang dan bumi sebagai salah satu planet
Bab 3. Teleskop Bamberg
 Bab 3 Teleskop Bamberg 3. 1 Teleskop Refraktor Teleskop optik berfungsi mengumpulkan dan memfokuskan cahaya dari bagian spektrum cahaya tampak elektromagnetik agar dapat langsung melihat gambar yang diperbesar.
Bab 3 Teleskop Bamberg 3. 1 Teleskop Refraktor Teleskop optik berfungsi mengumpulkan dan memfokuskan cahaya dari bagian spektrum cahaya tampak elektromagnetik agar dapat langsung melihat gambar yang diperbesar.
BAB III METODE PENELITIAN
 26 BAB III METODE PENELITIAN 3.1 Metode Penelitian Metode yang digunakan dalam penelitian ini adalah studi observasi monitoring, yaitu dengan melakukan pengamatan dalam interval waktu tertentu dengan mengukur
26 BAB III METODE PENELITIAN 3.1 Metode Penelitian Metode yang digunakan dalam penelitian ini adalah studi observasi monitoring, yaitu dengan melakukan pengamatan dalam interval waktu tertentu dengan mengukur
INFORMASI ASTRONOMIS HILAL DAN MATAHARI SAAT MATAHARI TERBENAM TANGGAL 8 DAN 9 SEPTEMBER 2010 PENENTU AWAL BULAN SYAWWAL 1431 H
 INFORMASI ASTRONOMIS HILAL DAN MATAHARI SAAT MATAHARI TERBENAM TANGGAL 8 DAN 9 SEPTEMBER 2010 PENENTU AWAL BULAN SYAWWAL 1431 H Keteraturan peredaran Bulan dalam mengelilingi Bumi juga Bumi dan Bulan dalam
INFORMASI ASTRONOMIS HILAL DAN MATAHARI SAAT MATAHARI TERBENAM TANGGAL 8 DAN 9 SEPTEMBER 2010 PENENTU AWAL BULAN SYAWWAL 1431 H Keteraturan peredaran Bulan dalam mengelilingi Bumi juga Bumi dan Bulan dalam
Abdul Rachman dan Thomas Djamaluddin Peneliti Matahari dan Antariksa Lembaga Penerbangan dan Antariksa Nasional (LAPAN)
 Abdul Rachman dan Thomas Djamaluddin Peneliti Matahari dan Antariksa Lembaga Penerbangan dan Antariksa Nasional (LAPAN) Disampaikan pada Diseminasi Hisab Rukyat di BPPR- LAPAN Pameungpeuk 30 Juli 2011
Abdul Rachman dan Thomas Djamaluddin Peneliti Matahari dan Antariksa Lembaga Penerbangan dan Antariksa Nasional (LAPAN) Disampaikan pada Diseminasi Hisab Rukyat di BPPR- LAPAN Pameungpeuk 30 Juli 2011
(Fenomena Matahari di Atas Ka bah) Pandapotan Harahap NIM: Abstrak
 MENENTUKAN ARAH KE SEBUAH KOTA DAN MENGHITUNG JARAK DUA BUAH KOTA MEAUI BAYANG-BAYANG TONGKAT OEH MATAHARI (Fenomena Matahari di Atas Ka bah) Pandapotan Harahap NIM: 765 Progran Studi Pengajaran Fisika
MENENTUKAN ARAH KE SEBUAH KOTA DAN MENGHITUNG JARAK DUA BUAH KOTA MEAUI BAYANG-BAYANG TONGKAT OEH MATAHARI (Fenomena Matahari di Atas Ka bah) Pandapotan Harahap NIM: 765 Progran Studi Pengajaran Fisika
Antiremed Kelas 9 Fisika
 Antiremed Kelas 9 Fisika Tata Surya - Latihan Ulangan Doc Name : AR09FIS0599 Version : 2012-10 halaman 1 01. Berikut ini adalah planet-planet pada tata surya kita. Urutan yang benar dari yang terdekat
Antiremed Kelas 9 Fisika Tata Surya - Latihan Ulangan Doc Name : AR09FIS0599 Version : 2012-10 halaman 1 01. Berikut ini adalah planet-planet pada tata surya kita. Urutan yang benar dari yang terdekat
GERAK EDAR BUMI & BULAN
 GERAK EDAR BUMI & BULAN Daftar isi : Pendahuluan Standar Kompetensi Kompetensi Dasar Indikator Materi : 1. Bentuk dan Ukuran Bumi 2. Pengaruh Rotasi Bumi 3. Pengaruh Revolusi Bumi 4. Bulan Sebagai Satelit
GERAK EDAR BUMI & BULAN Daftar isi : Pendahuluan Standar Kompetensi Kompetensi Dasar Indikator Materi : 1. Bentuk dan Ukuran Bumi 2. Pengaruh Rotasi Bumi 3. Pengaruh Revolusi Bumi 4. Bulan Sebagai Satelit
Ronde Analisis Data. P (φ) = P 0 + P t cos φ dengan P t = 2πP 0r cp B
 Halaman 1 dari 6 (D1) Binary Pulsar Dalam pencarian sistematis selama beberapa dekade, astronom telah menemukan sejumlah besar milisecond pulsar (periode rotasi < 10 ms). Sebagian besar pulsar ini ditemukan
Halaman 1 dari 6 (D1) Binary Pulsar Dalam pencarian sistematis selama beberapa dekade, astronom telah menemukan sejumlah besar milisecond pulsar (periode rotasi < 10 ms). Sebagian besar pulsar ini ditemukan
Soal Ujian Olimpiade Astronomi Kabupaten-Kota Tingkat SMA, 2008
 Soal Ujian Olimpiade Astronomi Kabupaten-Kota Tingkat SMA, 008 Waktu : 150 menit Nama : Sekolah: kabupaten/kota : Provinsi: Tanggal Lahir: Kelas (tahun ajaran 007/008): DAFTAR KONSTANTA Konstanta gravitasi,
Soal Ujian Olimpiade Astronomi Kabupaten-Kota Tingkat SMA, 008 Waktu : 150 menit Nama : Sekolah: kabupaten/kota : Provinsi: Tanggal Lahir: Kelas (tahun ajaran 007/008): DAFTAR KONSTANTA Konstanta gravitasi,
SELEKSI TINGKAT PROVINSI CALON PESERTA INTERNATIONAL ASTRONOMY OLYMPIAD (IAO) TAHUN 2009
 DEPARTEMEN PENDIDIKAN NASIONAL DIRJEN MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS SELEKSI TINGKAT PROVINSI CALON PESERTA INTERNATIONAL ASTRONOMY OLYMPIAD (IAO) TAHUN
DEPARTEMEN PENDIDIKAN NASIONAL DIRJEN MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS SELEKSI TINGKAT PROVINSI CALON PESERTA INTERNATIONAL ASTRONOMY OLYMPIAD (IAO) TAHUN
INFORMASI HILAL SAAT MATAHARI TERBENAM TANGGAL 2 JUNI 2011 M PENENTU AWAL BULAN RAJAB 1432 H
 INFORMASI HILAL SAAT MATAHARI TERBENAM TANGGAL 2 JUNI 2011 M PENENTU AWAL BULAN RAJAB 1432 H Keteraturan peredaran Bulan dalam mengelilingi Bumi juga Bumi dan Bulan dalam mengelilingi Matahari memungkinkan
INFORMASI HILAL SAAT MATAHARI TERBENAM TANGGAL 2 JUNI 2011 M PENENTU AWAL BULAN RAJAB 1432 H Keteraturan peredaran Bulan dalam mengelilingi Bumi juga Bumi dan Bulan dalam mengelilingi Matahari memungkinkan
Makalah Rotasi dan Revolusi bumi
 1 Makalah Rotasi dan Revolusi bumi Guna memenuhi Tugas Mata Pelajaran Ilmu Pengetahuan Alam Disusun oleh Ketua Anggota : Syalmi : Yola Prawita Oti Mulyani Anggi Mutia Kelas : VII.4 SMP NEGERI 2 TOBOALI
1 Makalah Rotasi dan Revolusi bumi Guna memenuhi Tugas Mata Pelajaran Ilmu Pengetahuan Alam Disusun oleh Ketua Anggota : Syalmi : Yola Prawita Oti Mulyani Anggi Mutia Kelas : VII.4 SMP NEGERI 2 TOBOALI
Bintang Ganda DND-2006
 Bintang Ganda Bintang ganda (double stars) adalah dua buah bintang yang terikat satu sama lain oleh gaya tarik gravitasi antar kedua bintang tersebut. Apabila sistem bintang ini lebih dari dua, maka disebut
Bintang Ganda Bintang ganda (double stars) adalah dua buah bintang yang terikat satu sama lain oleh gaya tarik gravitasi antar kedua bintang tersebut. Apabila sistem bintang ini lebih dari dua, maka disebut
KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS
 KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS Nama Kelas & Sekolah Provinsi Kabupaten/Kota Tanggal Lahir Tanda Tangan Naskah ini
KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SEKOLAH MENENGAH ATAS Nama Kelas & Sekolah Provinsi Kabupaten/Kota Tanggal Lahir Tanda Tangan Naskah ini
: Jarak titik pusat benda langit, sampai dengan Equator langit, di ukur sepanjang lingkaran waktu, dinamakan Deklinasi. Jika benda langit itu
 Al-daqaiq al-tamkiniyyah (Ar.) : Tenggang waktu yang diperlukan oleh Matahari sejak piringan atasnya menyentuh ufuk hakiki sampai terlepas dari ufuk mar i Altitude (ing) Bayang Asar Bujur tempat Deklinasi
Al-daqaiq al-tamkiniyyah (Ar.) : Tenggang waktu yang diperlukan oleh Matahari sejak piringan atasnya menyentuh ufuk hakiki sampai terlepas dari ufuk mar i Altitude (ing) Bayang Asar Bujur tempat Deklinasi
4. Orbit dalam Medan Gaya Pusat. AS 2201 Mekanika Benda Langit
 4. Orbit dalam Medan Gaya Pusat AS 2201 Mekanika Benda Langit 4. Orbit dalam Medan Gaya Pusat 4.1 Pendahuluan Pada bab ini dibahas gerak benda langit dalam medan potensial umum, misalnya potensial sebagai
4. Orbit dalam Medan Gaya Pusat AS 2201 Mekanika Benda Langit 4. Orbit dalam Medan Gaya Pusat 4.1 Pendahuluan Pada bab ini dibahas gerak benda langit dalam medan potensial umum, misalnya potensial sebagai
BAB I SISTEM KOORDINAT
 BAB I SISTEM KOORDINAT 1.1 Sistem Koordinat Sistem koordinat adalah suatu cara ang digunakan untuk menentukan letak suatu titik pada bidang ( R ) atau ruang ( R ). Beberapa macam sistem koordinat ang kita
BAB I SISTEM KOORDINAT 1.1 Sistem Koordinat Sistem koordinat adalah suatu cara ang digunakan untuk menentukan letak suatu titik pada bidang ( R ) atau ruang ( R ). Beberapa macam sistem koordinat ang kita
Matematika Astronomi: Bagaimana Matematika Mempelajari Alam 1
 Matematika Astronomi: Bagaimana Matematika Mempelajari Alam 1 Ariyadi Wijaya ([email protected]) Abstrak Manfaat fenomena astronomi untuk kehidupan manusia menyebabkan pengkajian astronomi telah menjadi
Matematika Astronomi: Bagaimana Matematika Mempelajari Alam 1 Ariyadi Wijaya ([email protected]) Abstrak Manfaat fenomena astronomi untuk kehidupan manusia menyebabkan pengkajian astronomi telah menjadi
PRISMA FISIKA, Vol. I, No. 1 (2013), Hal. 1-7 ISSN : Visualisasi Efek Relativistik Pada Gerak Planet
 PRISMA FISIKA, Vol. I, No. 1 (13), Hal. 1-7 ISSN : 337-8 Visualisasi Efek Relativistik Pada Gerak Planet Nurul Asri 1, Hasanuddin 1, Joko Sampurno 1, Azrul Azwar 1 1 Program Studi Fisika, FMIPA, Universitas
PRISMA FISIKA, Vol. I, No. 1 (13), Hal. 1-7 ISSN : 337-8 Visualisasi Efek Relativistik Pada Gerak Planet Nurul Asri 1, Hasanuddin 1, Joko Sampurno 1, Azrul Azwar 1 1 Program Studi Fisika, FMIPA, Universitas
DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA
 Dapatkan soal-soal lainnya di http://forum.pelatihan-osn.com DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA Solusi Tes Olimpiade Sains Nasional
Dapatkan soal-soal lainnya di http://forum.pelatihan-osn.com DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDRAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT PEMBINAAN SMA Solusi Tes Olimpiade Sains Nasional
SMP kelas 9 - FISIKA BAB 4. SISTEM TATA SURYALatihan Soal 4.2. Pernyataan tersebut yang termasuk ciri ciri dari bumi di tunjukkan pada nomor...
 SMP kelas 9 - FISIKA BAB 4. SISTEM TATA SURYALatihan Soal 4.2 1. Perhatikan pernyataan berikut! 1. Melakukan revolusi terhadap matahari 2. Memiliki satelit berupa cincin 3. Mengelilingi matahari pada orbitnya
SMP kelas 9 - FISIKA BAB 4. SISTEM TATA SURYALatihan Soal 4.2 1. Perhatikan pernyataan berikut! 1. Melakukan revolusi terhadap matahari 2. Memiliki satelit berupa cincin 3. Mengelilingi matahari pada orbitnya
A. Peta 1. Pengertian Peta 2. Syarat Peta
 A. Peta Dalam kehidupan sehari-hari kamu tentu membutuhkan peta, misalnya saja mencari daerah yang terkena bencana alam setelah kamu mendengar beritanya di televisi, sewaktu mudik untuk memudahkan rute
A. Peta Dalam kehidupan sehari-hari kamu tentu membutuhkan peta, misalnya saja mencari daerah yang terkena bencana alam setelah kamu mendengar beritanya di televisi, sewaktu mudik untuk memudahkan rute
KEMENTRIAN PENDIDIKAN DAN KEBUDAYAAN DITJEN MANAJEMEN PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA
 KEMENTRIAN PENDIDIKAN DAN KEBUDAYAAN DITJEN MANAJEMEN PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA Olimpiade Sains Nasional Bidang Astronomi 2012 ESSAY Solusi Teori 1) [IR] Tekanan (P) untuk atmosfer planet
KEMENTRIAN PENDIDIKAN DAN KEBUDAYAAN DITJEN MANAJEMEN PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA Olimpiade Sains Nasional Bidang Astronomi 2012 ESSAY Solusi Teori 1) [IR] Tekanan (P) untuk atmosfer planet
BAB IV ANALISIS SISTEM HISAB AWAL BULAN KAMARIAH ALMANAK NAUTIKA DAN ASTRONOMICAL ALGORITHMS JEAN MEEUS
 150 BAB IV ANALISIS SISTEM HISAB AWAL BULAN KAMARIAH ALMANAK NAUTIKA DAN ASTRONOMICAL ALGORITHMS JEAN MEEUS Pada bab ini, penulis akan menganalisis tentang sistem hisab Almanak Nautika dan Astronomical
150 BAB IV ANALISIS SISTEM HISAB AWAL BULAN KAMARIAH ALMANAK NAUTIKA DAN ASTRONOMICAL ALGORITHMS JEAN MEEUS Pada bab ini, penulis akan menganalisis tentang sistem hisab Almanak Nautika dan Astronomical
KEMENTRIAN PENDIDIKAN DAN KEBUDAYAAN DITJEN MANAJEMEN PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA
 KEMENTRIAN PENDIDIKAN DAN KEBUDAYAAN DITJEN MANAJEMEN PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA Olimpiade Sains Nasional Bidang Astronomi 2012 Tes Teori Waktu 180 menit Nomor Peserta Provinsi Tanggal
KEMENTRIAN PENDIDIKAN DAN KEBUDAYAAN DITJEN MANAJEMEN PENDIDIKAN MENENGAH DIREKTORAT PEMBINAAN SMA Olimpiade Sains Nasional Bidang Astronomi 2012 Tes Teori Waktu 180 menit Nomor Peserta Provinsi Tanggal
BAB III METODE PENELITIAN
 BAB III METODE PENELITIAN 1. Metode Penelitian Penelitian menggunakan metode deskriptif melalui pendekatan kuantitatif. Fenomena yang ada merupakan fenomena alam berupa kumpulan bintang-bintang dalam gugus
BAB III METODE PENELITIAN 1. Metode Penelitian Penelitian menggunakan metode deskriptif melalui pendekatan kuantitatif. Fenomena yang ada merupakan fenomena alam berupa kumpulan bintang-bintang dalam gugus
FI322 Ilmu Pengetahuan Bumi dan Antariksa
 Materi Keahlian (MKKPS), bagi mahasiswa prodi Pendidikan Fisika. Pilihan (MKPPS), bagi mahasiswa prodi Fisika. Tambahan (MKKT), bagi mahasiswa di luar Jurusan Pendidikan Fisika. 3 SKS. Fisika Umum, Fisika
Materi Keahlian (MKKPS), bagi mahasiswa prodi Pendidikan Fisika. Pilihan (MKPPS), bagi mahasiswa prodi Fisika. Tambahan (MKKT), bagi mahasiswa di luar Jurusan Pendidikan Fisika. 3 SKS. Fisika Umum, Fisika
Bumi berotasi. Getak Harian - dari timur ke barat. - periodanya 24 jam. - sejajar ekuator langit.
 Gerak Bumi Animasi Bumi berotasi Bola langit melakukan gerak semu, arahnya berlawanan dgn arah gerak rotasi bumi Getak Harian - dari timur ke barat. - periodanya 24 jam. - sejajar ekuator langit. Di ekuator,
Gerak Bumi Animasi Bumi berotasi Bola langit melakukan gerak semu, arahnya berlawanan dgn arah gerak rotasi bumi Getak Harian - dari timur ke barat. - periodanya 24 jam. - sejajar ekuator langit. Di ekuator,
BAB IV ANALISIS METODE HISAB AWAL BULAN KAMARIAH QOTRUN NADA DALAM KITAB METHODA AL-QOTRU
 BAB IV ANALISIS METODE HISAB AWAL BULAN KAMARIAH QOTRUN NADA DALAM KITAB METHODA AL-QOTRU A. Analisis Metode dan Dasar Penentuan Hisab Awal Bulan Kamariah Qotrun Nada dalam Kitab Methoda Al-Qotru Hisab
BAB IV ANALISIS METODE HISAB AWAL BULAN KAMARIAH QOTRUN NADA DALAM KITAB METHODA AL-QOTRU A. Analisis Metode dan Dasar Penentuan Hisab Awal Bulan Kamariah Qotrun Nada dalam Kitab Methoda Al-Qotru Hisab
MENYENANGI MATEMATIKA DAN SAINS MELALUI ASTRONOMI* 1
 MENYENANGI MATEMATIKA DAN SAINS MELALUI ASTRONOMI* 1 Oleh Judhistira Aria Utama Laboratorium Bumi dan Antariksa Jurusan Pendidikan Fisika Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam Universitas
MENYENANGI MATEMATIKA DAN SAINS MELALUI ASTRONOMI* 1 Oleh Judhistira Aria Utama Laboratorium Bumi dan Antariksa Jurusan Pendidikan Fisika Fakultas Pendidikan Matematika dan Ilmu Pengetahuan Alam Universitas
INFORMASI HILAL SAAT MATAHARI TERBENAM TANGGAL 23 JANUARI 2012 M PENENTU AWAL BULAN RABI UL AWAL 1433 H
 INFORMASI HILAL SAAT MATAHARI TERBENAM TANGGAL 23 JANUARI 2012 M PENENTU AWAL BULAN RABI UL AWAL 1433 H Keteraturan peredaran Bulan dalam mengelilingi Bumi juga Bumi dan Bulan dalam mengelilingi Matahari
INFORMASI HILAL SAAT MATAHARI TERBENAM TANGGAL 23 JANUARI 2012 M PENENTU AWAL BULAN RABI UL AWAL 1433 H Keteraturan peredaran Bulan dalam mengelilingi Bumi juga Bumi dan Bulan dalam mengelilingi Matahari
BAB IV ANALISIS KOMPARASI ALGORITMA EQUATION OF TIME JEAN MEEUS DAN SISTEM NEWCOMB
 BAB IV ANALISIS KOMPARASI ALGORITMA EQUATION OF TIME JEAN MEEUS DAN SISTEM NEWCOMB A. Uji Komparasi dan Analisis Hasil Perhitungan Equation of Time Jean Meeus dan Newcomb Menggunakan Parameter Almanak
BAB IV ANALISIS KOMPARASI ALGORITMA EQUATION OF TIME JEAN MEEUS DAN SISTEM NEWCOMB A. Uji Komparasi dan Analisis Hasil Perhitungan Equation of Time Jean Meeus dan Newcomb Menggunakan Parameter Almanak
PROGRAM APLIKASI FALAKIYAH DENGAN fx-7400g PLUS
 PROGRAM APLIKASI FALAKIYAH DENGAN fx-7400g PLUS Bagian III : Menghitung Deklinasi Matahari dan Equation of Time A. Pendahuluan Yang disebut dengan deklinasi (declination) adalah jarak sudut antara sebuah
PROGRAM APLIKASI FALAKIYAH DENGAN fx-7400g PLUS Bagian III : Menghitung Deklinasi Matahari dan Equation of Time A. Pendahuluan Yang disebut dengan deklinasi (declination) adalah jarak sudut antara sebuah
SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2014 TINGKAT PROVINSI
 HAK CIPTA DILINDUNGI UNDANG-UNDANG SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2014 TINGKAT PROVINSI BIDANG ASTRONOMI Waktu : 210 Menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL
HAK CIPTA DILINDUNGI UNDANG-UNDANG SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 2014 TINGKAT PROVINSI BIDANG ASTRONOMI Waktu : 210 Menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL
2. Untuk interval 0 < x < 360, nilai x yang nantinya akan memenuhi persamaan trigonometri cos x 2 sin x = 2 3 cos adalah
 Soal Babak Semifinal OMITS 007. Hubungan antara a dan b agar fungsi f x = a sin x + b cos x mempunyai nilai stasioner di x = π adalah a. a = b b. a = b d. a = b e. a = b a = b. Untuk interval 0 < x < 60,
Soal Babak Semifinal OMITS 007. Hubungan antara a dan b agar fungsi f x = a sin x + b cos x mempunyai nilai stasioner di x = π adalah a. a = b b. a = b d. a = b e. a = b a = b. Untuk interval 0 < x < 60,
DINAMIKA BENDA LANGIT
 DINAMIKA BENDA LANGIT CHATIEF KUNJAYA KK A S T R O N O M I, I N S T I T U T T E K N O L O G I B A N D U N G TPOA, Kunjaya 2014 KOMPETENSI DASAR X.3.3 Menganalisis besaran-besaran fisis pada gerak lurus
DINAMIKA BENDA LANGIT CHATIEF KUNJAYA KK A S T R O N O M I, I N S T I T U T T E K N O L O G I B A N D U N G TPOA, Kunjaya 2014 KOMPETENSI DASAR X.3.3 Menganalisis besaran-besaran fisis pada gerak lurus
UNIT 13: GERAK BENDA LANGIT
 MATERI KULIAH IPA-1 JURUSAN PENDIDIKAN IPA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM FOTO YANG RELEVAN UNIT 13: GERAK BENDA LANGIT I Introduction 5 Latar Belakang Pada K-13 Kkelas VII terdapat KD sebagai
MATERI KULIAH IPA-1 JURUSAN PENDIDIKAN IPA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM FOTO YANG RELEVAN UNIT 13: GERAK BENDA LANGIT I Introduction 5 Latar Belakang Pada K-13 Kkelas VII terdapat KD sebagai
Satuan Besaran dalam Astronomi. Dr. Chatief Kunjaya KK Astronomi ITB
 Satuan Besaran dalam Astronomi Dr. Chatief Kunjaya KK Astronomi ITB Kompetensi Dasar X.3.1 Memahami hakikat fisika dan prinsipprinsip pengukuran (ketepatan, ketelitian dan aturan angka penting) X.4.1 Menyajikan
Satuan Besaran dalam Astronomi Dr. Chatief Kunjaya KK Astronomi ITB Kompetensi Dasar X.3.1 Memahami hakikat fisika dan prinsipprinsip pengukuran (ketepatan, ketelitian dan aturan angka penting) X.4.1 Menyajikan
IPA TERPADU KLAS VIII BAB 14 BUMI, BULAN, DAN MATAHARI
 IPA TERPADU KLAS VIII BAB 14 BUMI, BULAN, DAN MATAHARI KOMPETENSI INTI 3. Memahami dan menerapkan pengetahuan (faktual, konseptual, dan prosedural) berdasarkan rasa ingin tahunya tentang ilmu pengetahuan,
IPA TERPADU KLAS VIII BAB 14 BUMI, BULAN, DAN MATAHARI KOMPETENSI INTI 3. Memahami dan menerapkan pengetahuan (faktual, konseptual, dan prosedural) berdasarkan rasa ingin tahunya tentang ilmu pengetahuan,
SOAL UJIAN PRAKTEK ASTRONOMI OLIMPIADE SAINS NASIONAL 2014 CALON PESERTA INTERNATIONAL EARTH SCIENCE OLYMPIAD (IESO) 2015
 SOAL UJIAN PRAKTEK ASTRONOMI OLIMPIADE SAINS NASIONAL 2014 CALON PESERTA INTERNATIONAL EARTH SCIENCE OLYMPIAD (IESO) 2015 Bidang : KEBUMIAN SUB BIDANG ASTRONOMI Materi : ANALISIS DATA (Langit Mendung)
SOAL UJIAN PRAKTEK ASTRONOMI OLIMPIADE SAINS NASIONAL 2014 CALON PESERTA INTERNATIONAL EARTH SCIENCE OLYMPIAD (IESO) 2015 Bidang : KEBUMIAN SUB BIDANG ASTRONOMI Materi : ANALISIS DATA (Langit Mendung)
BAB IV ANALISIS PEDOMAN WAKTU SHALAT SEPANJANG MASA KARYA SAĀDOE DDIN DJAMBEK. A. Analisis Metode Hisab Awal Waktu Salat Saādoe ddin Djambek dalam
 BAB IV ANALISIS PEDOMAN WAKTU SHALAT SEPANJANG MASA KARYA SAĀDOE DDIN DJAMBEK A. Analisis Metode Hisab Awal Waktu Salat Saādoe ddin Djambek dalam Pembuatan Pedoman Waktu Shalat Sepanjang Masa Saādoe ddin
BAB IV ANALISIS PEDOMAN WAKTU SHALAT SEPANJANG MASA KARYA SAĀDOE DDIN DJAMBEK A. Analisis Metode Hisab Awal Waktu Salat Saādoe ddin Djambek dalam Pembuatan Pedoman Waktu Shalat Sepanjang Masa Saādoe ddin
3. ORBIT KEPLERIAN. AS 2201 Mekanika Benda Langit. Monday, February 17,
 3. ORBIT KEPLERIAN AS 2201 Mekanika Benda Langit 1 3.1 PENDAHULUAN Mekanika Newton pada mulanya dimanfaatkan untuk menentukan gerak orbit benda dalam Tatasurya. Misalkan Matahari bermassa M pada titik
3. ORBIT KEPLERIAN AS 2201 Mekanika Benda Langit 1 3.1 PENDAHULUAN Mekanika Newton pada mulanya dimanfaatkan untuk menentukan gerak orbit benda dalam Tatasurya. Misalkan Matahari bermassa M pada titik
Gerhana Bulan Total 31 Januari 2018
 Gerhana Bulan Total 31 Januari 2018 Rhorom Priyatikanto Pusat Sains Antariksa Lembaga Penerbangan dan Antariksa Nasional Bandung, Indonesia Pendahuluan Matahari, Bulan, bintang, dan 5 planet adalah objek
Gerhana Bulan Total 31 Januari 2018 Rhorom Priyatikanto Pusat Sains Antariksa Lembaga Penerbangan dan Antariksa Nasional Bandung, Indonesia Pendahuluan Matahari, Bulan, bintang, dan 5 planet adalah objek
Pengenalan Geogebra. Oleh: Hazrul Iswadi. Disampaikan pada seminar internal Departemen MIPA. Tanggal 10 September 2011
 Pengenalan Geogebra Oleh: Hazrul Iswadi Disampaikan pada seminar internal Departemen MIPA Tanggal 10 September 2011 Departemen MIPA Universitas Surabaya A. Apa itu GeoGebra? GeoGebra adalah software gratis
Pengenalan Geogebra Oleh: Hazrul Iswadi Disampaikan pada seminar internal Departemen MIPA Tanggal 10 September 2011 Departemen MIPA Universitas Surabaya A. Apa itu GeoGebra? GeoGebra adalah software gratis
Klik. Korona pada Matahari
 Klik Korona pada Matahari Klik Kromosfer pada Matahari Klik TATA SURYA Susunan Matahari dan anggota tata surya yang mengitarinya. Anggota Tata Surya 1. Planet 2. Asteroid 3. Satelit 4. Meteoroid 5. Komet
Klik Korona pada Matahari Klik Kromosfer pada Matahari Klik TATA SURYA Susunan Matahari dan anggota tata surya yang mengitarinya. Anggota Tata Surya 1. Planet 2. Asteroid 3. Satelit 4. Meteoroid 5. Komet
SOAL SELEKSI OLIMPIADE SAINS TINGKAT KABUPATEN/KOTA 2014 CALON TIM OLIMPIADE ASTRONOMI INDONESIA 2015
 HAK CIPTA DILINDUNGI UNDANG-UNDANG SOAL SELEKSI OLIMPIADE SAINS TINGKAT KABUPATEN/KOTA 2014 CALON TIM OLIMPIADE ASTRONOMI INDONESIA 2015 Bidang Astronomi Waktu : 150 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN
HAK CIPTA DILINDUNGI UNDANG-UNDANG SOAL SELEKSI OLIMPIADE SAINS TINGKAT KABUPATEN/KOTA 2014 CALON TIM OLIMPIADE ASTRONOMI INDONESIA 2015 Bidang Astronomi Waktu : 150 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN
RENCANA PELAKSANAAN PEMBELAJARAN : HUKUM NEWTON TENTANG GRAVITASI
 RENCANA PELAKSANAAN PEMBELAJARAN NAMA SEKOLAH MATA PELAJARAN MATERI POKOK KELAS/SEMESTER WAKTU : SMA LABORATORIUM UPI : FISIKA : HUKUM NEWTON TENTANG GRAVITASI : XI/I : 3 X 4 JP + 2 JP A. KOMPETENSI INTI
RENCANA PELAKSANAAN PEMBELAJARAN NAMA SEKOLAH MATA PELAJARAN MATERI POKOK KELAS/SEMESTER WAKTU : SMA LABORATORIUM UPI : FISIKA : HUKUM NEWTON TENTANG GRAVITASI : XI/I : 3 X 4 JP + 2 JP A. KOMPETENSI INTI
HUKUM NEWTON TENTANG GRAVITASI DAN GERAK PLANET
 HUKUM NEWTON TENTANG GRAVITASI DAN GERAK PLANET HUKUM NEWTON TENTANG GRAVITASI DAN GERAK PLANET Kompetensi Dasar 3.2 Mengevaluasi pemikiran dirinya terhadap keteraturan gerak planet dalam tatasurya berdasarkan
HUKUM NEWTON TENTANG GRAVITASI DAN GERAK PLANET HUKUM NEWTON TENTANG GRAVITASI DAN GERAK PLANET Kompetensi Dasar 3.2 Mengevaluasi pemikiran dirinya terhadap keteraturan gerak planet dalam tatasurya berdasarkan
3. MEKANIKA BENDA LANGIT
 3. MEKANIKA BENDA LANGIT 3.1. ELIPS Sebelum belajar Mekanika Benda Langit lebih lanjut, terlebih dahulu perlu diketahui salah satu bentuk irisan kerucut yaitu tentang elips. Gambar 3.1. Geometri Elips
3. MEKANIKA BENDA LANGIT 3.1. ELIPS Sebelum belajar Mekanika Benda Langit lebih lanjut, terlebih dahulu perlu diketahui salah satu bentuk irisan kerucut yaitu tentang elips. Gambar 3.1. Geometri Elips
Draft Marking Scheme. (Berdasarkan Solusi OSP Astronomi 2013)
 Draft arking Scheme (Berdasarkan Solusi OSP Astronomi 013) A. C No A B C D E 1 X X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 1 X 13 X 14 X 15 X 16 X 17 X 18 19 X 0 X 1 X X 3 X 4 X 5 X Berdasarkan dokumen Petunjuk
Draft arking Scheme (Berdasarkan Solusi OSP Astronomi 013) A. C No A B C D E 1 X X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 11 X 1 X 13 X 14 X 15 X 16 X 17 X 18 19 X 0 X 1 X X 3 X 4 X 5 X Berdasarkan dokumen Petunjuk
Horizon Lokal Dan Jam Matahari
 Horizon Lokal Dan Jam Matahari Rosa M. Ros International Astronomical Union Technical University of Catalonia, Barcelona, Spain Tujuan Memahami gerak harian Matahari Memahami gerak tahunan Matahari Memahami
Horizon Lokal Dan Jam Matahari Rosa M. Ros International Astronomical Union Technical University of Catalonia, Barcelona, Spain Tujuan Memahami gerak harian Matahari Memahami gerak tahunan Matahari Memahami
"Setiap planet bergerak dengan lintasan elips, Matahari berada di salah satu fokusnya."
 Johannes Kepler merupakan seorang tokoh penting dalam revolusi ilmiah adalah seorang astronom Jerman, matematikawan dan astrolog. Dia paling dikenal melalui hukum gerakan planetnya. Dia kadang dirujuk
Johannes Kepler merupakan seorang tokoh penting dalam revolusi ilmiah adalah seorang astronom Jerman, matematikawan dan astrolog. Dia paling dikenal melalui hukum gerakan planetnya. Dia kadang dirujuk
GAYA GESEK. Gaya Gesek Gaya Gesek Statis Gaya Gesek Kinetik
 GAYA GESEK (Rumus) Gaya Gesek Gaya Gesek Statis Gaya Gesek Kinetik f = gaya gesek f s = gaya gesek statis f k = gaya gesek kinetik μ = koefisien gesekan μ s = koefisien gesekan statis μ k = koefisien gesekan
GAYA GESEK (Rumus) Gaya Gesek Gaya Gesek Statis Gaya Gesek Kinetik f = gaya gesek f s = gaya gesek statis f k = gaya gesek kinetik μ = koefisien gesekan μ s = koefisien gesekan statis μ k = koefisien gesekan
ZAARI BIN MOHAMAD HBSC4203_V2 - EARTH AND SPACE / BUMI DAN ANGKASA BUMI DAN ANGKASA A. PENDAHULUAN
 BUMI DAN ANGKASA A. PENDAHULUAN Seperti yang kita ketahui, selain planet bumi, di alam semesta terdapat banyak lagi benda-benda lain di langit. Kenampakan objek-objek samawi lain di langit yang umumnya
BUMI DAN ANGKASA A. PENDAHULUAN Seperti yang kita ketahui, selain planet bumi, di alam semesta terdapat banyak lagi benda-benda lain di langit. Kenampakan objek-objek samawi lain di langit yang umumnya
SOAL SELEKSI PESERTA OLIMPIADE SAINS NASIONAL BIDANG ASTRONOMI
 SOAL SELEKSI PESERTA OLIMPIADE SAINS NASIONAL BIDANG ASTRONOMI Waktu Jumlah Soal : 150 menit : 30 Soal 1. Bintang A memiliki tingkat kecemerlangan tiga kali lebih besar dibandingkan dengan Bintang B. Bintang
SOAL SELEKSI PESERTA OLIMPIADE SAINS NASIONAL BIDANG ASTRONOMI Waktu Jumlah Soal : 150 menit : 30 Soal 1. Bintang A memiliki tingkat kecemerlangan tiga kali lebih besar dibandingkan dengan Bintang B. Bintang
KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN
 Hak Cipta Dilindungi Undang-undang SOLUSI SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 014 TINGKAT PROVINSI ASTRONOMI Waktu : 180 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL
Hak Cipta Dilindungi Undang-undang SOLUSI SOAL UJIAN SELEKSI CALON PESERTA OLIMPIADE SAINS NASIONAL 014 TINGKAT PROVINSI ASTRONOMI Waktu : 180 menit KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL
Jika sebuah sistem berosilasi dengan simpangan maksimum (amplitudo) A, memiliki total energi sistem yang tetap yaitu
 A. TEORI SINGKAT A.1. TEORI SINGKAT OSILASI Osilasi adalah gerakan bolak balik di sekitar suatu titik kesetimbangan. Ada osilasi yang memenuhi hubungan sederhana dan dinamakan gerak harmonik sederhana.
A. TEORI SINGKAT A.1. TEORI SINGKAT OSILASI Osilasi adalah gerakan bolak balik di sekitar suatu titik kesetimbangan. Ada osilasi yang memenuhi hubungan sederhana dan dinamakan gerak harmonik sederhana.
GRAFIK (CHART) Aplikasi Manajemen Perkantoran B 1
 GRAFIK (CHART) Grafik (Chart) biasanya sering digunakan untuk mengetahui suatu kenaikan atau penurunan dari angka-angka yang terjadi pada suatu data, apakah data tersebut semakin lama semakin meningkat
GRAFIK (CHART) Grafik (Chart) biasanya sering digunakan untuk mengetahui suatu kenaikan atau penurunan dari angka-angka yang terjadi pada suatu data, apakah data tersebut semakin lama semakin meningkat
APLIKASI DERET FOURIER UNTUK MENGETAHUI WAKTU TERBIT, KULMINASI, DAN TERBENAM MATAHARI SKRIPSI. Diajukan untuk Memenuhi Salah Satu Syarat
 APLIKASI DERET FOURIER UNTUK MENGETAHUI WAKTU TERBIT, KULMINASI, DAN TERBENAM MATAHARI SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Guna Memperoleh Gelar Sarjana Strata Satu (S-1) Oleh: NURUL ISHMAH
APLIKASI DERET FOURIER UNTUK MENGETAHUI WAKTU TERBIT, KULMINASI, DAN TERBENAM MATAHARI SKRIPSI Diajukan untuk Memenuhi Salah Satu Syarat Guna Memperoleh Gelar Sarjana Strata Satu (S-1) Oleh: NURUL ISHMAH
ILMU PENGETAHUAN BUMI DAN ANTARIKSA
 ILMU PENGETAHUAN BUMI DAN ANTARIKSA Ilmu Pengetahuan Bumi dan Antariksa I. DESKRIPSI Mata kuliah ini adalah Mata Kuliah Keahlian Program Studi (MKKPS) yang merupakan mata kuliah wajib bagi mahasiswa prodi
ILMU PENGETAHUAN BUMI DAN ANTARIKSA Ilmu Pengetahuan Bumi dan Antariksa I. DESKRIPSI Mata kuliah ini adalah Mata Kuliah Keahlian Program Studi (MKKPS) yang merupakan mata kuliah wajib bagi mahasiswa prodi
KELOMPOK 1 Anggi Juliansa ( ) Reza AlFajri ( )
 BUMI DAN TATA SURYA KELOMPOK 1 Anggi Juliansa (121020220001) Reza AlFajri (121020220008) Alam semesta ini terdiri dari semua materi termasuk tenaga dan radiasi serta hal yang telah diketahui dan baru dalam
BUMI DAN TATA SURYA KELOMPOK 1 Anggi Juliansa (121020220001) Reza AlFajri (121020220008) Alam semesta ini terdiri dari semua materi termasuk tenaga dan radiasi serta hal yang telah diketahui dan baru dalam
MEKANIKA BENDA LANGIT MARIANO N., S.SI.
 MEKANIKA BENDA LANGIT MARIANO N., S.SI. MEKANIKA BENDA LANGIT Adalah ilmu yang mempelajari gerakan benda-benda langit secara kinematika maupun dinamika : Posisi Kecepatan Percepatan Interaksi Gaya Energi
MEKANIKA BENDA LANGIT MARIANO N., S.SI. MEKANIKA BENDA LANGIT Adalah ilmu yang mempelajari gerakan benda-benda langit secara kinematika maupun dinamika : Posisi Kecepatan Percepatan Interaksi Gaya Energi
