PANGKAT TAK SEBENARNYA
|
|
|
- Ridwan Yuwono
- 8 tahun lalu
- Tontonan:
Transkripsi
1 PANGKAT TAK SEBENARNYA
2
3 Bab 5 Pangkat Tak Sebenarnya Sumber: www6.fheberswalde.de Pada bab ini, kamu akan diajak untuk memahami sifat-sifat bilangan berpangkat dan bentuk akar serta penggunaannya dalam pemecahan masalah sederhana dengan cara mengidentifikasi sifatsifat bilangan berpangkat dan bentuk akar, melakukan operasi aljabar yang melibatkan bilangan berpangkat bulat dan bentuk akar, serta memecahkan masalah sederhana yang berkaitan dengan bilangan berpangkat dan bentuk akar. Di Kelas VII kamu telah mempelajari sifat-sifat perkalian dan pembagian bilangan bulat berpangkat bilangan bulat positif. Pada bab ini sifat-sifat tersebut akan dikembangkan sampai bilangan rasional berpangkat bilangan bulat dan bentuk akar. Konsep-konsep bilangan berpangkat dan bentuk akar banyak digunakan dalam bidang ilmu dan teknologi, seperti pada contoh berikut. Jari-jari penampang melintang sebuah batang tumbuhan A. Bilangan Rasional Berpangkat Bilangan Bulat B. Bentuk Akar dan Pangkat Pecahan 5 x cm. Adapun pada musim panas, ukurannya menyusut x cm. Setelah memdikotil pada musim dingin adalah pelajari bab ini, kamu dapat menghitung penurunan luas penampang tumbuhan dikotil tersebut pada musim panas. 111 Diagram Alur Bilangan Berpangkat terdiri atas Pangkat Tak Sebenarnya Pangkat Sebenarnya adalah adalah Pangkat Bilangan Bulat Positif Pangkat Nol sifat Pangkat Bilangan Bulat Negatif definisi definisi
4 am an = am + n am = am n an a m n a0 = 1, a bilangan rasional dan a 0 = am n = an m pan + qam = an (p + qam n) pan qam = an (p qam n) pam qan = an(pam n q) Pangkat Pecahan a n = 1 an dapat diubah menjadi sifat a bilangan rasional, a 0, dan n bilangan bulat positif 1 1 n m 1. p. m n. p p m n Bentuk Akar 1 = pm 1 m n = p
5 = p 1 n n = n = p m pm n m Tes Apersepsi Awal Sebelum mempelajari materi bab ini, kerjakanlah soal-soal berikut di buku latihanmu. 1.. Tentukan nilai dari bilangan berpangkat berikut. a. 7 c. ( 11) b. 1 d. ( 15) Tentukan nilai dari akar bilangan berikut. a. 81 c b. d. 65 Selesaikan soal-soal berikut. a. 5 + ( ) b. 8 1 ( ) c. d. ( ) ( ) ( )4 Tentukan nilai dari bilangan berpangkat berikut. a. () b. () Selesaikan soal-soal berikut. a. (4) (15) b. () + ()4
6 Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX A. Bilangan Rasional Berpangkat Bilangan Bulat 1. Bilangan Rasional Di Kelas VII, kamu telah mempelajari konsep bilangan rasional. Agar tidak lupa, konsep tersebut akan dipelajari kembali pada bab ini. Untuk itu, pahami kembali definisi bilangan rasional berikut. Definisi 5.1 Bilangan rasional ialah bilangan yang dapat dinyatakan dalam bentuk a, dengan a dan b adalah bilangan bulat b serta b 0. Bilangan 1, 1,,,, dan 5 merupakan bilangan rasional karena memenuhi bentuk seperti pada Definisi Pengertian Bilangan Rasional Berpangkat Bilangan Bulat Positif Dalam kehidupan sehari-hari, kadang-kadang kamu harus mengalikan bilangan-bilangan berikut: ( ) ( ) ( ) ( ) (1,5) (1,5) (1,5) (1,5) (1,5) Perkalian berulang tersebut akan lebih sederhana jika ditulis dalam bentuk bilangan berpangkat, seperti berikut. ditulis dan dibaca "tiga pangkat dua" ditulis 5 dan dibaca "lima pangkat tiga". ( ) ( ) ( ) ( ) ditulis ( )4 dan dibaca "negatif dua pangkat empat". Coba kamu tentukan bentuk bilangan berpangkat dari perkalian berulang (1,5) (1,5) (1,5) (1,5) (1,5). Penulisan perkalian berulang dalam bentuk bilangan berpangkat tersebut memperjelas definisi berikut. Definisi 5. Jika a bilangan rasional dan n bilangan bulat positif maka perkalian berulang n faktor dari a ialah a a a a... a dituli a n Tugas untukmu Coba kamu selidiki apakah bilangan-bilangan berikut merupakan bilangan rasional? a. 0,5 b. 0,... c. 0, d. 1, e. 0, f. Tuliskan hasil penyelidikanmu pada buku latihan, kemudian kumpulkan kepada gurumu. InfoMatika Pangkat dua dari suatu bilangan yang digit terakhirnya 5 dapat dihitung dengan rumus n (n + 1) + 5 Dalam hal ini + berarti angka-angkanya didekatkan. Misalnya, berapa nilai dari 45? 45 berarti x n=4 4 (4 + 1) x = 05 Jadi, 45 = 05 Dengan penalaran yang sama seperti perhitungan tersebut, hitunglah a. 75 b. 85 n faktor a Pangkat Tak Sebenarnya 11
7 TechnoMath Dengan menggunakan Calculator Scientific tipe FX-570W kamu dapat menentukan nilai (4,9) dengan menekan tomboltombol berikut secara berurutan. ( 4 9 ) x Pada Definisi 5., an disebut bilangan berpangkat dengan a sebagai bilangan pokok dan n sebagai pangkat (eksponen). Contoh b. ( )4 Pada layar akan muncul tampilan Selanjutnya, untuk mengetahui hasilnya tekan tombol = sehingga pada layar akan muncul tampilan. Tugas untukmu Salin dan lengkapilah perkalian berikut. 1.,54,5.. ) (... ) = ( faktor = (..... ) Misalkan, a adalah bilangan rasional. a a5 = ( ) (... ) faktor... faktor = ( )... faktor = a... Berdasarkan uraian tersebut dapatkah kamu menerka sifat umum perkalian bilangan berpangkat? Cobalah nyatakan sifat tersebut dengan kata-katamu sendiri. Kemudian, ujilah dugaanmu untuk mengalikan bilangan berpangkat sebarang. 114 d. Penyelesaian: a. 7 = = 49 7 = 4 b. ( )4 = ( ) ( ) ( ) ( ) = 9 9 = 81 c. (4) = ( ) = (9 9) = 81 d.. =
8 8 7 Sebuah bak mandi berbentuk kubus dan mempunyai panjang rusuk 9, dm. Berapa mililiter volume bak mandi tersebut? Penyelesaian: Diketahui: Panjang rusuk bak mandi (p) = 9, dm Ditanyakan: Volume bak mandi (V) dalam satuan ml. V = p = (9,) = 9, 9, 9, = 84,64 9, = 778,688 Volume bak mandi itu adalah 778,688 dm atau 778,688 liter. Diketahui 1 liter = 1000 ml sehingga 778,688 liter = 778, ml = ml. Jadi, volume bak mandi tersebut adalah ml.... faktor... faktor =,5 Nyatakan bilangan berpangkat berikut dalam perkalian berulang, kemudian hitunglah. a. 7 c. (4). Sifat Bilangan Rasional Berpangkat Bilangan Bulat Positif a. Sifat Perkalian Bilangan Berpangkat Pelajari operasi hitung berikut. = (1 4 ) ({ ) ffakktor ffakktor = = + ( ) faktor a Jadi, = +. Sekarang, lakukan Tugas untukmu di samping. Perkalian bilangan berpangkat tersebut memperjelas sifat berikut ini. Sifat 5.1 Jika a bilangan rasional dan m, n bilangan bulat positif maka am an = am+n Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX Siapa Berani? Contoh a. 5 5 = 5+ = 55 b. ( )4 ( )5 = ( )4+5 = ( )9 c. 4 tidak dapat disederhanakan karena bilangan pokoknya tidak sama. d. y y = y+ = y5, dengan y = bilangan rasional. Ketinggian suatu benda dapat ditentukan dengan menggunakan rumus gerak jatuh bebas, yaitu h = 1 gt. Dalam hal ini h = ketinggian benda, g = percepatan gravitasi bumi, dan t = waktu benda sampai jatuh ke tanah. Sebuah benda dijatuhkan dari puncak sebuah gedung. Hasil pengukuran menunjukkan bahwa waktu benda sampai jatuh ke tanah adalah 4,9 detik. Jika percepatan gravitasi bumi di tempat itu 9,8 m/det, berapa meterkah tinggi gedung tersebut? Penyelesaian: Diketahui: t = 4,9 detik dan g = 9,8 m/det Ditanyakan: h =? h = 1 gt = 1 9,8 (4,9) = 4,9 (4,9)
9 Salin dan lengkapilah pembagian bilangan berikut..... fa to 64 7faktor 8or 4... faktor... faktor = 1.. =... faktor Pelajari operasi hitung berikut.. Misalnya, a adalah bilangan rasional..... fa to 64 7faktor 8or (... ) a5 = (... ) a 14 5 fa a or 6 7faktor 4 48 = {... faktor ffakktor ( 5 ) fakto fakt ktor kto } = 14 = 5 = ( 5 ) faktor a { ffakktor =.... fa to 64 7faktor 8or (... ) (... ) faktor fak akto t r... faktor Selanjutnya, lakukan Tugas untukmu di samping. Pembagian bilangan berpangkat tersebut memenuhi sifat berikut. m positif maka a n = am n dengan m > n..... fa kttor tor 64 7ffaktor 4 8 (... ) = 1.. = a 5 Jadi, = 5 Sifat 5. Jika a bilangan rasional, a 0, dan m, n bilangan bulat (..... ) fa kttor tor.... fa to 64 7ffaktor faktor 8or = (... ) (... ) (... ) 14
10 b. Sifat Pembagian Bilangan Berpangkat Tugas untukmu = (... ) = (4,9)1+ = (4,9) = 117,649 Jadi, tinggi gedung tersebut adalah 117,649 meter. 5 Panjang rusuk sebuah kubus adalah 5 cm. Kemudian, panjang rusuk kubus tersebut diperpanjang menjadi 5 kali panjang rusuk semula. Berapa liter volume kubus yang baru? Berdasarkan uraian tersebut, coba kamu terka sifat umum pembagian bilangan berpangkat. Nyatakan sifat tersebut dengan kata-katamu sendiri. Kemudian, ujilah dugaanmu untuk menghitung pembagian dua bilangan berpangkat sebarang. a Pangkat Tak Sebenarnya 115 Contoh a. 7 = 7 4 = = 7 4 b. ( 5)6 = ( 5)6 4 = ( 5) = 5 ( 5)4 c. p5 = p5 = p p Percepatan sentripetal dari sebuah benda yang bergerak v Sumber: CD Image Tugas untukmu m = 16 m/det v = 57, 6 km =
11 Salin dan lengkapilah perpangkatan berikut (54) = faktor.. ) = ( faktor (... ) ) ( faktor... faktor... = 5 = faktor (a)4 = faktor... ) (..... ) = ( faktor (... ) 14 4 (... ) faktor... faktor... = 14.. = a faktor Kemudian, ujilah dugaanmu untuk memangkatkan bilangan berpangkat sebarang. Berdasarkan uraian tersebut, dapatkah kamu menduga sifat umum perpangkatan bilangan berpangkat? Cobalah nyatakan sifat tersebut dengan kata-katamu sendiri. 116 jam a.600 det Ditanyakan as? as = v = 16 = 16 1 = 161 = 16 r 16 Jadi, percepatan sentripetalnya adalah 16 m/det
12 . Misalnya, a adalah bilangan rasional.... faktor melingkar dirumuskan as = r. Dalam hal ini as = percepatan sentripetal bersatuan m/det, v = kecepatan benda bersatuan m/det, dan r = jarak benda ke pusat lingkaran bersatuan meter. Sebuah mobil bergerak di suatu tikungan yang berbentuk seperempat lingkaran dengan jari-jari 16 m. Mobil melaju dengan kecepatan tetap 57,6 km/jam. Berapa m/det percepatan sentripetal mobil tersebut? Penyelesaian: Diketahui: r = 16 m c. Sifat Perpangkatan Bilangan Berpangkat Pelajari operasi hitung berikut ini. () = 1 ffakktor = (1 4 ) (1 4 ) = 1 4 ffakktor faktor a ( ) faktor a = Jadi, () = = Sekarang, kerjakan Tugas untukmu di samping. Perpangkatan bilangan berpangkat yang telah kamu pelajari tersebut memperjelas sifat berikut. Sifat 5. Jika a bilangan rasional dan m, n bilangan bulat positif maka (am)n = am n = an m Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX Contoh (4) = 4 = 8 a. ( c b. 5 1 = 1 4 = ( ) = ( )1
13 15 = ) Energi kinetik (Ek) sebuah benda bermassa m kg yang bergerak dengan kecepatan v m/det dirumuskan Ek = 1 mv. Sebuah benda bermassa 6 kg bergerak dengan kecepatan 7 m/det. Berapa joule energi kinetik benda tersebut? Penyelesaian: Diketahui: m = 6 kg v = 7 m/det = m/det Ditanyakan: Ek =? Ek = 1 1 mv = 6 () = = 6 = 7 =.187 Jadi, energi kinetiknya adalah.187 joule. Tugas untukmu d. Sifat Perpangkatan dari Bentuk Perkalian Pelajarilah operasi hitung berikut. ( ) = (1 ) ( 4) 4 (4 4 ) Salin dan lengkapilah operasi hitung berikut. 1. ( 5)4 = fakto f r... faktor =( = 1 4 ) (1 4 ) ffakktor = ( ) (..... ) 14 faktor a... faktor Jadi, ( ) =. Sekarang, kerjakan Tugas untukmu di samping. Perpangkatan dari bentuk perkalian yang telah kamu pelajari tersebut memperjelas sifat berikut. Sifat 5.4 Jika n bilangan bulat positif dan a, b bilangan rasional maka (a b)n = an bn. Misalkan, a dan b bilangan rasional.... (a b)5 = faktor
14 = ( ) (..... ) faktor Contoh a. ( 5) = 5 = 4 5 = 100 b. {( ) ) = ( ) = 7 8 = 16 c. ( pq)4 = ( )4 p4 q4 = 81p4q4 Suatu alat listrik mempunyai hambatan 10 ohm dialiri arus 10 ampere selama menit. Berapa joule besarnya energi listrik yang digunakan?... faktor = faktor = Berdasarkan uraian tersebut coba kamu terka sifat umum perpangkatan dari bentuk perkalian tersebut. Nyatakan sifat itu dengan kata-katamu sendiri. Pangkat Tak Sebenarnya 117 Tugas untukmu Penyelesaian: Diketahui: R = 10 ohm I = 10 ampere t = menit = 10 detik Ditanyakan W? W = I R t = ( 10) = (10) 10 1, 10 = 9, = 1,6 108 =, Jadi, energi listrik yang digunakan sebesar, joule. Bersama kelompok belajarmu, coba kamu selidiki mengapa pada Sifat 5.5 nilai b tidak boleh sama dengan nol. Presentasikan hasil penyelidikanmu di depan kelas bergantian dengan kelompok yang lain. e. Sifat Perpangkatan dari Bentuk Pembagian Tugas untukmu Salin dan lengkapilah operasi hitung berikut Untuk memahami sifat perpangkatan dari bentuk pembagian, pelajarilah operasi hitung berikut dengan saksama. = faktor
15 ... faktor =... = faktor.... fa aktor to 64 7faktor 8or (... ) (... ) 14 = a... b faktor Berdasarkan uraian tersebut coba kamu terka sifat umum perpangkatan dari bentuk pembagian itu. Nyatakan sifat tersebut dengan katakatamu sendiri. ffakktor Sifat distributif pada bentuk aljabar adalah a (b + c) = ab + ac. Sifat 5.5 Jika a, b bilangan rasional, b 0, dan n bilangan bulat n positif maka a b n = an. b Contoh f. Catatan = Sekarang, kerjakan Tugas untukmu di samping. Perpangkatan dari bentuk pembagian yang telah kamu pelajari itu memperjelas sifat berikut Jadi,
16 . Misalkan, a dan b bilangan rasional fak f ktor } = = = { { ffakktor.... fa to 64 7faktor 8or... (... ) = 5... (... ) 14 a b 7 7 = = 4 7 = ( 4. pq r = p q 4 pq = r r 4 ) = Sifat Penjumlahan dan Pengurangan Bilangan Berpangkat Sebelum mempelajari sifat penjumlahan dan pengurangan bilangan berpangkat, dapatkah kamu menyederhanakan penjumlahan bilangan berpangkat berikut? a c b. ( ) + ( )5 Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX Cocokkan hasilnya dengan jawaban berikut. a = 5 (1 + ) (sifat distributif ) 5 5 = 10 = 10 b. ( ) + ( )5 = ( ) (1 + ( )) (sifat distributif ) = ( ) 10 = 10 ( ) 5 c = 5 ( + 5) (sifat distributif ) = 5 7 = 7 5 Uraian tersebut sesuai dengan konsep penjumlahan bilangan berpangkat seperti berikut. Edward Waring ( ) Sifat 5.6 Jika a, p, q adalah bilangan rasional dan m, n adalah bilangan bulat positif, dengan m n maka pan + qam = an(p + qam n) Konsep penjumlahan dua bilangan berpangkat tersebut berlaku
17 juga untuk pengurangan dua bilangan berpangkat seperti berikut. Sifat 5.7 Jika a, p, q adalah bilangan rasional dan m, n adalah bilangan bulat positif, dengan m n maka pan qam = an(p qam n) pam qan = an(pam n q) Contoh = 5 (1 + ) = 5 5 = = 55 (1 5) = 55 ( 4) = = 75 ( 7 ) = = (sifat 5.6) Setiap bilangan bulat merupakan bilangan pangkat tiga dari bilangan itu sendiri atau merupakan jumlah dari beberapa bilangan pangkat tiga. Pernyataan ini diungkapkan oleh seorang matematikawan Inggris, Edward Waring, pada tahun Pernyataan tersebut dapat dibuktikan kebenarannya. Jika diambil sebarang bilangan bulat, bilangan tersebut dapat dinyatakan sebagai bilangan bulat berpangkat tiga. Misalnya, = ( 5) dan 0 = ( ) + ( ) + ( ) + ( ). Sumber: Ensiklopedi Matematika & Peradaban Manusia, 00 (sifat 5.7) (sifat 5.6) Tugas untukmu 4. Sifat Bilangan Rasional Berpangkat Bilangan Bulat Negatif dan Nol 1. Gunakan Sifat 5. untuk Berdasarkan Sifat 5., telah dipelajari bahwa untuk a adalah bilangan rasional, a 0, dan m, n adalah bilangan bulat am = am n. an a5. a8. Dengan menuliskan ke dalam bentuk faktorfaktornya, sederhanamenyederhanakan a. Pengertian Pangkat Bilangan Bulat Negatif positif dengan m > n, berlaku InfoMatika kanlah a5. a8 Berdasarkan kedua langkah tersebut, apa yang dapat kamu simpulkan? Pangkat Tak Sebenarnya 119 Siapa Berani? Sifat tersebut dapat dikembangkan untuk m < n. Sebagai contoh, amatilah bentuk berikut.
18 Bilangan sempurna adalah bilangan yang jumlah seluruh faktornya sama dengan dua kali bilangan tersebut. Sebagai contoh, 8 merupakan bilangan sempurna karena jumlah seluruh faktornya sama dengan 8, yaitu = = 56 = 8 Untuk mengetahui bilangan sempurna, salah satunya dapat menggunakan rumus p (P p+1 1). Dalam hal ini p merupakan bilangan prima. Coba kamu tentukan paling sedikit dua buah bilangan sempurna lainnya (selain 8) dengan menggunakan rumus tersebut. a = a 5 = a... (1) a 5 Dengan cara menuliskan ke dalam bentuk faktorfaktornya, pembagian tersebut dapat dituliskan sebagai berikut. a a a a = = a a a a5 a a a a a a a a 1 1 =... () =1 a a a Berdasarkan (1) dan () dapat disimpulkan bahwa a = 1. a Dengan demikian, kamu dapat mengubah bilangan rasional berpangkat bilangan bulat negatif ke dalam bentuk bilangan rasional berpangkat bilangan bulat positif dan sebaliknya. Secara umum, untuk bilangan berpangkat n, dengan n adalah bilangan bulat positif dapat ditulis seperti berikut. 1 = a n, a 0 an Sekarang, amati bentuk perpangkatan berikut yang dihitung dengan menggunakan kalkulator. InfoMatika t t cokelat hitam merah perak Nilai dari komponen resistor ditandai oleh sebuah sistem warna garis. Inilah cara untuk menuliskan bilangan yang besar dalam benda yang kecil. Dua garis yang pertama menunjukkan sebuah bagian dan yang ketiga mewakili operasi perkalian dengan pangkat 10. Adapun garis yang keempat menunjukkan toleransi nilai. Sumber: Ensiklopedi Matematika & Peradaban Manusia, a a 1 4 = 0,15 = 1 = = 0,5 = 1 = 0, = 1 = t 9 Uraian tersebut memenuhi definisi bilangan rasional berpangkat bilangan bulat negatif seperti
19 definisi berikut. Definisi 5. Jika a bilangan rasional, a 0, dan n adalah bilangan bulat positif maka a n = 1n a Contoh 5.8 Ubahlah bentuk pangkat berikut menjadi bentuk pangkat positif. a. 5 b. Penyelesaian: a. 5 = 1 5 b. = 1 Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX Sifat pangkat bilangan bulat positif dari Sifat 5.1 sampai dengan Sifat 5.5 berlaku juga untuk bilangan berpangkat bilangan bulat negatif, dengan a, b adalah bilangan rasional dan m, n adalah bilangan bulat negatif. Coba kamu tuliskan kelima sifat tersebut di buku tugasmu. Contoh 5.9 a = = 5 = 5 5 = 5 b. ( ( ) = ( ) 4 = ( ) = (( ) 1) = )4 1 1 = 1 = 9 1 Siapa Berani? 1. Ubahlah bentuk pangkat berikut menjadi bentuk pangkat positif. a b. ( ) c. ( 8) d Selesaikan soal berikut. Kemudian, ubahlah hasilnya ke bentuk pangkat negatif. b. Pengertian Pangkat Nol b. Kamu telah mempelajari Sifat 5. bilangan rasional berc. Sebagai contoh, a 5 = a5 5 = a0... (1) a Dengan cara menuliskan ke dalam bentuk faktor-faktornya, pembagian tersebut dapat dituliskan sebagai berikut. a5 = a a a a a = 1 a a a a a a5
20 ... () Berdasarkan (1) dan () dapat disimpulkan bahwa a0 = 1. Uraian tersebut memenuhi konsep bilangan berpangkat nol seperti definisi berikut. Definisi 5.4 a0 = 1, dengan a bilangan rasional dan a 0 Contoh 5.10 Hitunglah bentuk perpangkatan bilangan rasional berikut Tugas untukmu Pada Definisi 5.4, disebutkan bahwa a0 = 1. Selidiki mengapa hal tersebut berlaku untuk a bilangan rasional dan a 0? Bagaimana jika a = 0? Tulis hasil penyelidikanmu pada buku tugasmu, kemudian kumpulkan pada gurumu. Siapa Berani? Sifat 5.1 sampai dengan Sifat 5.5 yang telah kamu pelajari pada bagian berlaku juga untuk bilangan berpangkat nol, dengan m = n = 0, a adalah bilangan rasional, dan a 0. Coba tuliskan kelima sifat tersebut. 1 a
21 5 4 m pangkat bilangan bulat positif dan negatif, yaitu a n = am n, dengan a bilangan rasional, m dan n adalah bilangan bulat, m 0, n 0, serta m n. Sekarang, amati sifat tersebut untuk m = n a. Ubahlah bentuk pangkat berikut menjadi bentuk pangkat positif. a. 5 7 b. 9 c. d. 4 5 (0,1) (0,15) 1 Pangkat Tak Sebenarnya 11 Penyelesaian: =
22 5 8 = 7 ( ) = = 5 = = = 5 4 = 4 = Tes Kompetensi 5.1 Kerjakan soal-soal berikut dalam buku latihanmu. 1. Hitunglah: a. 5 : 4. 5 b. c. (0,5) (0,5)4
23 d. ( 7) e.. 4 Tentukan R jika R1 = Hitunglah dalam bentuk yang paling sederhana. Volume sebuah kerucut dinyatakan dengan rumus V = t alas kerucut dan t = tinggi kerucut. 4. R= 1 r Jika r = 1 d, dalam hal ini d = diameter alas kerucut, nyatakan: a. V dalam ¾, d, dan t; b. t dalam V, ¾ dan r; c. d dalam ¾, V, dan t; d. t dalam ¾, V, dan d. Hambatan total R dari sebuah rangkaian seri paralel ditentukan oleh persamaan 1
24 1 R R 6. 1 ¾ rt, dengan r = jari-jari 1 1 R R4, R = ¾, dan R4 = ¾. Diketahui produksi semen (x) sebuah pabrik memenuhi persamaan x = 5 4 t 106 dengan t bilangan bulat positif yang menyatakan waktu berjalan dalam tahun. Jika keuntungan perusahaan dinyatakan p = 5 105, oleh p dari persamaan x dan nyatakan hasilnya 1, R = 1 7. berapakah keuntungan perusahaan yang diperoleh selama tahun? Gunakanlah Sifat 5.6 dan 5.7 untuk menyederhanakan bilangan berpangkat berikut. a b c. ( 5)6 ( 5)5 d Hambatan sebuah alat listrik (R) bersatuan ohm dirumuskan R = 8. V. Dalam hal ini P V = tegangan listrik bersatuan volt, dan P = daya listrik bersatuan watt. Pada sebuah alat listrik tertulis 0 volt, 0 watt. Berapa ohm hambatan alat listrik tersebut? Besarnya energi listrik yang digunakan pada sebuah alat listrik dirumuskan W = I Rt. Dalam hal ini W = energi listrik bersatuan joule, I = kuat arus listrik Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX
25 9. bersatuan ampere, R = hambatan listrik bersatuan ohm, dan t = waktu bersatuan detik. Suatu alat listrik mempunyai hambatan 10 ohm dialiri arus 10 ampere selama 5 menit. Berapa joule besarnya energi listrik yang digunakan? Sebuah penampungan air berbentuk kubus dengan panjang rusuk 1,5 10 cm. Berapa liter volume penampungan air tersebut? 10. Panjang sebuah karet gelang () dirumuskan sebagai berikut. = (4a ) 5 ( 9)4 dengan a merupakan bilangan 1,,, 4, dan 5 yang menyatakan jenis karet gelang. Jenis karet gelang manakah yang memiliki ukuran terpanjang? B. Bentuk Akar dan Pangkat Pecahan 1. Bilangan Real A Di Subbab A kamu telah mempelajari konsep bilangan rasional. Agar kamu lebih memahami konsep bilangan rasional, coba kamu selidiki apakah bilangan-bilangan berikut merupakan bilangan rasional? a. c. 0, b. 0, d. ¾ Sekarang, pelajarilah Gambar 5.1. Gambar tersebut memperlihatkan sebuah segitiga sikusiku istimewa dengan besar sudut lancipnya 45 dan panjang sisi siku-sikunya 1 satuan panjang. Panjang sisi AC dapat ditentukan dengan menggunakan Dalil Pythagoras seperti berikut. (AC) = (AB) + (BC) AC = 1 1 =. Jadi, panjang sisi AC adalah satuan panjang. Amati bilangan tersebut. Dengan menggunakan kalkulator, akan diperoleh nilai = 1, Apakah merupakan bilangan rasional? Coba kamu cari nilainilai a dan b agar = a, dalam hal ini a dan b b bilangan bulat dan b 0. Ternyata, tidak ada nilai a dan b yang memenuhi a = b, sehingga bukan bilangan rasional. Jadi, merupakan bilangan irasional. Gabungan dari himpunan bilangan rasional dan himpunan bilangan irasional merupakan himpunan bilangan real B 1 C
26 Gambar 5.1 Catatan Hubungan antara macam-macam bilangan dapat disajikan seperti diagram berikut. Bilangan Real Bilangan Rasional Bilangan Bulat Bilangan Cacah Bilangan Bulat Positif (Bilangan Asli) Bilangan Irasional Bilangan Pecahan Bilangan Bulat Negatif Bilangan Nol Pangkat Tak Sebenarnya 1. Pengertian Bentuk Akar Untuk memahami pengertian bentuk akar, pelajarilah perhitungan-perhitungan berikut ini. Siapa Berani? 4 = Bentuk 4 x dengan x 0 dapat merupakan bentuk akar atau bukan bentuk akar. Tentukan paling sedikit dua nilai x agar bentuk tersebut merupakan a. bentuk akar, b. bukan bentuk akar. Tugas untukmu Bentuk akar hanyalah sebagian kecil dari anggota-anggota himpunan bilangan irasional. Contoh bilangan irasional yang bukan bentuk akar yaitu ¾ dan e. Carilah informasi mengenai bilangan ¾ dan e. Kemudian, buatlah laporan dari tugas tersebut dan kumpulkan. Siapa Berani? Perhatikan balok berikut. H G F E D A = Berapakah 6, 9 = 16 = 4 = 4
27 5 = 5 64, dan 81? 5 = 49, Perhitungan akar pangkat bilangan tersebut memenuhi definisi berikut. Definisi 5.5 a = a, bil a r 0 a, bil a 0 Amati contoh-contoh berikut. 1. Misalkan, a = (a > 0) Nilai a = =. Misalkan, a = (a < 0) Nilai a = ( ) = ( ) = Sekarang, adakah akar pangkat yang tidak memenuhi? Akar pangkat bilangan yang tidak memenuhi Definisi 5.5 dinamakan bentuk akar, seperti,, 5, 7, dan 8. Bentuk akar tersebut merupakan bilangan irasional.. Menyederhanakan Bentuk Akar Sebuah bentuk akar dapat disederhanakan menjadi perkalian dua buah akar pangkat bilangan, dengan salah satu akar pangkat bilangan memenuhi Definisi 5.5. Amati dan pelajari contoh berikut. 8 = 4 = 4 = = 18 = 9 = 9 = = Berdasarkan perhitungan tersebut, dapatkah kamu menemukan sifat berikut? Sifat 5.8 C ab a B Diketahui AB = 8 cm, BC = 4 cm, dan CG = 6 cm. Hitunglah panjang diagonal sisi AC dan diagonal ruang AG dalam bentuk akar yang paling sederhana. 14 = b, dengan a dan b adalah bilangan rasional positif. Contoh = 4 = 4 = 4 = 4 6 = 4 6 = 6
28 Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX 4. Operasi Aljabar pada Bentuk Akar a. Penjumlahan dan Pengurangan Bentuk Akar Di buku Kelas VII Bab, kamu telah mempelajari penjumlahan dan pengurangan bentuk aljabar, misalnya x + x = ( + )x = 5x... (1) 5y y = (5 )y = y... () Konsep tersebut berlaku juga untuk bentuk akar, misalnya... () + = ( + ) = 5... (4) 5 = (5 ) = Berdasarkan kedua contoh tersebut dapatkah kamu menerka sifat umum penjumlahan dan pengurangan bentuk akar? Nyatakan sifat tersebut dengan kata-katamu sendiri. Penjumlahan dan pengurangan bentuk akar tersebut memperjelas sifat berikut. Sifat 5.9 Siapa Berani? Hitunglah operasi bentuk akar berikut dengan terlebih dahulu menyederhanakan bentuk akarnya. a. a c b c = (a + b) c a c b c = (a b) c dengan a, b, c adalah bilangan rasional dan c 0. + b c. + 8 d Contoh = (4 + ) = (Tidak dapat dijumlahkan karena tidak meme-. nuhi aturan penjumlahan bentuk akar) b. Perkalian Bentuk Akar Dengan menggunakan Sifat 5.8, kamu dapat menghitung perkalian bentuk akar berikut. = = 6
29 = = 9 = Sederhanakan bentuk akar berikut. 5 6 = 5 6 = 0 6 Ketiga perkalian tersebut memenuhi sifat perkalian bentuk akar, yang secara umum ditulis seperti berikut. Sifat 5.10 a b Siapa Berani? a. b. c. d. e c d = ac bd dengan a, b, c, d adalah bilangan rasional, b 0, dan d 0. Pangkat Tak Sebenarnya 15 Contoh 5.1 Sederhanakan bentuk-bentuk berikut. b. 5 a. Penyelesaian: a. Ingat perkalian suku dua. (a + b) (a b) = a ab + ab b = a b Oleh karena itu, Sederhanakan bentuk akar berikut b. 150
30 5 7 c Pada Sifat 5.11, dituliskan persamaan b = = = c. Pembagian Bentuk Akar Untuk memahami pembagian bentuk akar, amati dan pelajarilah uraian berikut. 100 : 4 = 10 : = 5 = 100 : 4 = 5 = : 9 = 6 : = = 6 : 9 = 4 =. Berdasarkan uraian tersebut, diperoleh hubungan berikut. 100 : 4 = 100 : 4 = : 9 = 6 : 9 =. Perhitungan tersebut menggambarkan sifat pembagian dalam bentuk akar seperti berikut. Sifat 5.11 a b dengan a dan b bilangan rasional, a 0, dan b > 0. Selidikilah bagaimana jika a dan b negatif? Berilah beberapa contoh, lalu amati. Kemudian, tuliskan hasil penyelidikanmu pada buku tugasmu dan kumpulkan pada gurumu. 16 5
31 Tugas untukmu a = = = = =1 b. Ingat, (a + b) = a + ab + b Oleh karena itu, Siapa Berani? a. a = b a atau b a = b a b dengan a dan b adalah bilangan rasional, a 0, dan b > 0. Contoh 5.14 a. 18 = 18 = 6 b. Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX 6 15 = 6 15 = 5
32 5. Merasionalkan Penyebut Suatu Pecahan Kamu telah mempelajari bahwa bentuk akar merupakan bilangan irasional, seperti, 5, + 5,, dan 5 +. Pecahan bentuk akar merupakan bilangan irasional juga Misalnya 1 1, 1,, 5, dan Penyebut pecahan-pecahan tersebut dapat diubah menjadi bilangan rasional. Cara merasionalkan setiap penyebut berlainan. Akan tetapi, prinsip dasarnya sama, yaitu mengalikan penyebut-penyebut tersebut dengan pasangan bentuk akar sekawannya sehingga diperoleh penyebut bilangan rasional. Berdasarkan contoh pecahan-pecahan bentuk akar tersebut, secara umum bentuk akar yang dapat dirasionalkan, a c c c c yaitu,,,, dan, dengan b a b a b b d b d a, b, c, dan d adalah bilangan rasional dan b > 0, d > 0. Penyebut dari pecahan-pecahan tersebut berturut-turut b,a b,a b, b d, dan b d. Apakah bentuk sekawan dari setiap penyebut itu? a. Bentuk sekawan dari b adalah b. b. Bentuk sekawan dari a + b adalah a b. c. Bentuk sekawan dari b + d adalah b d. Perkalian bentuk akar dengan sekawannya akan menghasilkan bilangan rasional. Berikut ini perkalian bentuk akar dengan pasangan sekawannya yang menghasilkan bilangan rasional. a. b.
33 b a b b = b b a b = a b d b d = b b = = a b d =b d dengan b, a b, dan b d adalah bilangan rasional. Sampai saat ini, kamu telah mempelajari perkalian penyebut pecahan bentuk akar dengan pasangan sekawannya sehingga diperoleh penyebut bilangan rasional. Sekarang, kamu akan mempelajari bagaimana penerapannya dalam merasionalkan penyebut dari pecahan bentuk akar. Secara umum, pecahan bentuk akar yang dapat dirasionalkan penyebutnya adalah c. a c c c, dan,,, b a b a b b d c b InfoNet Kamu dapat menambah wawasanmu tentang materi dalam bab ini dari internet dengan mengunjungi alamat: manajemen.klanis.or.id/ warehouse/bab%01%0 bilangan%0pangkat.doc. d Pangkat Tak Sebenarnya 17 Pecahan tersebut masing-masing dirasionalkan dengan mengalikan pembilang dan penyebutnya dengan bentuk akar sekawan dari penyebutnya, yaitu sebagai berikut. a. a = a b b b b Ingat, b b 1 = a b = a b = a b b Uji Kecerdikan Kerjakan soal-soal berikut. Kemudian, pasangkan hasilnya dengan jawaban yang
34 bersesuaian dengan cara menuliskan hurufhuruf soal pada kotak yang tersedia. Jika kamu menjawab dengan benar, kamu akan memperoleh kalimat pernyataan dari seorang matematikawan Jerman, Carl Friedrich Gauss. A. 4 6 E. H. ( 5) I. 4 K. M. c. 15 1/ /9 1/4 7 N. 4 : 44 R. 5
35 T. U. Ingat, a b a b d b c e. b d b b d d = c b b d d d d b b d = c b b d d d c =
36 1 b b c = Contoh 5.15 Sederhanakan penyebut pecahan-pecahan berikut dengan merasionalkan penyebutnya. a. 10 1/9 a Penyelesaian: 40 6 b c b 56 = c a b b b b = c a b = c a a b a b a b c c a b c = = a b a b a b a b a b d.
37 1/9 a a a 1/6 6 b b c = a 16/81 6 c b. b b b. 10 = = 5 = 10 5 = = 6 5 = = 5+ 5
38 6. Pangkat Pecahan Kamu telah mempelajari bilangan rasional berpangkat bilangan bulat positif, nol, dan bilangan bulat negatif. Selanjutnya, kamu akan mempelajari bilangan berpangkat pecahan. Misalkan, 18 Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX pandanglah persamaan 9n =. Ini berarti 9 dipangkatkan n sama dengan. Selain itu, 9n = dapat juga ditulis dalam bentuk ()n = n = 1 1 Artinya, n = 1 atau n =. Jadi, jika 9n =, sama artinya 1 dengan 9 =. 1 1 adalah eksponen pecahan. 1 Bilangan 9 dinamakan bilangan berpangkat pecahan. Sebelumnya, kamu telah mengetahui bahwa 9 = dan Pada bentuk 9, bilangan =. Jadi, 9 = 9 =. Secara umum, jika an = p dengan a, p adalah bilangan real 1 dan n adalah bilangan bulat, dengan n > 0 maka a = p n. Definisikan a = n p (dibaca: "a adalah akar pangkat n dari p"). Pada definisi tersebut berlaku ketentuan berikut. Catatan (i) p merupakan bilangan real positif dan nol untuk n bilangan genap. (ii) p merupakan semua bilangan real untuk n bilangan ganjil. Contoh: Jika 15k = 5 maka (5)k = 5 ¾ 5k = 51 ¾ k = 1 ¾ k = 1 1 Jadi, 15 = 5, atau 15 = 5. Dengan menggunakan pengembangan Sifat 5., kamu dapat menentukan hubungan antara akar pangkat suatu bilangan dan bilangan berpangkat pecahan seperti berikut. 1
39 pn n 1 = pn n n = p n = p1 = p p 1 n Bilangan berpangkat tak sebenarnya meliputi, bilangan berpangkat nol, bilangan berpangkat bilangan bulat negatif, dan bilangan berpangkat pecahan seperti 1, dan =p Bilangan berpangkat bilangan bulat positif disebut juga bilangan berpangkat sebenarnya, seperti, ( ), n 1, 5, 0, 50,, 10, dan 1
40 5, (0,), 1. 1 p n adalah akar pangkat n dari p atau dituliskan n p = pn. 1 p n disebut bilangan berpangkat pecahan. 1 Pada p n berlaku ketentuan berikut. (i) p merupakan bilangan real positif dan nol, untuk n bilangan genap. (ii) p merupakan semua bilangan real untuk n bilangan ganjil. Secara umum, untuk bilangan berpangkat pecahan, berlaku sifat berikut. Pangkat Tak Sebenarnya 19 Sifat 5.1 Uji Kecerdikan Penjualan sepeda motor pada suatu dealer mengikuti persamaan p Sifat n 1 m = p m 1 m n pn = p ms 1 n
41 = pm 1 n = n pm Sifat 5.14 p = t. m Dalam hal ini, t adalah bilangan bulat positif yang menyatakan waktu dalam tahun. a. Hitung banyaknya sepeda motor yang terjual pada tahun ke-4. b. Apakah penjualan terus meningkat dari tahun ke tahun? Jika ya, bagaimana pendapatmu mengenai dampaknya terhadap lingkungan? m 1 = pn µ = 1 sm p n = pn n m p Berdasarkan Sifat 5.1 dan 5.14, terlihat bahwa m pn = pm = n n m p
42 Contoh Sederhanakanlah bentuk-bentuk akar berikut. 5 b. a. 8 Penyelesaian: 8 = a. b. = = = 1 = 5 5 = = 8 4= 8 4. = 4 = 4 = 4 Ubahlah bentuk akar berikut menjadi pangkat pecahan. a. 5 b. 5 81
43 Penyelesaian: 4 Hal Penting. eksponen polinem bilangan berpangkat pangkat negatif pangkat pecahan bentuk akar 5 b = 4 = 5 a. 5 = 5 Ubahlah pangkat pecahan berikut menjadi bentuk akar. 1 a. 1 4 Penyelesaian: 6 c. = a. b = 1 6 = 1 b. c. = =
44 8 = 6 Contoh 5.17 x Jari-jari penampang melintang sebuah batang tumbuhan dikotil 5 x x x 10 x cm. Adapun pada musim pada musim dingin adalah panas, ukurannya tersebut menyusut sejauh x cm, seperti pada gambar di samping. Hitunglah penurunan luas penampang tumbuhan dikotil tersebut pada musim panas. Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX Penyelesaian: Langkah 1 Menuliskan apa yang diketahui dan yang ditanyakan soal tersebut. 5 x cm 5 x Jari-jari batang setelah menyusut r = Diketahui: Jari-jari batang mula-mula = r1 = cm x Ditanyakan: Penurunan luas penampang (¾L) Langkah Menentukan konsep yang akan digunakan untuk menjawab soal. Pada soal ini, konsep yang digunakan adalah luas daerah lingkaran dan operasi pada bentuk akar. Langkah Menyelesaikan soal. ¾L = Luas mula-mula Luas batang setelah menyusut 5 x = πr1 πr = = 5 x 4 x 5 x = 5 x 4
45 x 9 16 πx = 4πx x= 4 4 x = x= 9 x 4 = 4πx + 5 x= 4 5 x 1. Sederhanakanlah soal-soal berikut. a. 8 b c. d e. 8 f.
46 g. Jadi, penurunan luas penampang tumbuhan tersebut = 4πx cm. Langkah 4 Memeriksa kembali jawaban yang telah diperoleh. Oleh karena ¾L = πr1 πr maka ¾L + πr = 4πx + Siapa Berani? Ubahlah bentuk akar berikut menjadi pangkat pecahan. a. a. Jadi, jawaban ¾L = 4πx cm tersebut benar karena ¾L + πr = πr1. 1 b. 16 d.. Ubahlah pangkat pecahan berikut menjadi bentuk akar. 1 = πr1 c. 11 b. 7 c. 115
47 Tes Kompetensi 5. Kerjakan soal-soal berikut dalam buku latihanmu. 1. Sederhanakan bentuk akar berikut a. c b. d. Hitunglah operasi-operasi berikut. a. 6 6 b. 7 c. 48 d Sederhanakan pecahan bentuk akar berikut dengan merasionalkan penyebutnya. a. b c. d Nyatakan soal-soal berikut dalam bentuk akar yang paling sederhana. 1 a. 10 b Pangkat Tak Sebenarnya
48 11 5. Sederhanakanlah soal-soal berikut dan nyatakan hasilnya dalam bentuk bilangan berpangkat rasional positif. a b ( 5) ( ) p= b. p = x 1 x bilangan Selidikilah apakah pernyataan berikut benar atau salah. Jelaskan hasil penyelidikanmu. a = a = ( )( ) 1 = Ubahlah persamaan tersebut dalam bentuk yang paling sederhana, tanpa menggunakan pangkat bilangan negatif. 7. Hitunglah p + q, p q, dan p q, serta sederhanakan hasilnya jika a. rasional untuk x =
49 c. b. 4 4 d Amati persamaan berikut. 1 a 9. Tunjukkan bahwa dan q = 1 dan q = Carilah nilai x untuk persamaan a ) a = ( = a 11. Sebuah kubus dengan R R Z panjang rusuk 6 cm disandarkan pada S dinding sehingga Q posisinya miring seperti pada gambar. Y P Jika PY = 4 cm dan RZ = 1 cm, berapa tinggi titik R dari lantai? 1. Sederhanakan bentuk a b untuk x 4x = 1. 4 a= 1, dan b = 1. Ringkasan Berikut ini contoh rangkuman dari sebagian materi pada bab ini. 1. Bilangan rasional ialah bilangan yang dapat
50 4. a b dinyatakan dalam bentuk, dengan a dan.. b adalah bilangan bulat serta b 0. Jika a adalah bilangan rasional dan m, n adalah bilangan bulat positif maka am an = am + n. Jika a adalah bilangan rasional, dengan a 0, dan m, n adalah bilangan bulat m positif maka a n = am n dengan m > n. a Jika a adalah bilangan rasional dan m, n adalah bilangan bulat positif maka (am)n = am n = an m. Jika a, p, q adalah bilangan rasional dan m, n adalah bilangan bulat positif dengan m n maka pan + qam = an (p + qam n). Jika a, p, q adalah bilangan rasional dan m, n adalah bilangan bulat positif dengan m n maka pan qam = an (p qam n); pam qan = an (pam n q). Coba kamu buat rangkuman dari materi yang telah kamu pelajari pada bab ini dengan katakatamu sendiri. Tuliskan rangkuman tersebut pada buku latihanmu. 1 Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX Refleksi 1... Buatlah kelompok yang terdiri atas 5 sampai 8 orang atau disesuaikan dengan kondisi kelasmu. Setiap anggota kelompok menceritakan tentang materi apa saja dari bab ini yang menurutmu paling mudah dan yang paling sulit dipahami berikut alasannya. Tuliskan hasilnya, kemudian presentasikan di depan kelas bergantian dengan kelompok lain. Tes Kompetensi Bab 5 Kerjakanlah pada buku tugasmu. Pilihlah salah satu jawaban yang paling tepat Nilai ( 6) sama dengan... a. 6 c b. d =... a b.
51 c d Dengan merasionalkan penyebutnya, 6 dapat disederhanakan bentuk menjadi... a. + c. d. b. 4 =... a. 7 b =... a. 5 b. 8 c. 6 d. 7 c. 5 d =... 8 a. 6 c. 6 b. 8 d =... a. c. b. 15 d Dengan merasionalkan penyebutnya, bentuk 6 dapat disederhanakan menjadi... d. a. c. b =... a. b. c. d. 8 5 =...
52 a. 5 b. 5 c. 5 5 d. Pangkat Tak Sebenarnya =... 9 c. a. 8 b = a. b. c. 5 d Dengan cara merasionalkan penyebutnya, bentuk akar menjadi... a a. b. c. d. dapat disederhanakan 17.
53 1 5 c. 5 1 d. b b. c. d a. b. c. d =... = =
54 a. b. c. d = a. b. c. d. =... a. d a. b. c. d a. b. c. d = Belajar Matematika Aktif dan Menyenangkan untuk Kelas IX 8 =...
55
Bilangan Berpangkat. Pangkat Bulat Negatif. a bilangan real. bilangan bulat positif
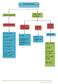 Pangkat sebenarnya Pangkat Tak sebenarnya Pangkat bulat positif Pangkat Bulat Negatif Pangkat Nol Pangkat pecaha a m x a n a m+n a m n an am (a m ) n a nxm p.a n + q. a m a n m n p + qa p.a n - q. a m
Pangkat sebenarnya Pangkat Tak sebenarnya Pangkat bulat positif Pangkat Bulat Negatif Pangkat Nol Pangkat pecaha a m x a n a m+n a m n an am (a m ) n a nxm p.a n + q. a m a n m n p + qa p.a n - q. a m
Pola (1) (2) (3) Banyak segilima pada pola ke-15 adalah. A. 235 C. 255 B. 250 D Yang merupakan bilangan terbesar adalah. A. C. B. D.
 SOAL SELEKSI AWAL 1. Suhu dalam sebuah lemari es adalah 15 o C di bawah nol. Pada saat mati listrik suhu dalam lemari es meningkat 2 o C setiap 120 detik. Jika listrik mati selama 210 detik, suhu dalam
SOAL SELEKSI AWAL 1. Suhu dalam sebuah lemari es adalah 15 o C di bawah nol. Pada saat mati listrik suhu dalam lemari es meningkat 2 o C setiap 120 detik. Jika listrik mati selama 210 detik, suhu dalam
Soal Babak Penyisihan MIC LOGIKA 2011
 Soal Babak Penyisihan MIC LOGIKA 2011 1. Jika adalah bilangan bulat dan angka puluhan dari adalah tujuh, maka angka satuan dari adalah... a. 1 c. 5 e. 9 b. 4 d. 6 2. ABCD adalah pesergi dengan panjang
Soal Babak Penyisihan MIC LOGIKA 2011 1. Jika adalah bilangan bulat dan angka puluhan dari adalah tujuh, maka angka satuan dari adalah... a. 1 c. 5 e. 9 b. 4 d. 6 2. ABCD adalah pesergi dengan panjang
PREDIKSI SOAL UJIAN NASIONAL MATEMATIKA SMP/MTs DAN PEMBAHASAN
 PREDIKSI SOAL UJIAN NASIONAL MATEMATIKA SMP/MTs DAN PEMBAHASAN. * Indikator SKL : Menyelesaikan masalah yang berkaitan dengan operasi tambah, kurang, kali, atau bagi pada bilangan. * Indikator Soal : Menentukan
PREDIKSI SOAL UJIAN NASIONAL MATEMATIKA SMP/MTs DAN PEMBAHASAN. * Indikator SKL : Menyelesaikan masalah yang berkaitan dengan operasi tambah, kurang, kali, atau bagi pada bilangan. * Indikator Soal : Menentukan
Sifat 1 Untuksebarang bilangan rasional a tak nol dan sebarang bilangan bulat m dan n, berlaku a m. a m = a m + n
 Bilangan Berpangkat Kita ingat kembali bahwa untuk bilangan-bilangan cacah a, m, dan n dengan a 0, berlaku: 1 a m = a a a a (sebanyak m faktor) a m a n = a m + n a 0 = 1, di mana a 0 Notasi-notasi di atas
Bilangan Berpangkat Kita ingat kembali bahwa untuk bilangan-bilangan cacah a, m, dan n dengan a 0, berlaku: 1 a m = a a a a (sebanyak m faktor) a m a n = a m + n a 0 = 1, di mana a 0 Notasi-notasi di atas
Sumber: Kamus Visual, 2004
 1 BILANGAN BULAT Pernahkah kalian memerhatikan termometer? Termometer adalah alat yang digunakan untuk mengukur suhu suatu zat. Pada pengukuran menggunakan termometer, untuk menyatakan suhu di bawah 0
1 BILANGAN BULAT Pernahkah kalian memerhatikan termometer? Termometer adalah alat yang digunakan untuk mengukur suhu suatu zat. Pada pengukuran menggunakan termometer, untuk menyatakan suhu di bawah 0
Latihan Ujian 2012 Matematika
 Latihan Ujian 2012 Matematika Hari/Tanggal : Minggu, 19 Februari 2012 Waktu : 120 menit Jumlah Soal : 60 soal Petunjuk Tulis nomor peserta dan nama Anda di tempat yang disediakan pada Lembar Jawaban. Materi
Latihan Ujian 2012 Matematika Hari/Tanggal : Minggu, 19 Februari 2012 Waktu : 120 menit Jumlah Soal : 60 soal Petunjuk Tulis nomor peserta dan nama Anda di tempat yang disediakan pada Lembar Jawaban. Materi
PEMERINTAH PROVINSI DAERAH KHUSUS IBUKOTA JAKARTA DINAS PENDIDIKAN MGMP MATEMATIKA SMP PROVINSI DKI JAKARTA SMPN... JAKARTA
 PEMERINTAH PROVINSI DAERAH KHUSUS IBUKOTA JAKARTA DINAS PENDIDIKAN MGMP MATEMATIKA SMP PROVINSI DKI JAKARTA SMPN... JAKARTA UJICOBA UJIAN NASIONAL TAHUN PELAJARAN 017/018 RAHASIA LEMBAR SOAL Mata Pelajaran
PEMERINTAH PROVINSI DAERAH KHUSUS IBUKOTA JAKARTA DINAS PENDIDIKAN MGMP MATEMATIKA SMP PROVINSI DKI JAKARTA SMPN... JAKARTA UJICOBA UJIAN NASIONAL TAHUN PELAJARAN 017/018 RAHASIA LEMBAR SOAL Mata Pelajaran
SOAL OSN MATEMATIKA SMP TINGKAT KABUPATEN 2012
 SOAL OSN MATEMATIKA SMP TINGKAT KABUPATEN 2012 BAGIAN A : PILIHAN GANDA SOAL 1 Pernyataan yang benar diantara pernyataan-pernyataan berikut adalah : A. {Ø} Ø D. {a,b} {a, b, {{a,b}}} B. {Ø} Ø E. {a,ø}
SOAL OSN MATEMATIKA SMP TINGKAT KABUPATEN 2012 BAGIAN A : PILIHAN GANDA SOAL 1 Pernyataan yang benar diantara pernyataan-pernyataan berikut adalah : A. {Ø} Ø D. {a,b} {a, b, {{a,b}}} B. {Ø} Ø E. {a,ø}
UJIAN NASIONAL SMP/MTs
 UJIAN NASIONAL SMP/MTs Tahun Pelajaran 2007/2008 Mata Pelajaran Jenjang : Matematika : SMP/MTs MATA PELAJARAN Hari/Tanggal : Selasa, 6 Mei 2008 Jam : 08.00-10.00 WAKTU PELAKSANAAN PETUNJUK UMUM 1. Isikan
UJIAN NASIONAL SMP/MTs Tahun Pelajaran 2007/2008 Mata Pelajaran Jenjang : Matematika : SMP/MTs MATA PELAJARAN Hari/Tanggal : Selasa, 6 Mei 2008 Jam : 08.00-10.00 WAKTU PELAKSANAAN PETUNJUK UMUM 1. Isikan
MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo Telepon/Fax (0275)
 KODE : 0/ 1A TUC1/01 MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo 54114 Telepon/Fax (075) 31405 UJI COBA KE 1 UJIAN NASIONAL 01 SMP Se KABUPATEN
KODE : 0/ 1A TUC1/01 MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo 54114 Telepon/Fax (075) 31405 UJI COBA KE 1 UJIAN NASIONAL 01 SMP Se KABUPATEN
Copyright all right reserved
 Latihan Soal UASBN SD/MI 011 Mata Ujian : Matematika Jumlah Soal : 40 1. Hasil dari 4 : 6 x (-5) =... -7-1. Najwa memiliki 1 bungkus permen yang akan dibagikan kepada 4 orang temanny Jika setiap bungkus
Latihan Soal UASBN SD/MI 011 Mata Ujian : Matematika Jumlah Soal : 40 1. Hasil dari 4 : 6 x (-5) =... -7-1. Najwa memiliki 1 bungkus permen yang akan dibagikan kepada 4 orang temanny Jika setiap bungkus
PAKET 3 CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs
 PAKET 3 CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs. * Kemampuan yang diuji. Menghitung hasil operasi tambah, kurang, kali dan bagi pada bilangan bulat Menentukan hasil operasi campuran bilangan bulat.
PAKET 3 CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs. * Kemampuan yang diuji. Menghitung hasil operasi tambah, kurang, kali dan bagi pada bilangan bulat Menentukan hasil operasi campuran bilangan bulat.
Copyright Hak Cipta dilindungi undang-undang
 Latihan Soal UN SMP/MTs Mata Pelajaran : Matematika Jumlah Soal : 0. Hasil dari.7 +.75 adalah. 5 c. 57 d 7. Suhu di dalam kulkas - 0 C. Pada saat mati lampu suhu di dalam kulkas naik 0 C setiap menit.
Latihan Soal UN SMP/MTs Mata Pelajaran : Matematika Jumlah Soal : 0. Hasil dari.7 +.75 adalah. 5 c. 57 d 7. Suhu di dalam kulkas - 0 C. Pada saat mati lampu suhu di dalam kulkas naik 0 C setiap menit.
SMP / MTs Mata Pelajaran : Matematika
 Latihan Soal Ujian Nasional 200 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika Dalam UN berlaku Petunjuk Umum seperti ini :. Isikan identitas Anda ke dalam Lembar
Latihan Soal Ujian Nasional 200 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika Dalam UN berlaku Petunjuk Umum seperti ini :. Isikan identitas Anda ke dalam Lembar
a. 10 c. 20 b. -10 d Indikator : Menyelesaikan soal cerita yang berkaitan dengan operasi Bilangan Bulat a c b d.
 1. Indikator : Menentukan hasil operasi campuran Bilangan Bulat : Hasil dari -20 + 5 x (-12) : (-6) =.. a. 10 c. 20 b. -10 d. 20 2. Indikator : Menyelesaikan soal cerita yang berkaitan dengan operasi Bilangan
1. Indikator : Menentukan hasil operasi campuran Bilangan Bulat : Hasil dari -20 + 5 x (-12) : (-6) =.. a. 10 c. 20 b. -10 d. 20 2. Indikator : Menyelesaikan soal cerita yang berkaitan dengan operasi Bilangan
Bab 1. Bilangan Bulat. Standar Kompetensi. 1. Memahami sifat-sifat operasi hitung bilangan dan pengunaannya dalam pemecahan masalah.
 Bab 1 Bilangan Bulat Standar Kompetensi 1. Memahami sifat-sifat operasi hitung bilangan dan pengunaannya dalam pemecahan masalah. Kompetensi Dasar 1.1. Melakukan operasi hitung bilangan pecahan. 1.2. Menggunakan
Bab 1 Bilangan Bulat Standar Kompetensi 1. Memahami sifat-sifat operasi hitung bilangan dan pengunaannya dalam pemecahan masalah. Kompetensi Dasar 1.1. Melakukan operasi hitung bilangan pecahan. 1.2. Menggunakan
Soal-soal dan Pembahasan UN Matematika SMP/MTs Tahun Pelajaran 2007/2008
 Soal-soal dan Pembahasan UN Matematika SMP/MTs Tahun Pelajaran 2007/2008 1. Hasil dari 1.764 + 3.375 adalah... A. 53 B. 57 C.63 D. 67 BAB VIII BILANGAN BERPANGKAT 4 2 15 1.764 3.375 4 x 4 16 1 3 1 1 64
Soal-soal dan Pembahasan UN Matematika SMP/MTs Tahun Pelajaran 2007/2008 1. Hasil dari 1.764 + 3.375 adalah... A. 53 B. 57 C.63 D. 67 BAB VIII BILANGAN BERPANGKAT 4 2 15 1.764 3.375 4 x 4 16 1 3 1 1 64
SOAL MATEMATIKA - SMP
 SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 200
SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 200
MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo Telepon/Fax (0275)
 KODE : 0/ 1B TUC1/016 MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo 4114 Telepon/Fax (07) 3140 UJI COBA KE 1 UJIAN NASIONAL 016 SMP Se KABUPATEN
KODE : 0/ 1B TUC1/016 MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo 4114 Telepon/Fax (07) 3140 UJI COBA KE 1 UJIAN NASIONAL 016 SMP Se KABUPATEN
BAB 5 Bilangan Berpangkat dan Bentuk Akar
 BAB 5 Bilangan Berpangkat dan Bentuk Akar Untuk materi ini mempunyai 3 Kompetensi Dasar yaitu: Kompetensi Dasar : 1. Mengidentifikasi sifat-sifat bilangan berpangkat dan bentuk akar 2. Melakukan operasi
BAB 5 Bilangan Berpangkat dan Bentuk Akar Untuk materi ini mempunyai 3 Kompetensi Dasar yaitu: Kompetensi Dasar : 1. Mengidentifikasi sifat-sifat bilangan berpangkat dan bentuk akar 2. Melakukan operasi
pagar kebun, ternyata masih kurang dan Pak Sulis membeli kawat lagi sebanyak 3 m.
 PREDIKSI UJIAN NASIONAL 207 [email protected] Pilihlah jawaban yang paling tepat!. Hasil dari - x (-2 + ) : (9 5) adalah... A. - B. - C. D. 2. Pak Sulis mempunyai persediaan kawat sepanjang 5 m. Ketika
PREDIKSI UJIAN NASIONAL 207 [email protected] Pilihlah jawaban yang paling tepat!. Hasil dari - x (-2 + ) : (9 5) adalah... A. - B. - C. D. 2. Pak Sulis mempunyai persediaan kawat sepanjang 5 m. Ketika
PENGERJAAN HITUNG BILANGAN BULAT
 M O D U L 1 PENGERJAAN HITUNG BILANGAN BULAT Standar Kompetensi : Melakukan operasi hitung bilangan bulat dalam pemecahan masalah Kompetensi Dasar : 1. Menggunakan sifat-sifat operasi hitung termasuk operasi
M O D U L 1 PENGERJAAN HITUNG BILANGAN BULAT Standar Kompetensi : Melakukan operasi hitung bilangan bulat dalam pemecahan masalah Kompetensi Dasar : 1. Menggunakan sifat-sifat operasi hitung termasuk operasi
PREDIKSI SOAL MATEMATIKA TAHUN
 PREDIKSI SOAL MATEMATIKA TAHUN 2014 PAKET 1. Hasil dari 3 2 7 21 2 : 31 2 adalah... A. B. C. D. 18 7 28 7 9 2 11 2 2. Dalam kompetisi matematika, setiap jawaban benar diberi skor 4, jawaban salah diberi
PREDIKSI SOAL MATEMATIKA TAHUN 2014 PAKET 1. Hasil dari 3 2 7 21 2 : 31 2 adalah... A. B. C. D. 18 7 28 7 9 2 11 2 2. Dalam kompetisi matematika, setiap jawaban benar diberi skor 4, jawaban salah diberi
3 OPERASI HITUNG BENTUK ALJABAR
 OPERASI HITUNG BENTUK ALJABAR Pada arena balap mobil, sebuah mobil balap mampu melaju dengan kecepatan (x + 10) km/jam selama 0,5 jam. Berapakah kecepatannya jika jarak yang ditempuh mobil tersebut 00
OPERASI HITUNG BENTUK ALJABAR Pada arena balap mobil, sebuah mobil balap mampu melaju dengan kecepatan (x + 10) km/jam selama 0,5 jam. Berapakah kecepatannya jika jarak yang ditempuh mobil tersebut 00
C. y = 2x - 10 D. y = 2x + 10
 1. Diantara himpunan berikut yang merupakan himpunan kosong adalah... A. { bilangan cacah antara 19 dan 20 } B. { bilangan genap yang habis dibagi bilangan ganjil } C. { bilangan kelipatan 3 yang bukan
1. Diantara himpunan berikut yang merupakan himpunan kosong adalah... A. { bilangan cacah antara 19 dan 20 } B. { bilangan genap yang habis dibagi bilangan ganjil } C. { bilangan kelipatan 3 yang bukan
Latihan Soal Ujian Nasional Sekolah Menengah Pertama / Madrasah Tsanawiyah. SMP / MTs Mata Pelajaran : Matematika
 Latihan Soal Ujian Nasional 00 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika Dalam UN berlaku Petunjuk Umum seperti ini :. Isikan identitas Anda ke dalam Lembar Jawaban
Latihan Soal Ujian Nasional 00 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika Dalam UN berlaku Petunjuk Umum seperti ini :. Isikan identitas Anda ke dalam Lembar Jawaban
Barisan dan Deret Bilangan
 Bab 6 Barisan dan Deret Bilangan Sumber: www.scatork.com Pada bab ini, kamu akan diajak untuk memahami barisan dan deret bilangan serta penggunaannya dalam pemecahan masalah dengan cara menentukan pola
Bab 6 Barisan dan Deret Bilangan Sumber: www.scatork.com Pada bab ini, kamu akan diajak untuk memahami barisan dan deret bilangan serta penggunaannya dalam pemecahan masalah dengan cara menentukan pola
UN SMP Matematika (A) 53 (B) 57 (C) 63 (D) 67
 UN SMP Matematika Doc Name: UNSMP2008MAT999 Version : 202-0 halaman 0. Hasil dari 3.764 3. 37 (A) 3 (B) 7 (C) 63 (D) 67 02. Suhu di dalam kulkas -2 0 C. Pada saat mati lampu suhu di dalam kulkas naik 3
UN SMP Matematika Doc Name: UNSMP2008MAT999 Version : 202-0 halaman 0. Hasil dari 3.764 3. 37 (A) 3 (B) 7 (C) 63 (D) 67 02. Suhu di dalam kulkas -2 0 C. Pada saat mati lampu suhu di dalam kulkas naik 3
FISIKA TRY OUT - IV UN SMA CENDANA MANDAU T.A 2008 / Waktu :90 Menit LEMBAR SOAL UN 56 HARI LAGI.
 TRY OUT - IV UN SMA CENDANA MANDAU T.A 2008 / LEMBAR SOAL FISIKA Waktu :90 Menit Petunjuk : a Periksa dan bacalah soal-soal sebelum menjawabnya. b Jumlah soal sebanyak 30 item pilihan objektif. c Kerjakan
TRY OUT - IV UN SMA CENDANA MANDAU T.A 2008 / LEMBAR SOAL FISIKA Waktu :90 Menit Petunjuk : a Periksa dan bacalah soal-soal sebelum menjawabnya. b Jumlah soal sebanyak 30 item pilihan objektif. c Kerjakan
Copyright Hak Cipta dilindungi undang-undang
 Pembahasan Latihan Soal UN SMP/MTs Mata Pelajaran : Matematika Jumlah Soal : 0 Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari bentuk faktorisasi prima dari bilangan dalam tanda akar.
Pembahasan Latihan Soal UN SMP/MTs Mata Pelajaran : Matematika Jumlah Soal : 0 Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari bentuk faktorisasi prima dari bilangan dalam tanda akar.
SOAL UN FISIKA DAN PENYELESAIANNYA 2005
 2. 1. Seorang siswa melakukan percobaan di laboratorium, melakukan pengukuran pelat tipis dengan menggunakan jangka sorong. Dari hasil pengukuran diperoleh panjang 2,23 cm dan lebar 36 cm, maka luas pelat
2. 1. Seorang siswa melakukan percobaan di laboratorium, melakukan pengukuran pelat tipis dengan menggunakan jangka sorong. Dari hasil pengukuran diperoleh panjang 2,23 cm dan lebar 36 cm, maka luas pelat
MATEMATIKA (Paket 2) Waktu : 120 Menit
 MATEMATIKA (Paket 2) Waktu : 20 Menit (025) 77 2606 Website : Pilihlah jawaban yang paling tepat!. Hasil dari A. B. D. 8 5 8 2 2 8 2 adalah. 2. Hasil dari A. B. D. 8 adalah.. Bentuk sederhana dari A. 2
MATEMATIKA (Paket 2) Waktu : 20 Menit (025) 77 2606 Website : Pilihlah jawaban yang paling tepat!. Hasil dari A. B. D. 8 5 8 2 2 8 2 adalah. 2. Hasil dari A. B. D. 8 adalah.. Bentuk sederhana dari A. 2
SOLUSI ISIAN SINGKAT
 SOLUSI ISIAN SINGKAT NO. s.d. 5. Jawaban: 9 Misalnya bilangan pecahan itu adalah x, maka 0x,... x 0,... 9x x 9 Jadi, bilangan pecahan itu adalah 9.. Jawaban:.080 o Jarum menit dalam jam berputar 60 o.
SOLUSI ISIAN SINGKAT NO. s.d. 5. Jawaban: 9 Misalnya bilangan pecahan itu adalah x, maka 0x,... x 0,... 9x x 9 Jadi, bilangan pecahan itu adalah 9.. Jawaban:.080 o Jarum menit dalam jam berputar 60 o.
PEMERINTAH KOTA YOGYAKARTA DINAS PENDIDIKAN
 DOKUMEN NEGARA RAHASIA B TAHUN PELAJARAN 06/07 MATEMATIKA PEMERINTAH KOTA YOGYAKARTA DINAS PENDIDIKAN 07 tpm_un_smp_yk_mtk-i-b_06/07 MATA PELAJARAN Mata Pelajaran : Matematika PELAKSANAAN Hari/Tanggal
DOKUMEN NEGARA RAHASIA B TAHUN PELAJARAN 06/07 MATEMATIKA PEMERINTAH KOTA YOGYAKARTA DINAS PENDIDIKAN 07 tpm_un_smp_yk_mtk-i-b_06/07 MATA PELAJARAN Mata Pelajaran : Matematika PELAKSANAAN Hari/Tanggal
MATA PELAJARAN PELAKSANAAN PETUNJUK UMUM
 MATA PELAJARAN Mata Pelajaran : Matematika PELAKSANAAN Hari/Tanggal : Selasa, 8 November 008 Jam :.0 7.0 PETUNJUK UMUM. Isikan identitas Anda ke dalam Lembar Jawaban Ujian Nasional (LJUN) yang tersedia
MATA PELAJARAN Mata Pelajaran : Matematika PELAKSANAAN Hari/Tanggal : Selasa, 8 November 008 Jam :.0 7.0 PETUNJUK UMUM. Isikan identitas Anda ke dalam Lembar Jawaban Ujian Nasional (LJUN) yang tersedia
Suku Banyak. A. Pengertian Suku Banyak B. Menentukan Nilai Suku Banyak C. Pembagian Suku Banyak D. Teorema Sisa E. Teorema Faktor
 Bab 5 Sumber: www.in.gr Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan fungsi komposisi dalam pemecahan masalah; menggunakan konsep, sifat, dan aturan fungsi invers
Bab 5 Sumber: www.in.gr Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan fungsi komposisi dalam pemecahan masalah; menggunakan konsep, sifat, dan aturan fungsi invers
Uji Kompetensi Semester 1
 A. Pilihlah jawaban yang paling tepat! Uji Kompetensi Semester 1 1. Sebuah benda bergerak lurus sepanjang sumbu x dengan persamaan posisi r = (2t 2 + 6t + 8)i m. Kecepatan benda tersebut adalah. a. (-4t
A. Pilihlah jawaban yang paling tepat! Uji Kompetensi Semester 1 1. Sebuah benda bergerak lurus sepanjang sumbu x dengan persamaan posisi r = (2t 2 + 6t + 8)i m. Kecepatan benda tersebut adalah. a. (-4t
TRY OUT 2 TAHUN PELAJARAN 2015/2016
 1 TRY OUT TAHUN PELAJARAN 015/016 SMP/MTs MATEMATIKA Musyawarah Guru Mata Pelajaran MGMP MATEMATIKA SMP/MTs DINAS PENDIDIKAN PEMUDA DAN OLAHRAGA KABUPATEN LEMBATA Mata Pelajaran Jenjang Hari/Tanggal Jam
1 TRY OUT TAHUN PELAJARAN 015/016 SMP/MTs MATEMATIKA Musyawarah Guru Mata Pelajaran MGMP MATEMATIKA SMP/MTs DINAS PENDIDIKAN PEMUDA DAN OLAHRAGA KABUPATEN LEMBATA Mata Pelajaran Jenjang Hari/Tanggal Jam
2. Di antara bilangan-bilangan berikut, hanya ada satu yang habis membagi , yaitu. c. 1 d.
 Halaman: 1 1. Akar pangkat empat dari 4 adalah a. 4 b. 4 c. 4 d. 4 2. Di antara bilangan-bilangan berikut, hanya ada satu yang habis membagi 100 000 064, yaitu a. 10404 b. 10408 c. 10804 d. 10808 3. Banyaknya
Halaman: 1 1. Akar pangkat empat dari 4 adalah a. 4 b. 4 c. 4 d. 4 2. Di antara bilangan-bilangan berikut, hanya ada satu yang habis membagi 100 000 064, yaitu a. 10404 b. 10408 c. 10804 d. 10808 3. Banyaknya
D. 80,28 cm² E. 80,80cm²
 1. Seorang siswa melakukan percobaan di laboratorium, melakukan pengukuran pelat tipis dengan menggunakan jangka sorong. Dari hasil pengukuran diperoleh panjang 2,23 cm dan lebar 36 cm, maka luas pelat
1. Seorang siswa melakukan percobaan di laboratorium, melakukan pengukuran pelat tipis dengan menggunakan jangka sorong. Dari hasil pengukuran diperoleh panjang 2,23 cm dan lebar 36 cm, maka luas pelat
Dari gambar jaring-jaring kubus di atas bujur sangkar nomor 6 sebagai alas, yang menjadi tutup kubus adalah bujur sangkar... A. 1
 1. Diketahui : A = { m, a, d, i, u, n } dan B = { m, e, n, a, d, o } Diagram Venn dari kedua himpunan di atas adalah... D. A B = {m, n, a, d} 2. Jika P = bilangan prima yang kurang dari Q = bilangan ganjil
1. Diketahui : A = { m, a, d, i, u, n } dan B = { m, e, n, a, d, o } Diagram Venn dari kedua himpunan di atas adalah... D. A B = {m, n, a, d} 2. Jika P = bilangan prima yang kurang dari Q = bilangan ganjil
pagar kebun, ternyata masih kurang dan Pak Sulis membeli kawat lagi sebanyak 3 m.
 PREDIKSI UJIAN NASIONAL 207 [email protected] Pilihlah jawaban yang paling tepat!. Hasil dari - x (-2 + 4) : (9 5) adalah... A. -4 B. - C. D. 4 - x (-2 + 4) : (9 5) = - x (-8) : (-6) = 24 : (-6) =
PREDIKSI UJIAN NASIONAL 207 [email protected] Pilihlah jawaban yang paling tepat!. Hasil dari - x (-2 + 4) : (9 5) adalah... A. -4 B. - C. D. 4 - x (-2 + 4) : (9 5) = - x (-8) : (-6) = 24 : (-6) =
Bab. Bilangan Riil. A. Macam-Macam Bilangan B. Operasi Hitung pada. Bilangan Riil. C. Operasi Hitung pada Bilangan Pecahan D.
 Bab I Sumber: upload.wikimedia.org Bilangan Riil Anda telah mempelajari konsep bilangan bulat di Kelas VII. Pada bab ini akan dibahas konsep bilangan riil yang merupakan pengembangan dari bilangan bulat.
Bab I Sumber: upload.wikimedia.org Bilangan Riil Anda telah mempelajari konsep bilangan bulat di Kelas VII. Pada bab ini akan dibahas konsep bilangan riil yang merupakan pengembangan dari bilangan bulat.
MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo Telepon/Fax (0275)
 KODE : 02 B / TUC /206 MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo 544 Telepon/Fax (0275) 2405 UJI COBA KE UJIAN NASIONAL 206 SMP Se KABUPATEN
KODE : 02 B / TUC /206 MUSYAWARAH KERJA KEPALA SEKOLAH (MKKS) SMP KABUPATEN PURWOREJO Sekretariat: Jl. Jendral Sudirman 8 Purworejo 544 Telepon/Fax (0275) 2405 UJI COBA KE UJIAN NASIONAL 206 SMP Se KABUPATEN
Bilangan Real. Modul 1 PENDAHULUAN
 Modul 1 Bilangan Real S PENDAHULUAN Drs. Soemoenar emesta pembicaraan Kalkulus adalah himpunan bilangan real. Jadi jika akan belajar kalkulus harus paham terlebih dahulu tentang bilangan real. Bagaimanakah
Modul 1 Bilangan Real S PENDAHULUAN Drs. Soemoenar emesta pembicaraan Kalkulus adalah himpunan bilangan real. Jadi jika akan belajar kalkulus harus paham terlebih dahulu tentang bilangan real. Bagaimanakah
MATEMATIKA (Paket 5) Waktu : 120 Menit
 MATEMATIKA (Paket 5) Waktu : 0 Menit (05) 477 606 Website : Pilihlah jawaban yang paling tepat!. Hasil dari 7 + 4 : 6 ( 7) adalah.... 00 C. 56 B. 56 D. 00. Hasil dari 4 6 5 : 5 8 4 B. 8 adalah.... C. 4
MATEMATIKA (Paket 5) Waktu : 0 Menit (05) 477 606 Website : Pilihlah jawaban yang paling tepat!. Hasil dari 7 + 4 : 6 ( 7) adalah.... 00 C. 56 B. 56 D. 00. Hasil dari 4 6 5 : 5 8 4 B. 8 adalah.... C. 4
PENDALAMAN MATERI MATEMATIKA S D. 3. Diketahui : a = 112, b = 175, c = 138 dan d = 225. Tentukan nilai ab+bc+ad+cd
 PRESTASI O S N IMO PENALAMAN MATERI MATEMATIKA S. Gambarlah urutan berikutnya. 5 x 4 : 6 + 8 x 35 : 4 + 63 : 9 x 40 =... 3. iketahui : a =, b = 75, c = 38 dan d = 5. Tentukan nilai ab+bc+ad+cd 4. Jika
PRESTASI O S N IMO PENALAMAN MATERI MATEMATIKA S. Gambarlah urutan berikutnya. 5 x 4 : 6 + 8 x 35 : 4 + 63 : 9 x 40 =... 3. iketahui : a =, b = 75, c = 38 dan d = 5. Tentukan nilai ab+bc+ad+cd 4. Jika
B. 26 September 1996 D. 28 September 1996
 1. Ditentukan A = {2, 3, 5, 7, 8, 11} Himpunan semesta yang mungkin adalah... A.{bilangan ganjil yang kurang dari 12} B.{bilangan asli yang kurang dari 12} C.{bilangan prima yang kurang dari 12} D.{bilangan
1. Ditentukan A = {2, 3, 5, 7, 8, 11} Himpunan semesta yang mungkin adalah... A.{bilangan ganjil yang kurang dari 12} B.{bilangan asli yang kurang dari 12} C.{bilangan prima yang kurang dari 12} D.{bilangan
LATIHAN ULANGAN AKHIR SEMESTER GANJIL SMP NEGERI 196 JAKARTA TAHUN PELAJARAN 2010/2011 LEMBAR SOAL
 LATIHAN ULANGAN AKHIR SEMESTER GANJIL SMP NEGERI JAKARTA TAHUN PELAJARAN 00/0 LEMBAR SOAL Mata Pelajaran : MATEMATIKA Hari / Tanggal : 0 November 00 W a k t u : 07.00 0.00 WIB (0 menit) K e l a s : IX
LATIHAN ULANGAN AKHIR SEMESTER GANJIL SMP NEGERI JAKARTA TAHUN PELAJARAN 00/0 LEMBAR SOAL Mata Pelajaran : MATEMATIKA Hari / Tanggal : 0 November 00 W a k t u : 07.00 0.00 WIB (0 menit) K e l a s : IX
NO SOAL PEMBAHASAN 1
 PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : C7 NO SOAL PEMBAHASAN Hasil dari 5 + ( : ) adalah... Urutan pengerjaan operasi hitung A. 9 Operasi hitung Urutan pengerjaan B. Dalam kurung C. 9 Pangkat ; Akar D.
PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : C7 NO SOAL PEMBAHASAN Hasil dari 5 + ( : ) adalah... Urutan pengerjaan operasi hitung A. 9 Operasi hitung Urutan pengerjaan B. Dalam kurung C. 9 Pangkat ; Akar D.
A. UNSUR - UNSUR ALJABAR
 PENGERTIAN ALJABAR Bentuk ALJABAR adalah suatu bentuk matematika yang dalam penyajiannya memuat hurufhuruf untuk mewakili bilangan yang belum diketahui. Bentuk aljabar dapat dimanfaatkan untuk menyelesaikan
PENGERTIAN ALJABAR Bentuk ALJABAR adalah suatu bentuk matematika yang dalam penyajiannya memuat hurufhuruf untuk mewakili bilangan yang belum diketahui. Bentuk aljabar dapat dimanfaatkan untuk menyelesaikan
UJIAN NASIONAL SMP/MTs TAHUN PELAJARAN 2004/2005
 UJIAN NASIONAL SMP/MTs TAHUN PELAJARAN 004/005 Mata Pelajaran : MATEMATIKA Hari/Tanggal : RABU, 8 JUNI 005 Waktu : 0 MENIT PETUNJUK UMUM. Periksa dan bacalah soal-soal sebelum kamu menjawab. Tulis nomor
UJIAN NASIONAL SMP/MTs TAHUN PELAJARAN 004/005 Mata Pelajaran : MATEMATIKA Hari/Tanggal : RABU, 8 JUNI 005 Waktu : 0 MENIT PETUNJUK UMUM. Periksa dan bacalah soal-soal sebelum kamu menjawab. Tulis nomor
MATEMATIKA EBTANAS TAHUN 1992
 MATEMATIKA EBTANAS TAHUN 99 EBT-SMP-9-0 Diketahui: A = {m, a, d, i, u, n} dan B = {m, a, n, a, d, o} Diagram Venn dari kedua himpunan di atas A. m a d o a m o i e e I d u a a u n e m i d o m i d a u n
MATEMATIKA EBTANAS TAHUN 99 EBT-SMP-9-0 Diketahui: A = {m, a, d, i, u, n} dan B = {m, a, n, a, d, o} Diagram Venn dari kedua himpunan di atas A. m a d o a m o i e e I d u a a u n e m i d o m i d a u n
SMP / MTs Mata Pelajaran : Matematika
 Kunci Jawaban Latihan Soal Ujian Nasional 010 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika 1. Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari
Kunci Jawaban Latihan Soal Ujian Nasional 010 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika 1. Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari
MATEMATIKA EBTANAS TAHUN 1993
 MATEMATIKA EBTANAS TAHUN 99 EBT-SMP-9-0 Ditentukan A = {v, o, k, a, l} ; B = {a, i, u, e, o} Diagram yang menyatakan hal tersebut di atas A. B. v o u v o i a k u k l I l a e v o u v o u a k a k l e l i
MATEMATIKA EBTANAS TAHUN 99 EBT-SMP-9-0 Ditentukan A = {v, o, k, a, l} ; B = {a, i, u, e, o} Diagram yang menyatakan hal tersebut di atas A. B. v o u v o i a k u k l I l a e v o u v o u a k a k l e l i
PEMBAHASAN SOAL-SOAL UN TAHUN 2012 KODE : A13 NO SOAL PEMBAHASAN 1
 PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : A SMP N Kalibagor Hasil dari 5 + [6 : ( )] adalah... Urutan pengerjaan operasi hitung A. 7 Operasi hitung Urutan pengerjaan B. 4 Dalam kurung C. Pangkat ; Akar D.
PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : A SMP N Kalibagor Hasil dari 5 + [6 : ( )] adalah... Urutan pengerjaan operasi hitung A. 7 Operasi hitung Urutan pengerjaan B. 4 Dalam kurung C. Pangkat ; Akar D.
LATIHAN SOAL VOLUME BALOK DAN KUBUS. setinggi 35 cm. Berapa liter air yang ada di dalam akuarium?
 LATIHAN SOAL VOLUME BALOK DAN KUBUS 1. Sebuah bak mempunyai ukuran panjang 60 cm, lebar 40 cm dan tinggi 30 cm. a. Berapa volume air untuk mengisi bak mandi agar penuh? b. Jika sebagian telah digunakan,
LATIHAN SOAL VOLUME BALOK DAN KUBUS 1. Sebuah bak mempunyai ukuran panjang 60 cm, lebar 40 cm dan tinggi 30 cm. a. Berapa volume air untuk mengisi bak mandi agar penuh? b. Jika sebagian telah digunakan,
DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP TRYOUT UN menit
 DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP P.18 TRYOUT UN 2013 Mata Pelajaran Matematika Hari/Tanggal Waktu 120 menit 1. Hasil dari 5 + [(-2) 4] adalah... a. -13 b. -3 c. 3 d. 13 2. Hasil
DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP P.18 TRYOUT UN 2013 Mata Pelajaran Matematika Hari/Tanggal Waktu 120 menit 1. Hasil dari 5 + [(-2) 4] adalah... a. -13 b. -3 c. 3 d. 13 2. Hasil
1 m, maka jumlah anak yatim yang menerima. menerima Bilangan 3 jika dinyatakan dalam bentuk akar menjadi... A. 9 3 C. 5 2 B. 6 3 D.
 PREDIKSI UCUN THP I Sukses Ujian Nasional 204 No. Kisi-Kisi Jabaran Soal Prediksi Soal Menentukan hasil operasi hitung campuran bilangan bulat 2 Menyelesaikan soal cerita yang berkaitan dengan pembagian
PREDIKSI UCUN THP I Sukses Ujian Nasional 204 No. Kisi-Kisi Jabaran Soal Prediksi Soal Menentukan hasil operasi hitung campuran bilangan bulat 2 Menyelesaikan soal cerita yang berkaitan dengan pembagian
Melakukan Operasi Hitung Bilangan Bulat dalam Pemecahan Masalah
 Bab 1 Melakukan Operasi Hitung Bilangan Bulat dalam Pemecahan Masalah Tujuan Pembelajaran Setelah mempelajari bab ini, diharapkan siswa dapat: 1. menguasai sifat-sifat operasi hitung bilangan bulat,. menjumlahkan
Bab 1 Melakukan Operasi Hitung Bilangan Bulat dalam Pemecahan Masalah Tujuan Pembelajaran Setelah mempelajari bab ini, diharapkan siswa dapat: 1. menguasai sifat-sifat operasi hitung bilangan bulat,. menjumlahkan
1. BARISAN ARITMATIKA
 MATEMATIKA DASAR ARITMATIKA BARISAN ARITMATIKA 1. BARISAN ARITMATIKA Sering disebut barisan hitung, adalah barisan bilangan yang setiap sukunya diperoleh dari suku sebelumnya dengan menambah atau mengurangi
MATEMATIKA DASAR ARITMATIKA BARISAN ARITMATIKA 1. BARISAN ARITMATIKA Sering disebut barisan hitung, adalah barisan bilangan yang setiap sukunya diperoleh dari suku sebelumnya dengan menambah atau mengurangi
abcde dengan a, c, e adalah bilangan genap dan b, d adalah bilangan ganjil? A B C D E. 3000
 Hal. 1 / 7 METHODIST-2 EDUCATION EXPO LOMBA SAINS PLUS ANTAR PELAJAR TINGKAT SMA SE-SUMATERA UTARA TAHUN 2015 BIDANG WAKTU : MATEMATIKA : 120 MENIT PETUNJUK : 1. Pilihlah jawaban yang benar dan tepat.
Hal. 1 / 7 METHODIST-2 EDUCATION EXPO LOMBA SAINS PLUS ANTAR PELAJAR TINGKAT SMA SE-SUMATERA UTARA TAHUN 2015 BIDANG WAKTU : MATEMATIKA : 120 MENIT PETUNJUK : 1. Pilihlah jawaban yang benar dan tepat.
Turunan Fungsi dan Aplikasinya
 Bab 8 Sumber: www.duniacyber.com Turunan Fungsi dan Aplikasinya Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan dalam perhitungan turunan fungsi; menggunakan turunan
Bab 8 Sumber: www.duniacyber.com Turunan Fungsi dan Aplikasinya Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan dalam perhitungan turunan fungsi; menggunakan turunan
A. LATIHAN SOAL UNTUK KELAS 9A
 A. LATIHAN SOAL UNTUK KELAS 9A. Hasil dari 5 ( 6) + 24 : 2 ( 3) =... A. -5 B. -6. 0 D. 6 2. Hasil dari 2 : 75% + 8,75 =... A. 4 B. 5. 6 D. 7 3. Uang Irna sama dengan 2 3 uang Tuti. Jika jumlah uang mereka
A. LATIHAN SOAL UNTUK KELAS 9A. Hasil dari 5 ( 6) + 24 : 2 ( 3) =... A. -5 B. -6. 0 D. 6 2. Hasil dari 2 : 75% + 8,75 =... A. 4 B. 5. 6 D. 7 3. Uang Irna sama dengan 2 3 uang Tuti. Jika jumlah uang mereka
Perbandingan paling sederhana 750 cm terhadap 2,25 km adalah...
 PREDIKSI UJIAN NASIONAL 08. Hasil dari Hasil dari 5 5. Perbandingan paling sederhana 750 cm terhadap,5 km 0 0 : 0 :.000 : 00 : 0.000. Perbandingan uang Ali dan Tuti adalah : sedangkan perbandingan Tuti
PREDIKSI UJIAN NASIONAL 08. Hasil dari Hasil dari 5 5. Perbandingan paling sederhana 750 cm terhadap,5 km 0 0 : 0 :.000 : 00 : 0.000. Perbandingan uang Ali dan Tuti adalah : sedangkan perbandingan Tuti
Ringkasan Materi Soal-soal dan Pembahasan MATEMATIKA. SD Kelas 4, 5, 6
 Ringkasan Materi Soal-soal dan Pembahasan MATEMATIKA SD Kelas 4, 5, 6 1 Matematika A. Operasi Hitung Bilangan... 3 B. Bilangan Ribuan... 5 C. Perkalian dan Pembagian Bilangan... 6 D. Kelipatan dan Faktor
Ringkasan Materi Soal-soal dan Pembahasan MATEMATIKA SD Kelas 4, 5, 6 1 Matematika A. Operasi Hitung Bilangan... 3 B. Bilangan Ribuan... 5 C. Perkalian dan Pembagian Bilangan... 6 D. Kelipatan dan Faktor
Perhatikan skema sistem bilangan berikut. Bilangan. Bilangan Rasional. Bilangan pecahan adalah bilangan yang berbentuk a b
 2 SISTEM BILANGAN Perhatikan skema sistem bilangan berikut Bilangan Bilangan Kompleks Bilangan Real Bilangan Rasional Bilangan Irasional Bilangan Bulat Bilangan Pecahan Bilangan bulat adalah bilangan yang
2 SISTEM BILANGAN Perhatikan skema sistem bilangan berikut Bilangan Bilangan Kompleks Bilangan Real Bilangan Rasional Bilangan Irasional Bilangan Bulat Bilangan Pecahan Bilangan bulat adalah bilangan yang
PEMBAHASAN SOAL-SOAL UN TAHUN 2012 KODE : A13 NO SOAL PEMBAHASAN 1
 Pembahasan UN 0 A3 by Alfa Kristanti PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : A3 Hasil dari 5 + [6 : ( 3)] adalah... Urutan pengerjaan operasi hitung A. 7 Operasi hitung Urutan pengerjaan B. 4 Dalam kurung
Pembahasan UN 0 A3 by Alfa Kristanti PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : A3 Hasil dari 5 + [6 : ( 3)] adalah... Urutan pengerjaan operasi hitung A. 7 Operasi hitung Urutan pengerjaan B. 4 Dalam kurung
SOAL MATEMATIKA - SMP
 SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 01 BAGIAN
SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 01 BAGIAN
PEMANTAPAN UJIAN NASIONAL Kerjakan dengan sungguh-sungguh dengan kejujuran hati!
 PEMANTAPAN UJIAN NASIONAL 2013 Kerjakan dengan sungguh-sungguh dengan kejujuran hati! 1. Hasil dari (-5 7) : 4 x (-5) + 8 adalah. A. -26 B. -23 C. 23 D. 26 (-5 7) : 4 x (-5) + 8 = -12 : 4 x (-5) + 8 =
PEMANTAPAN UJIAN NASIONAL 2013 Kerjakan dengan sungguh-sungguh dengan kejujuran hati! 1. Hasil dari (-5 7) : 4 x (-5) + 8 adalah. A. -26 B. -23 C. 23 D. 26 (-5 7) : 4 x (-5) + 8 = -12 : 4 x (-5) + 8 =
SOAL PREDIKSI MATEMATIKA TAHUN
 SOAL PREDIKSI MATEMATIKA TAHUN 2014 PAKET 1. Hasil dari 5 2 7-21 4 : 31 2 adalah... A. 3 3 14 B. 3 9 14 C. 4 3 14 D. 4 9 14 2. Dalam kompetisi matematika, setiap jawaban benar diberi skor 3, jawaban salah
SOAL PREDIKSI MATEMATIKA TAHUN 2014 PAKET 1. Hasil dari 5 2 7-21 4 : 31 2 adalah... A. 3 3 14 B. 3 9 14 C. 4 3 14 D. 4 9 14 2. Dalam kompetisi matematika, setiap jawaban benar diberi skor 3, jawaban salah
(a) 32 (b) 36 (c) 40 (d) 44
 Halaman:. Jika n = 8, maka n0 n bernilai... (a) kurang dari 00 (b) (d) lebih dari 00. Penumpang suatu pesawat terdiri dari anak-anak dari berbagai negara, 6 orang dari Indonesia yang termasuk dari anak-anak
Halaman:. Jika n = 8, maka n0 n bernilai... (a) kurang dari 00 (b) (d) lebih dari 00. Penumpang suatu pesawat terdiri dari anak-anak dari berbagai negara, 6 orang dari Indonesia yang termasuk dari anak-anak
PEMBAHASAN SOAL-SOAL UN TAHUN 2012 KODE : C37 NO SOAL PEMBAHASAN 1
 PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : C7 SMP N Kalibagor NO SOAL PEMBAHASAN Hasil dari 5 + ( : ) adalah... Urutan pengerjaan operasi hitung A. 9 Operasi hitung Urutan pengerjaan B. Dalam kurung C. 9 Pangkat
PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : C7 SMP N Kalibagor NO SOAL PEMBAHASAN Hasil dari 5 + ( : ) adalah... Urutan pengerjaan operasi hitung A. 9 Operasi hitung Urutan pengerjaan B. Dalam kurung C. 9 Pangkat
PEMBAHASAN SOAL-SOAL UN TAHUN 2012 KODE : C32 NO SOAL PEMBAHASAN. Ingat!
 Pembahasan UN 0 C by Alfa Kristanti PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : C NO SOAL PEMBAHASAN Hasil dari 6 adalah... A. 48. a = a a a B. 7. = C. 08. = D. 6 6 = 6 = 6 = 6 = 6 Hasil dari 8 adalah... A.
Pembahasan UN 0 C by Alfa Kristanti PEMBAHASAN SOAL-SOAL UN TAHUN 0 KODE : C NO SOAL PEMBAHASAN Hasil dari 6 adalah... A. 48. a = a a a B. 7. = C. 08. = D. 6 6 = 6 = 6 = 6 = 6 Hasil dari 8 adalah... A.
Bab 1. Bilangan Bulat
 Bilangan Bulat Bab 1 Sebuah kotak kue berbentuk kubus. Jika volumenya 729 cm, berapa sentimeter panjang rusuk kotak kue tersebut? Agar kamu dapat menjawabnya, kamu harus mengetahui nilai akar pangkat tiga
Bilangan Bulat Bab 1 Sebuah kotak kue berbentuk kubus. Jika volumenya 729 cm, berapa sentimeter panjang rusuk kotak kue tersebut? Agar kamu dapat menjawabnya, kamu harus mengetahui nilai akar pangkat tiga
DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP TRYOUT UN menit
 DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP P.04 TRYOUT UN 01 Mata Pelajaran Matematika Hari/Tanggal Waktu 10 menit 1. Hasil dari -15 + (-1 : ) adalah... a -19 b -11 c -9 d 9. Hasil dari
DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP P.04 TRYOUT UN 01 Mata Pelajaran Matematika Hari/Tanggal Waktu 10 menit 1. Hasil dari -15 + (-1 : ) adalah... a -19 b -11 c -9 d 9. Hasil dari
GMBB. SMA.GEC.Novsupriyanto93.wordpress.com Page 1
 1. Sebuah benda bermassa 1 kg berputar dengan kecepatan sudut 120 rpm. Jika jari-jari putaran benda adalah 2 meter percepatan sentripetal gerak benda tersebut adalah a. 32π 2 m/s 2 b. 42 π 2 m/s 2 c. 52π
1. Sebuah benda bermassa 1 kg berputar dengan kecepatan sudut 120 rpm. Jika jari-jari putaran benda adalah 2 meter percepatan sentripetal gerak benda tersebut adalah a. 32π 2 m/s 2 b. 42 π 2 m/s 2 c. 52π
SOAL MATEMATIKA - SMP
 SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 2005
SOAL MATEMATIKA - SMP OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA KEMENTERIAN PENDIDIKAN DAN KEBUDAYAAN DIREKTORAT JENDERAL PENDIDIKAN DASAR DIREKTORAT PEMBINAAN SEKOLAH MENENGAH PERTAMA TAHUN 2005
semua ada tentang sekolah dasar
 CONTOH SOAL DAN KISI-KISI UJIAN NASIONAL SD/MI TAHUN 2012/2013 MATA PELAJARAN MATEMATIKA No Kompetensi Indikator Soal Jawaban 1 Memahami konsep dan operasi hitung bilangan bulat serta dapat menggunakannya
CONTOH SOAL DAN KISI-KISI UJIAN NASIONAL SD/MI TAHUN 2012/2013 MATA PELAJARAN MATEMATIKA No Kompetensi Indikator Soal Jawaban 1 Memahami konsep dan operasi hitung bilangan bulat serta dapat menggunakannya
SELEKSI OLIMPIADE MATEMATIKA INDONESIA 2004 TINGKAT PROVINSI
 SELEKSI OLIMPIADE MATEMATIKA INDONESIA 2004 TINGKAT PROVINSI Bidang Matematika Bagian Pertama Waktu : 90 Menit DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT
SELEKSI OLIMPIADE MATEMATIKA INDONESIA 2004 TINGKAT PROVINSI Bidang Matematika Bagian Pertama Waktu : 90 Menit DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT
SOAL DAN PEMBAHASAN UJIAN NASIONAL MATEMATIKA SMP/MTs TAHUN PELAJARAN 2015/2016-TANGGAL 10 Mei 2016
 SOAL DAN PEMBAHASAN UJIAN NASIONAL MATEMATIKA SMP/MTs TAHUN PELAJARAN 0/06-TANGGAL 0 Mei 06. Tanda berarti kalikan bilangan kedua dengan, kemudian jumlahkan hasilnya dengan dua kali bilangan pertama. Hasil
SOAL DAN PEMBAHASAN UJIAN NASIONAL MATEMATIKA SMP/MTs TAHUN PELAJARAN 0/06-TANGGAL 0 Mei 06. Tanda berarti kalikan bilangan kedua dengan, kemudian jumlahkan hasilnya dengan dua kali bilangan pertama. Hasil
SOAL UN FISIKA DAN PENYELESAIANNYA 2007
 1. Suatu segi empat setelah diukur dengan menggunakan alat yang berbeda panjang 0,42 cm, lebar 0,5 cm. Maka luas segi empat tersebut dengan penulisan angka penting 2. adalah... A. 0,41 B. 0,21 C. 0,20
1. Suatu segi empat setelah diukur dengan menggunakan alat yang berbeda panjang 0,42 cm, lebar 0,5 cm. Maka luas segi empat tersebut dengan penulisan angka penting 2. adalah... A. 0,41 B. 0,21 C. 0,20
SEKOLAH TINGGI ILMU STATISTIK BADAN PUSAT STATISTIK SOAL UJIAN MASUK PROGRAM D-IV TAHUN AKADEMIK 2011/2012 MINGGU, 5 JUNI 2011 MATEMATIKA 90 MENIT
 SEKOLAH TINGGI ILMU STATISTIK BADAN PUSAT STATISTIK SOAL UJIAN MASUK PROGRAM D-IV TAHUN AKADEMIK 2011/2012 MINGGU, 5 JUNI 2011 MATEMATIKA 90 MENIT Petunjuk Di bawah setiap soal dicantumkan 5 kemungkinan
SEKOLAH TINGGI ILMU STATISTIK BADAN PUSAT STATISTIK SOAL UJIAN MASUK PROGRAM D-IV TAHUN AKADEMIK 2011/2012 MINGGU, 5 JUNI 2011 MATEMATIKA 90 MENIT Petunjuk Di bawah setiap soal dicantumkan 5 kemungkinan
SELEKSI OLIMPIADE TINGKAT PROVINSI 2009 TIM OLIMPIADE MATEMATIKA INDONESIA 2010
 Dapatkan soal-soal lainnya di http://forum.pelatihan-osn.com SELEKSI OLIMPIADE TINGKAT PROVINSI 2009 TIM OLIMPIADE MATEMATIKA INDONESIA 2010 Waktu : 210 Menit DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT
Dapatkan soal-soal lainnya di http://forum.pelatihan-osn.com SELEKSI OLIMPIADE TINGKAT PROVINSI 2009 TIM OLIMPIADE MATEMATIKA INDONESIA 2010 Waktu : 210 Menit DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT
PEMANTAPAN UJIAN NASIONAL Kerjakan dengan sungguh-sungguh dengan kejujuran hati!
 PEMANTAPAN UJIAN NASIONAL 203 Kerjakan dengan sungguh-sungguh dengan kejujuran hati!. Hasil dari (-5 7) : 4 x (-5) + 8 adalah. A. -26 B. -23 C. 23 D. 26 2. Perbandingan banyak kelereng Taris dan Fauzan
PEMANTAPAN UJIAN NASIONAL 203 Kerjakan dengan sungguh-sungguh dengan kejujuran hati!. Hasil dari (-5 7) : 4 x (-5) + 8 adalah. A. -26 B. -23 C. 23 D. 26 2. Perbandingan banyak kelereng Taris dan Fauzan
P 54 TRY OUT 4 UJIAN NASIONAL TAHUN PELAJARAN 2011/2012 MATEMATIKA (E-3) SMK KELOMPOK KEAHLIAN TEKNOLOGI, KESEHATAN DAN PERTANIAN UTAMA
 TRY OUT 4 UJIAN NASIONAL TAHUN PELAJARAN 2011/2012 MATEMATIKA (E-3) SMK KELOMPOK KEAHLIAN TEKNOLOGI, KESEHATAN DAN PERTANIAN P 54 UTAMA SMK NEGERI 2 MAGELANG PROVINSI JAWA TENGAH TAHUN 2012 Mata Pelajaran
TRY OUT 4 UJIAN NASIONAL TAHUN PELAJARAN 2011/2012 MATEMATIKA (E-3) SMK KELOMPOK KEAHLIAN TEKNOLOGI, KESEHATAN DAN PERTANIAN P 54 UTAMA SMK NEGERI 2 MAGELANG PROVINSI JAWA TENGAH TAHUN 2012 Mata Pelajaran
Soal-soal dan Pembahasan UASBN Matematika SD/MI Tahun Pelajaran 2009/2010
 Soal-soal dan Pembahasan UASBN Matematika SD/MI Tahun Pelajaran 2009/2010 1. Hasil dari 576 + 712 376 =... A. 348 B. 912 C. 1.288 D. 1.652 BAB I Bilangan Penjumlahan dan pengurangan derajatnya sama, pengerjaannya
Soal-soal dan Pembahasan UASBN Matematika SD/MI Tahun Pelajaran 2009/2010 1. Hasil dari 576 + 712 376 =... A. 348 B. 912 C. 1.288 D. 1.652 BAB I Bilangan Penjumlahan dan pengurangan derajatnya sama, pengerjaannya
DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP TRYOUT UN menit
 DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP P.06 TRYOUT UN 2013 Mata Pelajaran Matematika Hari/Tanggal Waktu 120 menit 1. Hasil dari 5 + [6 : (-3)] adalah... a 7 b 4 c 3 d -2 2. Hasil
DINAS PENDIDIKAN KABUPATEN MALANG MGMP MATEMATIKA SMPN SATAP P.06 TRYOUT UN 2013 Mata Pelajaran Matematika Hari/Tanggal Waktu 120 menit 1. Hasil dari 5 + [6 : (-3)] adalah... a 7 b 4 c 3 d -2 2. Hasil
TEOREMA PYTHAGORAS. Kata-Kata Kunci: teorema Pythagoras tripel Pythagoras segitiga siku-siku istimewa. Sumber: Indonesian Heritage, 2002
 5 TEOREM PYTHGORS Sumber: Indonesian Heritage, 00 Pernahkah kalian memerhatikan para tukang kayu atau tukang bangunan? Dalam bekerja, mereka banyak memanfaatkan teorema Pythagoras. oba perhatikan kerangka
5 TEOREM PYTHGORS Sumber: Indonesian Heritage, 00 Pernahkah kalian memerhatikan para tukang kayu atau tukang bangunan? Dalam bekerja, mereka banyak memanfaatkan teorema Pythagoras. oba perhatikan kerangka
1. Sebuah mobil memiliki kecepatan awal sebesar 6 m/s. Setelah 1 menit, kecepatan mobil tersebut menjadi 9 m/s. Berapakah percepatan mobil tersebut?
 1. Sebuah mobil memiliki kecepatan awal sebesar 6 m/s. Setelah 1 menit, kecepatan mobil tersebut menjadi 9 m/s. Berapakah percepatan mobil tersebut? a. 0,4 m/s 2 c. 3 m/s 2 b. 0,05 m/s 2 d. 15 m/s 2 2.
1. Sebuah mobil memiliki kecepatan awal sebesar 6 m/s. Setelah 1 menit, kecepatan mobil tersebut menjadi 9 m/s. Berapakah percepatan mobil tersebut? a. 0,4 m/s 2 c. 3 m/s 2 b. 0,05 m/s 2 d. 15 m/s 2 2.
A. MENGHITUNG LUAS BERBAGAI BANGUN DATAR
 A. MENGHITUNG LUAS BERBAGAI BANGUN DATAR Dalam bab ini kamu akan mempelajari: 1. menghitung luas bangun datar; 2. menghitung luas segi banyak; 3. menghitung luas gabungan dua bangun datar; dan 4. menghitung
A. MENGHITUNG LUAS BERBAGAI BANGUN DATAR Dalam bab ini kamu akan mempelajari: 1. menghitung luas bangun datar; 2. menghitung luas segi banyak; 3. menghitung luas gabungan dua bangun datar; dan 4. menghitung
KUMPULAN SOAL MATEMATIKA KELAS VIII (BSE DEWI N)
 KUMPULAN SOAL MATEMATIKA KELAS VIII (BSE DEWI N) Kumpulan Soal Matematika Kelas VIII (BSE Dewi N) Faktorisasi Suku Aljabar A. Pilihlah salah satu jawaban yang tepat. 1. Pada bentuk aljabar 2x2 + 3xy y2
KUMPULAN SOAL MATEMATIKA KELAS VIII (BSE DEWI N) Kumpulan Soal Matematika Kelas VIII (BSE Dewi N) Faktorisasi Suku Aljabar A. Pilihlah salah satu jawaban yang tepat. 1. Pada bentuk aljabar 2x2 + 3xy y2
Menghitung Volume Kubus dan Balok dan Menggunakannya dalam Pemecahan Masalah
 Bab 4 Menghitung Volume Kubus dan Balok dan Menggunakannya dalam Pemecahan Masalah Tujuan Pembelajaran Setelah mempelajari bab ini, diharapkan siswa dapat:. mengenal satuan volume; 2. mengubah satuan volume
Bab 4 Menghitung Volume Kubus dan Balok dan Menggunakannya dalam Pemecahan Masalah Tujuan Pembelajaran Setelah mempelajari bab ini, diharapkan siswa dapat:. mengenal satuan volume; 2. mengubah satuan volume
PREDIKSI UAS 1 FISIKA KELAS X TAHUN 2013/ Besaran-besaran berikut yang merupakan besaran pokok adalah a. Panjang, lebar,luas,volume
 PREDIKSI UAS 1 FISIKA KELAS X TAHUN 2013/2014 A. PILIHAN GANDA 1. Besaran-besaran berikut yang merupakan besaran pokok adalah a. Panjang, lebar,luas,volume d. Panjang, lebar, tinggi, tebal b. Kecepatan,waktu,jarak,energi
PREDIKSI UAS 1 FISIKA KELAS X TAHUN 2013/2014 A. PILIHAN GANDA 1. Besaran-besaran berikut yang merupakan besaran pokok adalah a. Panjang, lebar,luas,volume d. Panjang, lebar, tinggi, tebal b. Kecepatan,waktu,jarak,energi
PREDIKSI SOAL MATEMATIKA TAHUN
 PREDIKSI SOAL MATEMATIKA TAHUN 2014 PAKET 1. Hasil dari 4 2 3 21 4 : 11 2 A. B. C. D. 19 6 29 8 37 8 37 6 adalah... 2. Dalam kompetisi fisika, setiap jawaban benar diberi skor 2, jawaban salah diberi skor
PREDIKSI SOAL MATEMATIKA TAHUN 2014 PAKET 1. Hasil dari 4 2 3 21 4 : 11 2 A. B. C. D. 19 6 29 8 37 8 37 6 adalah... 2. Dalam kompetisi fisika, setiap jawaban benar diberi skor 2, jawaban salah diberi skor
MATEMATIKA. *Untuk Kalangan Sendiri
 MATEMATIKA *Untuk Kalangan Sendiri 1 PENJUMLAHAN 1 1 5 4 6 + 3 8 7 3 = 0 5 8 6 Caranya: 3 8 7 3 + 1. Disusun lurus dari satuan 4 4 5 9 2. Urutan yang kosong diberi angka 0 3. Ditambahkan dari satuan (
MATEMATIKA *Untuk Kalangan Sendiri 1 PENJUMLAHAN 1 1 5 4 6 + 3 8 7 3 = 0 5 8 6 Caranya: 3 8 7 3 + 1. Disusun lurus dari satuan 4 4 5 9 2. Urutan yang kosong diberi angka 0 3. Ditambahkan dari satuan (
Bahan Ajar untuk Guru Kelas 5 Rasio dan Proporsi
 Bahan Ajar untuk Guru Kelas 5 Rasio dan Proporsi Bilangan-bilangan rasional dat diinterpretasikan sebagai sebuah rasio. Sebagai contoh, rasio jumlah pria dan jumlah wanita adalah 1 dan 2, maksudnya bahwa
Bahan Ajar untuk Guru Kelas 5 Rasio dan Proporsi Bilangan-bilangan rasional dat diinterpretasikan sebagai sebuah rasio. Sebagai contoh, rasio jumlah pria dan jumlah wanita adalah 1 dan 2, maksudnya bahwa
KUMPULAN SOAL MATEMATIKA SMP KELAS 8
 KUMPULAN SOAL MATEMATIKA SMP KELAS 8 Dirangkum oleh Moch. Fatkoer Rohman Website: http://fatkoer.co.cc http://zonamatematika.co,cc Email: [email protected] 009 Evaluasi Bab 1 Untuk nomor 1 sampai 5 pilihlah
KUMPULAN SOAL MATEMATIKA SMP KELAS 8 Dirangkum oleh Moch. Fatkoer Rohman Website: http://fatkoer.co.cc http://zonamatematika.co,cc Email: [email protected] 009 Evaluasi Bab 1 Untuk nomor 1 sampai 5 pilihlah
PAKET 2 CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs
 PAKET CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs 1. * Kemampuan yang diuji. Menghitung hasil operasi tambah, kurang, kali dan bagi pada bilangan bulat Menentukan hasil operasi campuran bilangan bulat.
PAKET CONTOH SOAL DAN PEMBAHASAN MATEMATIKA SMP/MTs 1. * Kemampuan yang diuji. Menghitung hasil operasi tambah, kurang, kali dan bagi pada bilangan bulat Menentukan hasil operasi campuran bilangan bulat.
