Transformasi Obyek (Kasus 2D)
|
|
|
- Iwan Setiabudi
- 9 tahun lalu
- Tontonan:
Transkripsi
1 Transformasi Obek (Kasus 2D) Grafika Komputer Semester Ganjil 28 Teknik Informatika ITS Ann Yuniarti - 28
2 Kompetensi. Mampu membangun tool untuk mentransformasi obek 2. Mampu memahami konsep transformasi affine ang merupakan kombinasi dari rotasi, penskalaan, dan translasi 3. Mampu mengimplementasikan konsep transformasi dalam sebuah program OpenGL Teknik Informatika ITS Ann Yuniarti
3 Referensi Computer Graphics using OpenGL, 3rd Edition, b: F.S. Hill, Jr. and Stephen M. Kelle Chapter 5 Computer Graphics with OpenGL, 3rd Edition, b: Donald Hearn and M.Pauline Baker Chapter 5 Teknik Informatika ITS Ann Yuniarti
4 Pokok Bahasan. Transformasi 2D Dasar. Translasi 2. Rotasi 3. Penskalaan 2. Kombinasi Transformasi 3. Transformasi Affine Teknik Informatika ITS Ann Yuniarti
5 Kegunaan Transformasi Me-reposisi ataupun me-resize obek Pada proses viewing, untuk mengubah worldcoordinate menjadi displa untuk suatu output device Untuk aplikasi-aplikasi tertentu: CAD mengatur orientasi dan ukuran suatu komponen pada suatu rancangan Animasi menggerakkan letak kamera atau obek pada sebuah laar sesuai path tertentu Teknik Informatika ITS Ann Yuniarti
6 Jenis-jenis Transformasi Transformasi Geometri Diterapkan pada deskripsi geometri suatu obek Gunana untuk mengubah posisi, orientasi, atau ukuran suatu obek Transformasi modeling Digunakan untuk membentuk sebuah laar atau membuat deskripsi hierarki suatu obek kompleks ang terdiri dari beberapa bagian Contoh: pesawat terdiri dari saap, ekor, mesin, dan lain-lain, dimana masing-masing dapat dispesifikasikan dalam komponen-komponen level ke-2 dan seterusna. Transformasi modeling mendeskripsikan bagaimana setiap komponen disusun untuk rancangan keseluruhan Teknik Informatika ITS Ann Yuniarti
7 2D Modeling Transformations Modeling Coordinates Scale Translate Scale Rotate Translate World Coordinates Teknik Informatika ITS Ann Yuniarti
8 2D Modeling Transformations Modeling Coordinates Let s look at this in detail World Coordinates Teknik Informatika ITS Ann Yuniarti
9 2D Modeling Transformations Modeling Coordinates Initial location at (, ) with - and -aes aligned Teknik Informatika ITS Ann Yuniarti
10 2D Modeling Transformations Modeling Coordinates Scale.3,.3 Rotate -9 Translate 5, 3 Teknik Informatika ITS Ann Yuniarti - 28
11 2D Modeling Transformations Modeling Coordinates Scale.3,.3 Rotate -9 Translate 5, 3 Teknik Informatika ITS Ann Yuniarti - 28
12 2D Modeling Transformations Modeling Coordinates Scale.3,.3 Rotate -9 Translate 5, 3 World Coordinates Teknik Informatika ITS Ann Yuniarti
13 Transformasi Geometri 2D Translasi 2D = + t, = + t (t, t ) disebut vektor translasi atau pergeseran Dalam bentuk matriks: ' P P' ' Persamaan translasi 2D: P = P + T Line, polgon translasi titik endpoints, render Untuk menghapus obek ang asli displa it in background color before translating it Circle, ellipse, spline curve translasi titik-titik ang mendefinisikan (misalna koordinat titik pusat), render obek hasil translasi di posisi ang baru T t t Teknik Informatika ITS Ann Yuniarti
14 Transformasi Geometri 2D Scaling 2D = s, = s Dalam bentuk matriks: ' ' s s Uniform scaling berarti skalar pengali sama untuk semua komponen: 2 Teknik Informatika ITS Ann Yuniarti
15 Transformasi Geometri 2D Non-uniform scaling: skalar ang berbeda untuk tiap komponen: X 2, Y.5 Teknik Informatika ITS Ann Yuniarti
16 Transformasi Geometri 2D ' ' r (, ) r (, ) cos sin sin cos Rotasi 2D = r cos (Φ + ) = r sin (Φ + ) Trig Identit = r cos(f) cos( ) r sin(f) sin( ) = r sin(f) cos( ) + r cos(f) sin( ) Original point = r cos (f) = r sin (f) Hasil substitusi = cos( ) - sin( ) = sin( ) + cos( ) Teknik Informatika ITS Ann Yuniarti
17 Transformasi Geometri 2D Shear 2D Shear pada arah relatif terhadap sumbu : = + sh, = Parameter sh dapat berupa bilangan real Dalam bentuk matriks: ' ' Shear pada arah relatif terhadap sumbu : =, = + sh Dalam bentuk matriks: ' ' sh sh Teknik Informatika ITS Ann Yuniarti
18 Transformasi Geometri 2D Reflection 2D Pencerminan terhadap garis = (sumbu ): =, = - Dalam bentuk matriks: ' ' Pencerminan terhadap garis = (sumbu ): = -, = Dalam bentuk matriks: ' Pencerminan terhadap titik pusat (, ): = -, = - Dalam bentuk matriks: ' ' ' Teknik Informatika ITS Ann Yuniarti
19 Basic 2D Transformations Translation: = + t = + t Scale: = * s = * s Rotation: = *cos(θ) - *sin(θ) = *sin(θ) + *cos(θ) Transformations can be combined (with simple algebra) Teknik Informatika ITS Ann Yuniarti
20 Basic 2D Transformations Translation: = + t = + t Scale: = * s = * s Rotation: = *cos(θ) - *sin(θ) = *sin(θ) + *cos(θ) Teknik Informatika ITS Ann Yuniarti
21 Basic 2D Transformations Translation: = + t = + t Scale: = * s = * s Rotation: = *cos(θ) - *sin(θ) = *sin(θ) + *cos(θ) (, ) = *s = *s (,) Teknik Informatika ITS Ann Yuniarti
22 Basic 2D Transformations Translation: = + t = + t Scale: = * s = * s Rotation: = *cos(θ) - *sin(θ) = *sin(θ) + *cos(θ) (, ) = (*s )*cos θ) - (*s )*sin(θ) = (*s )*sin(θ) + (*s )*cos(θ) Teknik Informatika ITS Ann Yuniarti
23 Basic 2D Transformations Translation: = + t = + t Scale: = * s = * s Rotation: = *cos(θ) - *sin(θ) = *sin(θ) + *cos(θ) (, ) = ((*s )*cos(θ) - (*s )*sin(θ)) + t = ((*s )*sin(θ) + (*s )*cos(θ)) + t Teknik Informatika ITS Ann Yuniarti
24 Basic 2D Transformations Translation: = + t = + t Scale: = * s = * s Rotation: = *cos(θ) - *sin(θ) = *sin(θ) + *cos(θ) = ((*s )*cos(θ) - (*s )*sin(θ)) + t = ((*s )*sin(θ) + (*s )*cos(θ)) + t Teknik Informatika ITS Ann Yuniarti
25 Matri Representation Represent 2D transformation b a matri a c b d Multipl matri b column vector appl transformation to point ' ' a c b d ' ' a c b d Teknik Informatika ITS Ann Yuniarti
26 Matri Representation Transformations combined b multiplication ' ' a c b d e g f h i k j l Matrices are a convenient and efficient wa to represent a sequence of transformations! Teknik Informatika ITS Ann Yuniarti
27 Teknik Informatika ITS 27 Ann Yuniarti Matrices What tpes of transformations can be represented with a 22 matri? 2D Identit? ' ' ' ' 2D Scale around (,)? s s * ' * ' s s ' '
28 22 Matrices What tpes of transformations can be represented with a 22 matri? 2D Rotate around (,)? ' ' cos sin * * sin cos * * ' ' cos sin sin cos 2D Shear? ' ' sh sh * * Teknik Informatika ITS Ann Yuniarti ' ' sh sh
29 Teknik Informatika ITS 29 Ann Yuniarti Matrices What tpes of transformations can be represented with a 22 matri? 2D Mirror about Y ais? ' ' ' ' 2D Mirror over (,)? ' ' ' '
30 22 Matrices What tpes of transformations can be represented with a 22 matri? 2D Translation? ' t ' t NO! Onl linear 2D transformations can be represented with a 22 matri Teknik Informatika ITS Ann Yuniarti
31 Linear Transformations Linear transformations are combinations of Scale, Rotation, Shear, and Mirror Properties of linear transformations: Satisfies: ' ' T( sp s2p2) st ( p) s2t ( p2) Origin maps to origin Lines map to lines Parallel lines remain parallel Ratios are preserved a c b d Teknik Informatika ITS Ann Yuniarti
32 Homogeneous Coordinates Q: How can we represent translation as a 33 matri? ' ' t t Teknik Informatika ITS Ann Yuniarti
33 Homogeneous Coordinates Homogeneous coordinates represent coordinates in 2 dimensions with a 3- vector homogeneous coords Homogeneous coordinates seem unintuitive, but the make graphics operations much easier Teknik Informatika ITS Ann Yuniarti
34 Homogeneous Coordinates Q: How can we represent translation as a 33 matri? ' ' A: Using the rightmost column: t t Translation t t Teknik Informatika ITS Ann Yuniarti
35 Translation Eample of translation Homogeneous Coordinates ' ' t t t t t = 2 t = Teknik Informatika ITS Ann Yuniarti
36 Homogeneous Coordinates Add a 3rd coordinate to ever 2D point (,, w) represents a point at location (/w, /w) (,, ) represents a point at infinit (,, ) is not allowed Convenient coordinate sstem to represent man useful transformations 2 2 (2,,) or (4,2,2) or (6,3,3) Teknik Informatika ITS Ann Yuniarti
37 Teknik Informatika ITS 37 Ann Yuniarti - 28 Basic 2D Transformations Basic 2D transformations as 33 matrices cos sin sin cos ' ' ' ' t t ' ' sh sh Translate Rotate Shear ' ' s s Scale
38 Affine Transformations Affine transformations are combinations of Linear transformations, and ' a b c Translations ' d e f w w Properties of affine transformations: Origin does not necessaril map to origin Lines map to lines Parallel lines remain parallel Ratios are preserved Teknik Informatika ITS Ann Yuniarti
39 Matri Composition Transformations can be combined b matri multiplication ' ' w' t t cos sin sin cos s s w p = T(t,t ) R( ) S(s,s ) p Teknik Informatika ITS Ann Yuniarti
40 Matri Composition Matrices are a convenient and efficient wa to represent a sequence of transformations General purpose representation Hardware matri multipl p = (T * (R * (S*p) ) ) p = (T*R*S) * p Teknik Informatika ITS Ann Yuniarti
41 Matri Composition Be aware: order of transformations matters Matri multiplication is not commutative p = T * R * S * p Global Local Teknik Informatika ITS Ann Yuniarti
42 Matri Composition What if we want to rotate and translate? E: Rotate line segment b 45 degrees about endpoint a and lengthen a a Teknik Informatika ITS Ann Yuniarti
43 Multiplication Order Wrong Wa Our line is defined b two endpoints Appling a rotation of 45 degrees, R(45), affects both points We could tr to translate both endpoints to return endpoint a to its original position, but b how much? a a Wrong R(45) a Correct T(-3) R(45) T(3) Teknik Informatika ITS Ann Yuniarti
44 Multiplication Order - Correct Isolate endpoint a from rotation effects a First translate line so a is at origin: T (-3) a Then rotate line 45 degrees: R(45) a Then translate back so a is where it was: T(3) a Teknik Informatika ITS Ann Yuniarti
45 Matri Composition Will this sequence of operations work? 3 cos(45) sin(45) sin(45) cos(45) 3 a a a' a' Teknik Informatika ITS Ann Yuniarti
46 Matri Composition After correctl ordering the matrices Multipl matrices together What results is one matri store it (on stack)! Multipl this matri b the vector of each verte All vertices easil transformed with one matri multipl Teknik Informatika ITS Ann Yuniarti
47 Reverse Rotations Q: How do ou undo a rotation of R( )? A: Appl the inverse of the rotation R - ( ) = R(- ) How to construct R-( ) = R(- ) Inside the rotation matri: cos( ) = cos(- ) The cosine elements of the inverse rotation matri are unchanged The sign of the sine elements will flip Therefore R - ( ) = R(- ) = R T ( ) Teknik Informatika ITS Ann Yuniarti
48 Teknik Informatika ITS Ann Yuniarti
49 #include <windows.h> #include <GL/glut.h> #include <stdlib.h> #include <math.h> GLsizei winwidth=6, winheight=6; //set initial displa window size GLfloat wcmin=.,wcma=225.; //set range for world coordinates GLfloat wcmin=.,wcma=225.; class wcpt2d { public: GLfloat,; }; tpedef GLfloat Matri33 [3][3]; Matri33 matcomposite; const GLdouble pi=3.459; void init(void) { glclearcolor(.,.,.,.); //set color of displa window to white } /* Construct the 3 b 3 identit matri */ void matri33setidentit (Matri33 matident33){ GLint row, col; for(row=;row<3;row++) for(col=;col<3;col++) matident33[row][col]=(row==col); } /* Premultipl matri m times matri m2, store result in m2. */ void matri33premultipl (Matri33 m, Matri33 m2) { GLint row, col; Matri33 mattemp; for(row=;row<3;row++) for(col=;col<3;col++) mattemp[row][col]=m[row][]*m2[][col]+m[row][]*m2[][col]+m[row][2]*m2[2][col]; for(row=;row<3;row++) for(col=;col<3;col++) m2[row][col]=mattemp[row][col];
50 void translate2d(glfloat t, GLfloat t){ Matri33 mattrans; matri33setidentit(mattrans); //initialize translation matri to identit mattrans[][2]=t; mattrans[][2]=t; matri33premultipl(mattrans,matcomposite);//concatenate mattrans with composite matri } void rotate2d(wcpt2d pivotpt, GLfloat theta){ Matri33 matrot; matri33setidentit(matrot); //initialize rotation matri to identit matrot[][]=cos(theta); matrot[][]=-sin(theta); matrot[][2]=pivotpt. * (-cos(theta))+pivotpt. * sin(theta); matrot[][]=sin(theta); matrot[][]=cos(theta); matrot[][2]=pivotpt. * (-cos(theta))-pivotpt. * sin(theta); matri33premultipl(matrot,matcomposite);//concatenate matrot with the composite matri } void scale2d(glfloat s, GLfloat s, wcpt2d fiedpt){ Matri33 matscale; matri33setidentit(matscale); //initialize scaling matri to identit matscale[][]=s; matscale[][2]=(-s)*fiedpt.; matscale[][]=s; matscale[][2]=(-s)*fiedpt.; matri33premultipl(matscale,matcomposite);//concatenate matscale with the composite matri } /* using the composite matri, calculate transformed coordinates. */ void transformverts2d(glint nverts, wcpt2d * verts){ GLint k; GLfloat temp; for(k=;k<nverts;k++){ temp=matcomposite[][]*verts[k].+matcomposite[][]*verts[k].+matcomposite[][2]; verts[k].=matcomposite[][]*verts[k].+matcomposite[][]*verts[k].+matcomposite[][ 2]; verts[k].=temp; } }
51 void triangle(wcpt2d *verts) { GLint k; glbegin(gl_triangles); for(k=;k<3;k++) glverte2f(verts[k].,verts[k].); glend(); } void displafcn(void){ GLint nverts=3; //define initial position for triangle wcpt2d verts[3]={{5.,25.},{5.,25.},{.,.}}; wcpt2d centroidpt; //calculate position of triangle centroid GLint k, Sum=, Sum=; for(k=;k<nverts;k++) { Sum+=verts[k].; Sum+=verts[k].; } centroidpt.=glfloat(sum)/glfloat(nverts); centroidpt.=glfloat(sum)/glfloat(nverts); wcpt2d pivpt,fiedpt; // set geometric transformation parameters pivpt=centroidpt; fiedpt=centroidpt; GLfloat t=., t=.; GLfloat s=.5, s=.5; GLdouble theta=pi/2.; glclear(gl_color_buffer_bit); //clear displa window glcolor3f(.,.,.); //set initial fill color to blue triangle(verts); //displa blue triangle matri33setidentit(matcomposite);//initialize composite matri to identit /* construct composite matri for transformation sequence */ scale2d(s,s,fiedpt); // first transformation: Scale. rotate2d(pivpt,theta); // second transformation: Rotate. translate2d(t,t); // final transformation: Translate. transformverts2d(nverts,verts);//appl composite matri to triangle vertices glcolor3f(.,.,.); //set color for transformed triangle triangle(verts); //displa red transformed triangle glflush(); }
52 void winreshapefcn(glint newwidth, GLint newheight){ glmatrimode(gl_projection); glloadidentit(); gluortho2d(wcmin,wcma,wcmin,wcma); glclear(gl_color_buffer_bit); } void main(int argc, char ** argv){ glutinit(&argc,argv); glutinitdisplamode(glut_single GLUT_RGB); glutinitwindowposition(5,5); glutinitwindowsize(winwidth,winheight); glutcreatewindow("geometric Transformation Sequence"); init(); glutdisplafunc(displafcn); glutreshapefunc(winreshapefcn); glutmainloop(); }
53 Some Interesting Images Teknik Informatika ITS Ann Yuniarti
54 Some Interesting Images Teknik Informatika ITS Ann Yuniarti
55 Tugas Kelas C Tulis sebuah program animasi ang mengimplementasikan prosedur rotasi 2D. Inputna sebuah polgon ang dirotasi terhadap sebuah pivot point menggunakan sudut ang kecil. Untuk meningkatkan kecepatan gunakan aproksimasi dari fungsi sin dan cos, dan untuk menghindari akumulasi error ang berlebihan reset nilai koordinat awal pada setiap putaran baru. Teknik Informatika ITS Ann Yuniarti
56 Tugas Kelas X Modifikasi contoh program sebelumna supaa: Parameter transformasi dapat dispesifikasikan sebagai input dari user Dapat diaplikasikan pada semua polgon dengan verteks-verteksna dispesikasikan oleh input dari user Urutan transformasi geometrik ditentukan oleh input dari user Teknik Informatika ITS Ann Yuniarti
57 Tugas Kelas A Implementasi program untuk membuat gambar: Untuk membuatna, buat sebuah fungsi ang menggambar polgon gambar (b) (seperlima dari bintang). Lalu transformasikan dengan rotasi untuk menggambar bintang secara keseluruhan. Teknik Informatika ITS Ann Yuniarti
58 Tugas Kelas B Implementasi program untuk membuat gambar: Untuk membuatna, buat sebuah fungsi ang menggambar sebuah motif (gambar kiri). Lalu transformasikan dengan refleksi untuk mendapatkan sebuah spoke ang utuh, lalu rotasi untuk menggambar snowflake secara keseluruhan. Teknik Informatika ITS Ann Yuniarti
Transformasi Obyek (Lanjutan)
 Transformasi Obek (Lanjutan) Grafika Komputer Semester Ganjil 28 Teknik Informatika ITS Ann Yuniarti - 28 Kompetensi. Mampu memahami konsep transformasi 3D 2. Mampu mengimplementasikan konsep transformasi
Transformasi Obek (Lanjutan) Grafika Komputer Semester Ganjil 28 Teknik Informatika ITS Ann Yuniarti - 28 Kompetensi. Mampu memahami konsep transformasi 3D 2. Mampu mengimplementasikan konsep transformasi
Esther Wibowo
 Esther Wibowo [email protected] Topik Hari Ini Dasar Transformasi Translation Pemindahan, Penggeseran Scaling Perubahan Ukuran Shear Distorsi? Rotation Pemutaran Representasi Matriks Transformasi
Esther Wibowo [email protected] Topik Hari Ini Dasar Transformasi Translation Pemindahan, Penggeseran Scaling Perubahan Ukuran Shear Distorsi? Rotation Pemutaran Representasi Matriks Transformasi
Pengertian. Transformasi geometric transformation. koordinat dari objek Transformasi dasar: Translasi Rotasi Penskalaan
 Pengertian Transformasi geometric transformation Transformasi = mengubah deskripsi koordinat dari objek Transformasi dasar: Translasi Rotasi Penskalaan Translasi Mengubah posisi objek: perpindahan lurus
Pengertian Transformasi geometric transformation Transformasi = mengubah deskripsi koordinat dari objek Transformasi dasar: Translasi Rotasi Penskalaan Translasi Mengubah posisi objek: perpindahan lurus
BAB V TRANSFORMASI 2D
 BAB V TRANSFORMASI 2D OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : Transformasi Dasar 2D 1. Translasi 2. Rotasi 3. Scalling Transformasi Lain 1. Refleksi 2. Shear TUJUAN DAN SASARAN: Setelah
BAB V TRANSFORMASI 2D OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : Transformasi Dasar 2D 1. Translasi 2. Rotasi 3. Scalling Transformasi Lain 1. Refleksi 2. Shear TUJUAN DAN SASARAN: Setelah
Tutorial 04 Modeling & Transformasi Proyeksi
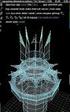 Tutorial 04 Modeling & Transformasi Proyeksi Secara substansi, Grafika Komputer adalah proses transformasi dari model 3D obyek berupa informasi geometri bentuk, informasi pose, warna, texture, dan pencahayaan
Tutorial 04 Modeling & Transformasi Proyeksi Secara substansi, Grafika Komputer adalah proses transformasi dari model 3D obyek berupa informasi geometri bentuk, informasi pose, warna, texture, dan pencahayaan
Grafika Komputer. Evangs Mailoa
 Grafika Komputer Evangs Mailoa Kumpulan polygon atau permukaan yang secara bersama-sama membentuk kulit dari suatu obyek. Dinyatakan dengan daftar poligon-poligon yang disertai dengan arah dari permukaan
Grafika Komputer Evangs Mailoa Kumpulan polygon atau permukaan yang secara bersama-sama membentuk kulit dari suatu obyek. Dinyatakan dengan daftar poligon-poligon yang disertai dengan arah dari permukaan
Transformasi Geometri Sederhana
 Transformasi Geometri Sederhana Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut dengan manipulasi. Perubahan gambar dengan mengubah koordinat
Transformasi Geometri Sederhana Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut dengan manipulasi. Perubahan gambar dengan mengubah koordinat
Gambar 1. Viewport pada layar
 No. : ST/EKA/PTI223/03 Revisi : 02 Hal. 1 dari 9 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi, balikan,
No. : ST/EKA/PTI223/03 Revisi : 02 Hal. 1 dari 9 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi, balikan,
BAB-7 TRANSFORMASI 2D
 BAB-7 TRANSFORMASI 2D Kita dapat melakukan transformasi terhadap objek, pada materi ini akan dibahas transformasi 2D yaitu translasi, skala, rotasi. By: I Gusti Ngurah Suryantara, S.Kom., M.Kom 7.1. PENDAHULUAN
BAB-7 TRANSFORMASI 2D Kita dapat melakukan transformasi terhadap objek, pada materi ini akan dibahas transformasi 2D yaitu translasi, skala, rotasi. By: I Gusti Ngurah Suryantara, S.Kom., M.Kom 7.1. PENDAHULUAN
Gasal 2011/2012 KOMPUTER GRAFIK (3SKS)
 Gaal 2/22 KOMPUTER GRAFIK (3SKS) CucunVer Angkoo,ST,MT :: Pertemuan ke :: General Tranformation A tranformation map point to other point and/or ector to other ector QT(P) 3 TRANSFORMASI 2D A Matrik Tranformai
Gaal 2/22 KOMPUTER GRAFIK (3SKS) CucunVer Angkoo,ST,MT :: Pertemuan ke :: General Tranformation A tranformation map point to other point and/or ector to other ector QT(P) 3 TRANSFORMASI 2D A Matrik Tranformai
Transformasi Datum dan Koordinat
 Transformasi Datum dan Koordinat Sistem Transformasi Koordinat RG091521 Lecture 6 Semester 1, 2013 Jurusan Pendahuluan Hubungan antara satu sistem koordinat dengan sistem lainnya diformulasikan dalam bentuk
Transformasi Datum dan Koordinat Sistem Transformasi Koordinat RG091521 Lecture 6 Semester 1, 2013 Jurusan Pendahuluan Hubungan antara satu sistem koordinat dengan sistem lainnya diformulasikan dalam bentuk
TRANSFORMASI. Tujuan transfomasi adalah:
 TRANSFORMASI Grafika komputer merupakan bidang yang menarik minat banyak orang. Salah sub bagian dari grafika komputer adalah pemodelan objek (object modelling). Dalam pemodelan objek dua dimensi (2D),didapati
TRANSFORMASI Grafika komputer merupakan bidang yang menarik minat banyak orang. Salah sub bagian dari grafika komputer adalah pemodelan objek (object modelling). Dalam pemodelan objek dua dimensi (2D),didapati
Gambar 1. Viewport pada layar
 No. : ST/EKA/PTI223/03 Revisi : 03 Senin 010210 Hal. 1 dari 5 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi,
No. : ST/EKA/PTI223/03 Revisi : 03 Senin 010210 Hal. 1 dari 5 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi,
Transformasi Geometri Sederhana. Farah Zakiyah Rahmanti 2014
 Transformasi Geometri Sederhana Farah Zakiyah Rahmanti 2014 Grafika Komputer TRANSFORMASI 2D Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut
Transformasi Geometri Sederhana Farah Zakiyah Rahmanti 2014 Grafika Komputer TRANSFORMASI 2D Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut
PETEMUAN KE-5 TRANSFORMASI-PANDANGAN (Viewing)
 PETEMUAN KE-5 TRANSFORMASI-PANDANGAN (Viewing) A.Tujuan 1. Dapat menggambar objek 3D 2. Dapat mentransformasikan objek 3D 3. Dapat menggunkan glviewport,glmodelview, glprojection, glfrustum B. Dasar Teori
PETEMUAN KE-5 TRANSFORMASI-PANDANGAN (Viewing) A.Tujuan 1. Dapat menggambar objek 3D 2. Dapat mentransformasikan objek 3D 3. Dapat menggunkan glviewport,glmodelview, glprojection, glfrustum B. Dasar Teori
Pengenalan OpenGL. Sintax Perintah OpenGL. Library yang Berhubungan dengan OpenGL
 Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
LAMPIRAN SOURCE CODE
 DAFTAR PUSTAKA Anonim. www.opengl.org (diakses pada tanggal 01 Juli 2015). Fadlisyah, et al. 2007. Pengantar Grafika Komputer. Yogyakarta: Andi. Haemel, Nicholas, et al. 2011. OpenGL super bible : comprehensive
DAFTAR PUSTAKA Anonim. www.opengl.org (diakses pada tanggal 01 Juli 2015). Fadlisyah, et al. 2007. Pengantar Grafika Komputer. Yogyakarta: Andi. Haemel, Nicholas, et al. 2011. OpenGL super bible : comprehensive
Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan
 A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan Perintah Arti Keterangan glvertex2i(x,y);
A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan Perintah Arti Keterangan glvertex2i(x,y);
PENGANTAR GRAFIKA KOMPUTER
 PENGANTAR GRAFIKA KOMPUTER Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Pengenalan grafika komputer
PENGANTAR GRAFIKA KOMPUTER Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Pengenalan grafika komputer
Aljabar Linear. & Matriks. Evangs Mailoa. Pert. 7-8
 Aljabar Linear & Matriks Pert. 7-8 Evangs Mailoa Yang dipelajari hari ini: Aritmatika Vektor Konsep Geometrik Titik, Garis dan Bidang Perkalian Titik Euclidean Vector Spaces I There are two major topics
Aljabar Linear & Matriks Pert. 7-8 Evangs Mailoa Yang dipelajari hari ini: Aritmatika Vektor Konsep Geometrik Titik, Garis dan Bidang Perkalian Titik Euclidean Vector Spaces I There are two major topics
OPENGL DALAM MICROSOFT VISUAL STUDIO EXPRESS Created by: Gideon
 OPENGL DALAM MICROSOFT VISUAL STUDIO EXPRESS 2012 Created by: Gideon Tutorial Open GL untuk membuat garis dengan program Microsoft Visual Studio Express 2012 OpenGL dengan Microsoft Visual Express 2012
OPENGL DALAM MICROSOFT VISUAL STUDIO EXPRESS 2012 Created by: Gideon Tutorial Open GL untuk membuat garis dengan program Microsoft Visual Studio Express 2012 OpenGL dengan Microsoft Visual Express 2012
Line VS Bezier Curve. Kurva Bezier. Other Curves. Drawing the Curve (1) Pertemuan: 06. Dosen Pembina Danang Junaedi Sriyani Violina IF-UTAMA 2
 Line VS Bezier Curve Kurva Bezier Pertemuan: 06 Dosen Pembina Danang Junaedi Sriyani Violina IF-UTAMA 1 IF-UTAMA 2 Other Curves Drawing the Curve (1) IF-UTAMA 3 IF-UTAMA 4 1 Drawing the Curve (2) Algoritma
Line VS Bezier Curve Kurva Bezier Pertemuan: 06 Dosen Pembina Danang Junaedi Sriyani Violina IF-UTAMA 1 IF-UTAMA 2 Other Curves Drawing the Curve (1) IF-UTAMA 3 IF-UTAMA 4 1 Drawing the Curve (2) Algoritma
Tutorial 09. Lighting
 Tutorial 09. Lighting Visualisasi tentu saja tidak akan terjadi bila tidak ada cahaya. Pencahayaan merupakan esensi dari visualisasi dan merupakan topik yang sangat kompleks. Hingga tahap ini lingkungan
Tutorial 09. Lighting Visualisasi tentu saja tidak akan terjadi bila tidak ada cahaya. Pencahayaan merupakan esensi dari visualisasi dan merupakan topik yang sangat kompleks. Hingga tahap ini lingkungan
Jawab: Titik awal (x 1, y 1 ) = A(2,1) dan Titik akhir (x 2, y 2 ) = B(8,5) dx = x 2 x 1 = 8 2 = 6 dan dy = y 2 y 1 = 5 1 = 4
 .. Algoritma DDA (Digital Diferential Analer ) DDA adalah algoritma pembentuk garis ang didasarkan pada perasamaan (-8). Garis dibuat menggunakan titik awal (, ) dan titik akhir (, ). Setiap koordinat
.. Algoritma DDA (Digital Diferential Analer ) DDA adalah algoritma pembentuk garis ang didasarkan pada perasamaan (-8). Garis dibuat menggunakan titik awal (, ) dan titik akhir (, ). Setiap koordinat
Bab 2 Output Primitif
 Bab Output Primitif.. Algoritma DDA (Digital Diferential Analer ) ===================================================================. Tentukan dua titik ang akan dihubungkan dalam pembentukan garis..
Bab Output Primitif.. Algoritma DDA (Digital Diferential Analer ) ===================================================================. Tentukan dua titik ang akan dihubungkan dalam pembentukan garis..
Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan
 No. : ST/EKA/PTI223/04 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL
No. : ST/EKA/PTI223/04 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL
Grafika Komputer. Evangs Mailoa
 Grafika Komputer Evangs Mailoa Translasi Skala Rotasi/Putar Konsep yang terpenting dalam grafika komputer adalah Transformasi Affine. Pada dasarnya, transformasi ini adalah memindahkan objek tanpa merusak
Grafika Komputer Evangs Mailoa Translasi Skala Rotasi/Putar Konsep yang terpenting dalam grafika komputer adalah Transformasi Affine. Pada dasarnya, transformasi ini adalah memindahkan objek tanpa merusak
PETEMUAN KE-3 PRIMITIVE DRAWING 2
 PETEMUAN KE-3 PRIMITIVE DRAWING 2 A.Tujuan 1. Dapat mengaplikasikan objek primitif dalam bentuk yang lain B. Dasar Teori Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam
PETEMUAN KE-3 PRIMITIVE DRAWING 2 A.Tujuan 1. Dapat mengaplikasikan objek primitif dalam bentuk yang lain B. Dasar Teori Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam
apa yang terjadi?. Kemudian lakukan pengantian beberapa bagian seperti sintak
 No. : ST/EKA/PTI223/02 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam praktikum hari ini lakukan penambahan
No. : ST/EKA/PTI223/02 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam praktikum hari ini lakukan penambahan
BAB II LINGKUNGAN PEMROGRAMAN GRAFIK DENGAN OPEN GL
 BAB II LINGKUNGAN PEMROGRAMAN GRAFIK DENGAN OPEN GL Pemrograman Grafis Pemrograman grafis adalah pemrograman yang digunakan untuk menghasilkan gambar pada komputer menggunakan library yang ada. Teknik-teknik
BAB II LINGKUNGAN PEMROGRAMAN GRAFIK DENGAN OPEN GL Pemrograman Grafis Pemrograman grafis adalah pemrograman yang digunakan untuk menghasilkan gambar pada komputer menggunakan library yang ada. Teknik-teknik
Geometri, Koordinat Homogen, dan Transformasi Affine. Computer Graphics #03#04#05
 Geometri, Koordinat Homogen, dan Transformasi Affine Computer Graphics #3#4#5 Ruang Lingkup Dasar Geometri Sistem Koordinat Viewport Drawing (Elemen Dasar dan rimitive Matriks Transformasi Affine Koordinat
Geometri, Koordinat Homogen, dan Transformasi Affine Computer Graphics #3#4#5 Ruang Lingkup Dasar Geometri Sistem Koordinat Viewport Drawing (Elemen Dasar dan rimitive Matriks Transformasi Affine Koordinat
Screw Theory and Reciprocity
 1 crew Theory and Reciprocity Latifah Nurahmi Definition of crew A spatial displacement of a rigid body can be expressed as a combination of a rotation about a line and a translation along the same line.
1 crew Theory and Reciprocity Latifah Nurahmi Definition of crew A spatial displacement of a rigid body can be expressed as a combination of a rotation about a line and a translation along the same line.
Euclidean n & Vector Spaces. Matrices & Vector Spaces
 Lecture 9 Euclidean n & Vector Spaces Delivered by: Filson Maratur Sidjabat [email protected] Matrices & Vector Spaces #4 th June 05 (90%*score / 0% extra points for HW-Q) Retake Quiz. Compute
Lecture 9 Euclidean n & Vector Spaces Delivered by: Filson Maratur Sidjabat [email protected] Matrices & Vector Spaces #4 th June 05 (90%*score / 0% extra points for HW-Q) Retake Quiz. Compute
TE Teknik Numerik Sistem Linear
 TE 9467 Teknik Numerik Sistem Linear Operator Linear Trihastuti Agustinah Bidang Studi Teknik Sistem Pengaturan Jurusan Teknik Elektro - FTI Institut Teknologi Sepuluh Nopember O U T L I N E. Objektif.
TE 9467 Teknik Numerik Sistem Linear Operator Linear Trihastuti Agustinah Bidang Studi Teknik Sistem Pengaturan Jurusan Teknik Elektro - FTI Institut Teknologi Sepuluh Nopember O U T L I N E. Objektif.
Pengenalan OpenGL. Sintax Perintah OpenGL. Library yang Berhubungan dengan OpenGL
 Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
TE Teknik Numerik Sistem Linear. Bidang Studi Teknik Sistem Pengaturan Jurusan Teknik Elektro - FTI Institut Teknologi Sepuluh Nopember
 TE9467 Teknik Numerik Sistem Linear Bidang Studi Teknik Sistem Pengaturan Jurusan Teknik Elektro - FTI Institut Teknologi Sepuluh Nopember O U T L I N E OBJEKTIF TEORI 3 CONTOH 4 SIMPULAN 5 LATIHAN OBJEKTIF
TE9467 Teknik Numerik Sistem Linear Bidang Studi Teknik Sistem Pengaturan Jurusan Teknik Elektro - FTI Institut Teknologi Sepuluh Nopember O U T L I N E OBJEKTIF TEORI 3 CONTOH 4 SIMPULAN 5 LATIHAN OBJEKTIF
SEBUAH TELAAH ELIPS DAN LINGKARAN MELALUI SEBUAH PENDEKATAN ALJABAR MATRIKS
 SEBUAH TELAAH ELIPS DAN LINGKARAN MELALUI SEBUAH PENDEKATAN ALJABAR MATRIKS Rahmat Sagara Sekolah Tinggi Keguruan dan Ilmu Pendidikan Kebangkitan Nasional Sampoerna School of Education Building Jl. Kapten
SEBUAH TELAAH ELIPS DAN LINGKARAN MELALUI SEBUAH PENDEKATAN ALJABAR MATRIKS Rahmat Sagara Sekolah Tinggi Keguruan dan Ilmu Pendidikan Kebangkitan Nasional Sampoerna School of Education Building Jl. Kapten
BAB IV IMPLEMENTASI DAN PENGUJIAN
 BAB IV IMPLEMENTASI DAN PENGUJIAN 4.1 Implementasi Tahapan implementasi bertujuan untuk memastikan apakah aplikasi yang dibuat dapat bekerja secara efektif dan efisien sesuai dengan yang diharapkan. Sebelum
BAB IV IMPLEMENTASI DAN PENGUJIAN 4.1 Implementasi Tahapan implementasi bertujuan untuk memastikan apakah aplikasi yang dibuat dapat bekerja secara efektif dan efisien sesuai dengan yang diharapkan. Sebelum
Computer Graphics PENGANTAR GRAFIKA 3D
 Computer Graphics PENGANTAR GRAFIKA 3D F A K ULTAS I L MU K O MPUTER 2 4 TUJUAN INSTRUKSIONAL KHUSUS. Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2- Dimensi 2. Mahasiswa mengerti
Computer Graphics PENGANTAR GRAFIKA 3D F A K ULTAS I L MU K O MPUTER 2 4 TUJUAN INSTRUKSIONAL KHUSUS. Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2- Dimensi 2. Mahasiswa mengerti
Pengantar Grafika 3D E D I T A N
 Pengantar Grafika 3D F A KULTAS I L M U K O M P UTER E D I T A N 2 5 TUJUAN INSTRUKSIONAL KHUSUS 2 Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2-Dimensi Mahasiswa mengerti
Pengantar Grafika 3D F A KULTAS I L M U K O M P UTER E D I T A N 2 5 TUJUAN INSTRUKSIONAL KHUSUS 2 Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2-Dimensi Mahasiswa mengerti
20. TRANSFORMASI. A. Translasi (Pergeseran) ; T = b. a y. a y. x atau. = b. = b
 . TRANSFORMASI A. Translasi (Pergeseran) ; T b a + b a atau b a B. Refleksi (Pencerminan). Bila M matriks refleksi berordo, maka: M atau M. Matriks M karena refleksi terhadap sumbu, sumbu, garis, dan garis
. TRANSFORMASI A. Translasi (Pergeseran) ; T b a + b a atau b a B. Refleksi (Pencerminan). Bila M matriks refleksi berordo, maka: M atau M. Matriks M karena refleksi terhadap sumbu, sumbu, garis, dan garis
Mata Kuliah: Geometri Analitik (3 SKS)
 Mata Kuliah: Geometri Analitik (3 SKS) PRAKTIKUM GEOMETRI ANALITIK Tujuan Umum: Mahasiswa dapat menggunakan program CABRI GEOMETRI II PLUS untuk menyelesaikan permasalahan-permasalahan dalam Geometri Analitik
Mata Kuliah: Geometri Analitik (3 SKS) PRAKTIKUM GEOMETRI ANALITIK Tujuan Umum: Mahasiswa dapat menggunakan program CABRI GEOMETRI II PLUS untuk menyelesaikan permasalahan-permasalahan dalam Geometri Analitik
Keseimbangan Torsi Coulomb
 Hukum Coulomb Keseimbangan Torsi Coulomb Perputaran ini untuk mencocokan dan mengukur torsi dalam serat dan sekaligus gaya yang menahan muatan Skala dipergunakan untuk membaca besarnya pemisahan muatan
Hukum Coulomb Keseimbangan Torsi Coulomb Perputaran ini untuk mencocokan dan mengukur torsi dalam serat dan sekaligus gaya yang menahan muatan Skala dipergunakan untuk membaca besarnya pemisahan muatan
PRIMITIVE DRAWING. Achmad Basuki Nana Ramadijanti
 PRIMITIVE DRAWING Achmad Basuki Nana Ramadijanti Materi Program Dasar dengan OpenGL Menggambar Titik Menggambar Garis Menggambar Polyline Menggambar Polygon Pewarnaan Struktur Dasar Program Grafik Dengan
PRIMITIVE DRAWING Achmad Basuki Nana Ramadijanti Materi Program Dasar dengan OpenGL Menggambar Titik Menggambar Garis Menggambar Polyline Menggambar Polygon Pewarnaan Struktur Dasar Program Grafik Dengan
Topik bahasan: 1. Membuat objek mudah dan kompleks dengan jaring poligon 2. Merender jaring poligon sebagai wireframe dan atau pejal dengan OpenGL
 Grafika-5 Pemodelan 3D dengan Jaring Poligon Tujuan Materi: Setelah mempelajari bab ini, Anda diharapkan dapat menjelaskan secara ringkas bagaimana membentuk objek 3D dengan jaring poligon (polygon meshes)
Grafika-5 Pemodelan 3D dengan Jaring Poligon Tujuan Materi: Setelah mempelajari bab ini, Anda diharapkan dapat menjelaskan secara ringkas bagaimana membentuk objek 3D dengan jaring poligon (polygon meshes)
Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc
 KALKULUS III Teorema Integral (Green s Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Kurva Tertutup Sederhana, Daerah Terhubung sederhana dan Berganda Suatu kurva tertutup sederhana adalah
KALKULUS III Teorema Integral (Green s Theorem) Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 Kurva Tertutup Sederhana, Daerah Terhubung sederhana dan Berganda Suatu kurva tertutup sederhana adalah
Tutorial 06. Texture Mapping & Blending
 Tutorial 06. Texture Mapping & Blending Hingga tahap ini, geometric primitive digambar dengan warna solid atau warna hasil interpolasi warnawarna vertex-nya. Texture mapping memungkinkan untuk menaruh
Tutorial 06. Texture Mapping & Blending Hingga tahap ini, geometric primitive digambar dengan warna solid atau warna hasil interpolasi warnawarna vertex-nya. Texture mapping memungkinkan untuk menaruh
BAB IV IMPLEMENTASI DAN PENGUJIAN SISTEM
 BAB IV IMPLEMENTASI DAN PENGUJIAN SISTEM Pada bab ini akan dibahas implementasi bertujuan memastikan apakah aplikasi yang dibuat berjalan sesuai yang penulis harapakan. Sebelum program diimplementasikan
BAB IV IMPLEMENTASI DAN PENGUJIAN SISTEM Pada bab ini akan dibahas implementasi bertujuan memastikan apakah aplikasi yang dibuat berjalan sesuai yang penulis harapakan. Sebelum program diimplementasikan
Simulasi Transformasi Linier pada Bidang 2D Dengan Menggunakan OpenGL API
 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Tugas Besar II IF2123 Aljabar Geometri Simulasi Transformasi Linier pada Bidang 2D Dengan Menggunakan
Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Tugas Besar II IF2123 Aljabar Geometri Simulasi Transformasi Linier pada Bidang 2D Dengan Menggunakan
BAB III ANALISIS DAN PERANCANGAN SISTEM PROGRAM SIMULASI PERAMBATAN GETARAN MENGGUNAKAN FRAKTAL 3D
 27 BAB III ANALISIS DAN PERANCANGAN SISTEM PROGRAM SIMULASI PERAMBATAN GETARAN MENGGUNAKAN FRAKTAL 3D 3.1. Analisis Kebutuhan Sistem Berikut ini merupakan gambaran umum sistem dimana terdapat tahap-tahap
27 BAB III ANALISIS DAN PERANCANGAN SISTEM PROGRAM SIMULASI PERAMBATAN GETARAN MENGGUNAKAN FRAKTAL 3D 3.1. Analisis Kebutuhan Sistem Berikut ini merupakan gambaran umum sistem dimana terdapat tahap-tahap
Swakalibrasi Kamera Menggunakan Matriks Fundamental
 Swakalibrasi Kamera Menggunakan Matriks Fundamental Eza Rahmanita, Eko Mulyanto 2, Moch. Hariadi 3 Program Studi Teknik Informatika, Universitas Trunojoyo Madura Jl. Raya Telang Po Bo 2 Kamal, Bangkalan
Swakalibrasi Kamera Menggunakan Matriks Fundamental Eza Rahmanita, Eko Mulyanto 2, Moch. Hariadi 3 Program Studi Teknik Informatika, Universitas Trunojoyo Madura Jl. Raya Telang Po Bo 2 Kamal, Bangkalan
PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN
 PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN Rudy Adipranata 1, Liliana 2, Gunawan Iteh Fakultas Teknologi Industri, Jurusan Teknik Informatika, Universitas Kristen Petra Jl. Siwalankerto
PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN Rudy Adipranata 1, Liliana 2, Gunawan Iteh Fakultas Teknologi Industri, Jurusan Teknik Informatika, Universitas Kristen Petra Jl. Siwalankerto
Simetri. Operasi Simetri 13/03/2015. Pertemuan ke-5 Kristalografi (Simetri: Simbol & Operasinya) Nurun Nayiroh, M.Si
 DIFRAKSI SINAR-X Pertemuan ke-5 Kristalografi (Simetri: Simbol & Operasinya) Nurun Nayiroh, M.Si Simetri Operasi simetri: Translasi Inversi (Pusat Simetri) Rotasi Pencerminan Screw Glide Muka kristal (review
DIFRAKSI SINAR-X Pertemuan ke-5 Kristalografi (Simetri: Simbol & Operasinya) Nurun Nayiroh, M.Si Simetri Operasi simetri: Translasi Inversi (Pusat Simetri) Rotasi Pencerminan Screw Glide Muka kristal (review
Melakukan Operasi Logika
 Melakukan Operasi Logika Hampir semua statemen C++ adalah ekspresi. Operator C++ selain +, -, /, * yakni operator logika. Pada dasarnya orang2 menghitung menggunakan operasi AND dan OR Mengapa Menggunakan
Melakukan Operasi Logika Hampir semua statemen C++ adalah ekspresi. Operator C++ selain +, -, /, * yakni operator logika. Pada dasarnya orang2 menghitung menggunakan operasi AND dan OR Mengapa Menggunakan
Matriks Sebagai Representasi Orientasi Objek 3D
 Matriks Sebagai Representasi Orientasi Objek 3D Cendhika Imantoro - 13514037 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Matriks Sebagai Representasi Orientasi Objek 3D Cendhika Imantoro - 13514037 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Materi Aljabar Linear Lanjut
 Materi Aljabar Linear Lanjut TRANSFORMASI LINIER DARI R n KE R m ; GEOMETRI TRANSFORMASI LINIER DARI R 2 KE R 2 Disusun oleh: Dwi Lestari, M.Sc email: [email protected] JURUSAN PENDIDIKAN MATEMATIKA
Materi Aljabar Linear Lanjut TRANSFORMASI LINIER DARI R n KE R m ; GEOMETRI TRANSFORMASI LINIER DARI R 2 KE R 2 Disusun oleh: Dwi Lestari, M.Sc email: [email protected] JURUSAN PENDIDIKAN MATEMATIKA
MENGGAMBAR GRAFIK DENGAN MICROSOFT MATHEMATICS 4.0 1
 MENGGAMBAR GRAFIK DENGAN MICROSOFT MATHEMATICS 4.0 1 Oleh Kuswari Hernawati Jurusan Pendidikan Matematika FMIPA UNY [email protected] PENDAHULUAN Microsoft Mathematics adalah program edukasi, yang dibuat
MENGGAMBAR GRAFIK DENGAN MICROSOFT MATHEMATICS 4.0 1 Oleh Kuswari Hernawati Jurusan Pendidikan Matematika FMIPA UNY [email protected] PENDAHULUAN Microsoft Mathematics adalah program edukasi, yang dibuat
LINEAR PROGRAMMING-1
 /5/ LINEAR PROGRAMMING- DR.MOHAMMAD ABDUL MUKHYI, SE., MM METODE KUANTITATIF Perumusan PL Ada tiga unsur dasar dari PL, ialah:. Fungsi Tujuan. Fungsi Pembatas (set ketidak samaan/pembatas strukturis) 3.
/5/ LINEAR PROGRAMMING- DR.MOHAMMAD ABDUL MUKHYI, SE., MM METODE KUANTITATIF Perumusan PL Ada tiga unsur dasar dari PL, ialah:. Fungsi Tujuan. Fungsi Pembatas (set ketidak samaan/pembatas strukturis) 3.
DAFTAR PUSTAKA. (diakses 1 maret 2016)
 DAFTAR PUSTAKA [1] http://www.surakarta.go.id/konten/bus-tingkat-werkudara# (diakses 28 februari 2016) [2] Anonim. www.opengl.org (diakses 1 maret 2016) [3] Haemel, Nicholas, et al. 2011. OpenGL super
DAFTAR PUSTAKA [1] http://www.surakarta.go.id/konten/bus-tingkat-werkudara# (diakses 28 februari 2016) [2] Anonim. www.opengl.org (diakses 1 maret 2016) [3] Haemel, Nicholas, et al. 2011. OpenGL super
PENENTUAN RUTE TERPENDEK DENGAN METODE FLOYD WARSHALL PADA PETA DIGITAL UNIVERSITAS SUMATERA UTARA SKRIPSI DHYMAS EKO PRASETYO
 PENENTUAN RUTE TERPENDEK DENGAN METODE FLOYD WARSHALL PADA PETA DIGITAL UNIVERSITAS SUMATERA UTARA SKRIPSI DHYMAS EKO PRASETYO 091402023 PROGRAM STUDI TEKNOLOGI INFORMASI FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI
PENENTUAN RUTE TERPENDEK DENGAN METODE FLOYD WARSHALL PADA PETA DIGITAL UNIVERSITAS SUMATERA UTARA SKRIPSI DHYMAS EKO PRASETYO 091402023 PROGRAM STUDI TEKNOLOGI INFORMASI FAKULTAS ILMU KOMPUTER DAN TEKNOLOGI
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB. SHEET PRAKTIKUM GRAFIKA KOMPUTER
 No. : ST/EKA/PTI275/05 Revisi : 02 1 P a g e A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer. Bagian dari komputasi
No. : ST/EKA/PTI275/05 Revisi : 02 1 P a g e A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer. Bagian dari komputasi
Program 1 /* Menampilkan Bayangan sebuah obyek sumber file */
 No. : ST/EKA/PTI223/10 Revisi : 01 Senin 010509 Hal. 1 dari 5 hal. Pengantar Untuk menghasilkan gambar yang realistik perlu memodelkan pencerminan dan pembiasan maupun memunculkan bayangan karena pengaruh
No. : ST/EKA/PTI223/10 Revisi : 01 Senin 010509 Hal. 1 dari 5 hal. Pengantar Untuk menghasilkan gambar yang realistik perlu memodelkan pencerminan dan pembiasan maupun memunculkan bayangan karena pengaruh
ORIENTASI PADA PRA PLOTTING PETA BERSISTEM KOORDINAT LOKAL TERHADAP SISTEM KOORDINAT FIX (TETAP)
 Orientasi pada Pra Plotting... ORIENTASI PADA PRA PLOTTING PETA BERSISTEM KOORDINAT LOKAL TERHADAP SISTEM KOORDINAT FIX (TETAP) Yuwono 1), AdiKurniawan 2) 1) Jurusan Teknik Geomatika, ITS, 2) Jurusan Teknik
Orientasi pada Pra Plotting... ORIENTASI PADA PRA PLOTTING PETA BERSISTEM KOORDINAT LOKAL TERHADAP SISTEM KOORDINAT FIX (TETAP) Yuwono 1), AdiKurniawan 2) 1) Jurusan Teknik Geomatika, ITS, 2) Jurusan Teknik
Vektor-Vektor. Ruang Berdimensi-2. Ruang Berdimensi-3
 Vektor-Vektor dalam Ruang Berdimensi-2 dan Ruang Berdimensi-3 Disusun oleh: Achmad Fachrurozi Albert Martin Sulistio Iffatul Mardhiyah Rifki Kosasih Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan
Vektor-Vektor dalam Ruang Berdimensi-2 dan Ruang Berdimensi-3 Disusun oleh: Achmad Fachrurozi Albert Martin Sulistio Iffatul Mardhiyah Rifki Kosasih Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan
/*Bismillahirrohmanirrohim _Fatimah_Rombel 2_Projek_Akhir_Komgraf*/ #include <stdio.h> #include <stdlib.h> #include <string.
 /*Bismillahirrohmanirrohim.. 5302413025_Fatimah_Rombel 2_Projek_Akhir_Komgraf*/ #include #include #include #include "SOIL.h" #include float z_pos = -5.0f; float
/*Bismillahirrohmanirrohim.. 5302413025_Fatimah_Rombel 2_Projek_Akhir_Komgraf*/ #include #include #include #include "SOIL.h" #include float z_pos = -5.0f; float
WATERMARKING CITRA DIGITAL YANG TAHAN TERHADAP GEOMETRIC ATTACKS
 WATERMARKING CITRA DIGITAL YANG TAHAN TERHADAP GEOMETRIC ATTACKS Disusun Oleh : Cosmas Surya Hadi (0822070) Jurusan Teknik Elektro, Fakultas Teknik, Jl. Prof. drg. Suria Sumantri, MPH No. 65, Bandung 40164,
WATERMARKING CITRA DIGITAL YANG TAHAN TERHADAP GEOMETRIC ATTACKS Disusun Oleh : Cosmas Surya Hadi (0822070) Jurusan Teknik Elektro, Fakultas Teknik, Jl. Prof. drg. Suria Sumantri, MPH No. 65, Bandung 40164,
TUGAS AKHIR DESAIN DAN IMPLEMENTASI GRAPHIC USER INTERFACE UNTUK MESIN CNC DENGAN TAMPILAN 3-D MENGGUNAKAN WPF DAN VISUAL BASIC 2008
 TUGAS AKHIR DESAIN DAN IMPLEMENTASI GRAPHIC USER INTERFACE UNTUK MESIN CNC DENGAN TAMPILAN 3-D MENGGUNAKAN WPF DAN VISUAL BASIC 2008 Oleh Ade Fadli NIM : 13204144 PROGRAM STUDI TEKNIK ELEKTRO SEKOLAH TEKNIK
TUGAS AKHIR DESAIN DAN IMPLEMENTASI GRAPHIC USER INTERFACE UNTUK MESIN CNC DENGAN TAMPILAN 3-D MENGGUNAKAN WPF DAN VISUAL BASIC 2008 Oleh Ade Fadli NIM : 13204144 PROGRAM STUDI TEKNIK ELEKTRO SEKOLAH TEKNIK
1. Pendahuluan Latar Belakang
 1. Pendahuluan 1.1. Latar Belakang Meningkatnya kebutuhan manusia akan sistem keamanan berbasis tracking yang dapat bekerja secara otomatis membuat ilmuwan mulai menciptakan berbagai macam teknologi dan
1. Pendahuluan 1.1. Latar Belakang Meningkatnya kebutuhan manusia akan sistem keamanan berbasis tracking yang dapat bekerja secara otomatis membuat ilmuwan mulai menciptakan berbagai macam teknologi dan
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB. SHEET PRAKTIKUM GRAFIKA KOMPUTER
 No. : ST/EKA/PTI223/05 Revisi : 02 Senin 010409 Hal. 1 dari 8 hal. A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer.
No. : ST/EKA/PTI223/05 Revisi : 02 Senin 010409 Hal. 1 dari 8 hal. A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer.
Penerapan Transformasi Geometri pada Karya Seni Indonesia
 Penerapan Transformasi Geometri pada Karya Seni Indonesia Letivany Aldina/13514067 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Penerapan Transformasi Geometri pada Karya Seni Indonesia Letivany Aldina/13514067 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
GRAFIKA GAME. Aditya Wikan Mahastama. Rangkuman Transformasi Dua Dimensi UNIV KRISTEN DUTA WACANA TEKNIK INFORMATIKA GENAP 1213
 GRAFIKA GAME Aditya Wikan Mahastama [email protected] Rangkuman Transformasi Dua Dimensi 5 UNIV KRISTEN DUTA WACANA TEKNIK INFORMATIKA GENAP 1213 Transformasi (Rangkuman) Grafika Komputer Semester Gasal
GRAFIKA GAME Aditya Wikan Mahastama [email protected] Rangkuman Transformasi Dua Dimensi 5 UNIV KRISTEN DUTA WACANA TEKNIK INFORMATIKA GENAP 1213 Transformasi (Rangkuman) Grafika Komputer Semester Gasal
DIAN PRATIWI. ST, MTI
 DIAN PRATIWI. ST, MTI PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Diterbitkan melalui Nida Dwi Karya Publishing PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Oleh: Dian Pratiwi, ST, MTI Copyright 2015
DIAN PRATIWI. ST, MTI PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Diterbitkan melalui Nida Dwi Karya Publishing PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Oleh: Dian Pratiwi, ST, MTI Copyright 2015
Penerapan Transformasi Lanjar pada Proses Pengolahan Gambar
 Penerapan Transformasi Lanjar pada Proses Pengolahan Gambar Pratama Nugraha Damanik 13513001 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
Penerapan Transformasi Lanjar pada Proses Pengolahan Gambar Pratama Nugraha Damanik 13513001 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
SATUAN ACARA PERKULIAHAN
 SATUAN ACARA PERKULIAHAN Mata Kuliah : PENGANTAR GRAFIK KOMPUTER & OLAH CITRA Fakultas : Ilmu Komputer Jurusan : S1 Sistem Informasi KODE MATA KULIAH / SKS : AK-011204 / 2 SKS PERTEMUAN POKOK BAHASAN &
SATUAN ACARA PERKULIAHAN Mata Kuliah : PENGANTAR GRAFIK KOMPUTER & OLAH CITRA Fakultas : Ilmu Komputer Jurusan : S1 Sistem Informasi KODE MATA KULIAH / SKS : AK-011204 / 2 SKS PERTEMUAN POKOK BAHASAN &
UNIVERSITAS BINA NUSANTARA SIMULASI KINEMATIKA LENGAN ROBOT INDUSTRI DENGAN 6 DERAJAT KEBEBASAN
 UNIVERSITAS BINA NUSANTARA Jurusan Sistem Komputer Skripsi Sarjana Komputer Semester Genap tahun 2003/2004 SIMULASI KINEMATIKA LENGAN ROBOT INDUSTRI DENGAN 6 DERAJAT KEBEBASAN Andy Rosady 0400530056 Riza
UNIVERSITAS BINA NUSANTARA Jurusan Sistem Komputer Skripsi Sarjana Komputer Semester Genap tahun 2003/2004 SIMULASI KINEMATIKA LENGAN ROBOT INDUSTRI DENGAN 6 DERAJAT KEBEBASAN Andy Rosady 0400530056 Riza
LAYOUT OBYEK MODUL 3 MENYUSUN, MENATA, MENGATUR, MENGUBAH OBYEK
 LAYOUT OBYEK MODUL 3 MENYUSUN, MENATA, MENGATUR, MENGUBAH OBYEK Pada bab sebelumnya kita sudah membicarakan tentang editing obyek dasar. Pada pembahasan tersebut adalah cara mudah dan cepat untuk melakukan
LAYOUT OBYEK MODUL 3 MENYUSUN, MENATA, MENGATUR, MENGUBAH OBYEK Pada bab sebelumnya kita sudah membicarakan tentang editing obyek dasar. Pada pembahasan tersebut adalah cara mudah dan cepat untuk melakukan
ABSTRAK. PDF created with FinePrint pdffactory Pro trial version
 ABSTRAK Scattering Parameters (S-Parameter) merupakan suatu metode pengukuran yang berhubungan dengan daya datang dan daya pantul. Dalam tugas akhir ini dibahas prinsip kerja S-Parameter yang berhubungan
ABSTRAK Scattering Parameters (S-Parameter) merupakan suatu metode pengukuran yang berhubungan dengan daya datang dan daya pantul. Dalam tugas akhir ini dibahas prinsip kerja S-Parameter yang berhubungan
Aplikasi Quartenion pada Game Engine
 Aplikasi Quartenion pada Game Engine Ali Akbar - 13514080 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia [email protected]
Aplikasi Quartenion pada Game Engine Ali Akbar - 13514080 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia [email protected]
Chapter 5 GENERAL VECTOR SPACE 5.1. REAL VECTOR SPACES 5.2. SUB SPACES
 Chapter 5 GENERAL VECTOR SPACE 5.1. REAL VECTOR SPACES 5.2. SUB SPACES Definisi : VECTOR SPACE Jika V adalah ruang vektor dimana u,v,w merupakan objek dalam V sebagai vektor, dan terdapat skalar k dan
Chapter 5 GENERAL VECTOR SPACE 5.1. REAL VECTOR SPACES 5.2. SUB SPACES Definisi : VECTOR SPACE Jika V adalah ruang vektor dimana u,v,w merupakan objek dalam V sebagai vektor, dan terdapat skalar k dan
TRANSFORMASI SUMBU KOORDINAT
 TRANSFORMASI SUMBU KOORDINAT Tujuan Pembelajaran Umum Mahasiswa mampu menyelesaikan analisa struktur dengan cara Analisa Struktur Metode Matriks (ASMM) 3.5 Pendahuluan Transformasi Sumbu Koordinat Tujuan
TRANSFORMASI SUMBU KOORDINAT Tujuan Pembelajaran Umum Mahasiswa mampu menyelesaikan analisa struktur dengan cara Analisa Struktur Metode Matriks (ASMM) 3.5 Pendahuluan Transformasi Sumbu Koordinat Tujuan
Drawing, Viewport, dan Transformasi. Pertemuan - 02
 Drawing, Viewport, dan Transformasi Pertemuan - 02 Ruang Lingkup Definisi Drawing Viewport Transfomasi Definisi Bagian dari grafik komputer meliputi: 1. Citra (Imaging) : mempelajari cara pengambilan dan
Drawing, Viewport, dan Transformasi Pertemuan - 02 Ruang Lingkup Definisi Drawing Viewport Transfomasi Definisi Bagian dari grafik komputer meliputi: 1. Citra (Imaging) : mempelajari cara pengambilan dan
TUGAS PENGANTAR GRAFIK KOMPUTER DAN OLAH CITRA
 TUGAS PENGANTAR GRAFIK KOMPUTER DAN OLAH CITRA NAMA : HERU SANJAYA NPM : 39110387 KELAS : 2DB23 Gambar dibawah ini adalah tampilan awal Code Blocks. Setelah itu, pilih menu Settings Compiler and Debugger.
TUGAS PENGANTAR GRAFIK KOMPUTER DAN OLAH CITRA NAMA : HERU SANJAYA NPM : 39110387 KELAS : 2DB23 Gambar dibawah ini adalah tampilan awal Code Blocks. Setelah itu, pilih menu Settings Compiler and Debugger.
Grafika Komputer. Evangs Mailoa
 Grafika Komputer Evangs Mailoa Yang dipelajari hari ini: Aritmatika Vektor Konsep Geometrik Titik, Garis dan Bidang Perkalian Titik Pengenalan Kenapa kita perlu belajar vektor? Kita butuh untuk mengetahui
Grafika Komputer Evangs Mailoa Yang dipelajari hari ini: Aritmatika Vektor Konsep Geometrik Titik, Garis dan Bidang Perkalian Titik Pengenalan Kenapa kita perlu belajar vektor? Kita butuh untuk mengetahui
19. TRANSFORMASI A. Translasi (Pergeseran) B. Refleksi (Pencerminan) C. Rotasi (Perputaran)
 9. TRANSFORMASI A. Translasi (Pergeseran) ; T = b a b a atau b a B. Refleksi (Pencerminan). Bila M matriks refleksi berordo, maka: M atau M. Matriks M karena refleksi terhadap sumbu, sumbu, garis =, dan
9. TRANSFORMASI A. Translasi (Pergeseran) ; T = b a b a atau b a B. Refleksi (Pencerminan). Bila M matriks refleksi berordo, maka: M atau M. Matriks M karena refleksi terhadap sumbu, sumbu, garis =, dan
SATUAN PERKULIAHAN. 10 menit -apersepsi -motivasi Diberikan dalam bahasa Inggris 100% 2 Kegiatan inti:
 I. IDENTITAS MATA KULIAH II. SATUAN PERKULIAHAN b. Materi pokok : Pengenalan Bentuk SPL dengan variabel d. Pertemuan ke : e. Waktu : menit STANDAR KOMPETENSI DAN INDIKATOR Mahasiswa memiliki keterampilan
I. IDENTITAS MATA KULIAH II. SATUAN PERKULIAHAN b. Materi pokok : Pengenalan Bentuk SPL dengan variabel d. Pertemuan ke : e. Waktu : menit STANDAR KOMPETENSI DAN INDIKATOR Mahasiswa memiliki keterampilan
Variable. Variable (cont) Variable (cont) Tipe Data
 Variable Variable (cont) Variable dapat didefinisikan sebagai bagian dari memory untuk menyimpan nilai yang telah ditentukan. Setiap variable memrlukan identifier yang dapat membedakannya dari variable
Variable Variable (cont) Variable dapat didefinisikan sebagai bagian dari memory untuk menyimpan nilai yang telah ditentukan. Setiap variable memrlukan identifier yang dapat membedakannya dari variable
Gambar 1. Contoh tekstur makrostruktur
 No. : ST/EKA/PTI223/08 Revisi : 02 Senin 010510 Hal. 1 dari 14 hal. Pengantar Tekstur adalah tampilan permukaan (corak) dari suatu benda yang dapat dinilai dengan cara dilihat atau diraba. Pada prakteknya,
No. : ST/EKA/PTI223/08 Revisi : 02 Senin 010510 Hal. 1 dari 14 hal. Pengantar Tekstur adalah tampilan permukaan (corak) dari suatu benda yang dapat dinilai dengan cara dilihat atau diraba. Pada prakteknya,
BAB 3 PERANCANGAN DAN PEMBUATAN. Engine akan dirancang agar memenuhi syarat maintainability, reusability dan
 13 BAB 3 PERANCANGAN DAN PEMBUATAN 3.1 Perancangan Engine Engine akan dirancang agar memenuhi syarat maintainability, reusability dan usability. Maintainability berarti kode program engine harus mudah
13 BAB 3 PERANCANGAN DAN PEMBUATAN 3.1 Perancangan Engine Engine akan dirancang agar memenuhi syarat maintainability, reusability dan usability. Maintainability berarti kode program engine harus mudah
APLIKASI MENGUBAH POLARISASI FRAME GAMBAR 2 DIMENSI MENJADI 3 DIMENSI
 APLIKASI MENGUBAH POLARISASI FRAME GAMBAR 2 DIMENSI MENJADI 3 DIMENSI ABDUL ARDI 41507110115 PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS ILMU KOMPUTER UNIVERSITAS MERCU BUANA JAKARTA 2014 APLIKASI MENGUBAH
APLIKASI MENGUBAH POLARISASI FRAME GAMBAR 2 DIMENSI MENJADI 3 DIMENSI ABDUL ARDI 41507110115 PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS ILMU KOMPUTER UNIVERSITAS MERCU BUANA JAKARTA 2014 APLIKASI MENGUBAH
Linear Discrimant Model
 (update 1 Februari 01) Lecture 3 Linear Discrimant Model Learning a Class from Examples (Alpaydin 009) Class C of a family car Prediction: Is car x a family car? Knowledge extraction: What do people expect
(update 1 Februari 01) Lecture 3 Linear Discrimant Model Learning a Class from Examples (Alpaydin 009) Class C of a family car Prediction: Is car x a family car? Knowledge extraction: What do people expect
PEMODELAN OBYEK DENGAN METODE KURVA PARAMETRIK
 PEMODELAN OBYEK DENGAN METODE KURVA PARAMETRIK Ina Agustina Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta
PEMODELAN OBYEK DENGAN METODE KURVA PARAMETRIK Ina Agustina Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta
ALJABAR LINEAR SUMANANG MUHTAR GOZALI KBK ANALISIS
 ALJABAR LINEAR SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam Shalawat serta salam
ALJABAR LINEAR SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam Shalawat serta salam
Titik hasil transformasi dapat diperoleh melalui rumus affine transformation.
 TRANSFORMASI 3D 1. PENDAHULUAN Transformasi 3D pada dasarnya hampir sama dengan transformasi 2D, hanya pada 3D kita menghitung sumbu Z. Sama seperti pada 2D, ada tiga transformasi dasar yang dapat dilakukan
TRANSFORMASI 3D 1. PENDAHULUAN Transformasi 3D pada dasarnya hampir sama dengan transformasi 2D, hanya pada 3D kita menghitung sumbu Z. Sama seperti pada 2D, ada tiga transformasi dasar yang dapat dilakukan
Pewarnaan dan Perputaran Polygon Untuk Objek Gambar Segi Tiga dan Segi Empat Menggunakan Program OPENGL 32
 Pewarnaan dan Perputaran Polygon Untuk Objek Gambar Segi Tiga dan Segi Empat Menggunakan Program OPENGL 32 Aqwam Rosadi Kardian, Bheta Agus Wardijono STMIK JAKARTA STI&K [email protected], [email protected]
Pewarnaan dan Perputaran Polygon Untuk Objek Gambar Segi Tiga dan Segi Empat Menggunakan Program OPENGL 32 Aqwam Rosadi Kardian, Bheta Agus Wardijono STMIK JAKARTA STI&K [email protected], [email protected]
Nama Soal Pembagian Ring Road Batas Waktu 1 detik Nama Berkas Ringroad[1..10].out Batas Memori 32 MB Tipe [output only] Sumber Brian Marshal
![Nama Soal Pembagian Ring Road Batas Waktu 1 detik Nama Berkas Ringroad[1..10].out Batas Memori 32 MB Tipe [output only] Sumber Brian Marshal Nama Soal Pembagian Ring Road Batas Waktu 1 detik Nama Berkas Ringroad[1..10].out Batas Memori 32 MB Tipe [output only] Sumber Brian Marshal](/thumbs/56/39098166.jpg) Nama Soal Pembagian Ring Road Batas Waktu 1 detik Nama Berkas Ringroad[1..10].out Batas Memori 32 MB Tipe [output only] Sumber Brian Marshal Deskripsi Soal Dalam rangka mensukseskan program Visit Indonesia,
Nama Soal Pembagian Ring Road Batas Waktu 1 detik Nama Berkas Ringroad[1..10].out Batas Memori 32 MB Tipe [output only] Sumber Brian Marshal Deskripsi Soal Dalam rangka mensukseskan program Visit Indonesia,
04-Ruang Vektor dan Subruang
 04-Ruang Vektor dan Subruang Vektor (1) Dosen: Anny Yuniarti, M.Comp.Sc Gasal 2011-2012 Anny2011 1 Agenda Bagian 1: Ruang Vektor Bagian 2: Nullspace of A: Solusi Ax = 0 Bagian 3: Rank dan Row-reduced-form
04-Ruang Vektor dan Subruang Vektor (1) Dosen: Anny Yuniarti, M.Comp.Sc Gasal 2011-2012 Anny2011 1 Agenda Bagian 1: Ruang Vektor Bagian 2: Nullspace of A: Solusi Ax = 0 Bagian 3: Rank dan Row-reduced-form
Muhammad Zidny Naf an, M.Kom. Gasal 2015/2016
 MKB3383 - Teknik Pengolahan Citra Transformasi Geometri Muhammad Zidny Naf an, M.Kom. Gasal 2015/2016 Outline Pengantar operasi geometrik Penggeseran citra Pemutaran citra Interpolasi piksel Zooming Pencerminan
MKB3383 - Teknik Pengolahan Citra Transformasi Geometri Muhammad Zidny Naf an, M.Kom. Gasal 2015/2016 Outline Pengantar operasi geometrik Penggeseran citra Pemutaran citra Interpolasi piksel Zooming Pencerminan
BAHAN PRAKTIKUM GEOGEBRA
 BAHAN PRAKTIKUM GEOGEBRA Berikut ini diberikan petunjuk praktikum pembelajaran Matematika Aljabar dan Kalkulus menggunakan Geogebra. Geogebra merupakan software yang berisi aplikasi aljabar dan geometri.
BAHAN PRAKTIKUM GEOGEBRA Berikut ini diberikan petunjuk praktikum pembelajaran Matematika Aljabar dan Kalkulus menggunakan Geogebra. Geogebra merupakan software yang berisi aplikasi aljabar dan geometri.
Perspective & Imaging Transformation
 Perspective & Imaging Transformation Perspective & Imaging Transformation y Y Bidang Citra x X (X,Y,Z) (x,y) Pusat Lensa z Z x Z - X 3 Camera coordinate system (x,y,z) dan World coordinate system (X,Y,Z)
Perspective & Imaging Transformation Perspective & Imaging Transformation y Y Bidang Citra x X (X,Y,Z) (x,y) Pusat Lensa z Z x Z - X 3 Camera coordinate system (x,y,z) dan World coordinate system (X,Y,Z)
T DAR INTEGRAL TAK MUTLAK
 INTEGRAL TAK MUTLAK T 515.43 DAR INTEGRAL TAK MUTLAK A B S T R A K Setiap teori integral selalu memuat masalah sebagai berikut. Jika untuk setiap n berlaku fungsi f» terintegral dan barisan fungsi {f n
INTEGRAL TAK MUTLAK T 515.43 DAR INTEGRAL TAK MUTLAK A B S T R A K Setiap teori integral selalu memuat masalah sebagai berikut. Jika untuk setiap n berlaku fungsi f» terintegral dan barisan fungsi {f n
