Bab II Tinjauan Pustaka
|
|
|
- Surya Susman
- 9 tahun lalu
- Tontonan:
Transkripsi
1 4 Bab II Tinauan Putaka II. Prilangan Sbidang Jalan dan Jalan Rl Prilangan bidang antara alan dngan alan rl (prlintaan) rupakan kau khuu pada uatu rua alan raya dngan tanggung awab untuk pngaturan dan prtibangan kaanan trbagi pada kpntingan alan dan alan rl. Pngudi kndaraan yang ndkat k uatu prlintaan haru iliki pandangan yang tidak trhalang k alur auk yang cukup untuk ungkinkan kontrol trhadap kndaraan. Slain ditinau dari gi klaatan, prlintaan uga brdapak trhadap tundaan kndaraan. Tundaan yang tradi pada prilangan bidang antara alan dan alan rl dipngaruhi olh aktor-aktor : () pngopraian krta yang liputi kcpatan, panang krta, dan rkuni krta yang lwat dala atu hari; () pngopraian alan yang liputi kcpatan kndaraan dan tingkat kpadatan aru; (3) kondii gotrik alan yang liputi lbar alan, ulah laur, dan kbradaan piah aru, kbradaan rubl trip, dan alur alan rl. II. Karaktritik Lalu Linta Lalu linta rupakan intraki antara bbrapa koponn yang bntuk uatu it yang trdiri dari alan, anuia, dan kndaraan. ntuk kbrhailan pngopraiannya, ktiga koponn ini haru kopatibl. ala knyataan harihari hal ini tidak prnah tradi, akibatnya it lalu linta alan ringkali gagal. Kclakaan, kactan, dan gangguan lalu linta rupakan contoh kgagalan it dan hapir ua kau dibabkan olh ktidakuaian antar ktiga koponn, atau antar atu koponn dan lingkungan diana it broprai. Ada tiga karaktritik prir dala tori aru lalu linta yang aling trkait, cara akrokopik diknal dngan aru (low), kcpatan (pd), dan krapatan (dnity), diana ktiga variabl ini nggabarkan kualita tingkat playanan yang dialai olh pngudi kndaraan (Martin dan Brian, 967).
2 5 A. Aru dan olu Aru lalu linta (low) adalah ulah kndaraan yang lintai atu titik pngaatan pada pnggal alan trtntu pada priod waktu trtntu, diukur dala atuan kndaraan pr atuan waktu. Sdangkan volu adalah ulah kndaraan yang lintai uatu rua alan pada priod waktu trtntu, diukur dala atuan kndaraan pr atuan waktu. olu biaanya dihitung dala kndaraan/hari atau kndaraan/a. olu dapat uga dinyatakan dala priod waktu yang lain. ala pbahaannya volu dibagi nadi : () volu harian (daily volu) olu harian ini digunakan bagai daar untuk prncanaan alan dan obrvai uu tntang trnd. Pngukuran volu harian dibdakan nadi : (a) Avrag Annual aily Traic (AAT), dala atuan vhicl pr hour (vph) rata-rata yakni volu yang diukur laa 4 a dala kurun waktu 365 hari. (b) Avrag Annual Wkday Traic (AAWT), dala atuan vhicl pr hour (vph) rata-rata yakni volu yang diukur laa 4 a pada hari kra laa atu bulan dala kurun waktu 365 hari. (c) Avrag aily Traic (AT), dala atuan vhicl pr hour (vph) rata-rata yakni volu yang diukur laa 4 a pnuh dala priod waktu trtntu yang lbih kcil dari atu tahun, ial na bulan, atu ui, inggu. (d) Avrag Wkday Traic (AWT), dala atuan vhicl pr hour (vph) rata-rata yakni volu yang diukur laa 4 a pada hari kra laa atu bulan dala kurun waktu kurang dari atu tahun. () volu a-an (hourly volu) Yakni uatu pngaatan trhadap aru lalu linta untuk nntukan a puncak laa priod pagi dan or yang biaanya tradi kibukan akibat orang prgi dan pulang kra. ari pngaatan trbut dapat diktahui aru yang paling bar yang dibut bagai a puncak. Aru
3 6 pada a puncak ini dipakai bagai daar untuk dain alan raya dan analii oprai lainnya. (3) volu pr ub a (ubhourly volu) Yakni aru yang diurvi dala priod waktu lbih kcil dari atu a. B. Kcpatan (Spd) Kcpatan adalah baran yang nunukkan arak yang ditpuh kndaraan dibagi waktu tpuh. Kcpatan uunya dibagi nadi tiga ni : () kcpatan tpat (pot pd) Adalah kcpatan kndaraan kndaraan pada uatu aat diukur dari uatu tpat yang ditntukan. () kcpatan brgrak (running pd) Adalah kcpatan kndaraan rata-rata pada uatu alur pada aat kndaraan brgrak dan didapat dngan bagi panang alur dibagi dngan laa waktu kndaraan brgrak npuh alur trbut. (3) kcpatan pralanan ( ourny pd) Adalah kcpatan kti kndaraan yang dang dala pralanan antara dua tpat, dan rupakan arak antara dua tpat dibagi dngan laa waktu bagi kndaraan untuk nylaikan pralanan antara dua tpat trbut, dngan laa waktu ini ncakup tiap waktu brhnti yang ditibulkan olh habatan (pnundaan) lalu linta. Panang linta pngaatan untuk urvai kcpatan tpat dapat dilihat pada Tabl II. brikut ini : Tabl II. Panang Lintaan Pngaatan yang ianurkan Kcpatan rata-rata aru lalu linta Panang lintaan (k/a) () < > Subr : irktorat Jndral Prhubungan arat, 990
4 7 ala prgrakan aru lalu linta, tiap kndaraan bralan pada kcpatan yang brbda. ngan dikian dala aru lalu linta tidak diknal kcpatan tunggal ttapi lbih diknal bagai ditribui dari kcpatan kndaraan tunggal. ari ditribui trbut ulah rata-rata atau nilai tipikal dapat digunakan untuk ngtahui karaktritik dari aru lalu linta. ala prhitungannya, kcpatan rata-rata dibdakan nadi : () Ti Man Spd ( t ) Adalah kcpatan rata-rata dari luruh kndaraan yang lwati uatu titik dari alan laa priod waktu trtntu. () Spac Man Spd ( ) Adalah kcpatan dari luruh kndaraan yang npati pnggalan alan laa priod waktu trtntu. Kduanya dapat dihitung dari rangkaian pngukuran waktu tpuh dan pngukuran arak nurut ruu di bawah ini (May, 990) : t n d t i i...(ii.) n n d i ti n...(ii.) Wadrop brikan praaan hubungan uu antara t + t dan adalah : σ...(ii.3) diana : pac an pd (k/a, /dt) t ti an pd (k/a, /dt) σ d t i n ipangan baku dari pac an pd arak tpuh (k, tr) waktu tpuh kndaraan (a, dtik) ulah kndaraan yang diaati
5 8 Sdangkan untuk nghitung barnya kcpatan rata-rata ruang dari kluruhan lalu linta kndaraan brotor digunakan ruu (Budiarto,998) : r n diana : MC. MC n + n MC L + n. L L + n + n H H. H...(II.4) r kcpatan rata-rata ruang dari luruh kndaraan (k/a) n MC n L n H MC ulah apl pada otor ulah apl kndaraan ringan ulah apl kndaraan brat kcpatan rata-rata ruang pda otor (k/a) L H kcpatan rata-rata ruang kndaraan ringan (k/a) kcpatan rata-rata ruang kndaraan brat (k/a) Slanutnya, untuk ndapatkan variabl krapatan () dilakukan dngan bagi ulah aru () dala atuan p dngan kcpatan rata-rata ruang kluruhan ( ). r C. Krapatan (nity) Krapatan didiniikan bagai ulah kndaraan yang npati uatu panang alan atau laur, cara uu dikprikan dala vhicl pr il (vp) atau vhicl pr il pr lan (vppl). Krapatan ulit diukur cara langung di lapangan, hingga nilai krapatan diprolh dari hubungan : Shingga...(II.5) diana : volu (knd/a) pac an pd (k/a) krapatan (knd/k)
6 9 II.3 Ekivalni Mobil Pnupang ntuk kprluan analia dan prhitungan dari aru lalu linta yang trdiri dari brbagai aca tip aka prlu dikonvrikan k dala atuan kndaraan ringan, yang diknal bagai atuan obil pnupang (p) dngan nggunakan aktor kivalni obil pnupang. P (997) ndiniikan atuan obil pnupang dan kivaln obil pnupang bagai brikut : () atuan obil pnupang (p) yaitu atuan aru diana aru dari brbagai tip kndaraan tlah diubah nadi kndaraan ringan (trauk obil pnupang dngan nggunakan p); () kivalni obil pnupang (p) yaitu aktor konvri brbagai ni kndaraan dibandingkan dngan obil pnupang atau kndaraan ringan lainnya hubungan dngan dapaknya pada prilaku lalu linta, diana untuk obil pnupang dan kndaraan ringan lainnya nilai p aa dngan,0. Nilai atuan obil pnupang pada darah rua nggunakan nilai kivaln alan prkotaan trbagi pada Bab 5 MKJI 997. Tabl II. Nilai p untuk Jalan Prkotaan Trbagi dan Satu Arah Subr : P, 997
7 0 iana klaiikai kndaraan yang diakud bagai brikut : () kndaraan ringan (L) yaitu kndaraan brotor bra dua dngan pat roda dngan arak a,0-3,0 tr, liputi obil pnupang, ikrobi, pick up, dan truk kcil uai klaiikai Bina Marga; () kndaraan brat (H) yaitu kndaraan brotor dngan lbih dari pat roda yang liputi bi, truk a, truk 3 a, dan truk kobinai uai it klaiikai Bina Marga; (3) pda otor (MC) yaitu kndaraan brotor dngan dua atau tiga roda yang liputi pda otor dan kndaraan roda tiga uai it klaiikai Bina Marga. II.4 Kapaita Kapaita didiniikan bagai aru akiu lalui uatu titik di alan yang dapat diprtahankan pr atuan a pada kondii trtntu. ntuk alan dua laur dua arah, kapaita ditntukan untuk aru dua arah (kobinai dua arah), ttapi untuk alan dngan banyak laur, aru dipiahkan pr arah dan kapaita ditntukan pr laur. Praaan daar untuk nntukan kapaita adalah bagai brikut : C C o x FC W x FC SP x FC SF x FC CS...(II.6) diana : C kapaita (p/a) C o kapaita daar (p/a) FC W aktor pnyuaian lbar alur lalu linta FC SP aktor pnyuaian piahan arah (hanya untuk alan tak trbagi), brnilai,0 untuk alan trbagi dan alan atu arah FC SF aktor pnyuaian habatan aping dan bahu alan/krb FC CS aktor pnyuaian ukuran kota
8 Tabl II.3 Kapaita aar (C o ) Subr : P, 997 Tabl II.4 Faktor Pnyuaian Kapaita untuk Lbar Jalur Lalu Linta (FC W ) Subr : P, 997
9 Tabl II.5 Faktor Pnyuaian Kapaita untuk Habatan Saping dan Jarak Krb Pnghalang (FC SF ) Subr : P, 997 Tabl II.6 Faktor Pnyuaian Kapaita untuk kuran Kota (FC CS ) Subr : P,997 II.5 Modl Hubungan Karaktritik Aru Lalu Linta Pndkatan tori dari prgrakan kndaraan di alan ring diabil dari prinip aliran luida. Hal ini dibabkan trdapatt kiripan antara aliran luida dan prgrakan aru pada kondii kpadatan tinggi. Modl yang prtaa diaukan dngan ngauikan nona kadaan tunggal (ingl rgi) ata rntang koplk dari kondii aliran aru yang liputi aru bba dan kondii aru act. Modl yang diaukan blakangan bruaha lbih prntaikan kondii bnarnya di lapangan dngan
10 3 prtibangkan pnggabungan dua kadaan, yaitu kadaan aru bba dan kadaan aru act dngan ngnalkan paratr tabahan. A. Modl Linir Grnhild Modl ini adalah odl yang paling awal trcatat dala uaha ngaati prilaku lalu linta. Grnhild ngadakan tudi pada alur alan di luar kota Ohio, diana kondii lalu linta nuhi yarat karna tanpa gangguan dan brgrak cara bba (tady tat condition). Grnhild ndapatkan hail bahwa hubungan antara kcpatan dan krapatan briat linir. Brdaarkan pnlitian-pnlitian lanutnya trdapat hubungan yang rat antara odl linir dngan kadaan data di lapangan. Hubungan linir kcpatan dan krapatan ini nadi hubungan yang paling populr dala tinauan prgrakan lalu linta, ngingat ungi hubungannya adalah yang paling drhana hingga udah ditrapkan. Modl ini dapat diabarkan bagai brikut :...(II.7) diana : kcpatan rata-rata ruang kcpatan rata-rata ruang kadaan aru bba (r low) krapatan pada aat act (a dnity) krapatan Pada aat kcpatan rupakan kcpatan aru bba (r low), pngudi dapat acu kndaraannya pada kcpatan yang diinginkannya dangkan pada aat kondii krapatan act (a dnity), kndaraan tidak dapat brgrak aa kali atau kondii kcpatan angat kcil. ntuk ndapatkan nilai kontanta dan, aka praaan (II.7) diubah nadi praaan linir y a + bx, dngan ialkan : y x a b
11 4 Hubungan antara aru dan krapatan diprolh dari ubtitui k praaan (II.7) didapat :...(II.8) Hubungan antara aru dan kcpatan diprolh dari ubtitui k praaan (II.7) didapat : -...(II.9) Harga aru akiu dapat dicari dngan nurunkan praaan (II.8) trhadap krapatan () dan nilai aru akiu tradi pada aat nilai krapatan akiu yakni pada aat nilai turunan prtaa (dirnial k-) trbut aa dngan nol. ntuk nilai 0 aka : 0
12 5...(II.0) Nilai diubtituikan k dala praaan (II.8) dngan kondii brubah nadi dan nadi, diprolh : 4...(II.) diana : aru akiu (knd/a) krapatan pada aat aru akiu (knd/k) Aru (p/a) tan θ θ 0 Kcpatan (k/a) 0 Krapatan (p/k) 0 Aru (p/a) Gabar II. Hubungan Antara Kcpatan, Aru dan Krapatan Modl Grnhild
13 6 Slanutnya hubungan antara ktiga kcpatan, volu dan krapatan digabarkan pada Gabar II.. Gabar ini nunukkan bntuk uu hubungan antara aru dngan kcpatan, aru dngan krapatan dan kcpatan dngan krapatan. Hubungan antara kcpatan dngan krapatan adalah onoton k bawah yang artinya apabila krapatan naik, aka kcpatan akan turun. Aru nadi nol ktika krapatan angat tinggi hingga tidak ungkinkan kndaraan untuk brgrak lagi. Ktika krapatan nilainya nol, aka tidak trdapat kndaraan di alan hingga aru uga nol. Antara kdua nilai-nilai ktri trbut dikbangkan hubungan antara kdua paratr trbut. Gabar II. nunukkan bbrapa titik pnting, yaitu tingkat volu nol tradi pada dua kondii brbda. Prtaa, ika tidak ada kndaraan di ailita, krapatan adalah nol dan tingkat aru adalah nol. Scara toriti, kcpatan pada aat kondii ini ditntukan olh pngudi prtaa (diauikan pada nilai yang tinggi). Kcpatan ini dinyatakan dala. Kdua, ika krapatan nadi bgitu tinggi hingga ua kndaraan haru brhnti, kcpatan adalah nol dan tingkat aru adalah nol. Karna tidak ada prgrakan dan kndaraan tidak dapat linta pada uatu titik di potongan alan. Krapatan diana ua kndaraan brhnti dibut krapatan act dinyatakan bagai. i antara kdua ktri trbut, dinaika aru lalu linta nghailkan pngaruh akiu. ngan ningkatnya aru dari nol, krapatan uga ningkat karna lbih banyak kndaraan di alan. Jika hal ini tradi, kcpatan nurun karna intraki antar kndaraan. Pnurunan ini diabaikan pada krapatan dan aru rndah dan dang. ngan ningkatnya krapatan, kurva ini nganurkan bahwa kcpatan nurun cukup brarti blu kapaita dicapai. Apabila krapatan naik dari nol, aka aru uga naik. Naun apabila krapatan tru naik akan dicapai uatu titik diana akan nybabkan pnurunan kcpatan dan aru. Titik akiu ini dinaakan kapaita. B. Modl Logarita Grnbrg Hubungan karaktritik aru lalu linta pada odl ini dibuat dngan ngauikan bahwa aru lalu linta punyai kaaan dngan aru luida. Pada tahun 959 Grnbrg ngadakan tudi yang dilakukan di trowongan
14 7 Lincoln dan nganalia hubungan antara kcpatan dan krapatan dngan nggunakan aui praaan kontinuita dari praaan grakan bnda cair/luida. Ruu daar dari Grnbrg adalah : c b...(ii.) diana c dan b rupakan nilai kontanta ngan nggunakan aui di ata Grnbrg ndapatkan hubungan antara kcpatan dan krapatan brbntuk logarita bagai brikut : ln...(ii.3) ntuk ndapatkan nilai kontanta dan, aka praaan (II.3) diubah nadi praaan linir y a + bx bagai brikut :. ln -. ln...(ii.4) ngan ialkan variabl-variablnya : y x ln a. ln b - ntuk ndapatkan hubungan antara aru dan krapatan aka diubtituikan k praaan (II.) :. ln -. ln. ln -. ln (ln ln ). ln ln...(ii.5)
15 8 Hubungan antara aru dan kcpatan didapat dari ubtitui k praaan (II.3) didapat :. ln. ln ln...(ii.6) Nilai krapatan pada aat aru akiu untuk odl Grnbrg dapat dicari dngan nurunkan praaan (II.5) trhadap krapatan () dan nyaakan hail dirnial trbut dngan nol hingga diprolh :.. ln + ln ln ntuk nilai 0 aka : 0 ln 0 ln
16 9 0 ln...(ii.7) Sdangkan nilai kcpatan pada aat volu akiu dicari dngan nurunkan praaan (II.6) trhadap kcpatan ( ) dan nyaakan hail dirnial trbut dngan nol hingga diprolh : + ntuk 0 aka : (II.8) Aru akiu pada tod Grnbrg dihitung dngan nggunakan ruu daar : x x...(ii.9)
17 0 C. Modl Ekponnial ndrwood ndrwood ngukakan uatu hipoti bahwa hubungan antara kcpatan dan krapatan rupakan hubungan kponnial dngan bntuk praaan bagai brikut :...(II.0) ntuk ndapatkan nilai kontanta dan, aka praaan (II.0) diubah nadi praaan linir y a + bx bagai brikut : ln ( ) ln (. ) ln ( ) ln ( ) -...(II.) ngan ialkan variabl-variablnya : y ln x a ln b - ntuk ndapatkan hubungan antara volu dan krapatan aka diubtituikan k praaan (II.0) :...(II.) Slanutnya dngan ngganti.. B. -/(-/A). B+A B dan didapat : A
18 Hubungan antara aru dan kcpatan didapat dngan ubtitui praaan (II.0) :.. Apabila kdua rua dinyatakan dala ungi logarita naturali, aka diprolh praaan : ln ( ) ln (. ) k ln ( ) ln ( )-... ln ( ) -.. ln ( ) ln...(ii.3) Nilai krapatan pada aat aru akiu dicari dngan nurunkan praaan (II.) trhadap krapatan () dan nyaakan hail dirnial trbut dngan nol hingga diprolh : +
19 ntuk 0 aka diprolh : (II.4) Sdangkan nilai kcpatan pada aat aru akiu dicari dngan nurunkan praaan (II.3) trhadap kcpatan ( ) dan nyaakan hail dirnial trbut dngan nol hingga diprolh : ln + ln - ln - ln ntuk 0 aka : 0 - ln 0 - ln...(ii.5) Karna tradi pada kondii akiu aka adalah.
20 3 Aru akiu pada tod ndrwood dihitung dngan nggunakan ruu daar : x x...(ii.6). Modl Northwtrn Modl hubungan volu, kcpatan dan krapatan yang kpat ini diuulkan olh klopok pnliti dari nivrita Northwtrn. Mrka lakukan obrvai lapangan dan ndapatkan odl hubungan kcpatan dan krapatan ndkati bntuk kurva S trbalik. Modl ini kudian dibri naa Modl Northwtrn. Bntuk praaannya rupakan hubungan kponnial kuadrati bagai brikut :...(II.7) Modl ini hapir aa dngan odl yang dikbangkan olh ndrwood, hanya baran nilai paratrnya brbda. ntuk ndapatkan nilai kontanta dan aka praaan (II.7) diubah nadi praaan linir y a + bx bagai brikut :. ln ln (. ) ln ln -...(II.8) ngan ialkan variabl-variablnya : y ln x a ln b -
21 4 ntuk ndapatkan hubungan antara aru dan krapatan aka diubtituikan k praaan (II.7) :.....(II.9) Hubungan antara aru dan kcpatan didapat dngan ubtitui praaan (II.7) :.. k Apabila kdua rua dinyatakan dala ungi logarita naturali, aka diprolh praaan : ln ( ) ln (. ln ( ) ln ( ) ( ). ln ( ) ( ) ln ( ) ) ln ln...(ii.30)
22 5 Nilai krapatan pada aat aru akiu dicari dngan nurunkan praaan (II.9) trhadap krapatan () dan nyaakan hail dirnial trbut dngan nol hingga diprolh :. + - ntuk 0 aka diprolh : (II.3) Sdangkan nilai kcpatan pada aat aru akiu dicari dngan nurunkan praaan (II.30) trhadap kcpatan ( ) dan nyaakan hail dirnial trbut dngan nol hingga diprolh : ln
23 6 + / / ln / ln - ln / ntuk 0 aka : 0 - ln / 0 - ln / 0 / ln...(ii.3) Karna tradi pada kondii akiu aka adalah. Aru akiu pada tod ndrwood dihitung dngan nggunakan ruu daar : x x...(ii.33)
24 7 II.6 Modl Antrian Ktika printaan lbihi kapaita untuk uatu priod waktu atau pada uatu waktu antar kdatangan yang lbih rndah dibandingkan dngan waktu playanan (pada tingkat ikrokopik) di uatu lokai trtntu, aka trbntuklah antrian. Antrian bia brupa antrian yang brgrak (oving quu) atau antrian yang brhnti (toppd quu). Pada daarnya klbihan kndaraan diipan pada darah uptra dari bottlnck atau darah playanan, dan kdatangannya ditunda laa priod waktu brikutnya. Ada dua tknik analii yang bia dipakai dala plaari pro antrian, yaitu hock wav analyi dan quuing analyi. Shock wav analyi dapat digunakan ktika pro printaan-kapaita adalah dtrinitic, dan trutaa cocok untuk valuai arak yang diprlukan untuk pro antrian dan untuk intraki pro antrian. Quuing analyi dapat digunakan baik untuk pro dtrinitic aupun pro tochatic, dan kndaraan yang brada di dala pro dianggap diipan dala antrian vrtikal. A. Shock Wav Analyi Salah atu bagian dala tudi ngnai nona lalu linta ialah iat-iat dari globang kut pada aru lalu linta. Globang kut didiniikan bagai bata kondii brbai ruang dan waktu ditandai dngan dikontinuita antara aru padat dan tak padat (May, 990). Sdangkan Lighthill dan Whitha prti dikutip dari Wohl dan Martin (967) nlakan bahwa globang kut trbntuk ktika pada buah rua alan trdapat aru dngan krapatan rndah yang diikuti olh aru dngan krapatan tinggi, diana kondii ini ungkin diakibatkan olh kclakaan, pngurangan ulah laur, atau alur auk rap. Mialnya aa prilaku lalu linta pada aat auki alan nypit, pada ipang brinyal ktika nyala lapu rah, atau pada prlintaan krta api. Pada prlintaan krta api, dikontinuita tradi aat krta linta (pintu prlintaan ditutup) dan adanya prlabatan bagai akibat pngurangan kcpatan olh kndaraan di dpannya karna adanya habatan brupa pngndali kcpatan (rubl trip) aupun alur rl (pada aat kondii prlintaan dibuka).
25 8 Kondii pada aat pintu prlintaan ditutup dapat digabarkan bagai brikut : () Kondii alan trtutup total Kondii ini tradi aat krta linta dan pintu prlintaan ditutup. Akibatnya nilai krapatan pada kondii aru yang auk (volu kbutuhan dand) brangur-angur nadi krapatan act. Kndaraan yang brada di dpan klopoknya ngurangi kcpatannya aat ndkati prlintaan, dan akhirnya brhnti hingga trbntuk antrian di blakangnya. () Pada aat pintu prlintaan dibuka, krapatan pada kondii act brangurangur kbali apai pada kadaan diana krapatan nuu k kondii akiu. (3) Pada tahap ini kcpatan globang kut ( ω BC ) akan nyuul kcpatan globang kut ( ω AB ), diana krapatan aat kondii act akan hilang dan aru akan kbali pada kondii noral blu adanya pnutupan. Tiga globang kut ulai pada aat t di gari hnti : ω A ( globang kut bntukan au), ω B (globang kut dia dpan), dan ω AB (globang kut bntukan undur). Kcpatan dari ktiga globang kut ini dinyatakan pada diagra Gabar II. (a) dan dapat dihitung dngan nggunakan ruuruu brikut : ω A A + μa...(ii.34) A ω ω B 0...(II.35) B B AB A A...(II.36) A B B B A diana : ω A globang kut dari kondii titik awal ( 0 dan 0) k titik A ( A, A )
26 9 ω B globang kut pada aat pintu prlintaan ditutup laa kndaraan brhnti hingga B 0 dan B krapatan aat act) ω AB globang kut aat nilai krapatan aru pada kondii volu kndaraan aa dngan volu kbutuhan ( A ) brangurangur nadi krapatan act ( B ). Kondii aru A, B, dan ini ttap apai waktu t pada aat pintu prlintaan dibuka. Aru (p/a/laur) C A A A A ω C C ω AB C C ω B ω AC ω BC B B Jarak ω C ω AB ω BC ω AC Rua yang ditinau t 0 t t t 3 t 4 Waktu Gabar II. Globang Kut Pada Prlintaan Krta Api Saat Pintu itutup
27 30 Kondii aru baru C pada waktu t di gari hnti ningkat dari nol apai aru nuh. Ini nybabkan dua globang kut baru, ω C (globang kut pulihan au) dan ω BC (globang kut pulihan undur), dangkan globang kut akhir adalah ω B (globang kut dia di. Kcpatan dua globang kut baru ini dapat cara grai dilihat pada Gabar II. (a) dan dihitung dngan praaan brikut ini : ω C C + μc...(ii.37) C B C ω C BC...(II.38) B C B C diana : ω C globang kut pada aat pintu prlintaan dibuka, kondii rua di dpan pintu prlintaan dari kondii aru dan krapatan nol prlahan brgrak arah dngan lalu linta k arah hilir apai pada kondii titik C ( C volu akiu kapaita, C krapatan akiu) ω BC globang kut dari kndaraan yang ngalai kondii brhnti aat pintu ditutup ulai brgrak diuul olh kndaraan diblakangnya apai kndaraan trakhir yang tidak ngalai antrian ttapi kcpatannya trpngaruh olh kcpatan aru di dpannya. Kondii aru, C, B, dan A ttap apai ω AB dan ω BC otong waktu t 3. Intrval waktu antara t dan t 3 dapat dihitung bagai brikut : ω AB t a r...(ii.39) ωbc ωab
28 3 t r t t a t 3 t b t 4 α β X A X B A Gabar II.3 Lokai Antrian dan Lokai Hilangnya Antrian B Lokai antrian dari gari hnti pada waktu t dapat dihitung bagai brikut : X A r. tan α...(ii.40) tan α A A...(II.4) Lokai hilangnya antrian dari gari hnti pada waktu t 3 dapat dihitung dngan ruu brikut : r ωbc. ωab X B...(II.4) 3600 ωbc ωab diana r laanya waktu pnutupan pintu prlintaan t t Rpon lalu linta yang tidak bia brgrak dngan gra bgitu pintu prlintaan dibuka ngakibatkan bbrapa kndaraan ungkin aih ngalai tundaan walaupuntidak ngalai antrian. Pada aat t 3 globang kut grak au baru ω AC trbntuk, dan dua globang kut grak undur ω AB dan ω BC brakhir. Globang kut ω AC dapat dihitung dngan ruu : A ω C AC...(II.43) A C
29 3 Kondii aru, C, dan A ttap apai waktu trtntu apai pintu prlintaan ditutup kbali, ttapi bblunya pada aat waktu t 4, globang kut bntukan au ω AC otong gari hnti dan aru di gari hnti nurun dari aru akiu C nadi A. Priod waktu dari ulai pintu prlintaan dibuka apai tingkat plpaan gari hnti turun dibawah nilai akiu ( t apai t 4 ) dapat dihitung bagai brikut : r. ωab ωbc tb +...(II.44) ωbc ωab ωac Julah kndaraan yang ngalai antrian : N (r + t a ) x A...(II.45) Tundaan yang tradi : T ½ x r x N...(II.46) Pada aat pintu dibuka kondii yang tradi dapat diaakan dngan kau bottlnck, diana rua yang blu trpngaruh prlintaan bagai darah uptra dan rua dngan prlintaan bagai downtra. ala Wohl (967) dilakan ika volu pada rua tanpa habatan lbih kcil daripada volu akiu pada bottlnck, aka akan tradi pnurunan kcpatan dan knaikan krapatan dari k laa kndaraan auki prlintaan. Walaupun tradi tundaan pada kndaraan ttapi hock wav tidak tradi. Knaikan volu pada uptra aih dapat ditapung olh bottlnck apai pada tingkat volu akiu bottlnck. Kcpatan globang kut pada downtra adalah nol. Jika volu akiu ini trlapaui aka tibullah antrian. Pada uatu titik auk bottlnck aru yang dibrikan olh diagra daar haru banding. Shingga untuk alan tanpa habatan, krapatan akan ningkat ncapai titik E. Kcpatan globang di E adalah ngati pngaruhnya trhadap alan utaa, dan dari ini akan dipantulkan k bawah k alan pndkat dari bottlnck. Pngaruh dari globang ini akan brtu dngan globang yang datang brgabung pada kiringan di C dan globang kut dari kcpatan ngati rlati trhadap alan. Pngaruh dari bottlnck akan brangurangur dipantulkan panang alan ika volu pada pndkat dianggap kontan.
30 33 Ini dapat dilakan bahwa antrian tidak dapat dikurangi laa aru auk kurang dari kapaita bottlnck. olu C B A C () untuk alan utaa E () untuk bagian bottlnck Krapatan Gabar II.4 Hubungan Antara olu dan Krapatan Pada Jalan dngan Bagian Bottlnck olu Spac Man Spd dari kndaraan yang ndkati antrian Kcpatan dari globang yang ndkat Kcpatan globang kut Kcpatan dari globang yang dipantulkan Spac Man Spd dari kndaraan dala antrian Krapatan Gabar II.5 Hubungan Antara olu dan Krapatan dan Hubungan Shock Wav Pada Situai Bottlnck
31 34 B. Analii Antrian (Quuing Analyi) ata aukan yang dibutuhkan pada analii antrian adalah : () nilai kdatangan rata-rata (an arrival valu), nilai ini nggabarkan rata-rata aru (kndaraan pr a) atau ti hadway (dtik pr kndaraan), itilah printaan (dand) atau aukan (input) biaanya nggantikan itilah kdatatangan (arrival); () ditribui kdatangan (arrival ditribution), dapat brupa ditribui dtrinitic atau ditribui probabilitic; (3) nilai playanan rata-rata (an rvic valu), itilah kapaita (capacity), kbrangkatan (dpatur), atau kluaran (output) biaanya nggantikan itilah playanan (rvic); (4) ditribui playanan (rvic ditribution); (5) diiplin antrian (quu diciplin). ala analii antrian prlu dilakukan trlbih dahulu klaiikai aukan karaktritik, yaitu : () Apabila ditribui kdatangan dan/atau ditribui playanan briat probabilitic dan waktu kdatangan rta playanan tiap individu tidak diktahui aka nggunakan tochatic quuing analyi () Apabila ditribui kdatangan dan ditribui playanan briat dtrinitic dan waktu kdatangan rta playanan diktahui aka digunakan dtrinitic quuing analyi trinitic quuing anayli dapat dibdakan nadi dua lvl yang brbda. Pada lvl ikrokopik, pola kdatangan dan playanan dianggap nru dangkan pada lvl akrokopik hal ini dianggap acak. Lvl ikrokopik biaanya dipilih ktika rata-rata kdatangan dan playanan tinggi dan lvl akrokopik ring dipilih ktika kdatangan dan playanan rndah. Pada prilangan bidang alan raya dan alan rl adalah alah atu contoh analii antrian dtrinitic pada tingkat akrokopik, diana kdatangan dan pola playanan dianggap nru. Pada Gabar II.6 a nggabarkan rata-rata kdatangan (λ) yang kontan laa priod tudi. Rata-rata playanan (μ) punyai dua kondii : nol ktika pintu prlintaan ditutup dan ningkat apai nilai rata-rata aru nuh () ktika pintu dibuka. Nilai rata-rata playanan
32 35 akan banding dngan aru nuh ktika tradi antrian. ngan kata lain, rata-rata playanan banding dngan rata-rata kdatangan ika kondii pintu trbuka. iiplin antrian yang dipakai adalah it FIFO. urai waktu antrian diulai dari awal pintu ditutup apai antrian brakhir (t q ). urai waktu antrian ini brguna untuk ngtahui apakah ada kndaraan di dala antrian yang tria atau bia dilpakan luruhnya. Ara A nggabarkan ulah kndaraan yang diipan laa priod waktu pintu ditutup. Saat pintu ulai dibuka, ara A ulai lua dan nggabarkan ulah kndaraan yang dilpakan. Ktika luaan A aa dngan luaan A aka antrian hilang. Sdangkan luaan A 3 nggabarkan ulah kndaraan yang dilayani laa pintu trbuka apai aat pintu ditutup kbali karna ada krta yang lwat. Julah kndaraan yang ngalai antrian digabarkan olh proyki vrtikal gitiga antrian. Kndaraan prtaa yang ngalai antrian adalah kndaraan yang datang tlah pintu ditutup. Sua kndaraan yang datang laa pintu ditutup aa prti yang datang pada aat pintu dibuka ttapi blu trbak antrian ngalai pro antrian dan dipaka untuk brhnti atau nurunkan kcpatannya. Panang antrian digabarkan olh arak vrtikal lalui gitiga. Pada aat awal pintu ditutup, panang antrian ningkat dari nol apai nilai akiu di akhir waktu pnutupan. Kudian panang antrian brkurang apai gari kdatangan brpotongan dngan gari playanan (panang antrian nadi nol). Hal ini brlangung apai priod waktu pnutupan pintu prlintaan kbali. Tundaan individu digabarkan olh arak horiontal yang otong gitiga. Kndaraan prtaa yang datang tlah awal pnutupan ngalai tundaan individu trbar. Stiap kndaraan yang datang tlah itu ngalai lbih kcil dan akin kcil tundaan individu apai antrian nghilang. May akai tknik dari aru nru untuk aalah pada bottlnck ntara (ialnya uatu rua alan yang brilangan dngan alan rl, atau alan atu laur yang trtutup karna adanya kclakaan). Kondii ini dapat dilakan dngan prilaku antrian laa atu iklu inyal lalu linta, diana durai tundaaan atau
33 36 pnutupan banding dngan intrval panang waktu pnutupan r dan waktu yang dibutuhkan olh antrian untuk habi tlah plpaan adalah t a. May dala Grlough (975) ruukan odl praaan atati untuk kondii alan dngan kondii aru nru yang cara prinip bia diaakan dngan kau bottlnck prti pada kau prlintaan krta api ini. urai antrian : S B t q r...(ii.47) S A Waktu plpaan antrian : t a t q r...(ii.48) Julah kndaraan yang ngalai tundaan : N A. t q...(ii.49) Julah akiu kndaraan dala antrian : N r ( A B )...(II.50) Julah rata-rata kndaraan dala antrian : N N /...(II.5) Total kndaraan dala atu waktu antrian : r (A - B )tq M...(II.5) Waktu rata-rata kndaraan trtunda : r T r B...(II.53) A Tundaan akiu pr kndaraan : T r B A...(II.54) diana : A rata-rata kdatangan lalu linta pada bagian hulu (uptra) S rata-rata aru nuh atau kapaita dari aru tak trganggu B aru rata-rata pada bagian hilir (downtra) laa r ( B < A < S ) r durai waktu tinauan, pada aat pintu prlintaan ditutup r adalah laa pnutupan
34 37 t a waktu plpaan antrian tlah awal pbukaan pintu prlintaan t q total waktu antrian r + t a S Rata-rata aru (p/a) λ A A A 3 μ 0 Pintu Pintu dibuka Pintu ditutup ditutup (a) Waktu Kdatangan λ Kndaraan kuulati N 0 N antrian μ λ Kbrangkatan μ r t o Waktu t q (b) Gabar II.6 iagra Antrian
35 38 II.7 Tundaan Tundaan nurut MKJI 997 dibut bagai waktu tpuh tabahan yang diprlukan untuk lwati uatu ipang dibandingkan trhadap ituai tanpa ipang. Brdaarkan dinii di ata, dapat diturunkan k dala praaan atati bagai brikut : W W 0 + T...(II.55) diana : W waktu tpuh total W 0 waktu tpuh pada kondii aru bba, rupakan waktu iniu yang diprlukan untuk npuh uatu rua alan trtntu T tundaan Tundaan trdiri dari Tundaan Lalu Linta (T T ) yaitu tundaan yang dibabkan olh pngaruh kndaraan lain, dan Tundaan Gotrik (T G ) yaitu tundaan yang dibabkan olh prlabatan dan prcpatan untuk lwati ailita prti pada pripangan dan trhnti karna lapu rah. Scara atati dapat dinyatakan bagai brikut : T T T + T G...(II.56) diana : T T T G tundaan lalu linta rata-rata tundaan gotri rata-rata Tundaan rupakan ukuran kinra kriti dari intrruptd low. Mnurut Taylor (996), ada dua dinii tundaan : () Tundaan brhnti (toppd dlay), yaitu tundaan yang dialai olh kndaraan yang bnar-bnar brhnti, yang ruuk pada tundaan antrian. () Tundaan kactan (congtion dlay), yaitu tundaan yang liputi tundaan akibat antrian dan yang dibabkan olh kndaraan yang ngurangi kcpatan karna intraki dngan kndaraan lainnya. Tundaan ini dapat diukur dngan nghitung liih antara ourny ti dan travl ti yang diinginkan.
36 39 ala tudi ini, tundaan didiniikan bagai tabahan waktu pralanan aat lalui prtuan bidang alan dan alan rl. Koponn tundaan trdiri dari prlabatan kndaraan, brhntinya kndaraan, dan prcpatan kbali pada kondii kcpatan ula, yang tradi akibat pnutupan pintu prlintaan aat krta lwat dan pada aat pintu dibuka (akibat kondii gotrik darah prlintaan). Shingga nilai tundaan total dapat dicari dari praaan brikut : T total T L + T L + T L3...(II.57) Shingga waktu tpuh total nadi : W W 0 + T L + T L + T L3...(II.58) diana : T total nilai tundaan total (dt/p) T L tundaan kndaraan diana pngudi bralan dngan kcpatan. yang diinginkan T L tundaan kndaraan akibat pnurunan kcpatan T L3 tundaan kndaraan akibat pnutupan pintu prlintaan Jarak Kndaraan dngan aru bba Kndaraan dngan kcpatan yang diinginkan T total W o T L T L T L3 Sta A Sta Waktu Gabar II.7 Tundaan Yang ialai Kndaraan Pada Prlintaan
37 40 Pada kondii diana aru yang auk bottlnck nurunkan kcpatannya aka tundaan yang tradi diakibatkan olh prbdaan kcpatan pada aat auki bottlnck (kcpatan awal) dan aat brada pada darah akhir bottlnck (kcpatan akhir). Waktu yang diprlukan bagi kndaraan untuk naikkan atau prlabat pada rata-rata prcpatan atau prlabatan dari kcpatan awal apai kcpatan akhir adalah : B w...(ii.59) a A Sdangkan arak yang diprlukan bagi kndaraan untuk naikkan atau prlabat pada rata-rata prcpatan atau prlabatan a dari kcpatan awal apai kcpatan akhir adalah : B w 0,733 a w x, (II.60) diana : A B a kcpatan pada prulaan prlabatan kcpatan pada akhir prlabatan rata-rata prlabatan Nilai prcpatan atau prlabatan brvariai trgantung pada pngudi, kndaraan, ituai lalu linta, ituai alan, dan untuk brbagai tingkat kcpatan yang brbda. Makiu dan noral rata-rata prcpatan atau prlabatan untuk obil pnupang pada prubahan kcpatan dan kondii dan yang brvariai dapat dilihat pada Tabl II.7 brikut ini : Tabl II.7 Makiu dan Noral Prcpatan Atau Prlabatan ntuk Mobil Pnupang (Mil pr a/dtik) Mdan Prubahan Kcpatan (il/a) atar 8,0 (3,3) 5,0 (3,3) 4,7 (3,3) 3,8 (,6),8 (,0) + % 7,8 4,6 4, 3,4,4 + 6% 6,7 3,7 3,4,5,5 + 0% 5,8,8,5,6 0,6 Subr : May, 990
38 4 II.8 Analii Statitik A. Prkiraan Julah Sapl ari data pngaatan yang diabil bagai apl dapat kita hitung nilai rata-ratanya dan prkiraan yang paling baik trhadap rata-rata populai adalah ratarata apl. Walaupun ulah apl yang bar dapat brikan hail prkiraan yang lbih baik dari nilai rata-rata populai ttapi ulah apl yang bar butuhkan lbih banyak waktu dan uaha dala pngupulan dan analiinya. Apabila nilai rata-rata apl ( x ) dipakai untuk nakir nilai ratarata populai (μ), aka barnya ulah apl adalah bagai brikut : t n...( II.6) ε diana : n ulah apl yang dibutuhkan ipangan baku yang diharapkan ε liit kalahan trtntu (galat) yang diprbolhkan dan dittapkan blunya olh pngguna t koiin tandar kalahan dari rata-rata yang dipakai bagai acuan untuk tingkat kprcayaan trtntu Barnya nilai t untuk brbagai tingkat kprcayaan dapat dilihat pada Tabl II.8. Tabl II.8 Nilai t ntuk Brbagai Tingkat Kprcayaan Tingkat kprcayaan yang t Praaan diharapkan (%) 68,3,00 n σ Subr : Pignataro, 973 σ 95,0,96 n 3,84 σ 95,5,00 n 4 σ 99,7 3,00 n 9
39 4 Apabila kita tidak punyai data awal ngnai kondii lokai pnlitian hingga ukar untuk nntukan nilai ipangan baku aka kita dapat nggunakan nilai ipangan baku pada Tabl II.8. Tabl ini prlihatkan bbrapa ipangan baku untuk ailita dan lokai yang brbda. Nilai-nilai ini bia digunakan untuk prkiraan pndahuluan dari ulah apl yang dibutuhkan ika tidak diktahui data blunya. Tabl II.9 Sipangan Baku Kcpatan Saat ntuk Prkiraan Julah Sapl Ara Lalu Linta Tip Jalan Raya Sipangan Baku (il pr a) Rural laur 5,3 4 laur 4, Intrdiat laur 5,3 4 laur 5,3 rban laur 4,8 4 laur 4,9 Subr : McShan, 990 B. Man, Mdian, dan Modu Rata-rata apl (an) didapat dari prhitungan luruh apl dibagi dngan ulah data. n i x i x...(ii.6) n Sdangkan untuk data brklopok rata-ratanya adalah : i x x i i...(ii.63) diana : x rata-rata apl (an) x i apl k-i n ulah apl i rkuni untuk nilai x i yang bruaian
40 43 Mdian nntukan ltak data tlah data itu diuun nurut urutan nilainya. Jika banyak data ganil, dian rupakan data paling tngah tlah data diurutkan. Sdangkan ika ulah data gnap, dian adalah rata-rata hitung dua data tngah. Jika data tlah diuun dala datar ditribui rkuni aka diannya : M b + p n F...(II.64) diana : M dian b bata bawah kla dian, ialah kla diana dian akan trltak p panang kla dian F ulah ua rkuni dngan tanda lbih kcil dari tanda kla dian rkuni kla dian Modu nyatakan nona yang paling banyak tradi, yaitu data yang punyai rkuni trbanyak. Jika data tlah diuun dala datar ditribui rkuni aka odunya : b Mo b + p...(ii.65) b + b diana : Mo odu b bata bawah kla dian, ialah kla diana dian akan trltak p panang kla odal b rkuni kla odal dikurangi rkuni kla intrval dngan tanda kla yang lbih kcil blu tanda kla odal b rkuni kla odal dikurangi rkuni kla intrval dngan tanda kla yang lbih bar udah tanda kla odal ala buat datar ditribui rkuni ada bbrapa hal yang prlu diprhatikan : - Rntang : adalah data trbar dikurangi data trkcil - Banyak kla intrval + 3,3 log (n)
41 44 diana n ulah apl rntang - Panang kla intrval p banyak kla C. ariani dan Sipangan Baku Sapl ariani dan ipangan baku apl adalah uatu ukuran yang nyatakan pnybaran dari apl, diruukan bagai brikut : n ( x x) i i...(ii.66) n - n ( x x) i i...(ii.67) n - ntuk data apl yang tlah diuun dala datar rkuni aka : ( x x) i i...(ii.68) n - diana : variani apl ipangan baku apl. Analii Rgri Linir Pada paangan variabl (x i,y i ), apabila y i rupakan variabl yang diaati (diukur tlah x i ditntukan) aka analii pnntuan y bagai ungi x dibut analii rgri. Apabila rataan dari pubah acak Y yang brkaitan linir dngan uatu nilai ttap x, aka praaan linir populai dinyatakan bagai : μ Y x α + βx...(ii.69) Koiin rgri linir α dan β rupakan dua paratr yang ditakir dari data apl. Bila takiran untuk kdua paratr trbut aing-aing dinyatakan dngan a dan b, aka μ Y x dapat ditakir dngan ŷ dari bntuk gari rgri brdaarkan apl atau gari kcocokan rgri. Hubungan antara variabl bba x dan variabl tidak bba y yang dicocokkan pada data prcobaan ditandai dngan praaan prdiki yang dibut praaan rgri.
42 45 ŷ a + bx...(ii.70) Barnya kontanta a dan b dapat dicari dari praaan-praaan di bawah ini : n b n x i x i y i i x i - x i ( x i ) - y i...(ii.7) a y b...(ii.7) diana : y i xi n n y i xi n ulah apl Sdangkan untuk nakir paratr σ yang nggabarkan variai acak atau variai galat prcobaan di kitar gari rgri dapat dicari bagai brikut : J xx J yy n ( xi x )...(II.73) i n ( yi y )...(II.74) i n J xy ( x - x ) ( y y )...(II.75) i i i JKG J yy + b J xy...(ii.76) JKG...(II.77) n diana : JKG ulah kuadrat galat J xx total ulah kuadrat x trkorki J yy total ulah kuadrat y trkorki J xy ulah kuadrat rgri JKR takiran takbia untuk σ dari data apl
43 46 E. Analii Korlai Analii korlai dilakukan untuk ngukur ratnya hubungan antara variabl y dan x dngan nggunakan uatu bilangan yang dibut koiin korlai. Nilai koiin korlai dihitung dngan praaan di bawah ini: n xiyi - xi yi r...(ii.78) { n x - ( x ) }{ n y - ( y ) } i i i i Barnya nilai r trltak antara - < r < +, ika harga r ndkati - atau + aka hubungan antara variabl y dan variabl x kuat, ttapi ika r ndkati 0 aka hubungan yang dihailkan lah dan brarti bahwa baik variabl x aupun variabl y adalah variabl bba. Tanda (-) nyatakan prtabahan nilai x nybabkan pnurunan y, dan tanda (+) nyatakan prtabahan nilai x nybabkan knaikan nilai y. Pngukuran untuk ngtahui auh ana ktpatan ungi rgri adalah dngan lihat nilai koiin dtrinai (r ) yang didapat dngan ngkuadratkan nilai koiin korlai. Nilai koiin dtrinai nyatakan propori variai kluruhan dala nilai pubah y yang dapat ditrangkan atau diakibatkan olh hubungan linir dngan nilai pubah acak x. F. i Signiikani i igniikani digunakan untuk nntukan linir atau tidaknya hubungan antara variabl bba dan tidak bba. i igniikai yang digunakan biaanya adalah i- t ( tudnt t tt) dan i- F (varianc ratio tt /Th F tt). i-t ungkinkan untuk pnguian dngan tandingan atu arah ntara ui-f trbata pada pnguian dngan tandingan dua arah. (a) i - t Ho : β β o variai dala y diakibatkan olh luktuai acak yang tidak trgantung pada nilai x H : β β o t / b - β J o xx...(ii.79) T punyai ditribui-t dngan draat kbbaan n-. Hipoti ditolak bila t > t α/ untuk tara kbrartian α.
44 47 (b) i- F Mial kita ingin ngui hipoti : Ho : β 0 variai dala y diakibatkan olh luktuai acak yang tidak H : β 0 trgantung pada nilai x ntuk ngui hipoti di ata kita hitung : JKR/ JKG/(n ) JKR...(II.80) dan nolak Ho pada tara kbrartian α bila > αˆ (, n-) Jika hipoti nol ditolak, yaitu bila nilai tatitik hitungan lbihi nilai kriti αˆ (,n-) aka dapat diipulkan bahwa trdapat ulah variai yang brarti dala rpon y yang dibabkan atau odl rupakan ungi linir. Bila tatitik brada dala darah pnriaan aka diipulkan bahwa data tidak brikan cukup dukungan kpada odl hingga odl trbut bukan rupakan ungi linir. G. itribui Noral itribui noral tandar adalah ditribui noral dngan rata-rata μ0 dan ipangan baku σ. Fungi dnitanya brbntuk : /z (z)...(ii.8) π Mngubah ditribui noral uu nadi ditribui noral baku ditpuh dngan nggunakan tranorai : Z X μ σ...(ii.8)
45 48 Kurva Noral u Kurva Noral Standar μ-3σ μ-σ μ-σ μ μ+σ μ+σ μ+3σ rata-rata μ 0 ipangan baku σ Gabar II.8 Kurva Nora u dan Standar
BAB IV VIBRASI KRISTAL
 BAB IV VIBRASI KRISTAL MATERI : Gtaran (Vibrai) Krital 4..praaan dipri untuk krital brbai atu ato. 4..kcpatan klopok (group vlocity) 4.3 praaan dipri untuk krital brbai dua ato. 4.4.cabang optik 4.5.cabang
BAB IV VIBRASI KRISTAL MATERI : Gtaran (Vibrai) Krital 4..praaan dipri untuk krital brbai atu ato. 4..kcpatan klopok (group vlocity) 4.3 praaan dipri untuk krital brbai dua ato. 4.4.cabang optik 4.5.cabang
Gambar 1 Sayatan transversal akar andromonoecious; lapisan periderm (p), xilem sekunder (xs)
 3 Gabar Sayatan tranvral akar androonociou; laian ridr (), xil kundr () Gabar Sayatan tranvral akar onociou; laian ridr (), xil kundr () Pngaatan Anatoi Batang Sayatan tranvral batang tanaan androonociou
3 Gabar Sayatan tranvral akar androonociou; laian ridr (), xil kundr () Gabar Sayatan tranvral akar onociou; laian ridr (), xil kundr () Pngaatan Anatoi Batang Sayatan tranvral batang tanaan androonociou
HASIL DAN PEMBAHASAN. Gambar 3 Proses penentuan perilaku api.
 6 yang diharapkan. Msin infrnsi disusun brdasarkan stratgi pnalaran yang akan digunakan dalam sistm dan rprsntasi pngtahuan. Msin infrnsi yang digunakan dalam pngmbangan sistm pakar ini adalah FIS. Implmntasi
6 yang diharapkan. Msin infrnsi disusun brdasarkan stratgi pnalaran yang akan digunakan dalam sistm dan rprsntasi pngtahuan. Msin infrnsi yang digunakan dalam pngmbangan sistm pakar ini adalah FIS. Implmntasi
UJI KESELARASAN FUNGSI (GOODNESS-OF-FIT TEST)
 UJI CHI KUADRAT PENDAHULUAN Distribusi chi kuadrat mrupakan mtod pngujian hipotsa trhadap prbdaan lbih dari proporsi. Contoh: manajr pmasaran suatu prusahaan ingin mngtahui apakah prbdaan proporsi pnjualan
UJI CHI KUADRAT PENDAHULUAN Distribusi chi kuadrat mrupakan mtod pngujian hipotsa trhadap prbdaan lbih dari proporsi. Contoh: manajr pmasaran suatu prusahaan ingin mngtahui apakah prbdaan proporsi pnjualan
Pertemuan XIV, XV VII. Garis Pengaruh
 ahan jar Statika ulyati, ST., T rtmuan X, X. Garis ngaruh. ndahuluan danya muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksi disbut bban brgrak. isalkan ada sbuah kndaraan mlalui
ahan jar Statika ulyati, ST., T rtmuan X, X. Garis ngaruh. ndahuluan danya muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksi disbut bban brgrak. isalkan ada sbuah kndaraan mlalui
JURNAL TEKNIK ITS Vol. 1, No. 1 (Sept. 2012) ISSN: B-103
 JURNAL EKNIK IS Vol., No. (Spt. ) ISSN: 3-97 B-3 Prancangan dan Iplntasi Kontrollr Pid-Fuzzy untuk Mnjaga Stabilitas Frkunsi gangan rbangkit Pada Pbangkit Listrik Kapasitas kva dngan Pnggrak Utaa Motor
JURNAL EKNIK IS Vol., No. (Spt. ) ISSN: 3-97 B-3 Prancangan dan Iplntasi Kontrollr Pid-Fuzzy untuk Mnjaga Stabilitas Frkunsi gangan rbangkit Pada Pbangkit Listrik Kapasitas kva dngan Pnggrak Utaa Motor
BAB I METODE NUMERIK SECARA UMUM
 BAB I METODE NUMERIK SECARA UMUM Aplikasi modl matmatika banyak muncul dalam brbagai disiplin ilmu pngtahuan, sprti isika, kimia, konomi, prsoalan rkayasa (tknik msin, sipil, lktro). Modl matmatika yang
BAB I METODE NUMERIK SECARA UMUM Aplikasi modl matmatika banyak muncul dalam brbagai disiplin ilmu pngtahuan, sprti isika, kimia, konomi, prsoalan rkayasa (tknik msin, sipil, lktro). Modl matmatika yang
IV. Konsolidasi. Pertemuan VII
 Prtmuan VII IV. Konsolidasi IV. Pndahuluan. Konsolidasi adalah pross brkurangnya volum atau brkurangnya rongga pori dari tanah jnuh brpmabilitas rndah akibat pmbbanan. Pross ini trjadi jika tanah jnuh
Prtmuan VII IV. Konsolidasi IV. Pndahuluan. Konsolidasi adalah pross brkurangnya volum atau brkurangnya rongga pori dari tanah jnuh brpmabilitas rndah akibat pmbbanan. Pross ini trjadi jika tanah jnuh
 Konsolidasi http://www.pwri.go.jp/ http://www.ashirportr.org Pmbbanan tanah jnuh brprmabilitas rndah akan mnaikkan tkanan air pori Air akan mngalir k lapisan tanah dngan tkanan pori yg lbih rndah Prmabilitas
Konsolidasi http://www.pwri.go.jp/ http://www.ashirportr.org Pmbbanan tanah jnuh brprmabilitas rndah akan mnaikkan tkanan air pori Air akan mngalir k lapisan tanah dngan tkanan pori yg lbih rndah Prmabilitas
Analisis Rangkaian Listrik
 Sudaryatno Sudirham Analisis Rangkaian Listrik Mnggunakan Transformasi Fourir - Sudaryatno Sudirham, Analisis Rangkaian Listrik (4) BAB Analisis Rangkaian Mnggunakan Transformasi Fourir Dngan pmbahasan
Sudaryatno Sudirham Analisis Rangkaian Listrik Mnggunakan Transformasi Fourir - Sudaryatno Sudirham, Analisis Rangkaian Listrik (4) BAB Analisis Rangkaian Mnggunakan Transformasi Fourir Dngan pmbahasan
II. LANDASAN TEORI. digunakan sebagai landasan teori pada penelitian ini. Teori dasar mengenai graf
 II. LANDASAN TEORI 2.1 Konsp Dasar Graf Pada bagian ini akan dibrikan konsp dasar graf dan dimnsi partisi graf yang digunakan sbagai landasan tori pada pnlitian ini. Tori dasar mngnai graf yang akan digunakan
II. LANDASAN TEORI 2.1 Konsp Dasar Graf Pada bagian ini akan dibrikan konsp dasar graf dan dimnsi partisi graf yang digunakan sbagai landasan tori pada pnlitian ini. Tori dasar mngnai graf yang akan digunakan
BAB IV HASIL PENELITIAN DAN PEMBAHASAN. Data penelitian diperoleh dari siswa kelas XII Jurusan Teknik Elektronika
 BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. DESKRIPSI DATA Data pnlitian diprolh dari siswa klas XII Jurusan Tknik Elktronika Industri SMK Ma arif 1 kbumn. Data variabl pngalaman praktik industri, kmandirian
BAB IV HASIL PENELITIAN DAN PEMBAHASAN A. DESKRIPSI DATA Data pnlitian diprolh dari siswa klas XII Jurusan Tknik Elktronika Industri SMK Ma arif 1 kbumn. Data variabl pngalaman praktik industri, kmandirian
Muatan Bergerak. Muatan hidup yang bergerak dari satu ujung ke ujung lain pada suatu
 Muatan rgrak Muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksik disbut bb bban brgrak Sbuah kndaraan mlalui suatu jmbatan, maka akan timbul prubahanbh nilai i raksi kimaupun gaya
Muatan rgrak Muatan hidup yang brgrak dari satu ujung k ujung lain pada suatu konstruksik disbut bb bban brgrak Sbuah kndaraan mlalui suatu jmbatan, maka akan timbul prubahanbh nilai i raksi kimaupun gaya
PENGARUH SEGMEN BOTTLENECK SISTEMATIK TERHADAP KARAKTERISTIK LALU LINTAS (STUDI KASUS: JL. JAMIN GINTING KM 14.5)
 PENGARUH EGEN BOTTLENECK ITEATIK TERHAAP KARAKTERITIK LALU LINTA (TUI KAU: JL. JAIN GINTING K 14.5) Kristian Napitupulu ahasiswa Program arjana Tknik ipil Fakultas Tknik Univrsitas umatra Utara Jln. Prpustakaan
PENGARUH EGEN BOTTLENECK ITEATIK TERHAAP KARAKTERITIK LALU LINTA (TUI KAU: JL. JAIN GINTING K 14.5) Kristian Napitupulu ahasiswa Program arjana Tknik ipil Fakultas Tknik Univrsitas umatra Utara Jln. Prpustakaan
Bab 6 Sumber dan Perambatan Galat
 Mtod Pnlitian Suradi Sirgar Bab 6 Sumbr dan Prambatan Galat 6. Sumbr galat. Data masukan, misal hasil pngukuran (galat bawaan). Slama komputasi (galat pross), galat ang timbul akibat komputasi 3. Galat
Mtod Pnlitian Suradi Sirgar Bab 6 Sumbr dan Prambatan Galat 6. Sumbr galat. Data masukan, misal hasil pngukuran (galat bawaan). Slama komputasi (galat pross), galat ang timbul akibat komputasi 3. Galat
PERANCANGAN DAN SIMULASI METODE DIRECT TORQUE CONTROL (DTC) UNTUK PENGATURAN KECEPATAN MOTOR INDUKSI TIGA FASA
 PERANCANGAN DAN SIULASI EODE DIREC ORQUE CONROL (DC) UNUK PENGAURAN KECEPAAN OOR INDUKSI IGA FASA Panji Kurniawan 67 Juruan knik Elktro FI, Intitut knologi Spuluh Nopmbr Kampu IS, Surabaya 6 -mail:[email protected]
PERANCANGAN DAN SIULASI EODE DIREC ORQUE CONROL (DC) UNUK PENGAURAN KECEPAAN OOR INDUKSI IGA FASA Panji Kurniawan 67 Juruan knik Elktro FI, Intitut knologi Spuluh Nopmbr Kampu IS, Surabaya 6 -mail:[email protected]
Oleh : Bustanul Arifin K BAB IV HASIL PENELITIAN. Nama N Mean Std. Deviation Minimum Maximum X ,97 3,
 Kpdulian trhadap sanitasi lingkungan diprdiksi dari tingkat pndidikan ibu dan pndapatan kluarga pada kluarga sjahtra I klurahan Krtn kcamatan Lawyan kota Surakarta Olh : Bustanul Arifin K.39817 BAB IV
Kpdulian trhadap sanitasi lingkungan diprdiksi dari tingkat pndidikan ibu dan pndapatan kluarga pada kluarga sjahtra I klurahan Krtn kcamatan Lawyan kota Surakarta Olh : Bustanul Arifin K.39817 BAB IV
Pembahasan Soal. Pak Anang SELEKSI MASUK UNIVERSITAS INDONESIA. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS. Disusun Oleh :
 Pmbahasan Soal SELEKSI MASUK UNIVERSITAS INDONESIA Disrtai TRIK SUPERKILAT dan LOGIKA PRAKTIS Disusun Olh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pmbahasan Soal SIMAK UI 2011 Matmatika
Pmbahasan Soal SELEKSI MASUK UNIVERSITAS INDONESIA Disrtai TRIK SUPERKILAT dan LOGIKA PRAKTIS Disusun Olh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pmbahasan Soal SIMAK UI 2011 Matmatika
BAB II TEORI DASAR 2.1 Pengertian Pasang Surut
 BAB II TEORI DASAR 2.1 Pngrtian Pasang Surut Pasang surut air laut (pasut) adalah pristiwa naik turunnya muka air scara priodik dngan rata-rata priodnya 12,4 jam (di bbrapa tmpat 24,8 jam) (Pond dan Pickard,
BAB II TEORI DASAR 2.1 Pngrtian Pasang Surut Pasang surut air laut (pasut) adalah pristiwa naik turunnya muka air scara priodik dngan rata-rata priodnya 12,4 jam (di bbrapa tmpat 24,8 jam) (Pond dan Pickard,
Variabel Indikator Deskriptor No. item Motivasi Belajar. 6. Kebiasaan dalam mengikuti pelajaran 7. Semangat dalam mengikuti pelajaran
 Lapiran Kisi-Kisi Skala MotivasiBlajar Variabl Indikator Dskriptor No it + - Motivasi Blajar Ktkunan dala blajar,,, Ult dala nghadapiksul itan Minat dan ktajaan prhatian dala blajar Brprstasi dala blajar
Lapiran Kisi-Kisi Skala MotivasiBlajar Variabl Indikator Dskriptor No it + - Motivasi Blajar Ktkunan dala blajar,,, Ult dala nghadapiksul itan Minat dan ktajaan prhatian dala blajar Brprstasi dala blajar
Aplikasi Integral. Panjang sebuah kurva w(y) sepanjang selang dapat ditemukan menggunakan persamaan
 Aplikasi Intgral Intgral dapat diaplikasikan k dalam banyak hal. Dari yang sdrhana, hingga aplikasi prhitungan yang sangat komplks. Brikut mrupakan aplikasi-aplikasi intgral yang tlah diklompokkan dalam
Aplikasi Intgral Intgral dapat diaplikasikan k dalam banyak hal. Dari yang sdrhana, hingga aplikasi prhitungan yang sangat komplks. Brikut mrupakan aplikasi-aplikasi intgral yang tlah diklompokkan dalam
Perancangan dan Implementasi Metode Kontrol Optimal LQR untuk Pengendalian Frekuensi pada Simulator Pembangkit Listrik Generator
 JURNAL EKNIK IS Vol., No. (Spt. ) ISSN: 3-97 A-66 Prancangan dan Iplntasi Mtod Kontrol Optial LQR untuk Pngndalian Frkunsi pada Siulator Pbangkit Listrik Gnrator Ahad Roni Utoo dan Mochaad Rali Jurusan
JURNAL EKNIK IS Vol., No. (Spt. ) ISSN: 3-97 A-66 Prancangan dan Iplntasi Mtod Kontrol Optial LQR untuk Pngndalian Frkunsi pada Siulator Pbangkit Listrik Gnrator Ahad Roni Utoo dan Mochaad Rali Jurusan
LAPORAN PRAKTIKUM FISIKA MODERN. JUDUL PRAKTIKUM PENENTUAN MUATAN SPESIFIK (e/m) ELEKTRON
 LAPORAN PRAKTIKUM FISIKA MODERN JUDUL PRAKTIKUM PENENTUAN MUATAN SPESIFIK (/) ELEKTRON OLEH: NAMA : THATHIT SUPRAYOGI NIM : 1303615513 OFFERING : N- KELOMPOK : PEMBIMBING : Dr. HARI WISODO, M. Si LABORATORIUM
LAPORAN PRAKTIKUM FISIKA MODERN JUDUL PRAKTIKUM PENENTUAN MUATAN SPESIFIK (/) ELEKTRON OLEH: NAMA : THATHIT SUPRAYOGI NIM : 1303615513 OFFERING : N- KELOMPOK : PEMBIMBING : Dr. HARI WISODO, M. Si LABORATORIUM
Model Matematik dari Spark Ignition Engine FIAT DEDRA V6
 AURALA Journal of Sintifi Modling & Coputation, Volu o. 0 ISS 00 Modl Matati dari Spar Ignition Engin FIA DEDRA V Irianto olitni Eltronia gri Surabaya Kapu IS Kputih Suolilo Surabaya 0 lp 0980 Fax 09 Abtra
AURALA Journal of Sintifi Modling & Coputation, Volu o. 0 ISS 00 Modl Matati dari Spar Ignition Engin FIA DEDRA V Irianto olitni Eltronia gri Surabaya Kapu IS Kputih Suolilo Surabaya 0 lp 0980 Fax 09 Abtra
PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON. Putri Anjarsari, S.Si., M.Pd
 PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON Putri Anjarsari, S.Si., M.Pd [email protected] PERKEMBANGAN TEORI ATOM Dmokritus Dalton Thomson Ruthrford Bohr Mkanika glombang Dmokritus
PERKEMBANGAN TEORI ATOM & PENEMUAN PROTON, NEUTRON, ELEKTRON Putri Anjarsari, S.Si., M.Pd [email protected] PERKEMBANGAN TEORI ATOM Dmokritus Dalton Thomson Ruthrford Bohr Mkanika glombang Dmokritus
Pada gambar 2 merupakan luasan bidang dua dimensi telah mengalami regangan. Salah satu titik yang menjadi titik acuan adalah titik P.
 nurunan Kcpatan Glombang dan Glombang S Glombang sismik mrupakan gtaran yang mrambat pada mdium batuan dan mnmbus lapisan bumi. njalaran mnybabkan dformasi batuan.strss atau tkanan didfinisikan gaya prsatuan
nurunan Kcpatan Glombang dan Glombang S Glombang sismik mrupakan gtaran yang mrambat pada mdium batuan dan mnmbus lapisan bumi. njalaran mnybabkan dformasi batuan.strss atau tkanan didfinisikan gaya prsatuan
BAB II TEGANGAN TINGGI IMPULS
 BAB II TEGANGAN TINGGI IMPULS 2. TEGANGAN IMPULS Tegangan Impul (impule voltage) adalah tegangan yang naik dalam waktu ingkat ekali kemudian diuul dengan penurunan yang relatif lambat menuju nol. Ada tiga
BAB II TEGANGAN TINGGI IMPULS 2. TEGANGAN IMPULS Tegangan Impul (impule voltage) adalah tegangan yang naik dalam waktu ingkat ekali kemudian diuul dengan penurunan yang relatif lambat menuju nol. Ada tiga
PROSIDING ISBN :
 S-2 ANALISA FAKTOR GAS BUANG KENDARAAN BERBAHAN BAKAR SOLAR MENGGUNAKAN RANCANGAN ACAK LENGKAP (Suatu Aplikai Matmatika dan Statitika Untuk Pnlitian Lingkungan) Dy Gunita 1, Lilik Slamt 2 1,2 LEMBAGA PENERBANGAN
S-2 ANALISA FAKTOR GAS BUANG KENDARAAN BERBAHAN BAKAR SOLAR MENGGUNAKAN RANCANGAN ACAK LENGKAP (Suatu Aplikai Matmatika dan Statitika Untuk Pnlitian Lingkungan) Dy Gunita 1, Lilik Slamt 2 1,2 LEMBAGA PENERBANGAN
Perancangan dan Implementasi Metode Kontrol Optimal LQR Untuk Pengendalian Frekuensi Pada Simulator Pembangkit Listrik Generator
 JURNAL EKNIK POMIS Vol., No., () -6 Prancangan dan Iplntasi Mtod Kontrol Optial LQR Untuk Pngndalian Pada Siulator Pbangkit Listrik Gnrator Ahad Roni Utoo, Mochaad Rali Jurusan knik Elktro, Fakultas knologi
JURNAL EKNIK POMIS Vol., No., () -6 Prancangan dan Iplntasi Mtod Kontrol Optial LQR Untuk Pngndalian Pada Siulator Pbangkit Listrik Gnrator Ahad Roni Utoo, Mochaad Rali Jurusan knik Elktro, Fakultas knologi
PENGARUH BAURAN PEMASARAN TERHADAP KEPUTUSAN PEMBELIAN (Survei Kepada Konsumen Sepatu Merek Converse di Kota Malang)
 PENGARUH BAURAN PEMASARAN TERHADAP KEPUTUSAN PEMBELIAN (Survi Kpada Konsun Spatu Mrk Convrs di Kota Malang) Mrry Blla Fbriana Edy ulianto Sunarti Fakultas Ilu Adinistrasi Univrsitas Brawijaya Malang [email protected]
PENGARUH BAURAN PEMASARAN TERHADAP KEPUTUSAN PEMBELIAN (Survi Kpada Konsun Spatu Mrk Convrs di Kota Malang) Mrry Blla Fbriana Edy ulianto Sunarti Fakultas Ilu Adinistrasi Univrsitas Brawijaya Malang [email protected]
8. Fungsi Logaritma Natural, Eksponensial, Hiperbolik
 8. Fungsi Logaritma Natural, Eksponnsial, Hiprbolik 8.. Fungsi Logarithma Natural. Sudaratno Sudirham Dfinisi. Logaritma natural adalah logaritma dngan mnggunakan basis bilangan. Bilangan ini, sprti halna
8. Fungsi Logaritma Natural, Eksponnsial, Hiprbolik 8.. Fungsi Logarithma Natural. Sudaratno Sudirham Dfinisi. Logaritma natural adalah logaritma dngan mnggunakan basis bilangan. Bilangan ini, sprti halna
Fisika Dasar II Listrik, Magnet, Gelombang dan Fisika Modern
 Fisika Dasar II Listrik, Magnt, Glombang dan Fisika Modrn Pokok Bahasan Mdan Listrik dan Dipol Listrik Abdul Waris Rizal Kurniadi Novitrian Sparisoma Viridi Mdan Listrik Artinya daripada ini... Mrka lbih
Fisika Dasar II Listrik, Magnt, Glombang dan Fisika Modrn Pokok Bahasan Mdan Listrik dan Dipol Listrik Abdul Waris Rizal Kurniadi Novitrian Sparisoma Viridi Mdan Listrik Artinya daripada ini... Mrka lbih
REGRESI LINEAR & KORELASI. Elty Sarvia, ST., MT. Fakultas Teknik Jurusan Teknik Industri Universitas Kristen Maranatha Bandung REGRESI
 9/08/0 REGREI LINEAR & KORELAI Elty arvia, T., MT. Fakultas Tknik Jurusan Tknik Industri Univrsitas Kristn Maranatha Bandung REGREI jauh ini,kita hanya mmbuat statistik dngan satu variabl pada waktu trtntu,
9/08/0 REGREI LINEAR & KORELAI Elty arvia, T., MT. Fakultas Tknik Jurusan Tknik Industri Univrsitas Kristn Maranatha Bandung REGREI jauh ini,kita hanya mmbuat statistik dngan satu variabl pada waktu trtntu,
BAB 2 DASAR TEORI 2.1 TEORI GELOMBANG LINIER. Bab 2 Teori Dasar
 BAB 2 DASAR TEORI Glombang air mrupakan manifstasi dari suatu rambatan nrgi yang mmiliki frkunsi dan priod. Glombang air yang trjadi di laut dapat disbabkan olh angin, grakan kapal, gmpa atau gaya gravitasi
BAB 2 DASAR TEORI Glombang air mrupakan manifstasi dari suatu rambatan nrgi yang mmiliki frkunsi dan priod. Glombang air yang trjadi di laut dapat disbabkan olh angin, grakan kapal, gmpa atau gaya gravitasi
BAB 2 DISTRIBUSI INDUK DAN DISTRIBUSI SAMPEL
 BAB DISTRIBUSI IDUK DA DISTRIBUSI SAMEL.. EDAHULUA Jika suatu bsaran mmiliki nilai ssungguhnya sdangkan hasil ukurnya adalah maka kita mngharapkan hasil pngamatan mndkati, namun knyataannya tidak slalu
BAB DISTRIBUSI IDUK DA DISTRIBUSI SAMEL.. EDAHULUA Jika suatu bsaran mmiliki nilai ssungguhnya sdangkan hasil ukurnya adalah maka kita mngharapkan hasil pngamatan mndkati, namun knyataannya tidak slalu
1. Diberikan fungsi permintaan dan penawaran sebuah barang, Q 25 2Q
 Matmatika Ekonomi I Jawaban Tuga I Matmatika Ekonomi I. Dibrikan fungi prmintaan an pnawaran buah barang, 0 ngan,, an brturut-turut aalah harga (alam rupiah), kuantita (jumlah) prmintaan an kuantita pnawaran.
Matmatika Ekonomi I Jawaban Tuga I Matmatika Ekonomi I. Dibrikan fungi prmintaan an pnawaran buah barang, 0 ngan,, an brturut-turut aalah harga (alam rupiah), kuantita (jumlah) prmintaan an kuantita pnawaran.
PENGARUH TEBAL RUSUK TERHADAP LAJU PERPINDAHAN PANAS KONVEKSI PADA RIBBED SQUARE CHANNEL. Akhmad Farid 1)
 Widya knika Vol.0 No.1; Mart 01 ISSN 1411 0660 : 6-10 PENGARUH EBAL RUSUK ERHADAP LAJU PERPINDAHAN PANAS KONVEKSI PADA RIBBED SQUARE HANNEL Akhad Farid 1) ABSRAK Pningkatan turbulni aliran fluida daat
Widya knika Vol.0 No.1; Mart 01 ISSN 1411 0660 : 6-10 PENGARUH EBAL RUSUK ERHADAP LAJU PERPINDAHAN PANAS KONVEKSI PADA RIBBED SQUARE HANNEL Akhad Farid 1) ABSRAK Pningkatan turbulni aliran fluida daat
BAB 5 E N E R G I. W = F II d...(5.1)
 5 E N E G I 5.1 Krja Kata krja iliki arti pada bahasa shari-hari. Ttapi dala fisika,krja dibri arti yang spsifik untuk ndskripsikan apa yang dihasilkan olh gaya ktika ia bkrja pada bnda sntara bnda trsbut
5 E N E G I 5.1 Krja Kata krja iliki arti pada bahasa shari-hari. Ttapi dala fisika,krja dibri arti yang spsifik untuk ndskripsikan apa yang dihasilkan olh gaya ktika ia bkrja pada bnda sntara bnda trsbut
1. Proses Normalisasi
 BAB IV PEMBAHASAN A. Pr-Procssing Pross pngolahan signal PCG sblum dilakukan kstaksi dan klasifikasi adalah pr-procssing. Signal PCG untuk data training dan data tsting trdapat dalam lampiran 5 (halaman
BAB IV PEMBAHASAN A. Pr-Procssing Pross pngolahan signal PCG sblum dilakukan kstaksi dan klasifikasi adalah pr-procssing. Signal PCG untuk data training dan data tsting trdapat dalam lampiran 5 (halaman
BAB IV ANALISA PENYEBAB PUTUSNYA RANTAI RECLAIM FEEDER
 BAB IV AALISA PEYEBAB PUTUSYA RATAI RECLAIM FEEDER Rclaim Fdr adalah buah min ang digunakan dalam itm pngiriman matrial (matrial input). Dalam hal ini, rclaim fdr mrupakan alat bantu pada itim konvor dalam
BAB IV AALISA PEYEBAB PUTUSYA RATAI RECLAIM FEEDER Rclaim Fdr adalah buah min ang digunakan dalam itm pngiriman matrial (matrial input). Dalam hal ini, rclaim fdr mrupakan alat bantu pada itim konvor dalam
OLEH: DESTRIYANTI TRI BUDIARTI YULLIA HESTIANA IRWAN SEPTEMBER GUNAWAN
 OLEH: DESTRIYANTI 7 58 TRI BUDIARTI 7 YULLIA HESTIANA 7 5 IRWAN SEPTEBER 7 46 GUNAWAN 7 KELAS : 6. L ATA KULIAH : ATEATIKA LANJUTAN DOSEN PENGASUH : FADLI, S.Si FAKULTAS KEGURUAN DAN ILU PENDIDIKAN UNIVERSITAS
OLEH: DESTRIYANTI 7 58 TRI BUDIARTI 7 YULLIA HESTIANA 7 5 IRWAN SEPTEBER 7 46 GUNAWAN 7 KELAS : 6. L ATA KULIAH : ATEATIKA LANJUTAN DOSEN PENGASUH : FADLI, S.Si FAKULTAS KEGURUAN DAN ILU PENDIDIKAN UNIVERSITAS
MENINGKATKAN KEMAMPUAN MENULIS DALAM PEMBELAJARAN BAHASA INDONESIA MELALUI MODEL EXAMPLE NON EXAMPLE DI KELAS V SEKOLAH DASAR NEGERI MEDAN
 MENINGKATKAN KEMAMPUAN MENULIS DALAM PEMBELAJARAN BAHASA INDONESIA MELALUI MODEL EXAMPLE NON EXAMPLE DI KELAS V SEKOLAH DASAR NEGERI MEDAN Eva Btty Simanjuntak, Lili Huaini Surl : [email protected]
MENINGKATKAN KEMAMPUAN MENULIS DALAM PEMBELAJARAN BAHASA INDONESIA MELALUI MODEL EXAMPLE NON EXAMPLE DI KELAS V SEKOLAH DASAR NEGERI MEDAN Eva Btty Simanjuntak, Lili Huaini Surl : [email protected]
Fungsi dan Grafik Diferensial dan Integral
 Sudarano Sudirham Sudi Mandiri Fungi dan Grafik Difrnial dan Ingral Sudarano Sudirham, Fungi dan Grafik, Difrnial dan Ingral Darublic 6 Pramaan Difrnial Ord Dua 6.. Pramaan Difrnial Linir Ord Dua Scara
Sudarano Sudirham Sudi Mandiri Fungi dan Grafik Difrnial dan Ingral Sudarano Sudirham, Fungi dan Grafik, Difrnial dan Ingral Darublic 6 Pramaan Difrnial Ord Dua 6.. Pramaan Difrnial Linir Ord Dua Scara
APLIKASI METODE ELEMEN HINGGA PADA ANALISIS STRUKTUR RANGKA BATANG
 Jurna Iiah MEDIA ENGINEERING Vo., No., Jui 0 ISSN 087-9334 (56-60) APLIKASI METODE ELEMEN HINGGA PADA ANALISIS STRKTR RANGKA BATANG Srvi O. Dapas Dosn Jurusan Tknik Sipi Fakutas Tknik nivrsitas Sa Ratuangi
Jurna Iiah MEDIA ENGINEERING Vo., No., Jui 0 ISSN 087-9334 (56-60) APLIKASI METODE ELEMEN HINGGA PADA ANALISIS STRKTR RANGKA BATANG Srvi O. Dapas Dosn Jurusan Tknik Sipi Fakutas Tknik nivrsitas Sa Ratuangi
TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER
 TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER HannaA Parhusip Cntr of Applid Mathmatics Program Studi Matmatika Industri dan Statistika Fakultas Sains dan Matmatika Univrsitas Kristn Sata
TINJAUAN ULANG EKSPANSI ASIMTOTIK UNTUK MASALAH BOUNDARY LAYER HannaA Parhusip Cntr of Applid Mathmatics Program Studi Matmatika Industri dan Statistika Fakultas Sains dan Matmatika Univrsitas Kristn Sata
PEMANFAATAN SALAK BONGKOK
 PEMANFAATAN SALAK BONGKOK (Salacca dulis Rinw) SEBAGAI DIVERSIFIKASI PENGOLAHAN PANGAN UNTUK MENINGKATKAN NILAI EKONOMIS BUAH LOKAL Ultilization Of Salak Bongkok As A Divrsifid Food Procssing To Incras
PEMANFAATAN SALAK BONGKOK (Salacca dulis Rinw) SEBAGAI DIVERSIFIKASI PENGOLAHAN PANGAN UNTUK MENINGKATKAN NILAI EKONOMIS BUAH LOKAL Ultilization Of Salak Bongkok As A Divrsifid Food Procssing To Incras
Mata Kuliah : Matematika Diskrit Program Studi : Teknik Informatika Minggu ke : 7
 Mata Kuliah : Matmatika Diskrit Program Studi : Tknik Informatika Minggu k : 7 MATRIK GRAPH Sbuah graph dapat kita sajikan dalam bntuk matrik, yaitu : a. Matrik titik (Adjacnt Matrix) b. Matrik rusuk (Edg
Mata Kuliah : Matmatika Diskrit Program Studi : Tknik Informatika Minggu k : 7 MATRIK GRAPH Sbuah graph dapat kita sajikan dalam bntuk matrik, yaitu : a. Matrik titik (Adjacnt Matrix) b. Matrik rusuk (Edg
Reduksi data gravitasi
 Modul 5 Rduksi data gravitasi Rduksi data gravitasi trdiri dari:. Rduksi g toritis. Rduksi fr air 3. Rduksi Bougur 4. Rduksi mdan/trrain. Rduksi g toritis Pnlaahan tntang konsp rduksi data gravitasi lbih
Modul 5 Rduksi data gravitasi Rduksi data gravitasi trdiri dari:. Rduksi g toritis. Rduksi fr air 3. Rduksi Bougur 4. Rduksi mdan/trrain. Rduksi g toritis Pnlaahan tntang konsp rduksi data gravitasi lbih
Materike April 2014
 Matrik-6 Pnggunaan Intgral Tak Tntu 10 April 014 Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna ( difrnsial Contoh ' ' '' ' Prsamaan Difrnsial dan Pnggunaanna
Matrik-6 Pnggunaan Intgral Tak Tntu 10 April 014 Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna ( difrnsial Contoh ' ' '' ' Prsamaan Difrnsial dan Pnggunaanna
IV. HASIL DAN PEMBAHASAN
 IV. HASIL DAN PEMBAHASAN A. KARAKTERISTIK MUTU DAN REOLOGI CPO AWAL Minyak sawit kasar (crud palm oil/cpo) mrupakan komoditas unggulan Indonsia yang juga brpran pnting dalam prdagangan dunia. Mngingat
IV. HASIL DAN PEMBAHASAN A. KARAKTERISTIK MUTU DAN REOLOGI CPO AWAL Minyak sawit kasar (crud palm oil/cpo) mrupakan komoditas unggulan Indonsia yang juga brpran pnting dalam prdagangan dunia. Mngingat
BAB I PENDAHULUAN. I.1. Latar Belakang
 Laboratoriu Hidrogeologi 015 BAB I PENDAHULUAN I.1. Latar Belakang Hidrogeologi (hidro- berarti air, dan -geologi berarti ilu engenai batuan) adalah erupakan perpaduan antara ilu geologi dengan ilu hidrolika
Laboratoriu Hidrogeologi 015 BAB I PENDAHULUAN I.1. Latar Belakang Hidrogeologi (hidro- berarti air, dan -geologi berarti ilu engenai batuan) adalah erupakan perpaduan antara ilu geologi dengan ilu hidrolika
Materi ke - 6. Penggunaan Integral Tak Tentu. 30 Maret 2015
 Matri k - 6 Pnggunaan Intgral Tak Tntu 30 Mart 015 Industrial Enginring UNS [email protected] Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna difrnsial Contoh '
Matri k - 6 Pnggunaan Intgral Tak Tntu 30 Mart 015 Industrial Enginring UNS [email protected] Prsamaan Difrnsial dan Pnggunaanna Prsamaan difrnsial mngaitkan suatu fungsi dngan turunanna difrnsial Contoh '
MA 2081 STATISTIKA DASAR SEMESTER I 2012/2013 KK STATISTIKA, FMIPA ITB
 MA 081 STATISTIKA DASAR SEMESTER I 01/013 KK STATISTIKA, FMIPA ITB UJIAN RE-EVALUASI Jum at, 1 Deember 01, 13.30 15.30 WIB (10 MENIT) Kela 01. Pengajar: Utriweni Mukhaiyar, Kela 0. Pengajar: Sumanto Winotoharjo
MA 081 STATISTIKA DASAR SEMESTER I 01/013 KK STATISTIKA, FMIPA ITB UJIAN RE-EVALUASI Jum at, 1 Deember 01, 13.30 15.30 WIB (10 MENIT) Kela 01. Pengajar: Utriweni Mukhaiyar, Kela 0. Pengajar: Sumanto Winotoharjo
BAB VIII METODA TEMPAT KEDUDUKAN AKAR
 6 BAB VIII METODA TEMPAT EDUDUAN AAR Dekripi : Bab ini memberikan gambaran ecara umum mengenai diagram tempat kedudukan akar dan ringkaan aturan umum untuk menggambarkan tempat kedudukan akar erta contohcontoh
6 BAB VIII METODA TEMPAT EDUDUAN AAR Dekripi : Bab ini memberikan gambaran ecara umum mengenai diagram tempat kedudukan akar dan ringkaan aturan umum untuk menggambarkan tempat kedudukan akar erta contohcontoh
Sinanglingtyas et al., Penerapan Metode Role Playing...
 Sinanglingtya t al., Pnrapan Mtod Rol Playing... Pnrapan Mtod Rol Playing untuk Mningkatkan Aktivita dan Hail Blajar Siwa Kla V dalam Pmblajaran PKn Pokok Bahaan Bntuk-Bntuk Kputuan Brama di SDN Tukum
Sinanglingtya t al., Pnrapan Mtod Rol Playing... Pnrapan Mtod Rol Playing untuk Mningkatkan Aktivita dan Hail Blajar Siwa Kla V dalam Pmblajaran PKn Pokok Bahaan Bntuk-Bntuk Kputuan Brama di SDN Tukum
Pengaruh Posisi Pipa Segi Empat dalam Aliran Fluida Terhadap Perpindahan Panas
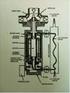 Pngaruh Posisi Pipa Sgi Empat dalam Aliran Fluida Trhadap Prpindahan Panas Kaprawi Jurusan Tknik Msin, Fakultas Tknik UNSRI, Palmbang E-mail: [email protected] ABSTRAK Sbuah pipa brpnampang sgi mpat dipasang
Pngaruh Posisi Pipa Sgi Empat dalam Aliran Fluida Trhadap Prpindahan Panas Kaprawi Jurusan Tknik Msin, Fakultas Tknik UNSRI, Palmbang E-mail: [email protected] ABSTRAK Sbuah pipa brpnampang sgi mpat dipasang
PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN
 JIMT ol. 9 No. 1 Juni 01 (Hal. 16 8) Jurnal Ilmiah Matmatika dan Trapan ISSN : 450 766X PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN Nurainun 1, S. Musdalifah,
JIMT ol. 9 No. 1 Juni 01 (Hal. 16 8) Jurnal Ilmiah Matmatika dan Trapan ISSN : 450 766X PELABELAN TOTAL SISI ANTI AJAIB SUPER (PTSAAS) PADA GABUNGAN GRAF BINTANG GANDA DAN LINTASAN Nurainun 1, S. Musdalifah,
model pengukuran yang menunjukkan ukur Pengukuran dalam B. Model Mode sama indikator dan 1 Pag
 Modl Modl Pngukuran dalam Pmodlan Prsamaan Struktural Wahyu Widhiarso Fakultas Psikologi UGM Tulisan ini akan mmbahas bbrapa modl dalam SEM yang unik. Dikatakan unik karna jarang dipakai. Tulisan hanya
Modl Modl Pngukuran dalam Pmodlan Prsamaan Struktural Wahyu Widhiarso Fakultas Psikologi UGM Tulisan ini akan mmbahas bbrapa modl dalam SEM yang unik. Dikatakan unik karna jarang dipakai. Tulisan hanya
ANALISIS LOG-LOGISTIK UNTUK MENGGAMBARKAN HUBUNGAN DOSIS-RESPON HERBISIDA PADA TIGA JENIS GULMA
 ANALISIS LOG-LOGISTIK UNTUK MENGGAMBARKAN HUBUNGAN DOSIS-RESPON HERBISIDA PADA TIGA JENIS GULMA Olh : Yanti Muliyaningsih G40026 PROGRAM STUDI STATISTIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT
ANALISIS LOG-LOGISTIK UNTUK MENGGAMBARKAN HUBUNGAN DOSIS-RESPON HERBISIDA PADA TIGA JENIS GULMA Olh : Yanti Muliyaningsih G40026 PROGRAM STUDI STATISTIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT
ELEKTROMAGNETIK TERAPAN 1. PROPAGASI GELOMBANG ELEKTROMAGNET (GELOMBANG DATAR)
 LKTROMAGNTIK TRAPAN 1. PROPAGASI GLOMBANG LKTROMAGNT (GLOMBANG DATAR) OUTLIN Propagai Glombang lktromagnt (Glombang Datar) PNDAULUAN Glombang Glombang adalah uatu fnomna alamiah ang trjadi dalam dimni
LKTROMAGNTIK TRAPAN 1. PROPAGASI GLOMBANG LKTROMAGNT (GLOMBANG DATAR) OUTLIN Propagai Glombang lktromagnt (Glombang Datar) PNDAULUAN Glombang Glombang adalah uatu fnomna alamiah ang trjadi dalam dimni
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde I
 Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
BAB III : ALAT-ALAT OPTIK
 BAB III : ALAT-ALAT OPTIK Pada bab ini mmbaa tntang bbrapa lat optik yang mnggunakan lna, prti : mata dan kacamata (lna kontak), lup (kaca pmbar), mikrokop, tropong (tlkop). III.. Mata manuia dan Kacamata
BAB III : ALAT-ALAT OPTIK Pada bab ini mmbaa tntang bbrapa lat optik yang mnggunakan lna, prti : mata dan kacamata (lna kontak), lup (kaca pmbar), mikrokop, tropong (tlkop). III.. Mata manuia dan Kacamata
Integral Fungsi Eksponen, Fungsi Trigonometri, Fungsi Logaritma
 Modul Intgral Fungsi Eksponn, Fungsi Trigonomtri, Fungsi Logaritma Dr. Subanar D PENDAHULUAN alam mata kuliah Kalkulus I Anda tlah mngnal bahwa intgrasi adalah pross balikan dari difrnsiasi. Jadi untuk
Modul Intgral Fungsi Eksponn, Fungsi Trigonomtri, Fungsi Logaritma Dr. Subanar D PENDAHULUAN alam mata kuliah Kalkulus I Anda tlah mngnal bahwa intgrasi adalah pross balikan dari difrnsiasi. Jadi untuk
BAB V DISTRIBUSI PROBABILITAS DISKRIT
 BAB V DISTRIBUSI ROBABILITAS DISKRIT 5.. Distribusi Uniform Disrit Bila variabl aca X mmilii nilai,,... dngan probabilitas yang sama, maa distribusi uniform disrit dinyataan sbagai: f (, ) ;,,... paramtr
BAB V DISTRIBUSI ROBABILITAS DISKRIT 5.. Distribusi Uniform Disrit Bila variabl aca X mmilii nilai,,... dngan probabilitas yang sama, maa distribusi uniform disrit dinyataan sbagai: f (, ) ;,,... paramtr
BAB 2 LANDASAN TEORI
 6 A ANDAAN TEORI Pngrtian MM Multi vl Markting MM adalah salah satu contoh unit usaha yang brpola bisnis unik, yang sdang brkmbang di dalam bidang pnjualan barangbarang kbutuhan manusia, mulai brupaya
6 A ANDAAN TEORI Pngrtian MM Multi vl Markting MM adalah salah satu contoh unit usaha yang brpola bisnis unik, yang sdang brkmbang di dalam bidang pnjualan barangbarang kbutuhan manusia, mulai brupaya
BAB I PENDAHULUAN 1.1.Latar Belakang
 BAB I PENDAHULUAN 1.1.Latar Blakang Sarana dan prasarana transportasi di suatu ngara mmpunyai pranan yang sangat pnting dalam pngmbangan suatu kawasan trtntu, baik konomi, sosial, budaya dan sbagainya.
BAB I PENDAHULUAN 1.1.Latar Blakang Sarana dan prasarana transportasi di suatu ngara mmpunyai pranan yang sangat pnting dalam pngmbangan suatu kawasan trtntu, baik konomi, sosial, budaya dan sbagainya.
Jurnal ICT Penelitian dan Penerapan Teknologi AKADEMI TELKOM SANDHY PUTRA JAKARTA
 Jurnal ICT Pnlitian dan Pnrapan Tknologi Jurnal ICT Pnlitian dan Pnrapan Tknologi AKADEMI TELKOM SANDHY PUTRA JAKARTA PENGUKURAN KUALITAS TRANSMISI SERAT OPTIK PT. TELKOMSEL PADA RUAS TELKOM KOTAMUBAGUUPAI
Jurnal ICT Pnlitian dan Pnrapan Tknologi Jurnal ICT Pnlitian dan Pnrapan Tknologi AKADEMI TELKOM SANDHY PUTRA JAKARTA PENGUKURAN KUALITAS TRANSMISI SERAT OPTIK PT. TELKOMSEL PADA RUAS TELKOM KOTAMUBAGUUPAI
BAB II TINJAUAN PUSTAKA. fungsi dari faktor produksi adalah fungsi dari modal (capital) dan tenaga kerja
 BAB II TINJAUAN USTAKA 2.1. Landasan Tori 2.1.1. nawaran Agrgat nawaran Agrgat atau Aggrgat Supply adalah jumlah total dari barang dan jasa yang ditawarkan dalam suatu prkonomian pada tingkat harga. Modl
BAB II TINJAUAN USTAKA 2.1. Landasan Tori 2.1.1. nawaran Agrgat nawaran Agrgat atau Aggrgat Supply adalah jumlah total dari barang dan jasa yang ditawarkan dalam suatu prkonomian pada tingkat harga. Modl
PENGARUH PARKIR KENDARAAN RODA EMPAT TERHADAP ARUS LALU LINTAS PADA RUAS JALAN RAYA TUNTANG - BATAS KOTA SALATIGA 1
 PENGARH PARKIR KENDARAAN RODA EMPAT TERHADAP ARS LAL LINTAS PADA RAS JALAN RAYA TNTANG - BATAS KOTA SALATIGA 1 Rahan Dwihari ABSTRACT The objective o the tudy i to analyi the eect o traic volue caued by
PENGARH PARKIR KENDARAAN RODA EMPAT TERHADAP ARS LAL LINTAS PADA RAS JALAN RAYA TNTANG - BATAS KOTA SALATIGA 1 Rahan Dwihari ABSTRACT The objective o the tudy i to analyi the eect o traic volue caued by
Gambar IV.6. Gambaran kontur bidang sesar yang menggambarkan bentuk ramp-flat-ramp pada border fault di Sub-cekungan Kiri.
 Pada pta struktur waktu (Gambar IV.4) trlihat bntuk ssar utama yang cukup unik dibagian tngah. Bntuk ini dipngaruhi olh konfigurasi Batuan Dasar yang dihasilkan olh struktur brumur Pra-Trsir. Pada pta
Pada pta struktur waktu (Gambar IV.4) trlihat bntuk ssar utama yang cukup unik dibagian tngah. Bntuk ini dipngaruhi olh konfigurasi Batuan Dasar yang dihasilkan olh struktur brumur Pra-Trsir. Pada pta
PENENTUAN NILAI e/m ELEKTRON
 Pnntuan Nilai E/m Elktron 013 PENENTUAN NILAI /m ELEKTRON Intan Masruroh S, Anita Susanti, Rza Ruzuqi, Zaky Alam Laboratorium Fisika Radiasi, Dpartmn Fisika Fakultas Sains Dan Tknologi, Univrsitas Airlangga
Pnntuan Nilai E/m Elktron 013 PENENTUAN NILAI /m ELEKTRON Intan Masruroh S, Anita Susanti, Rza Ruzuqi, Zaky Alam Laboratorium Fisika Radiasi, Dpartmn Fisika Fakultas Sains Dan Tknologi, Univrsitas Airlangga
BAB 2 LANDASAN TEORI
 6 BAB LANDASAN TEORI Pada bab ini akan diuraikan mngnai tori dan trminologi graph, yaitu bntuk-bntuk khusus suatu graph. Di sini uga akan dilaskan mngnai minimum spanning tr, pmrograman 0-, dan aplikasi
6 BAB LANDASAN TEORI Pada bab ini akan diuraikan mngnai tori dan trminologi graph, yaitu bntuk-bntuk khusus suatu graph. Di sini uga akan dilaskan mngnai minimum spanning tr, pmrograman 0-, dan aplikasi
STUDI KELAYAKAN SARANA DAN PRASARANA PRAKTIK UJIAN KOMPETENSI PROGAM KEAHLIAN TEKNIK KENDARAAN RINGAN SMK SWASTA TERAKREDITASI B SE-KABUPATEN SLEMAN
 92 Jurnal Pndidikan Tknik Otomotif, Edii XIII, Nomor 2, Tahun 2016 STUDI KELAYAKAN SARANA DAN PRASARANA PRAKTIK UJIAN KOMPETENSI PROGAM KEAHLIAN TEKNIK KENDARAAN RINGAN SMK SWASTA TERAKREDITASI B SE-KABUPATEN
92 Jurnal Pndidikan Tknik Otomotif, Edii XIII, Nomor 2, Tahun 2016 STUDI KELAYAKAN SARANA DAN PRASARANA PRAKTIK UJIAN KOMPETENSI PROGAM KEAHLIAN TEKNIK KENDARAAN RINGAN SMK SWASTA TERAKREDITASI B SE-KABUPATEN
Penyelesaian Soal Ujian Tengah Semester 2008
 Penyeleaian Soal Ujian Tengah Semeter 008 Soal A Curah hujan harian maximum tahunan elama periode 978.d. 007 di Staiun Godean Yogyakarta diajikan pada tabel di bawah ini. kedalaman hujan (mm) rekueni 5
Penyeleaian Soal Ujian Tengah Semeter 008 Soal A Curah hujan harian maximum tahunan elama periode 978.d. 007 di Staiun Godean Yogyakarta diajikan pada tabel di bawah ini. kedalaman hujan (mm) rekueni 5
Deret Fourier, Transformasi Fourier dan DFT
 Drt Fourir, Transformasi Fourir dan DFT A. Drt Fourir Drt fourir adalah drt yang digunakan dalam bidang rkayasa. Drt ini prtama kali ditmukan olh sorang ilmuan prancis Jan-Baptist Josph Fourir (1768-18).
Drt Fourir, Transformasi Fourir dan DFT A. Drt Fourir Drt fourir adalah drt yang digunakan dalam bidang rkayasa. Drt ini prtama kali ditmukan olh sorang ilmuan prancis Jan-Baptist Josph Fourir (1768-18).
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI. MICRO BUBBLE GENERATOR Micro Bubbl Gnrator (MBG) mrupakan suatu alat yang difungsikan untuk mnghasilkan glmbung udara dalam ukuran mikro, yaitu glmbung dngan diamtr 00 μm []. Aplikasi
BAB II LANDASAN TEORI. MICRO BUBBLE GENERATOR Micro Bubbl Gnrator (MBG) mrupakan suatu alat yang difungsikan untuk mnghasilkan glmbung udara dalam ukuran mikro, yaitu glmbung dngan diamtr 00 μm []. Aplikasi
+ = R R γ P II.3 Beberapa Percobaan dengan Soap Films Soap film yang diregangkan sepanjang kawat. Berbentuk planar, karena tekanan di kedua
 Bab II KAPILAITAS (CAPILLAITY) (CAPILLAITY) Olh : NISA NUINA VALEIE 1406 01 809 Bab II. Kapilaritas (Capillarity) II.1 Tgangan Prmukaan dan Enrgi Bbas Prmukaan II. Prsamaan Young dan Laplac II.3 Bbrapa
Bab II KAPILAITAS (CAPILLAITY) (CAPILLAITY) Olh : NISA NUINA VALEIE 1406 01 809 Bab II. Kapilaritas (Capillarity) II.1 Tgangan Prmukaan dan Enrgi Bbas Prmukaan II. Prsamaan Young dan Laplac II.3 Bbrapa
ANALISIS KINERJA STRUKTUR PADA BANGUNAN BERTINGKAT BERATURAN DAN KETIDAK BERATURAN HORIZONTAL SESUAI SNI
 ANALISIS KINERJA STRUKTUR PADA BANGUNAN BERTINGKAT BERATURAN DAN KETIDAK BERATURAN HORIZONTAL SESUAI SNI 03-1726-2012 Hotma L Purba Jurusan Tknik Sipil,Univrsitas Sriwijaya Korspondnsi pnulis : [email protected]
ANALISIS KINERJA STRUKTUR PADA BANGUNAN BERTINGKAT BERATURAN DAN KETIDAK BERATURAN HORIZONTAL SESUAI SNI 03-1726-2012 Hotma L Purba Jurusan Tknik Sipil,Univrsitas Sriwijaya Korspondnsi pnulis : [email protected]
MODUL PERKULIAHAN REKAYASA FONDASI 1. Penurunan Tanah pada Fondasi Dangkal. Fakultas Program Studi Tatap Muka Kode MK Disusun Oleh
 MODUL PERKULIAHAN REKAYASA FONDASI 1 Pnurunan Tanah pada Fondasi Dangkal Fakultas Program Studi Tatap Muka Kod MK Disusun Olh Tknik Prnanaan Tknik A41117AB dan Dsain Sipil 9 Abstrat Modul ini brisi bbrapa
MODUL PERKULIAHAN REKAYASA FONDASI 1 Pnurunan Tanah pada Fondasi Dangkal Fakultas Program Studi Tatap Muka Kod MK Disusun Olh Tknik Prnanaan Tknik A41117AB dan Dsain Sipil 9 Abstrat Modul ini brisi bbrapa
OPTIMISASI KAPASITOR PADA SELF EXCITED INDUCTION GENERATOR DENGAN METODE PARTICLE SWARM OPTIMIZATION
 Poiding SENTA 015 Politknik Ngi Malang Volu 7 SSN: 085-347 OPTMSAS KAPASTOR PADA SE ECTED NDUCTON GENERATOR DENGAN METODE PARTCE SWARM OPTMATON Nita ndiani Ptiwi 1, Ddt Canda Riawan, Hi Suyo Atoo 3 1,,3
Poiding SENTA 015 Politknik Ngi Malang Volu 7 SSN: 085-347 OPTMSAS KAPASTOR PADA SE ECTED NDUCTON GENERATOR DENGAN METODE PARTCE SWARM OPTMATON Nita ndiani Ptiwi 1, Ddt Canda Riawan, Hi Suyo Atoo 3 1,,3
PROSES PEMANENAN DENGAN MODEL LOGISTIK STUDI KASUS PADA PTP. NUSANTARA IX
 Prosiding SPMIPA. pp. 3-39, 006 ISBN : 979.704.47.0 PROSES PEMANENAN DENGAN MODEL LOGISTIK STUDI KASUS PADA PTP. NUSANTARA IX Eka Ariani, Agus Rusgiyono Jurusan Matmatika FMIPA Univrsitas Dipongoro Jl.
Prosiding SPMIPA. pp. 3-39, 006 ISBN : 979.704.47.0 PROSES PEMANENAN DENGAN MODEL LOGISTIK STUDI KASUS PADA PTP. NUSANTARA IX Eka Ariani, Agus Rusgiyono Jurusan Matmatika FMIPA Univrsitas Dipongoro Jl.
PMMC utk Arus Bolak-Balik
 PMMC utk Aru Bolak-Balik Penggunaan PMMC eperhatikan polarita tegangan. Hanya dpt eneria aru dc, tdk ac. Utk ac berfrekueni rendah (. Hertz), pointer beruaha engikuti harga eaat aru ac : ½ iklu poitif
PMMC utk Aru Bolak-Balik Penggunaan PMMC eperhatikan polarita tegangan. Hanya dpt eneria aru dc, tdk ac. Utk ac berfrekueni rendah (. Hertz), pointer beruaha engikuti harga eaat aru ac : ½ iklu poitif
MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL
 ISSN : 407 846 -ISSN : 460 846 MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL Chrish Rikardo *, Taufik Limansyah, Dharma Lsmono Magistr Tknik Industri,
ISSN : 407 846 -ISSN : 460 846 MODEL PERSEDIAAN DETERMINISTIK DENGAN MEMPERTIMBANGKAN MASA KADALUARSA DAN PENURUNAN HARGA JUAL Chrish Rikardo *, Taufik Limansyah, Dharma Lsmono Magistr Tknik Industri,
ROKET AIR SMA NEGERI 21 MAKASSAR
 ALAT PERAGA FISIKA ROKET AIR SMA NEGERI 21 MAKASSAR I. PENDAHULUAN 1. Latar Blakang Trkadang di waktu snggang srang siswa tatkala kbanyakan mrka mnggunakannya untuk brmalas-malasan, mlakukan hal yang tak
ALAT PERAGA FISIKA ROKET AIR SMA NEGERI 21 MAKASSAR I. PENDAHULUAN 1. Latar Blakang Trkadang di waktu snggang srang siswa tatkala kbanyakan mrka mnggunakannya untuk brmalas-malasan, mlakukan hal yang tak
TEORI ANTRIAN. Pertemuan Ke-12. Riani Lubis. Universitas Komputer Indonesia
 TEORI ANTRIAN MATA KULIAH RISET OPERASIONAL Pertemuan Ke-12 Riani Lubi Juruan Teknik Informatika Univerita Komputer Indoneia Pendahuluan (1) Pertamakali dipublikaikan pada tahun 1909 oleh Agner Kraup Erlang
TEORI ANTRIAN MATA KULIAH RISET OPERASIONAL Pertemuan Ke-12 Riani Lubi Juruan Teknik Informatika Univerita Komputer Indoneia Pendahuluan (1) Pertamakali dipublikaikan pada tahun 1909 oleh Agner Kraup Erlang
VI. EFISIENSI PRODUKSI DAN PERILAKU RISIKO PRODUKTIVITAS PETANI PADA USAHATANI CABAI MERAH
 VI. EFISIENSI PRODUKSI DAN PERILAKU RISIKO PRODUKTIVITAS PETANI PADA USAHATANI CABAI MERAH.. Faktor-Faktor yang Mmpngaruhi Produktivitas Cabai Mrah dan Nilai Elastisitas Input trhadap Produktivitas...
VI. EFISIENSI PRODUKSI DAN PERILAKU RISIKO PRODUKTIVITAS PETANI PADA USAHATANI CABAI MERAH.. Faktor-Faktor yang Mmpngaruhi Produktivitas Cabai Mrah dan Nilai Elastisitas Input trhadap Produktivitas...
MINAT SISWA TERHADAP EKSTRAKURIKULER OLAHRAGA BOLA VOLI DI SMA N 2 KABUPATEN PACITAN
 Artikl Skripsi MINAT SISWA TERHADAP EKSTRAKURIKULER OLAHRAGA BOLA VOLI DI SMA N 2 KABUPATEN PACITAN SKRIPSI Diajukan Untuk Mmnuhi Sbagian Syarat Guna Mmprolh Glar Sarjana Pndidikan (S.Pd.) Pada Jurusan
Artikl Skripsi MINAT SISWA TERHADAP EKSTRAKURIKULER OLAHRAGA BOLA VOLI DI SMA N 2 KABUPATEN PACITAN SKRIPSI Diajukan Untuk Mmnuhi Sbagian Syarat Guna Mmprolh Glar Sarjana Pndidikan (S.Pd.) Pada Jurusan
Catatan Kuliah 8 Memahami dan Menganalisa Optimisasi Pertumbuhan
 Caaan Kuliah 8 Mahai dan Mnganalisa Opiisasi Prubuhan. Sia dari Fungsi Eksponnsial Fungsi ksponnsial adalah ungsi ang variabl bbasna uncul sbagai pangka. Bnuk uu : b ; b > diana : variabl dpndn Conoh :
Caaan Kuliah 8 Mahai dan Mnganalisa Opiisasi Prubuhan. Sia dari Fungsi Eksponnsial Fungsi ksponnsial adalah ungsi ang variabl bbasna uncul sbagai pangka. Bnuk uu : b ; b > diana : variabl dpndn Conoh :
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB 1 PENDAHULUAN 1.1 Latar Blakang Di dalam dunia bisnis yang smakin ktat saat ini prusahaan dituntut untuk mmiliki banyak kunggulan komptitif agar dapat brsaing dngan yang lainnya. Maka dari itu, prusahaan
BAB 1 PENDAHULUAN 1.1 Latar Blakang Di dalam dunia bisnis yang smakin ktat saat ini prusahaan dituntut untuk mmiliki banyak kunggulan komptitif agar dapat brsaing dngan yang lainnya. Maka dari itu, prusahaan
BAB II Dioda dan Rangkaian Dioda
 BAB II Dioda dan Rangkaian Dioda 2.1. Pendahuluan Dioda adalah komponen elektronika yang teruun dari bahan emikonduktor tipe-p dan tipe-n ehingga mempunyai ifat dari bahan emikonduktor ebagai berikut.
BAB II Dioda dan Rangkaian Dioda 2.1. Pendahuluan Dioda adalah komponen elektronika yang teruun dari bahan emikonduktor tipe-p dan tipe-n ehingga mempunyai ifat dari bahan emikonduktor ebagai berikut.
Presentasi 2. Isi: Solusi Persamaan Diferensial pada Saluran Transmisi
 Prsntasi Isi: Solusi Prsamaan Difrnsial pada Saluran Transmisi Rprsntasi sinyal dalam bntuk phasor Pmikiran Dasar Sinyal harmonis mudah untuk diturunkan dan diintgralkan Smua sinyal fungsi waktu bisa dirprsntasikan
Prsntasi Isi: Solusi Prsamaan Difrnsial pada Saluran Transmisi Rprsntasi sinyal dalam bntuk phasor Pmikiran Dasar Sinyal harmonis mudah untuk diturunkan dan diintgralkan Smua sinyal fungsi waktu bisa dirprsntasikan
BAB II TINJAUAN KEPUSTAKAAN
 BAB II TINJAUAN KEPUTAKAAN II.1 PENDAHULUAN Yild lin adalah suatu pmcahan yang dapat digunakan dalam plat bton dimana trjadinya tgangan llh dan rotasi scara plastis muncul. Tori ini dapat digunakan dalam
BAB II TINJAUAN KEPUTAKAAN II.1 PENDAHULUAN Yild lin adalah suatu pmcahan yang dapat digunakan dalam plat bton dimana trjadinya tgangan llh dan rotasi scara plastis muncul. Tori ini dapat digunakan dalam
Kontrol Trakcing Laras Meriam 57mm dengan Menggunakan Hybrid Kontrol Logika Fuzzy - PID
 129 Kontrol Trakcing Laras Mriam 57mm dngan Mnggunakan Hybrid Kontrol Logika Fuzzy - PID Jki Saputra, M. Aziz Muslim, dan Rini Nur Hasanah Abstrak Laras mriam adalah salah satu bagian bsar dari kontruksi
129 Kontrol Trakcing Laras Mriam 57mm dngan Mnggunakan Hybrid Kontrol Logika Fuzzy - PID Jki Saputra, M. Aziz Muslim, dan Rini Nur Hasanah Abstrak Laras mriam adalah salah satu bagian bsar dari kontruksi
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Peatnya perkembangan ilmu pengetahuan dan teknologi membuat matematika menjadi angat penting artinya, bahkan dapat dikatakan bahwa perkembangan ilmu pengetahuan dan
BAB 1 PENDAHULUAN 1.1 Latar Belakang Peatnya perkembangan ilmu pengetahuan dan teknologi membuat matematika menjadi angat penting artinya, bahkan dapat dikatakan bahwa perkembangan ilmu pengetahuan dan
ALAT-ALAT SAMBUNG MEKANIS PADA KAYU: PAKU DAN BAUT OLEH: EVALINA HERAWATI, S.Hut, M.Si NIP
 Karya Tulis ALAT-ALAT SAMBUNG MEKANIS PAA KAYU: PAKU AN BAUT OLEH: EVALINA HERAWATI, S.Hut, M.Si NIP. 13 303 840 EPARTEMEN KEHUTANAN FAKULTAS PERTANIAN UNIVERSITAS SUMATERA UTARA MEAN 008 Evalina Hrawati
Karya Tulis ALAT-ALAT SAMBUNG MEKANIS PAA KAYU: PAKU AN BAUT OLEH: EVALINA HERAWATI, S.Hut, M.Si NIP. 13 303 840 EPARTEMEN KEHUTANAN FAKULTAS PERTANIAN UNIVERSITAS SUMATERA UTARA MEAN 008 Evalina Hrawati
Bab 1 Ruang Vektor. I. 1 Ruang Vektor R n. 1. Ruang berdimensi satu R 1 = R = kumpulan bilangan real Menyatakan suatu garis bilangan;
 Bab Ruang Vktor I. Ruang Vktor R n. Ruang brdimnsi satu R = R = kumpulan bilangan ral Mnyatakan suatu garis bilangan; -3 - - 0. Ruang brdimnsi dua R = bidang datar ; Stiap vktor di R dinyatakan sbagai
Bab Ruang Vktor I. Ruang Vktor R n. Ruang brdimnsi satu R = R = kumpulan bilangan ral Mnyatakan suatu garis bilangan; -3 - - 0. Ruang brdimnsi dua R = bidang datar ; Stiap vktor di R dinyatakan sbagai
