Catatan Kuliah (2 sks) MX 324 Pengantar Teori Graf
|
|
|
- Suryadi Widjaja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 Catatan Kuliah (2 sks) MX 324 Pengantar Teori Graf (Draft Versi Desember 2008 ) Oleh: Didit Budi Nugroho, M.Si. Program Studi Matematika Fakultas Sains dan Matematika Universitas Kristen Satya Wacana
2 DAFTAR ISI DAFTAR GAMBAR DAFTAR TABEL KATA PENGANTAR ii iii iv 1 De nisi dan Konsep Fundamental De nisi-de nisi Dasar Operasi Graf Lintasan dan Lingkaran Lingkaran Hamilton dan Jalan Euler Pohon dan Hutan Pohon dan Hutan Rentangan Soal-soal untuk Bab Pohon Rentangan Minimal Pengantar Pohon Rentangan Minimal Soal-soal untuk Bab Algoritma Pencarian Pengantar Depth-First Search Breadth-First Search Masalah Lintasan Terpendek Soal-soal untuk Bab Graf Berarah Pengantar Jaringan dan Arus Teorema Max-Flow-Min-Cut Soal-soal untuk Bab DAFTAR PUSTAKA 47 i
3 DAFTAR GAMBAR 1.1 Graf dengan sisi ganda dan gelang Dua graf yang isomor k Suatu lintasan P 6 di graf G (a) Graf tidak terhubung G 1 ; dan (b) graf terhubung G (a) T 1 bukan pohon; (b) T 2 adalah pohon Pohon-pohon yang tidak isomor k sampai dengan enam titik Subpohon T 1 dan T 2 yang diperoleh dari T dengan menghapus satu sisi x (a) Graf tangga; (b) pohon rentangan; (c) hutan rentangan Suatu graf terhubung berbobot dengan 6 titik dan 7 sisi Suatu graf terhubung berbobot dengan 9 titik dan 16 sisi Suatu graf tidak terhubung dengan 7 titik dan 6 sisi Suatu graf terhubung dengan 10 titik dan 11 sisi Suatu graf berbobot dengan 8 titik dan 15 sisi Graf berarah dengan 5 titik Suatu graf berarah tanpa sisi ganda dan loop Jaringan dengan sumber a dan target akhir z ii
4 DAFTAR TABEL 1.1 Pembentukan pohon rentangan dari graf dalam Gambar 1.8(a) menggunakan Algoritma Greedy Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2 menggunakan Algoritma Prim Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2 menggunakan Algoritma Kruskal Pembentukan pohon berakar (T; v 1 ) dari graf dalam Gambar 3.2 berdasarkan Algoritma Depth-First Search Pembentukan pohon berakar (T; v 1 ) dari graf dalam Gambar 3.2 berdasarkan Algoritma Breadth-First Search Pencarian lintasan terpendek dari titik u untuk graf dalam Gambar 3.3 berdasarkan Algoritma Lintasan Terpendek Dijkstra iii
5 KATA PENGANTAR Naskah ini ditulis selama satu semester ketika penulis mengajar Pengantar Teori Graf di Program Studi Matematika dan Pendidikan Matematika, Universitas Kristen Satya Wacana, Salatiga, pada Semester I tahun Catatan ini membentuk naskah dasar untuk kuliah MX 324 Pengantar Teori Graf. Teori Graf adalah suatu bidang dari Matematika Diskrit yang mempelajari bentuk (dinamakan graf) yang terdiri dari suatu himpunan titik-titik yang dihubungkan oleh garis (dinamakan sisi). Teori Graf dan aplikasinya tidak hanya dijumpai dalam cabang-cabang matematika, tetapi juga dalam disiplin-disiplin ilmiah seperti teknik, ilmu komputer, riset operasi, dan manajemen sains. Naskah ini difokuskan pada beberapa aplikasi dari teori graf dan menyajikan algoritma-algoritma graf yang biasanya digunakan untuk menyelesaikan masalah dalam aplikasi. Keseluruhan dari naskah ini berkaitan dengan algoritma graf, seperti Algoritma Greedy untuk pencarian pohon, Algoritma Prim dan Kruskal untuk pencarian pohon rentangan minimal, Algoritma Dijkstra untuk masalah lintasan terpendek, dan terakhir adalah Algoritma Ford-Fulkerson untuk mencari arus maksimum dari suatu jaringan. Salatiga, Desember 2008 Didit B. Nugroho iv
6 Bab 1 De nisi dan Konsep Fundamental Tujuan Pembelajaran: Mengetahui sifat-sifat dasar dari teori graf. Mengetahui operasi-operasi graf. Mengetahui tentang jalan, trail, lintasan, lingkaran, pohon, dan hutan dalam suatu graf. Mengetahui tentang lingkaran Hamilton dan jalan Euler. Mengaplikasikan Algoritma Greedy untuk mencari pohon rentangan dari suatu graf. 1.1 De nisi-de nisi Dasar Di [7], de nisi non-formal dari graf (graph) dalam kamus Webster (1913) diberikan seperti berikut ini. De nisi 1.1 Graf mempunyai dua pengertian: 1. Suatu kurva atau permukaan, letak (locus) dari suatu titik dimana koordinatkoordinatnya merupakan variabel-variabel dalam persamaan letak. 2. Suatu diagram yang melambangkan suatu sistem keterhubungan berdasarkan titik (spot), semua dapat saling dibedakan dan beberapa dihubungkan oleh garis sejenis. De nisi non-formal dari graf pada poin 2 adalah pengertian yang digunakan dalam naskah ini. Secara sederhana, suatu graf merupakan suatu koleksi titik-titik (vertices), bersama-sama dengan beberapa sisi (edges) yang menghubungkan beberapa titik tersebut. Gambar 1.1: Graf dengan sisi ganda dan gelang. Sebagai contoh, graf G dalam Gambar 1.1 mempunyai titik-titik v 1 ; v 2 ; v 3 ; v 4 ; v 5, sedangkan sisi-sisinya dinyatakan oleh e 1 = fv 1 ; v 2 g, e 2 = fv 2 ; v 3 g, e 3 = fv 3 ; v 4 g, 1
7 Bab 1. De nisi dan Konsep Fundamental 2 e 4 = fv 1 ; v 4 g, e 5 = fv 1 ; v 4 g, e 6 = fv 4 ; v 5 g, e 7 =fv 5 ; v 5 g. Secara khusus, sembarang sisi dapat dinyatakan sebagai 2-himpunan bagian dari himpunan semua titik; dengan kata lain, suatu himpunan bagian yang terdiri dari anggota (tidak perlu berbeda) dari himpunan semua titik. Secara formal, graf G pada himpunan V dan E dapat dide nisikan seperti berikut ini. De nisi 1.2 (formal) Suatu graf G adalah pasangan himpunan V dan E, dituliskan G = (V; E), dimana V adalah suatu himpunan berhingga dan E adalah koleksi dari 2-himpunan bagian dari V. Anggota-anggota V dikenal sebagai titik dan anggota-anggota dari E dikenal sebagai sisi. Jadi, dalam contoh sebelumnya dipunyai V = V (G) = fv 1 ; v 2 ; v 3 ; v 4 ; v 5 g dan E = E (G) = fe 1 ; e 2 ; e 3 ; e 4 ; e 5 ; e 6 ; e 7 g. Banyaknya titik dalam graf dinamakan order dan dituliskan sebagai jv j, sedangkan banyaknya sisi dituliskan sebagai jej. Suatu graf berorder 0 dinamakan graf kosong (empty graph), dan yang berorder 1 dinamakan graf trivial. De nisi 1.3 Graf G 1 = (V 1 ; E 1 ) adalah suatu subgraf dari G 2 = (V 2 ; E 2 ) jika V 1 V 2 dan E 1 E 2. Graf berikut ini: mempunyai subgraf antara lain Diperhatikan kembali graf G dalam Gambar 1.1. Sisi-sisi yang mempunyai titiktitik ujung sama, e 4 dan e 5 dinamakan sisi ganda (parallel edges atau multiple edges). Jika suatu sisi menghubungkan titik yang sama, sisi tersebut dinamakan gelang (loop), seperti e 7. De nisi 1.4 Suatu graf yang mempunyai sisi ganda dan atau gelang dinamakan multigraf. Suatu graf yang tidak mempunyai sisi ganda dan gelang disebut graf sederhana (simple graph). De nisi 1.5 Dua titik x; y 2 V dikatakan bertetangga (adjacent) jika fx; yg 2 E, dengan kata lain, jika x dan y dihubungkan oleh suatu sisi.
8 Bab 1. De nisi dan Konsep Fundamental 3 De nisi 1.6 Dua sisi, misalnya e 1 dan e 2, dikatakan bertetangga jika keduanya mempunyai suatu titik ujung yang sama, misalnya z, artinya e 1 = fu; zg dan e 2 = fv; zg. De nisi 1.7 Untuk sembarang sisi e = fx; yg, sisi e dikatakan bersisian (incidency) dengan titik x dan y. Bisa juga dikatakan bahwa titik x dan y bersisian dengan e. Sebagai contoh, pada graf G dalam Gambar 1.1, v 3 dan v 2 bertetangga karena dihubungkan oleh sisi e 2, sedangkan v 2 dan v 4 tidak bertetangga karena tidak ada sisi fv 2 ; v 4 g. Sisi e 2 bertetangga dengan sisi e 3 karena keduanya mempunyai titik v 3 sebagai ujung yang sama. Jika semua titik pada graf G adalah bertetangga, maka G dinamakan graf lengkap. Suatu graf lengkap dengan n titik dituliskan sebagai K n. Lima graf lengkap pertama diberikan seperti berikut: De nisi 1.8 Diambil G = (V; E) adalah suatu multigraf dengan himpunan titik V = fv 1, v 2, :::, v n g dan himpunan sisi E = fe 1, e 2, :::, e p g. Matriks ketetanggaan (adjacency matrix) dari G adalah suatu matriks A (G) = [a ij ] berukuran n n dimana masukan-(i; j) diberikan oleh a ij = banyaknya sisi yang menghubungkan v i dan v j ; dan matriks kebersisian (incidence matrix) dari G adalah suatu matriks S (G) = [s ij ] berukuran n p dimana masukan-(i; j) diberikan oleh 1 jika vi bersisian dengan e s ij = j. 0 jika v i tidak bersisian dengan e j Dicatat bahwa matriks A (G) adalah simetris, artinya A t = A. Sebagai contoh, multigraf
9 Bab 1. De nisi dan Konsep Fundamental 4 dapat dinyatakan oleh matriks ketetanggaan dan matriks kebersisian berturut-turut: A = , S = De nisi 1.9 Derajat (degree atau valency) dari suatu titik v, dituliskan (v), adalah banyaknya sisi yang bersisian dengan titik v. Secara khusus, titik berderajat nol dikatakan terasing (isolated) dan titik berderajat 1 dinamakan titik pendant. Dicatat bahwa dalam De nisi 1.9 setiap gelang pada suatu titik berkontribusi 2 untuk (v). Sebagai contoh, pada graf dalam Gambar 1.1 dipunyai (v 3 ) = 2, (v 4 ) = 4, (v 5 ) = 3, dan seterusnya. Teorema 1.10 Jumlah dari semua derajat titik pada sembarang graf G = (V; E) adalah dua kali banyaknya sisi, artinya X (v) = 2 jej v2v dengan jej menyatakan banyaknya sisi. Bukti. Hasil secara langsung mengikuti seperti berikut ini. Jika kita menjumlahkan semua derajat titik dalam G, kita menghitung setiap sisi tepat dua kali: sekali dari setiap ujung-ujungnya. Akibat 1.11 Jumlah dari semua derajat titik pada sembarang graf adalah bilangan bulat positif genap. Bukti. Jelas. Akibat 1.12 Banyaknya titik berderajat ganjil dalam suatu graf adalah genap. Bukti. Diambil V e dan V o yang berturut-turut menyatakan koleksi titik-titik berderajat genap dan ganjil untuk graf G. Berdasarkan Teorema 1.10 diperoleh X X (v) + (v) = 2 jej : v2v e v2v o Untuk setiap v 2 V e, derajat (v) adalah genap. Akibatnya X v2v e (v) adalah genap. Karena (v) ganjil untuk setiap v 2 V 0, maka jv 0 j haruslah genap. Sekarang diperhatikan dua graf dalam Gambar 1.2. Kedua graf tersebut pada dasarnya adalah sama. Untuk menerima hal ini diberikan pengertian isomor k (isomorphic) dari dua graf seperti berikut ini.
10 Bab 1. De nisi dan Konsep Fundamental 5 Gambar 1.2: Dua graf yang isomor k. De nisi 1.13 Dua graf G 1 = (V 1 ; E 1 ) dan G 2 = (V 2 ; E 2 ) dikatakan isomor k, dituliskan G 1 ' G 2, jika terdapat suatu fungsi bijektif (1-1 dan pada) : V 1! V 2 sedemikian sehingga untuk setiap u; v 2 V 1 berlaku fu; vg 2 E 1 jika dan hanya jika f (u) ; (v)g 2 E 2. Suatu fungsi yang demikian dinamakan suatu isomor sma (isomorphism). Secara cepat, dua graf dalam Gambar 1.2 adalah isomor k, dan suatu isomor sma diberikan oleh (a) = v 2 ; (b) = v 1 ; (c) = v 3 ; (d) = v 4 : (1.1) Ini bisa ditunjukkan seperti berikut. Diambil fungsi yang dide nisikan oleh (1.1). Di G 1 dipunyai himpunan sisi E 1 = ffa; bg ; fa; cg ; fa; dg ; fb; dg ; fc; dgg ; sehingga menggunakan fungsi diperoleh sisi-sisi f (a) ; (b)g = fv 2 ; v 1 g ; f (a) ; (c)g = fv 2 ; v 3 g ; f (a) ; (d)g = fv 2 ; v 4 g ; f (b) ; (d)g = fv 1 ; v 4 g ; f (c) ; (d)g = fv 3 ; v 4 g : Karena gabungan dari semua sisi yang diperoleh melalui sama dengan himpunan sisi E 2 di G 2, maka disimpulkan bahwa fungsi yang dide nisikan oleh (1.1) adalah isomor sma dari G 1 ke G Operasi Graf De nisi 1.14 Komplemen (complement) dari suatu graf sederhana G = (V; E) adalah graf sederhana G = V; E dimana sisi-sisi di E secara tepat adalah sisi-sisi yang tidak ada di G. Sebagai contoh, diberikan suatu graf dengan komplemennya seperti berikut:
11 Bab 1. De nisi dan Konsep Fundamental 6 De nisi 1.15 Diberikan graf-graf sederhana G 1 = (V 1 ; E 1 ) dan G 2 = (V 2 ; E 2 ) dimana V 2 V Jumlahan kedua graf adalah G 1 + G 2 = (V 1 [ V 2 ; E 1 [ E 2 [ E) dimana E adalah himpunan sisi-sisi baru yang menghubungkan setiap titik di G 1 dengan setiap titik di G Jika V 2 V 1, dide nisikan suatu graf beda (di erence graph) G 1 G 2 = (V 1 ; E 3 ) (graf sederhana) dimana E 3 adalah himpunan sisi-sisi dari G 1 yang tidak ada di G 2. Contoh dari selisih dan jumlahan dua graf diberikan seperti berikut: Terdapat beberapa operasi biner antara dua graf sederhana G 1 G 2 = (V 2 ; E 2 ) : = (V 1 ; E 1 ) dan (i) Gabungan: G 1 [ G 2 = (V 1 [ V 2 ; E 1 [ V 2 ) (graf sederhana). (ii) Irisan: G 1 \ G 2 = (V 1 \ V 2 ; E 1 \ V 2 ) (graf sederhana). (iii) Jumlahan ring: G 1 G 2 adalah subgraf dari G 1 [ G 2 dimana himpunan sisinya E 1 E 2 = (E 1 E 2 ) [ (E 2 E 1 ) dan himpunan titiknya terdiri dari setiap titik-titik ujung dari sisi-sisi di E 1 E 2. Untuk graf-graf
12 Bab 1. De nisi dan Konsep Fundamental 7 dipunyai Dicatat bahwa untuk suatu bilangan asli n dan sembarang graf G dipunyai ng = G [ G [{z [ G}. n kali 1.3 Lintasan dan Lingkaran Diambil G = (V; E) sebagai suatu graf dengan himpunan V = fv 1 ; v 2 ; :::g dan E = fe 1 ; e 2 ; :::g. De nisi 1.16 Suatu jalan (walk) dalam graf G adalah suatu barisan bergantian (titik dan sisi) tak kosong berhingga v 0 ; e 1 ; v 1 ; :::; v k 1 ; e k ; v k sedemikian sehingga e i = fv i 1 ; v i g 2 E, untuk setiap i = 1; :::; k. Secara khusus, apabila graf G adalah sederhana, jalan dapat dinyatakan sebagai suatu barisan titiktitik v 0 ; v 1 ; :::; v k 1 ; v k sedemikian sehingga fv i 1 ; v i g 2 E, untuk setiap i = 1; :::; k. Dicatat bahwa suatu jalan bisa melalui sembarang titik atau sisi lebih dari satu kali. Jika v 0 = v k, maka jalan dikatakan tertutup, jika tidak dikatakan terbuka. Untuk graf dalam Gambar 1.1, barisan v 3, e 3, v 4, e 4, v 1, e 4, v 4, e 5, v 1, e 4, v 4, e 6, v 5 adalah jalan terbuka dan barisan v 3, e 2, v 2, e 1, v 1, e 5, v 4, e 4, v 1, e 5, v 4, e 3, v 3 adalah jalan tertutup. De nisi 1.17 Suatu jalan adalah trail jika semua sisi-sisinya berbeda. Suatu trail adalah tertutup jika titik-titik ujungnya sama, jika tidak maka dikatakan terbuka. Sebagai contoh, pada graf dalam Gambar 1.1 jalan v 2, e 2, v 3, e 3, v 4, e 4, v 1, e 5, v 4, e 6, v 5 adalah suatu trail meskipun titik v 4 muncul dua kali. De nisi 1.18 Suatu lintasan (path) adalah suatu trail dengan semua titiknya berbeda. De nisi 1.19 Banyaknya sisi dalam lintasan dinamakan panjang lintasan. Lintasan dengan panjang n dinotasikan dengan P n. Suatu contoh untuk lintasan diberikan dalam Gambar 1.3, dan ini dapat dituliskan sebagai P 6 = v 1 ; v 4 ; v 3 ; v 5 ; v 6 ; v 7 ; v 8.
13 Bab 1. De nisi dan Konsep Fundamental 8 Gambar 1.3: Suatu lintasan P 6 di graf G. De nisi 1.20 Lingkaran (cycle) adalah suatu trail tertutup dengan semua titik-titiknya, kecuali titik-titik ujung, berbeda. Lingkaran dinyatakan oleh barisan berputar titik-titik seperti C = v 0 ; v 1 ; :::; v k ; v 0. Panjang suatu lingkaran adalah banyaknya sisi atau titik. Lingkaran dengan panjang n dinotasikan dengan C n. Tiga lingkaran pertama diberikan seperti berikut: De nisi 1.21 Jarak antara dua titik u dan v di graf G, dinotasikan dengan d (u; v), adalah panjang dari lintasan terpendek antara kedua titik tersebut. De nisi 1.22 Diameter dari graf G, dinotasikan diam(g), adalah lintasan terpanjang antara sembarang dua titik di G. Pada graf G dalam Gambar 1.3, jarak antara titik v 1 dan v 5 adalah 2 karena lintasan terpendeknya v 1 ; v 4 ; v 5 atau v 1 ; v 6 ; v 5. Untuk diameter dari graf G yaitu diam (G) = 7 yang bisa diperoleh dari lintasan terpanjang v 1 ; v 4 ; v 2 ; v 3 ; v 5 ; v 6 ; v 7 ; v 8. Berdasarkan bahasan di atas, sifat-sifat dari lintasan dan lingkaran: 1. dalam lintasan, derajat dari setiap titik adalah 2, kecuali untuk titik-titik ujung yang berderajat 1, 2. dalam lingkaran, derajat dari setiap titik adalah 2, 3. banyak sisi pada lintasan adalah kurang satu dari banyaknya titik, sedangkan banyak sisi pada lingkaran sama dengan banyak titik. De nisi 1.23 Dua titik u dan v dalam graf G dikatakan terhubung jika terdapat suatu lintasan dari u ke v. De nisi 1.24 Suatu graf tak kosong adalah terhubung jika sembarang dua titiknya dihubungkan oleh suatu lintasan.
14 Bab 1. De nisi dan Konsep Fundamental 9 Gambar 1.4: (a) Graf tidak terhubung G 1 ; dan (b) graf terhubung G 2. Dalam Gambar 1.4, graf G 1 adalah tidak terhubung karena terdapat dua titik (misalnya v 1 dan v 7 ) yang tidak dihubungkan oleh suatu lintasan. Dalam kasus ini graf G 1 dikatakan mempunyai dua komponen, karena dapat dinyatakan 1. V = V 1 [ V 2 dimana V 1 \ V 2 =? ; dan 2. E = E 1 [ E 2 dimana E 1 \ E 2 =?; untuk V 1 = fv 1 ; v 2 ; v 3 ; v 4 g dan V 2 = fv 5 ; v 6 ; v 7 g. 1.4 Lingkaran Hamilton dan Jalan Euler Pada suatu waktu, matematikawan Hamilton dan Euler pergi berlibur. Mereka mengunjungi negara dengan 7 kota (titik) yang dihubungkan oleh suatu sistem jalan (sisi) yang digambarkan oleh graf di bawah ini. Hamilton hanya ingin mengunjungi setiap kota sekali dan kembali ke kota awal dia berangkat. Berbeda dengan Hamilton, Euler tertarik dalam hal melewati setiap jalan tepat sekali dan tidak memikirkan apakah akhir perjalanannya pada kota yang berbeda atau tidak dari kota awal dia berangkat. De nisi 1.25 Suatu lingkaran Hamilton dalam suatu graf G = (V; E) adalah suatu lingkaran yang memuat semua titik di V. De nisi 1.26 Suatu jalan Euler dalam suatu graf G = (V; E) adalah suatu jalan yang menggunakan setiap sisi di E tepat satu kali. Bisa diperiksa bahwa graf di atas mempunyai lingkaran Hamilton, misalnya v 1, v 2, v 3, v 6, v 7, v 5, v 4, v 1. Lebih lanjut jalan Euler tidak ditemukan pada graf tersebut.
15 Bab 1. De nisi dan Konsep Fundamental 10 Berikut ini diberikan teorema (tanpa bukti) untuk menentukan apakah suatu graf mempunyai lingkaran Hamilton atau jalan Euler. Teorema 1.27 (Dirac 1952) Setiap graf G = (V; E) dengan titik n 3 dan (G) = min f (v) : v 2 V g n 2 mempunyai lingkaran Hamilton. Teorema 1.28 Suatu graf terhubung adalah Euler jika dan hanya jika setiap titik mempunyai derajat genap. Akibat 1.29 Suatu graf terhubung adalah Euler jika dan hanya jika setiap titik mempunyai derajat genap atau terdapat tepat dua titik berderajat ganjil. 1.5 Pohon dan Hutan De nisi 1.30 Suatu graf T = (V; E) dinamakan pohon jika memenuhi kondisi berikut: 1. T adalah terhubung; dan 2. T tidak mempunyai lingkaran. Gambar 1.5: (a) T 1 bukan pohon; (b) T 2 adalah pohon. Dalam Gambar 1.5, graf T 1 bukan pohon karena terdapat lingkaran C 3 = v 3 ; v 4 ; v 5, sedangkan T 2 adalah pohon berdasarkan De nisi Lebih lanjut, pohon-pohon yang tidak isomor k sampai dengan enam titik diberikan dalam Gambar 1.6. Gambar 1.6: Pohon-pohon yang tidak isomor k sampai dengan enam titik.
16 Bab 1. De nisi dan Konsep Fundamental 11 Dua sifat sederhana berikut ini diperoleh berdasarkan de nisi yang sudah diberikan. Teorema 1.31 Jika graf T = (V; E) adalah pohon dengan minimal dua titik, maka untuk setiap pasang titik berbeda x; y 2 V terdapat lintasan tunggal dari x ke y. Bukti. Diandaikan terdapat dua lintasan berbeda dari x ke y: maka terdapat i 2 N sehingga x = v 0 ; v 1 ; v 2 ; :::; v r = y, dan x = u 0 ; u 1 ; u 2 ; :::; u s = y, v 0 = u 0 ; v 1 = u 1 ; :::; v i = u i, tapi v i+1 6= u i+1 : Sekarang diperhatikan titik-titik v i+1, v i+2,..., v r. Karena kedua lintasan berakhir di y, maka terdapat nilai terkecil j 2 fi + 1, i + 2,..., rg sedemikian sehingga v j = u l untuk suatu l 2 fi + 1, i + 2,..., sg. Jadi dua lintasan tersebut memberikan suatu lingkaran v i ; v i+1 ; :::; v j 1 ; u l ; u l 1 ; :::; u i+1 ; v i yang kontradiksi dengan hipotesis bahwa T adalah pohon. Teorema 1.32 Jika T = (V; E) adalah suatu pohon dengan n titik, maka pohon mempunyai n 1 sisi. Bukti. Digunakan induksi pada banyaknya titik dari T = (V; E). (i) Jelas bahwa hasil adalah benar untuk jv j = 1. (ii) Diandaikan bahwa hasil benar untuk jv j k. Diambil T = (V; E) dengan jv j = k + 1. Jika satu sisi dari T dihapus, maka graf mempunyai dua komponen: T 1 = (V 1 ; E 1 ) dan T 2 = (V 2 ; E 2 ) : Jelas bahwa jv 1 j k dan jv 2 j k, sehingga dari hipotesis induksi diperoleh je 1 j = jv 1 j 1 dan je 2 j = jv 2 j 1: Dicatat bahwa jv j = jv 1 j + jv 2 j dan jej = je 1 j + je 2 j + 1: Karena itu jej = jv j 1.
17 Bab 1. De nisi dan Konsep Fundamental 12 Gambar 1.7: Subpohon T 1 dan T 2 yang diperoleh dari T dengan menghapus satu sisi x. De nisi 1.33 Suatu hutan (forest) F = ft 1 ; :::; T N g adalah suatu himpunan dari N\ pohon-pohon T k = (V k ; E k ) dimana V k =?, atau dengan kata lain komponen dari F adalah pohon. k=1 Sebagai contoh, empat pohon berikut ini bersama-sama akan membentuk hutan. 1.6 Pohon dan Hutan Rentangan De nisi 1.34 Diberikan graf terhubung G = V (V; E). 1. Pohon rentangan (spanning tree) dari graf G adalah suatu pohon dari G yang memuat semua titik di G. 2. Hutan rentangan (spanning forest) dari graf G adalah suatu hutan dari G yang memuat semua titik di G. Diperhatikan graf yang dinyatakan oleh Gambar 1.8. Setiap graf di bagian (b) dan (c) berturut-turut menyatakan suatu pohon dan hutan rentangan dari graf di bagian (a). Dari contoh ini jelas bahwa pohon dan hutan rentangan dari suatu graf belum tentu tunggal. Teorema 1.35 Jika graf terhubung G = (V; E) memenuhi jej = jv j adalah pohon. 1, maka graf G Bukti. Diambil G adalah sembarang pohon terhubung dengan n titik dan n 1 sisi. Dimisalkan G 0 adalah suatu pohon rentangan dalam G, maka G 0 juga mempunyai n titik dan n 1 sisi. Karena itu G 0 = G. Pertanyaan yang lazim adalah bagaimana kita bisa mendapatkan suatu pohon rentangan untuk sembarang graf terhubung. Untuk melakukan ini, diaplikasikan Algoritma Greedy seperti di bawah ini. Algoritma Greedy membangun suatu penyelesaian
18 Bab 1. De nisi dan Konsep Fundamental 13 Gambar 1.8: (a) Graf tangga; (b) pohon rentangan; (c) hutan rentangan. sebagian demi sebagian dan selalu memilih bagian berikutnya yang memberikan manfaat segera dan paling jelas [3]. Algoritma Greedy untuk pohon rentangan. Input: Graf terhubung G = (V; E) dimana jv j = n. Output: Pohon rentangan T dari G. (1) Diambil sembarang titik u di V (G) dan dimasukkan u ke V (T ). (2) Dibentuk V (G) V (T ). Dipilih suatu titik y 2 V (G) V (T ) dan y bertetangga dengan suatu titik x 2 V (T ). Selanjutnya dimasukkan sisi fx; yg ke E (T ). (3) Diulangi langkah (2) sebanyak (n 2) kali sampai semua titik di V (G) termuat dalam pohon. Sebagai contoh, Tabel 1.1 menyajikan penyelesaian pohon rentangan dari graf dalam Gambar 1.8(a) menggunakan Algoritma Greedy. Jadi, diperoleh suatu pohon rentangan dari graf dalam Gambar 1.8(a) seperti berikut ini.
19 Bab 1. De nisi dan Konsep Fundamental 14 Tabel 1.1: Pembentukan pohon rentangan dari graf dalam Gambar 1.8(a) menggunakan Algoritma Greedy. sisi yang ditam- Langkah V (G) nv (T ) y V (T ) bahkan pada T 1 u = v 5 fv 5 g 2 fv 1 ; v 2 ; v 3 ; v 4 ; v 6 g v 4 fv 5 ; v 4 g fv 5 ; v 4 g 3 fv 1 ; v 2 ; v 3 ; v 6 g v 6 fv 5 ; v 4 ; v 6 g fv 5 ; v 6 g 4 fv 1 ; v 2 ; v 3 g v 2 fv 5 ; v 4 ; v 6 ; v 2 g fv 5 ; v 2 g 5 fv 1 ; v 3 g v 1 fv 5 ; v 4 ; v 6 ; v 2 ; v 1 g fv 4 ; v 1 g 6 fv 3 g v 3 fv 5 ; v 4 ; v 6 ; v 2 ; v 1 ; v 3 g fv 6 ; v 3 g Proposisi 1.36 Algoritma Greedy selalu bisa mengkonstruksi suatu pohon rentangan. Bukti. Perlu ditunjukkan bahwa di sembarang tingkat, suatu titik baru di V selalu dapat dihubungkan ke pohon parsial menggunakan suatu sisi di E. Untuk melihat ini, diambil S yang menyatakan himpunan titik-titik dalam pohon parsial di sembarang tingkat. Diasumsikan bahwa S 6=? agar selalu bisa dipilih suatu titik awal. Diandaikan bahwa S 6= V. Dibuktikan sebaliknya bahwa suatu titik tambahan di V tidak bisa dihubungkan ke pohon parsial. Karena itu tidak ada sisi di E mempunyai satu titik di S dan titik lainnya di V ns. Akibatnya tidak ada lintasan dari sembarang titik di S ke sembarang titik di V ns, yang berarti G tidak terhubung. Ini kontradiksi dengan kenyataan bahwa G adalah terhubung. 1.7 Soal-soal untuk Bab 1 1. Gambarkan suatu graf yang dinyatakan oleh matriks ketetanggaan berikut ini Gambarkan suatu graf sederhana dengan 6 titik dan 10 sisi. 3. Konstruksi suatu graf dengan 5 titik dan 6 sisi yang tidak memuat lingkaran C Berapa banyak sisi dari graf lengkap K n? Berikan penjelasan. 5. Untuk setiap daftar berikut ini, tentukan apakah mungkin bahwa daftar tersebut menyatakan derajat-derajat dari semua titik dari suatu graf sederhana. Jika ya, gambarkan graf tersebut. Jika tidak, berikan penjelasan
20 Bab 1. De nisi dan Konsep Fundamental 15 (a) 2, 2, 2, 3 (b) 2, 2, 4, 4, 4 (c) 1, 2, 2, 3, 4 (d) 1, 2, 3, 4 (e) 5; 2; 3; 2; 4 (f) 4; 4; 3; 2; 3 (g) 3; 3; 2; 3; 2 (h) 4; 4; 1; 3; 2 6. Tentukan 11 graf (sederhana) berbeda dengan 4 titik? 7. Tentukan semua graf (sederhana) berbeda dengan 5 titik dan 2 sisi? Bagaimana dengan 3 sisi? Berapa banyak sisi maksimum pada suatu graf sederhana dengan 5 titik yang dapat dibuat? 8. Buktikan bahwa pasangan graf berikut ini adalah isomor k. 9. Periksa apakah pasangan graf di bawah isomor k? Jika ya, tentukan isomor smanya. 10. Berapa banyak sisi yang dipunyai oleh komplemen dari suatu graf dengan n titik dan m sisi? 11. Untuk setiap operasi graf di bawah ini, gambarkan graf dari hasil operasinya. (a) K 4 K 2 (b) C 5 + K 1 (c) 5K 1 + P 2 (d) K 3 [ K 1 (e) K 3 [ K 1 (f) (K 3 [ K 1 ) K 3 [ K 1 (g) K 4 [ 2K 2 (h) K 4 [ 2K 2 (i) (K 4 [ 2K 2 ) K 4 [ 2K Tentukan rumus untuk diameter dari graf K n. 13. Untuk nilai n 2 N yang mana sedemikian sehingga graf lengkap K n mempunyai suatu jalan Euler? 14. Berapa banyak pohon rentangan dari graf C n? 15. Tentukan banyaknya pohon rentangan dari setiap graf roda (wheel) berikut ini.
21 Bab 1. De nisi dan Konsep Fundamental Apakah pada graf K 5 dan W 5 terdapat lingkaran Hamilton atau jalan Euler? 17. Pada graf K 5, tentukan suatu lingkaran Hamilton yang juga merupakan jalan Euler. 18. Periksa apakah ada lingkaran Hamilton atau jalan Euler dalam graf yang dinyatakan oleh matriks ketetanggaan berikut ini Gambarkan semua pohon dengan tujuh titik yang tidak isomor s. 20. Aplikasikan Algoritma Greedy untuk mencari suatu pohon rentangan dari graf terhubung berikut ini
22 Bab 2 Pohon Rentangan Minimal Tujuan Pembelajaran: Mengetahui tentang graf berbobot. Mengetahui tentang pohon rentangan minimal. Mengetahui aplikasi-aplikasi dari pohon. Mengaplikasikan Algoritma Prim dan Kruskal untuk pencarian pohon rentangan minimal. 2.1 Pengantar Pada bab ini akan diperhatikan masalah pohon rentangan ketika sisi-sisi dari suatu graf terhubung mempunyai bobot. De nisi 2.1 Diandaikan bahwa G = (V; E) adalah suatu graf. Sembarang fungsi bertipe w : E! N dinamakan fungsi bobot. Graf G, bersama-sama dengan fungsi w : E! N, dinamakan graf berbobot (weighted graph). Gambar 2.1: Suatu graf terhubung berbobot dengan 6 titik dan 7 sisi. Sebagai contoh, diperhatikan graf berbobot dalam Gambar 2.1. Graf mempunyai fungsi bobot w : E! N, dimana dan E = ffv 1 ; v 2 g ; fv 1 ; v 4 g ; fv 2 ; v 3 g ; fv 2 ; v 5 g ; fv 3 ; v 6 g ; fv 4 ; v 5 g ; fv 5 ; v 6 gg w (fv 1 ; v 2 g) = 3; w (fv 1 ; v 4 g) = 2; w (fv 2 ; v 3 g) = 5; w (fv 2 ; v 5 g) = 1; w (fv 3 ; v 6 g) = 4; w (fv 4 ; v 5 g) = 6; w (fv 5 ; v 6 g) = 7: 17
23 Bab 2. Pohon Rentangan Minimal 18 De nisi 2.2 Diandaikan bahwa G = (V; E), bersama-sama dengan fungsi w : E! N, membentuk suatu graf berbobot. Lebih lanjut diandaikan bahwa G adalah terhubung dan T adalah suatu pohon rentangan dari G. Nilai w (T ) = X e2t w (e) ; jumlahan bobot dari sisi-sisi di T, dinamakan bobot dari pohon rentangan T. 2.2 Pohon Rentangan Minimal Secara jelas, untuk sembarang pohon rentangan T dari G dipunyai w (T ) 2 N. Jelas juga bahwa hanya terdapat berhingga pohon rentangan T dari G. Karena itu pasti ada satu pohon rentangan T dimana nilai w (T ) adalah terkecil diantara semua pohon rentangan dari G. De nisi 2.3 Diandaikan bahwa G = (V; E) adalah terhubung dan bersama-sama dengan fungsi w : E! N membentuk suatu graf berbobot. Suatu pohon rentangan T dari G, untuk yang mana bobot w (T ) adalah terkecil diantara semua pohon rentangan dari G, dinamakan suatu pohon rentangan minimal (minimal spanning tree) dari G. Dicatat bahwa pohon rentangan minimal dari suatu graf terhubung berbobot mungkin tidak tunggal. Diperhatikan, sebagai contoh, suatu graf terhubung dimana semua sisinya mempunyai bobot sama, maka jelas bahwa setiap pohon rentangan adalah minimal. Sekarang pertanyaannya adalah bagaimana membangun suatu pohon rentangan minimal dari sembarang graf terhubung berbobot. Jawaban diperoleh dengan memodi kasi Algoritma Greedy di Subbab 1.6. Dalam hal ini ada dua algoritma, yaitu Algoritma Prim dan Algoritma Kruskal. Menurut [12], Algoritma Prim ditemukan pada tahun 1930 oleh matematikawan Vojt¼ech Jarník ( ) dan kemudian secara terpisah oleh ilmuwan komputer Robert C. Prim pada tahun 1957 dan ditemukan kembali oleh Dijkstra pada tahun Karena itu algoritma ini sering dinamakan Algoritma DJP atau Algoritma Jarník. Algoritma Prim membentuk suatu pohon rentangan minimal dengan cara mengambil satu sisi pada setiap langkah pembentukan. Ketentuannya adalah bahwa satu sisi yang diambil harus bersisian dengan suatu titik di pohon pada langkah sebelumnya, memiliki bobot minimal, dan tidak membentuk lingkaran di pohon. Berikut ini adalah algoritmanya. Algoritma Prim untuk suatu pohon rentangan minimal. Input: Graf terhubung G = (V; E) dengan jv j = n, dan dilengkapi fungsi bobot w : E! N. Output: Pohon rentangan minimal T dari G. (1) Dibuat T dengan mengambil satu sisi di E (G) yang berbobot mimimal. (2) Dipilih satu sisi fu; vg 2 E (G) ne (T ) yang bersisian dengan suatu titik di E (T ), memiliki bobot minimal, dan tidak membentuk lingkaran di T. Selanjutnya dimasukkan fu; vg ke dalam E (T ).
24 Bab 2. Pohon Rentangan Minimal 19 (3) Diulangi langkah (2) sebanyak (n 3) kali sampai semua titik di V (G) termuat dalam pohon. Gambar 2.2: Suatu graf terhubung berbobot dengan 9 titik dan 16 sisi. Tabel 2.1: Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2 menggunakan Algoritma Prim. Sisi fu; vg yang Bobot Langkah ditambahkan pada E (T ) w (fu; vg) V (T ) 1 fv 1 ; v 2 g 1 fv 1 ; v 2 g 2 fv 1 ; v 4 g 1 fv 1 ; v 2 ; v 4 g 3 fv 2 ; v 3 g 1 fv 1 ; v 2 ; v 3 ; v 4 g 4 fv 3 ; v 5 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 g 5 fv 5 ; v 7 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 7 g 6 fv 7 ; v 8 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 7 ; v 8 g 7 fv 8 ; v 6 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 6 ; v 7 ; v 8 g 8 fv 6 ; v 9 g 2 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 6 ; v 7 ; v 8 ; v 9 g Sebagai contoh, diperhatikan graf terhubung berbobot dalam Gambar 2.2. Pembentukan pohon rentangan minimal menggunakan Algoritma Prim disajikan dalam Tabel 2.1, dengan pohon rentangan minimalnya seperti di bawah ini. Proposisi 2.4 Algoritma Prim selalu bisa mengkonstruksi suatu pohon rentangan minimal.
25 Bab 2. Pohon Rentangan Minimal 20 Bukti. Diandaikan bahwa T adalah suatu pohon rentangan dari G yang dibangun oleh algoritma Prim. Akan ditunjukkan bahwa w (T ) w (U) untuk sembarang pohon rentangan U dari G. Diandaikan bahwa sisi-sisi dari T dalam urutan konstruksi adalah e 1 ; e 2 ; :::; e n 1, dimana jv j = n. Jika U = T, maka jelas bahwa hasil adalah benar dan bukti selesai. Sekarang, tanpa kehilangan keumuman, diandaikan bahwa U 6= T, yang berarti T memuat suatu sisi yang tidak ada di U. Diandaikan bahwa e 1 ; e 2 ; :::; e k 1 2 U dan e k =2 U. Dinotasikan S adalah himpunan titik-titik dari pohon parsial yang membentuk sisisisi e 1 ; e 2 ; :::; e k 1, dan diambil e k = fx; yg, dimana x 2 S dan y 2 V ns. Karena U adalah suatu pohon rentangan dari G, berarti terdapat suatu lintasan di U dari x ke y yang pasti memuat suatu sisi e dengan satu titik di S dan titik lainnya di V ns. Dalam pandangan algoritma haruslah dipunyai w (e k ) w (e), jika tidak maka sisi e akan dipilih lebih dulu daripada e k dalam konstruksi dari T berdasarkan algoritma. Sekarang dihapus sisi e dari U dan diganti dengan e k. Selanjutnya diperoleh suatu pohon rentangan baru U 1 dari G, dimana Lebih jauh, w (U 1 ) = w (U) w (e) + w (e k ) w (U). e 1 ; e 2 ; :::; e k 1 ; e k 2 U 1 : Jika U 1 6= T, maka proses di atas diulang dan diperoleh suatu barisan dari pohon rentangan U 1 ; U 2 ; ::: dari G, yang masing-masing memuat suatu bagian dari barisan e 1 ; e 2 ; :::; e n 1 dan lebih panjang daripada yang mendahului. Karena itu proses pasti berhenti dengan suatu pohon rentangan U m = T. Secara jelas seperti yang diinginkan. w (U) w (U 1 ) w (U 2 ) w (U m ) = T Algoritma kedua, yaitu Algoritma Kruskal, pertama kali muncul pada tahun 1956 dalam sebuah tulisan yang ditulis oleh Joseph Kruskal [5]. Algoritma ini membangun suatu pohon rentangan minimal dimana pada setiap langkah pembentukan mungkin tidak terbentuk pohon tetapi hutan. Berikut ini adalah algoritmanya. Algoritma Kruskal untuk suatu pohon rentangan minimal. Input: Graf terhubung G = (V; E) dengan jv j = n, dan dilengkapi fungsi bobot w : E! N. Output: Pohon rentangan minimal T dari G. (1) Dibuat T dengan mengambil satu sisi di E (G) yang berbobot mimimal. (2) Dipilih satu sisi fu; vg 2 E (G) ne (T ) yang memiliki bobot minimal dan tidak membentuk lingkaran di T. Selanjutnya dimasukkan fu; vg ke dalam E (T ). (3) Diulangi langkah (2) sebanyak (n 3) kali sampai semua titik di V (G) termuat dalam pohon.
26 Bab 2. Pohon Rentangan Minimal 21 Tabel 2.2: Pembentukan pohon rentangan minimal dari graf dalam Gambar 2.2 menggunakan Algoritma Kruskal. Sisi fu; vg yang Bobot Langkah ditambahkan pada E (T ) w (fu; vg) V (T ) 1 fv 1 ; v 2 g 1 fv 1 ; v 2 g 2 fv 3 ; v 5 g 1 fv 1 ; v 2 ; v 3 ; v 5 g 3 fv 2 ; v 4 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 g 4 fv 2 ; v 3 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 g 5 fv 4 ; v 7 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 7 g 6 fv 7 ; v 8 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 7 ; v 8 g 7 fv 8 ; v 6 g 1 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 6 ; v 7 ; v 8 g 8 fv 6 ; v 9 g 2 fv 1 ; v 2 ; v 3 ; v 4 ; v 5 ; v 6 ; v 7 ; v 8 ; v 9 g Diperhatikan kembali graf dalam Gambar 2.2. Pohon rentangan minimalnya dapat dibentuk menggunakan Algoritma Kruskal seperti pada Tabel 2.2 dengan hasil akhirnya seperti di bawah ini. Dicatat bahwa pohon rentangan minimal yang diperoleh dari dua algoritma di atas adalah tidak identik, tetapi bobot minimal dari kedua pohon rentangan yang dihasilkan adalah sama. Proposisi 2.5 Algoritma Kruskal selalu bisa mengkonstruksi suatu pohon rentangan minimal. Bukti. Diandaikan bahwa T adalah suatu pohon rentangan dari G yang dibangun oleh algoritma Kruskal, dan sisi-sisi dari T dalam urutan konstruksi adalah e 1 ; e 2 ; :::; e n 1, dimana jv j = n. Diambil U adalah sembarang pohon rentangan minimal dari G. Jika U = T, maka jelas bahwa hasil adalah benar dan bukti selesai. Sekarang, tanpa kehilangan keumuman, diandaikan bahwa U 6= T, yang berarti T memuat suatu sisi yang tidak ada di U. Diandaikan bahwa e 1 ; e 2 ; :::; e k 1 2 U dan e k =2 U. Ditambahkan suatu sisi e k ke U, maka ini akan menghasilkan suatu lingkaran. Jika dihapus suatu sisi berbeda e =2 T dari lingkaran tersebut, maka akan diperoleh kembali suatu pohon rentangan U 1. Dalam pandangan algoritma haruslah dipunyai w (e k )
27 Bab 2. Pohon Rentangan Minimal 22 w (e), jika tidak maka sisi e akan dipilih lebih dulu daripada e k dalam konstruksi dari T berdasarkan algoritma. Ini berarti bahwa pohon rentangan baru U 1 memenuhi w (U 1 ) = w (U) w (e) + w (e k ) w (U). Karena U adalah suatu pohon rentangan minimal dari G, maka w (U 1 ) = w (U), sehingga U 1 juga merupakan suatu pohon rentangan minimal dari G. Lebih jauh, e 1 ; e 2 ; :::; e k 1 ; e k 2 U 1 : Jika U 1 6= T, maka proses di atas diulang dan diperoleh suatu barisan dari pohon rentangan minimal U 1 ; U 2 ; ::: dari G, yang masing-masing memuat suatu bagian dari barisan e 1 ; e 2 ; :::; e n 1 dan lebih panjang daripada yang mendahului. Karena itu proses pasti berhenti dengan suatu pohon rentangan U m = T. 2.3 Soal-soal untuk Bab 2 1. Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini. 2. Aplikasikan algoritma Kruskal untuk mencari suatu pohon rentangan minimal dari graf berbobot dalam Soal Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini. 4. Aplikasikan algoritma Kruskal untuk mencari suatu pohon rentangan minimal dari graf berbobot dalam Soal 3.
28 Bab 2. Pohon Rentangan Minimal Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini. 6. Aplikasikan algoritma Kruskal untuk mencari suatu pohon rentangan minimal dari graf berbobot dalam Soal Aplikasikan algoritma Prim untuk mencari suatu pohon rentangan minimal dari graf berbobot berikut ini. 8. Aplikasikan algoritma Kruskal untuk mencari suatu pohon rentangan minimal dari graf berbobot dalam Soal 7.
29 Bab 3 Algoritma Pencarian Tujuan Pembelajaran: Mengaplikasikan strategi-strategi pencarian pohon dari satu titik khusus untuk graf terhubung. Mengaplikasikan Algoritma Dijkstra untuk memecahkan masalah lintasan terpendek. 3.1 Pengantar Dalam banyak kejadian kita ingin mengunjungi setiap titik tepat satu kali dalam suatu urutan yang khusus. Proses mengunjungi titik-titik dari suatu pohon dalam suatu urutan khusus dinamakan dinamakan pencarian (searching) atau melakukan suatu pencarian pohon. Seringkali proses ini dinamakan pelintasan (traversal). Dalam bab ini diberikan strategi-strategi dalam mencari suatu lintasan dari satu titik tertentu ke titik-titik lainnya untuk suatu graf terhubung dan graf terhubung berbobot. 3.2 Depth-First Search Gambar 3.1: Suatu graf tidak terhubung dengan 7 titik dan 6 sisi. Diperhatikan graf yang direpresentasikan dalam Gambar 3.1. Diandaikan bahwa ingin dicari semua titik u di graf sedemikian sehingga ada suatu lintasan dari titik v 1 ke titik u. Ini bisa didapatkan seperti berikut ini. (1) Dimulai dari titik v 1, bergerak ke suatu titik tetangga v 2 dan dengan segera bergerak ke titik tetangga v 3. Dari sini disimpulkan bahwa ada suatu lintasan dari titik v 1 ke titik v 2 atau v 3. Dalam kasus ini v 1 dinamakan orang tua (parent) dari v 2 atau sebaliknya v 2 adalah anak (child) dari v 1, sedangkan v 2 dinamakan orang tua (parent) dari v 3 24
30 Bab 3. Algoritma Pencarian 25 (2) Karena tidak ada titik tetangga baru dari titik v 3, maka kembali ke titik v 2. Karena tidak ada tetanga baru dari titik v 2, maka kembali ke titik v 1. (3) Dimulai dari titik v 1 lagi, bergerak ke titik tetangga v 5 dan segera bergerak ke titik tetangga v 4. Dari sini disimpulkan bahwa ada suatu lintasan dari titik v 1 ke titik v 2, v 3, v 4, atau v 5. (4) Karena tidak ada titik tetangga baru dari titik v 4, maka kembali ke titik v 5. (5) Dimulai dari titik v 5 dan bergerak ke titik tetangga v 6. Dari sini disimpulkan bahwa ada suatu lintasan dari titik v 1 ke titik v 2, v 3, v 4, v 5 atau v 6. (6) Karena tidak ada titik tetangga baru dari titik v 6, maka kembali ke titik v 5. Karena tidak ada titik tetangga baru dari titik v 5, maka kembali ke titik v 1. Karena tidak ada titik tetangga baru dari titik v 1, maka proses berhenti. Disimpulkan bahwa ada suatu lintasan dari titik v 1 ke titik v 2, v 3, v 4, v 5 atau v 6. Dicatat bahwa hasil dari proses di atas adalah suatu pohon rentangan dari graf yang direpresentasikan oleh graf di bawah ini. Proses di atas merupakan suatu contoh dari strategi yang dikenal sebagai Depth-First Search, yang dapat dipandang sebagai suatu metode pertumbuhan-pohon khusus (special tree-growing method). Diaplikasikan dari suatu titik u di suatu graf G, proses tersebut akan memberikan suatu pohon rentangan dari komponen graf G yang memuat titik u. Dalam hal ini titik u tersebut biasanya dinamakan akar dari pohon rentangan. Algoritma Depth-First Search. Input: Graf terhubung G = (V; E), V = fv 1, v 2,..., v n g. Output: Pohon rentangan berakar (T; u) untuk G, dengan u 2 V (G). (1) Ditetapkan titik u sebagai v. (2) Dipilih v i, dengan i adalah indeks terkecil, sedemikian sehingga fv; v i g 2 V dan v i belum pernah dipilih sebelumnya. Jika tidak ditemukan v i, lanjut ke langkah (3). Jika v i ada, dimasukkan sisi fv; v i g ke T dan ditetapkan v i sebagai v, selanjutnya kembali ke langkah (2). (3) Jika v = u, maka proses berhenti dan pohon T adalah suatu pohon rentangan berakar u. Tetapi jika v 6= u, maka mundur dari v ke orang tuanya, misalnya w, selanjutnya tetapkan w sebagai v dan kembali ke langkah (2).
31 Bab 3. Algoritma Pencarian 26 Gambar 3.2: Suatu graf terhubung dengan 10 titik dan 11 sisi. Tabel 3.1: Pembentukan pohon berakar (T; v 1 ) dari graf dalam Gambar 3.2 berdasarkan Algoritma Depth-First Search. Titik v sebagai Tetangga dari v Titik v i sebagai Sisi yang ditam- Langkah orang tua di V (G) nv (T ) anak dari v bahkan pada E (T ) 1 v 1 v 2 v 2 fv 1 ; v 2 g 2 v 2 v 3 ; v 5 v 3 fv 2 ; v 3 g 3 v 3 4 v 2 v 5 v 5 fv 2 ; v 5 g 5 v 5 v 4 ; v 6 ; v 7 v 4 fv 5 ; v 4 g 6 v 4 v 7 v 7 fv 4 ; v 7 g 7 v 7 v 6 ; v 9 v 6 fv 7 ; v 6 g 8 v 6 9 v 7 v 9 v 9 fv 7 ; v 9 g 10 v 9 v 8 ; v 10 v 8 fv 9 ; v 8 g 11 v 8 12 v 9 v 10 v 10 fv 9 ; v 10 g Sebagai contoh, Algoritma Depth-First Search untuk mencari pohon berakar v 1 dari graf yang dinyatakan dalam Gambar 3.2 adalah seperti dalam Tabel 3.1. Proses tersebut menghasilkan pohon rentangan di bawah ini.
32 Bab 3. Algoritma Pencarian Breadth-First Search Diperhatikan kembali graf dalam Gambar 3.1. Diandaikan lagi bahwa kita ingin mencari semua titik u sedemikian sehingga ada suatu lintasan dari titik v 1 ke titik u. Kita bisa mendapatkannya seperti berikut ini. (1) Dimulai dari titik v 1, dan berjalan ke semua titik baru yang bertetangga dengan v 1, yaitu v 2, v 5, dan v 6. (2) Berikutnya dimulai dari v 2, dan berjalan ke semua titik baru yang bertetangga dengan v 2, yaitu hanya v 3. (3) Berikutnya dimulai dari v 5, dan berjalan ke semua titik baru yang bertetangga dengan v 5, yaitu hanya v 4. (4) Berikutnya dimulai dari v 6, dan berjalan ke semua titik baru yang bertetangga dengan v 6, yaitu tidak ada. (5) Berikutnya dimulai dari v 3, dan berjalan ke semua titik baru yang bertetangga dengan v 3, yaitu tidak ada. (6) Berikutnya dimulai dari v 4, dan berjalan ke semua titik baru yang bertetangga dengan v 4, yaitu tidak ada. (7) Karena titik v 4 merupakan titik terakhir dalam daftar v 1, v 2, v 5, v 6, v 3, v 4 (dalam urutan pencapaian), maka proses berhenti. Dicatat bahwa hasil dari proses di atas adalah suatu pohon rentangan dari graf yang direpresentasikan oleh garf di bawah ini. Proses di atas merupakan suatu contoh dari strategi yang dikenal sebagai Breadth- First Search, yang dapat dipandang sebagai suatu metode pertumbuhan-pohon khusus. Diaplikasikan dari suatu titik u di graf G, strategi tersebut juga akan memberikan suatu pohon rentangan dari komponen graf G yang memuat titik u. Algoritma Breadth-First Search. Input: Graf terhubung G = (V; E), V = fv 1, v 2,..., v n g. Output: Pohon rentangan berakar (T; u) untuk G, dengan u 2 V (G). (1) Dimulai dengan barisan titik Q = u 2 V. (2) Jika Q adalah barisan kosong, maka proses berhenti. Tetapi jika Q bukan barisan kosong, maka dihapus titik terdepan dari Q, misalnya v, dan selanjutnya ke langkah (3).
33 Bab 3. Algoritma Pencarian 28 (3) Jika terdapat titik w bertetangga dengan v dan w belum pernah masuk barisan, maka masukkan semua sisi fv; wg ke T, tambahkan semua titik w ke bagian akhir dari Q, dan kembali ke langkah (2). Jika tidak ada titik yang bertetangga dengan v yang belum pernah masuk barisan, maka kembali ke langkah (2). Tabel 3.2: Pembentukan pohon berakar (T; v 1 ) dari graf dalam Gambar 3.2 berdasarkan Algoritma Breadth-First Search. v (titik terdepan w (tetangga v Sisi yang ditam- Langkah dari Q) dan tidak di V (T )) Q bahkan pada E (T ) 1 v 1 2 v 1 v 2 v 2 fv 1 ; v 2 g 3 v 2 v 3 ; v 5 v 3 ; v 5 fv 2 ; v 3 g ; fv 2 ; v 5 g 4 v 3 v 5 5 v 5 v 4 ; v 6 ; v 7 v 4 ; v 6 ; v 7 fv 5 ; v 4 g ; fv 5 ; v 6 g ; fv 5 ; v 7 g 6 v 4 v 6 ; v 7 7 v 6 v 7 8 v 7 v 9 v 9 fv 7 ; v 9 g 9 v 9 v 8 ; v 10 v 8 ; v 10 fv 9 ; v 8 g ; fv 9 ; v 10 g 10 v 8 v v 10 Sebagai contoh, akan digunakan Algoritma Breadth-First Search untuk mencari pohon rentangan dari graf dalam Gambar 3.2. Dimulai dari titik v 1, dan dalam kasus ini digunakan ketentuan bahwa ketika kita mempunyai suatu pilihan dari titik-titik maka kita mengambil titik yang mempunyai penomoran lebih rendah. Proses pencarian disajikan dalam Tabel 3.2 dan pohon rentangan yang dihasilkan adalah seperti di bawah ini. Dicatat bahwa pohon rentangan yang diperoleh dari dua algoritma di atas adalah tidak identik, meskipun digunakan ketentuan yang sama dengan memperhatikan pilihan pertama titik-titik dengan penomoran yang lebih rendah.
34 Bab 3. Algoritma Pencarian Masalah Lintasan Terpendek Diperhatikan suatu graf terhubung G = (V; E), dengan fungsi bobot w : E! N. Untuk sembarang pasangan titik berbeda x; y 2 V dan untuk sembarang lintasan dari x ke y, diperhatikan nilai dari v 0 (= x) ; v 1 ; :::; v r (= y) rx w (fv i 1 ; v i g) ; (3.1) i=1 yaitu jumlahan dari bobot-bobot sisi yang membentuk lintasan. Kita tertarik untuk dalam meminimalkan nilai dari (3.1) atas semua lintasan dari x ke y. Diperhatikan bahwa jika kita memikirkan bobot dari suatu sisi sebagai panjang, maka kita mencoba mencari suatu lintasan terpendek dari x ke y. Algoritma yang digunakan untuk menyelesaikan masalah tersebut adalah variasi dari Algoritma Breadth- First Search. Untuk memahami ide pokok dari algoritma yang akan digunakan, diperhatikan analogi berikut ini. Diperhatikan tiga kota A, B, dan C. Diandaikan bahwa informasi berikut ini mengenai waktu perjalanan antara kota-kota tersebut: AB BC AC x y z Informasi tersebut dapat direpresentasikan dengan gambar berikut ini. Jelas bahwa waktu perjalanan antara A dan C tidak bisa melebih minfz; x + yg. Sekarang diandaikan bahwa u adalah suatu titik di graf terhubung berbobot G = (V; E). Untuk setiap titik x 2 V, diandaikan bahwa lintasan terpendek dari u ke x tidak melebihi l (x). Jika diambil y sebagai suatu titik di graf, dan p sebagai suatu titik yang bertetangga dengan y, maka jelas bahwa lintasan terpendek dari u ke y tidak melebihi min fl (y) ; l (p) + w (fp; yg)g : (3.2) Hal ini diilustrasikan oleh gambar di bawah ini.
35 Bab 3. Algoritma Pencarian 30 Oleh karena itu kita dapat mengganti informasi l (y) dengan minimum (3.2). Berikut ini diberikan Algoritma Dijkstra untuk memecahkan masalah lintasan terpendek untuk suatu graf terhubung berbobot. Algoritma Dijkstra pertama kali muncul pada tahun 1959 dalam sebuah tulisan yang ditulis oleh Edsger Dijkstra [12]. Algoritma Lintasan Terpendek Dijkstra. Input: Graf terhubung G = (V; E) yang dilengkapi suatu fungsi bobot w : E! N. Suatu titik khusus u 2 V (G). Output: Panjang semua lintasan terpendek dari u ke titik-titik lain: l : V (G) n fug! N. (1) Diambil l (u) = 0, dan dituliskan l (x) = 1 untuk setiap titik x 2 V dan x 6= u. Selanjutnya dimasukkan u ke V (T ). (2) Diperhatikan semua titik y 2 V (G) n V (T ) dan bertetangga dengan u. Diganti nilai dari l (y) dengan minfl (y), l (u) + w (fu; yg)g. Diamati pada nilai baru dari l (y) untuk setiap titik y 2 V (G) n V (T ), dan dipilih suatu titik v dimana l (v) l (y) untuk semua titik y. Selanjutnya ditambahkan sisi yang muncul untuk nilai baru dari l (v) ke E (T ). (3) Jika V (T ) = V (G), maka proses berhenti. Lintasan tunggal dari u ke sembarang titik x 6= u menyatakan lintasan terpendek dari u ke x. Jika V (T ) 6= V (G), maka ditetapkan v = u dan kembali ke langkah (2). Gambar 3.3: Suatu graf berbobot dengan 8 titik dan 15 sisi. Sebagai contoh, diperhatikan diperhatikan graf berbobot dalam Gambar 3.3. Dimisalkan titik awalnya adalah u, maka dipunyai proses Dijkstra seperti dalam Tabel 3.3. Nilai-nilai l (v) menyatakan panjang lintasan terpendek dari u ke titik v yang diperhatikan. Dari proses ini juga diperoleh pohon rentangan seperti di bawah ini. Berikut ini diberikan contoh penghitungan untuk langkah 2 dan 3.
36 Bab 3. Algoritma Pencarian 31 Tabel 3.3: Pencarian lintasan terpendek dari titik u untuk graf dalam Gambar 3.3 berdasarkan Algoritma Lintasan Terpendek Dijkstra. Langkah l (u) l (a) l (b) l (c) l (d) l (e) l (f) l (g) v l (v) sisi baru u c 1 fu; cg a 2 fu; ag f 2 fc; f g b 3 fc; bg e 3 fc; eg d 4 fb; dg 8 4 g 4 fe; gg pada langkah 2: Diperhatikan tetangga dari u, yaitu a, b, dan c. Dihitung nilai baru untuk: l (a) : min fl (a) ; l (u) + w (fu; ag)g = min f1; 0 + 2g = 2; l (b) : min fl (b) ; l (u) + w (fu; bg)g = min f1; 0 + 3g = 3; l (c) : min fl (c) ; l (u) + w (fu; cg)g = min f1; 0 + 1g = 1: Diperoleh titik c dimana l (c) l (a) ; l (b). pada langkah 3: Diperhatikan tetangga dari c selain u, yaitu b, e, dan f. Dihitung nilai baru untuk: l (b) : min fl (b) ; l (c) + w (fc; bg)g = min f3; 1 + 2g = 3; l (e) : min fl (e) ; l (c) + w (fc; eg)g = min f1; 1 + 2g = 3; l (f) : min fl (f) ; l (c) + w (fc; fg)g = min f1; 1 + 1g = 2: Diperoleh titik f dimana l (f) l (a) ; l (b) ; l (e). 3.5 Soal-soal untuk Bab 3 1. Aplikasikan Algoritma Depth-First Search untuk graf pada Soal 1 dalam Bab Diperhatikan graf G yang dide nisikan oleh matriks ketetanggaan berikut ini
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI.. Definisi Graf Secara matematis, graf G didefinisikan sebagai pasangan himpunan (V,E) ditulis dengan notasi G = (V, E), yang dalam hal ini: V = himpunan tidak-kosong dari simpul-simpul
BAB II LANDASAN TEORI.. Definisi Graf Secara matematis, graf G didefinisikan sebagai pasangan himpunan (V,E) ditulis dengan notasi G = (V, E), yang dalam hal ini: V = himpunan tidak-kosong dari simpul-simpul
Gambar 6. Graf lengkap K n
 . Jenis-jenis Graf Tertentu Ada beberapa graf khusus yang sering dijumpai. Beberapa diantaranya adalah sebagai berikut. a. Graf Lengkap (Graf Komplit) Graf lengkap ialah graf sederhana yang setiap titiknya
. Jenis-jenis Graf Tertentu Ada beberapa graf khusus yang sering dijumpai. Beberapa diantaranya adalah sebagai berikut. a. Graf Lengkap (Graf Komplit) Graf lengkap ialah graf sederhana yang setiap titiknya
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU. Oleh: Kartika Yulianti, S.Pd., M.Si.
 HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
LOGIKA DAN ALGORITMA
 LOGIKA DAN ALGORITMA DASAR DASAR TEORI GRAF Kelahiran Teori Graf Sejarah Graf : masalah jembatan Königsberg (tahun 736) C A D B Gbr. Masalah Jembatan Königsberg Graf yang merepresentasikan jembatan Königsberg
LOGIKA DAN ALGORITMA DASAR DASAR TEORI GRAF Kelahiran Teori Graf Sejarah Graf : masalah jembatan Königsberg (tahun 736) C A D B Gbr. Masalah Jembatan Königsberg Graf yang merepresentasikan jembatan Königsberg
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
LANDASAN TEORI. Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan. kromatik lokasi sebagai landasan teori pada penelitian ini.
 6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
Kode MK/ Matematika Diskrit
 Kode MK/ Matematika Diskrit TEORI GRAF 1 8/29/2014 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 2 8/29/2014 1 TEORI GRAF Tujuan Mahasiswa memahami konsep
Kode MK/ Matematika Diskrit TEORI GRAF 1 8/29/2014 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 2 8/29/2014 1 TEORI GRAF Tujuan Mahasiswa memahami konsep
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
MATEMATIKA DISKRIT II ( 2 SKS)
 MATEMATIKA DISKRIT II ( 2 SKS) Rabu, 18.50 20.20 Ruang Hard Disk PERTEMUAN XI, XII RELASI Dosen Lie Jasa 1 Matematika Diskrit Graf (lanjutan) 2 Lintasan dan Sirkuit Euler Lintasan Euler ialah lintasan
MATEMATIKA DISKRIT II ( 2 SKS) Rabu, 18.50 20.20 Ruang Hard Disk PERTEMUAN XI, XII RELASI Dosen Lie Jasa 1 Matematika Diskrit Graf (lanjutan) 2 Lintasan dan Sirkuit Euler Lintasan Euler ialah lintasan
BAB 2 GRAF PRIMITIF. 2.1 Definisi Graf
 BAB 2 GRAF PRIMITIF Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkait graf, matriks adjency, terhubung, primitifitas, dan scrambling index sebagai landasan teori yang menjadi acuan
BAB 2 GRAF PRIMITIF Pada Bagian ini akan dijelaskan beberapa definisi dan teorema terkait graf, matriks adjency, terhubung, primitifitas, dan scrambling index sebagai landasan teori yang menjadi acuan
PENGETAHUAN DASAR TEORI GRAF
 PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Konsep Dasar Teori Graph 2.1.1 Graph Tak Berarah dan Digraph Suatu Graph Tak Berarah (Undirected Graph) merupakan kumpulan dari titik yang disebut verteks dan segmen garis yang
BAB II LANDASAN TEORI 2.1 Konsep Dasar Teori Graph 2.1.1 Graph Tak Berarah dan Digraph Suatu Graph Tak Berarah (Undirected Graph) merupakan kumpulan dari titik yang disebut verteks dan segmen garis yang
BAB II TINJAUAN PUSTAKA. kromatik lokasi sebagai landasan teori dari penelitian ini.
 BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
BAB 2 DEGREE CONSTRAINED MINIMUM SPANNING TREE. Pada bab ini diberikan beberapa konsep dasar seperti beberapa definisi dan teorema
 BAB 2 DEGREE CONSTRAINED MINIMUM SPANNING TREE Pada bab ini diberikan beberapa konsep dasar seperti beberapa definisi dan teorema sebagai landasan berfikir dalam melakukan penelitian ini dan akan mempermudah
BAB 2 DEGREE CONSTRAINED MINIMUM SPANNING TREE Pada bab ini diberikan beberapa konsep dasar seperti beberapa definisi dan teorema sebagai landasan berfikir dalam melakukan penelitian ini dan akan mempermudah
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM
 ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
Graph. Rembang. Kudus. Brebes Tegal. Demak Semarang. Pemalang. Kendal. Pekalongan Blora. Slawi. Purwodadi. Temanggung Salatiga Wonosobo Purbalingga
 TEORI GRAPH Graph Graph Graph digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar berikut ini sebuah graph yang menyatakan peta jaringan jalan raya yang
TEORI GRAPH Graph Graph Graph digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar berikut ini sebuah graph yang menyatakan peta jaringan jalan raya yang
Dasar-Dasar Teori Graf. Sistem Informasi Universitas Gunadarma 2012/2013
 Dasar-Dasar Teori Graf Sistem Informasi Universitas Gunadarma 2012/2013 Teori Graf Teori Graf mulai dikenal saat matematikawan kebangsaan Swiss bernama Leonhard Euler, yang berhasil mengungkapkan Misteri
Dasar-Dasar Teori Graf Sistem Informasi Universitas Gunadarma 2012/2013 Teori Graf Teori Graf mulai dikenal saat matematikawan kebangsaan Swiss bernama Leonhard Euler, yang berhasil mengungkapkan Misteri
Struktur dan Organisasi Data 2 G R A P H
 G R A P H Graf adalah : Himpunan V (Vertex) yang elemennya disebut simpul (atau point atau node atau titik) Himpunan E (Edge) yang merupakan pasangan tak urut dari simpul, anggotanya disebut ruas (rusuk
G R A P H Graf adalah : Himpunan V (Vertex) yang elemennya disebut simpul (atau point atau node atau titik) Himpunan E (Edge) yang merupakan pasangan tak urut dari simpul, anggotanya disebut ruas (rusuk
Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik
 BAB II DASAR TEORI 2.1 Teori Dasar Graf 2.1.1 Graf dan Graf Sederhana Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik yang tak kosong dan E adalah himpunan sisi. Untuk selanjutnya,
BAB II DASAR TEORI 2.1 Teori Dasar Graf 2.1.1 Graf dan Graf Sederhana Suatu graf G adalah pasangan himpunan (V, E), dimana V adalah himpunan titik yang tak kosong dan E adalah himpunan sisi. Untuk selanjutnya,
Studi Algoritma Optimasi dalam Graf Berbobot
 Studi Algoritma Optimasi dalam Graf Berbobot Vandy Putrandika NIM : 13505001 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : if15001@students.if.itb.ac.id
Studi Algoritma Optimasi dalam Graf Berbobot Vandy Putrandika NIM : 13505001 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : if15001@students.if.itb.ac.id
v 3 e 2 e 4 e 6 e 3 v 4
 5 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan dimensi partisi graf sebagai landasan teori dari penelitian ini... Konsep Dasar Graf Pada bagian ini akan diberikan
5 II. TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan dimensi partisi graf sebagai landasan teori dari penelitian ini... Konsep Dasar Graf Pada bagian ini akan diberikan
BAB I PENDAHULUAN. himpunan bagian bilangan cacah yang disebut label. Pertama kali diperkenalkan
 1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
II. TINJAUAN PUSTAKA. kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini
 5 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf, graf pohon dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini 2.1 KONSEP DASAR GRAF Konsep
5 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf, graf pohon dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini 2.1 KONSEP DASAR GRAF Konsep
KONSEP DASAR GRAF DAN GRAF POHON. Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf
 II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
BAB 2 TINJAUAN PUSTAKA
 BAB 2 TINJAUAN PUSTAKA Pada bagian ini akan dijelaskan beberapa konsep dasar yang berkaitan dengan permasalahan, seperti definisi dan teorema yang dijadikan landasan dalam penelitian ini. 2.1 Graf Graf
BAB 2 TINJAUAN PUSTAKA Pada bagian ini akan dijelaskan beberapa konsep dasar yang berkaitan dengan permasalahan, seperti definisi dan teorema yang dijadikan landasan dalam penelitian ini. 2.1 Graf Graf
PERBANDINGAN ALGORTIMA PRIM DAN KRUSKAL DALAM MENENTUKAN POHON RENTANG MINIMUM
 PERBANDINGAN ALGORTIMA PRIM DAN KRUSKAL DALAM MENENTUKAN POHON RENTANG MINIMUM Kodirun 1 1 Jurusan Matematika FMIPA Universitas Haluoleo, Kendari e-mail: kodirun_zuhry@yahoo.com Abstrak Masalah yang sering
PERBANDINGAN ALGORTIMA PRIM DAN KRUSKAL DALAM MENENTUKAN POHON RENTANG MINIMUM Kodirun 1 1 Jurusan Matematika FMIPA Universitas Haluoleo, Kendari e-mail: kodirun_zuhry@yahoo.com Abstrak Masalah yang sering
merupakan himpunan sisi-sisi tidak berarah pada. (Yaoyuenyong et al. 2002)
 dari elemen graf yang disebut verteks (node, point), sedangkan, atau biasa disebut (), adalah himpunan pasangan tak terurut yang menghubungkan dua elemen subset dari yang disebut sisi (edge, line). Setiap
dari elemen graf yang disebut verteks (node, point), sedangkan, atau biasa disebut (), adalah himpunan pasangan tak terurut yang menghubungkan dua elemen subset dari yang disebut sisi (edge, line). Setiap
TINJAUAN PUSTAKA. Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi
 II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Sebelum memulai pembahasan lebih lanjut, pertama-tama haruslah dijelaskan apa yang dimaksud dengan traveling salesman problem atau dalam bahasa Indonesia disebut sebagai persoalan
BAB 2 LANDASAN TEORI Sebelum memulai pembahasan lebih lanjut, pertama-tama haruslah dijelaskan apa yang dimaksud dengan traveling salesman problem atau dalam bahasa Indonesia disebut sebagai persoalan
Aplikasi Algoritma Dijkstra dalam Pencarian Lintasan Terpendek Graf
 Aplikasi Algoritma Dijkstra dalam Pencarian Lintasan Terpendek Graf Nur Fajriah Rachmah - 0609 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan
Aplikasi Algoritma Dijkstra dalam Pencarian Lintasan Terpendek Graf Nur Fajriah Rachmah - 0609 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan
Graf. Matematika Diskrit. Materi ke-5
 Graf Materi ke-5 Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya
Graf Materi ke-5 Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Terminologi graf Tereminologi termasuk istilah yang berkaitan dengan graf. Di bawah ini akan dijelaskan beberapa definisi yang sering dipakai terminologi. 2.1.1 Graf Definisi
BAB II LANDASAN TEORI 2.1 Terminologi graf Tereminologi termasuk istilah yang berkaitan dengan graf. Di bawah ini akan dijelaskan beberapa definisi yang sering dipakai terminologi. 2.1.1 Graf Definisi
GRAF. Graph seperti dimaksud diatas, ditulis sebagai G(E,V).
 GRAF GRAF Suatu Graph mengandung 2 himpunan, yaitu : 1. Himpunan V yang elemennya disebut simpul (Vertex atau Point atau Node atau Titik) 2. Himpunan E yang merupakan pasangan tak urut dari simpul. Anggotanya
GRAF GRAF Suatu Graph mengandung 2 himpunan, yaitu : 1. Himpunan V yang elemennya disebut simpul (Vertex atau Point atau Node atau Titik) 2. Himpunan E yang merupakan pasangan tak urut dari simpul. Anggotanya
MA3051 Pengantar Teori Graf. Semester /2014 Pengajar: Hilda Assiyatun
 MA3051 Pengantar Teori Graf Semester 1 2013/2014 Pengajar: Hilda Assiyatun Bab 1: Graf dan subgraf Graf G : tripel terurut VG, E G, ψ G ) V G himpunan titik (vertex) E G himpunan sisi (edge) ψ G fungsi
MA3051 Pengantar Teori Graf Semester 1 2013/2014 Pengajar: Hilda Assiyatun Bab 1: Graf dan subgraf Graf G : tripel terurut VG, E G, ψ G ) V G himpunan titik (vertex) E G himpunan sisi (edge) ψ G fungsi
Algoritma Brute-Force dan Greedy dalam Pemrosesan Graf
 Algoritma Brute-Force dan Greedy dalam Pemrosesan Graf Marvin Jerremy Budiman / 13515076 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Algoritma Brute-Force dan Greedy dalam Pemrosesan Graf Marvin Jerremy Budiman / 13515076 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
BAB 2 LANDASAN TEORI
 4 BAB 2 LANDASAN TEORI 2.1 Pengertian Kemacetan Kemacetan adalah situasi atau keadaan tersendatnya atau bahkan terhentinya lalu lintas yang disebabkan oleh banyaknya jumlah kendaraan melebihi kapasitas
4 BAB 2 LANDASAN TEORI 2.1 Pengertian Kemacetan Kemacetan adalah situasi atau keadaan tersendatnya atau bahkan terhentinya lalu lintas yang disebabkan oleh banyaknya jumlah kendaraan melebihi kapasitas
Penerapan Algoritma Steiner Tree dalam Konstruksi Jaringan Pipa Gas
 Penerapan Algoritma Steiner Tree dalam Konstruksi Jaringan Pipa Gas Achmad Baihaqi, NIM: 13508030 Program Studi Teknik Informatika Institut Teknologi Bandung Jalan Ganesa 10 Bandung e-mail: baihaqi@students.itb.ac.id
Penerapan Algoritma Steiner Tree dalam Konstruksi Jaringan Pipa Gas Achmad Baihaqi, NIM: 13508030 Program Studi Teknik Informatika Institut Teknologi Bandung Jalan Ganesa 10 Bandung e-mail: baihaqi@students.itb.ac.id
INTRODUCTION TO GRAPH THEORY LECTURE 2
 INTRODUCTION TO GRAPH THEORY LECTURE Operasi-Operasi Pada Graph Union Misal G dan H adalah dua graph yang saling asing. Union G H adalah graph dengan V(G H)=V(G) V(H) dan E(G H)=E(G) E(H). Join Join dari
INTRODUCTION TO GRAPH THEORY LECTURE Operasi-Operasi Pada Graph Union Misal G dan H adalah dua graph yang saling asing. Union G H adalah graph dengan V(G H)=V(G) V(H) dan E(G H)=E(G) E(H). Join Join dari
Representasi Graph Isomorfisme. sub-bab 8.3
 Representasi Graph Isomorfisme sub-bab 8.3 Representasi graph:. Adjacency list. Adjacency matrix 3. Incidence matrix Contoh: undirected graph Adjacency list : tiap vertex v :, 3, di-link dengan 3:,, 5
Representasi Graph Isomorfisme sub-bab 8.3 Representasi graph:. Adjacency list. Adjacency matrix 3. Incidence matrix Contoh: undirected graph Adjacency list : tiap vertex v :, 3, di-link dengan 3:,, 5
BAB II KAJIAN PUSTAKA
 BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi dan konsep dasar dalam teori graf dan pelabelan graf yang akan digunakan pada bab selanjutnya. 2.1 Definisi dan Istilah Dalam Teori Graf
BAB II LANDASAN TEORI Pada bab ini akan diberikan beberapa definisi dan konsep dasar dalam teori graf dan pelabelan graf yang akan digunakan pada bab selanjutnya. 2.1 Definisi dan Istilah Dalam Teori Graf
LATIHAN ALGORITMA-INTEGER
 LATIHAN ALGORITMA-INTEGER Nyatakan PBB(295,70) = 5 sebagai kombinasi lanjar 295 dan 70 Tentukan inversi dari 27(mod 7) Tentukan solusi kekongruenan lanjar dari 27.x kongruen 1(mod 7) dengan cara 1 ( cara
LATIHAN ALGORITMA-INTEGER Nyatakan PBB(295,70) = 5 sebagai kombinasi lanjar 295 dan 70 Tentukan inversi dari 27(mod 7) Tentukan solusi kekongruenan lanjar dari 27.x kongruen 1(mod 7) dengan cara 1 ( cara
Graf. Program Studi Teknik Informatika FTI-ITP
 Graf Program Studi Teknik Informatika FTI-ITP Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan
Graf Program Studi Teknik Informatika FTI-ITP Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan
APLIKASI PEWARNAAN SIMPUL GRAF UNTUK MENGATASI KONFLIK PENJADWALAN MATA KULIAH DI FMIPA UNY
 APLIKASI PEWARNAAN SIMPUL GRAF UNTUK MENGATASI KONFLIK PENJADWALAN MATA KULIAH DI FMIPA UNY Latar belakang Masalah Pada setiap awal semester bagian pendidikan fakultas Matematika dan Ilmu Pengetahuan Universitas
APLIKASI PEWARNAAN SIMPUL GRAF UNTUK MENGATASI KONFLIK PENJADWALAN MATA KULIAH DI FMIPA UNY Latar belakang Masalah Pada setiap awal semester bagian pendidikan fakultas Matematika dan Ilmu Pengetahuan Universitas
Pohon. Modul 4 PENDAHULUAN. alam modul-modul sebelumnya Anda telah mempelajari graph terhubung tanpa sikel, misalnya model graph untuk molekul C 4
 Modul 4 Pohon Dr. Nanang Priatna, M.Pd. D PENDAHULUAN alam modul-modul sebelumnya Anda telah mempelajari graph terhubung tanpa sikel, misalnya model graph untuk molekul C 4 H 10, hierarki administrasi
Modul 4 Pohon Dr. Nanang Priatna, M.Pd. D PENDAHULUAN alam modul-modul sebelumnya Anda telah mempelajari graph terhubung tanpa sikel, misalnya model graph untuk molekul C 4 H 10, hierarki administrasi
MEMBANDINGKAN KEMANGKUSAN ALGORITMA PRIM DAN ALGORITMA KRUSKAL DALAM PEMECAHAN MASALAH POHON MERENTANG MINIMUM
 MEMBANDINGKAN KEMANGKUSAN ALGORITMA PRIM DAN ALGORITMA KRUSKAL DALAM PEMECAHAN MASALAH POHON MERENTANG MINIMUM Pudy Prima (13508047) Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika
MEMBANDINGKAN KEMANGKUSAN ALGORITMA PRIM DAN ALGORITMA KRUSKAL DALAM PEMECAHAN MASALAH POHON MERENTANG MINIMUM Pudy Prima (13508047) Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika
UNIVERSITAS GUNADARMA
 UNIVERSITAS GUNADARMA SK No. 92 / Dikti / Kep /1996 Fakultas Ilmu Komputer, Teknologi Industri, Ekonomi,Teknik Sipil & Perencanaan, Psikologi, Sastra Program Diploma (D3) Manajemen Informatika, Teknik
UNIVERSITAS GUNADARMA SK No. 92 / Dikti / Kep /1996 Fakultas Ilmu Komputer, Teknologi Industri, Ekonomi,Teknik Sipil & Perencanaan, Psikologi, Sastra Program Diploma (D3) Manajemen Informatika, Teknik
LANDASAN TEORI. Bab Konsep Dasar Graf. Definisi Graf
 Bab 2 LANDASAN TEORI 2.1. Konsep Dasar Graf Definisi Graf Suatu graf G terdiri atas himpunan yang tidak kosong dari elemen elemen yang disebut titik atau simpul (vertex), dan suatu daftar pasangan vertex
Bab 2 LANDASAN TEORI 2.1. Konsep Dasar Graf Definisi Graf Suatu graf G terdiri atas himpunan yang tidak kosong dari elemen elemen yang disebut titik atau simpul (vertex), dan suatu daftar pasangan vertex
Permodelan Pohon Merentang Minimum Dengan Menggunakan Algoritma Prim dan Algoritma Kruskal
 Permodelan Pohon Merentang Minimum Dengan Menggunakan Algoritma Prim dan Algoritma Kruskal Salman Muhammad Ibadurrahman NIM : 13506106 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha
Permodelan Pohon Merentang Minimum Dengan Menggunakan Algoritma Prim dan Algoritma Kruskal Salman Muhammad Ibadurrahman NIM : 13506106 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha
II. KONSEP DASAR GRAF DAN GRAF POHON. Graf G adalah himpunan terurut ( V(G), E(G)), dengan V(G) menyatakan
 II. KONSEP DASAR GRAF DAN GRAF POHON 2.1 Konsep Dasar Graf Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989). Graf G adalah himpunan terurut ( V(G), E(G)), dengan
II. KONSEP DASAR GRAF DAN GRAF POHON 2.1 Konsep Dasar Graf Teori dasar mengenai graf yang akan digunakan dalam penelitian ini diambil dari Deo (1989). Graf G adalah himpunan terurut ( V(G), E(G)), dengan
Graf dan Analisa Algoritma. Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017
 Graf dan Analisa Algoritma Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017 Who Am I? Stya Putra Pratama, CHFI, EDRP Pendidikan - Universitas Gunadarma S1-2007 Teknik Informatika S2-2012
Graf dan Analisa Algoritma Pertemuan #01 - Dasar-Dasar Teori Graf Universitas Gunadarma 2017 Who Am I? Stya Putra Pratama, CHFI, EDRP Pendidikan - Universitas Gunadarma S1-2007 Teknik Informatika S2-2012
TINJAUAN PUSTAKA. Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada
 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
7. PENGANTAR TEORI GRAF
 Definisi : Secara umum merupakan kumpulan titik dan garis. Sebuah garf G terdiri dari: 1. Sebuah himpunan V=V(G) yang memiliki elemen2 yg dinamakan verteks/titik/node. 2. Sebuah kumpulan E=E(G) merupakan
Definisi : Secara umum merupakan kumpulan titik dan garis. Sebuah garf G terdiri dari: 1. Sebuah himpunan V=V(G) yang memiliki elemen2 yg dinamakan verteks/titik/node. 2. Sebuah kumpulan E=E(G) merupakan
BAB 2 LANDASAN TEORI. yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang
 BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya
BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya
PENGERTIAN GRAPH. G 1 adalah graph dengan V(G) = { 1, 2, 3, 4 } E(G) = { (1, 2), (1, 3), (2, 3), (2, 4), (3, 4) } Graph 2
 PENGERTIAN GRAPH 1. DEFINISI GRAPH Graph G adalah pasangan terurut dua himpunan (V(G), E(G)), V(G) himpunan berhingga dan tak kosong dari obyek-obyek yang disebut himpunan titik (vertex) dan E(G) himpunan
PENGERTIAN GRAPH 1. DEFINISI GRAPH Graph G adalah pasangan terurut dua himpunan (V(G), E(G)), V(G) himpunan berhingga dan tak kosong dari obyek-obyek yang disebut himpunan titik (vertex) dan E(G) himpunan
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM
 ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
x 6 x 5 x 3 x 2 x 4 V 3 x 1 V 1
 . PENGANTAR TEORI GRAF Definisi : Secara umum merupakan kumpulan titik dan garis. NET terdiri atas : 1. Himpunan titik (tidak boleh kosong) 2. Himpunan garis (directed line) 3. Setiap directed line menentukan
. PENGANTAR TEORI GRAF Definisi : Secara umum merupakan kumpulan titik dan garis. NET terdiri atas : 1. Himpunan titik (tidak boleh kosong) 2. Himpunan garis (directed line) 3. Setiap directed line menentukan
II. LANDASAN TEORI. Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan
 4 II. LANDASAN TEORI Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan Konisberg yang kemudian menghasilkan konsep graf Eulerian merupakan awal dari lahirnya teori graf. Euler mengilustrasikan
4 II. LANDASAN TEORI Ide Leonard Euler di tahun 1736 untuk menyelesaikan masalah jembatan Konisberg yang kemudian menghasilkan konsep graf Eulerian merupakan awal dari lahirnya teori graf. Euler mengilustrasikan
Pertemuan 12. Teori Graf
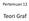 Pertemuan 2 Teori Graf Derajat Definisi Misalkan adalah titik dalam suatu Graf G. Derajat titik (simbol d()) adalah jumlah garis yang berhubungan dengan titik dan garis suatu loop dihitung dua kali. Derajat
Pertemuan 2 Teori Graf Derajat Definisi Misalkan adalah titik dalam suatu Graf G. Derajat titik (simbol d()) adalah jumlah garis yang berhubungan dengan titik dan garis suatu loop dihitung dua kali. Derajat
2. TINJAUAN PUSTAKA. Chartrand dan Zhang (2005) yaitu sebagai berikut: himpunan tak kosong dan berhingga dari objek-objek yang disebut titik
 2. TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf Pada bagian ini akan diberikan konsep dasar graf yang diambil dari buku Chartrand dan Zhang (2005) yaitu sebagai berikut: Suatu Graf G adalah suatu pasangan himpunan
2. TINJAUAN PUSTAKA 2.1 Konsep Dasar Graf Pada bagian ini akan diberikan konsep dasar graf yang diambil dari buku Chartrand dan Zhang (2005) yaitu sebagai berikut: Suatu Graf G adalah suatu pasangan himpunan
Termilogi Pada Pohon Berakar 10 Pohon Berakar Terurut
 KATA PENGANTAR Puji syukur penyusun panjatkan ke hadirat Allah Subhanahu wata?ala, karena berkat rahmat-nya kami bisa menyelesaikan makalah yang berjudul Catatan Seorang Kuli Panggul. Makalah ini diajukan
KATA PENGANTAR Puji syukur penyusun panjatkan ke hadirat Allah Subhanahu wata?ala, karena berkat rahmat-nya kami bisa menyelesaikan makalah yang berjudul Catatan Seorang Kuli Panggul. Makalah ini diajukan
BAB 2 GRAF PRIMITIF. Gambar 2.1. Contoh Graf
 BAB 2 GRAF PRIMITIF Pada bagian ini akan dijelaskan mengenai definisi graf, istilah-istilah dalam graf, matriks ketetanggaan, graf terhubung, primitivitas graf, dan scrambling index. 2.1 Definisi Graf
BAB 2 GRAF PRIMITIF Pada bagian ini akan dijelaskan mengenai definisi graf, istilah-istilah dalam graf, matriks ketetanggaan, graf terhubung, primitivitas graf, dan scrambling index. 2.1 Definisi Graf
BAB 2 GRAF PRIMITIF. 2.1 Definisi Graf
 BAB 2 GRAF PRIMITIF Pada bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan definisi graf,
BAB 2 GRAF PRIMITIF Pada bab ini akan dijelaskan beberapa konsep dasar seperti definisi dan teorema yang dijadikan landasan teori dalam penelitian ini. Konsep dasar tersebut berkaitan dengan definisi graf,
Graph. Matematika Informatika 4. Onggo
 Matematika Informatika 4 Onggo Wiryawan @OnggoWr Definisi adalah struktur diskrit yang mengandung vertex dan edge yang menghubungkan vertex-vertex tersebut. vertex edge 2 Jenis-jenis Definisi 1: Suatu
Matematika Informatika 4 Onggo Wiryawan @OnggoWr Definisi adalah struktur diskrit yang mengandung vertex dan edge yang menghubungkan vertex-vertex tersebut. vertex edge 2 Jenis-jenis Definisi 1: Suatu
GRAF. V3 e5. V = {v 1, v 2, v 3, v 4 } E = {e 1, e 2, e 3, e 4, e 5 } E = {(v 1,v 2 ), (v 1,v 2 ), (v 1,v 3 ), (v 2,v 3 ), (v 3,v 3 )}
 GRAF Graf G(V,E) didefinisikan sebagai pasangan himpunan (V,E), dengan V adalah himpunan berhingga dan tidak kosong dari simpul-simpul (verteks atau node). Dan E adalah himpunan berhingga dari busur (vertices
GRAF Graf G(V,E) didefinisikan sebagai pasangan himpunan (V,E), dengan V adalah himpunan berhingga dan tidak kosong dari simpul-simpul (verteks atau node). Dan E adalah himpunan berhingga dari busur (vertices
NASKAH UJIAN UTAMA. JENJANG/PROG. STUDI : DIPLOMA TIGA / MANAJEMEN INFORMATIKA HARI / TANGGAL : Kamis / 18 FEBRUARI 2016
 NASKAH UJIAN UTAMA MATA UJIAN : LOGIKA DAN ALGORITMA JENJANG/PROG. STUDI : DIPLOMA TIGA / MANAJEMEN INFORMATIKA HARI / TANGGAL : Kamis / 18 FEBRUARI 2016 NASKAH UJIAN INI TERDIRI DARI 80 SOAL PILIHAN GANDA
NASKAH UJIAN UTAMA MATA UJIAN : LOGIKA DAN ALGORITMA JENJANG/PROG. STUDI : DIPLOMA TIGA / MANAJEMEN INFORMATIKA HARI / TANGGAL : Kamis / 18 FEBRUARI 2016 NASKAH UJIAN INI TERDIRI DARI 80 SOAL PILIHAN GANDA
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan himpunan dan beberapa definisi yang berkaitan dengan himpunan, serta konsep dasar dan teori graf yang akan digunakan pada bab selanjutnya. 2.1 Himpunan
BAB 2 LANDASAN TEORI Pada bab ini akan dijelaskan himpunan dan beberapa definisi yang berkaitan dengan himpunan, serta konsep dasar dan teori graf yang akan digunakan pada bab selanjutnya. 2.1 Himpunan
TEORI GRAF UNIVERSITAS MUHAMMADIYAH JEMBER ILHAM SAIFUDIN PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK. Selasa, 13 Desember 2016
 PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS MUHAMMADIYAH JEMBER TEORI GRAF ILHAM SAIFUDIN Selasa, 13 Desember 2016 Universitas Muhammadiyah Jember Pendahuluan 1 OUTLINE 2 Definisi Graf
PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS MUHAMMADIYAH JEMBER TEORI GRAF ILHAM SAIFUDIN Selasa, 13 Desember 2016 Universitas Muhammadiyah Jember Pendahuluan 1 OUTLINE 2 Definisi Graf
ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY. Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin
 ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin hasma_ba@yahoo.com Abstract Graf yang memuat semua siklus dari yang terkecil sampai
ALTERNATIF PEMBUKTIAN DAN PENERAPAN TEOREMA BONDY Hasmawati Jurusan Matematika, Fakultas Mipa Universitas Hasanuddin hasma_ba@yahoo.com Abstract Graf yang memuat semua siklus dari yang terkecil sampai
BAB II LANDASAN TEORI
 15 BAB II LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Graf Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang
15 BAB II LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Graf Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang
Graf dan Operasi graf
 6 Bab II Graf dan Operasi graf Dalam subbab ini akan diberikan konsep dasar, definisi dan notasi pada teori graf yang dipergunakan dalam penulisan disertasi ini. Konsep dasar tersebut ditulis sesuai dengan
6 Bab II Graf dan Operasi graf Dalam subbab ini akan diberikan konsep dasar, definisi dan notasi pada teori graf yang dipergunakan dalam penulisan disertasi ini. Konsep dasar tersebut ditulis sesuai dengan
Penerapan Teori Graf Pada Algoritma Routing
 Penerapan Teori Graf Pada Algoritma Routing Indra Siregar 13508605 Program Studi Teknik Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan Ganesha 10, Bandung
Penerapan Teori Graf Pada Algoritma Routing Indra Siregar 13508605 Program Studi Teknik Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan Ganesha 10, Bandung
Bagaimana merepresentasikan struktur berikut? A E
 Bagaimana merepresentasikan struktur berikut? B D A E F C G Bagaimana merepresentasikan struktur berikut? Contoh-contoh aplikasi graf Peta (jaringan jalan dan hubungan antar kota) Jaringan komputer Jaringan
Bagaimana merepresentasikan struktur berikut? B D A E F C G Bagaimana merepresentasikan struktur berikut? Contoh-contoh aplikasi graf Peta (jaringan jalan dan hubungan antar kota) Jaringan komputer Jaringan
BAB 2 LANDASAN TEORI
 BAB LANDASAN TEORI. Teori Graf Teori graf merupakan pokok bahasan yang sudah tua usianya namun memiliki banyak terapan sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan
BAB LANDASAN TEORI. Teori Graf Teori graf merupakan pokok bahasan yang sudah tua usianya namun memiliki banyak terapan sampai saat ini. Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan
Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Demak Semarang. Kend al. Salatiga.
 GRAF PENDAHULUAN Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya yang menghubungkan
GRAF PENDAHULUAN Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya yang menghubungkan
BAB 2 LANDASAN TEORITIS
 xvi BAB 2 LANDASAN TEORITIS Dalam penulisan laporan tugas akhir ini, penulis akan memberikan beberapa pengertian yang berhubungan dengan judul penelitian yang penulis ajukan, karena tanpa pengertian yang
xvi BAB 2 LANDASAN TEORITIS Dalam penulisan laporan tugas akhir ini, penulis akan memberikan beberapa pengertian yang berhubungan dengan judul penelitian yang penulis ajukan, karena tanpa pengertian yang
8/29/2014. Kode MK/ Nama MK. Matematika Diskrit 2 8/29/2014
 Kode MK/ Nama MK Matematika Diskrit 1 8/29/2014 2 8/29/2014 1 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 3 8/29/2014 POHON DAN PEWARNAAN GRAF Tujuan Mahasiswa
Kode MK/ Nama MK Matematika Diskrit 1 8/29/2014 2 8/29/2014 1 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 3 8/29/2014 POHON DAN PEWARNAAN GRAF Tujuan Mahasiswa
BAB II TEORI GRAF DAN PELABELAN GRAF. Dalam bab ini akan diberikan beberapa definisi dan konsep dasar dari
 BAB II TEORI GRAF DAN PELABELAN GRAF Dalam bab ini akan diberikan beberapa definisi dan konsep dasar dari teori graf, serta akan dijelaskan beberapa jenis pelabelan graf yang akan digunakan pada bab-bab
BAB II TEORI GRAF DAN PELABELAN GRAF Dalam bab ini akan diberikan beberapa definisi dan konsep dasar dari teori graf, serta akan dijelaskan beberapa jenis pelabelan graf yang akan digunakan pada bab-bab
Bab 2. Teori Dasar. 2.1 Definisi Graf
 Bab 2 Teori Dasar Pada bagian ini diberikan definisi-definisi dasar dalam teori graf berikut penjabaran mengenai kompleksitas algoritma beserta contohnya yang akan digunakan dalam tugas akhir ini. Berikut
Bab 2 Teori Dasar Pada bagian ini diberikan definisi-definisi dasar dalam teori graf berikut penjabaran mengenai kompleksitas algoritma beserta contohnya yang akan digunakan dalam tugas akhir ini. Berikut
BAB I PENDAHULUAN 1.1 Latar Belakang Masalah
 BAB I PENDAHULUAN. Latar Belakang Masalah Seiring perkembangan zaman, maka perkembangan ilmu pengetahuan berkembang pesat, begitu pula dengan ilmu matematika. Salah satu cabang ilmu matematika yang memiliki
BAB I PENDAHULUAN. Latar Belakang Masalah Seiring perkembangan zaman, maka perkembangan ilmu pengetahuan berkembang pesat, begitu pula dengan ilmu matematika. Salah satu cabang ilmu matematika yang memiliki
Pertemuan 11 GRAPH, MATRIK PENYAJIAN GRAPH
 Pertemuan 11 GRAPH, MATRIK PENYAJIAN GRAPH GRAPH Suatu Graph mengandung 2 himpunan, yaitu : 1. Himpunan V yang elemennya disebut simpul (Vertex atau Point atau Node atau Titik) 2. Himpunan E yang merupakan
Pertemuan 11 GRAPH, MATRIK PENYAJIAN GRAPH GRAPH Suatu Graph mengandung 2 himpunan, yaitu : 1. Himpunan V yang elemennya disebut simpul (Vertex atau Point atau Node atau Titik) 2. Himpunan E yang merupakan
Aplikasi Pohon dan Graf dalam Kaderisasi
 Aplikasi Pohon dan Graf dalam Kaderisasi Jonathan - 13512031 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Aplikasi Pohon dan Graf dalam Kaderisasi Jonathan - 13512031 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
BAB II LANDASAN TEORI
 5 BAB II LANDASAN TEORI.1 Sejarah Graf Menurut catatan sejarah, masalah jembatan KÖnigsberg adalah masalah yang pertama kali menggunakan graf (tahun 1736). Di kota KÖnigsberg (sebelah timur Negara bagian
5 BAB II LANDASAN TEORI.1 Sejarah Graf Menurut catatan sejarah, masalah jembatan KÖnigsberg adalah masalah yang pertama kali menggunakan graf (tahun 1736). Di kota KÖnigsberg (sebelah timur Negara bagian
Bab 2 LANDASAN TEORI. 2.1 Definisi Graf
 Bab 2 LANDASAN TEORI 2.1 Definisi Graf Suatu graf G terdiri dari himpunan tak kosong terbatas dari objek yang dinamakan titik dan himpunan pasangan (boleh kosong) dari titik G yang dinamakan sisi. Himpunan
Bab 2 LANDASAN TEORI 2.1 Definisi Graf Suatu graf G terdiri dari himpunan tak kosong terbatas dari objek yang dinamakan titik dan himpunan pasangan (boleh kosong) dari titik G yang dinamakan sisi. Himpunan
Aplikasi Shortest Path dengan Menggunakan Graf dalam Kehidupan Sehari-hari
 Aplikasi Shortest Path dengan Menggunakan Graf dalam Kehidupan Sehari-hari Andika Mediputra NIM : 13509057 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Aplikasi Shortest Path dengan Menggunakan Graf dalam Kehidupan Sehari-hari Andika Mediputra NIM : 13509057 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
BAB II TINJAUAN PUSTAKA. sepasang titik. Himpunan titik di G dinotasikan dengan V(G) dan himpunan
 5 BAB II TINJAUAN PUSTAKA A. Teori Graf 1. Dasar-dasar Graf Graf G didefinisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G = (V, E), dimana V adalah himpunan titik yang tidak kosong (vertex)
5 BAB II TINJAUAN PUSTAKA A. Teori Graf 1. Dasar-dasar Graf Graf G didefinisikan sebagai pasangan himpunan (V, E) ditulis dengan notasi G = (V, E), dimana V adalah himpunan titik yang tidak kosong (vertex)
BAB 2. Konsep Dasar. 2.1 Definisi graf
 BAB 2 Konsep Dasar 21 Definisi graf Suatu graf G = (V(G), E(G)) didefinisikan sebagai pasangan himpunan 2 titik V(G) dan himpunan sisi E(G) dengan V(G) dan E(G) [ VG ( )] Sebagai contoh, graf G 1 = (V(G
BAB 2 Konsep Dasar 21 Definisi graf Suatu graf G = (V(G), E(G)) didefinisikan sebagai pasangan himpunan 2 titik V(G) dan himpunan sisi E(G) dengan V(G) dan E(G) [ VG ( )] Sebagai contoh, graf G 1 = (V(G
III. BILANGAN KROMATIK LOKASI GRAF. Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.(2002). = ( ) {1,2,3,, } dengan syarat
 III. BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.00). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan
III. BILANGAN KROMATIK LOKASI GRAF Bilangan kromatik lokasi graf pertama kali dikaji oleh Chartrand dkk.00). Konsep ini merupakan pengembangan dari konsep dimensi partisi dan pewarnaan graf. Pewarnaan
BAB II LANDASAN TEORI. Teori graf dikenal sejak abad ke-18 Masehi. Saat ini teori graf telah
 BAB II LANDASAN TEORI 2.1. Pendahuluan Teori graf dikenal sejak abad ke-18 Masehi. Saat ini teori graf telah berkembang sangat pesat dan digunakan untuk menyelesaikan persoalanpersoalan pada berbagai bidang
BAB II LANDASAN TEORI 2.1. Pendahuluan Teori graf dikenal sejak abad ke-18 Masehi. Saat ini teori graf telah berkembang sangat pesat dan digunakan untuk menyelesaikan persoalanpersoalan pada berbagai bidang
Konsep. Graph adalah suatu diagram yang memuat informasi tertentu. Contoh : Struktur organisasi
 GRPH 1 Konsep Graph adalah suatu diagram yang memuat informasi tertentu. Contoh : Struktur organisasi 2 Contoh Graph agan alir pengambilan mata kuliah 3 Contoh Graph Peta 4 5 Dasar-dasar Graph Suatu graph
GRPH 1 Konsep Graph adalah suatu diagram yang memuat informasi tertentu. Contoh : Struktur organisasi 2 Contoh Graph agan alir pengambilan mata kuliah 3 Contoh Graph Peta 4 5 Dasar-dasar Graph Suatu graph
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Teori graf adalah cabang kajian matematika yang mempelajari sifat-sifat graf. Secara sederhana, suatu graf adalah himpunan benda-benda yang disebut titik yang terhubung
BAB 1 PENDAHULUAN 1.1 Latar Belakang Teori graf adalah cabang kajian matematika yang mempelajari sifat-sifat graf. Secara sederhana, suatu graf adalah himpunan benda-benda yang disebut titik yang terhubung
47 Matematika Diskrit BAB IV TEORI GRAF
 47 BAB IV TEOI GAF Teori graf merupakan pokok bahasan yang banyak penerapannya pada masa kini. emakaian teori graf telah banyak dirasakan dalam berbagai ilmu, antara lain : optimisasi jaringan, ekonomi,
47 BAB IV TEOI GAF Teori graf merupakan pokok bahasan yang banyak penerapannya pada masa kini. emakaian teori graf telah banyak dirasakan dalam berbagai ilmu, antara lain : optimisasi jaringan, ekonomi,
MIDDLE PADA BEBERAPA GRAF KHUSUS
 PELABELAN DAN PEMBENTUKAN GRAF MIDDLE PADA BEBERAPA GRAF KHUSUS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Meliana Deta Anggraeni 4111409019
PELABELAN DAN PEMBENTUKAN GRAF MIDDLE PADA BEBERAPA GRAF KHUSUS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Meliana Deta Anggraeni 4111409019
RENCANA PEMBELAJARAN SEMESTER (RPS)
 RENCANA PEMBELAJARAN SEMESTER (RPS) MUG2A3 Matematika Diskrit Disusun oleh: Dede Tarwidi, M.Si., M.Sc. PROGRAM STUDI S1 ILMU KOMPUTASI FAKULTAS INFORMATIKA TELKOM UNIVERSITY LEMBAR PENGESAHAN Rencana Pembelajaran
RENCANA PEMBELAJARAN SEMESTER (RPS) MUG2A3 Matematika Diskrit Disusun oleh: Dede Tarwidi, M.Si., M.Sc. PROGRAM STUDI S1 ILMU KOMPUTASI FAKULTAS INFORMATIKA TELKOM UNIVERSITY LEMBAR PENGESAHAN Rencana Pembelajaran
Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah
 BAB II KAJIAN TEORI II.1 Teori-teori Dasar Graf II.1.1 Definisi Graf Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah himpunan tak kosong dari titik graf G, dan E, himpunan sisi
BAB II KAJIAN TEORI II.1 Teori-teori Dasar Graf II.1.1 Definisi Graf Sebuah graf sederhana G adalah pasangan terurut G = (V, E) dengan V adalah himpunan tak kosong dari titik graf G, dan E, himpunan sisi
SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * CHARACTERISTIC OF THE GRAPH THAT CONTAINS ALL CYCLES Nur Rohmah Oktaviani Putri
 SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin CHARACTERISTIC OF THE GRAPH THAT CONTAINS
SIFAT SIFAT GRAF YANG MEMUAT SEMUA SIKLUS Nur Rohmah Oktaviani Putri * Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Hasanuddin CHARACTERISTIC OF THE GRAPH THAT CONTAINS
TEORI DASAR GRAF 1. Teori Graf
 TEORI SR GRF 1 Obyektif : 1. Mengerti apa yang dimaksud dengan Graf 2. Memahami operasi yang dilakukan pada Graf 3. Mengerti derajat dan keterhubungan Graf Teori Graf Teori Graf mulai dikenal pada saat
TEORI SR GRF 1 Obyektif : 1. Mengerti apa yang dimaksud dengan Graf 2. Memahami operasi yang dilakukan pada Graf 3. Mengerti derajat dan keterhubungan Graf Teori Graf Teori Graf mulai dikenal pada saat
ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH
 ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH Hasmawati, Jusmawati Massalesse, Hendra, Muhamad Hasbi Jurusan Matematika FMIPA Universitas Hasanudin
ALTERNATIF PEMBUKTIAN PENGEMBANGAN TEOREMA DIRAC UNTUK GRAF BERORDE KURANG ATAU SAMA DENGAN SEPULUH Hasmawati, Jusmawati Massalesse, Hendra, Muhamad Hasbi Jurusan Matematika FMIPA Universitas Hasanudin
Aplikasi Pohon Merentang Minimum dalam Rute Jalur Kereta Api di Pulau Jawa
 Aplikasi Pohon Merentang Minimum dalam Rute Jalur Kereta Api di Pulau Jawa Darwin Prasetio ( 001 ) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Aplikasi Pohon Merentang Minimum dalam Rute Jalur Kereta Api di Pulau Jawa Darwin Prasetio ( 001 ) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
