8/29/2014. Kode MK/ Nama MK. Matematika Diskrit 2 8/29/2014
|
|
|
- Utami Widjaja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 Kode MK/ Nama MK Matematika Diskrit 1 8/29/ /29/2014 1
2 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 3 8/29/2014 POHON DAN PEWARNAAN GRAF Tujuan Mahasiswa memahami konsep pohon dan pewarnaan graf. Mahasiswa memahami aplikasi minimum spanning tree maupun pewarnaan graf. Mahasiswa mampu memahami dan meyelesaikan berbagai persoalan dan fenomena yang terkait dengan pohon dan pewarnaan graf. 4 8/29/2014 2
3 Definisi Pohon (tree) merupakan salah satu bentuk khusus dari struktur suatu graf. Misalkan A merupakan sebuah himpunan berhingga simpul (vertex) pada suatu graf G yang terhubung. Untuk setiap pasangan simpul di A dapat ditentukan suatu lintasan yang menghubungkan pasangan simpul tersebut. 5 8/29/2014 Definisi (2) Suatu graf terhubung yang setiap pasangan simpulnya hanya dapat dihubungkan oleh satu lintasan tertentu, maka graf tersebut dinamakan pohon (tree). Dengan kata lain, pohon merupakan graf takberarah yang terhubung dan tidak memiliki siklus maupun sirkuit. 6 8/29/2014 3
4 Definisi (3) Contoh : Gambar G1 dan G2 adalah pohon, G3 bukan pohon 7 8/29/2014 Definisi (4) Hutan (forest) merupakan kumpulan pohon yang saling lepas. Dengan kata lain, hutan merupakan graf tidak terhubung yang tidak mengandung sirkuit. Setiap komponen di dalam graf terhubung tersebut adalah pohon. 8 8/29/2014 4
5 Beberapa sifat pohon : Misalkan G merupakan suatu graf dengan n buah simpul dan tepat n 1 buah sisi. Jika G tidak mempunyai sirkuit maka G merupakan pohon. Suatu pohon dengan n buah simpul mempunyai n 1 buah sisi. Setiap pasang simpul di dalam suatu pohon terhubung dengan lintasan tunggal. Misalkan G adalah graf sederhana dengan jumlah simpul n, jika G tidak mengandung sirkuit maka penambahan satu sisi pada graf hanya akan membuat satu sirkuit. 9 8/29/2014 Pohon Merentang Minimum (Minimun Spenning Tree) Spanning Tree dari suatu graf terhubung merupakan subgraf merentang (spanning subgraph) yang berupa pohon. Pohon merentang diperoleh dengan cara menghilangkan sirkuit di dalam graf tersebut. Gambar Graf dan Spanning Tree 10 8/29/2014 5
6 Pohon Merentang Minimum (Minimun Spenning Tree) (2) Terlihat bahwa T1, T2, T3, T4 merupakan spanning tree dari graf G. Perlu diperhatikan bahwa setiap graf terhubung berbobot paling sedikit mempunyai satu buah spanning tree. Pohon rentang yang memiliki bobot minimum dinamakan pohon merentang minimum (minimum spanning tree). Salah satu contoh aplikasi spanning tree adalah menentukan rangkaian jalan dengan jarak total seminimum mungkin yang menghubungkan semua kota sehingga setiap kota tetap terhubung satu sama lain. 11 8/29/2014 Cara Menentukan Minimum Spanning Tree 1. Algoritma Prim 2. Algoritma Kruskal 12 8/29/2014 6
7 Algoritma Prim Langkah-Langkah Algoritma Prim Pilih sisi dari graf G yang berbobot minimum, masukkan ke dalam T. Pilih sisi (u, v) dalam G yang mempunyai bobot minimum dan bersisian dengan simpul di T, dengan syarat sisi tersebut tidak membentuk sirkuit di T. Masukkan (u, v) ke dalam T. Ulangi langkah 2 sebanyak n 2 kali. 13 8/29/2014 Algoritma Prim (2) Jumlah langkah seluruhnya dalam algoritma Prim adalah sebanyak jumlah sisi di dalam spanning tree dengan n buah simpul, yaitu (n 1) buah. Contoh 5.1 : Tentukan minimum spanning tree dari graf dibawah ini : 14 8/29/2014 7
8 Algoritma Prim (3) Jawab : Pilih sisi fg sehingga kita mempunyai T ({f, g}, fg) Langkah selanjutnya dapat dipilih sisi ef karena sisi tersebut berbobot minimum yang bersisian dengan simpul f. Selanjutnya pilih sisi ae atau gh karena sisi tersebut berbobot minimum yang bersisian dengan simpul pada T, yaitu e dan g. 15 8/29/2014 Algoritma Prim (4) Jika proses ini dilanjutkan terus maka akan diperoleh minimum spanning tree seperti dibawah ini : Terlihat bahwa spanning tree tersebut mempunyai total bobot = /29/2014 8
9 Algoritma Kruskal Langkah-langkah dalam algoritma Kruskal agak berbeda dengan algoritma Prim. Pada algoritma Kruskal, semua sisi dengan bobot yang minimal dimasukan kedalam T secara berurutan. 17 8/29/2014 Algoritma Kruskal (2) Langkah-Langkah Algoritma Kruskal : Langkah I : T berbentuk seperti pohon berikut Langkah II : memasukan sisi-sisi yang berbobot 3 kedalam sehingga T berbentuk 18 8/29/2014 9
10 Algoritma Kruskal (3) Langkah III : memasukan sisi-sisi yang berbobot 4 kedalam sehingga akhirnya diperoleh minimum spanning tree berikut : 19 8/29/2014 Pohon Berakar Pada suatu pohon, yang sisi-sisinya diberi arah sehingga menyerupai graf berarah, maka simpul yang terhubung dengan semua simpul pada pohon tersebut dinamakan akar. 20 8/29/
11 Pohon Berakar (2) Suatu pohon yang satu buah simpulnya diperlakukan sebagai akar maka pohon tersebut dinamakan pohon berakar (rooted tree), lihat gambar (a). Simpul yang berlaku sebagai akar mempunyai derajat masuk sama dengan nol. Sementara itu, simpul yang lain pada pohon itu memiliki derajat masuk sama dengan satu. Pada suatu pohon berakar, Simpul yang memiliki derajat keluar sama dengan nol dinamakan daun. Selanjutnya, komponen arah biasanya diabaikan sehingga pohon berakar digambarkan seperti graf tak berarah pada gambar 5.3 (b) 21 8/29/2014 Terminologi Pohon Berakar a. Anak (child atau children) dan Orangtua (parent) Jika ada satu sisi antara dua simpul maka simpul yang lebih dekat dengan akar dinamakan orang tua sedangkan sisi yang lain dinamakan anak. Pada gambar 5.3 terlihat bahwa b, c, dan d adalah anak-anak simpul a, dan a merupakan orangtua dari anak-anak itu. Sementara itu, g dan h merupakan anak dari d, sedangkan d merupakan orang tua dari g dan h. Selanjutnya, a dinamakan leluhur (ancestor) dari e, f, g dan h. sedangkan e, f, g dan h dinamakan keturunan (descendant) dari a. Sementara itu, f adalah saudara kandung (sibling) e, tetapi, g bukan saudara kandung e, karena orangtua mereka berbeda. 22 8/29/
12 Terminologi Pohon Berakar (2) b. Lintasan (path) Lintasan dari a ke h adalah a, d, h. dengan panjang lintasannya adalah 2. Pada suatu pohon, lintasan antara dua simpul sembarang adalah unik, yaitu hanya ada satu lintasan. 23 8/29/2014 Terminologi Pohon Berakar (3) c. Subtree (Upapohon) Misalkan d adalah suatu simpul pada pohon, maka subgraf (pohon) yang terdiri dari d bersama dengan seluruh keturunannya dinamakan subtree. Pada contoh dibawah ini, yang di dalam lingkaran merupakan subtree dari pohon utamanya. 24 8/29/
13 Terminologi Pohon Berakar (4) d. Derajat (degree) Derajat sebuah simpul adalah jumlah anak pada simpul tersebut. Pada gambar sebelumnya : Simpul yang berderajat 0 adalah simpul c, e, f, g, dan h Tak ada simpul yang berderajat 1. Simpul yang berderajat 2 adalah simpul b dan d. Simpul yang berderajat 3 adalah simpul a. Jadi, derajat yang dimaksudkan di sini adalah derajatkeluar. Derajat maksimum dari semua simpul merupakan derajat pohon itu sendiri. Jadi, pohon pada gambar sebelumnya berderajat /29/2014 Terminologi Pohon Berakar (5) e. Daun (leaf) Simpul yang berderajat nol (atau tidak mempunyai anak) disebut daun. Simpul c, e, f, g dan h adalah daun. f. Simpul Dalam (internal vertex) Simpul (selain akar) yang mempunyai anak disebut simpul dalam. Simpul b dan d dinamakan simpul dalam. g. Tingkat (level) Akar mempunyai level sama dengan 0, sedangkan simpul yang lain bergantung pada posisi masing-masing. Misalkan, pada gambar sebelumnya, terlihat bahwa b, c dan d berada pada tingkat 2. Sedangkan e, f, g dan h berada pada tingkat /29/
14 Pohon Berakar (3) Pohon berakar yang urutan anak-anaknya penting (diperhatikan) maka pohon yang demikian dinamakan pohon terurut (ordered tree). Sedangkan, pohon berakar yang setiap simpul cabangnya mempunyai paling banyak n buah anak disebut pohon n-ary. Jika n = 2, pohonnnya disebut pohon biner (binary tree). 27 8/29/2014 Contoh Pohon Biner 1. Pohon Ekspresi Ekspresi aritmetika (a * b) ((c + d) / e) dapat dinyatakan dalam suatu pohon biner, dimana peubah sebagai daun dan operator aritmetika sebagai simpul dalam dan akar. 28 8/29/
15 Contoh Pohon Biner (2) 2. Pohon keputusan (Decision Tree) Suatu pohon dimana internal vertexnya berkorespondensi dengan sebuah keputusan dinamakan pohon keputusan. Salah satu kegunaan pohon keputusan adalah dalam memilah-milah kompleksitas dari berbagai jenis algoritma. 29 8/29/2014 Contoh Pohon Biner (3) 3. Kode awalan (prefix code) Kode awalan merupakan himpunan kode (salah satunya adalah kode biner) sedemikian sehingga tidak ada anggota himpunan yang merupakan awalan dari kode yang lain. Contoh : {001, 010, 011, 11} merupakan kode awalan, jika dinyatakan dalam pohon biner, yaitu : /29/
16 Contoh Pohon Biner (4) 4. Kode Hufman Pengkodean Hufman sering sekali digunakan dalam bidang kompresi data. Perhatikan tabel kode ASCII berikut ini : Jadi rangkaian bit untuk string ADABACA, dapat direpresentasikan dalam bentuk : Panjang kode dari string tersebut adalah 7 8 = 56 bit (7 byte). 31 8/29/2014 Contoh Pohon Biner (5) 4. Kode Hufman (Lanjutan) Simbol Kekerapan Peluang Kode Huffman A 4 4/7 0 B 1 1/7 10 C 1 1/7 11 D 1 1/7 110 Sehingga rangkaian bit untuk string ADABACA : atau yang semula panjangnya 56 bit cukup dituliskan dalam 11 bit. 32 8/29/
17 Penelusuran Pohon Biner Misalkan, berikut ini adalah pohon biner dimana A merupakan akar pohon biner tersebut. Sementara itu, S dan T merupakan upapohon (subtree) dari pohon biner. 33 8/29/2014 Jenis Penelusuran Pohon Biner 1. Preorder : A, S, T - kunjungi A - kunjungi S secara preorder - kunjungi T secara preorder 2. Inorder : S, A, T - kunjungi S secara inorder - kunjungi A - kunjungi T secara inorder 3. Postorder : S, T, A - kunjungi S secara postorder - kunjungi T secara postorder - kunjungi A 34 8/29/
18 Jenis Penelusuran Pohon Biner (2) Contoh : Tentukan hasil penelusuran preorder, inorder, dan postorder dari pohon di bawah ini : 35 8/29/2014 Jenis Penelusuran Pohon Biner (3) Jawab : preorder : * a b / + c d e (prefix) inorder : a * b c + d / e (infix) postorder : a b * c d + e / (postfix) 36 8/29/
19 Pewarnaan Graf Pewarnaan dari suatu graf G merupakan suatu pemetaan dari sekumpulan warna ke beberapa simpul (vertex) yang ada pada graf G sedemikian sehingga simpul yang bertetangga memiliki warna yang berbeda. Selain pewarnaan simpul, dikenal pula pewarnaan sisi pada suatu graf. Namun dalam bab ini hanya akan difokuskan pada pewarnaan simpul. Suatu graf G dikatakan berwarna n jika terdapat n warna dalam pewarnaan graf G tersebut. Banyak warna minimum yang diperlukan dalam pewarnaan suatu graf dinamakan bilangan kromatik, yang dinotasikan oleh (G) ( : dibaca chi). 37 8/29/2014 Pewarnaan Graf (2) Contoh : Bilangan kromatik suatu graf lengkap-n (Kn) adalah n. Hal ini disebabkan karena setiap simpul pada graf lengkap adalah bertetangga. Jadi (Kn) = n. Perhatikan graf lengkap dengan 5 simpul berikut ini : maka untuk mewarnai graf tersebut diperlukan 5 warna. 38 8/29/
20 Pewarnaan Graf (3) Algoritma Welch-Powell dalam pewarnaan suatu graf G dapat diilustrasikan sebagai berikut : 1. Urutkan semua simpul pada graf G berdasarkan derajat masing-masing simpul, dari besar menjadi kecil. Urutan tersebut tidak unik karena beberapa simpul mungkin mempunyai derajat yang sama. 2. Gunakan warna pertama untuk mewarnai simpul pertama dan simpul lain yang berada pada urutan sepanjang simpul tersebut tidak bertetangga dengan simpul sebelumnya. 39 8/29/2014 Pewarnaan Graf (4) 3. Berikan warna kedua untuk mewarnai simpul pada urutan tertinggi (yang belum diwarnai), lakukan seperti point sebelumnya. 4. Seperti point ketiga, dilakukan terus menerus sehingga setiap simpul pada graf tersebut menjadi berwarna semua. 5. Algoritma Welch-Powell hanya memberikan batas atas untuk bilangan kromatik. Dengan demikian, algoritma ini tidak selalu memberikan jumlah warna minimum yang diperlukan dalam pewarnaan graf. 40 8/29/
21 Pewarnaan Graf (5) Contoh : Gunakan algoritma Welch-Powell untuk pewarnaan graf berikut ini : 41 8/29/2014 Pewarnaan Graf (6) Contoh : (Lanjutan) Terlihat bahwa urutan derajat masing-masing simpul adalah sebagai berikut : a b c d e f Dengan demikian, dapat dilakukan pewarnaan sebagai berikut : Warna I untuk simpul : b, f Warna II untuk simpul : a, d, e Warna III untuk simpul : c 42 8/29/
22 Pewarnaan Graf (7) Misalkan G merupakan suatu graf, pernyataan berikut adalah ekivalen: G merupakan graf bipartite Bilangan kromatik G adalah dua ( (G) = 2 ) Setiap sirkuit dari G mempunyai panjang yang genap 43 8/29/2014 Pewarnaan Graf (7) Contoh : Perhatikan graf bipartit K3,3 : Pewarnaan pada graf tersebut dapat dilakukan dengan menggunakan dua warna, yaitu : - Warna I untuk simpul a, b, c - Warna II untuk simpul d, e, f 44 8/29/
23 Pewarnaan Graf (8) Contoh : (Lanjutan) Sementara itu, jika kita ingin membuat suatu sirkuit pada graf tersebut, maka sirkuit tersebut akan melewati 3 atau 5 simpul yang lain sebelum kembali ke simpul awal. Sehingga sirkuit tersebut memiliki panjang yang genap 45 8/29/2014 Pewarnaan Peta (Map Coloring) Sebelum membahas tentang pewarnaan daera pada suatu graf planar, perhatikan beberapa definisi yang akan disampaikan terkait dengan graf planar berikut ini: Area r1, r2, r3, r4, dan r5 dinamakan daerah (region) dari graf planar tersebut. Dua buah daerah dalam suatu graf planar dikatakan bertetangga jika mereka paling sedikit mempunyai sebuah sisi bersama. 46 8/29/
24 Pewarnaan Peta (Map Coloring) (2) Contoh daerah yang bertetangga adalah : - r1 dan r2 - r2 dan r3 - r2 dan r5 - r4 dan r5 - r1 dan r5 - r2 dan r4 47 8/29/2014 Pewarnaan Peta (Map Coloring) (3) Sementara itu, contoh daerah yang tidak bertetangga adalah : r1 dan r4 r5 dan r3 r3 dan r4 Jumlah daerah yang bertetangga dengan suatu daerah pada suatu graf dieroleh dengan cara menghitung jumlah daerah yang palig sedikit mempunyai satu sisi bersama dengan daerah tersebut. 48 8/29/
25 Pewarnaan Peta (Map Coloring) (4) Dengan demikian, masing-masing daerah pada graf tersebut mempunyai daerah tetangga sebagai berikut: r1 mempunyai 2 daerah tetangga yaitu r2 dan r5 r2 mempunyai 3 daerah tetangga yaitu r1, r3 dan r5 r3 mempunyai 1 daerah tetangga yaitu r2 r4 mempunyai 2 daerah tetangga yaitu r2 dan r5 r5 mempunyai 3 daerah tetangga yaitu r1, r2 dan r4 Pewarnaan daerah (peta) pada suatu graf planar G merupakan pemetaan sekumpulan warna ke beberapa daerah yang berada pada graf planar tersebut sedemikian sehingga daerah yang bertetangga tidak memiliki warna yang sama. 49 8/29/2014 Pewarnaan Peta (Map Coloring) (5) Contoh : Perhatikan graf planar berikut ini : Lakukan pewarnaan daerah dengan menggunakan : a. 3 warna b. 2 warna 50 8/29/
26 Pewarnaan Peta (Map Coloring) (5) Jawab : a. Pewarnaan graf dengan 3 warna : Warna I untuk daerah r1 dan r4 Warna II untuk daerah r2 Warna III untuk daerah r3 dan r5 b. Pewarnaan graf dengan 2 warna, tidak mungkin dapat dilakukan. Hal ini disebabkan karena daerah r2, r4 dan r5 bertetangga satu sama lain, sehingga harus diberikan warna yang berbeda. 51 8/29/2014 Pewarnaan Peta (Map Coloring) (6) Dual dari pewarnaan peta adalah berupa pewarnaan simpul dari suatu graf planar. Perhatikan bahwa suatu pewarnaan pada graf G akan menghubungkan ke suatu pewarnaan simpul dari dual G*. Dengan kata lain, sebuah peta G adalah berwarna n jika dan hanya jika graf planar dari dual G* dengan warna n. Agar kebih jelas, perhatikan contoh graf berikut : 52 8/29/
27 Pewarnaan Peta (Map Coloring) (7) Pilih sebuah simpul dalam setiap daerah pada graf tersebut, hubungkan dua simpul tersebut dengan suatu sisi jika dua daerah tersebut saling bertetangga. 53 8/29/2014 Pewarnaan Peta (Map Coloring) (8) Jika kita gambarkan graf yang terbentuk maka diperoleh graf sebagai berikut : Jadi, pewarnaan peta dapat direpresentasikan dalam pewarnaan simpul. Yang lebih penting dalam pewarnaan ini adalah model graf yang diberikan merupakan representasi dari permasalahan nyata. 54 8/29/
28 Rangkuman Suatu graf terhubung yang setiap pasangan simpulnya hanya dapat dihubungkan oleh satu lintasan tertentu, maka graf tersebut dinamakan pohon (tree). Dengan kata lain, pohon merupakan graf takberarah yang terhubung dan tidak memiliki siklus maupun sirkuit. Spanning Tree dari suatu graf terhubung merupakan subgraf merentang (spanning subgraph) yang berupa pohon. Pohon rentang yang memiliki bobot minimum dinamakan pohon merentang minimum (minimum spanning tree). 55 8/29/2014 Rangkuman (2) Ada beberapa terminologi pohon yang perlu diketahui, antara lain : akar, daun, subtree, lintasan terpendek, dan lain lain. Untuk menentukan minimum spanning tree terdapat dua algoritma, yaitu Prim dan Kruskal. Pewarnaan dari suatu graf G merupakan suatu pemetaan dari sekumpulan warna ke beberapa simpul (vertex) yang ada pada graf G sedemikian sehingga simpul yang bertetangga memiliki warna yang berbeda. Selain pewarnaan simpul, dikenal pula pewarnaan sisi pada suatu graf. 56 8/29/
29 Rangkuman (3) Banyak warna minimum yang diperlukan dalam pewarnaan suatu graf dinamakan bilangan kromatik, yang dinotasikan oleh ( : dibaca chi). (G) Pewarnaan peta (map) merupakan dual dari pewarnaan simpul suatu graf. 57 8/29/2014 THANK YOU 58 8/29/
Definisi. Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit. pohon pohon bukan pohon bukan pohon
 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan pohon
1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan pohon
Pohon (TREE) Matematika Deskrit. Hasanuddin Sirait, MT 1
 Pohon (TREE) Matematika Deskrit By @Ir. Hasanuddin Sirait, MT 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon
Pohon (TREE) Matematika Deskrit By @Ir. Hasanuddin Sirait, MT 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon
Matematika Diskret (Pohon) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs.
 Matematika Diskret (Pohon) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon
Matematika Diskret (Pohon) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon
DEFINISI. Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit. pohon pohon bukan pohon bukan pohon 2
 1 POHON DEFINISI Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan
1 POHON DEFINISI Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan
Pohon (Tree) Universitas Gunadarma Sistem Informasi 2012/2013
 Pohon (Tree) Universitas Gunadarma Sistem Informasi 2012/2013 Pohon (Tree) Pohon (Tree) didefinisikan sebagai graf terhubung yang tidak mengandung sirkuit. Karena merupakan graf terhubung, maka pohon selalu
Pohon (Tree) Universitas Gunadarma Sistem Informasi 2012/2013 Pohon (Tree) Pohon (Tree) didefinisikan sebagai graf terhubung yang tidak mengandung sirkuit. Karena merupakan graf terhubung, maka pohon selalu
TERAPAN POHON BINER 1
 TERAPAN POHON BINER 1 Terapan pohon biner di dalam ilmu komputer sangat banyak, diantaranya : 1. Pohon ekspresi 2. Pohon keputusan 3. Kode Prefiks 4. Kode Huffman 5. Pohon pencarian biner 2 Pohon Ekspresi
TERAPAN POHON BINER 1 Terapan pohon biner di dalam ilmu komputer sangat banyak, diantaranya : 1. Pohon ekspresi 2. Pohon keputusan 3. Kode Prefiks 4. Kode Huffman 5. Pohon pencarian biner 2 Pohon Ekspresi
Termilogi Pada Pohon Berakar 10 Pohon Berakar Terurut
 KATA PENGANTAR Puji syukur penyusun panjatkan ke hadirat Allah Subhanahu wata?ala, karena berkat rahmat-nya kami bisa menyelesaikan makalah yang berjudul Catatan Seorang Kuli Panggul. Makalah ini diajukan
KATA PENGANTAR Puji syukur penyusun panjatkan ke hadirat Allah Subhanahu wata?ala, karena berkat rahmat-nya kami bisa menyelesaikan makalah yang berjudul Catatan Seorang Kuli Panggul. Makalah ini diajukan
Pohon. Bahan Kuliah IF2120 Matematika Diskrit. Program Studi Teknik Informatika ITB. Rinaldi M/IF2120 Matdis 1
 Pohon Bahan Kuliah IF2120 Matematika Diskrit Program Studi Teknik Informatika ITB Rinaldi M/IF2120 Matdis 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a
Pohon Bahan Kuliah IF2120 Matematika Diskrit Program Studi Teknik Informatika ITB Rinaldi M/IF2120 Matdis 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a
Definisi. Pohon adalah graf tak-berarah, terhubung, dan tidak mengandung sirkuit. pohon pohon bukan pohon bukan pohon (ada sikuit) (tdk terhubung)
 POHON (TREE) Pohon Definisi Pohon adalah graf tak-berarah, terhubung, dan tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon (ada sikuit) (tdk
POHON (TREE) Pohon Definisi Pohon adalah graf tak-berarah, terhubung, dan tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon (ada sikuit) (tdk
TUGAS MAKALAH INDIVIDUAL. Mata Kuliah : Matematika Diskrit / IF2153 Nama : Dwitiyo Abhirama NIM :
 TUGAS MAKALAH INDIVIDUAL Mata Kuliah : Matematika Diskrit / IF2153 Nama : Dwitiyo Abhirama NIM : 13505013 Institut Teknologi Bandung Desember 2006 Penggunaan Struktur Pohon dalam Informatika Dwitiyo Abhirama
TUGAS MAKALAH INDIVIDUAL Mata Kuliah : Matematika Diskrit / IF2153 Nama : Dwitiyo Abhirama NIM : 13505013 Institut Teknologi Bandung Desember 2006 Penggunaan Struktur Pohon dalam Informatika Dwitiyo Abhirama
B C D E F G H I J K L M N O P Q R S T. Tinaliah, S.Kom POHON BINER
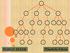 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z POHON BINER Tinaliah, S.Kom DEFINISI Pohon (dalam struktur data) struktur berisi sekumpulan elemen dimana salah satu elemen adalah akar (root) dan elemen-elemen
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z POHON BINER Tinaliah, S.Kom DEFINISI Pohon (dalam struktur data) struktur berisi sekumpulan elemen dimana salah satu elemen adalah akar (root) dan elemen-elemen
Algoritma Prim dengan Algoritma Greedy dalam Pohon Merentang Minimum
 Algoritma Prim dengan Algoritma Greedy dalam Pohon Merentang Minimum Made Mahendra Adyatman 13505015 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung
Algoritma Prim dengan Algoritma Greedy dalam Pohon Merentang Minimum Made Mahendra Adyatman 13505015 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung
BAB IV POHON. Diktat Algoritma dan Struktur Data 2
 iktat lgoritma dan Struktur ata 2 V POON efinisi Pohon Struktur pohon merupakan kumpulan elemen yang salah satu elemennya disebut akar dan sisa elemennya terpecah menjadi sejumlah himpunan yang saling
iktat lgoritma dan Struktur ata 2 V POON efinisi Pohon Struktur pohon merupakan kumpulan elemen yang salah satu elemennya disebut akar dan sisa elemennya terpecah menjadi sejumlah himpunan yang saling
P o h o n. Definisi. Oleh: Panca Mudji Rahardjo. Pohon. Adalah graf tak berarah terhubung yang tidak mengandung sirkuit.
 P o h o n Oleh: Panca Mudji Rahardjo Definisi Pohon Adalah graf tak berarah terhubung yang tidak mengandung sirkuit. Contoh: G 1 dan G 2 pohon, G 3 dan G 4 bukan pohon. 1 Definisi Hutan (forest) Adalah
P o h o n Oleh: Panca Mudji Rahardjo Definisi Pohon Adalah graf tak berarah terhubung yang tidak mengandung sirkuit. Contoh: G 1 dan G 2 pohon, G 3 dan G 4 bukan pohon. 1 Definisi Hutan (forest) Adalah
MATEMATIKA DISKRIT II ( 2 SKS)
 MATEMATIKA DISKRIT II ( 2 SKS) Rabu, 18.50 20.20 Ruang Hard Disk PERTEMUAN XI, XII RELASI Dosen Lie Jasa 1 Matematika Diskrit Graf (lanjutan) 2 Lintasan dan Sirkuit Euler Lintasan Euler ialah lintasan
MATEMATIKA DISKRIT II ( 2 SKS) Rabu, 18.50 20.20 Ruang Hard Disk PERTEMUAN XI, XII RELASI Dosen Lie Jasa 1 Matematika Diskrit Graf (lanjutan) 2 Lintasan dan Sirkuit Euler Lintasan Euler ialah lintasan
Sebuah pewarnaan dari graph G adalah sebuah pemetaan warna-warna ke simpulsimpul dari G sedemikian hingga simpul relasinya mempunyai warna warna yang
 Sebuah pewarnaan dari graph G adalah sebuah pemetaan warna-warna ke simpulsimpul dari G sedemikian hingga simpul relasinya mempunyai warna warna yang berbeda. Bilangan kromatik dari G adalah jumlah warna
Sebuah pewarnaan dari graph G adalah sebuah pemetaan warna-warna ke simpulsimpul dari G sedemikian hingga simpul relasinya mempunyai warna warna yang berbeda. Bilangan kromatik dari G adalah jumlah warna
I. LAMPIRAN TUGAS. Mata kuliah : Matematika Diskrit Program Studi : Sistem Informasi PA-31 Dosen Pengasuh : Ir. Bahder Djohan, MSc
 I. LAMPIRAN TUGAS. Mata kuliah : Matematika Diskrit Program Studi : Sistem Informasi PA- Dosen Pengasuh : Ir. Bahder Djohan, MSc Tugas ke Pertemuan TIK Soal-soal Tugas. Mendefinisikan Proposisi Membedakan
I. LAMPIRAN TUGAS. Mata kuliah : Matematika Diskrit Program Studi : Sistem Informasi PA- Dosen Pengasuh : Ir. Bahder Djohan, MSc Tugas ke Pertemuan TIK Soal-soal Tugas. Mendefinisikan Proposisi Membedakan
METODE POHON BINER HUFFMAN UNTUK KOMPRESI DATA STRING KARAKTER
 METODE POHON BINER HUFFMAN UNTUK KOMPRESI DATA STRING KARAKTER Muqtafi Akhmad (13508059) Teknik Informatika ITB Bandung e-mail: if18059@students.if.itb.ac.id ABSTRAK Dalam makalah ini akan dibahas tentang
METODE POHON BINER HUFFMAN UNTUK KOMPRESI DATA STRING KARAKTER Muqtafi Akhmad (13508059) Teknik Informatika ITB Bandung e-mail: if18059@students.if.itb.ac.id ABSTRAK Dalam makalah ini akan dibahas tentang
Pemanfaatan Pohon Biner dalam Pencarian Nama Pengguna pada Situs Jejaring Sosial
 Pemanfaatan Pohon Biner dalam Pencarian Nama Pengguna pada Situs Jejaring Sosial Stephen (35225) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Pemanfaatan Pohon Biner dalam Pencarian Nama Pengguna pada Situs Jejaring Sosial Stephen (35225) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Gambar 6. Graf lengkap K n
 . Jenis-jenis Graf Tertentu Ada beberapa graf khusus yang sering dijumpai. Beberapa diantaranya adalah sebagai berikut. a. Graf Lengkap (Graf Komplit) Graf lengkap ialah graf sederhana yang setiap titiknya
. Jenis-jenis Graf Tertentu Ada beberapa graf khusus yang sering dijumpai. Beberapa diantaranya adalah sebagai berikut. a. Graf Lengkap (Graf Komplit) Graf lengkap ialah graf sederhana yang setiap titiknya
Teori Pohon. Begin at the beginning and go on /ll you come to the end: then stop. Lewis Caroll, Alice s Adventures in Wonderland, 1865
 Teori Pohon Begin at the beginning and go on /ll you come to the end: then stop. Lewis Caroll, Alice s Adventures in Wonderland, 1865 1 Pohon Suatu graf tak berarah terhubung yang Hdak memiliki sirkuit
Teori Pohon Begin at the beginning and go on /ll you come to the end: then stop. Lewis Caroll, Alice s Adventures in Wonderland, 1865 1 Pohon Suatu graf tak berarah terhubung yang Hdak memiliki sirkuit
BAB I PENDAHULUAN. himpunan bagian bilangan cacah yang disebut label. Pertama kali diperkenalkan
 1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
PENGETAHUAN DASAR TEORI GRAF
 PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
PENGETAHUAN DASAR TEORI GRAF 1 Sejarah Singkat dan Beberapa Pengertian Dasar Teori Graf Teori graf lahir pada tahun 1736 melalui makalah tulisan Leonard Euler seorang ahli matematika dari Swiss. Euler
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
BAB II TINJAUAN PUSTAKA 2.1 Graf (Graph) Graf G didefinisikan sebagai pasangan himpunan (V, E) yang dinotasikan dalam bentuk G = {V(G), E(G)}, dimana V(G) adalah himpunan vertex (simpul) yang tidak kosong
RENCANA PEMBELAJARAN SEMESTER (RPS)
 RENCANA PEMBELAJARAN SEMESTER (RPS) MUG2A3 Matematika Diskrit Disusun oleh: Dede Tarwidi, M.Si., M.Sc. PROGRAM STUDI S1 ILMU KOMPUTASI FAKULTAS INFORMATIKA TELKOM UNIVERSITY LEMBAR PENGESAHAN Rencana Pembelajaran
RENCANA PEMBELAJARAN SEMESTER (RPS) MUG2A3 Matematika Diskrit Disusun oleh: Dede Tarwidi, M.Si., M.Sc. PROGRAM STUDI S1 ILMU KOMPUTASI FAKULTAS INFORMATIKA TELKOM UNIVERSITY LEMBAR PENGESAHAN Rencana Pembelajaran
RENCANA PEMBELAJARAN SEMESTER (RPS)
 RENCANA PEMBELAJARAN SEMESTER (RPS) MUG2A3 MATEMATIKA DISKRET Disusun oleh: Tim Dosen Matematika Diskret PROGRAM STUDI S1 TEKNIK INFORMATIKA FAKULTAS INFORMATIKA TELKOM UNIVERSITY LEMBAR PENGESAHAN Rencana
RENCANA PEMBELAJARAN SEMESTER (RPS) MUG2A3 MATEMATIKA DISKRET Disusun oleh: Tim Dosen Matematika Diskret PROGRAM STUDI S1 TEKNIK INFORMATIKA FAKULTAS INFORMATIKA TELKOM UNIVERSITY LEMBAR PENGESAHAN Rencana
BAB VII POHON BINAR POHON
 BAB VII POHON BINAR POHON Pohon atau tree adalah salah satu bentuk graph terhubung yang tidak mengandung sirkuit. Karena merupakan graph terhubung, maka pada pohon selalu terdapat path atau jalur yang
BAB VII POHON BINAR POHON Pohon atau tree adalah salah satu bentuk graph terhubung yang tidak mengandung sirkuit. Karena merupakan graph terhubung, maka pada pohon selalu terdapat path atau jalur yang
 BAB 2. LANDASAN TEORI 2.1. Algoritma Huffman Algortima Huffman adalah algoritma yang dikembangkan oleh David A. Huffman pada jurnal yang ditulisnya sebagai prasyarat kelulusannya di MIT. Konsep dasar dari
BAB 2. LANDASAN TEORI 2.1. Algoritma Huffman Algortima Huffman adalah algoritma yang dikembangkan oleh David A. Huffman pada jurnal yang ditulisnya sebagai prasyarat kelulusannya di MIT. Konsep dasar dari
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
BAB 2 LANDASAN TEORI 2.1 Teori Graf 2.1.1 Defenisi Graf Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya
Pertemuan 9 STRUKTUR POHON & KUNJUNGAN POHON BINER
 Pertemuan 9 STRUKTUR POHON & KUNJUNGAN POHON BINER DEFINISI POHON (TREE) Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang
Pertemuan 9 STRUKTUR POHON & KUNJUNGAN POHON BINER DEFINISI POHON (TREE) Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang
Aplikasi Pohon pada Pohon Binatang (Animal Tree)
 Aplikasi Pohon pada Pohon Binatang (Animal Tree) Cilvia Sianora Putri (13512027) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Aplikasi Pohon pada Pohon Binatang (Animal Tree) Cilvia Sianora Putri (13512027) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Implementasi Skema Pohon Biner yang Persistent dalam Pemrograman Fungsional
 Implementasi Skema Pohon Biner yang Persistent dalam Pemrograman Fungsional Azby Khilfi M. NIM : 13506018 Sekolah Teknik Elektro dan Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail
Implementasi Skema Pohon Biner yang Persistent dalam Pemrograman Fungsional Azby Khilfi M. NIM : 13506018 Sekolah Teknik Elektro dan Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail
Kode MK/ Matematika Diskrit
 Kode MK/ Matematika Diskrit TEORI GRAF 1 8/29/2014 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 2 8/29/2014 1 TEORI GRAF Tujuan Mahasiswa memahami konsep
Kode MK/ Matematika Diskrit TEORI GRAF 1 8/29/2014 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 2 8/29/2014 1 TEORI GRAF Tujuan Mahasiswa memahami konsep
Kompleksitas Algoritma dari Algoritma Pembentukan pohon Huffman Code Sederhana
 Kompleksitas Algoritma dari Algoritma Pembentukan pohon Huffman Code Sederhana Muhammad Fiqri Muthohar NIM : 13506084 1) 1) Jurusan Teknik Informatika ITB, Bandung, email: fiqri@arc.itb.ac.id Abstrak makalah
Kompleksitas Algoritma dari Algoritma Pembentukan pohon Huffman Code Sederhana Muhammad Fiqri Muthohar NIM : 13506084 1) 1) Jurusan Teknik Informatika ITB, Bandung, email: fiqri@arc.itb.ac.id Abstrak makalah
STRUKTUR POHON & KUNJUNGAN POHON BINER
 STRUKTUR POHON & KUNJUNGAN POHON BINER Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang saling terkait Istilah istilah Dalam
STRUKTUR POHON & KUNJUNGAN POHON BINER Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang saling terkait Istilah istilah Dalam
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM
 ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
Aplikasi Pohon dan Graf dalam Kaderisasi
 Aplikasi Pohon dan Graf dalam Kaderisasi Jonathan - 13512031 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Aplikasi Pohon dan Graf dalam Kaderisasi Jonathan - 13512031 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Penggunaan Pohon Biner Sebagai Struktur Data untuk Pencarian
 Penggunaan Pohon Biner Sebagai Struktur Data untuk Pencarian Rita Wijaya/13509098 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Penggunaan Pohon Biner Sebagai Struktur Data untuk Pencarian Rita Wijaya/13509098 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
BAB VII Tujuan 7.1 Deskripsi dari Binary Tree
 A VII Tree Tujuan 1. Mempelajari variasi bagian-bagian dari tree sebagai suatu bentuk struktur tak linier 2. Mempelajari beberapa hubungan fakta yang direpresentasikan dalam sebuah tree, sehingga mampu
A VII Tree Tujuan 1. Mempelajari variasi bagian-bagian dari tree sebagai suatu bentuk struktur tak linier 2. Mempelajari beberapa hubungan fakta yang direpresentasikan dalam sebuah tree, sehingga mampu
Soal dan Jawaban Materi Graf, Pohon, dan Kompleksitas Algoritma
 Soal dan Jawaban Materi Graf, Pohon, dan Kompleksitas Algoritma POHON 1. Ubahlah graf berikut ini dengan menggunakan algoritma prim agar menjadi pohon merentang minimum dan tentukan bobot nya! 2. Diberikan
Soal dan Jawaban Materi Graf, Pohon, dan Kompleksitas Algoritma POHON 1. Ubahlah graf berikut ini dengan menggunakan algoritma prim agar menjadi pohon merentang minimum dan tentukan bobot nya! 2. Diberikan
Pohon (Tree) Contoh :
 POHON (TREE) Pohon (Tree) didefinisikan sebagai graph terhubung yang tidak mengandung sirkuit. Sedangkan Hutan (Forest) adalah graph yang tidak mengandung sirkuit. Jadi pohon adalah hutan yang terhubung.
POHON (TREE) Pohon (Tree) didefinisikan sebagai graph terhubung yang tidak mengandung sirkuit. Sedangkan Hutan (Forest) adalah graph yang tidak mengandung sirkuit. Jadi pohon adalah hutan yang terhubung.
TINJAUAN PUSTAKA. Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada
 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
Variasi Pohon Pencarian Biner Seimbang
 Variasi Pohon Pencarian Biner Seimbang Tony 13516010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia buddy90_lost@yahoo.co.id
Variasi Pohon Pencarian Biner Seimbang Tony 13516010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia buddy90_lost@yahoo.co.id
Ringkasan mengenai Tree (Dari beberapa referensi lain) Nina Valentika
 Ringkasan mengenai Tree (Dari beberapa referensi lain) Nina Valentika December 31, 2015 0.1 Pendahuluan Figure 1: Contoh Tree. Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan
Ringkasan mengenai Tree (Dari beberapa referensi lain) Nina Valentika December 31, 2015 0.1 Pendahuluan Figure 1: Contoh Tree. Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
BAB 2 LANDASAN TEORI 2.1 Konsep Dasar Graf Definisi 2.1.1 Sebuah graf didefinisikan sebagai pasangan terurut himpunan dimana: 1. adalah sebuah himpunan tidak kosong yang berhingga yang anggotaanggotanya
Aplikasi Pohon Keputusan dalam Pemilihan Penerima Beasiswa UKT
 Aplikasi Pohon Keputusan dalam Pemilihan Penerima Beasiswa UKT Renjira Naufhal Dhiaegana 135160141 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Aplikasi Pohon Keputusan dalam Pemilihan Penerima Beasiswa UKT Renjira Naufhal Dhiaegana 135160141 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Penyandian (Encoding) dan Penguraian Sandi (Decoding) Menggunakan Huffman Coding
 Penyandian (Encoding) dan Penguraian Sandi (Decoding) Menggunakan Huffman Coding Nama : Irwan Kurniawan NIM : 135 06 090 1) Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10,
Penyandian (Encoding) dan Penguraian Sandi (Decoding) Menggunakan Huffman Coding Nama : Irwan Kurniawan NIM : 135 06 090 1) Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10,
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU. Oleh: Kartika Yulianti, S.Pd., M.Si.
 HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
HAND OUT MATA KULIAH TEORI GRAF (MT 424) JILID SATU Oleh: Kartika Yulianti, S.Pd., M.Si. JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS PENDIDIKAN MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS PENDIDIKAN INDONESIA
BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP
 Jurnal Matematika UNAND Vol. VI No. 1 Hal. 90 96 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP AFIFAH DWI PUTRI, NARWEN Program Studi Matematika,
Jurnal Matematika UNAND Vol. VI No. 1 Hal. 90 96 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND BILANGAN KROMATIK LOKASI UNTUK GRAF POHON n-ary LENGKAP AFIFAH DWI PUTRI, NARWEN Program Studi Matematika,
Penerapan Pohon Biner dalam Proses Pengamanan Peer to Peer
 Penerapan Pohon Biner dalam Proses Pengamanan Peer to Peer Eka Yusrianto Toisutta - NIM : 13504116 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganesha 10, Bandung email: if14116@students.if.itb.ac.id
Penerapan Pohon Biner dalam Proses Pengamanan Peer to Peer Eka Yusrianto Toisutta - NIM : 13504116 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganesha 10, Bandung email: if14116@students.if.itb.ac.id
APLIKASI PEWARNAAN SIMPUL GRAF UNTUK MENGATASI KONFLIK PENJADWALAN MATA KULIAH DI FMIPA UNY
 APLIKASI PEWARNAAN SIMPUL GRAF UNTUK MENGATASI KONFLIK PENJADWALAN MATA KULIAH DI FMIPA UNY Latar belakang Masalah Pada setiap awal semester bagian pendidikan fakultas Matematika dan Ilmu Pengetahuan Universitas
APLIKASI PEWARNAAN SIMPUL GRAF UNTUK MENGATASI KONFLIK PENJADWALAN MATA KULIAH DI FMIPA UNY Latar belakang Masalah Pada setiap awal semester bagian pendidikan fakultas Matematika dan Ilmu Pengetahuan Universitas
I. PENDAHULUAN. Gambar 1. Contoh-contoh graf
 Quad Tree dan Contoh-Contoh Penerapannya Muhammad Reza Mandala Putra - 13509003 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan Ganesha 10 Bandung
Quad Tree dan Contoh-Contoh Penerapannya Muhammad Reza Mandala Putra - 13509003 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan Ganesha 10 Bandung
PEMAMPATAN DATA DENGAN KODE HUFFMAN (APLIKASI POHON BINER)
 PEAPATAN DATA DENGAN KODE HUFFAN (APLIKASI POHON BINER) Winda Winanti (350507) Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 0, Bandung E-mail : if507@students.if.itb.ac.id Abstraksi
PEAPATAN DATA DENGAN KODE HUFFAN (APLIKASI POHON BINER) Winda Winanti (350507) Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 0, Bandung E-mail : if507@students.if.itb.ac.id Abstraksi
Mata Kuliah : Matematika Diskrit Program Studi : Teknik Informatika Minggu ke : 8
 POHON / TREE Dalam dunia informatika, pohon memegang peranan penting bagi seorang programmer untuk menggambarkan hasil karyanya. Bagi seorang user, setiap kali berhadapan dengan monitor untuk menjalankan
POHON / TREE Dalam dunia informatika, pohon memegang peranan penting bagi seorang programmer untuk menggambarkan hasil karyanya. Bagi seorang user, setiap kali berhadapan dengan monitor untuk menjalankan
LANDASAN TEORI. Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan. kromatik lokasi sebagai landasan teori pada penelitian ini.
 6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
6 II. LANDASAN TEORI Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada sub bab ini akan diberikan
Pohon dan Aplikasinya dalam Bagan Silsilah Keturunan
 Pohon dan Aplikasinya dalam Bagan Silsilah Keturunan Edmund Ophie 13512095 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Pohon dan Aplikasinya dalam Bagan Silsilah Keturunan Edmund Ophie 13512095 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI.. Definisi Graf Secara matematis, graf G didefinisikan sebagai pasangan himpunan (V,E) ditulis dengan notasi G = (V, E), yang dalam hal ini: V = himpunan tidak-kosong dari simpul-simpul
BAB II LANDASAN TEORI.. Definisi Graf Secara matematis, graf G didefinisikan sebagai pasangan himpunan (V,E) ditulis dengan notasi G = (V, E), yang dalam hal ini: V = himpunan tidak-kosong dari simpul-simpul
Kata Pengantar... Daftar Isi... Apakah Matematika Diskrit Itu? Logika... 1
 Daftar Isi Kata Pengantar... Daftar Isi... Apakah Matematika Diskrit Itu?... iii v xi 1. Logika... 1 1.1 Proposisi... 2 1.2 Mengkombinasikan Proposisi... 4 1.3 Tabel kebenaran... 6 1.4 Disjungsi Eksklusif...
Daftar Isi Kata Pengantar... Daftar Isi... Apakah Matematika Diskrit Itu?... iii v xi 1. Logika... 1 1.1 Proposisi... 2 1.2 Mengkombinasikan Proposisi... 4 1.3 Tabel kebenaran... 6 1.4 Disjungsi Eksklusif...
Penggunaan Algoritma Greedy dalam Membangun Pohon Merentang Minimum
 Penggunaan Algoritma Greedy dalam Membangun Pohon Merentang Minimum Gerard Edwin Theodorus - 13507079 Jurusan Teknik Informatika ITB, Bandung, email: if17079@students.if.itb.ac.id Abstract Makalah ini
Penggunaan Algoritma Greedy dalam Membangun Pohon Merentang Minimum Gerard Edwin Theodorus - 13507079 Jurusan Teknik Informatika ITB, Bandung, email: if17079@students.if.itb.ac.id Abstract Makalah ini
Tree. Perhatikan pula contoh tree di bawah ini : Level. Level 2. Level 3. Level 4. Level 5
 TR (POHON) Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan terutama untuk merepresentasikan hubungan data yang bersifat hierarkis antara elemenelemennya. efinisi tree : Kumpulan
TR (POHON) Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan terutama untuk merepresentasikan hubungan data yang bersifat hierarkis antara elemenelemennya. efinisi tree : Kumpulan
ALGORITMA DAN STRUKTUR DATA
 Modul ke: 10 Fitrianingsih Fakultas FASILKOM ALGORITMA DAN STRUKTUR DATA JENIS-JENIS TREE SKom., MMSI Program Studi Sistem Informasi JENIS-JENIS TREE Pohon (Tree) adalah graf terhubung yang tidak mengandung
Modul ke: 10 Fitrianingsih Fakultas FASILKOM ALGORITMA DAN STRUKTUR DATA JENIS-JENIS TREE SKom., MMSI Program Studi Sistem Informasi JENIS-JENIS TREE Pohon (Tree) adalah graf terhubung yang tidak mengandung
TEORI GRAF UNIVERSITAS MUHAMMADIYAH JEMBER ILHAM SAIFUDIN PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK. Selasa, 13 Desember 2016
 PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS MUHAMMADIYAH JEMBER TEORI GRAF ILHAM SAIFUDIN Selasa, 13 Desember 2016 Universitas Muhammadiyah Jember Pendahuluan 1 OUTLINE 2 Definisi Graf
PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS MUHAMMADIYAH JEMBER TEORI GRAF ILHAM SAIFUDIN Selasa, 13 Desember 2016 Universitas Muhammadiyah Jember Pendahuluan 1 OUTLINE 2 Definisi Graf
SATUAN ACARA PERKULIAHAN MATA KULIAH LOGIKA DAN ALGORITMA (MI/D3) KODE: IT SKS: 3 SKS. Kemampuan Akhir Yang Diharapkan
 SATUAN ACARA PERKULIAHAN MATA KULIAH LOGIKA DAN ALGORITMA (MI/D3) KODE: IT013323 SKS: 3 SKS Pertemuan Ke Pokok Bahasan dan TIU Sub Pokok Bahasan dan Sasaran Belajar Kean Akhir Yang Diharapkan Strategi
SATUAN ACARA PERKULIAHAN MATA KULIAH LOGIKA DAN ALGORITMA (MI/D3) KODE: IT013323 SKS: 3 SKS Pertemuan Ke Pokok Bahasan dan TIU Sub Pokok Bahasan dan Sasaran Belajar Kean Akhir Yang Diharapkan Strategi
Studi Algoritma Optimasi dalam Graf Berbobot
 Studi Algoritma Optimasi dalam Graf Berbobot Vandy Putrandika NIM : 13505001 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : if15001@students.if.itb.ac.id
Studi Algoritma Optimasi dalam Graf Berbobot Vandy Putrandika NIM : 13505001 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : if15001@students.if.itb.ac.id
Tenia Wahyuningrum, S.Kom. MT Sisilia Thya Safitri, S.T.,M.T.
 tree Tenia Wahyuningrum, S.Kom. MT Sisilia Thya Safitri, S.T.,M.T Tree Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Tree merepresentasikan
tree Tenia Wahyuningrum, S.Kom. MT Sisilia Thya Safitri, S.T.,M.T Tree Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Tree merepresentasikan
KONSEP DASAR GRAF DAN GRAF POHON. Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf
 II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
II. KONSEP DASAR GRAF DAN GRAF POHON Pada bab ini akan dijabarkan teori graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori pada penelitian ini. 2.1 Konsep Dasar Graf Pada bagian ini
Penerapan strategi runut-balik dalam penyelesaian permainan puzzle geser
 Penerapan strategi runut-balik dalam penyelesaian permainan puzzle geser Dimas Angga 13510046 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penerapan strategi runut-balik dalam penyelesaian permainan puzzle geser Dimas Angga 13510046 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
RENCANA PEMBELAJARAN SEMESTER (Kelas Teori)
 RENCANA PEMBELAJARAN SEMESTER (Kelas Teori) Fakultas : Teknik Industri Jurusan : Teknik Informatika Mata Kuliah & Kode : Matematika Diskrit SKS : Teori : 3 Praktik : - Semester & Waktu : Sem : 1 Waktu
RENCANA PEMBELAJARAN SEMESTER (Kelas Teori) Fakultas : Teknik Industri Jurusan : Teknik Informatika Mata Kuliah & Kode : Matematika Diskrit SKS : Teori : 3 Praktik : - Semester & Waktu : Sem : 1 Waktu
Penggunaan Pohon Huffman Sebagai Sarana Kompresi Lossless Data
 Penggunaan Pohon Huffman Sebagai Sarana Kompresi Lossless Data Aditya Rizkiadi Chernadi - 13506049 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Penggunaan Pohon Huffman Sebagai Sarana Kompresi Lossless Data Aditya Rizkiadi Chernadi - 13506049 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
SILABUS MATA KULIAH MATEMATIKA DISKRIT
 Kode Formulir : FM-STMIK MDP-KUL-04.02/R3 SILABUS MATA KULIAH MATEMATIKA DISKRIT A. IDENTITAS MATA KULIAH Program Studi : Sistem Informasi Mata Kuliah : Matematika Diskrit Kode : SP 245 Bobot : 4 (empat)
Kode Formulir : FM-STMIK MDP-KUL-04.02/R3 SILABUS MATA KULIAH MATEMATIKA DISKRIT A. IDENTITAS MATA KULIAH Program Studi : Sistem Informasi Mata Kuliah : Matematika Diskrit Kode : SP 245 Bobot : 4 (empat)
RENCANA PEMBELAJARAN SEMESTER PROGRAM STUDI TEKNIK ELEKTRO FAKULTAS TEKNIK ELEKRO TELKOM UNIVERSITY
 RENCANA PEMBELAJARAN SEMESTER PROGRAM STUDI TEKNIK ELEKTRO FAKULTAS TEKNIK ELEKRO TELKOM UNIVERSITY MATA KULIAH KODE RUMPUN MK BOBOT (SKS) SEMESTER DIREVISI Matematika Diskrit FEH2J3 3 sks 3 atau 4 22
RENCANA PEMBELAJARAN SEMESTER PROGRAM STUDI TEKNIK ELEKTRO FAKULTAS TEKNIK ELEKRO TELKOM UNIVERSITY MATA KULIAH KODE RUMPUN MK BOBOT (SKS) SEMESTER DIREVISI Matematika Diskrit FEH2J3 3 sks 3 atau 4 22
LOGIKA DAN ALGORITMA
 LOGIKA DAN ALGORITMA DASAR DASAR TEORI GRAF Kelahiran Teori Graf Sejarah Graf : masalah jembatan Königsberg (tahun 736) C A D B Gbr. Masalah Jembatan Königsberg Graf yang merepresentasikan jembatan Königsberg
LOGIKA DAN ALGORITMA DASAR DASAR TEORI GRAF Kelahiran Teori Graf Sejarah Graf : masalah jembatan Königsberg (tahun 736) C A D B Gbr. Masalah Jembatan Königsberg Graf yang merepresentasikan jembatan Königsberg
BAB VI PEWARNAAN GRAF.. Gambar 1 memperlihatkan sebuah graf, dengan χ ( G) = 3.
 112 BAB VI PEWARNAAN GRAF 6.1. Pendahuluan Ada tiga macam pewarnaan graf, yaitu pewarnaan simpul, pewarnaan sisi, dan pewarnaan wilayah (region). Yang akan kita bahas adalah pewarnaan simpul dan pewarnaan
112 BAB VI PEWARNAAN GRAF 6.1. Pendahuluan Ada tiga macam pewarnaan graf, yaitu pewarnaan simpul, pewarnaan sisi, dan pewarnaan wilayah (region). Yang akan kita bahas adalah pewarnaan simpul dan pewarnaan
Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem
 Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem Arie Tando (13510018) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem Arie Tando (13510018) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
6. TREE / BINARY TREE
 6. TREE / BINARY TREE TUJUAN PRAKTIKUM 1. Praktikan mengenal Struktur data Tree. 2. Praktikan mengenal jenis-jenis tree, seperti binary tree. 3. Praktikan mengenal istilah-istilah yang terdapat didalam
6. TREE / BINARY TREE TUJUAN PRAKTIKUM 1. Praktikan mengenal Struktur data Tree. 2. Praktikan mengenal jenis-jenis tree, seperti binary tree. 3. Praktikan mengenal istilah-istilah yang terdapat didalam
PEWARNAAN GRAF SEBAGAI METODE PENJADWALAN KEGIATAN PERKULIAHAN
 PEWARNAAN GRAF SEBAGAI METODE PENJADWALAN KEGIATAN PERKULIAHAN Eric Cahya Lesmana - 13508097 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesa
PEWARNAAN GRAF SEBAGAI METODE PENJADWALAN KEGIATAN PERKULIAHAN Eric Cahya Lesmana - 13508097 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesa
Pertemuan 15 REVIEW & QUIS
 Pertemuan 15 REVIEW & QUIS 1. Simpul Khusus pada pohon yang memiliki derajat keluar >= 0, dan derajat masuk = 0, adalah. a. Node / simpul d. edge / ruas b. Root / akar e. level c. Leaf / daun 2. Jika suatu
Pertemuan 15 REVIEW & QUIS 1. Simpul Khusus pada pohon yang memiliki derajat keluar >= 0, dan derajat masuk = 0, adalah. a. Node / simpul d. edge / ruas b. Root / akar e. level c. Leaf / daun 2. Jika suatu
Aplikasi Pohon dalam Pengambilan Keputusan oleh Sebuah Perusahaan
 Aplikasi Pohon dalam Pengambilan Keputusan oleh Sebuah Perusahaan Ahmad Aidin (13513020) Program Sarjana Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Aplikasi Pohon dalam Pengambilan Keputusan oleh Sebuah Perusahaan Ahmad Aidin (13513020) Program Sarjana Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Algoritma Brute-Force dan Greedy dalam Pemrosesan Graf
 Algoritma Brute-Force dan Greedy dalam Pemrosesan Graf Marvin Jerremy Budiman / 13515076 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Algoritma Brute-Force dan Greedy dalam Pemrosesan Graf Marvin Jerremy Budiman / 13515076 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
TINJAUAN PUSTAKA. Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi
 II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
PERBANDINGAN ALGORTIMA PRIM DAN KRUSKAL DALAM MENENTUKAN POHON RENTANG MINIMUM
 PERBANDINGAN ALGORTIMA PRIM DAN KRUSKAL DALAM MENENTUKAN POHON RENTANG MINIMUM Kodirun 1 1 Jurusan Matematika FMIPA Universitas Haluoleo, Kendari e-mail: kodirun_zuhry@yahoo.com Abstrak Masalah yang sering
PERBANDINGAN ALGORTIMA PRIM DAN KRUSKAL DALAM MENENTUKAN POHON RENTANG MINIMUM Kodirun 1 1 Jurusan Matematika FMIPA Universitas Haluoleo, Kendari e-mail: kodirun_zuhry@yahoo.com Abstrak Masalah yang sering
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM
 ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
ANALISIS JARINGAN LISTRIK DI PERUMAHAN JEMBER PERMAI DENGAN MENGGUNAKAN ALGORITMA PRIM SKRIPSI diajukan guna melengkapi tugas akhir dan memenuhi salah satu syarat untuk menyelesaikan Program Studi Pendidikan
Penerapan Pewarnaan Graf pada Permainan Real- Time Strategy
 Penerapan Pewarnaan Graf pada Permainan Real- Time Strategy Kurniandha Sukma Yunastrian / 13516106 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Penerapan Pewarnaan Graf pada Permainan Real- Time Strategy Kurniandha Sukma Yunastrian / 13516106 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Teori Dasar Graf (Lanjutan)
 Teori Dasar Graf (Lanjutan) MATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. Matriks-matriks yang dapat menyajikan
Teori Dasar Graf (Lanjutan) MATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. Matriks-matriks yang dapat menyajikan
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Graf adalah salah satu metode yang sering digunakan untuk mencari solusi dari permasalahan diskrit dalam dunia nyata. Dalam kehidupan sehari-hari, graf digunakan untuk
BAB 1 PENDAHULUAN 1.1 Latar Belakang Graf adalah salah satu metode yang sering digunakan untuk mencari solusi dari permasalahan diskrit dalam dunia nyata. Dalam kehidupan sehari-hari, graf digunakan untuk
BAB II TINJAUAN PUSTAKA. kromatik lokasi sebagai landasan teori dari penelitian ini.
 BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
BAB II TINJAUAN PUSTAKA Pada bab ini akan diberikan beberapa konsep dasar teori graf dan bilangan kromatik lokasi sebagai landasan teori dari penelitian ini. 2.1 Konsep Dasar Graf Beberapa konsep dasar
SATUAN ACARA PERKULIAHAN MATA KULIAH GRAPH & ANALISIS ALGORITMA (SI / S1) KODE / SKS : KK / 3 SKS
 Pertemuan ke Pokok Bahasan dan TIU Sub Pokok Bahasan dan TIK 1 Pendahuluan Penjelasan mengenai ruang lingkup mata kuliah, sasaran, tujuan dan kompetensi lulusan 2 1. Dasar-dasar 1.1. Kelahiran Teori Graph
Pertemuan ke Pokok Bahasan dan TIU Sub Pokok Bahasan dan TIK 1 Pendahuluan Penjelasan mengenai ruang lingkup mata kuliah, sasaran, tujuan dan kompetensi lulusan 2 1. Dasar-dasar 1.1. Kelahiran Teori Graph
- Tree Adalah graph tak berarah yang terhubung dan tidak memuat cycle. Suatu Tree paling sedikit mengandung satu vertex. Contoh :
 Kuliah 5, 6 MODUL 3 - Tree Adalah graph tak berarah yang terhubung dan tidak memuat cycle. Suatu Tree paling sedikit mengandung satu vertex. Contoh : Tree dgn vertex (a) Tree dgn vertex (b) Tree dgn 3
Kuliah 5, 6 MODUL 3 - Tree Adalah graph tak berarah yang terhubung dan tidak memuat cycle. Suatu Tree paling sedikit mengandung satu vertex. Contoh : Tree dgn vertex (a) Tree dgn vertex (b) Tree dgn 3
BAB III KONSEP DASAR TEORI GRAF. Teori graf adalah salah satu cabang matematika yang terus berkembang
 BAB III KONSEP DASAR TEORI GRAF Teori graf adalah salah satu cabang matematika yang terus berkembang dengan pesat. Teori ini sangat berguna untuk mengembangkan model-model terstruktur dalam berbagai keadaan.
BAB III KONSEP DASAR TEORI GRAF Teori graf adalah salah satu cabang matematika yang terus berkembang dengan pesat. Teori ini sangat berguna untuk mengembangkan model-model terstruktur dalam berbagai keadaan.
Graf untuk soal nomor 7
 Program Studi Teknik Informatika Nama : Sekolah Teknik Elektro dan Informatika NIM : Institut Teknologi Bandung T.tangan: Solusi Kuis ke-4 IF2120 Matematika Diskrit (3 SKS) Graf, Pohon, dan Kompleksitas
Program Studi Teknik Informatika Nama : Sekolah Teknik Elektro dan Informatika NIM : Institut Teknologi Bandung T.tangan: Solusi Kuis ke-4 IF2120 Matematika Diskrit (3 SKS) Graf, Pohon, dan Kompleksitas
Penerapan Pohon dan Himpunan dalam Klasifikasi Bahasa
 Penerapan Pohon dan Himpunan dalam Klasifikasi Bahasa Jeremia Jason Lasiman - 13514021 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penerapan Pohon dan Himpunan dalam Klasifikasi Bahasa Jeremia Jason Lasiman - 13514021 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
BAB II KAJIAN PUSTAKA
 BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
BAB II KAJIAN PUSTAKA A. Logika Fuzzy Logika fuzzy pertama kali dikembangkan oleh Prof. Lotfi A. Zadeh, seorang peneliti dari Universitas California, pada tahun 1960-an. Logika fuzzy dikembangkan dari
Pohon. Modul 4 PENDAHULUAN. alam modul-modul sebelumnya Anda telah mempelajari graph terhubung tanpa sikel, misalnya model graph untuk molekul C 4
 Modul 4 Pohon Dr. Nanang Priatna, M.Pd. D PENDAHULUAN alam modul-modul sebelumnya Anda telah mempelajari graph terhubung tanpa sikel, misalnya model graph untuk molekul C 4 H 10, hierarki administrasi
Modul 4 Pohon Dr. Nanang Priatna, M.Pd. D PENDAHULUAN alam modul-modul sebelumnya Anda telah mempelajari graph terhubung tanpa sikel, misalnya model graph untuk molekul C 4 H 10, hierarki administrasi
Teori Dasar Graf (Lanjutan)
 Teori Dasar Graf (Lanjutan) ATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. atriks-matriks yang dapat menyajikan
Teori Dasar Graf (Lanjutan) ATRIKS DAN GRAF Untuk menyelesaikan suatu permasalahan model graf dengan bantuan komputer, maka graf tersebut disajikan dalam bentuk matriks. atriks-matriks yang dapat menyajikan
FAKULTAS TEKNOLOGI KOMUNIKASI DAN INFORMATIKA UNIVERSITAS NASIONAL
 FAKULTAS TEKNOLOGI KOMUNIKASI DAN INFORMATIKA UNIVERSITAS NASIONAL RENCANA PEMBELAJARAN MATA KULIAH : Konsep Struktur Data dan Algoritma SEM: Genap KODE: 08030221 SKS: 2 JURUSAN : Teknik Informatika DOSEN:
FAKULTAS TEKNOLOGI KOMUNIKASI DAN INFORMATIKA UNIVERSITAS NASIONAL RENCANA PEMBELAJARAN MATA KULIAH : Konsep Struktur Data dan Algoritma SEM: Genap KODE: 08030221 SKS: 2 JURUSAN : Teknik Informatika DOSEN:
`BAB II LANDASAN TEORI
 `BAB II LANDASAN TEORI Landasan teori yang digunakan sebagai materi pendukung untuk menyelesaikan permasalahan yang dibahas dalam Bab IV adalah teori graf, subgraf, subgraf komplit, graf terhubung, graf
`BAB II LANDASAN TEORI Landasan teori yang digunakan sebagai materi pendukung untuk menyelesaikan permasalahan yang dibahas dalam Bab IV adalah teori graf, subgraf, subgraf komplit, graf terhubung, graf
Penyelesaian Traveling Salesman Problem dengan Algoritma Heuristik
 Penyelesaian Traveling Salesman Problem dengan Algoritma Heuristik Filman Ferdian - 13507091 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan Ganesha
Penyelesaian Traveling Salesman Problem dengan Algoritma Heuristik Filman Ferdian - 13507091 Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jalan Ganesha
Penggunaan Perwarnaan Graf dalam Mencari Solusi Sudoku
 Penggunaan Perwarnaan Graf dalam Mencari Solusi Sudoku Mahdan Ahmad Fauzi Al-Hasan - 13510104 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penggunaan Perwarnaan Graf dalam Mencari Solusi Sudoku Mahdan Ahmad Fauzi Al-Hasan - 13510104 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Graf. Matematika Diskrit. Materi ke-5
 Graf Materi ke-5 Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya
Graf Materi ke-5 Pendahuluan Graf digunakan untuk merepresentasikan objek-objek diskrit dan hubungan antara objek-objek tersebut. Gambar di bawah ini sebuah graf yang menyatakan peta jaringan jalan raya
RENCANA PEMBELAJARAN
 ISO 91 : 28 Disusun Oleh Diperiksa Oleh Disetujui Oleh Tanggal Berlaku 1 September 2015 Diana, M.Kom A.Haidar Mirza, M.Kom M. Izman Hardiansyah, Ph.D Mata Kuliah : Matematika Diskrit Semester :2 Kode :
ISO 91 : 28 Disusun Oleh Diperiksa Oleh Disetujui Oleh Tanggal Berlaku 1 September 2015 Diana, M.Kom A.Haidar Mirza, M.Kom M. Izman Hardiansyah, Ph.D Mata Kuliah : Matematika Diskrit Semester :2 Kode :
