Organisasi Berkas Sekuensial Berindeks
|
|
|
- Dewi Rachman
- 9 tahun lalu
- Tontonan:
Transkripsi
1 Organisasi Berkas Sekuensial Berindeks
2 Definisi Organisasi Berkas ini mirip dengan Organisasi Berkas Sekuensial dimana setiap rekaman disusun secara beruntun di dalam file, hanya saja ada tambahan indeks yang digunakan untuk mencatat posisi atau alamat dari suatu kunci rekaman di dalam file Indeks memiliki dua bagian, yaitu : Kunci Alamat Indeks digunakan untuk melakukan lookup dari kunci yang ada ke alamat penyimpanan rekaman Untuk alasan performa, indeks harus selalu terurut berdasarkan kunci
3 Single-Level Indexing Pengindeksan dengan hanya menggunakan sebuah indeks indeks berkas ADE 102 BCA CNN CNN ADE NFL SDN SDN NFL 105 BCA 106
4 Multi-Level Indexing Pengindeksan dengan menggunakan beberapa indeks yang saling terhubung Indeks yang berlevel tinggi merupakan detail dari indeks yang berlevel lebih rendah level 1 level 2 level 3 berkas
5 Implementasi Indeks Dengan Tabel Dengan AVL-Tree Dengan B-Tree
6 Indexing dengan Tabel Indeks dibentuk dari sebuah tabel dengan dua kolom, yaitu kolom kunci dan kolom alamat Merupakan implementasi indeks yang paling sederhana, namun dibutuhkan kerja ekstra untuk pemeliharaannya, yaitu menjaga agar tabel tetap dalam keadaan terurut
7 Indexing dengan AVL-Tree Indeks dibentuk menggunakan struktur Binary Search Tree (BST) Dengan cara ini, maintenance indeks lebih mudah karena AVL-Tree selalu menjaga agar selalu dalam keadaan terurut
8 Definisi Tree Dalam ilmu komputer, Tree adalah suatu struktur data yang banyak dipakai untuk mengemulasikan suatu struktur pohon yang terdiri dari serangkaian simpul data yang saling terhubung Tree merupakan bentuk khusus dari graph, dimana dalam tree tidak ada hubungan antar simpul yang tertutup (sirkular)
9 Terminologi Terminologi Tree E H B F I A C L J D G M K Setiap data disimpan di dalam bagian yg dinamakan simpul (node) Dalam contoh di samping, node adalah setiap lingkaran yang berisi huruf Setiap node dihubungkan dengan suatu sisi (edge) atau cabang Pada contoh di samping, sisi atau cabang adalah setiap garis yang menghubungkan setiap lingkaran Level dari suatu node dalam tree didefinisikan sebagai jarak suatu node dari node teratas dalam tree tersebut Dalam contoh, node A memiliki level 0, sementara pada level 2 terdapat nodenode E, F dan G
10 Hubungan Antar Node E H B F I A C L J D G M K Node yang berada di atas node lain dan terhubung oleh sebuah cabang dinamakan orang tua (parent) dari node di bawahnya Dalam contoh, node E dan node F memiliki parent node B, sementara node D adalah parent dari node G Node yang berada di bawah merupakan anak (child) dari node di atasnya yang terhubung cabang Dalam contoh, node K adalah child dari node G, sementara node J memiliki dua buah child, yaitu node L dan M
11 Hubungan Antar Node E H B F I A C L J D G M K Seluruh node yang berada di bawah hirarki suatu node X dinamakan turunan (descendant) dari node X Dalam contoh, semua node dari B hingga M merupakan descendant dari node A, sementara node D memiliki descendant node G dan K Node-node yang memiliki descendant node X dinamakan ancestor dari node X Dalam contoh, node A merupakan ancestor dari semua node lainnya, sementara node H memiliki ancestor F, B dan A
12 Hubungan Antar Node E H B F I A C L J D G M K Node-node yang memiliki parent yang sama dinamakan saudara (siblings) Dalam contoh, node L dan M merupakan siblings, karena sama-sama memiliki parent yang sama yaitu node J
13 Node-Node Khusus E H B F I A C L J D G M K Node yang paling atas dinamakan akar (root), yaitu satu-satunya node dalam tree yang tidak memiliki parent Pada contoh, node A adalah root Node yang tidak memiliki anak dinamakan daun (leaf) Pada contoh, node yang merupakan daun adalah node-node C, E, H, I, K, L dan M Node selain daun dinamakan Internal Nodes
14 Tinggi Suatu Tree E H B F I A C L J D G M K Tinggi atau height atau order dari suatu tree adalah jarak dari root ke daun yang paling jauh Tree yang hanya memiliki satu node saja (root sekaligus daun) dikatakan memiliki tinggi 0 Tree pada contoh di samping memiliki tinggi 4, yang merupakan jarak (banyaknya sisi) dari root (node A) ke daun terjauh (node L atau M)
15 Sub-Tree E H B F I A C L J D G M K Sub-tree merupakan suatu struktur tree yang berada di dalam struktur tree lainnya Sub-tree dari suatu node adalah sub-tree yang root-nya adalah anak node tersebut Pada contoh, node A memiliki 3 sub-tree, yaitu sub-tree yang memiliki root node B, sub-tree yang hanya terdiri dari satu node C dan sub-tree yang memiliki root node D Sub-tree yang dibentuk dari node-node berwarna abu-abu pada contoh merupakan sub-tree dari node F Daun pasti tidak memiliki sub-tree
16 Binary Tree A B C D E F G Binary Tree atau Pohon Biner adalah sebuah tree yang setiap nodenya maksimal hanya memiliki dua anak Pada contoh, Node A memiliki 2 anak Node B memiliki 1 anak Node C memiliki 2 anak Node D memiliki 0 anak Node E memiliki 1 anak Node F memiliki 0 anak Node G memiliki 0 anak
17 Sub-Tree Kiri & Sub-Tree Kanan A B C D E F G Setiap anak pada suatu node di binary tree dinamakan sebagai anak kiri (left child) dan anak kanan (right child) Pada contoh, Node A memiliki anak kiri node B dan anak kanan node C Node D merupakan anak kiri dari node B Node E tidak memiliki anak kiri Sub-tree yang dibentuk dari anak kiri suatu node dinamakan sub-tree kiri dan sub-tree kanan adalah sub-tree yang dibentuk dari anak kanan Dari contoh, sub-tree yang dibentuk dari node-node berwarna abu-abu merupakan sub-tree kanan dari node A
18 Balance Factor A B C D E F G Faktor Keseimbangan (Balance Factor / BF) suatu node pada binary tree adalah tinggi subtree kanan dikurangi tinggi sub-tree kiri Biasanya BF ditulis menggunakan tanda (negatif atau positif) kecuali untuk nilai 0 (nol) Jika suatu node tidak memiliki sub-tree pada suatu sisinya maka dianggap tinggi sub-tree node pada sisi tersebut adalah -1 Pada contoh, node A memiliki BF = +1 yang didapat dari 2 dikurangi 1 Node B memiliki BF = -1 yang didapat dari -1 dikurangi 0 Suatu daun pasti memiliki BF = 0
19 Pohon Penuh & Pohon Sempurna B A D C E Pohon Penuh (Full Binary Tree) adalah sebuah binary tree yang setiap node internalnya pasti memiliki dua anak D F B E G A F C G Pohon Sempurna (Perfect Binary Tree) adalah pohon penuh yang semua daunnya berada pada level yang sama, sehingga semua node memiliki BF = 0
20 Pohon Seimbang D B A E C F Pohon Seimbang (Balanced Tree) adalah pohon biner yang semua nodenya hanya memiliki BF antara -1, 0, atau +1 saja Pada contoh, G Node A dan B memiliki BF = -1 Node C dan D memiliki BF = +1 Node E, F dan G memiliki BF = 0
21 Pohon Terurut Pohon Terurut (Ordered Tree) adalah sebuah pohon biner yang setiap node pada sub-tree kiri nilainya lebih kecil dari nilai parent-nya dan setiap node pada subtree kanan memiliki nilai lebih besar dari parentnya
22 Binary Search Tree (BST) BST adalah jenis pohon terurut yang digunakan untuk menyimpan data sehingga memudahkan pencarian kembali data tersebut Gambar di bawah adalah ilustrasi penyisipan setiap node pada BST jika data yang masuk berturut-turut adalah 5, 3, 4, 7, 8, 1, dan 9 Pencarian data pada BST dimulai dari root ke bawah, dengan ketentuan jika nilai yang dicari lebih kecil dari nilai pada node maka pencarian dilanjutkan ke sub-tree kiri dan jika nilainya lebih besar dari nilai node maka pencarian berlanjut ke sub-tree kanan
23 Keseimbangan BST BST yang umum tidak memperhatikan masalah keseimbangan pohon Contohnya BST di samping bukanlah pohon seimbang, karena ada node (dengan nilai 7) yang memiliki BF = +2 Hal ini membuat pencarian suatu nilai pada BST menjadi tidak merata Supaya pencarian menjadi lebih merata sebaiknya sebuah BST dijadikan pohon yang seimbang
24 AVL-Tree AVL-Tree dinamakan berdasarkan dua orang penemunya, G.M. Adelson-Velsky dan E.M. Lendis AVL-Tree adalah sebuah self-balancing binary search tree, atau BST yang dengan sendirinya selalu seimbang Setiap ada penambahan nilai baru maka AVL- Tree akan secara otomatis melakukan pemeriksaan apakah masih seimbang atau tidak Jika tidak seimbang, untuk menyeimbangkan kembali dilakukan rotasi node
25 Arah Keseimbangan Tree A Suatu tree atau sub-tree disebut berat ke kiri jika root-nya memiliki BF < -1 B C Suatu tree atau sub-tree disebut berat ke kanan jika root-nya memiliki BF > +1 D Pemberat dari suatu tree atau sub-tree adalah daun yang memiliki jarak terjauh E Dalam contoh, tree tersebut dikatakan berat ke kanan dengan pemberat node E Sub-tree dengan root C dikatakan berat ke kiri dengan pemberat node E
26 Arah Keseimbangan Tree B E A D C Cabang pemberat dari suatu tree jika ada adalah cabang kedua yang menghubungkan root dengan pemberatnya Dalam contoh, Cabang pemberat tree adalah cabang yang menghubungkan node C dan node D Cabang pemberat sub-tree dengan root C adalah cabang yang menghubungkan node D dan node E
27 Arah Keseimbangan Tree B A D C Suatu tree disebut berat masuk jika cabang pemberatnya berbeda arah dengan cabang di atasnya Suatu tree disebut berat keluar jika cabang pemberatnya sama arahnya dengan cabang di atasnya E Pada contoh, Tree tersebut dikatakan berat masuk Sub-tree dengan root C dikatakan berat keluar
28 Aturan I Rotasi Node Root akan diganti oleh salah satu node pada jalur root node pemberat, dengan aturan : Jika tree berat keluar, node kedua (anak dari root) akan naik menggantikan root Jika tree berat masuk, maka node ketiga (cucu root) naik menggantikan root, sub-tree root lama pada arah pemberat menjadi subtree dari root baru
29 Aturan II Rotasi Node Root yang lama akan menjadi anak dari root yang baru pada sisi yang berlawanan dari arah keseimbangan (pemberat) tree Jika tree berat ke kiri, maka root lama menjadi anak kanan dari root yang baru Jika tree berat ke kanan, maka root lama menjadi anak kiri dari root baru
30 Aturan III Rotasi Node Jika root yang baru jadi memiliki tiga subtree, pindahkan sub-tree tengah ke salah satu anaknya, dengan ketentuan : Jika tadinya merupakan sub-tree kiri maka menjadi sub-tree kanan dari anak kiri Jika tadinya merupakan sub-tree kanan maka menjadi sub-tree kiri dari anak kanan
31 A B Berat Keluar -2 5 C D Node 5 dikatakan berat ke kiri karena BF-nya negatif Node 5 dikatakan berat keluar karena cabang 3-4 sama arahnya dengan cabang 4-5 yang ada di atasnya Aturan I : karena berat keluar maka node kedua (node 4) naik menggantikan node 5 Aturan II : karena berat ke kiri maka node 5 menjadi anak kanan dari penggantinya (node 4) Sub-tree A, B dan D posisinya tetap Aturan III : sub-tree C yang tadinya adalah sub-tree kanan dari node 4 berpindah menjadi sub-tree kiri dari node 5 4 A B C D
32 A B Berat Masuk 5 C D Node 3 dikatakan berat ke kanan karena BF-nya positif Node 5 dikatakan berat masuk karena cabang 4-5 berbeda arahnya dengan cabang di atasnya (cabang 5-3) Aturan I : karena berat masuk maka node ketiga (node 4) naik menggantikan node 3, dan node 5 menjadi anak kanannya Aturan II : karena berat ke kanan maka node 3 menjadi anak kiri dari penggantinya (node 4) Sub-tree A dan D posisinya tetap Aturan III : sub-tree B yang tadinya adalah sub-tree kiri dari node 4 berpindah menjadi sub-tree kanan dari node 3, sementara sub-tree C yang tadinya adalah sub-tree kanan dari node 4 berpindah menjadi sub-tree kiri dari node 5 4 A B C D
33 Langkah-Langkah Penambahan Kunci Baru pada AVL-Tree Penambahan kunci baru menganut aturan seperti pada BST, setiap kunci baru akan membentuk sebuah daun baru Dari daun yang baru terbentuk tersebut, telusuri dan hitung BF node-node ancestor-nya sampai menemui satu di antara tiga kondisi berikut : Mencapai root Menemukan node yang BF-nya nol Menemukan node yang tidak seimbang Jika menemukan node yang tidak seimbang, lakukan rotasi node pada node tersebut
34 Contoh Pembentukan AVL- Keys : 5, 2, 4 Tree
35 Lanjutan Pembentukan AVL-Tree Keys : 6,
36 Lanjutan Pembentukan AVL-Tree Keys :
37 Lanjutan Pembentukan AVL-Tree Keys : 3, 1,
38 B-Tree B-Tree diciptakan oleh Rudolf Bayer dan Ed McCreight Penciptanya tidak menjelaskan arti dari B pada B-Tree, bisa jadi singkatan dari Bayer atau Boeing, tempat Bayer bekerja Ada yang mengartikan B pada B-Tree sebagai Balanced Saat ini, B-Tree merupakan implementasi yang paling banyak digunakan
39 Definisi B-Tree B-Tree adalah sebuah struktur pohon multicabang yang dapat menyimpan lebih dari satu nilai pada setiap nodenya dan setiap daunnya berada pada level yang sama (seimbang) Setiap node pada B-Tree dapat menyimpan lebih dari satu nilai, namun ada kapasitas maksimalnya Kapasitas maksimal nilai yang dapat disimpan di tiap node inilah yang menentukan ordo atau order dari B-Tree
40 Order B-Tree Definisi dari Order B-Tree tidak jelas dan bervariasi dalam berbagai sumber menyebutkan bahwa B-Tree order n adalah B-Tree yang tiap nodenya dapat menyimpan nilai sebanyak n sampai 2n menyebutkan bahwa B-Tree order n adalah B-Tree yang setiap nodenya maksimal memiliki n anak atau dengan kata lain setiap nodenya maksimal dapat menyimpan n-1 nilai juga menyatakan bahwa order menentukan banyaknya anak maksimal di tiap node Sumber lain ada yang menyebutkan B-Tree order n adalah B-Tree yang setiap nodenya maksimal menyimpan n nilai atau ada juga yang menyebutkan 2n nilai
41 Bentuk Umum B-Tree Node x y... z... A B C Sub-Trees Sebuah B-Tree yang tidak kosong paling tidak memiliki sebuah node (yaitu root) yang minimal menyimpan satu nilai Nilai-nilai pada node B-Tree tersusun urut secara ascending atau menaik, pada contoh, x < y < < z Setiap nilai pada node internal pasti memiliki anak di sebelah kiri dan kanannya, pada contoh sub-tree A adalah anak kiri dari x dan sub-tree B adalah anak kanan x sekaligus anak kiri dari y Nilai-nilai pada sub-tree kiri harus lebih kecil dari nilai parent dan nilainilai pada sub-tree kanan lebih besar dari nilai parent, pada contoh, A < x < B < y < < z < C
42 Contoh Bentuk B-Tree
43 Langkah-Langkah Menambahkan Kunci Baru pada B-Tree 1. Jika B-Tree masih kosong, akan dibuat node baru sebagai root dan kunci baru dimasukkan pada root tersebut 2. Telusuri Node-node pada B-Tree dengan mencocokkan nilai pada node dengan kunci baru sampai ditemukan daun 3. Sisipkan kunci baru pada daun tersebut pada posisi yang tepat 4. Jika ada node yang menyimpan nilai lebih banyak dari kapasitas yang diperbolehkan maka terjadi illegal state 5. Jika terjadi illegal state maka lakukan operasi split sampai tidak ada illegal state lagi
44 Operasi Split pada Node B- Tree Operasi Split dilakukan pada suatu node yang mengalami illegal state Nilai yang berada di tengah (sebut saja x) naik ke node di atasnya (jika tidak ada, maka membuat node baru) Nilai-nilai di sebelah kiri dan kanan memisahkan diri menjadi node-node terpisah, yang merupakan anak kiri dan anak kanan dari x
45 Ilustrasi Operasi Split (1) Semula node hanya terdiri dari dua nilai saja, yaitu 56 dan 67 Ketika nilai baru (34) muncul maka terjadi illegal state Nilai yang tengah (56) naik ke atas (membuat node baru) Kedua nilai lainnya (34 dan 67) memisahkan diri ke nodenode di kiri dan kanan
46 Ilustrasi Operasi Split (2) Dari contoh sebelumnya, ditambahkan nilai-nilai 40 dan 10, sehingga terjadi illegal state pada daun di kiri Nilai yang tengah (34) naik ke node atasnya, bergabung dengan nilai 56 Nilai 10 membentuk node sendiri yang merupakan anak kiri dari 34, sementara nilai 40 membentuk node yang menjadi anak kanan 34 sekaligus anak kiri 56
47 Ilustrasi Operasi Split (3) Dari contoh sebelumnya, ditambahkan nilai-nilai 75 dan 99 sehingga terjadi illegal state Ketika nilai yang di tengah (75) naik ke node atasnya maka menjadikan node tersebut mengalami illegal state juga Operasi split dilakukan lagi pada node tersebut sehingga nilai yang di tengah (56) naik membentuk node baru dan seterusnya
Pertemuan 9 STRUKTUR POHON & KUNJUNGAN POHON BINER
 Pertemuan 9 STRUKTUR POHON & KUNJUNGAN POHON BINER DEFINISI POHON (TREE) Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang
Pertemuan 9 STRUKTUR POHON & KUNJUNGAN POHON BINER DEFINISI POHON (TREE) Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang
Lecture Notes On Algorithms and Data Structures. Oleh Thompson Susabda Ngoen
 Lecture Notes On Algorithms and Data Structures AVL TREE Oleh Thompson Susabda Ngoen Universitas Bina Nusantara Fakultas Ilmu Komputer 2003 Thompson S.N. AVL TREE 1 AVL TREE Binary Search Tree BST dibuat
Lecture Notes On Algorithms and Data Structures AVL TREE Oleh Thompson Susabda Ngoen Universitas Bina Nusantara Fakultas Ilmu Komputer 2003 Thompson S.N. AVL TREE 1 AVL TREE Binary Search Tree BST dibuat
STRUKTUR POHON & KUNJUNGAN POHON BINER
 STRUKTUR POHON & KUNJUNGAN POHON BINER Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang saling terkait Istilah istilah Dalam
STRUKTUR POHON & KUNJUNGAN POHON BINER Pohon (Tree) termasuk struktur non linear yang didefinisikan sebagai data yang terorganisir dari suatu item informasi cabang yang saling terkait Istilah istilah Dalam
BAB VII POHON BINAR POHON
 BAB VII POHON BINAR POHON Pohon atau tree adalah salah satu bentuk graph terhubung yang tidak mengandung sirkuit. Karena merupakan graph terhubung, maka pada pohon selalu terdapat path atau jalur yang
BAB VII POHON BINAR POHON Pohon atau tree adalah salah satu bentuk graph terhubung yang tidak mengandung sirkuit. Karena merupakan graph terhubung, maka pada pohon selalu terdapat path atau jalur yang
B C D E F G H I J K L M N O P Q R S T. Tinaliah, S.Kom POHON BINER
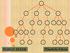 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z POHON BINER Tinaliah, S.Kom DEFINISI Pohon (dalam struktur data) struktur berisi sekumpulan elemen dimana salah satu elemen adalah akar (root) dan elemen-elemen
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z POHON BINER Tinaliah, S.Kom DEFINISI Pohon (dalam struktur data) struktur berisi sekumpulan elemen dimana salah satu elemen adalah akar (root) dan elemen-elemen
STRUKTUR POHON (TREE) Pohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit.
 Pertemuan 9 STRUKTUR POHON (TREE) ISTILAH-ISTILAH DASAR Pohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit. Karena merupakan Graph terhubung, maka pada Pohon (Tree)
Pertemuan 9 STRUKTUR POHON (TREE) ISTILAH-ISTILAH DASAR Pohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit. Karena merupakan Graph terhubung, maka pada Pohon (Tree)
TREE STRUCTURE (Struktur Pohon)
 TREE STRUCTURE (Struktur Pohon) Dalam ilmu komputer, tree adalah sebuah struktur data yang secara bentuk menyerupai sebuah pohon, yang terdiri dari serangkaian node (simpul) yang saling berhubungan. Node-node
TREE STRUCTURE (Struktur Pohon) Dalam ilmu komputer, tree adalah sebuah struktur data yang secara bentuk menyerupai sebuah pohon, yang terdiri dari serangkaian node (simpul) yang saling berhubungan. Node-node
Pohon (Tree) Universitas Gunadarma Sistem Informasi 2012/2013
 Pohon (Tree) Universitas Gunadarma Sistem Informasi 2012/2013 Pohon (Tree) Pohon (Tree) didefinisikan sebagai graf terhubung yang tidak mengandung sirkuit. Karena merupakan graf terhubung, maka pohon selalu
Pohon (Tree) Universitas Gunadarma Sistem Informasi 2012/2013 Pohon (Tree) Pohon (Tree) didefinisikan sebagai graf terhubung yang tidak mengandung sirkuit. Karena merupakan graf terhubung, maka pohon selalu
STRUKTUR POHON (TREE) Pohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit.
 Pertemuan 9 STRUKTUR POHON (TREE) ISTILAH-ISTILAH DASAR Pohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit. Karena merupakan Graph terhubung, maka pada Pohon (Tree)
Pertemuan 9 STRUKTUR POHON (TREE) ISTILAH-ISTILAH DASAR Pohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit. Karena merupakan Graph terhubung, maka pada Pohon (Tree)
Tree. Perhatikan pula contoh tree di bawah ini : Level. Level 2. Level 3. Level 4. Level 5
 TR (POHON) Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan terutama untuk merepresentasikan hubungan data yang bersifat hierarkis antara elemenelemennya. efinisi tree : Kumpulan
TR (POHON) Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan terutama untuk merepresentasikan hubungan data yang bersifat hierarkis antara elemenelemennya. efinisi tree : Kumpulan
Ringkasan mengenai Tree (Dari beberapa referensi lain) Nina Valentika
 Ringkasan mengenai Tree (Dari beberapa referensi lain) Nina Valentika December 31, 2015 0.1 Pendahuluan Figure 1: Contoh Tree. Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan
Ringkasan mengenai Tree (Dari beberapa referensi lain) Nina Valentika December 31, 2015 0.1 Pendahuluan Figure 1: Contoh Tree. Tree/pohon merupakan struktur data yang tidak linear/non linear yang digunakan
Soal Pendahuluan Modul 3
 1. Apa yang dimaksud dengan tree? PENGERTIAN TREE Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Struktur pohon adalah suatu cara
1. Apa yang dimaksud dengan tree? PENGERTIAN TREE Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Struktur pohon adalah suatu cara
Algoritma dan Struktur Data. Click to edit Master subtitle style Konsep Tree
 Algoritma dan Struktur Data Click to edit Master subtitle style Konsep Tree Basic Tree Concepts Tree berisi himpunan node dan garis berarah yang disebut branch yang menghubungkan dua node. Banyaknya branch
Algoritma dan Struktur Data Click to edit Master subtitle style Konsep Tree Basic Tree Concepts Tree berisi himpunan node dan garis berarah yang disebut branch yang menghubungkan dua node. Banyaknya branch
Pemrograman Algoritma Dan Struktur Data
 MODUL PERKULIAHAN Modul ke: 14Fakultas Agus FASILKOM Pemrograman Algoritma Dan Struktur Data ADT BINARY TREE Hamdi.S.Kom,MMSI Program Studi Teknik Informatika ISTILAH-ISTILAH DASAR Pohon atau Tree adalah
MODUL PERKULIAHAN Modul ke: 14Fakultas Agus FASILKOM Pemrograman Algoritma Dan Struktur Data ADT BINARY TREE Hamdi.S.Kom,MMSI Program Studi Teknik Informatika ISTILAH-ISTILAH DASAR Pohon atau Tree adalah
METODE AVL TREE UNTUK PENYEIMBANGAN TINGGI BINARY TREE
 METODE AVL TREE UNTUK PENYEIMBANGAN TINGGI BINARY TREE Suwanty 1 Octara Pribadi 2 Program Studi Teknik Informatika 1,2 STMIK TIME 1,2 Jalan Merbabu No. 32 AA-BB Medan 1,2 e-mail : [email protected]
METODE AVL TREE UNTUK PENYEIMBANGAN TINGGI BINARY TREE Suwanty 1 Octara Pribadi 2 Program Studi Teknik Informatika 1,2 STMIK TIME 1,2 Jalan Merbabu No. 32 AA-BB Medan 1,2 e-mail : [email protected]
DIKTAT KULIAH ALGORITMA dan STRUKTUR DATA II
 Pertemuan 13 Waktu : 135 menit Tujuan Pembelajaran : Mahasiswa mampu menjelaskan teknik pemrograman menggunakan Tree. Substansi Materi : Tree Tabulasi Kegiatan Perkuliahan No Tahap Kegiatan Kegiatan Pengajar
Pertemuan 13 Waktu : 135 menit Tujuan Pembelajaran : Mahasiswa mampu menjelaskan teknik pemrograman menggunakan Tree. Substansi Materi : Tree Tabulasi Kegiatan Perkuliahan No Tahap Kegiatan Kegiatan Pengajar
ALGORITMA DAN STRUKTUR DATA
 Modul ke: 10 Fitrianingsih Fakultas FASILKOM ALGORITMA DAN STRUKTUR DATA JENIS-JENIS TREE SKom., MMSI Program Studi Sistem Informasi JENIS-JENIS TREE Pohon (Tree) adalah graf terhubung yang tidak mengandung
Modul ke: 10 Fitrianingsih Fakultas FASILKOM ALGORITMA DAN STRUKTUR DATA JENIS-JENIS TREE SKom., MMSI Program Studi Sistem Informasi JENIS-JENIS TREE Pohon (Tree) adalah graf terhubung yang tidak mengandung
Tree (Struktur Data) Nisa ul Hafidhoh, MT
 Tree (Struktur Data) Nisa ul Hafidhoh, MT Struktur Data Linier 1 5 8 9 2 ARRAY 0 1 2 3 n Head Tail QUEUE O U T 1 2 3 4 STACK 4 3 2 1 I N 10 8 14 LINKED LIST Struktur Tree Struktur Tree adalah struktur
Tree (Struktur Data) Nisa ul Hafidhoh, MT Struktur Data Linier 1 5 8 9 2 ARRAY 0 1 2 3 n Head Tail QUEUE O U T 1 2 3 4 STACK 4 3 2 1 I N 10 8 14 LINKED LIST Struktur Tree Struktur Tree adalah struktur
Pohon dan Pohon Biner
 Pertemuan 14 Pohon dan Pohon Biner P r a j a n t o W a h y u A d i [email protected] +6285 641 73 00 22 Rencana Kegiatan Perkuliahan Semester # Pokok Bahasan 1 Pengenalan Struktur Data 2 ADT Stack
Pertemuan 14 Pohon dan Pohon Biner P r a j a n t o W a h y u A d i [email protected] +6285 641 73 00 22 Rencana Kegiatan Perkuliahan Semester # Pokok Bahasan 1 Pengenalan Struktur Data 2 ADT Stack
Algoritma dan Struktur Data. Binary Tree & Binary Search Tree (BST)
 Algoritma dan Struktur Data Binary Tree & Binary Search Tree (BST) Teknik Informatika Universitas Muhammadiyah Malang 2016 Outline Tree Binary tree Istilah pada tree Operasi dasar binary tree BST Definisi
Algoritma dan Struktur Data Binary Tree & Binary Search Tree (BST) Teknik Informatika Universitas Muhammadiyah Malang 2016 Outline Tree Binary tree Istilah pada tree Operasi dasar binary tree BST Definisi
A B C E F G K Contoh Tree
 Tree TREE Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hierarkis (hubungan one to many) antara elemen-elemen. Tree biasa didefinisikan sebagai kumpulan
Tree TREE Tree merupakan salah satu bentuk struktur data tidak linear yang menggambarkan hubungan yang bersifat hierarkis (hubungan one to many) antara elemen-elemen. Tree biasa didefinisikan sebagai kumpulan
MODUL PRAKTIKUM STRUKTUR DATA
 MODUL PRAKTIKUM STRUKTUR DATA TREE (POHON) Oleh : SUPRAPTO, S.Kom PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS PGRI RONGGOLAWE (UNIROW) TUBAN 2012/2013 MODUL V TREE (POHON) 5.1. TREE (POHON)
MODUL PRAKTIKUM STRUKTUR DATA TREE (POHON) Oleh : SUPRAPTO, S.Kom PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNIK UNIVERSITAS PGRI RONGGOLAWE (UNIROW) TUBAN 2012/2013 MODUL V TREE (POHON) 5.1. TREE (POHON)
Organisasi File Multi Key y( (Index)
 Organisasi File Multi Key y( (Index) Pengertian Organisasi berkas yang memperbolehkan record diakses oleh lebih dari satu key field disebut organisasi berkas dengan banyak key. Ada banyak teknik yang dipakai
Organisasi File Multi Key y( (Index) Pengertian Organisasi berkas yang memperbolehkan record diakses oleh lebih dari satu key field disebut organisasi berkas dengan banyak key. Ada banyak teknik yang dipakai
BAB IV POHON. Diktat Algoritma dan Struktur Data 2
 iktat lgoritma dan Struktur ata 2 V POON efinisi Pohon Struktur pohon merupakan kumpulan elemen yang salah satu elemennya disebut akar dan sisa elemennya terpecah menjadi sejumlah himpunan yang saling
iktat lgoritma dan Struktur ata 2 V POON efinisi Pohon Struktur pohon merupakan kumpulan elemen yang salah satu elemennya disebut akar dan sisa elemennya terpecah menjadi sejumlah himpunan yang saling
BINARY SEARCH TREE. TUJUAN UMUM Mahasiswa memahami binary search Tree
 BINARY SEARCH TREE TUJUAN UMUM Mahasiswa memahami binary search Tree Tujuan Khusus Bentuk Khusus Binary Tree Rekursive pada Binary Tree Tree Traversal Operasi pada Binary Tree Implementasi Binary Tree
BINARY SEARCH TREE TUJUAN UMUM Mahasiswa memahami binary search Tree Tujuan Khusus Bentuk Khusus Binary Tree Rekursive pada Binary Tree Tree Traversal Operasi pada Binary Tree Implementasi Binary Tree
Variasi Pohon Pencarian Biner Seimbang
 Variasi Pohon Pencarian Biner Seimbang Tony 13516010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia [email protected]
Variasi Pohon Pencarian Biner Seimbang Tony 13516010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia [email protected]
POHON CARI BINER (Binary Search Tree)
 POHON CARI BINER (Binary Search Tree) 50 24 70 10 41 61 90 3 12 35 47 55 67 80 99 POHON CARI BINER (Binary Search Tree) Definisi : bila N adalah simpul dari pohon maka nilai semua simpul pada subpohon
POHON CARI BINER (Binary Search Tree) 50 24 70 10 41 61 90 3 12 35 47 55 67 80 99 POHON CARI BINER (Binary Search Tree) Definisi : bila N adalah simpul dari pohon maka nilai semua simpul pada subpohon
Termilogi Pada Pohon Berakar 10 Pohon Berakar Terurut
 KATA PENGANTAR Puji syukur penyusun panjatkan ke hadirat Allah Subhanahu wata?ala, karena berkat rahmat-nya kami bisa menyelesaikan makalah yang berjudul Catatan Seorang Kuli Panggul. Makalah ini diajukan
KATA PENGANTAR Puji syukur penyusun panjatkan ke hadirat Allah Subhanahu wata?ala, karena berkat rahmat-nya kami bisa menyelesaikan makalah yang berjudul Catatan Seorang Kuli Panggul. Makalah ini diajukan
Silsilah keluarga Hasil pertandingan yang berbentuk turnamen Struktur organisasi dari sebuah perusahaan. B.1 Pohon Biner (Binary Tree)
 PRAKTIKUM 25 BINARY TREE A. TUJUAN Mahasiswa diharapkan mampu : 1. Memahami konsep dari BinaryTree 2. Memahami cara membangun Binary Tree secara manual 3. Memahami konsep dan implementasi dari menghitung
PRAKTIKUM 25 BINARY TREE A. TUJUAN Mahasiswa diharapkan mampu : 1. Memahami konsep dari BinaryTree 2. Memahami cara membangun Binary Tree secara manual 3. Memahami konsep dan implementasi dari menghitung
Buku Ajar Struktur Data
 B a g i a n 5 Tujuan Instruksional Khusus Pokok Bahasan Mahasiswa mampu menjelaskan struktur data nonlinier Tree. Mahasiswa mampu memahami operasi pada struktur data Tree Struktur data Tree secara umum.
B a g i a n 5 Tujuan Instruksional Khusus Pokok Bahasan Mahasiswa mampu menjelaskan struktur data nonlinier Tree. Mahasiswa mampu memahami operasi pada struktur data Tree Struktur data Tree secara umum.
Algoritma dan Struktur Data. Tree
 Algoritma dan Struktur Data Tree Outline 1. Apakah Tree Structure itu? 2. Binary Tree & implementasinya 3. Tree Traversal 4. Implementasi tree (selain binary tree) Apakah Tree Structure itu? Struktur data
Algoritma dan Struktur Data Tree Outline 1. Apakah Tree Structure itu? 2. Binary Tree & implementasinya 3. Tree Traversal 4. Implementasi tree (selain binary tree) Apakah Tree Structure itu? Struktur data
KUM 6 IMPLEMENTASI BINARY TREE
 PRAKTIKUM KUM 6 IMPLEMENTASI BINARY TREE TUJUAN PEMBELAJARAN: 1. Mengimplementasikan struktur data Binary Tree menggunakan linked list. 2. Mampu mengimplementasikan beragam operasi pada struktur data binary
PRAKTIKUM KUM 6 IMPLEMENTASI BINARY TREE TUJUAN PEMBELAJARAN: 1. Mengimplementasikan struktur data Binary Tree menggunakan linked list. 2. Mampu mengimplementasikan beragam operasi pada struktur data binary
BAB IX TREE (POHON) ISTILAH DASAR
 Modul 9 Struktur Data (rie) - 1 IX TREE (POHON) Struktur pada tree (pohon) tidak linear seperti pada struktur linked list, stack, dan queue. Setiap node pada tree mempunyai tingkatan, yaitu orang tua (parent)
Modul 9 Struktur Data (rie) - 1 IX TREE (POHON) Struktur pada tree (pohon) tidak linear seperti pada struktur linked list, stack, dan queue. Setiap node pada tree mempunyai tingkatan, yaitu orang tua (parent)
IT234 Algoritma dan Struktur Data. Tree
 IT234 Algoritma dan Struktur Data Tree Fakultas Teknologi Informasi Universitas Kristen Satya Wacana @2008 Tree Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya
IT234 Algoritma dan Struktur Data Tree Fakultas Teknologi Informasi Universitas Kristen Satya Wacana @2008 Tree Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya
JAWABAN TUGAS MATRIKULASI STRUKTUR DATA. DOSEN Bpk. Krisna Adiyarta, M.Sc
 Page 1 of 5 Struktur Data Matrikulasi JAWABAN TUGAS MATRIKULASI STRUKTUR DATA DOSEN Bpk. Krisna Adiyarta, M.Sc KELAS XA Disusun Oleh No NIM NAMA 1. 1211600075 NURHALIM 2. 1211600182 M. IMAN WAHYUDI 3.
Page 1 of 5 Struktur Data Matrikulasi JAWABAN TUGAS MATRIKULASI STRUKTUR DATA DOSEN Bpk. Krisna Adiyarta, M.Sc KELAS XA Disusun Oleh No NIM NAMA 1. 1211600075 NURHALIM 2. 1211600182 M. IMAN WAHYUDI 3.
DEFINISI. Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit. pohon pohon bukan pohon bukan pohon 2
 1 POHON DEFINISI Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan
1 POHON DEFINISI Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan
STRUKTUR DATA. By : Sri Rezeki Candra Nursari 2 SKS
 STRUKTUR DATA By : Sri Rezeki Candra Nursari 2 SKS Literatur Sjukani Moh., (2007), Struktur Data (Algoritma & Struktur Data 2) dengan C, C++, Mitra Wacana Media Utami Ema. dkk, (2007), Struktur Data (Konsep
STRUKTUR DATA By : Sri Rezeki Candra Nursari 2 SKS Literatur Sjukani Moh., (2007), Struktur Data (Algoritma & Struktur Data 2) dengan C, C++, Mitra Wacana Media Utami Ema. dkk, (2007), Struktur Data (Konsep
TERAPAN POHON BINER 1
 TERAPAN POHON BINER 1 Terapan pohon biner di dalam ilmu komputer sangat banyak, diantaranya : 1. Pohon ekspresi 2. Pohon keputusan 3. Kode Prefiks 4. Kode Huffman 5. Pohon pencarian biner 2 Pohon Ekspresi
TERAPAN POHON BINER 1 Terapan pohon biner di dalam ilmu komputer sangat banyak, diantaranya : 1. Pohon ekspresi 2. Pohon keputusan 3. Kode Prefiks 4. Kode Huffman 5. Pohon pencarian biner 2 Pohon Ekspresi
Outline. Struktur Data & Algoritme (Data Structures & Algorithms) Pengantar. Definisi. 2-3 Trees
 Struktur Data & Algoritme (Data Structures & Algorithms) 2-3 Trees Outline Pengantar Definisi 2-3 Tree Operasi: Search Insert Delete (a,b)-tree Denny ([email protected]) Suryana Setiawan ([email protected])
Struktur Data & Algoritme (Data Structures & Algorithms) 2-3 Trees Outline Pengantar Definisi 2-3 Tree Operasi: Search Insert Delete (a,b)-tree Denny ([email protected]) Suryana Setiawan ([email protected])
STRUKTUR DATA. By : Sri Rezeki Candra Nursari 2 SKS
 STRUKTUR DATA By : Sri Rezeki Candra Nursari 2 SKS Literatur Sjukani Moh., (2007), Struktur Data (Algoritma & Struktur Data 2) dengan C, C++, Mitra Wacana Media Utami Ema. dkk, (2007), Struktur Data (Konsep
STRUKTUR DATA By : Sri Rezeki Candra Nursari 2 SKS Literatur Sjukani Moh., (2007), Struktur Data (Algoritma & Struktur Data 2) dengan C, C++, Mitra Wacana Media Utami Ema. dkk, (2007), Struktur Data (Konsep
TREE ALGORITMA & STRUKTUR DATA. Materi ASD Fakultas Teknik Elektro & Komputer UKSW (www.uksw.edu) Download Dari :
 TREE ALGORITMA & STRUKTUR DATA Materi ASD Fakultas Teknik Elektro & Komputer UKSW (www.uksw.edu) Download Dari : http://ambonmemanggil.blogspot.com 1 TREE ISTILAH-ISTILAH DASAR: tree : kumpulan elemen
TREE ALGORITMA & STRUKTUR DATA Materi ASD Fakultas Teknik Elektro & Komputer UKSW (www.uksw.edu) Download Dari : http://ambonmemanggil.blogspot.com 1 TREE ISTILAH-ISTILAH DASAR: tree : kumpulan elemen
Definisi. Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit. pohon pohon bukan pohon bukan pohon
 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan pohon
1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon 2 Hutan (forest) adalah - kumpulan pohon
Penerapan Teori Pohon Dalam Kajian Struktur Data
 Penerapan Teori Pohon Dalam Kajian Struktur Data Khoirush Sholih Ridhwaana Akbar NIM : 13505120 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : [email protected]
Penerapan Teori Pohon Dalam Kajian Struktur Data Khoirush Sholih Ridhwaana Akbar NIM : 13505120 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : [email protected]
SATUAN ACARA PERKULIAHAN (SAP) Mata Kuliah : Struktur Data Kode : TIS3213 Semester : III Waktu : 2 x 3 x 50 Menit Pertemuan : 10 & 11
 . Kompetensi 1. Utama STUN R PERKULIHN (SP) Mata Kuliah : Struktur Data Kode : TIS3213 Semester : III Waktu : 2 x 3 x 50 Menit Pertemuan : 10 & 11 Mahasiswa dapat memahami tentang konsep pemrograman menggunakan
. Kompetensi 1. Utama STUN R PERKULIHN (SP) Mata Kuliah : Struktur Data Kode : TIS3213 Semester : III Waktu : 2 x 3 x 50 Menit Pertemuan : 10 & 11 Mahasiswa dapat memahami tentang konsep pemrograman menggunakan
Struktur Data Tree/Pohon dalam Bahasa Java
 Struktur Data Tree/Pohon dalam Bahasa Java Jeffrey Hermanto Halimsetiawan [email protected] tutorialpemrograman.wordpress.com 22 Maret 2009 tutorialpemrograman.wordpress.com - 2009 1 Tree merupakan
Struktur Data Tree/Pohon dalam Bahasa Java Jeffrey Hermanto Halimsetiawan [email protected] tutorialpemrograman.wordpress.com 22 Maret 2009 tutorialpemrograman.wordpress.com - 2009 1 Tree merupakan
Pohon. Bahan Kuliah IF2120 Matematika Diskrit. Program Studi Teknik Informatika ITB. Rinaldi M/IF2120 Matdis 1
 Pohon Bahan Kuliah IF2120 Matematika Diskrit Program Studi Teknik Informatika ITB Rinaldi M/IF2120 Matdis 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a
Pohon Bahan Kuliah IF2120 Matematika Diskrit Program Studi Teknik Informatika ITB Rinaldi M/IF2120 Matdis 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a
Binary Tree. Binary Tree dapat digambarkan berdasarkan kondisinya, sebagai berikut: Pointer ke akar (root) dari tree
 Binary Tree Pendahuluan Binary Tree adalah struktur data yang hampir mirip juga dengan Linked List untuk menyimpan koleksi dari data. Linked List dapat dianalogikan sebagai rantai linier sedangkan Binary
Binary Tree Pendahuluan Binary Tree adalah struktur data yang hampir mirip juga dengan Linked List untuk menyimpan koleksi dari data. Linked List dapat dianalogikan sebagai rantai linier sedangkan Binary
Pertemuan 9 STRUKTUR POHON (TREE) Sifat utama Pohon Berakar ISTILAH-ISTILAH DASAR
 ertemuan 9 STUKTU OHON (TEE) ISTILH-ISTILH DS ohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit. Karena merupakan Graph terhubung, maka pada ohon (Tree) selalu terdapat
ertemuan 9 STUKTU OHON (TEE) ISTILH-ISTILH DS ohon atau Tree adalah salah satu bentuk Graph terhubung yang tidak mengandung sirkuit. Karena merupakan Graph terhubung, maka pada ohon (Tree) selalu terdapat
- Tree Adalah graph tak berarah yang terhubung dan tidak memuat cycle. Suatu Tree paling sedikit mengandung satu vertex. Contoh :
 Kuliah 5, 6 MODUL 3 - Tree Adalah graph tak berarah yang terhubung dan tidak memuat cycle. Suatu Tree paling sedikit mengandung satu vertex. Contoh : Tree dgn vertex (a) Tree dgn vertex (b) Tree dgn 3
Kuliah 5, 6 MODUL 3 - Tree Adalah graph tak berarah yang terhubung dan tidak memuat cycle. Suatu Tree paling sedikit mengandung satu vertex. Contoh : Tree dgn vertex (a) Tree dgn vertex (b) Tree dgn 3
Binary Search Tree (BST)
 PROGRAM STUDI INFORMATIKA Universitas Syiah Kuala Struktur Data dan Algoritma Binary Search Tree (BST) Dr. Taufik Fuadi Abidin, M.Tech [email protected] Binary Tree Binary Tree adalah struktur
PROGRAM STUDI INFORMATIKA Universitas Syiah Kuala Struktur Data dan Algoritma Binary Search Tree (BST) Dr. Taufik Fuadi Abidin, M.Tech [email protected] Binary Tree Binary Tree adalah struktur
Pohon (TREE) Matematika Deskrit. Hasanuddin Sirait, MT 1
 Pohon (TREE) Matematika Deskrit By @Ir. Hasanuddin Sirait, MT 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon
Pohon (TREE) Matematika Deskrit By @Ir. Hasanuddin Sirait, MT 1 Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon
Tenia Wahyuningrum, S.Kom. MT Sisilia Thya Safitri, S.T.,M.T.
 tree Tenia Wahyuningrum, S.Kom. MT Sisilia Thya Safitri, S.T.,M.T Tree Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Tree merepresentasikan
tree Tenia Wahyuningrum, S.Kom. MT Sisilia Thya Safitri, S.T.,M.T Tree Kumpulan node yang saling terhubung satu sama lain dalam suatu kesatuan yang membentuk layakya struktur sebuah pohon. Tree merepresentasikan
13/12/2013. Binary Tree. Contoh Tree
 Binary Tree Contoh Tree 1 Struktur Tree Tree adalah struktur hirarki yang menempatkan elemen pada simpul pada cabang2nya yang dimulai dari root. Node (simpul) dalam tree dibagi dalam level dari tertinggi
Binary Tree Contoh Tree 1 Struktur Tree Tree adalah struktur hirarki yang menempatkan elemen pada simpul pada cabang2nya yang dimulai dari root. Node (simpul) dalam tree dibagi dalam level dari tertinggi
Matematika Diskret (Pohon) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs.
 Matematika Diskret (Pohon) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon
Matematika Diskret (Pohon) Instruktur : Ferry Wahyu Wibowo, S.Si., M.Cs. Definisi Pohon adalah graf tak-berarah terhubung yang tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon
Aplikasi Pohon pada Pohon Binatang (Animal Tree)
 Aplikasi Pohon pada Pohon Binatang (Animal Tree) Cilvia Sianora Putri (13512027) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Aplikasi Pohon pada Pohon Binatang (Animal Tree) Cilvia Sianora Putri (13512027) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Aplikasi Pohon Pencarian Biner Seimbang sebagai Memo Table Dynamic Programming
 Aplikasi Pohon Pencarian Biner Seimbang sebagai Memo Table Dynamic Programming Reinhard Benjamin Linardi, 13515011 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Aplikasi Pohon Pencarian Biner Seimbang sebagai Memo Table Dynamic Programming Reinhard Benjamin Linardi, 13515011 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Definisi. Pohon adalah graf tak-berarah, terhubung, dan tidak mengandung sirkuit. pohon pohon bukan pohon bukan pohon (ada sikuit) (tdk terhubung)
 POHON (TREE) Pohon Definisi Pohon adalah graf tak-berarah, terhubung, dan tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon (ada sikuit) (tdk
POHON (TREE) Pohon Definisi Pohon adalah graf tak-berarah, terhubung, dan tidak mengandung sirkuit a b a b a b a b c d c d c d c d e f e f e f e f pohon pohon bukan pohon bukan pohon (ada sikuit) (tdk
sistem basis data ti ti ukdw Indexing Materi Minggu ke-10 Teknik Informatika Universitas Kristen Duta Wacana Yogyakarta 04/07/13 budi susanto 1
 Indexing Materi Minggu ke-10 Teknik Informatika Universitas Kristen Duta Wacana Yogyakarta 04/07/13 budi susanto 1 Tujuan Memahami Tujuan Index pada Database Memahami model dasar Index Memahami algoritma
Indexing Materi Minggu ke-10 Teknik Informatika Universitas Kristen Duta Wacana Yogyakarta 04/07/13 budi susanto 1 Tujuan Memahami Tujuan Index pada Database Memahami model dasar Index Memahami algoritma
Implementasi Skema Pohon Biner yang Persistent dalam Pemrograman Fungsional
 Implementasi Skema Pohon Biner yang Persistent dalam Pemrograman Fungsional Azby Khilfi M. NIM : 13506018 Sekolah Teknik Elektro dan Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail
Implementasi Skema Pohon Biner yang Persistent dalam Pemrograman Fungsional Azby Khilfi M. NIM : 13506018 Sekolah Teknik Elektro dan Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail
Binary Tree. Binary Tree dapat digambarkan berdasarkan kondisinya, sebagai berikut: Pointer ke akar (root) dari tree
 Binary Tree Pendahuluan Binary Tree adalah struktur data yang hampir mirip juga dengan Linked List untuk menyimpan koleksi dari data. Linked List dapat dianalogikan sebagai rantai linier sedangkan Binary
Binary Tree Pendahuluan Binary Tree adalah struktur data yang hampir mirip juga dengan Linked List untuk menyimpan koleksi dari data. Linked List dapat dianalogikan sebagai rantai linier sedangkan Binary
OPERASI LOGIKA PADA GENERAL TREE MENGGUNAKAN FUNGSI REKURSIF
 OPERASI LOGIKA PADA GENERAL TREE MENGGUNAKAN FUNGSI REKURSIF Lutfi Hakim (1), Eko Mulyanto Yuniarno (2) Mahasiswa Jurusan Teknik Elektro (1), Dosen Pembimbing (2) Institut Teknologi Sepuluh Nopember (ITS)
OPERASI LOGIKA PADA GENERAL TREE MENGGUNAKAN FUNGSI REKURSIF Lutfi Hakim (1), Eko Mulyanto Yuniarno (2) Mahasiswa Jurusan Teknik Elektro (1), Dosen Pembimbing (2) Institut Teknologi Sepuluh Nopember (ITS)
Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem
 Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem Arie Tando (13510018) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem Arie Tando (13510018) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
IKI 20100: Struktur Data & Algoritma
 IKI 20100: Struktur Data & Algoritma B Tree Ruli Manurung & Ade Azurat ( Setiawan (acknowledgments: Denny, Suryana Fasilkom UI Ruli Manurung & Ade Azurat Fasilkom UI - IKI20100 2007/2008 Ganjil Minggu
IKI 20100: Struktur Data & Algoritma B Tree Ruli Manurung & Ade Azurat ( Setiawan (acknowledgments: Denny, Suryana Fasilkom UI Ruli Manurung & Ade Azurat Fasilkom UI - IKI20100 2007/2008 Ganjil Minggu
Penerapan Pohon Biner dalam Proses Pengamanan Peer to Peer
 Penerapan Pohon Biner dalam Proses Pengamanan Peer to Peer Eka Yusrianto Toisutta - NIM : 13504116 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganesha 10, Bandung email: [email protected]
Penerapan Pohon Biner dalam Proses Pengamanan Peer to Peer Eka Yusrianto Toisutta - NIM : 13504116 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganesha 10, Bandung email: [email protected]
8/29/2014. Kode MK/ Nama MK. Matematika Diskrit 2 8/29/2014
 Kode MK/ Nama MK Matematika Diskrit 1 8/29/2014 2 8/29/2014 1 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 3 8/29/2014 POHON DAN PEWARNAAN GRAF Tujuan Mahasiswa
Kode MK/ Nama MK Matematika Diskrit 1 8/29/2014 2 8/29/2014 1 Cakupan Himpunan, Relasi dan fungsi Kombinatorial Teori graf Pohon (Tree) dan pewarnaan graf 3 8/29/2014 POHON DAN PEWARNAAN GRAF Tujuan Mahasiswa
Binary Tree kosong Gambar 1. Binary Tree dalam kondisi kosong
 PRAKTIKUM 25-26 BINARY TREEDAN TRAVERSAL BINARY TREE A. TUJUAN Mahasiswa diharapkan mampu : 1. Memahami konsep dari BinaryTree dantraversalbinary Tree 2. Memahami proses traversal pada Binary Tree 3. Memahami
PRAKTIKUM 25-26 BINARY TREEDAN TRAVERSAL BINARY TREE A. TUJUAN Mahasiswa diharapkan mampu : 1. Memahami konsep dari BinaryTree dantraversalbinary Tree 2. Memahami proses traversal pada Binary Tree 3. Memahami
P o h o n. Definisi. Oleh: Panca Mudji Rahardjo. Pohon. Adalah graf tak berarah terhubung yang tidak mengandung sirkuit.
 P o h o n Oleh: Panca Mudji Rahardjo Definisi Pohon Adalah graf tak berarah terhubung yang tidak mengandung sirkuit. Contoh: G 1 dan G 2 pohon, G 3 dan G 4 bukan pohon. 1 Definisi Hutan (forest) Adalah
P o h o n Oleh: Panca Mudji Rahardjo Definisi Pohon Adalah graf tak berarah terhubung yang tidak mengandung sirkuit. Contoh: G 1 dan G 2 pohon, G 3 dan G 4 bukan pohon. 1 Definisi Hutan (forest) Adalah
TUGAS MAKALAH INDIVIDUAL. Mata Kuliah : Matematika Diskrit / IF2153 Nama : Dwitiyo Abhirama NIM :
 TUGAS MAKALAH INDIVIDUAL Mata Kuliah : Matematika Diskrit / IF2153 Nama : Dwitiyo Abhirama NIM : 13505013 Institut Teknologi Bandung Desember 2006 Penggunaan Struktur Pohon dalam Informatika Dwitiyo Abhirama
TUGAS MAKALAH INDIVIDUAL Mata Kuliah : Matematika Diskrit / IF2153 Nama : Dwitiyo Abhirama NIM : 13505013 Institut Teknologi Bandung Desember 2006 Penggunaan Struktur Pohon dalam Informatika Dwitiyo Abhirama
Pemodelan dan Pengelolaan Data Klasifikasi Tanaman Menggunakan Pohon
 Pemodelan dan Pengelolaan Data Klasifikasi Tanaman Menggunakan Pohon Febri Ardiansyah (13505099) Program Studi Teknik Informatika Institut Teknologi Bandung Jl. Ganesha no 10,Bandung [email protected]
Pemodelan dan Pengelolaan Data Klasifikasi Tanaman Menggunakan Pohon Febri Ardiansyah (13505099) Program Studi Teknik Informatika Institut Teknologi Bandung Jl. Ganesha no 10,Bandung [email protected]
ANALISIS ALGORITMA BINARY SEARCH
 ANALISIS ALGORITMA BINARY SEARCH Metode Binary search Binary search merupakan salah satu algoritma untuk melalukan pencarian pada array yang sudah terurut. Jika kita tidak mengetahui informasi bagaimana
ANALISIS ALGORITMA BINARY SEARCH Metode Binary search Binary search merupakan salah satu algoritma untuk melalukan pencarian pada array yang sudah terurut. Jika kita tidak mengetahui informasi bagaimana
2. Mahasiswa dapat membuat dan menggunakan array dan linked list dalam suatu kasus.
 1 ARRAY & LINKED LIST MODUL 1 Standar kompetensi: 1. Mahasiswa mengetahui perbedaan array dan linked list. 2. Mahasiswa dapat membuat dan menggunakan array dan linked list dalam suatu kasus. 3. Mahasiswa
1 ARRAY & LINKED LIST MODUL 1 Standar kompetensi: 1. Mahasiswa mengetahui perbedaan array dan linked list. 2. Mahasiswa dapat membuat dan menggunakan array dan linked list dalam suatu kasus. 3. Mahasiswa
BAB I PENDAHULUAN. himpunan bagian bilangan cacah yang disebut label. Pertama kali diperkenalkan
 1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
1 BAB I PENDAHULUAN 1.1. Latar Belakang Pelabelan graf merupakan suatu topik dalam teori graf. Objek kajiannya berupa graf yang secara umum direpresentasikan oleh titik dan sisi serta himpunan bagian bilangan
Aplikasi Pohon Keputusan dalam Pemilihan Penerima Beasiswa UKT
 Aplikasi Pohon Keputusan dalam Pemilihan Penerima Beasiswa UKT Renjira Naufhal Dhiaegana 135160141 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Aplikasi Pohon Keputusan dalam Pemilihan Penerima Beasiswa UKT Renjira Naufhal Dhiaegana 135160141 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Politeknik Elektronika Negeri Surabaya
 Politeknik Elektronika Negeri Surabaya PRAKTIKUM 28 BINARY SEARCH TREE 2 A. TUJUAN Mahasiswa diharapkan mampu : 1. Memahami konsep menghapus node pada Binary Search Tree. Node yang dihapus adalah node
Politeknik Elektronika Negeri Surabaya PRAKTIKUM 28 BINARY SEARCH TREE 2 A. TUJUAN Mahasiswa diharapkan mampu : 1. Memahami konsep menghapus node pada Binary Search Tree. Node yang dihapus adalah node
Mata Kuliah : Matematika Diskrit Program Studi : Teknik Informatika Minggu ke : 8
 POHON / TREE Dalam dunia informatika, pohon memegang peranan penting bagi seorang programmer untuk menggambarkan hasil karyanya. Bagi seorang user, setiap kali berhadapan dengan monitor untuk menjalankan
POHON / TREE Dalam dunia informatika, pohon memegang peranan penting bagi seorang programmer untuk menggambarkan hasil karyanya. Bagi seorang user, setiap kali berhadapan dengan monitor untuk menjalankan
BAB VII Tujuan 7.1 Deskripsi dari Binary Tree
 A VII Tree Tujuan 1. Mempelajari variasi bagian-bagian dari tree sebagai suatu bentuk struktur tak linier 2. Mempelajari beberapa hubungan fakta yang direpresentasikan dalam sebuah tree, sehingga mampu
A VII Tree Tujuan 1. Mempelajari variasi bagian-bagian dari tree sebagai suatu bentuk struktur tak linier 2. Mempelajari beberapa hubungan fakta yang direpresentasikan dalam sebuah tree, sehingga mampu
BAB 7 POHON BINAR R S U
 BAB 7 POHON BINAR Pohon (Tree) adalah graf terhubung yang tidak mengandung sirkuit. Karena merupakan graf terhubung maka pada pohon selalu terdapat path atau jalur yang menghubungkan kedua simpul di dalam
BAB 7 POHON BINAR Pohon (Tree) adalah graf terhubung yang tidak mengandung sirkuit. Karena merupakan graf terhubung maka pada pohon selalu terdapat path atau jalur yang menghubungkan kedua simpul di dalam
ALGORITMA PENCARIAN (1)
 ALGORITMA PENCARIAN (1) Permasalahan, Ruang Keadaan, Pencarian Farah Zakiyah Rahmanti Diperbarui 2016 Overview Deskripsi Permasalahan dalam Kecerdasan Buatan Definisi Permasalahan Pencarian Breadth First
ALGORITMA PENCARIAN (1) Permasalahan, Ruang Keadaan, Pencarian Farah Zakiyah Rahmanti Diperbarui 2016 Overview Deskripsi Permasalahan dalam Kecerdasan Buatan Definisi Permasalahan Pencarian Breadth First
METODE POHON BINER HUFFMAN UNTUK KOMPRESI DATA STRING KARAKTER
 METODE POHON BINER HUFFMAN UNTUK KOMPRESI DATA STRING KARAKTER Muqtafi Akhmad (13508059) Teknik Informatika ITB Bandung e-mail: [email protected] ABSTRAK Dalam makalah ini akan dibahas tentang
METODE POHON BINER HUFFMAN UNTUK KOMPRESI DATA STRING KARAKTER Muqtafi Akhmad (13508059) Teknik Informatika ITB Bandung e-mail: [email protected] ABSTRAK Dalam makalah ini akan dibahas tentang
Koleksi Hirarkis Tree
 Koleksi Hirarkis Tree Husni Didasarkan pada buku: Fundamentals of Python: From First Programs Through Data Structures Okyektif Menjelaskan perbedaan antara pohon dan tipe koleksi lain menggunakan terminologi
Koleksi Hirarkis Tree Husni Didasarkan pada buku: Fundamentals of Python: From First Programs Through Data Structures Okyektif Menjelaskan perbedaan antara pohon dan tipe koleksi lain menggunakan terminologi
HEAP. Heap dan Operasinya. Oleh Andri Heryandi
 HEAP Heap adalah sebuah binary tree dengan ketentuan sebagai berikut : Tree harus complete binary tree - Semua level tree mempunyai simpul maksimum kecuali pada level terakhir. - Pada level terakhir, node
HEAP Heap adalah sebuah binary tree dengan ketentuan sebagai berikut : Tree harus complete binary tree - Semua level tree mempunyai simpul maksimum kecuali pada level terakhir. - Pada level terakhir, node
Struktur Data dan Algoritma
 Struktur Data dan Algoritma Binary Search Tree Suryana Setiawan, Ruli Manurung & Ade Azurat ( Denny (acknowledgments: Fasilkom UI SUR HMM AA Fasilkom UI - IKI20100/ IKI80110P 2009/2010 Ganjil Minggu 9
Struktur Data dan Algoritma Binary Search Tree Suryana Setiawan, Ruli Manurung & Ade Azurat ( Denny (acknowledgments: Fasilkom UI SUR HMM AA Fasilkom UI - IKI20100/ IKI80110P 2009/2010 Ganjil Minggu 9
Cara Kerja B-tree dan Aplikasinya
 Cara Kerja B-tree dan Aplikasinya Paskasius Wahyu Wibisono - 13510085 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Cara Kerja B-tree dan Aplikasinya Paskasius Wahyu Wibisono - 13510085 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Hal penting dalam menentukan keberhasilan sistem cerdas adalah kesuksesan dalam pencarian.
 Hal penting dalam menentukan keberhasilan sistem cerdas adalah kesuksesan dalam pencarian. 3 Teknik Search menentukan simpul mana yang dibuat lebih dulu dan mana yang kemudian sampai ditemukannya simpul
Hal penting dalam menentukan keberhasilan sistem cerdas adalah kesuksesan dalam pencarian. 3 Teknik Search menentukan simpul mana yang dibuat lebih dulu dan mana yang kemudian sampai ditemukannya simpul
Kecerdasan Buatan. Penyelesaian Masalah dengan Pencarian... Pertemuan 02. Husni
 Kecerdasan Buatan Pertemuan 02 Penyelesaian Masalah dengan Pencarian... Husni [email protected] http://komputasi.wordpress.com S1 Teknik Informatika, STMIK AMIKOM, 2013 Outline Konsep Pencarian Pencarian
Kecerdasan Buatan Pertemuan 02 Penyelesaian Masalah dengan Pencarian... Husni [email protected] http://komputasi.wordpress.com S1 Teknik Informatika, STMIK AMIKOM, 2013 Outline Konsep Pencarian Pencarian
STRUKTUR DATA. By : Sri Rezeki Candra Nursari 2 SKS
 STRUKTUR DATA By : Sri Rezeki Candra Nursari 2 SKS Literatur Sjukani Moh., (2007), Struktur Data (Algoritma & Struktur Data 2) dengan C, C++, Mitra Wacana Media Utami Ema. dkk, (2007), Struktur Data (Konsep
STRUKTUR DATA By : Sri Rezeki Candra Nursari 2 SKS Literatur Sjukani Moh., (2007), Struktur Data (Algoritma & Struktur Data 2) dengan C, C++, Mitra Wacana Media Utami Ema. dkk, (2007), Struktur Data (Konsep
Heap Tree dan Kegunaannya dalam Heap Sort
 Heap Tree dan Kegunaannya dalam Heap Sort Efendy Chalikdjen 1, Hermanto Ong 2, Satria Putra Sajuthi 3 Laboratorium Ilmu dan Rekayasa Komputasi Departemen Teknik Informatika, Institut Teknologi Bandung
Heap Tree dan Kegunaannya dalam Heap Sort Efendy Chalikdjen 1, Hermanto Ong 2, Satria Putra Sajuthi 3 Laboratorium Ilmu dan Rekayasa Komputasi Departemen Teknik Informatika, Institut Teknologi Bandung
Struktur Data & Algoritma
 Struktur Data & Algoritma AVL Tree Suryana Setiawan, Ruli Manurung & Ade Azurat ( Denny (acknowledgments: Fasilkom UI SUR HMM AA Fasilkom UI - IKI20100/ IKI80110P Semester Ganjil 2009/2010 1 Tujuan Memahami
Struktur Data & Algoritma AVL Tree Suryana Setiawan, Ruli Manurung & Ade Azurat ( Denny (acknowledgments: Fasilkom UI SUR HMM AA Fasilkom UI - IKI20100/ IKI80110P Semester Ganjil 2009/2010 1 Tujuan Memahami
Kecerdasan Buatan Penyelesaian Masalah dengan Pencarian
 Kecerdasan Buatan Pertemuan 02 Penyelesaian Masalah dengan Pencarian Kelas 10-S1TI-03, 04, 05 Husni [email protected] http://komputasi.wordpress.com S1 Teknik Informatika, STMIK AMIKOM, 2012 Outline Pendahuluan
Kecerdasan Buatan Pertemuan 02 Penyelesaian Masalah dengan Pencarian Kelas 10-S1TI-03, 04, 05 Husni [email protected] http://komputasi.wordpress.com S1 Teknik Informatika, STMIK AMIKOM, 2012 Outline Pendahuluan
Pemanfaatan Pohon Biner dalam Pencarian Nama Pengguna pada Situs Jejaring Sosial
 Pemanfaatan Pohon Biner dalam Pencarian Nama Pengguna pada Situs Jejaring Sosial Stephen (35225) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Pemanfaatan Pohon Biner dalam Pencarian Nama Pengguna pada Situs Jejaring Sosial Stephen (35225) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Organisasi File Semester Ganjil 2014 Fak. Teknik Jurusan Teknik Informatika. Caca E. Supriana, S.Si.,MT. Si
 Organisasi File Semester Ganjil 2014 Fak. Teknik Jurusan Teknik Informatika Universitas i Pasundan Caca E. Supriana, S.Si.,MT. Si [email protected] 1 Pendahuluan DBMS harus menyimpan data di
Organisasi File Semester Ganjil 2014 Fak. Teknik Jurusan Teknik Informatika Universitas i Pasundan Caca E. Supriana, S.Si.,MT. Si [email protected] 1 Pendahuluan DBMS harus menyimpan data di
PENCARIAN KITAB BESERTA PASAL PADA ALKITAB BERDASARKAN KATA DENGAN MENGGUNAKAN STRUKTUR DATA TRIE
 PENCARIAN KITAB BESERTA PASAL PADA ALKITAB BERDASARKAN KATA DENGAN MENGGUNAKAN STRUKTUR DATA TRIE Ir. Suhatati Tjandra Abstrak Proses pengambilan informasi (information retrieval) merupakan hal yang sangat
PENCARIAN KITAB BESERTA PASAL PADA ALKITAB BERDASARKAN KATA DENGAN MENGGUNAKAN STRUKTUR DATA TRIE Ir. Suhatati Tjandra Abstrak Proses pengambilan informasi (information retrieval) merupakan hal yang sangat
Penerapan BFS dan DFS pada Pencarian Solusi
 Penerapan BFS dan DFS pada Pencarian Solusi Bahan Kuliah IF2151 Strategi Algoritmik Oleh: Rinaldi Munir 1 Pengorganisasian Solusi Kemungkinan2 solusi dari persoalan membentuk ruang solusi (solution space)
Penerapan BFS dan DFS pada Pencarian Solusi Bahan Kuliah IF2151 Strategi Algoritmik Oleh: Rinaldi Munir 1 Pengorganisasian Solusi Kemungkinan2 solusi dari persoalan membentuk ruang solusi (solution space)
Aplikasi Pohon Keputusan pada Permainan Catur
 Aplikasi Pohon Keputusan pada Permainan Catur Christian Anthony Setyawan 13514085 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Aplikasi Pohon Keputusan pada Permainan Catur Christian Anthony Setyawan 13514085 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Topic Complexity of Hashing Search & Binary Search Tree Algorithm
 Topic Complexity of Hashing Search & Binary Search Tree Algorithm Febriansyah Kurniawan M. Nasir Suyanto Searching a list of values is a common task. An application program might retrieve a student record,
Topic Complexity of Hashing Search & Binary Search Tree Algorithm Febriansyah Kurniawan M. Nasir Suyanto Searching a list of values is a common task. An application program might retrieve a student record,
Dasar Kerja Pengaplikasian Self-balancing Binary Search Tree untuk Pencarian sebagai Struktur Data yang Lebih Mangkus dan Sangkir
 1 Dasar Kerja Pengaplikasian Self-balancing Binary Search Tree untuk Pencarian sebagai Struktur Data yang Lebih Mangkus dan Sangkir Michell Setyawati Handaka (135 08 045) Program Studi Teknik Informatika
1 Dasar Kerja Pengaplikasian Self-balancing Binary Search Tree untuk Pencarian sebagai Struktur Data yang Lebih Mangkus dan Sangkir Michell Setyawati Handaka (135 08 045) Program Studi Teknik Informatika
MAKALAH DESAIN DAN ANALISIS ALGORITMA BINARY TREE DISUSUN OLEH : 1. Nadim Achmad ( ) 2. Dzurratul Ulya ( )
 MAKALAH DESAIN DAN ANALISIS ALGORITMA BINARY TREE DISUSUN OLEH : 1. Nadim Achmad (105060 807111009) 2. Dzurratul Ulya (105060807111120) 3. Safer Yusuf (105060803111004 ) PROGRAM TEKNOLOGI INFORMASI DAN
MAKALAH DESAIN DAN ANALISIS ALGORITMA BINARY TREE DISUSUN OLEH : 1. Nadim Achmad (105060 807111009) 2. Dzurratul Ulya (105060807111120) 3. Safer Yusuf (105060803111004 ) PROGRAM TEKNOLOGI INFORMASI DAN
Pohon (Tree) Contoh :
 POHON (TREE) Pohon (Tree) didefinisikan sebagai graph terhubung yang tidak mengandung sirkuit. Sedangkan Hutan (Forest) adalah graph yang tidak mengandung sirkuit. Jadi pohon adalah hutan yang terhubung.
POHON (TREE) Pohon (Tree) didefinisikan sebagai graph terhubung yang tidak mengandung sirkuit. Sedangkan Hutan (Forest) adalah graph yang tidak mengandung sirkuit. Jadi pohon adalah hutan yang terhubung.
Tujuan Instruksional
 Pertemuan 4 P E N C A R I A N T A N P A I N F O R M A S I B F S D F S U N I F O R M S E A R C H I T E R A T I V E D E E P E N I N G B I D I R E C T I O N A L S E A R C H Tujuan Instruksional Mahasiswa
Pertemuan 4 P E N C A R I A N T A N P A I N F O R M A S I B F S D F S U N I F O R M S E A R C H I T E R A T I V E D E E P E N I N G B I D I R E C T I O N A L S E A R C H Tujuan Instruksional Mahasiswa
POHON BINAR 7.1 POHON. Gambar 7.1. Contoh pohon berakar
 POHON BINAR 7.1 POHON Pohon atau tree adalah salah satu bentuk graph terhubung yang tidak mengandung sirkuit. Karena merupakan graph terhubung, maka pada pohon selalu terdapat path atau jalur yang menghubungkan
POHON BINAR 7.1 POHON Pohon atau tree adalah salah satu bentuk graph terhubung yang tidak mengandung sirkuit. Karena merupakan graph terhubung, maka pada pohon selalu terdapat path atau jalur yang menghubungkan
