Pengantar Computer Graphics Algoritma Dasar
|
|
|
- Agus Gunardi
- 8 tahun lalu
- Tontonan:
Transkripsi
1 Ha Pengantar Computer Graphics Algoritma Dasar Vincent Suhartono Bacaan Teknologi Informasi
2 Pengantar Computer Graphics Algoritma Dasar Penulis: Vincent Suhartono Bacaan Teknologi Informasi
3 Pengantar Computer Graphics: Bacaan Teknologi Informasi Penulis : Vincent Suhartono ISBN : Editor : Claudia Clarentia Ciptohartono Penunting : Totok Sutoo Desain Sampul dan Tata Letak : Claudia Clarentia Ciptohartono Penerbit : CV Mulia Jaa Redaksi : Jalan Anggajaa II No. 29-A, Condong Catur Kabupaten Sleman, Yogakarta Telp : [email protected] Cetakan Pertama April 26 Hak Cipta dilindungi undang-undang Dilarang memperbanak kara tulis ini dalam bentuk dan dengan cara apapun tanpa ijin tertulis dari penerbit. 2
4 KATA PENGANTAR Puji sukur, penulis panjatkan kehadirat Allah YME ang telah memberikan segala karunia ang tak terhingga sehingga penulis dapat menelesaikan buku ini. Buku ini ditulis dengan maksud untuk membantu pelajar dan mahasiswa sehingga dapat mengerti dan memahami seluk beluk Computer Graphics meskipun hana dalam bentuk teori ang masih sangat mendasar. Terima kasih sebesar-besarna kepada semua pihak ang telah membantu dalam pembuatan buku ini, aitu:. Universitas Dian Nuswantoro 2. Koordinator Matakuliah Computer Graphics 3. Teman-teman ang tidak dapat disebutkan satu per satu namana Kami menadari bahwa dalam buku ini masih memiliki sejumlah kekurangan. Oleh karena itu, saran dan komentar sangat dinantikan untuk perbaikan selanjutna. Meskipun demikian, kami tetap berharap semoga buku ini dapat membantu dan bermanfaat. Semarang, 2 Januari 26 Penulis iii 3
5 DAFTAR ISI KATA PENGANTAR... iii DAFTAR ISI... iv DAFTAR GAMBAR... vii DAFTAR TABEL... i Bab... 2 Pendahuluan Aplikasi Computer Graphics Graphics Languages Sistem Pemrograman Grafis Komponen Graphics Librar Ringkasan Bab Soal-Soal Latihan Bab Spesifikasi Graphics Primitif Piel (Picture Element) Warna Garis Bab Algoritma, Analisa, dan Tampilan Graphics Dua Dimensi (2D) Algoritma Brute Force Algoritma DDA (Digital Diferential Analzer) Algoritma Bressenham Lingkaran Simetris Delapan Titik Algoritma Midpoint Polgon iv 4
6 3.6 Filling Polgon Scan Line Polgon Fill Algorithms Boundar-Fill Algorithm Flood-Fill Algorithm... 8 Ringkasan Bab 3... Soal-Soal Latihan... Bab Atribut Output Primitif Atribut Titik Atribut Garis Tipe Garis Ukuran Garis Pen dan Brush Warna Garis... 7 Ringkasan Bab Soal-Soal Latihan... 9 Bab Transformasi Geometri Translasi (Pergeseran) Scalling (Penskalaan) Rotasi (Perputaran) Sistem Koordinat Homogen 2D Komposisi Matrik Transformasi 2D Transformasi Geometri 3D Ringkasan Bab Soal-Soal Latihan... 4 Daftar Istilah v
7 Daftar Pustaka Biografi Penulis vi 6
8 DAFTAR GAMBAR Gambar. Aplikasi grafika komputer pada bidang hiburan berupa film-film animasi 3D... 4 Gambar. 2 (a) Visualisasi Scientific (b) Visualisasi aliran turbulen dari angin topan... 5 Gambar. 3 Pembelajaran transformasi Fourier untuk peningkatan kualitas citra... 7 Gambar. 4 Gambar kartun, digambar menggunakan Paint under window... 8 Gambar. 5 Hasil perbaikan citra ang terkena noise domain frekuensi menggunakan transformasi Fourier... 9 Gambar. 6 GUI dari aplikasi-aplikasi pada sistem operasi Windows XP... 2 Gambar. 7 Sistem Pemrograman Grafis Gambar 2. Laar berisi M baris piksel dan N kolom piksel. Sebuah piksel (titik hitam) terletak pd (3,2) Gambar 2. 2 Garis lurus ang melalui titik P (, ) dan P 2( 2, 2). 34 Gambar 3. Pembulatan nilai dilakukan karena posisi piel adalah bulat (integer) Gambar 3. 2 Titik-titik pembentuk garis hasil perhitungan menggunakan algoritma Brute Force digambar pada raster graphics Gambar 3. 3 (a) Garis dengan kemiringan m >, tampak bahwa garis tidak kontinu (b) setelah dilakukan interpolasi garis menjadi kontinu Gambar 3. 4 Titik-titik pembentuk garis hasil perhitungan menggunakan algoritma DDA digambar pada raster graphics vii 7
9 Gambar 3. 5 Garis mempunai kemiringan < m <, pada titik = p+, garis berada diantara dua titik E dan NE ang mempunai titik tengah di M Gambar 3. 6 Titik-titik pembentuk garis dengan kemiringan < m <, hasil perhitungan menggunakan algoritma Bressenham ang digambar pada raster graphics Gambar 3. 7 Titik-titik pembentuk garis dengan kemiringan < m <, hasil perhitungan menggunakan algoritma Bressenham ang digambar pada raster graphics Gambar 3. 8 Terjadina gaps ang disebabkan adana perubahan gradient menghasilkan posisi koordinat piksel ang tidak merata Gambar 3. 9 Delapan titik simetris pada lingkaran Gambar 3. Garis lingkaran berada diantara titik ( k+, k) dan ( k+, k ) Gambar 3. Posisi piksel pada pembentukan lingkaran dengan titik pusat (,) dan jari-jari Gambar 3. 2 Polgon sederhana dan polgon tidak sederhana 83 Gambar 3. 3 : Permukaan bola, torus dan teko ang terbentuk dari banak polgon Gambar 3. 4 Metode scan-line Gambar 3. 5 Aturan paritas ganjil-genap untuk mengisi warna 86 Gambar 3. 6 Perhitungan paritas pada verteks a, b, c, dan d Gambar 3. 7 Polgon dengan sisi-sisi horisontal Gambar Gambar Gambar Gambar Gambar Gambar viii 8
10 Gambar Gambar Gambar Gambar Gambar Gambar Gambar Gambar Gambar Gambar Gambar Gambar Gambar Metode Boundar-Fill... 3 Gambar Gambar Gambar Gambar Gambar Gambar Gambar Gambar penggantian warna obek menggunakan Flood-Fill Algorithm. (a) lingkaran berwarna merah, segitiga berwarna hijau dan persegi berwarna biru. Obek tersebut warnana diubah menjadi (b) lingkaran berwarna abu-abu, segitiga berwarna kuning dan persegi berwarna coklat... 8 Gambar 4. Tpe garis : solid line, dashed line, dotted line dan dashed-dotted line... 5 i 9
11 Gambar 4. 2 Ukuran garis dari ¼ pt sampai dengan 6 pt pada software aplikasi Microsoft Word Gambar 4. 3 Beberapa bentuk pen atau brush pada paket program aplikasi Paint... 6 Gambar Gambar Gambar Gambar Gambar
12 DAFTAR TABEL Tabel Tabel Tabel Tabel Tabel i
13 Bab Pendahuluan TUJUAN PEMBELAJARAN Agar pembaca mempunai wawasan mengenai aplikasi grafika komputer di berbagai bidang. OUTCOME PEMBELAJARAN Pembaca mampu menjelaskan pengertian grafika komputer dan bisa memberikan beberapa contoh aplikasi grafika komputer di berbagai bidang. Pendahuluan Berbagai informasi ang divisualisasikan dalam bentuk gambar sudah ada jauh sebelum komputer ditemukan. Sebagai contoh, gambar-gambar zaman purba ang masih terdapat pada guagua, juga tulisan Hieroglph pada zaman mesir kuno juga dalam bentuk gambar. Pepatah mengatakan bahwa: Satu gambar dapat menerangkan kata dan tentu lebih bisa menerangkan bilangan. Suatu laporan (informasi) ang disajikan dalam bentuk angkaangka sangat menulitkan pembaca untuk bisa memahami secara cepat, bahkan konsentrasi akan menurun dalam waktu ang tidak begitu lama. Untuk menghindari hal ini maka informasi tersebut 2
14 perlu diubah hingga menjadi suatu gambaran grafis, sehingga jauh lebih mudah untuk dicerna. Masalah ini menjadi sangat penting jika laporan tadi akan dipergunakan sebagai acuan pengambilan keputusan, seperti misalna untuk pembelian. Presentasi ang baik biasana disertai dengan visualisasi terutama untuk tabel dengan bilangan ang sangat banak. Juga arah pengembangan komputer sendiri tidak lepas dari visualisasi grafis. Sebagai contoh adalah GUI (Graphical User Interface), ang kita pakai setiap hari dalam penggunaan komputer. Lebih jauh lagi komputer sebagai bagian dari multimedia dan broadcasting dituntut untuk dapat mengolah gambar ang bergerak (video). Pengetahuan tentang grafik programming sangat diperlukan bahkan sebagai sarat untuk pengolahan gambar. Sehingga perlu adana pengantar atau penggalian kembali topik akan grafika komputer. Grafika komputer (Computer graphics) adalah bagian dari ilmu komputer ang mempelajari cara-cara pembuatan dan manipulasi gambar secara digital, sehingga dapat memudahkan komunikasi antara manusia dan komputer, atau manusia dengan manusia melalui gambar-gambar, bagan-bagan, tabel dan lain-lain. Teknikteknik ang dipelajari dalam grafika komputer adalah teknik-teknik bagaimana membuat atau menciptakan gambar dengan menggunakan komputer. Bentuk sederhana dari grafika komputer adalah grafika komputer 2D, dengan teknik-teknik tertentu kemudian berkembang menjadi grafika komputer 3D. 3
15 . Aplikasi Computer Graphics Peran grafika komputer dalam menghasilkan gambar sangat penting sekali untuk perkembangan berbagai software aplikasi. Banak sekali aplikasi-aplikasi tertentu ang memanfaatkan grafika komputer, diantarana adalah:. Hiburan (Entertainment) Saat ini grafika komputer banak digunakan untuk menunjang pembuatan film, video musik, taangan televisi, motion picture, animasi, dan game (permainan). Gambar. Aplikasi grafika komputer pada bidang hiburan berupa film-film animasi 3D Sumber: com/28/2/ upinipinbajubaru.jpg 4
16 2. Visualisasi Visualisasi (visualization) adalah teknik-teknik dalam pembuatan gambar, diagram atau animasi untuk mengkomunikasikan suatu informasi. Pada saat ini visualisasi telah menjadi cara ang efektif dalam mengkomunikasikan data atau ide abstrak maupun nata sehingga cepat berkembang dan banak dipakai untuk keperluan ilmu pengetahuan, rekaasa, visualisasi disain produk, pendidikan, multimedia interaktif, kedokteran, dan lain-lain. Gambar. 2 (a) Visualisasi Scientific (b) Visualisasi aliran turbulen dari angin topan Sumber : 5
17 3. Computer-Aided Design (CAD) Grafika komputer digunakan dalam proses analisis dan desain, khususna untuk sistem arsitektural dan engineering dalam bentuk aplikasi CAD (Computer-Aided Design). CAD banak digunakan untuk mendesain bangunan, mobil, kapal, pesawat terbang, gedung, komputer, alat-alat elektronik, peralatan rumah tangga, dan berbagai produk lainna. Contoh perangkat lunak : AutoCAD, 3D Studio Ma dan lain-lain. 4. Computer-Aided Sofware Engineering (CASE) CASE digunakan dalam bidang sofware engineering. CASE biasana digunakan untuk memodelkan user requirement, pemodelan basisdata, workflow dalam proses bisnis, struktur program, dan sebagaina. Contoh perangkat lunak: Rational Rose, SBase Power Designer dan lain-lain. 5. Virtual Realit Virtual Realit adalah lingkungan virtual ang seakan-akan sama seperti lingkungan nata. Pada lingkungan ini user dapat berinteraksi dengan objek-objek dalam lingkungan 3-D. Dibutuhkan perangkat keras khusus untuk memberikan efek pemandangan 3-D dan membuat user mampu beriteraksi dengan objek-objek ang berada di lingkungan tersebut. Contoh: aplikasi Virtual Realit pilot trainer ang digunakan untuk latihan mengendarai pesawat terbang. Aplikasi ini dapat memberikan keutungan berupa mengurangi resiko cedera selama latihan, mengurangi biaa penerbangan, melatih pilot- 6
18 pilot pemula sebelum melakukan penerbangan ang sesungguhna. 6. Pendidikan dan Pelatihan Komputer digunakan sebagai alat bantu pendidikan dan pelatihan, misalna untuk membuat model-model proses fisika dan kimia, fungsi-fungsi psikologi, simulasi, dan sebagaina sehingga memudahkan sesorang untuk memahami bagaimana operasi atau proses ang terjadi dalam suatu sistem. Contoh: pembelajaran transformasi Fourier untuk peningkatan kualitas citra. Gambar. 3 Pembelajaran transformasi Fourier untuk peningkatan kualitas citra 7. Computer Art Computer art adalah penggunaan komputer grafis untuk menghasilkan kara-kara seni. Sebagai contoh grafika komputer digunakan untuk desktop publishing (cover buku), advertising (logo perusahaan), desain tekstil dan lain 7
19 sebagaina menggunakan perangkat lunak CorelDraw, Macromedia Freehand atau Adobe Ilustrator. Grafika komputer digunakan untuk pembuatan bermacam-macam gambar kartun sesuai dengan gagasan atau imajinasi seorang seniman menggunakan perangkat lunak ang berbasis paint contoh Paint, Corel Paint Shop Pro dan Adobe Photoshop. Gambar. 4 Gambar kartun, digambar menggunakan Paint under window 8. Pengolahan Citra Digital Pengolahan citra digital adalah teknik-teknik untuk mengolah citra digital. Pengolahan ang dilakukan meliputi, peningkatan kualitas citra, perbaikan citra, segmentasi citra, pengenalan pola menggunakan fitur-fitur ang ada dalam suatu citra. Contoh: perbaikan citra sehingga menjadi lebih jelas. 8
20 Gambar. 5 Hasil perbaikan citra ang terkena noise domain frekuensi menggunakan transformasi Fourier 9. Graphical User Interface (GUI) Graphical User Inteface adalah antarmuka grafis ang berguna untuk mempermudah interaksi antara manusia dengan komputer dan alat-alat ang dikendalikan oleh komputer. Gambar.6 menunjukkan GUI berupa window-window ang digunakan pada sistem operasi Windows XP. 9
21 Gambar. 6 GUI dari aplikasi-aplikasi pada sistem operasi Windows XP.2 Graphics Languages ) IGL (Interactive Graphics Librar) Salah satu paket grafis ang mengandung pustaka fungsi grafis ang lengkap. 2) GKS (Graphical Kernel Sstem) Rutin-rutin perangkat independen ang umum digunakan. Menggunakan pustaka UIS (User Interface Sstem) untuk pelaksanaan ditingkat low level. 3) HPGL (Hewlett Packard Graphics Librar) 2
22 Kumpulan Instruksi untuk berbagai fungsi output grafis untuk Plotter. 4) ReGIS (Remote Graphics Instruction Set) Khusus dikembangkan untuk pemrograman di terminal seri TV. 5) PHIGS (Programmer s Hierarchical Interactive Graphics Standard) Sebuah perangkat untuk keperluan umum dan merupakan paket grafis ang handal untuk mendukung sebagian besar bahasa pemrograman ang umum digunakan. 6) SG-GL (Silicon Graphics - Graphics Librar) Berisi rutin-rutin ang cepat dan efisien ang dikembangkan oleh Silicon Graphics (misalna OpenGL) 7) Computer-Aided Design (CAD) Alat grafis untuk menggambar, desain berbantukan komputer dan Manufaktur 8) PC-Graphics Untuk pemrograman grafis pada lingkungan DOS dan Windows. Contohna adalah: MVisual Basic, Visual C + + dengan GUI. 2
23 .3 Sistem Pemrograman Grafis Pada sstem pemrograman grafis, user menginput data (berupa program) melalui piranti input dan menggunakan software tertentu, kemudian software memanggil graphics librar untuk mendapatkan instruksi-instruksi ang cepat, selanjutna hasil dari program ditampilkan dilaar berupa gambar sesuai dengan apa ang diprogram. Gambar. 7 Sistem Pemrograman Grafis.4 Komponen Graphics Librar ) Fungsi Output - Fungsi untuk menggambar primitif grafik, misalna titik, garis, kurva lengkung, poligon, teks dan lainlain. 2) Atribut Output - Fungsi untuk men-set atribut, misalna tebal garis, isi warna, tinggi tkes dan lain-lain. 22
24 3) Fungsi Kontrol Fungsi untuk menangani event handling, error processing, I/O control dan lain-lain. 4) Operasi File Fungsi untuk menimpan dan mengambil output grafik. 5) Fungsi Matematika and Graphics - Transformasi, hidden line removal, rendering, clipping, window to viewport mapping, segments dan lain-lain. 6) Inquir functions - Fungsi untuk memberitahukan tentang status dan setting dari alat-alat output ang bekerja saat ini. 23
25 Ringkasan Bab Grafika komputer (Computer graphics) adalah bagian dari ilmu komputer ang mempelajari cara-cara pembuatan dan manipulasi gambar secara digital, sehingga dapat memudahkan komunikasi antara manusia dan komputer, atau manusia dengan manusia melalui gambar-gambar, baganbagan, tabel dan lain-lain. Grafika computer telah banak di aplikasikan di berbagai bidang diantarana adalah bidang hiburan, visualisasi, CAD (Computer- Aided Design), Virtual Realit, Pendidikan dan Pelatihan, Computer Art, Pengolahan Citra Digital, Graphical User Interface (GUI), dan sebagaina. 24
26 Soal-Soal Latihan. Jelaskan dan berikan contohna peran grafika komputer dibidang : a. Hiburan b. Visualisasi c. CAD (Computer-Aided Design) d. Virtual Realit e. Pendidikan dan Pelatihan f. Computer Art g. Pengolahan Citra Digital h. Graphical User Interface (GUI). 2. Jelaskan peran grafika komputer untuk visualisasi pada teknologi informasi khususna komputer! 3. Sebutkan beberapa bahasa pemrograman ang bisa digunakan untuk mengimplementasikan teori-teori grafika komputer! 25
27 Bab 2 Spesifikasi Graphics Primitif TUJUAN PEMBELAJARAN Agar pembaca mengetahui definisi graphics primitif. Agar pembaca memahami primitif geometri titik dan garis. Agar pembaca memahami algoritma Area Filling scan line dan Boundar Fill OUTCOME PEMBELAJARAN Pembaca dapat menjelaskan dan memberikan contoh tentang definisi graphics primitif. Pembaca dapat menjelaskan primitif geometri titik dan garis. Pembaca dapat menjelaskan perbedaan algoritma Area Filling scan line dan Boundar Fill. Pendahuluan Graphics primitif adalah struktur dasar geometri ang paling sederhana dari gambar grafika komputer. Titik dan garis adalah contoh dari output primitif ang dapat digunakan untuk membentuk gambar, misalna lingkaran, kerucut, permukaan berbentuk persegi, kurva dan permukaan berbentuk lengkung, warna area dan karakter, dan lain-lain. Gambar-gambar seperti 26
28 rumah, tembok, gedung dan lain-lain merupakan obek ang lengkap ang ditempatkan pada koordinat tertentu pada laar, dimana obek-obek tadi sebenarna tersusun dari kumpulan titik dan garis sebagai penusunna. 2. Piel (Picture Element) Piel adalah elemen gambar terkecil berupa sebuah titik ang ditempatkan dilaar. Jumlah kolom piksel = N (,) Sistem Koordinat Piksel berada di posisi (3,2) Gambar 2. Laar berisi M baris piksel dan N kolom piksel. Sebuah piksel (titik hitam) terletak pd (3,2). Gambar 2. menunjukkan sebuah piksel mempunai koordinat (3,2) pada laar. Jumlah Piksel untuk setiap gambar tergantung dari kemampuan Graphics card. Terdapat beberapa tampilan format gambar: 27
29 Standart -maksimal -maksimal Jumlah keseluruhan Piel VGA SVGA XGA SXGA Tabel 2. Sebagai pembanding adalah taangan televisi standart dengan jumlah titik gambar sebesar 4. Piksel. Bandingkan dengan WebCam standar VGA dan juga dengan HP ang memiliki fasilitas perekam 2 Mega Piksel. Resolusi Piksel adalah jumlah N piksel persatuan lebar () kali panjang () ( : width, height ) Jika laar mempunai dimensi p inchi sepanjang dan q inchi sepanjang, maka : resolusi- = N p piel/inchi (ppi) Persamaan 2 - resolusi- = M piel/inchi (ppi) q Persamaan
30 Aspek rasio = resolusi resolusi ( Height : Width ) Persamaan 2-3 Frame buffer adalah area memor tempat informasi gambar disimpan. Jika sstem mempunai n bit memori untuk tiap-tiap piksel, maka ukuran frame buffer adalah = H W n / 8 bte. Jumlah warna ang bisa ditampilkan secara bersama-sama dilaar adalah 2 n. Sistem dikatakan mempunai n bit planes. Screen Mode Piels Screen Bit Colors Memor Ratio planes CGA(med res) 322 4: K CGA(high res) 642 4:3 28K EGA : K VGA : K Super VGA- 86 4: M.44M Super VGA :3 6 65K.57M Tabel
31 Atribut dari piksel adalah warnana (indeks warna) i, dimana i 2 n. Biasana indeks warna ang bernilai melambangkan warna hitam. Monitor monokrom ang mempunai satu bit plane hana bisa menampilkan dua warna, aitu warna hitam () sebagai background dan warna putih () sebagai foreground. Monitor monokrom ang mempunai 8 bit plane bisa menampilkan 256 warna ang berbeda, ang disebut dengan grascale dengan indeks warna dimulai dari (hitam) sampai dengan 255 (putih). Contoh 2. Diketahui sebuah sistem dengan 28 X 24 frame buffer, mempunai 4 bits per piksel. jika sistem tersebut dapat mentransfer data 4 bits per detik, berapa lama waktu ang dibutuhkan untuk loading? Jawab: Jumlah piksel pada frame buffer = = 372 piksel Jumlah bit pada frame buffer = 372 piksel 4 bit /piksel = bit Waktu loadingna = bit bit / sekon 4 524,28 sekon 3
32 2.2 Warna Sudah dikatakan diatas bahwa warna merupakan atribut dari piksel. Selain piksel, ang lebih penting diperhitungkan lagi adalah warna dari piksel itu sendiri. Setiap piksel mengandung informasi mengenai warna dengan jumlah ang beragam. Pada awalna saat teknik penggambaran belum begitu maju, hana disediakan 6 kemungkinan warna setiap Pikselna. Tetapi Graphics card sekarang ini sudah mampu menampilkan gambar dengan berbagai macam kedalaman seperti pada tabel dibawah ini: Jumlah Bte setiap Piel Jumlah warna ang mampu ditampikan Color Qualit (8 bit) 2 (6 bit) 3 (24 bit) 4 (32 bit) Low Medium High Highest Tabel 2. 3 Untuk menampilkan suatu gambar pada laar monitor sering kali tidak cukup hana dengan 256 tampilan warna. Tetapi jika jumlah tampilan warna diperbesar maka memerlukan ruang (memori) lebih banak lagi. Lihat tabel kebutuhan memori di bawah ini: 3
33 /- B / 2 B / 3 B / 4 B / Piksel Format Piksel Piksel Piksel kb 6 kb 9 kb 2 kb kb 938 kb 46 kb 876 kb kb 536 kb 234 kb 372 kb kb 2622 kb 3933 kb 5244 kb Tabel 2. 4 Untuk menampilkan gambar pada laar monitor tabung sehingga tanpa efek kerdipan (flicker-free) diperlukan pengulangan taang sebanak 75 kali dalam satu detik. Bisa dicoba pada laar monitor, turunkan frekuensi monitor anda pada penetelan: displa settings advanced Monitor Screen refresh rate = 6. Terasa kerdipan ang mengganggu dan tidak naman di mata. Pengulangan taangan per detik ang begitu tinggi (lebih besar dari 75) pada resolusi (ketajaman gambar) ang tinggi pula, dapat menebabkan kesulitan dalam memindahkan gambar dari graphic card ke laar monitor (diperlukan transfer-rate ang besar). Berbeda dengan laer LCD (Liquid Crstal Displa). Pada laer LCD tidak dijumpai efek kerdipan (flicker) sehingga tidak memerlukan frekuensi pengulangan gambar ang tinggi. Hana saja, ang masih 32
34 menjadi masalah pada laar LCD adalah sudut pandang ang terbatas, dela time, dan tinggina harga. Secara teknis warna pada pesawat televisi tidak dipindahkan dalam bentuk Bte untuk setiap elemen gambarna, akan tetapi sudah berupa sinal warna analog. Sebagai pembanding Photo-CD ang dikeluarkan oleh Kodak memiliki resolusi sebesar 25 3 Piksel dengan kedalaman 3 Bte warna. Perbandingan ke tiga format dapat dilihat pada tabel dibawah ini: Televisi standar Gambar komputer (6 8 3 Bte) Photo-CD 8 kilo Bte.5 Mega Bte 2 Mega Bte 2.3 Garis Tabel 2. 5 Software untuk menggambar garis lurus pada setiap paket grafika komputer secara tradisi sebagai fungsi elementarna sudah tersedia, tetapi ada baikna kita simak lebih seksama bagaimana algoritma sebagai dasar penggambaran titik-titik pada raster graphics. Raster graphics diartikan sebagai grafik ang dibangun atas dasar titik-titik pada kolom dan baris ang 33
35 juga mengandung informasi warna. Gambar 2.2 adalah sebuah garis lurus ang melalui titik (, ) dan ( 2, 2). Gambar 2. 2 Garis lurus ang melalui titik P (, ) dan P 2( 2, 2) Secara umum garis lurus dinatakan dalam persamaan : = m + c Persamaan 2-4 dimana : m adalah gradient dan c adalah konstanta. Bila garis melalui titik (, ) dan titik ( 2, 2) maka gradien m dihitung menggunakan persamaan (2-5) m 2 2 Persamaan
36 Persamaan garis bergradien m ang melewati titik (, ) adalah: m ( ) Persamaan 2-6 Berdasarkan persamaan (2-4), garis ang melalui titik (, ) dan titik ( 2, 2) dapat ditulis sebagai berikut, c m. m 2. 2 atau 2 m 2 ) ( atau 2 m Persamaan 2-7 bila =, maka persamaan (2-7) menjadi m 2 Persamaan 2-8 Algoritma untuk menggambar garis pada komputer didasarkan pada persamaan (2-6) dan (2-8). Tugas dari algoritma pembentuk garis adalah menentukan titiktitik diantara dua titik ujung (, ) dan ( 2, 2) ang akan digambar sebagai garis. 35
37 Kriteria algoritma pembentuk garis ang baik: ) Garis antara dua titik ujung tersebut sebisa mungkin harus lurus. 2) Kerapatan titik-titik konstan (tidak ada gap antara dua titik ang bersebelahan). 3) Kerapatan titik-titik tidak tergantung pada kemiringan garis. 4) Waktu proses algoritma harus cepat. 36
38 Bab 3 Algoritma, Analisa, dan Tampilan Graphics Dua Dimensi (2D) TUJUAN PEMBELAJARAN Agar pembaca memahami algoritma pembentukan garis brute force, DDA (Digital Diferential Analzer ) dan Bressenham. Agar pembaca memahami algoritma pembentukan lingkaran. Agar pembaca memahami algoritma Area Filling scan line dan Boundar Fill. OUTCOME PEMBELAJARAN Pembaca dapat menjelaskan perbedaan algoritma pembentukan garis brute force, DDA dan Bressenham. Pembaca dapat menjelaskan algoritma pembentukan lingkaran. Pembaca dapat menjelaskan perbedaan algoritma Area Filling scan line dan Boundar Fill. 37
39 Pendahuluan Output primitif adalah struktur dasar geometri ang paling sederhana dari gambar grafika komputer. Titik dan garis adalah contoh dari output primitif ang dapat digunakan untuk membentuk gambar, misalna lingkaran, kerucut, permukaan berbentuk persegi, kurva dan permukaan berbentuk lengkung, warna area dan karakter, dan lain-lain. Gambar-gambar seperti rumah, tembok, gedung dan lain-lain merupakan obek ang lengkap ang ditempatkan pada koordinat tertentu pada laar, dimana obek-obek tadi sebenarna tersusun dari kumpulan titik dan garis sebagai penusunna. 3. Algoritma Brute Force Algoritma brute force untuk membentuk garis didasarkan pada persamaan (2-6), aitu :. Tentukan dua titik ujung (, ) dan ( 2, 2) 2. Jika = 2 (garis vertikal), maka (a) = + dan tetap (b) gambar titik (,) di laar (c) Selesai 3. Jika = 2 (garis horisontal), maka (a) = + dan tetap (b) gambar titik (,) di laar (c) Selesai {anggap 2 >, (jika sebalikna, gantilah 2 dengan )} 38
40 4. Hitung kemiringan garis m = ( 2 )/( 2 ) 5. N = = 7. Ulang sebanak N kali: (a) m ( ) (b) lakukan pembulatan a = Round(), (c) gambar titik (, a) di laar (d) = + 8. selesai Perhatikan langkah 7(b), karena posisi piksel adalah integer (bilangan bulat), dan nilai gradien m biasana pecahan, maka nilai adalah bilangan pecahan, sehingga kita perlu melakukan pembulatan terhadap nilai. Perhatikan Gambar 2.3 berikut. Garis ang ( i+,round( i+m)) ( i, i) ( i+, i+m) ( i, Round( i)) Gambar 3. Pembulatan nilai dilakukan karena posisi piel adalah bulat (integer) 39
41 Contoh 2.2 Diketahui 2 buah titik A(2,) dan titik B(8,5) bila titik A sebagai titik awal dan titik B sebagai titik akhir, maka buatlah garis ang menghubungkan titik tersebut dengan menggunakan algoritma Brute Force. Jawab:. titik ujung (, ) = (2,) dan ( 2, 2) = (8,5) 2. tidak dipenuhi 3. tidak dipenuhi 4. m = (5 )/(8 2) =,67 5. N = = 7 6. untuk = 2 =,67 ( 2) + 7. Ulang sebanak 7 kali iterasi ke-: = 2; =,67. (2 2) + = pembulatan: = gambar titik (2,) di laar = 2 + = 3 =================================================== iterasi ke-2: = 3; =,67. (3 2) + =,67 4
42 pembulatan: = 2 gambar titik (3,2) di laar. = 3 + = 4 =================================================== iterasi ke-3: = 4; =,67. (4 2) + = 2,34 pembulatan: = 2 gambar titik (4,2) di laar. = 4 + = 5 =================================================== iterasi ke-4: = 5; =,67. (5 2) + = 3, pembulatan: = 3 gambar titik (5,3) di laar. = 5 + = 6 =================================================== iterasi ke-5: = 6; =,67. (3 2) + = 3,68 pembulatan: = 4 gambar titik (6,4) di laar. 4
43 = 6 + = 7 =================================================== iterasi ke-6: = 7; =,67. (7 2) + =4,35 pembulatan: = 4 gambar titik (7,4) di laar. = 7 + = 8 ================================================ iterasi ke-7: = 8; =,67. (7 2) + =5,2 pembulatan: = 5 gambar titik (8,5) di laar. Maka diperoleh titik-titik pembentuk garis : (2,), (3,2), (4,2), (5,3), (6,4), (7,4), (8,5). 42
44 Gambar 3. 2 Titik-titik pembentuk garis hasil perhitungan menggunakan algoritma Brute Force digambar pada raster graphics. Masalah : Untuk kemiringan m >, garis menjadi tidak kontinu (Gambar 2.5(a)) ang mengakibatkan terjadina gap antar piksel, sehingga diperlukan interpolasi (Gambar 2.5(b)). (a) (b) Gambar 3. 3 (a) Garis dengan kemiringan m >, tampak bahwa garis tidak kontinu (b) setelah dilakukan interpolasi garis menjadi kontinu. 43
45 Selain menggunakan interpolasi, untuk kemiringan garis m >, tukarlah dengan maka sudah tidak terjadi gap antara titik ang satu dengan ang lain. Sehingga algoritma pembentukan garis untuk m > adalah sebagai berikut :. Tentukan dua titik ujung (, ) dan ( 2, 2) 2. Jika = 2 (garis vertikal), maka (a) = + dan tetap (b) gambar titik (,) di laar (c) Selesai 3. Jika = 2 (garis horisontal), maka (a) = + dan tetap (b) gambar titik (,) di laar (c) Selesai {anggap 2 >, (jika sebalikna, gantilah 2 dengan )} 4. Hitung kemiringan garis m = ( 2 ) /( 2 ) 5. N = = 7. Ulang sebanak N kali: m ( ) (a) (b) lakukan pembulatan a = Round(), (c) gambar titik ( a,) di laar 44
46 (d) = + 8. selesai Contoh 2.3 Diketahui 2 buah titik A(4,3) dan titik B(7,8) bila titik A sebagai titik awal dan titik B sebagai titik akhir, maka buatlah garis ang menghubungkan titik tersebut dengan menggunakan algoritma Brute Force. Jawab:. titik ujung A(4,3) dan B(7,8) 2. tidak dipenuhi 3. tidak dipenuhi 4. m = (7 4)/(8 3) =,6 5. N = = 6 6. untuk = 3 dan =,6. ( 3) Ulang sebanak 6 kali iterasi ke-: = 3; =,6. (3 3) + 4 =4 pembulatan: = 4 gambar titik (4,3) di laar. = 3 + = 4 45
47 ============================================= iterasi ke-2: = 4; =,6. (4 3) + 4 =4,6 pembulatan: = 5 gambar titik (5,4) di laar. = 4 + = 5 ============================================= iterasi ke-3: = 5; =,6. (5 3) + 4 =5,2 pembulatan: = 5 gambar titik (5,5) di laar. = 5 + = 6 ============================================= iterasi ke-4: = 6; =,6. (6 3) + 4 =5,8 pembulatan: = 6 gambar titik (6,6) di laar. = 6 + = 7 ============================================= iterasi ke-5: 46
48 = 7; =,6. (7 3) + 4 =6,4 pembulatan: = 6 gambar titik (6,7) di laar. = 7 + = 8 ============================================= iterasi ke-6: = 8; =,6. (8 3) + 4 =7 pembulatan: = 7 gambar titik (7,8) di laar. = 8 + = 9 titik-titik pembentuk garis : (4,3), (5,4), (5,5), (6,6), (6,7), (7,8). Kelemahan algoritma Brute Force : Algoritma ini terlalu lambat karena: pada setiap iterasi terdapat perkalian bilangan pecahan (floating point), penjumlahan bilangan pecahan, dan proses pembulatan angka pecahan menjadi bulat (integer). 47
49 3.2 Algoritma DDA (Digital Diferential Analzer) DDA adalah algoritma pembentuk garis ang didasarkan pada perasamaan (2-8). Garis dibuat menggunakan titik awal (, ) dan titik akhir ( 2, 2). Setiap koordinat titik ( k, k) ang membentuk garis diperoleh dari perhitungan, kemudian hasil perhitungan dikonversikan menjadi nilai integer. Algoritma ini bisa digunakan untuk menghitung garis dengan semua kemiringan. { < m < ; m> ; < m < ; m < }. Berikut adalah langkah-langkah pembentukan garis berdasarkan algoritma DDA:. Tentukan dua titik ang akan dihubungkan dalam pembentukan garis. 2. Tentukan salah satuna sebagai titik awal (, ) dan ang lain sebagai titik akhir ( 2, 2). 3. Hitung : d = 2 dan d = 2 4. Tentukan step, dengan ketentuan berikut: - bila d > d maka step = d - bila tidak, maka step = d 5. Hitung penambahan koordinat piksel dengan persamaan: _inc = d / step _inc = d / step 6. Koordinat selanjutna : = + _inc = + _inc 48
50 7. Lakukan pembulatan u = Round(), v = Round(), kemudian plot piksel (u, v) pada laar 8. Ulangi point 6 dan 7 untuk menentukan posisi piksel berikutna sampai = 2 dan = 2. Contoh 2.4 Diketahui 2 buah titik A(2,) dan titik B(8,5) bila titik A sebagai titik awal dan titik B sebagai titik akhir, maka buatlah garis ang menghubungkan titik tersebut dengan menggunakan algoritma DDA. Jawab: Titik awal (, ) = A(2,) dan Titik akhir ( 2, 2) = B(8,5) d = 2 = 8 2 = 6 dan d = 2 = 5 = 4 Karena: d > d, maka step = d = 6 _inc = d / step = 6/6 = _inc = d / step = 4/6 =,67 ================================================= Iterasi ke-: (,) = (2,) +_inc = 2 + = 3 +_inc = +,67 =,67 Koordinat selanjutna : (,) = (3;,67) 49
51 Pembulatan (3;,67) (3,2). Gambar titik (3,2) dilaar ================================================= Iterasi ke-2: (,) = (3;,67) +_inc = 3 + = 4 +_inc =,67 +,67 = 2,34 Koordinat selanjutna : (,) = (4; 2,34) Pembulatan (4; 2,34) (4,2). Gambar titik (4,2) dilaar ================================================= Iterasi ke-3: (,) = (4; 2,34) A+_inc = 4 + = 5 A+_inc = 2,34 +,67= 3, Koordinat selanjutna : (,) = (5; 3,) Pembulatan (5; 3,) (5,3). Gambar titik (5,3) dilaar ================================================= Iterasi ke-4: (,) = (5; 3,) A+_inc = 5 + = 6 A+_inc = 3, +,67 = 3,68 Koordinat selanjutna : (,) = (6; 3,68) Pembulatan (6; 3,68) (6,4). Gambar titik (6,4) dilaar ================================================= 5
52 Iterasi ke-5: (,) = (6; 3,68) A+_inc = 6 + = 7 A+_inc = 3,68 +,67 = 4,35 Koordinat selanjutna : (,) = (7; 4,35) Pembulatan (7; 4,35) (7,4). Gambar titik (7,4) dilaar ================================================= Iterasi ke-6: (,) = (7; 4,35) A+_inc = 7 + = 8 A+_inc = 4,35 +,67 = 5,2 Koordinat selanjutna : (,) = (8; 5,2) Pembulatan (8; 5,2) (8,5). Gambar titik (8,5) dilaar Karena = 2 = 8, maka iterasi dihentikan, sehingga diperoleh titik-titik pembentuk garis sebagai berikut: (2,), (3,2), (4,2), (5,3), (6,4), (7,4) dan (8,5). ================================================= Bila digambar pada raster graphics diperoleh gambar 2.6: 5
53 Gambar 3. 4 Titik-titik pembentuk garis hasil perhitungan menggunakan algoritma DDA digambar pada raster graphics. Kelebihan Algoritma DDA dibanding Algoritma Brute Force Algoritma DDA lebih cepat dibanding dengan algoritma Brute Force dan baik digunakan untuk kemiringan garis m >. Kelemahan Algoritma DDA Prosedur untuk menggambar garis masih menggunakan fungsi pembulatan maupun, sehingga memerlukan waktu. variabel, maupun m memerlukan kemiringan merupakan nilai pecahan. bilangan real karena 52
54 3.3 Algoritma Bressenham J.E. Bressenham pada th.965 mengumumkan penemuan algoritma untuk mengoptimalkan gambar garis pada raster. Algoritma garis Bressenham disebut juga Midpoint Line Algorithm. Algoritma temuanna tidak lagi menggunakan floating point arihtmetic, sehingga tidak perlu membulatkan nilai posisi piksel setiap waktu dan dalam pengulangan (looping) hana menggunakan pengoperasian incremental. Algoritma ini hampir dapat dipergunakan dan diimplementasikan pada semua hardware dan software untuk keperluan penggambaran garis. Algoritma Bressenham dapat memperbaiki pengendalian plotter, sehingga dia mendapatkan hak paten. Algoritma ini hana berlaku untuk nilai kemiringan garis : < m <. Perhatikan Gambar 2.7. Misalkan kemiringan garis m, ang besarna adalah < m <, titik awal garis di (, ) dan titik akhir garis di (, ). Anggap posisi titik sekarang ( p, p) dan sekarang kita harus memilih antara titik E (East) atau NE (Northeast). Misalkan Q adalah titik potong garis dengan garis = p+, dan M adalah titik tengah antara E dan NE. Jika titik tengah M terletak diatas garis, E dipilih, tetapi jika titik tengah M terletak dibawah garis, maka NE dipilih. 53
55 NE Garis aktual E M ( p, p) = p + Gambar 3. 5 Garis mempunai kemiringan < m <, pada titik = p+, garis berada diantara dua titik E dan NE ang mempunai titik tengah di M. Dalam hal ini kita harus menentukan apakah garis berada diatas titik tengah M atau dibawah titik tengah M. Untuk melakukan ini, kita amati bahwa setiap garis bisa dinatakan sebagai berikut; F(, ) = a + b + c = Persamaan 3 - Hitung: d = dan d =, maka garis juga bisa ditulis sebagai: = m + B = (d/d) + B atau (d/d) + B = 54
56 Kalikan dengan d menjadi (d) (d) + (d)b = Diperoleh a = d, b = d dan c = (d)b. Jika F(, ) =, maka (, ) terletak pada garis Jika F(, ) >, maka (, ) terletak dibawah garis jika F(, ) <, maka (, ) terletak diatas garis Untuk menerapkan kriteria midpoint, kita hitung: F(M) = F( p +, p + ½) = a ( p + ) + b ( p + ½) + c Dan menguji tanda dari d = F(M). Jika d >, M terletak dibawah garis, maka NE dipilih. Jika d =, pilih E ( sebenarna memilih NE juga bisa) Jika d <, M terletak diatas garis, maka E dipilih. Misalkan E dipilih, M bertambah satu langkah dalam arah, dan kita mempunai d baru misalna d baru. d baru = F( p + 2, p + ½) = a ( p + 2) + b ( p + ½) + c d lama = F( p +, p + ½) = a ( p + ) + b ( p + ½) + c jadi d baru d lama = a = d. Jadi setelah E dipilih, pertambahan untuk mendapatkan d ang baru adalah a = d. Misalkan NE dipilih, M adalah pertambahan satu langkah kearah dan sehingga 55
57 d baru = F( p + 2, p + 3/2) = a ( p + 2) + b ( p +3/2) + c d lama = F( p +, p + ½) = a ( p + ) + b ( p + ½) + c jadi d baru d lama = a + b = d d. Untuk memulai algoritma, titik awal adalah ( p, p ) = (, ). Untuk menghitung nilai d ang pertama untuk memulai algoritma, midpoint pertama adalah ( +, + ½) dan F(M) = F( +, + ½) = a ( + ) + b ( + ½)+ c = a + b + c + a + b/2 = + a + b/2 karena (, ) terletak pada garis. Jadi kita mulai dari d = a + b/2 = d d/2 Untuk menghilangkan pecahan, definisikan F dengan mengalikan 2, diperoleh F(,) = 2 (a + b + c) =. Definisi ini akan menebabkan nilai d menjadi d = 2d d Dengan begini algoritma midpoint Bresenham (untuk kemiringan < m < ) adalah : ) Tentukan dua titik ang akan dihubungkan dalam pembentukan garis. 2) Tentukan salah satu sebagai titik awal (, ) dan titik akhir (, ). 3) Hitung d, d, 2 d dan 2 d 2 d 4) Hitung parameter : po = 2 d d 5) Untuk setiap k sepanjang jalur garis, dimulai dengan k = 56
58 - bila p k < maka titik selanjutna adalah: ( k+, k) dan p k+ = p k + 2 d - bila tidak, titik selanjutna adalah: ( k+, k+) dan p k+ = p k + 2 d 2 d 6) Ulangi nomor 5 untuk menentukan posisi piksel berikutna, sampai = dan =. Contoh 2.5 Diketahui 2 buah titik A(2,) dan titik B(8,5) bila titik A sebagai titik awal dan titik B sebagai titik akhir, maka buatlah garis ang menghubungkan titik tersebut dengan menggunakan algoritma Bressenham. Jawab: Titik awal (, ) = A(2,) dan Titik akhir (, ) = B(8,5) d = = 8 2 = 6 dan d = = 5 = 4 m = d/ d = 4/6 ; kemiringan garis berada diantara dan : < m < 2 d = 2.6 = 2 ; 2 d = 2.4 = 8 dan 2 d 2 d = 8 2 = 4 p o = 2 d d = 8 6 = 2 57
59 ================================================= Iterasi ke- ( k = ): Titik awal = (2,) Po = 2 >, maka titik selanjutna adalah = 2 + = 3 dan = + = 2, koordinat selanjutna : (3,2) p = p + 2 d 2 d = 2 4 = 2 ================================================= Iterasi ke-2 ( k = ): Titik awal = (3,2) P = 2 <, maka titik selanjutna adalah = 3 + = 4 dan = 2, koordinat selanjutna : (4,2) p 2 = p + 2 d = = 6 ================================================= Iterasi ke-3 ( k = 2): Titik awal = (4,2) P 2 = 6 >, maka titik selanjutna adalah = 4 + = 5 dan = 2 + = 3, koordinat selanjutna : (5,3) p 3 = p d 2 d = 6 4 = 2 ================================================= 58
60 Iterasi ke-4 ( k = 3): Titik awal = (5,3) P 3 = 2 >, maka titik selanjutna adalah = 5 + = 6 dan = 3 + = 4, koordinat selanjutna : (6,4) p 4 = p d 2 d = 2 4 = 2 ================================================= Iterasi ke-5 ( k = 4): Titik awal = (6,4) P 3 = 2 <, maka titik selanjutna adalah = 6 + = 7 dan = 4, koordinat selanjutna : (7,4) p 5 = p d = = 6 ================================================= Iterasi ke-6 ( k = 5): Titik awal = (7,4) P 5 = 6 >, maka titik selanjutna adalah = 7 + = 8 dan = 4 + = 5, koordinat selanjutna : (8,5) ================================================= 59
61 Karena = 2 = 8, maka iterasi dihentikan, sehingga diperoleh titik-titik penusun garis sebagai berikut: (2,), (3,2), (4,2), (5,3), (6,4), (7,4) dan (8,5). Bila digambar pada raster graphics diperoleh Gambar 2.8: Gambar 3. 6 Titik-titik pembentuk garis dengan kemiringan < m <, hasil perhitungan menggunakan algoritma Bressenham ang digambar pada raster graphics. Untuk kemiringan < m <, kita tinggal mengganti komponen berikut: Untuk setiap k sepanjang jalur garis, dimulai dengan k = - bila p k < maka titik selanjutna adalah: ( k+, k) dan p k+ = p k + 2 d - bila tidak, titik selanjutna adalah: ( k+, k ) dan p k+ = p k + 2 d 2 d 6
62 Contoh 2.6 Diketahui 2 buah titik A(2,9) dan titik B(8,5) bila titik A sebagai titik awal dan titik B sebagai titik akhir, maka buatlah garis ang menghubungkan titik tersebut dengan menggunakan algoritma Bressenham. Jawab: Titik awal (, ) = A(2,9) dan Titik akhir (, ) = B(8,5) d = = 8 2 = 6 dan d = = 5 9 = 4 m = d/ d = 4/6 dan : < m < ; kemiringan garis berada diantara 2 d = 2.6 = 2 ; 2 d = 2. 4 = 8 dan 2 d 2 d = 8 2 = 4 p o = 2 d d = 8 6 = 2 ================================================= Iterasi ke- ( k = ): Titik awal = (2,9) Po = 2 >, maka titik selanjutna adalah = 2 + = 3 dan = 9 = 8, koordinat selanjutna : (3,8) p = p + 2 d 2 d = 2 4 = 2 ================================================= 6
63 Iterasi ke-2 ( k = ): Titik awal = (3,8) P = 2 <, maka titik selanjutna adalah = 3 + = 4 dan = 8, koordinat selanjutna : (4,8) p 2 = p + 2 d = = 6 ================================================= Iterasi ke-3 ( k = 2): Titik awal = (4,8) P 2 = 6 >, maka titik selanjutna adalah = 4 + = 5 dan = 8 = 7, koordinat selanjutna : (5,7) p 3 = p d 2 d = = 6 4 = 2 ================================================= Iterasi ke-4 ( k = 3): Titik awal = (5,7) P 2 = 2 >, maka titik selanjutna adalah = 5 + = 6 dan = 7 = 6, koordinat selanjutna : (6,6) p 4 = p d 2 d = = 2 4 = 2 ================================================= Iterasi ke-5 ( k = 4): 62
64 Titik awal = (6,6) P 4 = 2 <, maka titik selanjutna adalah = 6 + = 7 dan = 6, koordinat selanjutna : (7,6) p 5 = p d = = 6 ================================================= Iterasi ke-6 ( k = 5): Titik awal = (7,6) P 5 = 6 >, maka titik selanjutna adalah = 7 + = 8 dan = 6 = 5, koordinat selanjutna : (8,5) p 6 = p d 2 d = 6 4 = 2 ================================================= Karena = 2 = 8, maka iterasi dihentikan, sehingga diperoleh titik-titik penusun garis sebagai berikut: (2,9), (3,8), (4,8), (5,7), (6,6), (7,6) dan (8,5). Bila digambar pada raster graphics diperoleh Gambar 2.9: 63
65 Gambar 3. 7 Titik-titik pembentuk garis dengan kemiringan < m <, hasil perhitungan menggunakan algoritma Bressenham ang digambar pada raster graphics. Untuk kemiringan garis m >, tukarlah dengan, sehingga algoritma pembentukan garis untuk m > adalah sebagai berikut:. Tentukan dua titik ang akan dihubungkan dalam pembentukan garis. 2. Tentukan salah satu sebagai titik awal (, ) dan titik akhir (, ). 3. Hitung d, d, 2 d dan 2 d 2 d 4. Hitung parameter : po = 2 d d 64
66 5. Untuk setiap k sepanjang jalur garis, dimulai dengan k = - bila p k < maka titik selanjutna adalah: ( k, k+) dan p k+ = p k + 2 d - bila tidak, titik selanjutna adalah: ( k+, k+) dan p k+ = p k + 2 d 2 d 6. Ulangi nomor 5 untuk menentukan posisi piksel berikutna, sampai = dan =. Contoh 2.7 Diketahui 2 buah titik A(2,) dan titik B(4,7) bila titik A sebagai titik awal dan titik B sebagai titik akhir, maka buatlah garis ang menghubungkan titik tersebut dengan menggunakan algoritma Bressenham. Jawab: Titik awal (, ) = A(2,) dan Titik akhir (, ) = B(4,7) d = = 4 2 = 2 dan d = = 7 = 6 m = d/ d = 6/2 ; kemiringan garis lebih besar dari : m > 2 d = 4 ; 2 d = 2 dan 2 d 2 d = 4 2 = 8 65
67 p o = 2 d d = 4 6 = 2 ================================================= Iterasi ke- ( k = ): Titik awal = (2,) p o = 2 <, maka titik selanjutna adalah = 2 dan = + = 2, koordinat selanjutna : (2,2) p = p o + 2 d = = 2 ================================================= Iterasi ke-2 ( k = ): Titik awal = (2,2) p = 2 >, maka titik selanjutna adalah = 2+ = 3 dan = 2 + = 3, koordinat selanjutna : (3,3) p 2 = p + 2 d 2 d = 2 8 = 6 ================================================= Iterasi ke-3 ( k = 2): Titik awal = (3,3) p 2 = 6 <, maka titik selanjutna adalah = 3 dan = 3 + = 4, koordinat selanjutna : (3,4) p 3 = p d = = 2 66
68 ================================================= Iterasi ke-4 ( k = 3): Titik awal = (3,4) p 3 = 2 <, maka titik selanjutna adalah = 3 dan = 4 + = 5, koordinat selanjutna : (3,5) p 4 = p d = 2 +4 = 2 ================================================= Iterasi ke-5 ( k = 4): Titik awal = (3,5) p 4 = 2 >, maka titik selanjutna adalah = 3+=4 dan = 5 + = 6, koordinat selanjutna : (4,6) p 5 = p d 2 d = 2 8 = 6 ================================================= Iterasi ke-6 ( k = 5): Titik awal = (4,6) p 5 = 6 <, maka titik selanjutna adalah = 4 dan = 6 + = 7, koordinat selanjutna : (4,7) p 6 = p d = = 2 ================================================= 67
69 Sampai disini iterasi dihentikan. Untuk kemiringan garis m <, kita tinggal mengganti komponen berikut: Untuk setiap k sepanjang jalur garis, dimulai dengan k = - bila p k < maka titik selanjutna adalah: ( k, k ) dan p k+ = p k + 2 d - bila tidak, titik selanjutna adalah: ( k+, k ) dan p k+ = p k + 2 d 2 d Contoh 2.8 Diketahui 2 buah titik A( 6,) dan titik B(,) bila titik A sebagai titik awal dan titik B sebagai titik akhir, maka buatlah garis ang menghubungkan titik tersebut dengan menggunakan algoritma Bressenham. Jawab: Titik awal (, ) = A( 6,) dan Titik akhir (, ) = B(,) d = = ( 6) = 6 dan d = = = m = d/ d = /6 : m < ; kemiringan garis lebih kecil dari 68
70 2 d = 2 ; 2 d = 2 dan 2 d 2 d = 2 2 = 8 p o = 2 d d = 2 = 2 ================================================= Iterasi ke- ( k = ): Titik awal = ( 6,) p o = 2 >, maka titik selanjutna adalah = 6 + = 5 dan : ( 5,9) = = 9, koordinat selanjutna p = p o + 2 d 2 d = 2 8 = 6 ================================================= Iterasi ke-2 ( k = ): Titik awal = ( 5,9) P = 6<, maka titik selanjutna adalah = 5 dan = 9 = 8, koordinat selanjutna : ( 5,8) p 2 = p + 2 d = = 6 ================================================= Iterasi ke-3 ( k = 2): Titik awal = ( 5,8) P 2 = 6 >, maka titik selanjutna adalah 69
71 = 5 + = 4 dan = 8 = 7, koordinat selanjutna : ( 4,7) p 3 = p d 2 d = 6 8 = 2 ================================================= Iterasi ke-4 ( k = 3): Titik awal = ( 4,7) P 3 = 2 <, maka titik selanjutna adalah = 4 dan = 7 = 6, koordinat selanjutna : ( 4,6) p 4 = p d = = ================================================= Iterasi ke-5 ( k = 4): Titik awal = ( 4,6) P 4 = >, maka titik selanjutna adalah = 4 + = 3 dan = 6 = 5, koordinat selanjutna : ( 3,5) p 5 = p d 2 d = 8 = 2 ================================================= Iterasi ke-6 ( k = 5): Titik awal = ( 3,5) P 5 = 2 >, maka titik selanjutna adalah 7
72 = 3 + = 2 dan = 5 = 4, koordinat selanjutna : ( 2,4) p 5 = p d 2 d = 2 8 = 6 ================================================= Iterasi ke-7 ( k = 6): Titik awal = ( 2,4) P 3 = 6 <, maka titik selanjutna adalah = 2 dan = 4 = 3, koordinat selanjutna : ( 2,3) p 4 = p d = = 6 ================================================= Iterasi ke-8 ( k = 7): Titik awal = ( 2,3) P 7 = 6 >, maka titik selanjutna adalah = 2 + = dan = 3 = 2, koordinat selanjutna : (,2) p 8 = p d 2 d = 6 8 = 2 ================================================= Iterasi ke-9 ( k = 8): Titik awal = (,2) P 8 = 2 <, maka titik selanjutna adalah = dan = 2 =, koordinat selanjutna : (,) 7
73 p 9 = p d = = ================================================= Iterasi ke- ( k = 9): Titik awal = (,) P 9 = >, maka titik selanjutna adalah = + = dan = =, koordinat selanjutna : (,) p = p d 2 d = 8 = 2 ================================================= Sampai disini iterasi dihentikan. 3.4 Lingkaran Persamaan umum lingkaran dengan pusat lingkaran ( p, p) dan jari-jari r adalah: ( p) ( p) r Persamaan 3-2 Atau [ r ( 2 p p ) 2 ] Persamaan 3-3 Untuk menggambar piksel-piksel dalam kurva lingkaran, dapat digunakan sumbu dari = ( p-r) sampai = ( p+r) sebagai parameter dan sumbu sebagai hasil dari persamaan (2-). 72
74 Algoritma ini memerlukan waktu operasi ang besar, karena mengandung operasi perkalian dua bilangan integer, membutuhkan fungsi SQRT (untuk menghitung akar suatu bilangan) dan fungsi ROUND (untuk membulatkan bilangan pecahan menjadi bilangan integer), dan menghasilkan posisi koordinat piksel ang tidak merata, karena terjadina gaps ang disebabkan adana perubahan gradient seperti tampak pada Gambar 3.8. Gambar 3. 8 Terjadina gaps ang disebabkan adana perubahan gradient menghasilkan posisi koordinat piksel ang tidak merata Untuk menghindari posisi koordinat piksel ang tidak merata, koordinat piksel (,) dinatakan dengan menggunakan koordinat polar dalam persamaan (3-4) r cos dan rsin p p Persamaan
75 Akan tetapi penggambaran lingkaran menggunakan persamaan (3-4) memerlukan waktu operasi ang besar karena mengandung operasi perkalian bilangan riel, perhitungan trigonometri, dan membutuhkan banak segmen garis Simetris Delapan Titik Pembuatan kurva lingkaran dapat dilakukan dengan menentukan titik awal (,) ang terletak pada lingkaran, maka tujuh titik ang lain (ang terletak pada lingkaran juga) dapat ditentukan sebagai berikut : (,), (, ), (, ), (,), (,), (, ), (, ) Sehingga terbentuk delapan titik: (, ), (,), (, ), (, ), (,), (,), (, ), (, ) Dengan demikian sebenarna hana diperlukan untuk menghitung segmen 45 dalam menentukan lingkaran selengkapna. (,) Gambar 3. 9 Delapan titik simetris pada lingkaran 74
76 3.4.2 Algoritma Midpoint Algoritma midpoint juga disebut algoritma lingkaran Bressenham. Pembentukan semua titik berdasarkan titik pusat dengan penambahan semua jalur di sekeliling lingkaran. Komputasi untuk membuat kurva lingkaran dimulai dengan mengidentifikasi bagian-bagian dari lingkaran ang dapat ditentukan dengan menggunakan sifat simetri, hal ini dilakukan dengan cara membagai lingkaran dengan masing-masing mempunai sudut sebesar 45, sehingga dalam sebuah lingkaran dibagi menjadi 8 bagian. Perhatikan Gambar 3.. Gambar 3. Garis lingkaran berada diantara titik ( k+, k) dan ( k+, k ) Anggap bahwa kita mempunai titik ( k, k). Selanjutna adalah memilih titik ( k+, k) atau ( k+, k ) ang paling mendekati lingkaran. Persamaan untuk lingkaran Sehingga,, f (, ),, f (, ) r jika (, ) didalam lingkaran jika (, ) terletak pada lingkaran jika (, ) terletak diluar lingkaran 75
77 76 Untuk memilih titik ( k+, k) atau ( k+, k ) ang paling mendekati lingkaran, kriteria ang digunakan adalah titik tengah ( k+, k ½ ) aitu Jika p k< titik tengah berada didalam lingkaran, maka titik ( k+, k) dipilih. Jika p k> titik tengah berada diluar lingkaran, maka titik ( k+, k ) dipilih. hitung Atau Dimana k+ adalah k atau k- tergantung tanda dari p k. Dalam hal ini kriteria pertama ang dihitung adalah Jika jari-jari lingkaran bernilai integer (bilangan bulat), kita bisa membulatkan nilai p menjadi berikut ) 2 ( ) ( ) 2, ( r f p k k k k k ] ) [( 2, r f p k k k k k ) ( ) ( ) ( k k k k k k k p p r r r r f p 4 5 ) 2 ( ) 2 (, 2 2 p r
78 Kemudian jika p k < maka: Jika p k > maka: Dari sini diperoleh langkah-langkah algoritma pembentuk lingkaran. p p Langkah-langkah Algoritma Lingkaran Midpoint adalah:. Tentukan jari-jari r dan pusat lingkaran ( p, p), kemudian setting sedemikian rupa sehingga titik awal berada pada: (, ) = (, r) 2. Hitung nilai parameter : 5 p r 4 p k k 2k p k k 2k 2k Jika jari-jari r pecahan p r Jika jari-jari r bulat 3. Untuk setiap posisi k, dimulai dengan k = berlaku ketentuan: - bila p k < maka titik selanjutna adalah ( k+, k) dan p k+ = p k + 2 k+ + 77
79 - bila tidak, titik selanjutna adalah ( k+, k ) dan p k+ = p k + 2 k+ + 2 k+ 4. Tentukan titik simetris pada ketujuh oktan ang lain 5. Gerakkan setiap posisi piksel (, ) pada garis lingkaran dengan titik pusat ( p, p) dan plot nilai koordinat : = + p, = + p 6. Ulangi langkah 3 sampai dengan 5 hingga Contoh 2.9 Buatlah gambar kurva lingkaran dengan pusat lingkaran (4,6) dan jari-jari 8, perhitungan berdasarkan dari oktan kuadran pertama dimana = sampai =. Koordinat titik awal dimulai dari (,r) = (,8). Karena jari-jari r bulat, maka gunakan P = r. Iterasi ke-: K = X = Y = r = 8 P = r = 8 = 7 Karena P <, maka : X = X + = + = dan Y = Y = 8, jadi Titik selanjutna : (,8) P = p = () + = 4 Dengan algoritma simetris delapan titik, maka diperoleh titiktitik berikut : 78
80 (,8), (,8), (, 8), (, 8), (8,), ( 8,), (8, ), ( 8, ) Gerakkan setiap posisi piksel (, ) pada garis lingkaran dengan titik pusat (4,6) diperoleh titik-titik berikut (5, 4), (3, 4), (5, 2), (3, 2), (2, 7), ( 4, 7), (2, 5), ( 4, 5) ================================================= Iterasi ke-2: K = X = Y = 8 P = 4 Karena P <, maka X 2 = X + = + = 2 dan Y 2 = Y = 8, jadi Titik selanjutna : (2,8) P 2 = p = (2) + = Dengan algoritma simetris delapan titik, maka diperoleh titiktitik berikut : (2,8), ( 2,8), (2, 8), ( 2, 8), (8,2), ( 8,2), (8, 2), ( 8, 2) Gerakkan setiap posisi piksel (, ) pada garis lingkaran dengan titik pusat (4,6) diperoleh titik-titik berikut (6, 4), (2, 4), (6, 2), (2, 2), (2, 8), ( 4, 8), (2, 4), ( 4, 4) ================================================= Iterasi ke-3: K = 2 X 2 = 2 Y 2 = 8 P 2 = Karena P 2 >, maka 79
81 X 3 = X 2 + = 2 + = 3 dan Y 3 = Y 2 = 8 = 7, jadi Titik selanjutna : (3,7) P 3 = p = + 2.(3) + 2.(7) = 6 Dengan algoritma simetris delapan titik, maka diperoleh titiktitik berikut : (3,7), ( 3,7), (3, 7), ( 3, 7), (7,3), ( 7,3), (7, 3), ( 7, 3) ================================================= Gerakkan setiap posisi piksel (, ) pada garis lingkaran dengan titik pusat (4,6) diperoleh titik-titik berikut (7, 3), (, 3), (7, ), (, ), (, 9), ( 3, 9), (, 3), ( 3, 3) Iterasi ke-4: K = 3 X 3 = 3 Y 3 = 7 P 3 = 6 Karena P 3 <, maka X 4 = X 3 + = 3 + = 4 dan Y 4 = Y 3 = 7, jadi Titik selanjutna : (4,7) P 4 = p = (4) + = 3 Dengan algoritma simetris delapan titik, maka diperoleh titiktitik berikut : (4,7), ( 4,7), (4, 7), ( 4, 7), (7,4), ( 7,4), (7, 4), ( 7, 4) Gerakkan setiap posisi piksel (, ) pada garis lingkaran dengan titik pusat (4,6) diperoleh titik-titik berikut (8, 3), (, 3), (8, ), (, ), (, ), ( 3, ), (, 2), ( 3, 2) 8
82 ================================================= Iterasi ke-5: K = 4 X 4 = 4 Y 4 = 7 P 4 = 3 Karena P 4 >, maka X 5 = X 4 + = 4 + = 5 dan Y 5 = Y 4 = 7 = 6, jadi Titik selanjutna : (5,6) P 5 = p = (5) + 2.(6) = 2 Dengan algoritma simetris delapan titik, maka diperoleh titiktitik berikut : (5,6), ( 5,6), (5, 6), ( 5, 6), (6,5), ( 6,5), (6, 5), ( 6, 5) Gerakkan setiap posisi piksel (, ) pada garis lingkaran dengan titik pusat (4,6) diperoleh titik-titik berikut (9, 2), (, 2), (9, ), (, ), (, ), ( 2, ), (, ), ( 2, ) ================================================= Iterasi ke-6: K = 5 X 5 = 5 Y 5 = 6 P 5 = 2 Karena P 5 >, maka X 6 = X 5 + = 5 + = 6 dan Y 6 = Y 5 = 6 = 5, jadi Titik selanjutna : (6,5) Iterasi dihentikan karena X > Y. 8
83 Bila digambar, hasil untuk oktan ke- ditunjukkan oleh gambar (3.). Gambar 3. Posisi piksel pada pembentukan lingkaran dengan titik pusat (,) dan jari-jari Polgon Polgon adalah kumpulan garis lurus ang saling menambung hingga membentuk suatu luasan. Garis-garis ini disebut edge (sisi polgon). Titik pertemuan tiap dua sisi disebut verteks. Biasana polgon dinatakan dengan koordinat verteks-verteks ini. Ada dua jenis polgon aitu polgon sederhana dan polgon tidak sederhana. Ciri polgon sederhana adalah tidak semua verteks berada pada bidang ang sama, tidak mempunai sisisisi ang berpotongan, dan tidak mempunai lubang. 82
84 (a) Gambar 3. 2 Polgon sederhana dan polgon tidak sederhana Polgon sederhana dibagi menjadi dua aitu conve polgon dan non conve polgon. Ciri conve polgon adalah semua sudut interiorna < 8 o, atau setiap segmen garis ang dihasilkan dari dua buah verteks sembarang dalam polgon berada didalam polgon. Bentuk polgon ang paling sederhana adalah segitiga, karena semua polgon dapat dipecah-pecah menjadi bagian ang terkecil aitu segitiga seperti pada Gambar 3.2(b). Mengapa polgon? Dengan polgon secara praktek kita bisa melakukan pendekatan untuk membentuk permukaan setiap obek 3-D, jika kita mempunai jumlah polgon ang cukup. Sebagai contoh permukaan bola, torus, dan teko seperti pada Gambar 3.3 dapat dibuat dari beberapa polgon. 83
85 Gambar 3. 3 : Permukaan bola, torus dan teko ang terbentuk dari banak polgon. 3.6 Filling Polgon Dalam grafis, pemberian warna dibutuhkan untuk mempercantik tampilan polgon. Karena itu diperlukan algoritma khusus untuk mengisi warna pada polgon tersebut. Teknik atau algoritma untuk pengisian warna pada polgon disebut filling polgon atau area filling. Ada dua macam dasar pendekatan filling polgon pada sistem raster aitu scan-line Polgon Fill Algorithm dan Boundar-Fill Algorithm: 3.6. Scan Line Polgon Fill Algorithms Pemberian warna pada polgon dilakukan dengan cara menscan secara horisontal dari kiri ke kanan. Hal ini dilakukan untuk mendapatkan titik potong dengan tepi polgon, kemudian mengurutkan nilai-nilai titik potong dari kiri ke kanan dan memberi warna pada piksel-piksel diantara dua pasangan berurutan ( - 2). Hal ini dilakukan dari garis scan ang paling bawah (nilai terkecil) hingga garis scan ang paling atas seperti pada Gambar 3.4. Metode ini bisa juga digunakan 84
86 untuk pengisian warna pada obek-obek sederhana lainna, misalna lingkaran, ellip dan lain-lain. Scanline terakhir Titik potong Scanline pertama Titik potong 2 Piksel-piksel diantara titik potong - 2 Gambar 3. 4 Metode scan-line Bagaimana kita tahu bahwa piksel tersebut berada didalam polgon atau diluar polgon? Inside-Outside test Perhatikan Gambar 3.5. Untuk mengidentifikasi bagian dalam dan bagian luar digunakan aturan paritas ganjil-genap ang biasa disebut sebagai odd-even rule atau odd parit rule. Semula kita men-set paritas dengan nilai genap. Setiap ditemukan titik potong nilai paritas dibalik, ang semula genap dibalik menjadi ganjil, sebalikna ang semula ganjil dibalik menjadi genap. Beri warna pada piksel jika paritasna Ganjil. 85
87 paritas ganjil paritas genap Gambar 3. 5 Aturan paritas ganjil-genap untuk mengisi warna Masalah: Pada Gambar 3.6(a), verteks a, b, c, dan d merupakan pertemuan dari dua buah segmen garis. Mengapa pada verteks a dan d dihitung sekali, sedangkan pada verteks b dan c dihitung dua kali? 86
88 2 a b c d 2 (a) a c b d (b) Gambar 3. 6 Perhitungan paritas pada verteks a, b, c, dan d. Solusi: Buatlah perputaran tepi polgon searah jarum jam seperti pada Gambar 2.6(b). Check, apabila pada suatu verteks arah anak 87
89 panahna berubah (pada verteks b dan c aitu: naik-turun atau turun-naik) maka pada verteks tersebut dihitung dua kali. Sebalikna jika arah anak panahna tidak berubah (pada verteks a dan d aitu: naik-naik atau turun-turun) maka pada verteks tersebut dihitung sekali. Masalah: Perhatikan Gambar 3.7(a), Bagaimana perhitungan tepi horisontal AB, CD, GF, dan HI? (a) (b) Gambar 3. 7 Polgon dengan sisi-sisi horisontal Solusi: Abaikan verteks-verteks ang terletak pada tepi horisontal, atau jangan dimasukkan dalam perhitungan paritas ganjil-genap, sehingga tampak seperti pada Gambar 3.7(b). 88
90 Algoritma scanline menggunakan kaidah paritas ganjil-genap: Tentukan titik potong garis scan dengan semua sisi polgon Urutkan titik potong tadi berdasarkan koordinat sumbu Warnai semua piksel diantara pasangan titik potong ( - 2) ang terletak didalam polgon menggunakan kaidah paritas ganjil-genap. Kelemahan algoritma ini adalah: Memerlukan biaa tinggi (big cost) karena pada setiap sisi polgon selalu dilakukan pengujian terhadap piksel-piksel. Solusi: Menggunakan konsep edge table (ET) Edge Table ( ET ), edge table (ET) adalah tabel ang berisi sisisisi polgon. Kita akan menggunakan dua edge table ang berbeda, aitu: Active Edge Table (AET) dan Global Edge Table (GET). (AET) digunakan untuk menimpan semua sisi polgon ang berpotongan dengan garis scan, sedangkan GET digunakan untuk menimpan semua sisi polgon dan mengupdate AET. Perhitungan titik potong dengan garis scan ma ) min ) 89
91 9 Kita tahu bahwa: Setiap garis scan ang baru berlaku : Kita perlu menghitung untuk setiap garis scan: Sehingga, Dan Maka min ma, m b m i i m b m b m b i i i i, i i m m m b m b i i i i
92 Ini adalah cara ang efisien untuk menghitung nilai. Active Edge Table (AET) Tabel berisi satu entr per sisi ang berpotongan dengan garis scan aktif. Pada setiap garis scan ang baru : o Hitung titik potong baru untuk semua sisi menggunakan rumus : o Tambahkan setiap sisi baru ang berpotongan o Hapus setiap sisi ang tidak berpotongan Untuk efisiensi Update AET, kita tetap menjaga GET. Global Edge Table (GET) Tabel ang berisi informasi tentang semua sisi-sisi polgon GET mempunai satu tempat unttuk setiap garis scan o Setiap tempat menimpan daftar sisi ang mempunai nilai min o Setiap sisi ditentukan hana dalam satu tempat Tiap-tiap entr dalam GET berisi o Nilai ma dari sisi o (nilai pada titik min) o Nilai pertambahan (/m) Scan Line Polgon Fill Algorithms menggunakan ET, GET dan AET. Tambahkan sisi-sisi polgon ke GET 2. Set ke koordinat terkecil dalam GET 9
93 3. Inisialisasi, set AET = kosong 4. Ulang sampai AET dan GET kosong a. Tambahkan sisi-sisi dari GET ke AET ang mana min =. b. Hilangkan sisi-sisi dari AET bila ma =. c. Urutkan AET berdasarkan d. Warnai piksel ang terletak diantara pasangan titik potong dalam AET e. Untuk setiap sisi dalam AET, ganti dengan + /m f. Set = + untuk bergerak ke garis scan berikutna Contoh 2. Diketahui polgon berikut, gunakan konsep edge table untuk mewarnai polgon tersebut. Gambar
94 Sisi-sisi pembentuk polgon: Gambar
95 Gambar 3. 2 AET ma,,/m 4, 2, 2/3 5, 2, /4 EA AB kiri = 2 kanan = 2 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = (2 2), hasilna adalah; 94
96 Gambar 3. 2 Gambar AET ma,,/m 4, 4/3, 2/3 EA 5, 9/4, /4 AB i+ = i + /m i+ = i + /m = 2 2/3 = 2 + /4 = 4/3 = 9/4 kiri = 4/3 dan kanan = 9/4 2 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = ( 2), hasilna adalah 95
97 Gambar Gambar AET ma,,/m 4, 2/3, 2/3 EA i+ = i + /m = 4/3 2/3 = 2/3 5, /4, /4 AB i+ = i + /m = 9/4 + /4 = /4 kiri = 2/3 dan kanan = /4 3 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = ( 3), hasilna adalah; 96
98 Gambar Gambar AET ma,,/m 8,, 3/4 EA = DE pada EA, ma = 4. EA harus dihapus dari AET. Dalam GET sisi DE tersimpan pada = 4. Jadi sisi EA diganti dengan sisi DE 5, /4, /4 AB i+ = i + /m = /4 + /4 = /4 kiri = dan kanan = /4 3 97
99 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = ( 3), hasilna adalah Gambar Gambar AET ma,,/m 8, 3/4, 3/4 DE i+ = i + /m = + 3/4 = 3/4 6, 3, 3 AB = BC pada AB, ma = 5. AB harus dihapus dari AET. Dalam GET sisi BC tersimpan pada = 5. Jadi sisi AB diganti dengan sisi BC kiri = 3/4 dan kanan = 3 98
100 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = ( 3), hasilna adalah; Gambar AET ma,,/m Gambar , 6/4, 3/4 DE 8, 6, 3/2 BC = CD pada BC, ma = 6. BC harus i+ = i + /m dihapus dari AET. Dalam GET sisi CD tersimpan pada = 6. Jadi sisi = 3/4 + 3/4 BC diganti dengan sisi CD = 6/4 kiri = 6/4 2 dan kanan = 6 99
101 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = (2 6), hasilna adalah; Gambar 3. 3 Gambar AET ma,,/m 8, 9/4, 3/4 DE i+ = i + /m = 6/4 + 3/4 = 9/4 8, 9/2, 3/2 CD i+ = i + /m = 6 3/2 = 9/2 kiri = 9/4 2 dan kanan = 9/2 5
102 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = (2 5), hasilna adalah; Gambar Gambar AET ma,,/m 8, 3, 3/4 DE i+ = i + /m = 9/4 + 3/4 = 3 8, 3, 3/2 CD i+ = i + /m = 9/2 3/2 = 3 kiri = 3 dan kanan = 3
103 Pewarnaan dilakukan diantara titik potong ( kiri kanan) = (3 3), hasilna adalah; Gambar Karena sisi polgon dalam GET ataupun AET sudah habis, maka proses dihentikan Boundar-Fill Algorithm Prosedur boundar-fill menerima tiga parameter aitu: koordinat titik (,), warna isi dan warna garis batas. Proses pengisian warna tertentu dimulai dari titik (,), kemudian memeriksa posisi titik tetanggana, apakah titik tetangga tersebut memiliki warna batas: o Jika tidak, warnai titik tersebut dengan warna tertentu. o Selanjutna periksa lagi posisi dan warna titik tetanggana. o Proses diulangi terus hingga seluruh titik pada area pengisian telah diuji. 2
104 Dengan teknik ini pengisian warna dimulai dari sebuah titik ang berada didalam area (,) polgon dan mewarnai piksel dari titik tetanggana hingga semua piksel ang berada didalam polgon telah diwarnai seperti pada Gambar 2.2. Gambar Metode Boundar-Fill Ada 2 macam cara untuk melihat titik tetangga, aitu : 4 tetangga, melihat titik ang berada diatas, bawah, kanan dan kiri 8 tetangga, melihat titik ang berada diatas, bawah, kanan, kiri, pojok kiri atas, pojok kiri bawah, pojok kanan atas dan pojok kanan bawah. 3
105 a) 4 - tetangga 4 X 2 3 Gambar b) 8 - tetangga X Gambar Contoh 2. diketahui : polgon = {(,), (2,,5), (5,4), (8,7), (,4), (,2), (,)}, lakukan Area Filling menggunakan algoritma Boundar Fill Algorithm 4-tetangga. Jawab: titik-titik sebagai pembentuk polgon = {(,), (2,,5), (5,4), (8,7), (,4), (,2), (,)}. Bila poligon tersebut digambar, diperoleh gambar berikut : 4
106 Gambar Misalkan titik awal pencarian adalah (3,3). Tandai titik (3,3) dengan warna tertentu, misalna warna merah. Lihat 4- tetanggana, aitu titik (3,2), (3,4), (2,3), (4,3) Gambar
107 Ke-4 tetangga tersebut bukan garis batas poligon, sehingga 4- titik tersebut diwarnai merah Gambar 3. 4 Titik ang telah diproses: (3,3) Titik ang belum diproses : (3,2), (3,4), (2,3), (4,3) Ambil titik (3,2). Titik ang telah diproses: (3,2), (3,3) Titik ang belum diproses : (3,4), (2,3), (4,3) 4-tetangga titik tersebut adalah (3,3), (3,), (2,2), (4,2). Terlihat bahwa titik (4,2) dan (2,2) bukan garis batas poligon, sehingga diwarnai dengan warna merah. Titik (3,3) sudah diwarnai. Titik (3,) adalah garis batas jadi tidak diwarnai. 6
108 Gambar Titik ang telah diproses: (3,3)(3,2) Titik ang belum diproses : (3,4), (2,3), (4,3) (2,2), (4,2) Ambil titik (3,4). 4-tetangga titik tersebut adalah (3,3), (3,5), (2,4), (4,4). Titik (3,3) sudah diwarnai. Titik (3,5), (2,4) dan (4,4) adalah garis batas jadi tidak diwarnai. Proses diulang sehingga seluruh bagian dalam poligon diwarnai dengan warna merah. 7
109 Gambar Flood-Fill Algorithm Terkadang kita ingin mewarnai ( atau memberi warna ang baru) pada sebuah area ang mempunai warna lebih dari satu. Perhatikan gambar 2.2 berikut: (a) (b) Gambar penggantian warna obek menggunakan Flood-Fill Algorithm. (a) lingkaran berwarna merah, segitiga berwarna hijau dan persegi berwarna biru. Obek tersebut warnana diubah menjadi (b) lingkaran berwarna abuabu, segitiga berwarna kuning dan persegi berwarna coklat 8
110 Algoritma ini dimulai dari titik ang berada didalam area (,) dan mengganti semua pikselna dengan warna baru sehingga bagian dalam area mempunai warna ang sama. Pengujian titik tetangga bisa menggunakan 4-tetangga atau 8-tetangga. 9
111 Ringkasan Bab 3 Output primitif adalah struktur dasar geometri ang paling sederhana dari gambar grafika komputer. Titik dan garis adalah contoh dari output primitif ang dapat digunakan untuk membentuk gambar, misalna lingkaran, kerucut, permukaan berbentuk persegi, kurva dan permukaan berbentuk lengkung, warna area dan karakter, dan lain-lain. Piksel adalah elemen gambar terkecil berupa sebuah titik ang ditempatkan dilaar. warna merupakan atribut dari piksel. Frame buffer adalah area memor tempat informasi gambar disimpan. Ada 3 algoritma untuk membentuk garis, aitu Algoritma brute force, DDA, dan Bressenham. Sedangkan untuk membentuk lingkaran digunakan algoritma lingkaran midpoint. Polgon adalah kumpulan garis lurus ang saling menambung hingga membentuk suatu luasan. Garis-garis ini disebut edge (sisi polgon). Titik pertemuan tiap dua sisi disebut verteks. Untuk mengisi warna pada polgon diperlukan algoritma khusus. Teknik atau algoritma untuk pengisian warna pada polgon disebut filling polgon atau area filling. Ada dua macam dasar pendekatan filling polgon pada sistem raster aitu scan-line Polgon Fill Algorithm dan Boundar-Fill Algorithm.
112 Soal-Soal Latihan. Apa ang dimaksud dengan output primitif? Sebutkan! 2. Diketahui 2 buah titik A dan titik B. Bila titik A sebagai titik awal dan titik B sebagai titik akhir, tentukan titik-titik antara ang menghubungkan titik A dan titik B sehingga membentuk garis AB dengan menggunakan (a) Algoritma brute force (b) algoritma DDA (c) algoritma Bressenham, jika : i) A(3,2) dan B(, 6) ii) A(3,2) dan B(7, 7) iii) A( 5, ) dan B(, ) iv) A( 5, 4) dan B(,) 3 Berdasarkan soal no.2, bagaimana menurut saudara, mana algoritma ang lebih baik, Algoritma brute force, algoritma DDA atau algoritma Bressenham? Mengapa? 4. (a) Buatlah gambar kurva lingkaran dengan pusat lingkaran (,) dan jari-jari 6, perhitungan berdasarkan dari oktan kuadran pertama dimana = sampai = r. Koordinat titik awal dimulai dari (,r) = (,6). Untuk mempermudah perhitungan gunakan P = r ( sekali lagi, ini hana untuk mempermudah perhitungan dalam contoh). (b) sama seperti soal (a), tetapi pusat lingkarang di P(2,5).
113 5. Diketahui : polgon = {(2,), (3,6), (5,4), (8,8), (,4), (2,2), (2,)}, lakukan Area Filling menggunakan (a) algoritma Scan Line Polgon (b) algoritma Boundar Fill. 2
114 Bab 4 Atribut Output Primitif TUJUAN PEMBELAJARAN Agar pembaca memahami pengertian atribut output primitive Agar pembaca memahami atribut titik Agar pembaca memahami atribut garis OUTCOME PEMBELAJARAN Pembaca bisa mendefinisikan pengertian output primitive Pembaca bisa menjelaskan atribut titik Pembaca bisa menjelaskan atribut garis Pendahuluan Setelah berhasil membangun output primitif, langkah selanjutna adalah melakukan pengaturan terhadap atribut output primitif. Atribut adalah semua parameter ang mempengaruhi bagaimana primitive grafis ditampilkan. Atribut dari output primitif dapat berupa: Ukuran garis batas Tipe garis batas 3
115 Warna garis batas Warna objek (Fill color / Area Filling) 4. Atribut Titik Atribut dasar untuk titik adalah ukuran dan warna. Ukuran titik direpresentasikan sebagai beberapa piksel. Sedangkan warna titik bisa berupa monokrom (hitam/putih), grascale (abu-abu), ataupun berwarna (RGB). titik ukuran 2 point, dengan warna biru titik ukuran 26 point, dengan warna abu-abu 4.2 Atribut Garis Atribut dasar untuk garis adalah tipe (tpe), tebal (width) dan warna (color). Dalam beberapa paket program aplikasi grafika seperti paint, photo shop, corel draw dan lain-lain, garis dapat ditampilkan dengan menggunakan pilihan pen atau brush. 4.3 Tipe Garis Garis memiliki beberapa tipe, seperti garis tanpa terputus (solid line), garis putus-putus (dashed line), garis titik-titik (dotted line) dan kombinasi garis dan titik (dash-dotted line). Garis putusputus dibuat dengan memberikan jarak dengan bagian solid ang sama. Garis titik-titik dapat dibuat dengan cara memberikan jarak ang lebih besar dari bagian solid line. Garis putus-putus dapat juga dihasilkan dari sstem raster 4
116 menggunakan piel mask, contohna akan menampilkan garis putus-putus dengan panjang dash 3 dan jarak antar dash 5. Gambar 4. memperlihatkan tipe-tipe garis: Solid line Dashed line Dotted line Gambar 4. Tpe garis : solid line, dashed line, dotted line dan dasheddotted line 4.3. Ukuran Garis Implementasi ukuran garis tergantung pada kemampuan device output ang digunakan. Pada video monitor garis tebal ditampilkan sebagai kumpulan garis sejajar ang berdekatan, sedangkan pada plotter akan menggunakan ukuran pen ang berbeda-beda. Pada raster, tebal garis standar diperoleh dengan cara menempatkan satu piel pada tiap posisi, seperti pada algortima Bressenham. Garis dengan ketebalan ang lain diperoleh dengan perkalian integer positif dan garis standar. Gambar 3-2 menunjukkan berbagai ukuran garis mulai ¼ pt sampai dengan 6 pt ang terdapat pada software aplikasi Microsoft Word. 5
117 Gambar 4. 2 Ukuran garis dari ¼ pt sampai dengan 6 pt pada software aplikasi Microsoft Word Pen dan Brush Penggunaan pen dan brush pada aplikasi tertentu terkadang sangat dibutuhkan. Pen dan Brush merupakan atribut lain dari garis ang mempunai beberapa kategori aitu, bentuk, ukuran dan pola. Beberapa bentuk pen atau brush dapat dilihat pada Gambar 4.3 (diambil dari aplikasi Paint) : Gambar 4. 3 Beberapa bentuk pen atau brush pada paket program aplikasi Paint 6
118 4.4 Warna Garis Pada sstem raster, piel merupakan komponen dasar penusun garis. Sehingga atribut warna garis ditentukan oleh atribut warna dari piel penusunna. Jumlah warna setiap piel bergantung pada jumlah bit ang tersedia per piel pada frame buffer. Bila satu piel mempunai jumlah bit, maka piel tersebut berwarna hitam atau putih. Artina piel tersebut mempunai 2 kemungkinan warna aitu hitam atau putih. Bila satu piel mempunai jumlah 8 bit, maka piel tersebut mempunai 256 kemungkinan warna atau biasa disebut sebagai grascale. Bila satu piel mempunai jumlah 24 bit, maka piel tersebut mempunai sekitar 6 juta kemungkinan warna atau biasa disebut sebagai true color atau RGB. 7
119 Ringkasan Bab 4 Atribut adalah semua parameter ang mempengaruhi bagaimana primitive grafis ditampilkan. Atribut dari output primitif dapat berupa: Ukuran garis batas Tipe garis batas Warna garis batas Warna objek (Fill color / Area Filling) Atribut dasar untuk titik adalah ukuran dan warna. Atribut dasar untuk garis adalah tipe (tpe), tebal (width) dan warna (color). 8
120 Soal-Soal Latihan. Buatlah algoritma untuk membuat garis dengan ketebalan tertentu. 2. Buatlah algoritma untuk membuat garis dengan ketebalan tertentu dan warna tertentu. 3. Buatlah algoritma untuk membuat garis dengan ketebalan tertentu, warna biru dan warna tepi garis adalah merah. 9
121 4. Ubahlah algoritma pembentukan garis DDA dan Bressenham untuk membuat garis putus-putus (dashed), garis titik-titik (dotted) dan garis putus-titik-titik. 2
122 Bab 5 Transformasi Geometri TUJUAN PEMBELAJARAN Pembaca bisa memahami konsep transformasi geometri 2-D dan 3-D: translasi, rotasi, Refleksi, Shear dan scalling. OUTCOME PEMBELAJARAN Pembaca bisa menghitung transformasi geometri 2-D secara manual Pendahuluan Transformasi geometri digunakan untuk memberikan metodemetode perubahan bentuk dan posisi dari sebuah obek. Sehingga transformasi merupakan alat ang paling mendasar ang digunakan untuk grafika komputer. Transformasi membantu menederhanakan tugas-tugas dari pemodelan geometri (geometric modeling), animasi, dan rendering. Transformasi ang paling banak digunakan di dalam grafika komputer adalah transformasi affin (affine tranformation), ang mempunai bentuk sangat sederhana. Sejumlah transformasi dasar dari transformasi affin antara lain adalah : penggeseran (translation), penskalaan (scaling), dan pemutaran (rotation). 2
123 5. Translasi (Pergeseran) Sebuah titik A(,) digeser searah sumbu X sejauh t dan searah sumbu Y sejauh t (perhatikan Gambar 5.), maka titik hasil pergeseran tersebut dapat ditulis sebagai berikut : = + t = + t atau dapat disusun sebagai berikut : = +. + t =. + + t atau dalam bentuk matriks : t. t 22
124 Contoh 5. Tentukan posisi dari segitiga ABC ang dibentuk oleh titik-titik A(2,2), B(,2) dan C(6,2) jika dilakukan penggeseran pada Jawab: Yaitu A (,9), B (8,9) dan C (4,9) 5.2 Scalling (Penskalaan) Penskalaan adalah proses untuk memperbesar atau memperkecil suatu obek atau gambar. Misalkan titik A(,) diskalakan terhadap titik P(a,b) dengan faktor skala sebesar S searah sumbu X dan sebesar S searah sumbu Y (perhatikan Gambar 5., 23
125 maka koordinat hasil penskalaan dapat ditentukan sebagai berikut : = S (-a) + a = S (-b) + b atau = S + a S a = S + b S b atau dalam bentuk matriks : S a S. S b S a b Jika pusat penskalaanna adalah sumbu koordinat P(,), maka a = dan b =, sehingga persamaanna menjadi : S. S Matrik penajian untuk penskalaan terhadap titik pusat P(,) adalah; S S =. S 24
126 Contoh 5.2 Tentukan posisi dari segitiga ABC ang dibentuk oleh titik-titik A(2,2), B(,2) dan C(6,2), jika dilakukan penskalaan dengan faktor skala Jawab: 4 2 terhadap titik pusat P(,) Yaitu A (8,4), B (4,4) dan C (24,24) 5.3 Rotasi (Perputaran) Seperti halna pergeseran dan penskalaan, untuk pemutaran sembarang obek dilakukan dengan pemutaran setiap titik ujung garis. Pemutaran searah jarum jam akan dinatakan dengan sudut negatif, sedangkan pemutaran berlawanan dengan jarum jam dinatakan dengan sudut postif. Dengan menganggap besarna sudut putar adalah, maka hasil pemutaran titik A(,) dengan pusat putar P(,) akan dihasilkan titik A (, ) seperti ang diperlihatkan pada Gambar 5.3 berikut: 25
127 cos sin. sin cos Matrik penajian untuk rotasi terhadap titik pusat P(,) adalah cos sin R =. sin cos Contoh 5.3 Tentukan posisi dari segitiga ABC ang dibentuk oleh titik-titik A(2,2), B(,2) dan C(6,2), jika dilakukan pemutaran dengan pusat sumbu koordinat dengan rotasi putarna 8 derajat berlawanan arah dengan arah jarum jam. Jawab : Yaitu A (-2, -2), B (-, -2) dan C (-6,-2) 5.4 Sistem Koordinat Homogen 2D Dari berbagai bentuk matrik penajian, terlihat bahwa hana transformasi translasi saja ang belum bisa dinatakan sebagai matrik penajian, karena diperlukan operasi perkalian dan penjumlahan, sedangkan pada jenis transformasi ang lain cukup diperlukan operasi perkalian matriks saja, sehingga perlu dicari suatu cara agar translasipun juga bisa dinatakan dalam 26
128 27 operasi perkalian matriks. Hal ini dapat dilakukan dengan dengan menggunakan sistem koordinat homogen. Sistem koordinat homogen adalah sistem koordinat ang mempunai satu dimensi lebih tinggi dari sistem koordinat ang ditinjau. Sebagai contoh, sistem koordinat homogen dari sistem koordinat dua dimensi adalah sistem koordinat 3 dimensi dengan cara menentukan salah satu sumbuna sebagai suatu konstanta. Dengan menggunakan sistem koordinat homogen, persamaan umum transformasi titik A(,) menjadi A (, ) dapat ditulis sebagai :. t d b t c a Dari persamaan tersebut, maka masing-masing transformasi diatas bisa dituliskan sebagai berikut : Matrik penajian Translasi : T = t t, sehingga = t t
129 28 Matrik penajian Scalling : S = S S, sehingga = S S Matrik penajian Rotasi: R = cos sin sin cos, sehingga = cos sin sin cos Contoh 5.4 Tentukan posisi dari segitiga ABC ang dibentuk oleh titik-titik A(,2), B(,8) dan C(3,2) jika dilakukan transformasi berikut : a) Translasi kearah sumbu = 4, kearah sumbu = 2 b) Scalling dengan skala kearah sumbu = 2, kearah sumbu = 2 c) Diputar 9 o berlawanan jarum jam Jawab:
130 29 a) = = diperoleh A (4,), B (4,6) dan C (7,) b) = = diperoleh A (2, 4), B (2, 6) dan C (6, 4) c) = cos9 sin 9 sin 9 cos = diperoleh A ( 2, ), B ( 8, ) dan C ( 2, 3) 5.5 Komposisi Matrik Transformasi 2D Dengan menggunakan matrik penajian, kita bisa menusun transformasi secara berurutan ang biasa disebut sebagai komposisi matrik tranformasi, aitu dengan cara menghitung
131 3 perkalian matrik penajian secara berurutan. Karena perkalian matrik tidak bersifat komutatif, maka urut-urutan perkalian matrik harus diperhatian (tidak boleh kebalik) karena menunjukkan urut-urutan transformasi ang dilakukan. Contoh 5.5 Sebuah segmen garis AB dimana A(,5) dan B(,) akan dirotasikan 9 o terhadap titik A. Bagaimana proses ini dilakukan? Apakah langsung dilakukan proses rotasi 9 o? Gambar 5. Jawab: Jika langsung dirotasikan 9 o hasilna sebagai berikut: 5 A B 5 A B cos(9) sin(9) sin(9) cos(9) 5 5
132 Diperoleh titik hasil transformasi : A (,5) dan B (,) B 5 5 A A B 5 5 Gambar 5. 2 Tentu saja hasil ini tidak seperti ang kita harapkan (hasilna salah). Cara ang benar adalah menggunakan komposisi transformasi, aitu (a) translasikan segmen garis tersebut hingga titik A (sebagai pusat rotasi) berada di titik asal (,). (b) Kemudian rotasikan 9 o terhadap titik asal, dan terakhir (c) translasikan titik A sehingga posisina berada di tempat semula. 5 5 A B A B 5 5 (a) (b) Gambar
133 32 (a) (b) Gambar 5. 4 Secara matematis dapat ditulis sebagai berikut : AB = T(5) R(9) T( 5) AB 5 cos(9) sin(9) sin(9) cos(9) cos(9) sin(9) sin(9) cos(9) A B A B
134 Diperoleh titik hasil transformasi : A (5,) dan B (5,5) 5 5 B A B A 5 5 Gambar 5. 5 Contoh 5.6 Tentukan posisi dari segitiga ABC ang dibentuk oleh titik-titik A(5,5), B(,5) dan C(8,) jika dilakukan komposisi transformasi berikut: penggeseran pada 6 6, dilanjutkan dengan rotasi 9º berlawanan jarum jam, kemudian diakhiri dengan penskalaan dengan faktor skala pusat P(,). Jawab: 3 3 terhadap titik Dalam hal ini kita harus menghitung matrik komposisi berikut S * R * T * 33
135 34 Proses dilakukan terhadap operasi translasi terlebih dahulu cos(9) sin(9) sin(9) cos(9) Diperoleh titik hasil transformasi: A ( 33, 33), B ( 33, 48) dan C ( 48, 42) 5.8 Transformasi Geometri 3D Transformasi geometri 3D merupakan pengembangan dari transformasi geometri 2D. Secara umum representasi transformasi pada 3D juga dibuat dalam bentuk matrik untuk memudahkan perhitungan. a) Translasi z (,, (,, z ) T (T, T, T z)
136 35 Dalam hal ini, z T z z T T Dalam bentuk matrik z T T T z z b) Penskalaan (Scalling) Dalam hal ini, z S z S S z.... z (,, (,, z ) T (S, S, S z)
137 36 Dalam bentuk matrik z S S S z z c) Rotasi Rotasi terhadap sumbu-z sebesar sudut Ө. Dalam hal ini, z z cos sin sin cos Dalam bentuk matrik rotasi terhadap sumbu-z sebesar sudut Ө. cos sin sin cos z z Dengan cara ang sama diperoleh rotasi terhadap sumbu- sebesar sudut Ө. z (,, (,, z )
138 37 cos sin sin cos z z z Dalam bentuk matrik rotasi terhadap sumbu- sebesar sudut Ө. cos sin sin cos z z rotasi terhadap sumbu- sebesar sudut Ө. cos sin sin cos z z z Dalam bentuk matrik rotasi terhadap sumbu- sebesar sudut Ө. cos sin sin cos z z
139 38 Ringkasan Bab 5 Transformasi geometri pada dasarna adalah proses ang mengubah kedudukan setiap titik ang membentuk obek. Transformasi ang banak digunakan di dalam grafika komputer adalah transformasi affin (affine tranformation), aitu: penggeseran (translation), penskalaan (scaling), pemutaran (rotation) dan shearing. Sistem koordinat homogen adalah sistem koordinat ang mempunai satu dimensi lebih tinggi dari sistem koordinat ang ditinjau. Berikut adalah bentuk matrik Tranformasi 2D Translasi : = t t Penskalaan : = S S Rotasi : = cos sin sin cos
140 39 Berikut adalah bentuk matrik Tranformasi 3D Translasi: z T T T z z Penskalaan: z S S S z z Rotasi terhadap sumbu-z : cos sin sin cos z z Rotasi terhadap sumbu-: cos sin sin cos z z Rotasi terhadap sumbu-: cos sin sin cos z z
141 Soal-Soal Latihan. Tentukan posisi dari segitiga ABC ang dibentuk oleh titiktitik A(3,25), B(8,5) dan C(6,2) jika dilakukan penggeseran pada Tentukan posisi dari segitiga ABC ang dibentuk oleh titiktitik A(23,42), B(3,22) dan C(6,2), jika dilakukan penskalaan dengan faktor skala P(,) 4 2 terhadap titik pusat 3. Tentukan posisi dari segitiga ABC ang dibentuk oleh titiktitik A(2,24), B(5,2) dan C(6,2), jika dilakukan pemutaran dengan pusat sumbu koordinat dengan rotasi putarna 3 derajat berlawanan arah dengan arah jarum jam. 4. Tentukan posisi dari segitiga ABC ang dibentuk oleh titiktitik A(,5,6), B(5,8,2) dan C(3,25,) jika dilakukan transformasi berikut : a) translasi kearah sumbu = 2, sumbu = 3, sumbu z = 4 4
142 b) Scalling dengan skala kearah sumbu = 5, sumbu = 3, sumbu z = 7 c) Diputar 45 o terhadap sumbu 4
143 Daftar Istilah AVI: AVI definisi Microsoft untuk Audio Video Interleave. Standar format file video untuk Platform Ms Windows. Binar: Salah satu jenis pada sistem Digital untuk menggambarkan pengkodean pada komputer, sehingga angka numerik hana dapat terdiri atas nilai nol dan satu (On atau Off) saja. CGI: Kependekan dari Computer Graphic Imager. Realtime: Istilah dalam dunia computer ang merupakan bagian dari jenis pengoperasian dimana penerimaan dan proses data begitu pula pengembalian hasil berlangsung begitu cepat sehingga berkesan bahwa input-proses-output serentak. Pada suatu Sistem-NLE pada saat penambahan efek dan overblending proses render segera dilaksanakan dan tanpa ada kesan interrupt (penundaan karena perhitungan render). Rendering: Proses perhitungan matematik sebagai hasil dari efek-efek transformasi untuk frame video (Contoh: perubahan ukuran, efek-efek baik image maupun video, pergerakan). Resolution: Jumlah Informasi pada satu Frame Video, biasana diukur dari jumlah piel horisontal dikalikan jumlah piel vertikal (Contoh misalna standar VGA dengan resolusi 6448 piel). Jika faktor-faktor lainna tidak ada perobahan maka resolusi ang lebih tinggi berarti kualitas gambar lebih baik. 42
144 Streaming: Pengiriman data video melalui internet atau jaringan lain, dimana video langsung dapat dilihat meskipun proses pengiriman masih berlangsung. 24-Bit-Color: Standar warna ang dewasa ini dipakai pada Komputer. Masing-masing komponen warna merah(red), hijau(green) dan biru(blue) disimpan pada informasi 8 Bit (3X8 Bit=24 Bit). Dengan komposisi warna 24 Bit dapat menghasilkan lebih dari satu juta (48576) variasi warna g. YCC: Suatu sinal Video ang terdiri atas Luminance Y - Komponen dan dua Crominance C -Komponen. 43
145 Daftar Pustaka Andreas Butz, Computergrafik, SS 25, Ludwig-Maimilians Universitaet Muenchen Asthana & Sinha, Computer Graphics for Scientists and Engineers, Second Revised Edition, New Age International Publishers, New Delhi, (Revised) 23 (Reprint), ISBN : Edhi Nugroho, Teori dan Praktek Grafika Komputer menggunakan DELPHI dan OpenGL, Penerbit Graha Ilmu, Yogakarta, Cetakan Pertama 25, ISBN : X Francis S.Hill Jr, Computer Graphics, Department of Electrical and Computer Engineering Universit of Massachusetts, Macmillan Publishing Compan, New York, 99, ISBN James Fole, Van Daam, dkk., Grundlagen der Computergraphik Einfuehrung, Konzepte, Methoden, Addison-Wesle Publishing Compan, Bonn,.Auflage 994, ISBN
146 Biografi Penulis Vincent Suhartono adalah pengajar di dua Fakultas aitu Fakultas Teknik Jurusan Elektro dan Fakultas Ilmu Komputer Jurusan Teknik Informatika. Pada saat ini menjabat sebagai Ketua Program Studi, Program Sarjana Teknik Biomedis, Universitas Dian Nuswantoro (UDINUS). Penulis pernah mengajar di Fakultas Teknik Jurusan Teknik Elektro Universitas Kristen Sata Wacana (UKSW) Salatiga. Dan sebelum terjun di dunia pendidikan, pernah sebagai praktisi dengan menjabat sebagai Electronic Data Processing (EDP) Manager pada perusahaan swasta asing (PMA) pada PT Floetotto Indonesia di Semarang. Penulis memiliki 3 gelar pendidikan di Jerman: Ing.-(grad) dari Fachhochschule Bielefeld, Dipl.-Ing. dan Dr.-Ing. dari Universitas Bremen. Bidang Kepakaran penulis adalah: Nachhrichtentechnik (Teknik Komunikasi), Künstliche Intelligenz (Intelligence Control - Robotik) dan Realzeit Programmierung (Real Time Operating Sstem). Sebagai Coauthor, penulis sudah terlibat dalam berbagai buku seperti; buku Teori Pengolahan Citra Digital (Ed.I, ANDI Offset UDINUS, Yogakarta-Semarang, 29 dengan ISBN: ) dan Kecerdasan Buatan (Ed.I, ANDI Offset UDINUS, Yogakarta-Semarang, 2 dengan ISBN: ). 45
Bab 2 Output Primitif
 Bab Output Primitif.. Algoritma DDA (Digital Diferential Analer ) ===================================================================. Tentukan dua titik ang akan dihubungkan dalam pembentukan garis..
Bab Output Primitif.. Algoritma DDA (Digital Diferential Analer ) ===================================================================. Tentukan dua titik ang akan dihubungkan dalam pembentukan garis..
Jawab: Titik awal (x 1, y 1 ) = A(2,1) dan Titik akhir (x 2, y 2 ) = B(8,5) dx = x 2 x 1 = 8 2 = 6 dan dy = y 2 y 1 = 5 1 = 4
 .. Algoritma DDA (Digital Diferential Analer ) DDA adalah algoritma pembentuk garis ang didasarkan pada perasamaan (-8). Garis dibuat menggunakan titik awal (, ) dan titik akhir (, ). Setiap koordinat
.. Algoritma DDA (Digital Diferential Analer ) DDA adalah algoritma pembentuk garis ang didasarkan pada perasamaan (-8). Garis dibuat menggunakan titik awal (, ) dan titik akhir (, ). Setiap koordinat
Computer Graphic. Output Primitif dan Algoritma Garis. Erwin Yudi Hidayat. Computer Graphics C Version 2 Ed by Donald Hearn
 Computer Graphic Output Primitif dan Algoritma Garis Erwin Yudi Hidayat [email protected] Computer Graphics C Version 2 Ed by Donald Hearn Addison Wesley is an imprint of [email protected] CG -
Computer Graphic Output Primitif dan Algoritma Garis Erwin Yudi Hidayat [email protected] Computer Graphics C Version 2 Ed by Donald Hearn Addison Wesley is an imprint of [email protected] CG -
Computer Graphic. Output Primitif dan Algoritma Garis. Erwin Yudi Hidayat.
 Computer Graphic Output Primitif dan Algoritma Garis Erwin Yudi Hidayat [email protected] Computer Graphics C Version 2 Ed by Donald Hearn Addison Wesley is an imprint of [email protected]
Computer Graphic Output Primitif dan Algoritma Garis Erwin Yudi Hidayat [email protected] Computer Graphics C Version 2 Ed by Donald Hearn Addison Wesley is an imprint of [email protected]
3. Jika y1 = y2 (garis horisontal), maka (a) x = x + 1 dan y tetap (b) gambar titik (x,y) di layar (c) Selesai
 .3.1 Algoritma Brute Force Algoritma brute force untuk membentuk garis didasarkan pada persamaan (-6), yaitu : 1. Tentukan dua titik ujung (x1,y1) dan (x,y). Jika x1 = x (garis vertikal), maka (a) y =
.3.1 Algoritma Brute Force Algoritma brute force untuk membentuk garis didasarkan pada persamaan (-6), yaitu : 1. Tentukan dua titik ujung (x1,y1) dan (x,y). Jika x1 = x (garis vertikal), maka (a) y =
10/10/2017. Teknologi Display SISTEM KOORDINAT DAN BENTUK DASAR GEOMETRI (OUTPUT PRIMITIF) CRT CRT. Raster Scan Display
 1 2 SISTEM KOORDINAT DAN BENTUK DASAR GEOMETRI (OUTPUT PRIMITIF) Teknologi Display Cathode Ray Tubes (CRT) Liquid Crystal Display (LCD) 3 4 CRT Elektron ditembakkan dari satu atau lebih electron gun Kemudian
1 2 SISTEM KOORDINAT DAN BENTUK DASAR GEOMETRI (OUTPUT PRIMITIF) Teknologi Display Cathode Ray Tubes (CRT) Liquid Crystal Display (LCD) 3 4 CRT Elektron ditembakkan dari satu atau lebih electron gun Kemudian
Aplikasi-aplikasi Grafika Komputer
 [IF 7021] Grafika Komputer Terapan Aplikasi-aplikasi Grafika Komputer Alfa Ryano 23507003 Program Magister Informatika - Sistem Informasi Sekolah Pascasarja Institut Teknologi Bandung 2008 Aplikasi-aplikasi
[IF 7021] Grafika Komputer Terapan Aplikasi-aplikasi Grafika Komputer Alfa Ryano 23507003 Program Magister Informatika - Sistem Informasi Sekolah Pascasarja Institut Teknologi Bandung 2008 Aplikasi-aplikasi
PAGI. SOAL PILIHAN GANDA : No
 PAGI SOAL PILIHAN GANDA : No. 1 35. 1. Salah satu contoh aplikasi Grafika Komputer adalah Virtual Reality. Yang dimaksud Virtual Reality adalah: a. lingkungan virtual seperti yang ada di dunia internet
PAGI SOAL PILIHAN GANDA : No. 1 35. 1. Salah satu contoh aplikasi Grafika Komputer adalah Virtual Reality. Yang dimaksud Virtual Reality adalah: a. lingkungan virtual seperti yang ada di dunia internet
JURUSAN TEKNIK INFORMATIKA FAKULTAS TEKNIK Universitas Widyatama UJIAN TENGAH SEMESTER T.A. 2008/2009
 JURUAN TEKNIK INFORMATIKA FAKULTA TEKNIK Universitas Widatama UJIAN TENGAH EMETER T.A. 8/9 Mata Kuliah : GRAFIKA KOMPUTER Hari/Tanggal : JUM AT, APRIL 9 Waktu : MENIT Dosen Penguji : TIM DOEN ifat : BUKA
JURUAN TEKNIK INFORMATIKA FAKULTA TEKNIK Universitas Widatama UJIAN TENGAH EMETER T.A. 8/9 Mata Kuliah : GRAFIKA KOMPUTER Hari/Tanggal : JUM AT, APRIL 9 Waktu : MENIT Dosen Penguji : TIM DOEN ifat : BUKA
Modul. Grafika Komputer. Disusun Oleh: Maya Amelia
 Modul Grafika Komputer Disusun Oleh: Maya Amelia Fakultas Ilmu Komputer Universitas Indo Global Mandiri 2012 DAFTAR ISI 1. PENGENALAN GRAFIKA KOMPUTER 1.1 Pengertian Grafika Komputer 1.2 Elemen-Elemen
Modul Grafika Komputer Disusun Oleh: Maya Amelia Fakultas Ilmu Komputer Universitas Indo Global Mandiri 2012 DAFTAR ISI 1. PENGENALAN GRAFIKA KOMPUTER 1.1 Pengertian Grafika Komputer 1.2 Elemen-Elemen
GRAFIK KOMPUTER DAN PENGOLAHAN CITRA. WAHYU PRATAMA, S.Kom., MMSI.
 GRAFIK KOMPUTER DAN PENGOLAHAN CITRA WAHYU PRATAMA, S.Kom., MMSI. PERTEMUAN 3 - GRAFKOM DAN PENGOLAHAN CITRA Output Primitive dan Atributnya Pengenalan Titik dan Garis. Atribut Output Primitive: Line Attributes,
GRAFIK KOMPUTER DAN PENGOLAHAN CITRA WAHYU PRATAMA, S.Kom., MMSI. PERTEMUAN 3 - GRAFKOM DAN PENGOLAHAN CITRA Output Primitive dan Atributnya Pengenalan Titik dan Garis. Atribut Output Primitive: Line Attributes,
BAB IV ATRIBUT OUTPUT PRIMITIF
 BAB IV ATRIBUT OUTPUT PRIMITIF OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : 1. Fungsi Warna 2. Fungsi dan Atribut Titik 3. Fungsi dan Atribut Garis 4. Fungsi dan Atribut Kurva TUJUAN DAN SASARAN:
BAB IV ATRIBUT OUTPUT PRIMITIF OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : 1. Fungsi Warna 2. Fungsi dan Atribut Titik 3. Fungsi dan Atribut Garis 4. Fungsi dan Atribut Kurva TUJUAN DAN SASARAN:
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1 Pengenalan Citra Citra adalah suatu representasi (gambaran), kemiripan atau imitasi dari suatu objek. Citra sebagai keluaran suatu sistem perekaman data dapat bersifat optik berupa
BAB 2 LANDASAN TEORI 2.1 Pengenalan Citra Citra adalah suatu representasi (gambaran), kemiripan atau imitasi dari suatu objek. Citra sebagai keluaran suatu sistem perekaman data dapat bersifat optik berupa
Sistem Multimedia. Image. Donny Reza, S.Kom
 Sistem Multimedia Image Donny Reza, S.Kom Image/Citra Image: representasi grafis dan visual dari suatu informasi yang dapat ditampilkan dalam layar komputer atau dicetak Berbagai bentuk image: Foto Gambar
Sistem Multimedia Image Donny Reza, S.Kom Image/Citra Image: representasi grafis dan visual dari suatu informasi yang dapat ditampilkan dalam layar komputer atau dicetak Berbagai bentuk image: Foto Gambar
Grafik Komputer dan Pengolahan Citra. Grafik Komputer : Geometri Primitive. Universitas Gunadarma Grafik Komputer : Geometri Primitive 1/12
 Grafik Komputer : Geometri Primitive Universitas Gunadarma 2006 Grafik Komputer : Geometri Primitive 1/12 Menggambar GARIS (1/11) Garis adalah kumpulan titik-titik ang tersusun sedemikian rupa sehingga
Grafik Komputer : Geometri Primitive Universitas Gunadarma 2006 Grafik Komputer : Geometri Primitive 1/12 Menggambar GARIS (1/11) Garis adalah kumpulan titik-titik ang tersusun sedemikian rupa sehingga
BAB III OUTPUT PRIMITIF
 BAB III OUTPUT PRIMITIF OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : 1. Primitif Grafis. Algoritma Pembentukan Garis 3. Algoritma Pembentukan Lingkaran 4. Algoritma Pembentukan Ellips TUJUAN
BAB III OUTPUT PRIMITIF OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : 1. Primitif Grafis. Algoritma Pembentukan Garis 3. Algoritma Pembentukan Lingkaran 4. Algoritma Pembentukan Ellips TUJUAN
ALGORITMA MIDPOINT UNTUK PENGGAMBARAN GRAFIK BERKECEPATANG TINGGI
 ALGORITMA MIDPOINT UNTUK PENGGAMBARAN GRAFIK BERKECEPATANG TINGGI Kartika Gunadi Fakultas Teknik, Jurusan Teknik Informatika - Universitas Kristen Petra e-mail: [email protected] ABSTRAK : Penggambaran
ALGORITMA MIDPOINT UNTUK PENGGAMBARAN GRAFIK BERKECEPATANG TINGGI Kartika Gunadi Fakultas Teknik, Jurusan Teknik Informatika - Universitas Kristen Petra e-mail: [email protected] ABSTRAK : Penggambaran
BAB 1. PENDAHULUAN 1.1 Latar Belakang 1.2 Rumusan Masalah 1.3 Tujuan
 BAB 1. PENDAHULUAN 1.1 Latar Belakang Sering kita jumpai dalam kehidupan sehari-hari dalam penyajian data menggunakan bentuk grafik. Grafik sering juga disebut sebagai diagram, bagan, maupun chart. Pada
BAB 1. PENDAHULUAN 1.1 Latar Belakang Sering kita jumpai dalam kehidupan sehari-hari dalam penyajian data menggunakan bentuk grafik. Grafik sering juga disebut sebagai diagram, bagan, maupun chart. Pada
Grafika Komputer. Pendahuluan. Dr. Ahmad Sabri Universitas Gunadarma
 Grafika Komputer Pendahuluan Dr. Ahmad Sabri Universitas Gunadarma Ruang lingkup Perangkat Gambar Disiplin ilmu Grafik Komputer Gambar Grafik komputer adalah gambar yang dihasilkan oleh komputer. Natural
Grafika Komputer Pendahuluan Dr. Ahmad Sabri Universitas Gunadarma Ruang lingkup Perangkat Gambar Disiplin ilmu Grafik Komputer Gambar Grafik komputer adalah gambar yang dihasilkan oleh komputer. Natural
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Grafika Komputer Grafika komputer atau dalam bahasa Inggris computer graphics dapat diartikan sebagai perangkat alat yang terdiri dari hardware dan software untuk membuat gambar,
BAB II LANDASAN TEORI 2.1 Grafika Komputer Grafika komputer atau dalam bahasa Inggris computer graphics dapat diartikan sebagai perangkat alat yang terdiri dari hardware dan software untuk membuat gambar,
Mata Kuliah : Grafik Komputer KONVERSI PEMINDAIAN
 Mata Kuliah : Grafik Komputer KONVERSI PEMINDAIAN Karmilasari Konversi Pemindaian/Konversi Scan Konversi pemindaian atau rasterisasi adalah proses menemukan piksel layar yang besinggungan dengan garis/poligon/
Mata Kuliah : Grafik Komputer KONVERSI PEMINDAIAN Karmilasari Konversi Pemindaian/Konversi Scan Konversi pemindaian atau rasterisasi adalah proses menemukan piksel layar yang besinggungan dengan garis/poligon/
BAB II Tinjauan Pustaka
 23 BAB II Tinjauan Pustaka II.1. Pengolahan Citra Digital Citra yang diperoleh dari lingkungan masih terdiri dari warna yang sangat komplek sehingga masih diperlukan proses lebih lanjut agar image tersebut
23 BAB II Tinjauan Pustaka II.1. Pengolahan Citra Digital Citra yang diperoleh dari lingkungan masih terdiri dari warna yang sangat komplek sehingga masih diperlukan proses lebih lanjut agar image tersebut
Bab 3 Metode dan Perancangan Sistem 3.1 Metode Pengembangan Sistem
 Bab 3 Metode dan Perancangan Sistem 3.1 Metode Pengembangan Sistem Metode yang digunakan untuk pengembangan sistem dalam penelitian ini adalah model proses Prototype. Model prototype (Prototyping model)
Bab 3 Metode dan Perancangan Sistem 3.1 Metode Pengembangan Sistem Metode yang digunakan untuk pengembangan sistem dalam penelitian ini adalah model proses Prototype. Model prototype (Prototyping model)
Definisi, Tujuan, dan Manfaat Desain Grafis
 Definisi, Tujuan, dan Manfaat Desain Grafis 1. Definisi Desain Grafis Desain grafis dapat diartikan sebagai media penyampaian informasi kepada yang membutuhkan (masyarakat) yang disampaikan dalam bentuk
Definisi, Tujuan, dan Manfaat Desain Grafis 1. Definisi Desain Grafis Desain grafis dapat diartikan sebagai media penyampaian informasi kepada yang membutuhkan (masyarakat) yang disampaikan dalam bentuk
MODUL MATEMATIKA II. Oleh: Dr. Eng. LILYA SUSANTI
 MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
Pendahuluan. Pengantar Grafika 3D. Primitif 3D. Sistem Koordinat 3D 12/7/2011
 /7/0 Pengantar Grafika 3D Pendahuluan Grafika Komputer dalam aplikasina terbagi menjadi : Grafika D Grafika 3D Aplikasi D banak dipakai dalam pembuatan grafik, peta, kreasi D ang banak membantu pemakai
/7/0 Pengantar Grafika 3D Pendahuluan Grafika Komputer dalam aplikasina terbagi menjadi : Grafika D Grafika 3D Aplikasi D banak dipakai dalam pembuatan grafik, peta, kreasi D ang banak membantu pemakai
BERANDA SK / KD INDIKATOR MATERI LATIHAN UJI KOMPETENSI REFERENSI PENYUSUN SELESAI TEKNOLOGI INFORMASI DAN KOMUNIKASI
 Loading 25% 100% 50% 75% TEKNOLOGI INFORMASI DAN KOMUNIKASI MENGENAL GRAFIS DAN PROGRAM APLIKASINYA MATA PELAJARAN TIK KELAS XII / SEMESTER GANJIL TEKNOLOGI INFORMASI DAN KOMUNIKASI STANDAR MENGGUNAKAN
Loading 25% 100% 50% 75% TEKNOLOGI INFORMASI DAN KOMUNIKASI MENGENAL GRAFIS DAN PROGRAM APLIKASINYA MATA PELAJARAN TIK KELAS XII / SEMESTER GANJIL TEKNOLOGI INFORMASI DAN KOMUNIKASI STANDAR MENGGUNAKAN
BAB 4 IMPLEMENTASI DAN EVALUASI. membutuhkan spesifikasi Perangkat Keras (Hardware) dan Perangkat Lunak (Software)
 108 BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Implementasi Implementasi majalah elektronik Bitmap beserta editor majalah ini akan membutuhkan spesifikasi Perangkat Keras (Hardware) dan Perangkat Lunak (Software)
108 BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Implementasi Implementasi majalah elektronik Bitmap beserta editor majalah ini akan membutuhkan spesifikasi Perangkat Keras (Hardware) dan Perangkat Lunak (Software)
Pendahuluan 9/7/2011. Overview. Deskripsi
 Pertemuan : I Dosen Pembina : Sriyani Violina Danang Junaedi Pendahuluan Overview Deskripsi Tujuan Instruksional Kaitan Materi Urutan Bahasan Penilaian Grade Referensi 2 Deskripsi Tujuan Instruksional
Pertemuan : I Dosen Pembina : Sriyani Violina Danang Junaedi Pendahuluan Overview Deskripsi Tujuan Instruksional Kaitan Materi Urutan Bahasan Penilaian Grade Referensi 2 Deskripsi Tujuan Instruksional
Interaksi Manusia dan Komputer (Pengantar User Interface) Dosen : Agus Aan Jiwa Permana, S.Kom, M.Cs
 Interaksi Manusia dan Komputer (Pengantar User Interface) Dosen : Agus Aan Jiwa Permana, S.Kom, M.Cs Gambar Ilustrasi CONTENTS: 1 2 3 PENGANTAR ANTARMUKA INPUT-OUTPUT PC JENIS PERANGKAT INPUT-OUTPUT PC
Interaksi Manusia dan Komputer (Pengantar User Interface) Dosen : Agus Aan Jiwa Permana, S.Kom, M.Cs Gambar Ilustrasi CONTENTS: 1 2 3 PENGANTAR ANTARMUKA INPUT-OUTPUT PC JENIS PERANGKAT INPUT-OUTPUT PC
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI Salah satu bidang pengolahan citra yang sedang populer dan banyak dipergunakan dalam pembuatan film sebagai spesial efek yang ditambahkan ke dalam sebuah film untuk menghasilkan film
BAB II LANDASAN TEORI Salah satu bidang pengolahan citra yang sedang populer dan banyak dipergunakan dalam pembuatan film sebagai spesial efek yang ditambahkan ke dalam sebuah film untuk menghasilkan film
BAB 4 IMPLEMENTASI DAN EVALUASI. menjalankan aplikasi ini adalah : Prosesor Pentium IV 2.6 Ghz. Graphic Card dengan memori minimum 64 MB
 BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Spesifikasi Perangkat Lunak Aplikasi 4.1.1 Spesifikasi Perangkat Keras Spesifikasi minimum dari perangkat keras yang dibutuhkan agar dapat menjalankan aplikasi ini adalah
BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Spesifikasi Perangkat Lunak Aplikasi 4.1.1 Spesifikasi Perangkat Keras Spesifikasi minimum dari perangkat keras yang dibutuhkan agar dapat menjalankan aplikasi ini adalah
Tipe dan Jenis Layar Komputer Grafik. By Ocvita Ardhiani.
 Tipe dan Jenis Layar Komputer Grafik By Ocvita Ardhiani. PENGERTIAN GRAFIKA KOMPUTER Grafika komputer adalah bidang dari komputasi visual dimana penggunaan komputer akan menghasilkan gambar visual secara
Tipe dan Jenis Layar Komputer Grafik By Ocvita Ardhiani. PENGERTIAN GRAFIKA KOMPUTER Grafika komputer adalah bidang dari komputasi visual dimana penggunaan komputer akan menghasilkan gambar visual secara
Komputer & Software Semester Ganjil 2014 Fak. Teknik Jurusan Teknik Informatika.
 Komputer & Software Semester Ganjil 2014 Fak. Teknik Jurusan Teknik Informatika Universitas i Pasundan Caca E Supriana S Si MT Caca E. Supriana, S.Si., MT. [email protected] Komputer Komputer
Komputer & Software Semester Ganjil 2014 Fak. Teknik Jurusan Teknik Informatika Universitas i Pasundan Caca E Supriana S Si MT Caca E. Supriana, S.Si., MT. [email protected] Komputer Komputer
Grafika 2 dimensi Transformasi 2 dimensi Penggeseran pada grafika Penskalaan Pemutaran grafika Shearing Sistem koordinat homogen Transformasi
 Komputer Grafik Daftar Pustaka Pokok Bahasan Pengenalan Grafika Komputer Definisi Sejarah Grafika Komputer Sistem Grafika komputer Penerapan Grafika Komputer Penggambaran Grafika Pengertian Pixel Tipe
Komputer Grafik Daftar Pustaka Pokok Bahasan Pengenalan Grafika Komputer Definisi Sejarah Grafika Komputer Sistem Grafika komputer Penerapan Grafika Komputer Penggambaran Grafika Pengertian Pixel Tipe
Mengapa menggunakan format image BITMAP & VECTOR?
 Mengapa menggunakan format image BITMAP & VECTOR? Gambar-gambar grafis yang diproses menggunakan komputer terbagi menjadi dua jenis, yaitu bitmap dan vektor. Jika ingin mendapatkan sebuah hasil cetak yang
Mengapa menggunakan format image BITMAP & VECTOR? Gambar-gambar grafis yang diproses menggunakan komputer terbagi menjadi dua jenis, yaitu bitmap dan vektor. Jika ingin mendapatkan sebuah hasil cetak yang
BAB III METODE PENELITIAN
 BAB III METODE PENELITIAN 3.1 Rancangan Penelitian Pengerjaan tugas akhir ini ditunjukkan dalam bentuk blok diagram pada gambar 3.1. Blok diagram ini menggambarkan proses dari sampel citra hingga output
BAB III METODE PENELITIAN 3.1 Rancangan Penelitian Pengerjaan tugas akhir ini ditunjukkan dalam bentuk blok diagram pada gambar 3.1. Blok diagram ini menggambarkan proses dari sampel citra hingga output
yang tak terdefinisikan dalam arti keberadaannya tidak perlu didefinisikan. yang sejajar dengan garis yang diberikan tersebut.
 3 Gariis Lurus Dalam geometri aksiomatik/euclide konsep garis merupakan salah satu unsur ang tak terdefinisikan dalam arti keberadaanna tidak perlu didefinisikan. Karakteristik suatu garis diberikan pada
3 Gariis Lurus Dalam geometri aksiomatik/euclide konsep garis merupakan salah satu unsur ang tak terdefinisikan dalam arti keberadaanna tidak perlu didefinisikan. Karakteristik suatu garis diberikan pada
BAB 1 PENDAHULUAN. 1.1 Latar Belakang
 14 BAB 1 PENDAHULUAN 1.1 Latar Belakang Grafika komputer tengah menjadi teknologi masa kini. Segala proses perancangan model-model objek saat ini telah banyak menggunakan bantuan komputer. Industri automotive
14 BAB 1 PENDAHULUAN 1.1 Latar Belakang Grafika komputer tengah menjadi teknologi masa kini. Segala proses perancangan model-model objek saat ini telah banyak menggunakan bantuan komputer. Industri automotive
GRAFIK KOMPUTER DAN PENGOLAHAN CITRA. WAHYU PRATAMA, S.Kom., MMSI.
 GRAFIK KOMPUTER DAN PENGOLAHAN CITRA WAHYU PRATAMA, S.Kom., MMSI. PERTEMUAN 1 - GRAFKOM DAN PENGOLAHAN CITRA Pendahuluan Konsep Grafik Komputer dan Pengolahan Citra. Perkembangan Implementasi Grafik Komputer
GRAFIK KOMPUTER DAN PENGOLAHAN CITRA WAHYU PRATAMA, S.Kom., MMSI. PERTEMUAN 1 - GRAFKOM DAN PENGOLAHAN CITRA Pendahuluan Konsep Grafik Komputer dan Pengolahan Citra. Perkembangan Implementasi Grafik Komputer
BAB III ANALISIS DAN PERANCANGAN
 BAB III ANALISIS DAN PERANCANGAN III.1. Analisa Masalah Simulasi 3D mempunyai fungsi utama untuk membuat pemodelan 3D. Dari pemodelan 3D dapat diciptakan karya yang spektakuler seperti special efek dari
BAB III ANALISIS DAN PERANCANGAN III.1. Analisa Masalah Simulasi 3D mempunyai fungsi utama untuk membuat pemodelan 3D. Dari pemodelan 3D dapat diciptakan karya yang spektakuler seperti special efek dari
Fungsi dan Grafik Diferensial dan Integral
 Sudaratno Sudirham Studi Mandiri Fungsi dan Grafik Diferensial dan Integral ii Darpublic BAB Fungsi Linier.. Fungsi Tetapan Fungsi tetapan bernilai tetap untuk rentang nilai x dari sampai +. Kita tuliskan
Sudaratno Sudirham Studi Mandiri Fungsi dan Grafik Diferensial dan Integral ii Darpublic BAB Fungsi Linier.. Fungsi Tetapan Fungsi tetapan bernilai tetap untuk rentang nilai x dari sampai +. Kita tuliskan
PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN
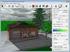 PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN Rudy Adipranata 1, Liliana 2, Gunawan Iteh Fakultas Teknologi Industri, Jurusan Teknik Informatika, Universitas Kristen Petra Jl. Siwalankerto
PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN Rudy Adipranata 1, Liliana 2, Gunawan Iteh Fakultas Teknologi Industri, Jurusan Teknik Informatika, Universitas Kristen Petra Jl. Siwalankerto
Computer Graphics PENGANTAR GRAFIKA 3D
 Computer Graphics PENGANTAR GRAFIKA 3D F A K ULTAS I L MU K O MPUTER 2 4 TUJUAN INSTRUKSIONAL KHUSUS. Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2- Dimensi 2. Mahasiswa mengerti
Computer Graphics PENGANTAR GRAFIKA 3D F A K ULTAS I L MU K O MPUTER 2 4 TUJUAN INSTRUKSIONAL KHUSUS. Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2- Dimensi 2. Mahasiswa mengerti
KATA PENGANTAR. Page 2. Bekasi, 29 Februari Penyusun
 KATA PENGANTAR Dengan menyebut nama Allah SWT yang Maha Pengasih lagi Maha Panyayang, Kami panjatkan puja dan puji syukur atas kehadirat-nya, yang telah melimpahkan rahmat, hidayah, dan inayah-nya kepada
KATA PENGANTAR Dengan menyebut nama Allah SWT yang Maha Pengasih lagi Maha Panyayang, Kami panjatkan puja dan puji syukur atas kehadirat-nya, yang telah melimpahkan rahmat, hidayah, dan inayah-nya kepada
BAB 2 LANDASAN TEORI
 BAB 2 LANDASAN TEORI 2.1. Citra Citra (image) sebagai salah satu komponen multimedia memegang peranan sangat penting sebagai bentuk informasi visual. Citra mempunyai karakteristik yang tidak dimiliki oleh
BAB 2 LANDASAN TEORI 2.1. Citra Citra (image) sebagai salah satu komponen multimedia memegang peranan sangat penting sebagai bentuk informasi visual. Citra mempunyai karakteristik yang tidak dimiliki oleh
BAB III ANALISA DAN PERANCANGAN
 BAB III ANALISA DAN PERANCANGAN 3.1 Rancangan Awal Pemodelan Blender merupakan software grafis 3 Dimensi yang sangat baik. Tidak hanya menyediakan fasilitas untuk membuat object 3D dengan mudah tapi juga
BAB III ANALISA DAN PERANCANGAN 3.1 Rancangan Awal Pemodelan Blender merupakan software grafis 3 Dimensi yang sangat baik. Tidak hanya menyediakan fasilitas untuk membuat object 3D dengan mudah tapi juga
BAB I PENDAHULUAN 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Objek tiga dimensi merupakan salah satu komponen multimedia yang memegang peranan sangat penting sebagai bentuk informasi visual. Objek tiga dimensi dibentuk oleh sekumpulan
BAB I PENDAHULUAN 1.1 Latar Belakang Objek tiga dimensi merupakan salah satu komponen multimedia yang memegang peranan sangat penting sebagai bentuk informasi visual. Objek tiga dimensi dibentuk oleh sekumpulan
BAB 2 LANDASAN TEORI
 8 BAB LANDASAN TEORI.. Pengertian citra Citra (image) menurut Schalkoff (989, p9) adalah fungsi dua dimensi ang dihasilkan dari penglihatan (viewing) suatu pemandangan, ang biasana disebut dengan gambar
8 BAB LANDASAN TEORI.. Pengertian citra Citra (image) menurut Schalkoff (989, p9) adalah fungsi dua dimensi ang dihasilkan dari penglihatan (viewing) suatu pemandangan, ang biasana disebut dengan gambar
MAKALAH APLIKASI KOMPUTER 1 SISTEM APLIKASI KOMPUTER GRAFIK KOMPUTER DAN KONSEP DASAR OLAH CITRA. Diajukan sebagai Tugas Mandiri Mata Kuliah NTM
 MAKALAH APLIKASI KOMPUTER 1 SISTEM APLIKASI KOMPUTER GRAFIK KOMPUTER DAN KONSEP DASAR OLAH CITRA Diajukan sebagai Tugas Mandiri Mata Kuliah NTM Semester Genap Tahun Akademik 2014 / 2015 Angkatan XIII Disusun
MAKALAH APLIKASI KOMPUTER 1 SISTEM APLIKASI KOMPUTER GRAFIK KOMPUTER DAN KONSEP DASAR OLAH CITRA Diajukan sebagai Tugas Mandiri Mata Kuliah NTM Semester Genap Tahun Akademik 2014 / 2015 Angkatan XIII Disusun
GRAPHICAL USER INTER-
 Ariesto Hadi Sutopo Ariesto Hadi Sutopo GRAPHICAL USER INTER- Setelah mempelajari bab ini, Anda diharapkan dapat: 1. Memahami konsep graphical interface 2. Membuat user interface yang baik 1 Pengantar
Ariesto Hadi Sutopo Ariesto Hadi Sutopo GRAPHICAL USER INTER- Setelah mempelajari bab ini, Anda diharapkan dapat: 1. Memahami konsep graphical interface 2. Membuat user interface yang baik 1 Pengantar
1. Pengertian Tentang Fungsi dan Grafik
 Darpublic Oktober 3 www.darpublic.com. Pengertian Tentang Fungsi dan Grafik Fungsi Apabila suatu besaran memiliki nilai ang tergantung dari nilai besaran lain, maka dikatakan bahwa besaran tersebut merupakan
Darpublic Oktober 3 www.darpublic.com. Pengertian Tentang Fungsi dan Grafik Fungsi Apabila suatu besaran memiliki nilai ang tergantung dari nilai besaran lain, maka dikatakan bahwa besaran tersebut merupakan
BAB II SISTEM MESIN PEMOTONG AKRILIK
 BAB II SISTEM MESIN PEMOTONG AKRILIK 2.1. Gambaran Mesin Pemotong Akrilik Mesin pemotong akrilik termasuk dalam jenis mesin CNC (Computer Numerical Control). Mesin CNC adalah sebuah mesin perkakas yang
BAB II SISTEM MESIN PEMOTONG AKRILIK 2.1. Gambaran Mesin Pemotong Akrilik Mesin pemotong akrilik termasuk dalam jenis mesin CNC (Computer Numerical Control). Mesin CNC adalah sebuah mesin perkakas yang
BAB III ANALISIS MASALAH DAN RANCANGAN PROGRAM
 BAB III ANALISIS MASALAH DAN RANCANGAN PROGRAM III.1. Analisa Masalah Simulasi 3D mempunyai fungsi utama untuk membuat pemodelan 3D. Dari pemodelan 3D dapat diciptakan karya yang spektakuler seperti special
BAB III ANALISIS MASALAH DAN RANCANGAN PROGRAM III.1. Analisa Masalah Simulasi 3D mempunyai fungsi utama untuk membuat pemodelan 3D. Dari pemodelan 3D dapat diciptakan karya yang spektakuler seperti special
Analisa Hasil Perbandingan Metode Low-Pass Filter Dengan Median Filter Untuk Optimalisasi Kualitas Citra Digital
 Analisa Hasil Perbandingan Metode Low-Pass Filter Dengan Median Filter Untuk Optimalisasi Kualitas Citra Digital Nurul Fuad 1, Yuliana Melita 2 Magister Teknologi Informasi Institut Saint Terapan & Teknologi
Analisa Hasil Perbandingan Metode Low-Pass Filter Dengan Median Filter Untuk Optimalisasi Kualitas Citra Digital Nurul Fuad 1, Yuliana Melita 2 Magister Teknologi Informasi Institut Saint Terapan & Teknologi
Pengantar Grafika 3D E D I T A N
 Pengantar Grafika 3D F A KULTAS I L M U K O M P UTER E D I T A N 2 5 TUJUAN INSTRUKSIONAL KHUSUS 2 Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2-Dimensi Mahasiswa mengerti
Pengantar Grafika 3D F A KULTAS I L M U K O M P UTER E D I T A N 2 5 TUJUAN INSTRUKSIONAL KHUSUS 2 Mahasiswa memahami Grafika 3-Dimensi dan dapat membedakan dengan Grafika 2-Dimensi Mahasiswa mengerti
Pada komputer grafik ada 3 macam sistem koordinat yang harus di perhatikan :
 Pada komputer grafik ada 3 macam sistem koordinat yang harus di perhatikan : Koordinat nyata Koordinat sistem (koordinat cartesian) Koordinat tampilan / layar Grafika Komputer Page 2 Adalah koordinat yang
Pada komputer grafik ada 3 macam sistem koordinat yang harus di perhatikan : Koordinat nyata Koordinat sistem (koordinat cartesian) Koordinat tampilan / layar Grafika Komputer Page 2 Adalah koordinat yang
Studi Digital Watermarking Citra Bitmap dalam Mode Warna Hue Saturation Lightness
 Studi Digital Watermarking Citra Bitmap dalam Mode Warna Hue Saturation Lightness Evan 13506089 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : [email protected]
Studi Digital Watermarking Citra Bitmap dalam Mode Warna Hue Saturation Lightness Evan 13506089 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : [email protected]
RENCANA PEMBELAJARAN SEMESTER (RPS)
 RENCANA PEMBELAJARAN SEMESTER (RPS) PKBM42002 GRAFIKA KOMPUTER PROGRAM STUDI D3 MANAJEMEN INFORMATIKA (MI) FAKULTAS ILMU KOMPUTER (FILKOM) UNIVERSITAS PUTRA INDONESIA YPTK LEMBAR PENGESAHAN Rencana Semester
RENCANA PEMBELAJARAN SEMESTER (RPS) PKBM42002 GRAFIKA KOMPUTER PROGRAM STUDI D3 MANAJEMEN INFORMATIKA (MI) FAKULTAS ILMU KOMPUTER (FILKOM) UNIVERSITAS PUTRA INDONESIA YPTK LEMBAR PENGESAHAN Rencana Semester
Transformasi Geometri Sederhana. Farah Zakiyah Rahmanti 2014
 Transformasi Geometri Sederhana Farah Zakiyah Rahmanti 2014 Grafika Komputer TRANSFORMASI 2D Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut
Transformasi Geometri Sederhana Farah Zakiyah Rahmanti 2014 Grafika Komputer TRANSFORMASI 2D Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut
BAB III METODOLOGI PENELITIAN. Penelitian ini menekankan pada objek virtual tiga dimensi gedung-gedung
 25 BAB III METODOLOGI PENELITIAN 3.1. Waktu dan Tempat Penelitian Penelitian ini menekankan pada objek virtual tiga dimensi gedung-gedung utama pada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
25 BAB III METODOLOGI PENELITIAN 3.1. Waktu dan Tempat Penelitian Penelitian ini menekankan pada objek virtual tiga dimensi gedung-gedung utama pada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
Pengertian. Transformasi geometric transformation. koordinat dari objek Transformasi dasar: Translasi Rotasi Penskalaan
 Pengertian Transformasi geometric transformation Transformasi = mengubah deskripsi koordinat dari objek Transformasi dasar: Translasi Rotasi Penskalaan Translasi Mengubah posisi objek: perpindahan lurus
Pengertian Transformasi geometric transformation Transformasi = mengubah deskripsi koordinat dari objek Transformasi dasar: Translasi Rotasi Penskalaan Translasi Mengubah posisi objek: perpindahan lurus
BAB I PERSYARATAN PRODUK
 BAB I PERSYARATAN PRODUK Pemrosesan gambar secara digital telah berkembang dengan cepat. Pengolahan gambar ini didukung dengan kemajuan teknologi perangkat keras yang signifikan. Produk produk pengolah
BAB I PERSYARATAN PRODUK Pemrosesan gambar secara digital telah berkembang dengan cepat. Pengolahan gambar ini didukung dengan kemajuan teknologi perangkat keras yang signifikan. Produk produk pengolah
BAB 2 LANDASAN TEORI
 7 BAB 2 LANDASAN TEORI 2.1 Citra Digital Citra digital merupakan sebuah fungsi intensitas cahaya, dimana harga x dan y merupakan koordinat spasial dan harga fungsi f tersebut pada setiap titik merupakan
7 BAB 2 LANDASAN TEORI 2.1 Citra Digital Citra digital merupakan sebuah fungsi intensitas cahaya, dimana harga x dan y merupakan koordinat spasial dan harga fungsi f tersebut pada setiap titik merupakan
BAB III TINJAUAN PUSTAKA. penjelasan-penjelasan mendetail beserta sumber-sumber teoritis yang berkaitan
 BAB III TINJAUAN PUSTAKA Dalam Bab III, Tinjauan Pustaka, penulis akan menerangkan tentang penjelasan-penjelasan mendetail beserta sumber-sumber teoritis yang berkaitan dengan pembuatan design 3D interior
BAB III TINJAUAN PUSTAKA Dalam Bab III, Tinjauan Pustaka, penulis akan menerangkan tentang penjelasan-penjelasan mendetail beserta sumber-sumber teoritis yang berkaitan dengan pembuatan design 3D interior
BAB V TRANSFORMASI 2D
 BAB V TRANSFORMASI 2D OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : Transformasi Dasar 2D 1. Translasi 2. Rotasi 3. Scalling Transformasi Lain 1. Refleksi 2. Shear TUJUAN DAN SASARAN: Setelah
BAB V TRANSFORMASI 2D OBJEKTIF : Pada Bab ini mahasiswa mempelajari tentang : Transformasi Dasar 2D 1. Translasi 2. Rotasi 3. Scalling Transformasi Lain 1. Refleksi 2. Shear TUJUAN DAN SASARAN: Setelah
BAB II DASAR TEORI. CV Dokumentasi CV berisi pengolahan citra, analisis struktur citra, motion dan tracking, pengenalan pola, dan kalibrasi kamera.
 BAB II DASAR TEORI Pada bab ini akan dibahas teori yang berkaitan dengan skripsi ini, meliputi pustaka OpenCV, citra, yaitu citra grayscale dan citra berwarna, pengolahan citra meliputi image enhancement
BAB II DASAR TEORI Pada bab ini akan dibahas teori yang berkaitan dengan skripsi ini, meliputi pustaka OpenCV, citra, yaitu citra grayscale dan citra berwarna, pengolahan citra meliputi image enhancement
Dasar-Dasar Menggambar dengan Flash (Objek dan Teks) Oleh: Ali Mahmudi
 Dasar-Dasar Menggambar dengan Flash (Objek dan Teks) Oleh: Ali Mahmudi Mengenal Macromedia Flash. Macromedia Flash MX merupakan perangkat lunak untuk merancang grafis dan animasi. Macromedia Flash MX merupakan
Dasar-Dasar Menggambar dengan Flash (Objek dan Teks) Oleh: Ali Mahmudi Mengenal Macromedia Flash. Macromedia Flash MX merupakan perangkat lunak untuk merancang grafis dan animasi. Macromedia Flash MX merupakan
GRAFIKA KOMPUTER BAB 1. PENGANTAR
 GRAFIKA KOMPUTER BAB 1. PENGANTAR Sistem Grafika Komputer Grafika komputer suatu bidang ilmu komputer yang mempelajari tentang cara cara untuk meningkatkan dan memudahkan komunikasi antara manusia dan
GRAFIKA KOMPUTER BAB 1. PENGANTAR Sistem Grafika Komputer Grafika komputer suatu bidang ilmu komputer yang mempelajari tentang cara cara untuk meningkatkan dan memudahkan komunikasi antara manusia dan
BAB 2 LANDASAN TEORI. tentang animasi. Animasi atau lebih akrab disebut dengan film animasi, adalah. gambar yang bergerak. (http://www.wikipedia.
 BAB 2 LANDASAN TEORI 2.1 ANIMASI Animasi memiliki banyak pengertian. Tiap orang memiliki pendapat yang berbeda tentang animasi. Animasi atau lebih akrab disebut dengan film animasi, adalah film yang merupakan
BAB 2 LANDASAN TEORI 2.1 ANIMASI Animasi memiliki banyak pengertian. Tiap orang memiliki pendapat yang berbeda tentang animasi. Animasi atau lebih akrab disebut dengan film animasi, adalah film yang merupakan
BAB 4 IMPLEMENTASI DAN EVALUASI. perangkat pendukung yang berupa piranti lunak dan perangkat keras. Adapun
 BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Implementasi Perangkat Ajar Dalam perancangan dan pembuatan perangkat ajar ini membutuhkan perangkat pendukung yang berupa piranti lunak dan perangkat keras. Adapun
BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Implementasi Perangkat Ajar Dalam perancangan dan pembuatan perangkat ajar ini membutuhkan perangkat pendukung yang berupa piranti lunak dan perangkat keras. Adapun
Animasi Objek 2 Dimensi GAMBAR BITMAP
 Animasi Objek 2 Dimensi `Animasi objek 2 Dimensi terdiri dari bitmap dan vektor.metode- metode ini menginterpretasikan input, menghitungnya dan menampilkannya pada output grafis seperti monitor.gambar
Animasi Objek 2 Dimensi `Animasi objek 2 Dimensi terdiri dari bitmap dan vektor.metode- metode ini menginterpretasikan input, menghitungnya dan menampilkannya pada output grafis seperti monitor.gambar
Materi. Pengantar Grafik & Multiedia. Tugas. Matakuliah Pengantar Teknologi Informasi. Graphic Techno. Hari syafran
 Materi Pengantar Grafik & Multiedia Tugas Matakuliah Pengantar Teknologi Informasi Graphic Techno Nama Anggota NPM/BP Hari syafran 2011610176 Hendro prasetyo 2011610177 Ahmad arif 2011610178 Dosen pembimbing
Materi Pengantar Grafik & Multiedia Tugas Matakuliah Pengantar Teknologi Informasi Graphic Techno Nama Anggota NPM/BP Hari syafran 2011610176 Hendro prasetyo 2011610177 Ahmad arif 2011610178 Dosen pembimbing
Sudaryatno Sudirham. Studi Mandiri. Fungsi dan Grafik. Darpublic
 Sudaratno Sudirham Studi Mandiri Fungsi dan Grafik ii Darpublic BAB 1 Pengertian Tentang Fungsi dan Grafik 1.1. Fungsi Apabila suatu besaran memiliki nilai ang tergantung dari nilai besaran lain, maka
Sudaratno Sudirham Studi Mandiri Fungsi dan Grafik ii Darpublic BAB 1 Pengertian Tentang Fungsi dan Grafik 1.1. Fungsi Apabila suatu besaran memiliki nilai ang tergantung dari nilai besaran lain, maka
TEKNIK PENGOLAHAN CITRA MENGGUNAKAN METODE KECERAHAN CITRA KONTRAS DAN PENAJAMAN CITRA DALAM MENGHASILKAN KUALITAS GAMBAR
 TEKNIK PENGOLAHAN CITRA MENGGUNAKAN METODE KECERAHAN CITRA KONTRAS DAN PENAJAMAN CITRA DALAM MENGHASILKAN KUALITAS GAMBAR Zulkifli Dosen Tetap Fakultas Ilmu Komputer Universitas Almuslim Email : [email protected]
TEKNIK PENGOLAHAN CITRA MENGGUNAKAN METODE KECERAHAN CITRA KONTRAS DAN PENAJAMAN CITRA DALAM MENGHASILKAN KUALITAS GAMBAR Zulkifli Dosen Tetap Fakultas Ilmu Komputer Universitas Almuslim Email : [email protected]
Bab III Perangkat Pengujian
 Bab III Perangkat Pengujian Persoalan utama dalam tugas akhir ini adalah bagaimana mengimplementasikan metode pengukuran jarak menggunakan pengolahan citra tunggal dengan bantuan laser pointer dalam suatu
Bab III Perangkat Pengujian Persoalan utama dalam tugas akhir ini adalah bagaimana mengimplementasikan metode pengukuran jarak menggunakan pengolahan citra tunggal dengan bantuan laser pointer dalam suatu
ANALISA ALGORITMA BOUNDARY FILL 4-CONNECTED DAN 8-CONNECTED PADA IMAGE DUA DIMENSI (2d)
 ISSN : 1978-6603 ANALISA ALGORITMA BOUNDARY FILL 4-CONNECTED DAN 8-CONNECTED PADA IMAGE DUA DIMENSI (2d) Herriyance *1, Hendryan Winata *2 #1 Program Studi Ilmu Komputer, Universitas Sumatera Utara #2
ISSN : 1978-6603 ANALISA ALGORITMA BOUNDARY FILL 4-CONNECTED DAN 8-CONNECTED PADA IMAGE DUA DIMENSI (2d) Herriyance *1, Hendryan Winata *2 #1 Program Studi Ilmu Komputer, Universitas Sumatera Utara #2
BAB II LANDASAN TEORI. Grafika komputer atau dalam bahasa Inggris computer graphics dapat
 BAB II LANDASAN TEORI 2.1 Grafika Komputer Grafika komputer atau dalam bahasa Inggris computer graphics dapat diartikan sebagai perangkat alat yang terdiri dari hardware dan software untuk membuat gambar,
BAB II LANDASAN TEORI 2.1 Grafika Komputer Grafika komputer atau dalam bahasa Inggris computer graphics dapat diartikan sebagai perangkat alat yang terdiri dari hardware dan software untuk membuat gambar,
Bab 1. Pendahuluan. menggunakan bantuan aplikasi CAD (Computer-Aided Design) untuk. menggunakan komputer ini disebut sebagai mesin Computer based
 Bab 1 Pendahuluan 1.1 Latar Belakang Masalah Seiring dengan kemajuan teknologi, komputer digunakan untuk berbagai keperluan, baik sebagai sarana untuk membantu pekerjaan maupun sarana hiburan. Penggunaannya
Bab 1 Pendahuluan 1.1 Latar Belakang Masalah Seiring dengan kemajuan teknologi, komputer digunakan untuk berbagai keperluan, baik sebagai sarana untuk membantu pekerjaan maupun sarana hiburan. Penggunaannya
BAB I PENDAHULUAN 1.2. Latar Belakang Masalah
 BAB I PENDAHULUAN Pada bab ini dijelaskan tujuan, latar belakang masalah, gambaran sistem, batasan masalah, perincian tugas yang dikerjakan dan garis besar penulisan skripsi. 1.1. Tujuan Merancang dan
BAB I PENDAHULUAN Pada bab ini dijelaskan tujuan, latar belakang masalah, gambaran sistem, batasan masalah, perincian tugas yang dikerjakan dan garis besar penulisan skripsi. 1.1. Tujuan Merancang dan
PENGENALAN TEKNOLOGI KOMPUTER
 PENGENALAN TEKNOLOGI KOMPUTER Komputer berasal dari bahasa latin computare yang mengandung arti menghitung Penggolongan Komputer a. Berdasarkan Data Yang Diolah 1. Komputer Analog 2. Komputer Digital 3.
PENGENALAN TEKNOLOGI KOMPUTER Komputer berasal dari bahasa latin computare yang mengandung arti menghitung Penggolongan Komputer a. Berdasarkan Data Yang Diolah 1. Komputer Analog 2. Komputer Digital 3.
PENDAHULUAN KALKULUS
 . BILANGAN REAL PENDAHULUAN KALKULUS Ada beberapa jenis bilangan ang telah kita kenal ketika di bangku sekolah. Bilangan-bilangan tersebut adalah bilangan asli, bulat, cacah, rasional, irrasional. Tahu
. BILANGAN REAL PENDAHULUAN KALKULUS Ada beberapa jenis bilangan ang telah kita kenal ketika di bangku sekolah. Bilangan-bilangan tersebut adalah bilangan asli, bulat, cacah, rasional, irrasional. Tahu
BAB I PENDAHULUAN. dengan teknik dan teori sintesis gambar (image) komputer. Komputer
 BAB I PENDAHULUAN III.1. Latar Belakang Grafika komputer adalah suatu cabang ilmu komputer yang berhadapan dengan teknik dan teori sintesis gambar (image) komputer. Komputer menghasilkan gambar dengan
BAB I PENDAHULUAN III.1. Latar Belakang Grafika komputer adalah suatu cabang ilmu komputer yang berhadapan dengan teknik dan teori sintesis gambar (image) komputer. Komputer menghasilkan gambar dengan
BAB IV HASIL DAN UJI COBA
 45 BAB IV HASIL DAN UJI COBA IV.1. Tampilan Hasil Laporan skripsi ini mencoba untuk membuat sebuah perancangan aplikasi permainan Color Memory menggunakan metode Brute Force. Dalam proses pembuatan aplikasi
45 BAB IV HASIL DAN UJI COBA IV.1. Tampilan Hasil Laporan skripsi ini mencoba untuk membuat sebuah perancangan aplikasi permainan Color Memory menggunakan metode Brute Force. Dalam proses pembuatan aplikasi
BAB III PERANCANGAN SISTEM. Pada dewasa sekarang ini sangat banyak terdapat sistem dimana sistem tersebut
 BAB III PERANCANGAN SISTEM 3.1 Definisi Masalah Pada dewasa sekarang ini sangat banyak terdapat sistem dimana sistem tersebut sudah terintegrasi dengan komputer, dengan terintegrasinya sistem tersebut
BAB III PERANCANGAN SISTEM 3.1 Definisi Masalah Pada dewasa sekarang ini sangat banyak terdapat sistem dimana sistem tersebut sudah terintegrasi dengan komputer, dengan terintegrasinya sistem tersebut
RENCANA PROGRAM KEGIATAN PERKULIAHAN SEMESTER (RPKPS)
 RENCANA PROGRAM KEGIATAN PERKULIAHAN SEMESTER (RPKPS) Kode / Nama Mata Kuliah : E124904/ Komputer Grafik Revisi 4 Satuan Kredit Semester : 2 SKS Tgl revisi : 16 Juli 2015 Jml Jam kuliah dalam seminggu
RENCANA PROGRAM KEGIATAN PERKULIAHAN SEMESTER (RPKPS) Kode / Nama Mata Kuliah : E124904/ Komputer Grafik Revisi 4 Satuan Kredit Semester : 2 SKS Tgl revisi : 16 Juli 2015 Jml Jam kuliah dalam seminggu
BAB III ANALISA MASALAH DAN PERANCANGAN PROGRAM
 BAB III ANALISA MASALAH DAN PERANCANGAN PROGRAM III.1. Analisa Masalah Kemajuan teknologi simulasi untuk menggambarkan suatu kejadian semakin pesat menuntut modernisasi di segala bidang. Tak terkecuali
BAB III ANALISA MASALAH DAN PERANCANGAN PROGRAM III.1. Analisa Masalah Kemajuan teknologi simulasi untuk menggambarkan suatu kejadian semakin pesat menuntut modernisasi di segala bidang. Tak terkecuali
Pertemuan 11. MONITOR dan MONITOR
 Pertemuan 11 MONITOR dan TROUBLESHOOTING MONITOR Jenis-jenis monitor Monitor merupakan komponen output yang digunakan untuk menampilkan teks atau gambar kelayar sehingga dapat dinikmati Oleh pemakai, monitor
Pertemuan 11 MONITOR dan TROUBLESHOOTING MONITOR Jenis-jenis monitor Monitor merupakan komponen output yang digunakan untuk menampilkan teks atau gambar kelayar sehingga dapat dinikmati Oleh pemakai, monitor
BAB 4 IMPLEMENTASI DAN EVALUASI
 BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Implementasi Program Aplikasi Pada bagian ini, Penulis akan menjelaskan kebutuhan spesifikasi perangkat keras dan perangkat lunak, serta menjelaskan bagaimana cara program
BAB 4 IMPLEMENTASI DAN EVALUASI 4.1 Implementasi Program Aplikasi Pada bagian ini, Penulis akan menjelaskan kebutuhan spesifikasi perangkat keras dan perangkat lunak, serta menjelaskan bagaimana cara program
BAB III ANALISA DAN PERANCANGAN
 BAB III ANALISA DAN PERANCANGAN III.1. Analisa Animasi 3D sangat banyak digunakan dalam pembuatan pemodelan 3D, karena animasi 3D mempunyai fungsi utama untuk membuat pemodelan 3D. Dari pemodelan 3D inilah
BAB III ANALISA DAN PERANCANGAN III.1. Analisa Animasi 3D sangat banyak digunakan dalam pembuatan pemodelan 3D, karena animasi 3D mempunyai fungsi utama untuk membuat pemodelan 3D. Dari pemodelan 3D inilah
BAB III ANALISIS MASALAH DAN PERANCANGAN PROGRAM
 BAB III ANALISIS MASALAH DAN PERANCANGAN PROGRAM III.1. Analisa Masalah Analisis sistem dapat didefinisikan sebagai Penguraian dari suatu sistem informasi yang utuh ke dalam bagian-bagian komponennya dengan
BAB III ANALISIS MASALAH DAN PERANCANGAN PROGRAM III.1. Analisa Masalah Analisis sistem dapat didefinisikan sebagai Penguraian dari suatu sistem informasi yang utuh ke dalam bagian-bagian komponennya dengan
BAB III METODE PENELITIAN
 BAB III METODE PENELITIAN 3.1 Rancangan Penelitian Tulisan Tangan angka Jawa Digitalisasi Pre-Processing ROI Scalling / Resize Shadow Feature Extraction Output Multi Layer Perceptron (MLP) Normalisasi
BAB III METODE PENELITIAN 3.1 Rancangan Penelitian Tulisan Tangan angka Jawa Digitalisasi Pre-Processing ROI Scalling / Resize Shadow Feature Extraction Output Multi Layer Perceptron (MLP) Normalisasi
Pertemuan 2 Representasi Citra
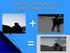 /29/23 FAKULTAS TEKNIK INFORMATIKA PENGOLAHAN CITRA DIGITAL ( DIGITAL IMAGE PROCESSING ) Pertemuan 2 Representasi Citra Representasi Citra citra Citra analog Citra digital Matrik dua dimensi yang terdiri
/29/23 FAKULTAS TEKNIK INFORMATIKA PENGOLAHAN CITRA DIGITAL ( DIGITAL IMAGE PROCESSING ) Pertemuan 2 Representasi Citra Representasi Citra citra Citra analog Citra digital Matrik dua dimensi yang terdiri
Perangkat Lunak Multimedia
 Perangkat Lunak Multimedia Perangkat lunak multimedia adalah komponen-komponen dalam data processing system, berupa program-program untuk mengontrol bekerjanya sistem komputer multimedia. Perangkat lunak
Perangkat Lunak Multimedia Perangkat lunak multimedia adalah komponen-komponen dalam data processing system, berupa program-program untuk mengontrol bekerjanya sistem komputer multimedia. Perangkat lunak
Bentuk Primitif. Esther Wibowo -
 Bentuk Primitif Esther Wibowo - [email protected] Bentuk Primitif Point - Titik Line - Garis Shape/Polygon - Bentuk bangun Text - Teks Titik Direpresentasikan dengan koordinat (x,y) Biasanya tidak
Bentuk Primitif Esther Wibowo - [email protected] Bentuk Primitif Point - Titik Line - Garis Shape/Polygon - Bentuk bangun Text - Teks Titik Direpresentasikan dengan koordinat (x,y) Biasanya tidak
AUGMENTED REALITY PERMAINAN BOLA PINGPONG MENGGUNAKAN FLARTOOLKIT. Prodi Teknik Elektro, Fakultas Teknik, Universitas Trunojoyo Madura 2
 AUGMENED REALIY PERMAINAN BOLA PINGPONG MENGGUNAKAN FLAROOLKI Haranto 1*, Septian Rahman Hakim 2 1,2 Prodi eknik Elektro, Fakultas eknik, Universitas runojoo Madura 2 Prodi Pendidikan Informatika, Fakultas
AUGMENED REALIY PERMAINAN BOLA PINGPONG MENGGUNAKAN FLAROOLKI Haranto 1*, Septian Rahman Hakim 2 1,2 Prodi eknik Elektro, Fakultas eknik, Universitas runojoo Madura 2 Prodi Pendidikan Informatika, Fakultas
BAB I PENDAHULUAN. baik dunia kerja maupun dunia pendidikan. Ditambah lagi dengan adanya dunia
 1 BAB I PENDAHULUAN I.1. Latar Belakang Saat ini perkembangan computer sudah semakin pesat, computer bukan lagi hal yang baru. Computer sudah menjadi peran utama dalam berbagai kegiatan baik dunia kerja
1 BAB I PENDAHULUAN I.1. Latar Belakang Saat ini perkembangan computer sudah semakin pesat, computer bukan lagi hal yang baru. Computer sudah menjadi peran utama dalam berbagai kegiatan baik dunia kerja
2 Akar Persamaan NonLinear
 2 Akar Persamaan NonLinear Beberapa metoda untuk mencari akar ang telah dikenal adalah dengan memfaktorkan atau dengan cara Horner Sebagai contoh, untuk mencari akar dari persamaan 2 6 = 0 ruas kiri difaktorkan
2 Akar Persamaan NonLinear Beberapa metoda untuk mencari akar ang telah dikenal adalah dengan memfaktorkan atau dengan cara Horner Sebagai contoh, untuk mencari akar dari persamaan 2 6 = 0 ruas kiri difaktorkan
Pengantar Grafika Komputer
 Kompetensi dan Referensi Pengantar Grafika Komputer G R A F I K A K O M P U T E R / P T I 2 7 5 /PENDIDIKAN TEKNIK INFORMATIKA/2 SKS Kompetensi Mahasiswa dapat merancang dan membangun sebuah aplikasi Grafika
Kompetensi dan Referensi Pengantar Grafika Komputer G R A F I K A K O M P U T E R / P T I 2 7 5 /PENDIDIKAN TEKNIK INFORMATIKA/2 SKS Kompetensi Mahasiswa dapat merancang dan membangun sebuah aplikasi Grafika
