PERTEMUAN 2 DASAR METODE NUMERIK

RENCANA PELAKSANAAN PEMBELAJARAN

7 RENCANA PELAKSANAAN PEMBELAJARAN M Peljrn : Memik Kels/ Semeser: XI Progrm IPA/ Aloksi Wku: 6 jm Peljrn ( Peremun) A. Sndr Kompeensi Menggunkn konsep i fungsi dn urunn fungsi dlm pemehn mslh. B. Kompeensi

MODUL VIII FISIKA MODERN Transformasi Lorentz

MODUL VIII FISIKA MODERN Trnsformsi Loren Tujun Insruksionl Umum : Agr mhsisw dp memhmi mengeni Trnsformsi Loren Tujun Insruksionl Khusus : Dp menjelskn enng kedu posul Einsein Dp menjelskn enng perbedn

INTEGRAL TAK-WAJAR. bentuk tak-tentu karena bentuk ini saling membantu dan tidak bersaing.

INTEGRAL TAK-WAJAR A. Tk Terhingg Seip ilngn sli merupkn ilngn erhingg dn dp menykn sesuu yng nykny erhingg. Arisoeles menykn hw ilngn sli n dp ernili seesr-esrny epi ep erhingg dn idk kn pernh sm dengn

r x = 0. Koefisien-koefisien persamaan yang dihasilkan adalah analitik pada x = 0. Jadi dapat kita gunakan metode deret pangkat.

Husn Arifh,M.Sc : Persmn Legendre Emil : [email protected] Persmn diferensil Legendre (1) 1 x 2 y 2xy + n n + 1 y = 0 Prmeter n pd (1) dlh bilngn rill yng diberikn. Setip penyelesin dri (1) dinmkn fungsi

Matematika EBTANAS Tahun 1987

Memik EBTANAS Thun 987 EBT-SMA-87-0 Himpunn penyelesin dri persmn : x + = x unuk x R dlh {, } {, } {, } {, } {, } EBT-SMA-87-0 Di bwh ini dlh gmbrpenmpng sebuh pip. Jik jri jri pip cm dn AB = 0 cm (AB

PROBLEM SOLVING TERKAIT DENGAN KELAS X SEMESTER 1 PADA STANDAR KOMPETENSI (SK) 1.

PROLEM SOLVING TERKIT DENGN KELS X SEMESTER PD STNDR KOMPETENSI (SK). LJR Memechkn mslh yng berkitn dengn bentuk pngkt, kr, dn logritm Oleh: Sigit Tri Guntoro. Du orng berselisih mengeni bnykny psngn bilngn

1) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persamaan kuadrat adalah seperti di bawah ini:

) BENTUK UMUM DAN BAGIAN-BAGIAN PERSAMAAN KUADRAT Bentuk umum persmn kudrt dlh seperti di bwh ini: b c dengn, b, c bilngn dn riil Dimn, disebut sebgi koefisien dri b disebut sebgi koefisien dri c disebut

CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. 3. Untuk k 2 didefinisikan bahwa a

CONTOH SOLUSI BEBERAPA SOAL OLIMPIADE MATEMATIKA Oleh: Wiworo, S.Si, M.M. Dikethui bhw,. Untuk k didefinisikn bhw k k k. Tentukn jumlh tk hingg dri. Kit mislkn S S. Dengn demikin kit dpt menuliskn Kedu

ANALISIS NUMERIK. Inter polasi. SPL simultan. Akar Persama. linear

ANALISIS NUMERIK Inter polsi SPL simultn Akr Persm n Non liner INTERPOLASI Tujun Interpolsi bergun untuk menksir hrg-hrg tengh ntr titik dt yng sudh tept. Interpolsi mempunyi orde tu derjt. Mcm Interpolsi

Integral Tak Wajar. Ayundyah Kesumawati. March 25, Prodi Statistika FMIPA-UII

Kesumwti Prodi Sttistik FMIPA-UII Mrch 25, 205 Sutu integrl tertentu b f (x)dx () diktkn wjr jik i memenuhi du syrt berikut: i. Bts integrsi dn b merupkn bilngn berhingg ii. fungsi f (x) terbts pd intervl

SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TAHUN 2002 TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 2003

SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TAHUN 00 TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 00 Bidng Memik Wku : 90 Meni DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH

BAB II PANGKAT, AKAR DAN LOGARITMA

BAB II PANGKAT, AKAR DAN LOGARITMA ILUSTRASI Sony kn membeli sebuh motor secr kredit, ketentun yng ditwrkn oleh perushn lesing dlh, ung muk sebesr Rp.500.000,00 dn ngsurn perbulnny sebesr Rp 365.000,00

Diana Holidah Bagian Farmasi Klinik dan Komunitas Fakultas Farmasi Universitas Jember

Din Holidh Bgin Frmsi Klinik dn Komunis Fkuls Frmsi Universis Jember Absorpsi Ob Absorpsi sisemik dri slurn cern ergnung pd:. Benuk sedin ble, kpsul, sirup dll b. Anomi fisiologi emp bsorpsi, melipui :

15. INTEGRAL SEBAGAI LIMIT

15. INTEGRAL SEBAGAI LIMIT 15.1 Jumlh Riemnn Dlm kulih Klkulus pd thun pertm, integrl Riemnn bisny diperkenlkn sebgi limit dri jumlh Riemnn, tidk mellui integrl Riemnn ts dn integrl Riemnn bwh. Hl ini

DETERMINAN. Misalkan A adalah suatu matriks persegi. a) Jika A memiliki satu baris atau satu kolom bilangan nol, maka det(a) = 0.

DETERMINAN Fungsi determinn dri sutu mtriks persegi A (dinotsikn dengn det(a) tu A ) didefinisikn sebgi jumlh dri semu hsil kli elementer bertnd dri A. Sementr, ngk tu bilngn dri det(a) disebut determinn

6. Himpunan Fungsi Ortogonal

6. Himpunn Fungsi Ortogonl Mislkn f periodik dengn periode, dn mulus bgin demi bgin pd [ π, π]. Jik S f N (θ) = N n= N c ne inθ, n =,, 2,..., dlh jumlh prsil dri deret Fourier f, mk kit telh menunjukkn

BAB II LANDASAN TEORI

BAB II LANDASAN TEORI Bb berikut ini kn disjikn mteri pendukung yng dpt membntu penulis untuk menyelesikn permslhn yng kn dibhs pd bb selnjutny. Adpun mteri pendukungny dlh pengertin mtriks, jenis-jenis

SOAL PILIHAN GANDA A. 10 B. 100 C D E

OLIMPIADE SAINS TAHUN 004 TINGKAT KABUPATEN/KOTA DIREKTORAT PENDIDIKAN LANJUTAN PERTAMA DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH DEPARTEMEN PENDIDIKAN NASIONAL BIDANG STUDI: MATEMATIKA. Ad du

BAB ALJABAR MARIX Dlm pokok bhsn ini kn disjikn dsr-dsr opersi ljbr mtrix yng berhubungn dengn nlisis struktur dengn menggunkn metode mtrix kekkun (stiffness method)... Pengertin Mtrix Mtrix merupkn sutu

Kerjakan di buku tugas. Tentukan hasil operasi berikut. a. A 2 d. (A B) (A + B) b. B 2 e. A (B + B t ) c. A B f. A t (A t + B t ) Tes Mandiri

Mmt Apliksi SMA Bhs Dikethui A = Tentukn hsil opersi berikut A c A A b A A d A Dikethui A = Tentukn hsil opersi berikut (A + B) c (B A) b A + AB + B d B BA + A Sol Terbuk Kerjkn di buku tugs Jik X = dn

matematika K-13 TEOREMA FAKTOR DAN OPERASI AKAR K e l a s

K-3 mtemtik K e l s XI TEOREMA FAKTOR DAN OPERASI AKAR Tujun Pemeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun erikut.. Memhmi teorem fktor.. Menentukn kr dn fktor liner suku nyk dengn

PELATIHAN INSTRUKTUR/PENGEMBANG SMU TANGGAL 28 JULI s.d. 10 AGUSTUS 2003 SUKU BANYAK. Oleh: Fadjar Shadiq, M.App.Sc.

PELATIHAN INSTRUKTUR/PENGEMBANG SMU TANGGAL 8 JULI s.d. 0 AGUSTUS 00 SUKU BANYAK Oleh: Fdjr Shdiq, M.App.Sc. DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH PUSAT PENGEMBANGAN

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA Yogyakarta 2011

Progrm Sudi M Kulih Pokok hsn : Memik : Geomeri : Kesengunn isusun oleh r. li Mhmudi FKULTS MTEMTIK N ILMU PENGETHUN LM UNIVERSITS NEGERI YOGYKRT Yogykr 0 Lemr Kegin Mhsisw Geomeri Lemr Kegin Mhsisw M

STRATEGI PENGAJARAN MATEMATIKA UNTUK MENENTUKAN AKAR-AKAR PERSAMAAN KUADRAT

Jurnl Vol II. No., Mret 08, hlm. 9-95 vilble online t www.jurnl.un.c.id/indeks/jmp STRTEGI PENGJRN MTEMTIK UNTUK MENENTUKN KR-KR PERSMN KUDRT Indh Purnm Putri, Symsudhuh, Ihd Hsbiyti 3 Progrm Studi Mgister

CHAPTER 1 EXPONENTS, ROOTS, AND LOGARITHMS

CHAPTER EXPONENTS, ROOTS, AND LOGARITHMS Indiktor (penunjuk): Mengubh bentuk pngkt negtif ke pngkt positif dn seblikny. (4 jp) A. EXPONENTS. Definition (ketentun): Positive Integers Exponents n = x x...

SIFAT-SIFAT LOGARITMA

K- Kels X mtemtik PEMINATAN SIFAT-SIFAT LOGARITMA Tujun Pembeljrn Setelh memeljri mteri ini, kmu dihrkn memiliki kemmun berikut.. Memhmi definisi logritm.. Dt menentukn nili logritm dengn menggunkn tbel

2. Paman mempunyai sebidang tanah yang luasnya 5 hektar. Tanah itu dibagikan kepada 3. Luas tanah yang diterima oleh mereka masing-masing = 5 :3 1

. Hitunglh 7 5. : b. 5 : c. 8 : 6 d. 8 9 7 7 7 5 77 77 77. : c. 8 : 6 : 6 6 9 9 9 6 54 8 40 7 b. 5: 5 d. 4: 4: 4 6 8 7 95 Husein Tmpoms, Rumus-rumus Dsr Mtemtik 4 :. Pmn mempunyi sebidng tnh yng lusny

matematika PEMINATAN Kelas X FUNGSI LOGARITMA K-13 A. Definisi Fungsi Logaritma

K-3 Kels mtemtik PEMINATAN FUNGSI LOGARITMA Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi definisi fungsi logritm.. Dpt menggunkn konsep fungsi logritm dlm menyelesikn

BAB: PENERAPAN INTEGRAL Topik: Volume Benda Putar (Khusus Kalkulus 1)

BAB: PENERAPAN INTEGRAL Topik: Volume Bend Putr (Khusus Klkulus ) Kompetensi yng diukur dlh kemmpun mhsisw menghitung volume bend putr dengn metode cincin, metode ckrm, tu metode kulit tbung.. UAS Klkulus,

KESALAHAN DALAM METODE NUMERIK

KESALAHAN DALAM METODE NUMERIK Mslh yng diselesikn menggunkn metode numerik psti menghsilkn solusi berbentuk ngk (numerik). Solusi dlm bentuk ngk tersebut merupkn solusi hmpirn tu pendektn dn bukn merupkn

PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER)

PENYELESAIAN SISTEM PERSAMAAN LINEAR DENGAN MENGGUNAKAN DETERMINAN (ATURAN CRAMER) Dikethui system Persmn Linier x+ x + x = x+ x + x = x+ x + x = dlm entuk mtriks x x x Penyelesin Dengn Aturn Crmer dlh

MODEL POTENSIAL 1 DIMENSI

MODEL POTENSIAL 1 DIMENSI 1. Sumur Potensil Tk Berhingg Kit tinju prtikel bermss m dengn energi positif, berd dlm sumur potensil stu dimensi dengn dinding potensil tk berhingg dn potensil didlmny nol,

PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA

K- Kels X mtemtik PEMINATAN PERSAMAAN DAN PERTIDAKSAMAAN LOGARITMA Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi definisi persmn dn pertidksmn logritm.. Dpt

VEKTOR. 1. Pengertian Vektor adalah besaran yang memiliki besar (nilai) dan arah. Vektor merupakan sebuah ruas garis yang

VEKTOR 1. Pengertin Vektor dlh besrn yng memiliki besr (nili dn rh. Vektor merupkn sebuh rus gris yng P berrh dn memiliki pnjng. Pnjng rus gris tersebut dlh pnjng vektor. Rus gris dri titik P dn berujung

PERTEMUAN 4 Metode Simpleks Kasus Maksimum

PERTEMUAN 4 Metode Simpleks Ksus Mksimum Untuk menyelesikn Persoln Progrm Linier dengn Metode Simpleks untuk fungsi tujun memksimumkn dn meminimumkn crny ered Model mtemtik dri Permslhn Progrm Linier dpt

Integral Kompleks (Bagian Kesatu)

Integrl Kompleks (Bgin Kestu) Supm Jurusn Mtemtik, FMIPA UGM Yogykrt 55281, INDONESIA Emil:[email protected], [email protected] (Pertemun Minggu XI) Outline 1 Fungsi Bernili Kompleks 2 Lintsn tu Kontur 3 Integrl

BAB 1 PERSAMAAN DAN PERTIDAKSAMAAN. Standar Kompetensi Mahasiswa memahami konsep dasar sistem bilangan real (R)

BAB PERSAMAAN DAN PERTIDAKSAMAAN Stndr Kompetensi Mhsisw memhmi konsep dsr sistem bilngn rel (R) sebgi semest untuk menentukn selesin persmn dn pertidksmn, dpt mengembngkn bentuk persmn dn pertidksmn yng

Matematika SMA (Program Studi IPA)

Smrt Solution UJIAN NASIONAL TAHUN PELAJARAN 2013/2014 Disusun Sesui Indiktor Kisi-Kisi UN 2013 Mtemtik SMA (Progrm Studi IPA) Disusun oleh : Pk Anng - Blogspot Pge 1 of 13 5. 2. Menyelesikn sol pliksi

LIMIT FUNGSI DAN KEKONTINUAN

LIMIT FUNGSI DAN KEKONTINUAN RANGKUMAN MATERI Sebelum memsuki mteri, perhtikn himpunn-himpunn berikut: ) Himpunn bilngn sli:,,,4,5,.... b) Himpunn bilngn bult:...,,,0,,,.... p c) Himpunn bilngn rsionl:

INTEGRAL FOURIER KED. Diasumsikan syarat-syarat berikut pada f(x): 1. f x memenuhi syarat Dirichlet pada setiap interval terhingga L, L.

INTEGRAL FOURIER Disumsikn syrt-syrt berikut pd f(x):. f x memenuhi syrt Dirichlet pd setip intervl terhingg L, L.. f x dx konvergen, yitu f(x) dpt diintegrsikn secr mutlk dlm (, ). Selnjutny, Teorem integrl

DETERMINAN DAN INVERS MATRIKS BLOK 2 2

Buletin Ilmih Mth. Stt. dn Terpnny (Bimster) Volume 06, No. 3(2017), hl 193 202. DETERMINAN DAN INVERS MATRIKS BLOK 2 2 Ilhmsyh, Helmi, Frnsiskus Frn INTISARI Mtriks blok merupkn mtriks persegi yng diblok

NILAI EIGEN DAN VEKTOR EIGEN

Pert 9 (mengjrkomputer.wordpress.com) NILAI EIGEN DAN VEKTOR EIGEN 9. Definisi Sebuh mtriks bujur sngkr dengn orde n n mislkn A, dn sebuh vektor kolom X. Vektor X dlh vektor dlm rung Euklidin n R yng dihubungkn

BAB 10. MATRIKS DAN DETERMINAN

Dessy Dwiynti, S.Si, MBA Mtemtik Ekonomi 1 BAB 10. MATRIKS DAN DETERMINAN 1. Pengertin mtriks Mtriks kumpuln bilngn yng disjikn secr tertur dlm bris dn kolom yng membentuk sutu persegi pnjng, sert termut

TRIGONOMETRI I. KOMPETENSI YANG DICAPAI

TRIGONOMETRI I. KOMPETENSI YANG DICAPAI Mhsisw dpt : 1. Membuktikn identits trigonometri.. Menghitung hubungn ntr sudut dn sisi segitig dengn Rumus Sinus. 3. Menghitung hubungn ntr sudut dn sisi segitig

SUKU BANYAK ( POLINOM)

SUKU BANYAK ( POLINOM) Bb 16 Skl 8.Menyelesikn mslh yng berkitn dengn teorem sis tu teorem fktor A. PENGERTIAN SUKU BANYAK. Bentuk x x x... x x, dengn 0 dn n { bil. cch} 1 0 disebut dengn Suku bnyk (Polinomil)

E. INTEGRASI BAGIAN ( PARSIAL )

E. INTEGRASI BAGIAN ( PARSIAL ) Integrsi gin (prsil) digunkn untuk mengintegrsikn sutu perklin fungsi yng msing-msing fungsiny ukn koefisien diferensil dri yng lin ( seperti yng sudh dihs pd su. B. D )

Solusi Pengayaan Matematika Edisi 4 Januari Pekan Ke-4, 2007 Nomor Soal: 31-40

Solusi Pengn Mtemtik Edisi 4 Jnuri Pekn Ke-4, 007 Nomor Sol: -40. Diberikn persmn 8 9 4 8 007 dn b, dengn b. Angk stun dri b dlh. A. B. C. D. 7 E. 9 Persmn 8 9 4 8 8 9 4 8 9 4 8 8 8 9 8 4 8 8 8 0 0 b tu

12. LUAS DAERAH DAN INTEGRAL

12. LUAS DAERAH DAN INTEGRAL 12.1 Lus Derh di Bwh Kurv Mslh menentukn lus derh (dn volume rung) telh dipeljri sejk er Pythgors dn Zeno, pd thun 500-n SM. Konsep integrl (yng terkit ert dengn lus derh)

Sistem Persamaan Linear Bagian 1

Sistem Persmn Liner Bgin. SISTEM PERSAMAAN LINEAR PENGANTAR Dlm bgin ini kn kit perkenlkn istilh dsr dn kit bhs sebuh metode untuk memechkn sistem-sistem persmn liner. Sebuh gris dlm bidng xy secr ljbr

Bab a. maka notasi determinan dari matriks A ditulis : det (A) atau. atau A.

Bb DETERMINAN MATRIKS Determinn sutu mtriks dlh sutu fungsi sklr dengn domin mtriks bujur sngkr. Dengn kt lin, determinn merupkn pemetn dengn domin berup mtriks bujur sngkr, sementr kodomin berup sutu

Bab 2 HUKUM KEKEKALAN. 2.1 Hukum Kekekalan Skalar

Bb 2 HUKUM KEKEKALAN 2.1 Hukum Kekekln Sklr Hukum kekekln mendeskripsikn dinmik suu kunis dlm sisem eruup. Khususny, hukum kekekln menykn bhw lju perubhn kumulif kunis ersebu hny ergnung pd fluks yng msuk,

Suku banyak. Akar-akar rasional dari

Suku nyk Algoritm pemgin suku nyk menentukn Teorem sis dn teorem fktor terdiri dri Pengertin dn nili suku nyk Hsil gi dn sis pemgin suku nyk Penggunn teorem sis Penggunn teorem fktor Derjd suku nyk pd

Penyelesaian Persamaan dengan Logaritma. Persamaan & Fungsi logaritma. Pengertian Logaritma 10/9/2013

10/9/013 Penyelesin Persmn dengn Logritm Persmn & Fungsi logritm Tim Dosen Mtemtik FTP Logritm dpt digunkn untuk mencri bilngn yng belum dikethui (bilngn x) dlm sebuh persmn, khususny persmn eksponensil

Rumus Luas Daerah Segi Empat Sembarang? Oleh: Al Jupri Dosen Jurusan Pendidikan Matematika Universitas Pendidikan Indonesia

Rumus Lus Derh Segi Empt Sembrng? Oleh: Al Jupri Dosen Jurusn Pendidikn Mtemtik Universits Pendidikn Indonesi Kit bisny lebih menyuki brng yng siftny serb gun dn efektif, stu brng untuk berbgi jenis keperlun.

Universitas Esa Unggul

ALJABAR LINIER DAN MATRIKS BHAN KULIAH DRA SURYARI PURNAMA, MM Universits Es Unggul Minggu I Mtriks Pokok Bhsn Sub Pokok Bhsn Tujun Instruksionl Umum Tujun Instruksionl Khusus : Pendhulun Mtriks : A. Pengertin

MA3231 Analisis Real

MA3231 Anlisis Rel Hendr Gunwn* *http://hgunwn82.wordpress.com Anlysis nd Geometry Group Bndung Institute of Technology Bndung, INDONESIA Progrm Studi S1 Mtemtik ITB, Semester II 2016/2017 HG* (*ITB Bndung)

Sistem Persamaan Linier

b I Sistem Persmn Linier I Sistem Persmn Linier TUJUN PEMELJRN: Mhsisw memhmi konsep-konsep tentng sistem persmn linier, eksistensi dn keunikn sistem persmn linier, keunikn sistem persmn linier homogen,

Volume Bangun Ruang. 1. Balok. Perhatikan gambar di atas. 1. Bangun apa saja yang ada di atas meja? 2. Termasuk bangun apa benda yang dibawa Tini?

Volume Bngun Rung Bend-bend di mej ini merupkn bngun rung. Kleng uu ini berbenuk p, y? Tono Tini Di kel V kmu elh mempeljri beberp jeni bngun rung. Blok Kubu Prim Lim Tbung Kerucu Tin Em... p, y? Perhikn

FISIKA BESARAN VEKTOR

K-3 Kels X FISIKA BESARAN VEKTOR TUJUAN PEMBELAJARAN Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi pengertin besrn vektor.. Mengusi konsep penjumlhn vektor dengn berbgi metode.

PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 1

PENGAYAAN MATEMATIKA SOLUSI SOAL-SOAL LATIHAN 6y y 8y. Dikethui R dn. Temukn nili y. y y 8y 6 Solusi: 6y y 8y y y 8y 6 6y y 8y 8y y 6 y 8 0 y y y 0 y y y 0 ( y ) ( y ) 0 y y 8y 6 ( y )(y ) 0 y 0tu y 0

Sistem Persamaan Linear

Sistem Persmn Liner Muhtdin, ST. MT. Metode Numerik & Komputsi. By : Muhtdin Persmn Aljbr Liner Simultn Metode Numerik & Komputsi. By : Muhtdin 9 Menyelesikn SPL sederhn Grphicl Method dri kedu persmn

Kesesuaian Persamaan Pola Intensitas Curah Hujan Sebagai Fungsi dari Durasi Hujan di Balai Pengamatan Dirgantara Pontianak

Kesesuin Persmn Pol nensis Curh Hujn Sebgi Fungsi dri Dursi Hujn di Bli Pengmn Dirgnr Ponink Ann Krin 1), M. shk Jumrng 1)* 1)Progrm Sudi Fisik, FMPA, Universis njungpur Jln Jendrl Ahmd Yni, Ponink, ndonesi

MATEMATIKA DASAR. 1. Jika x 1 dan x 2 adalah penyelesaian. persamaan Diketahui x 1 dan x 2 akar-akar persamaan 6x 2 5x + 2m 5 = 0.

MATEMATIKA ASAR. Jik dn dlh penyelesin persmn mk ( ).. E. B 7 6 6 + - ( + ) ( ). ( ) ( ) 7. Jik dn y b dengn, y > + y, mk. + y + b log b. + b log b b E. + log b E log dn y log b + y + y log + log b log

SISTEM BILANGAN REAL. 1. Sifat Aljabar Bilangan Real

SISTEM BILANGAN REAL Dlm terminologi Aljbr Abstrk, sistem bilngn rel disebut dengn field (lpngn) pd opersi penjumlhn dn perklin. Sutu opersi biner bis ditulis dengn sutu psngn terurut (, b) yng unik dri

7. Ruang L 2 (a, b) f(x) 2 dx < }.

7. Rung L (, b) Rung L (, b) didefinisikn sebgi rung semu fungsi f yng kudrtny terintegrlkn pd [, b], ykni L (, b) := {f : b f(x) dx < }. Rung ini menckup fungsi-fungsi f yng tk terbts pd [, b] tetpi f

M A T R I K S. Oleh: Dimas Rahadian AM, S.TP. M.Sc.

M T R I K S Oleh Dims Rhdin M, S.TP. M.Sc Emil [email protected] JURUSN ILMU DN TEKNOLOGI PNGN UNIVERSITS SEBELS MRET SURKRT DEFINISI... Mtriks dlh susunn bilngn berbentuk jjrn segi empt siku-siku yng

INTEGRAL. Bogor, Departemen Matematika FMIPA IPB. (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, / 45

INTEGRAL Deprtemen Mtemtik FMIPA IPB Bogor, 2012 (Deprtemen Mtemtik FMIPA IPB) Klkulus I Bogor, 2012 1 / 45 Topik Bhsn 1 Pendhulun 2 Anti-turunn 3 Lus di Bwh Kurv 4 Integrl Tentu 5 Teorem Dsr Klkulus 6

14. SIFAT-SIFAT INTEGRAL RIEMANN

4. SIFAT-SIFAT INTEGRAL RIEMANN 4. Sift-sift Dsr Integrl Riemnn Pd bb ini kit kn mempeljri sift-sift dsr integrl Riemnn. Sift pertm dlh sift kelinern, yng dinytkn dlm Proposisi. Sepnjng bb ini, I menytkn

ω = kecepatan sudut poros engkol

Kerj Untuk Mengtsi Gesekn 1. Pomp Tnp Bejn Udr Telh dijelskn pd bgin muk bhw pd wl dn khir lngkh hisp mupun lngkh tekn, tidk terjdi kerugin hed kibt gesekn. Kerugin hed mksimum hny terjdi pd pertenghn

Solusi Pengayaan Matematika Edisi 3 Januari Pekan Ke-3, 2008 Nomor Soal: 21-30

Solusi Pengn Mtemtik Edisi Jnuri Pekn Ke-, 00 Nomor Sol: -0. Crilh himpunn penelesin dri sistem persmn log log. () log Misln 0 ( )( ) 0 tu, mk persmn () menjdi: log tu log log log log tu log log log log

BAB IV BILANGAN BERPANGKAT DAN BENTUK AKAR

BAB IV BILANGAN BERPANGKAT DAN BENTUK AKAR Pet Konsep Bilngn Berpngkt dn Bentuk Akr mempeljri Bilngn berpngkt meliputi Bentuk kr meliputi Sift Opersi Mersionlkn Opersi Sift Kt Kunci. Pngkt 2. Akr 3. Sift

METODE TRAPESIUM TERKOREKSI KOMPOSIT UNTUK MENYELESAIKAN PERSAMAAN INTEGRAL VOLTERRA LINEAR JENIS KEDUA. Fitra Anugrah 1, Zulkarnain 2 ABSTRACT

METODE TRAPESIUM TERKOREKSI KOMPOSIT UNTUK MENYELESAIKAN PERSAMAAN INTEGRAL VOLTERRA LINEAR JENIS KEDUA Fitr Anugrh 1, Zulkrnin 2 1 Mhsisw Progrm Studi S1 Mtemtik 2 Dosen Jurusn Mtemtik Fkults Mtemtik

matematika WAJIB Kelas X RASIO TRIGONOMETRI Kurikulum 2013 A. Definisi Trigonometri

Kurikulum 0 Kels X mtemtik WAJIB RASIO TRIGONOMETRI Tujun Pembeljrn Setelh mempeljri mteri ini, kmu dihrpkn memiliki kemmpun berikut.. Memhmi rsio-rsio trigonometri yng meliputi sinus, kosinus, tngen,

4. Perkalian Matriks. Riki 3 2 Fera 2 5. Data harga bolpoin dan buku (dinyatakan oleh matriks Q), yaitu

Sift-Sift Perklin Sklr Mislkn dn b sklr, D dn H mtriks sebrng dengn ordo sm, mk berlku sift-sift sebgi berikut. D + H (D + H) 2. D + bd ( + b)d 3. (bd) (b)d 4. Perklin Mtriks Du buh mtriks tu lebih selin

PENDETEKSIAN PENCILAN ADITIF DAN INOVATIF DALAM DATA DERET WAKTU MELALUI METODE ITERATIF

Forum Sisik dn Kompusi, Vol No., 8 ISSN : 85-85 PENDEEKSIAN PENCILAN ADIF DAN INOVIF DALAM DA DERE WAKU MELALUI MEODE ERIF Kusmn Sdik, Erfini, Noviyni WP Depremen Sisik FMIPA Insiu Pernin Bogor E-mil :

Aljabar Linear Elementer

ljbr Liner Elementer M SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi

TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 2009

SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA TIM OLIMPIADE MATEMATIKA INDONESIA TAHUN 009 Bidng Mtemtik Wktu :,5 Jm DEPARTEMEN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT

DERET TAK HINGGA. Deret Geometri Suatu deret yang berbentuk: Dengan a 0 dinamakan deret geometri. Kekonvergenan: divergen jika r 1 Bukti:

DERET TAK HINGGA Cooh dere k higg : + + 3 + = k= k u k. Bris jumlh prsil S, deg S = + + 3 + + = k= k Defiisi Dere k higg, k= k, koverge d mempuyi jumlh S, pbil bris jumlh-jumlh prsil S koverge meuju S.

Materi V. Determianan dinotasikan berupa pembatas dua gris lurus,

Mteri V Tujun : 1. Mhsisw dpt mengenli determinn.. Mhsisw dpt merubh persmn linier menjdi persmn determinn.. Mhsisw menelesikn determinn ordo du. Mhsisw mmpu menelesikn determinn ordo tig. Mhsisw mengethui

NILAI EIGEN DAN VEKTOR EIGEN

Hl di 9 NILAI EIGEN DAN VEKTOR EIGEN 7. Definisi Sebuh mtiks buju sngk dengn ode n n mislkn A, dn sebuh vekto kolom X. Vekto X dlh vekto dlm ung Euklidin dengn sebuh pesmn: n R yng dihubungkn AX X (7.)

Modul 9. PENELITIAN OPERASIONAL PEMROGRAMAN DINAMIS. Oleh : Eliyani PROGRAM KELAS KARYAWAN PROGRAM STUDI TEKNIK INDUSTRI FAKULTAS TEKNOLOGI INDUSTRI

Modul 9. PENELITIAN OPERASIONAL Oleh : Eliyni PROGRAM KELAS KARYAWAN PROGRAM STUDI TEKNIK INDUSTRI FAKULTAS TEKNOLOGI INDUSTRI UNIVERSITAS MERCU BUANA http://www.mercubun.c.id JAKARTA 7 Pendhulun Pemrogrmn

METODE ALTERNATIF BARU UNTUK MENGHITUNG DETERMINAN MATRIKS ORDE 3 X 3

METODE ALTERNATIF BARU UNTUK MENGHITUNG DETERMINAN MATRIKS ORDE 3 X 3 Glng Ismu Hndoko 1, M Ntsir 2, Sigit Sugirto 2 1 Mhsisw Progrm S1 Mtemtik 2 Dosen Jurusn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm

Aljabar Linear Elementer

ljbr Liner Elementer M3 3 SKS Silbus : Bb I Mtriks dn Opersiny Bb II Determinn Mtriks Bb III Sistem Persmn Liner Bb IV Vektor di Bidng dn di Rung Bb V Rung Vektor Bb VI Rung Hsil Kli Dlm Bb VII Trnsformsi

3. LIMIT DAN KEKONTINUAN. INF228 Kalkulus Dasar

. LIMIT DAN KEKONTINUAN INF8 Klkulus Dsr . Limit Fungsi di Stu Titik Pengertin it secr intuisi Perhtikn ungsi Fungsi dits tidk terdeinisi di =, kren di titik tersebut berbentuk 0/0. Tpi msih bis ditnykn

,, % ,, % -0: 0 -0: 0! 2 % 26, &

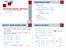PERSAMAAN LINIER GAUSS-SIEDEL METHOD Simultneous Liner Equtions Oleh : Purwnto,S.Si Bentuk Umum x + x + 3 x 3 + + n x n = b Sebuh persmn linier dengn : n peubh : x, x, x 3,, x n n konstnt :,, 3,, n Contoh

Matriks yang mempunyai jumlah baris sama dengan jumlah kolomnya disebut matriks bujur sangkar (square matrix). contoh :

TRIKS. PENGERTIN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom diseut

METODE ANALISIS HOMOTOPI UNTUK MENYELESAIKAN PERSAMAAN INTEGRAL LINEAR ABSTRACT

METODE ANALISIS HOMOTOPI UNTUK MENYELESAIKAN PERSAMAAN INTEGRAL LINEAR Azhrr Fortun Drno 1, Symsudhuh 2, Aziskhn 2 1 Mhsisw Progrm Studi S1 Mtemtik 2 Dosen Jurusn Mtemtik Fkults Mtemtik dn Ilmu Pengethun

SIMAK UI 2011 Matematika Dasar

SIMAK UI 0 Mtemtik Dsr Kode Sol Doc. Nme: SIMAKUI0MATDAS999 Version: 0-0 hlmn 0. Sebuh segitig sm kki mempunyi ls 0 cm dn tinggi 5 cm. Jik dlm segitig tersebut dibut persegi pnjng dengn ls terletk pd ls

PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT

PERSAMAAN KUADRAT, FUNGSI KUADRAT DAN PERTIDAKSAMAAN KUADRAT Persmn Kudrt. Bentuk Umum Persmn Kudrt Mislkn,, Є R dn 0 mk persmn yng erentuk 0 dinmkn persmn kudrt dlm peuh. Dlm persmn kudrt 0, dlh koefisien

Materi IX A. Pendahuluan

Mteri IX Tujun :. Mhsisw dpt memhmi vektor. Mhsisw mmpu mengunkn vektor dlm persoln sederhn 3. Mhsisw mengimplementsikn konsep vektor pd rngkin listrik. Pendhulun Sudh menjdi kesepktn umum hw untuk menentukn

didefinisikan sebagai bilangan yang dapat ditulis dengan b

1 PENDAHULUAN 1.1 Sistem Bilngn Rel Untuk mempeljri klkulus perlu memhmi hsn tentng system ilngn rel, kren klkulus didsrkn pd system ilngn rel dn siftsiftny. Sistem ilngn yng pling sederhn dlh ilngn sli,

BAB 4 IMPLEMENTASI HASIL PENELITIAN. Rancangan ini dibuat dan dites pada konfigurasi hardware sebagai berikut :

BAB 4 IMPLEMENTASI HASIL PENELITIAN 4.1 Spesifiksi Hrdwre dn Softwre Rncngn ini diut dn dites pd konfigursi hrdwre segi erikut : Processor : AMD Athlon XP 1,4 Gytes. Memory : 18 Mytes. Hrddisk : 0 Gytes.

Skew- Semifield dan Beberapa Sifatnya 1

Skew- Semifield dn Beberp Siftny K r y t i Jurusn Pendidikn Mtemtik Fkults Mtemtik dn Ilmu Pengethun Alm Universits Negeri Yogykrt E-mil: [email protected] Abstrk Sutu field ( lpngn ) F dlh struktur ljbr

MA3231 Analisis Real

MA3231 Anlisis Rel Hendr Gunwn* *http://hgunwn82.wordpress.com Anlysis nd Geometry Group Bndung Institute of Technology Bndung, INDONESIA Progrm Studi S1 Mtemtik ITB, Semester II 2016/2017 HG* (*ITB Bndung)

A. PENGERTIAN B. DETERMINAN MATRIKS

ATRIKS A. PENGERTIAN triks dlh sutu deretn elemen yng mementuk empt persegi pnjng, terdiri dri m ris dn n kolom. Elemen terseut dpt erentuk koefisien, ilngn tu simul. triks yng mempunyi m ris dn n kolom

SUKU BANYAK ( POLINOM)

SUKU BANYAK ( POLINOM) B 15 A. PENGERTIAN SUKU BANYAK. Bentuk 1 0 x x x x x, dengn 0 dn n { il. cch } n diseut dengn Suku nyk (Polinomil) dlm x erderjt n ( n dlh pngkt tertinggi dri x),,,., diseut keofisien