PERANCANGAN POLIHEDRA DENGAN METODE JARING POLIGON
|
|
|
- Hartono Hartanto
- 9 tahun lalu
- Tontonan:
Transkripsi
1 PERANCANGAN POLIHEDRA DENGAN METODE JARING POLIGON Ina Agustina, Agus Iskandar Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta Abstract Conceptually polygon method is being used to design 3D object. By using Open GL facility we can design many complex polygon to create any object that has a large advantages. Keywords: Open GL, polygon, 3D object Abstrak Secara konseptual, jaring poligon digunakan di grafika computer untuk menghasilkan objek 3D. Manakala seniman patung mengunakan jaring kawat untuk menghasilkan objek 3D. jika seniman mengubah-ubah bentuk patung dengan jaring kawat, tetapi penciptaan objek 3D dengan computer dilakukan dengan memanipulasi jaring poligon baik dengan pemrograman dan juga pemahaman geometri 3D. jaring poligon adalah permukaan yang dibuat dari kumpulan muka-muka poligon. Kata kunci: Open GL, poligon, obyek 3D I. PENDAHULUAN Ilustrasi yang terbaik untuk menggambarkan jaring poligon adalah dengan menggunakan kawat yang dihubung-hubungkan membentuk jaring kawat untuk membuat objek tertentu., misalnya objek orang (baca jaring kawat patung). Bentuk jaring kawat ini sama dengan seri dari jaring kawat poligon yang dihubungkan antara satu dengan yang lainnya. Kawat cukup fleksibel untuk membentuk objek lain yang lebih kompleks dan pejal. Seniman menggunakan tanah liat dan plester untuk menyelesaikan jaring kawat patung tersebut. Secara konseptual, jaring poligon digunakan di grafika computer untuk menghasilkan objek 3D. Manakala seniman patung mengunakan jaring kawat untuk menghasilkan objek 3D. jika seniman mengubah-ubah bentuk patung dengan jaring kawat, tetapi penciptaan objek 3D dengan computer dilakukan dengan memanipulasi jaring poligon baik dengan pemrograman dan juga pemahaman geometri 3D. jaring poligon adalah permukaan yang dibuat dari kumpulan muka-muka poligon. II. TEORI DASAR Pemodelan dengan Jaring Pilogon Pada bagian ini, akan dipelajari konsep dan istilah jaring, vector normal, muka (permukaan), dan pejal.jaring dapat digunakan untuk membuat kulit dari objek pejal. Jika jaring mentupi ruangan maka akan menghasilkan sebuah benda pejal. Ada dua cara untuk perwakilan jaring yaitu metoda daftar titk (vertex list method) dan metoda daftar muka (face list method). Kedua cara ini berbeda. 33
2 Masing-masing pilogon diwarnai dengan warna yang berbeda-beda sehingga dapat dilihat jaringannya. Masing-masing pilogon dapat dinyatakan dalam bentuk pejal atau tidak pejal tergantung pada coraknya. Pendefinisian Jaring Poligon Ada beberapa cara pendefinisian jaring. Untuk kubus dapat diwakili dengan membuat satu daftar yang berisi daftar masing-masing poligon, lokasi titik dan normal untuk masing-masing titik. Dengan perwakilan ini, kubus terdiri dari 24 titik, 24 normal dan 6 permukaan. Daftar ini dapat menciptakan data berlebih-lebihan karena ada beberapa titik normal yang didaftarkan lebih dari satu kali. Untuk itu, lebih baik digunakan metoda lain yaitu membuat 3 daftar (tidak dengan satu daftar). Ke tiga daftar tersebut adalah (1) daftar untuk titik, (2) daftar untuk permukaan dan (3) daftar normal. Dengan metoda ini, sebuah kubus terdiri dari (1) 8 buah titik, (2) 6 buah permukaan dan (3) 6 buah normal. (1) Daftar titik Titik x, y, z 0-1.0,-1.0, ,-1.0, , 1.0, , 1.0, ,-1.0, , 1.0, , 1.0, ,-1.0,-1.0 (2) Daftar normal Normal nx, ny, nz 0 0.0, 0.0, , 0.0, , 1.0, , -1.0, , 0.0, , 0.0, 0.0 (3) Daftar muka Muka titik normal 0(depan) 0,1,2,3 0,0,0,0 1(belakang) 4,5,6,7 1,1,1,1 2(atas) 5,3,2,6 2,2,2,2 3(bawah) 4,7,1,0 3,3,3,3 4(kanan) 7,6,2,1 4,4,4,4 5(kiri) 4,0,3,5 5,5,5,5 Selain itu, diperlukan lintasan muka yaitu untuk menentukan : Bagian dalam polygon Bagian luar dari pejal Letak arah normal Lintasan muka mengikuti arah jarum jam sebagaimana terlihat dari luar objek. Dalam polygon akan selalu ada pada sebelah kiri anda. 34
3 Penghitungan Normal Mengapa grafika computer membutuhkan normal? Normal mengatakan pada anda letak bagian permukaan sebelah luar Normal digunakan utnuk menghitung seberapa banyak sinar cahaya mengenai permukaan bagian luar Normal menentukan seberapa licinnya permukaan dirender. Dua cara menentukan normal: Cara pertama: Tentukan perkalian silang dengan menggunakan tiga (3) titik pada sebuah bidang (permukaan). Oleh karena itu, jika vector sejajar dengan perkalian silang maka nilainya akan kecil dan tidak akurat. Selain itu. Polygon mungkin tidak planar sempurna. Cara kedua: gunakan metoda Newell N- 1 m x = S (y i - y berikut(i) )(z i - z berikut(i) ) t=0 N- 1 m y = S (z i - z berikut(i) )(x i - x berikut(i) ) t=0 N- 1 m z = S (x i - x berikut(i) )(y i - y berikut(i) ) t=0 Sekarang anda telah dapat menghitung normal, namun apa gunanya jika anda tidak dapat menggunakannya dalam grafika computer! OpenGL menggunakan vector normal untuk penentuan permukaan luar, penghalusan (smoothing), pencahayaan (lightning) dan pemberian bayangan (shading).gambar 6.2 menunjukkan objek 3D yaitu sebuah kubus tanpa pencahayaan. Sedangkan Gambar 6.3 menunjukkan objek yang sama dengan pencahayaan. Untuk itu, pastikan anda menguasai cara menghitung vector normal. Gambar 2.1.a Objek 3D pejal tanpa pencahayaan Gambar 2.1.b Objek 3D pejal dengan pencahayaan 35
4 III. METODE SIMULASI Langkah-langkah pembuatan program ini hampir sama yang telah dibicarakan dalam Bab 2. Yang perlu diubah hanyalah isi dari fungsi Inisialisasi( ) dan Gambarku( ) yang terletak di class COpenGLku8Doc. Perubahannya adalah: void COpenGLku8Doc :: Inisialisasi( ) glloadidentity( ); glclear(gl_color_buffer_bit); //hidupkan pencahayaan glenable(gl_lightning); glenable(gl_light0); glshademodel(gl_smooth); glenable(gl_depth_test); glenable(gl_normalize); glclearcolor(1, 1, 1, 0); glviewport(0, 0, 600, 600); GLfloat intensitascahaya[ ] = 0.9f, 0.9f, 0.9f, 1.0f; GLfloat posisicahaya [ ] =...; gllightfv(gl_light0, GL_POSITION, posisicahaya); gllightfv(gl_light0, GL_POSITION, intensitascahaya); glmatrixmode(gl_projection); glloadidentity( ); glortho( -2, 2, -2, 2, -2, 2.0); glmatrixmode(gl_modelview); glloadidentity( ); void COpenGLku8Doc :: GambarKu( ) glclear(gl_color_buffer_bit GL_DEPTH_BUFFER_BIT); GLfloat bahan_ambient[ ] = 0, 0.2f, 0.3f, 1; GLfloat bahan_diffuse[ ] = 0.6f, 0.6f, 0.6f, 1.0f; GLfloat bahan_specular[ ] = 1.0f, 1.0f, 1.0f, 1.0f; GLfloat bahan_shininess[ ] = 90.0f; glmaterialfv(gl_front, GL_AMBIENT, bahan_ambient); glmaterialfv(gl_front, GL_DIFFUSE, bahan_diffuse); glmaterialfv(gl_front, GL_SPECULAR, bahan_specular); glmaterialfv(gl_front, GL_SHININESS, bahan_shininess); glrotated(30, 0, 1, 1); glrotated(15, 1, 1, 0); glpushmatrix( ); glbegin(gl_quads); //Muka depan glnormal3f( 0.0f, 0.0f, 1.0f); glvertex3f(-1.0f, -1.0f, 1.0f); glvertex3f( 1.0f, -1.0f, 1.0f); glvertex3f( 1.0f, 1.0f, 1.0f); glverte x3f(-1.0f, 1.0f, 1.0f); //Muka belakang glnormal3f( 0.0f, 0.0f, -1.0f); glvertex3f(-1.0f, -1.0f, -1.0f); glvertex3f(-1.0f, 1.0f, -1.0f); glvertex3f( 1.0f, 1.0f, -1.0f); glvertex3f( 1.0f, -1.0f, -1.0f); //Muka atas glnormal3f( 0.0f, 1.0f, 0.0f); glvertex3f(-1.0f, 1.0f, -1.0f); glvertex3f(-1.0f, 1.0f, 1.0f); glvertex3f( 1.0f, 1.0f, 1.0f); glvertex3f( 1.0f, 1.0f, -1.0f); // permulaan // pengga mbaran Quads // Normal menuju Anda // Titik 1 (depan) // Titik 2 (depan) // Titik 3 (depan) // Titik 4 (depan) // Normal meninggalkan // Anda // Titik 1 (belakang) // Titik 2 (belakang) // Titik 3 (belakang) // Titik 4 (belakang) // Normal berarah atas // Titik 1 (atas) // Titik 2 (atas) // Titik 3 (atas) // Titik 4 (atas) 36
5 //Muka bawah glnormal3f( 0.0f, -1.0f, 0.0f); glvertex3f(-1.0f, -1.0f, -1.0f); glvertex3f( 1.0f, -1.0f, -1.0f); glvertex3f( 1.0f, -1.0f, 1.0f); glvertex3f(-1.0f, -1.0f, 1.0f); //Muka kanan glnormal3f( 1.0f, 0.0f, 0.0f); glvertex3f( 1.0f, -1.0f, -1.0f); glvertex3f( 1.0f, 1.0f, -1.0f); glvertex3f( 1.0f, 1.0f, 1.0f); glvertex3f( 1.0f, -1.0f, 1.0f); //Muka kiri glnormal3f(-1.0f, 0.0f, 0.0f); glvertex3f(-1.0f, -1.0f, -1.0f); glvertex3f(-1.0f, -1.0f, 1.0f); glvertex3f(-1.0f, 1.0f, 1.0f); glvertex3f(-1.0f, 1.0f, -1.0f); glend( ); // Normal berarah bawah // Titik 1 (bawah) // Titik 2 (bawah) // Titik 3 (bawah) // Titik 4 (bawah) // Normal berarah kanan // Titik 1 (kanan) // Titik 2 (kanan) // Titik 3 (kanan) // Titik 4 (kanan) // Normal berarah kiri // Titik 1 (kiri) // Titik 2 (kiri) // Titik 3 (kiri) // Titik 4 (kiri) glpopmatrix( ); glflush( ); hasil keluaran dari program ini seperti pada gambar : Gambar 3.1 Kubus dengan pencahayaan. Property Jaring: Kepadatan Menyatakan sebuah objek pejal jika permukaannya tertutup ruang positif dan terhingga. Keterkaitan Antara bagian polygon yang satu dengan yang lain yang membentuk objek 3D dihubungkan satu sama lain. Atau dengan kata lain terikat satu sama lain dan jika tidak terhubung maka pastilah lebih dari satu objek. Kesederhanaan 37
6 Sederhana, jika pejal maka objek 3D tersebut tanpa lubang. Bidang Objek 3D dapat terdiri dari banyak bidang artinya setiap permukaan pada sebuah bagian objek mewakili sebuah bidang. Kecembungan Objek 3D dapat dibuat peck dengan menambahkan property cembung dan cekung. Pendefinisian Polihedra Polihedra adalah sebuah jaring yang mempunyai ruang terhingga dan tertutup (contohnya: tidak ada celah di antaranya). OpenGL menyediakan sejumlah fungsi yang dapat menggambar polihedra sederhana yaitu tetrahedron, octahedron, dodecahedron dan isocahedron (Tabel 6.1.) Oleh karena itu, jika membuat objek pejal dengan bayak muka dan bervariasi maka dibutuhkan untuk mendefinisikan jarring khusus sesuai dengan kebutuhan. Pada gambar berikut ini, merupakan contoh gambar dari Polihedra Isocahedron Pejal Di mana pada gambar ini mempunyai 10 bidang sisi : Gambar 3.2 Polihedra Isocahedron pejal. IV. ANALISA DAN PEMBAHASAN Polihedra Polihedra adalah sebuah jarring yang mempunyai ruang terhingga dan tertutup (contohnya: tidak ada celah di antaranya). OpenGL menyediakan sejumlah fungsi yang dapat menggambar polihedra sederhana yaitu tetrahedron, octahedron, dodecahedron dan isocahedron (Tabel 6.1.) Oleh karena itu, jika membuat objek pejal dengan bayak muka dan bervariasi maka dibutuhkan untuk mendefinisikan jarring khusus sesuai dengan kebutuhan. Prisma adalah polihedra yang memiliki bentuk kesimetrisan tertentu dan oleh karena itu mudah dijelaskan. Prisma didefinisikan sebagai sapuan atau penaikan poligon secara garis lurus. Antiprisma (gambar 6.5)mempunyai poligon atas dan bawah yang sama, tetapi polygon bawah diputar sepanjang n/180 derajad. 38
7 Gambar 4.1 Polihedra Isocahedron pejal. Contoh program dengan opengl dan Visual C++ untuk menampilkan objek 3D Polihedra. Tetrahedron, Octahedron yaitu Tetrahedron, Octahedron, Dodecahedron dan Icosahedron dengan tampilan sketsa kawat saja. Langkah1: Ubahlah isi dari fungsi inisialisasi() dan Gambarku() yang terletak di class COpenGLku8Doc. Perubahannya adalah: void COpenGLku8Doc::Inisialisasi() int w = 800, h = 600; glshademodel (GL_FLAT); glclearcolor (1.0, 1.0, 1.0, 0.0); glclearaccum (0.0, 0.0, 0.0, 0.0); glviewport (0, 0, w, h); glmatrixmode (GL_PROJECTION); glloadidentity (); gluperspective (60.0, (GLfloat) w/(glfloat) h, 1.0, 20.0); glmatrixmode (GL_MODELVIEW); void COpenGLku8Doc::GambarKu() glclear (GL_COLOR_BUFFER_BIT); glcolor3f (0, 0, 1); glpushmatrix(); gltranslatef (0.0, 1.0, -8.0); glutwiretetrahedron(); glpopmatrix(); glpushmatrix(); gltranslatef (2.0, 1.0, -8.0); glutwireoctahedron(); glpopmatrix(); glpushmatrix(); gltranslatef (2.5f, -2.5f, -8.0); glutwiredodecahedron(); glpopmatrix(); glpushmatrix(); gltranslatef (0.0, 1.0, -8.0); glutwireicosahedron(); glpopmatrix(); glflush(); 39
8 Hasil output program : Gambar 4.2 Output ekskusi program. V. KESIMPULAN Polihedra adalah sebuah jaring yang mempunyai ruang terhingga dan tertutup. Polihedra merupakan penggambaran dari unsur jaring polygon, dengan menggunakan kawat (jaring) yang dihubung-hubungkan membentuk jaring kawat untuk membuat objek tertentu. Polihedra mempunyai beberapa jenis bentuk penggambaran, seperti tetrahedron, octahedron, dodecahedron, dan isocahedron. Pada pembuatan polihedra diatas, kita dapat menemui beberapa fungsi yang dapat menggambar polihedra dalam bentuk jaring maupun bentuk pejal berisi, yaitu:glutwiretetrahedron(),glutsolidtetrahedron(),glutwireoctahedron(),glutsolidoctahedron(), glutwiredodecahedron(),glutsoliddodecahedron(),glutwireisocahedron(), glutsolidisocahedron(). Selain beberapa fungsi untuk menggambar suatu bentuk polihedra, kita juga dapat menggambar bentuk objek dengan menggunakan fungsi-fungsi khusus seperti kubus, bola, dan teko dalam bentuk jaring maupun bentuk pejal. Fungsi-fungsi tersebut yaitu glutwirecube (Gl double isi),glutsolidcube(gldoublesisi),glutwiresphere(gldoubler,glintiver,glintihor),glutsolidspher e(gldoubler,glintiver,glintihor),glutwiretorus(gldouble inr, GLdouble outr, GLintiV er, GLintiHor), glutsolidtorus(gldouble inr, GLdouble outr, GLintiVer, GLintiHor). Sehingga Dengan menggunakan fungsi-fungsi tersebut kita dapat melihat objek-objek yang dapat dibangun oleh suatu polihedra. DAFTAR PUSTAKA [1] Suyoto.. Teori dan Pemr ograman Grafika Komputer.. [2] Compile program dengan Ctrl+F7, lalu Run program dengan Ctrl+F5. [3] REFERENSI [4] Basuki, Achmad dan Nana Ramadijanti, Grafika Komputer: Teori dan Implementasi, Andi Yogyakarta, [5] Hill, F.S, Computer Graphic Using OpenGl, Second Edition, Prentice Hall, [6] Kadir, Abdul, Pemrograman C++, Andi Yogyakarta, [7] Bambang wirawan, Paulus, Grafik Komputer dengan C, Jakarta : Penerbit Andi, [8] http :\\ [9] http :\\ \opengl [10] http :\\ \yoav Lahav 40
9 VISUALISASI OBYEK 3D DENGAN METODE PROYEKSI GEOMETRI Rahmad Abdul Jabbar Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta Abstract Projection is method to displaying an 3D object on a define plane. On this paper we use OpenGL in order to design some of 3D object with a simple source code. Keywords: OpenGL, 3D obyek, projection. Abstrak Proyeksi dapat diartikan sebagai suatu cara untuk menampilkan objek 3D pada suatu bidang 2D. Dalam makalah ini akan diuraikan cara mengoperasikan opengl untuk mendesain berbagai contoh obyek 3D dengan piranti tersebut. Kata kunci: OpenGL, obyek 3D, proyeksi I. PENDAHULUAN Teknik-teknik yang dipelajari dalam grafika komputer adalah teknik-teknik bagaimana membuat atau menciptakan gamabar dengan menggunakan komputer. Ada perbedaan yang sangat mendasar antar foto dan gambar, dimana pada foto semua detail objek terlihat sedangkan gambar (baik gamabar manusia atau gamabar komputer) tidak dapat memperlihatkan semua detail yang dianggap penting dalam menunjukkan pola suatu gambar. Grafika komputer merupakan perangkat (tool) dasar yang digunakan untuk membuat ga mabar dengan komputer. Dengan menggunakan perangkat ini, penciptaan gamabar dapat dilakukan, bahkan dimudahkan, dengan menggunakan komputer. Ada beberapa program sederhana sampai program yang sangat kompleks guna membuat gambar komputer, antara lain paint, Adobe Photoshop, Auto Cad, Macromedia Freehand MX, dan lain-lain. Kali ini kita akan membahas Visualaisasi 3 Dimensi dengan Proyeksi Geometri Seni, entertainment, dan publishing seperti produksi film, animasi, spesial effect, game komputer, web browsing, buku, slide, dan majalah. Image processing atau pengolahan citra digital, yang dalam hal ini grafika komputer dapat digunakan misalnya seperti dalam coding (permindahan data citra menjadi data vector) yang banayak digunakan untuk keperluan GIS. Menampilkan proses yang sedang berjalan (process monitoring). Menampilkan simulasi, yang dalam hal ini grafik yang dihasilkan berupa grafik visualisasi proses. Seperti dalam simulasi perempatan jalan, grafik komputer digunakan untuk melakukan visualisasi secara detail secara detail bagaimana kedatangan mobil, pengaturan lampu lalu - lintas, dan semua item didalamnya. 41
10 CAD (Computer Aided Design). Satu program CAD yang paling banyak digunakan dalam dunia teknik, yaitu AUTOCAD, dimana grafik komputer dapat menunjukka n rancangan atau design pola atau design layout. Visulisasi analisis sains, yang dalam hal ini grafik komputer dapat digunakan sebagai sarana untuk menunjukkan proses ilmiah. 2.1 Objek Dalam 3 Dimensi II. LANDASAN TEORI Yang dimaksud dengan grafik 3 dimensi (3D) adalah setiap titik yang membentuk suatu objek yang diproses dan mempunyai 3 sumbu koordinat, yaitu x, y dan z. pada gambar dibawah ini dapat dibedakan komposisi sumbu koordinat antara grafik 2 dimensi dan grafik 3 dimensi. Gambar 2.1 Sumbu grafik 2 dan 3 dimensi. Elemen terkecil (titik) untuk menampilkan objek atau gambar pada grafik komputer 3D disebut Voxel, singkatan dari Volume Elemen. Elemen terkecil pada grafik 2D disebut Pixel, singkatan dari Picture Element. Bentuk dasar gambar geometri 3D anatar lain: 1. Titik (Voxel) 2. Garis 3. Bidang Segi tiga Segi empat Lingkaran, dan lain-lain 4. Volume Prisma Piramid Kotak Bola Dadu/Kubus, dan lain-lain. Titik yang terdapat didalam sistem koordinat 3D dapat dilihat pada gambar dibawah ini. Dimana titik P mempunyai 3 sumbu yang diwakili oleh variable x, y, dan z. Contoh: Sumbu x = 10, y = 11, z = 12 42
11 Maka titik P (x,y,z) ditulis seperti Y P(10, 11, 12) X P(x,y,z) Z Gambar 2.2 Sketsa obyek 3D. Untuk menggambar objek 3D yang sudah didefinisikan dapat dilakukan dengan memperhatikan bahwa: Objek 3D terdiri dari titik-titik dan face -face. Penggambaran dilakukan pada setiap face menggunakan polygon. Polygon dibentuk dari titik yang terdapat pada sebuah face. Titik-titk dinyatakan pada struktur 3D, sedangkan layar komputer dalam struktur 2D sehingga diperlukan konversi dari 3D menjadi 2D. Untuk menggambar objek 3D, untuk setiap face perlu dilakukan pengubahan titik 3D menjadi vector 3D, agar mudah ditransformasikan. Setelah proses pengolahan vector maka bentuk vector 3D menjadi 2D. Sumbu Z adalah sumbu yang searah dengan garis mata sehingga diperlukan transformasikan untuk menampilkan sumbu ini. Untuk hal ini perlu dilakukan rotasi sumbu. Dalam konversi, arah Z tidak diambil Konversi vector 3D menjadi titik 2D adalah perubahan struktur data dari vector 3D yang sudah diolah dengan transformasi menjadi struktur data titik 2D agar siap digambar kelayar komputer. Hal ini karena bagaimanapun juga layar komputer adalah 2D. Implementasi konversi vector 3D menjadi 2D: Gambar 2.3 Konversi dimensi. 43
12 point3d_t vector2point2d vector3d_t vec) point2d_t pnt; pnt.x=vec.v [0]; pnt.y=vec.v [1]; return pnt; Seperti telah dibahas diatas, proses pengolahan (transformasi) tidak dapat dilakukan terhadap data titik, tetapi dilakukan terhadap data vector sehingga untuk mengolah atau melakukan transformasi terlebih dahulu data titik 3D diubah menjadi 2D dan baru kemudian ditransformasikan. Proyeksi dapat diartikan sebagai suatu cara untuk menampilkan objek 3D pada suatu bidang 2D.Dalam konteks komputer grafik kita menghadapi permasalahan yang hampir sama dengan pelukis atau arsitek. Hanya saja komputer grafik memiliki kelebihan, yakni kita dapat langsung merekam data suatu objek dalam bentuk sebenarnya, yaitu 3D. Objek tersebut dapat kita manipulasi dengan tetap mempertahankan informasi tentang objek tersebut dengan tetap berbentuk 3D. Masalah baru timbul pada saat kita ingin menampilkan gambar tersebut, baik pada layar komputer maupun saat dicetak diatas kertas. Objek yang datanya berbentuk 3D harus kita tampilkan hanya 2 dimensi. Oleh karena itu kita harus melakukan konversi dari 3D ke 2D. konversi itu disebut proyeksi. Dalam melakukan proyeksi kita dapat memilih ke bidang mana objek 3D akan diproyeksikan. Pilihan tersebut adalah: Bidang X dan Y Bidang X dan Z Bidang Y dan Z Untuk memproyeksikan objek pada bidang X dan Y dilakukan dengan mengambil data koordinat X dan Y sementara data bidang Z diabaikan. Begitu pula secra analog berlaku seterusnya untuk bidang X dan Z. proyeksi seperti ini sayangnya tidak mencerminkan gambar suatu objek 3D. untuk mendapatkan efek 3D dapat dilakukan berbagai cara, misalnya: Sebuah gambar kotak yang akan ditampilkan pertama-tama dirotasikan pada sumbu X sebesar 20 derajat. Setelah itu baru diproyeksikan. Dengan cara ini paling tidak kita sudah mendapatkan efe k 3D, Beragam bentuk proyeksi antara lain: Paralel(orthogonal) Perspektif Vector3D_t point2vector(point3d_t pnt) vector3d_t vec; vec.v [0] = pnt.x; vec.v [1] = pnt.y; vec.v [2] = pnt.z; vec.v [3] = 1.; return vec; 44
13 Oblique Cavalier Cabinet Axonometrik(Perspektif militer) Isometrik Diametrik Model-model proyeksi: CARBINET CAVALIER ISOMETRIK DIMETRIK TRIMETRIK AXONOMETRIK Gambar 2.4 Model-model proyeksi. Proyeksi parallel merupakan teknik proyeksi yang paling sederhana dan mudah pengimplementasiannya. Biasanya proyeksi seperti ini dig unakan untuk keperluan gambar teknik, seperti untuk gambar teknik mesin, rumah, dan lainya. Proyeksi parallel dapat dilakukan pada 3 arah sumbu koordinat, yaitu pada sumbu x,y, dan z. Cara melakukan proyeksi orthographic adalah sebagai berikut: Nilai sumbu x dikonversikan menjadi 0 Nilai sumbu y dikonversikan menjadi 0 45
14 Nilai sumbu z dikonversikan menjadi 0 Matriks proyeksi pada sumbu x ditulis: T = Matriks proyeksi pada sumbu y ditulis: T = Matriks proyeksi pada sumbu z ditulis: T = Untuk memperbaiki tampilan, selain menggunakan proyeksi parallel, dapat juga dilakukan dengan merotasi objek dengan sudut terte ntu seperti pada proyeksi oblique. Umumnya proyeksi ini dilakukan dari sumbu z dengan sudut ß pada salah satu sumbu lainya dan dengan faktor perpendekan K pada sumbu z. Matriks transformasi dengan sumbu z = 0 ditulis: T = k.cos(ß) k.sin(ß) Proyeksi ini mempunyai sudut ß = 45º dan faktor perpendekan K = 1. sumbu miring yang ditampilakan biasanya adalah sumbu z. Matriks transformasi dengan sumbu z = 0 ditulis: [ T ] = cos(45) sin(45) Sin 45º = Cos 45º = 1/v 2, dapat juga ditulis seperti:
15 [ T ] = 1/v2 1/v Mirip dengan Proyeksi cavalier, hanya saja bagian dari sumbu dalam proses transformasi mengecil. Proyeksi ini mempunyai sudut = 45º dan factor perpendekan K = ½. Sumbu miring yang ditampilkan biasanya adalah sumbu z. Matriks transformasi dengan sumbu z=0 ditulis: [ T ] = 1/2v 2 1/2v contoh: misal sebuah kotak seperti pada Gambar 13.5 dengan data koordinat setiap titiknya sebagai berikut: P(x,y,z) Y P1(0,0,0) P2(0,0,1) P3(0,1,0) P4(0,1,1) P5(1,0,0) X P6(1,0,1) Z P7(1,1,0) Gambar 2.4 Proyeksi cabinet P8(1,1,1). Untuk mendapatkan tampilan pada layar dengan proyeksi cabinet, langkah pertama adalah mengendalikan kedelapan titik yang membentuk kotak dengan matriks proyeksi cabinet. Dalam matriks, kita dapat melihat bahwa pada baris proyeksi arah kolom Z mempunyai nilai 0. itu berarti nilai perhitungan titik yang kita dapati sudah langsung diproyeksi dengan arah z dan hasil proyeksinya adalah pada bidang X dan Y. Proyeksi axonomatrik dapat diartikan sebagai suatu objek yang dirotasi pada satu atau beberapa sumbu dan setelah itu barulah objek tersebut diproyeksi secara orthogonal (paralel). Umumnya, sumbu objek yang diproyeksikan akan diperpendek. Ketiga sumbu x,y, dan z diperpendek. Artinya, bidang yang diproyeksi memotong ketiga sumbu dengan sudut yang sama. Objek dirotasi pada sumbu y dengan sudut 45º dan pada sumbu x dengan sudut 35,26º. Matriks tranformasi untuk proyeksi isometric: 47
16 0, , , [ T ] = , , , , Gambar 2.5 Matriks Transformasi Ada dua sumbu koordinat yang diperpendek dengan ukuran yang sama dan pada umunya yang dipilih adalah sumbu X dan Y. bidang proyeksi berpotongan dengan 2 sumbu dengan besar sudut yang sama. Biasanya x dan y diperpendek dengan faktor ½ sumbu z. Artinya: Rotasi pada sumbu y sebaesar 22,20º dan Rotasi pada sumbu x sebaesar 22,70º. Matriks tras nformasi untuk proyeksi dimetrik: 0, , , [ T ] = , , , , Gambar 2. 6 lemari dengan proyeksi Dimetrik. 48
17 /* * select.c * This is an illustration of the selection mode and * name stack, which detects whether objects which collide * with a viewing volume. First, four triangles and a * rectangular box representing a viewing volume are drawn * (drawscene routine). The green triangle and yellow * triangles appear to lie within the viewing volume, but * the red triangle appears to lie outside it. Then the * selection mode is entered (selectobjects routine). * Drawing to the screen ceases. To see if any collisions * occur, the four triangles are called. In this example, * the green triangle causes one hit with the name 1, and * the yellow triangles cause one hit with the name 3. */ #include <GL/glut.h> #include <stdlib.h> #include <stdio.h> /* draw a triangle with vertices at (x1, y1), (x2, y2) * and (x3, y3) at z units away from the origin. */ void drawtriangle (GLfloat x1, GLfloat y1, GLfloat x2, GLfloat y2, GLfloat x3, GLfloat y3, GLfloat z) glbegin (GL_TRIANGLES); glvertex3f (x1, y1, z); glvertex3f (x2, y2, z); glvertex3f (x3, y3, z); glend (); /* draw a rectangular box with these outer x, y, and z values */ void drawviewvolume (GLfloat x1, GLfloat x2, GLfloat y1, GLfloat y2, GLfloat z1, GLfloat z2) glcolor3f (1.0, 1.0, 1.0); glbegin (GL_LINE_LOOP); glvertex3f (x1, y1, -z1); glvertex3f (x2, y1, -z1); glvertex3f (x2, y2, -z1); glvertex3f (x1, y2, -z1); glend (); glbegin (GL_LINE_LOOP); glvertex3f (x1, y1, -z2); glvertex3f (x2, y1, -z2); glvertex3f (x2, y2, -z2); glvertex3f (x1, y2, -z2); glend (); glbegin (GL_LINES); /* 4 lines */ glvertex3f (x1, y1, -z1); glvertex3f (x1, y1, -z2); glvertex3f (x1, y2, -z1); glvertex3f (x1, y2, -z2); glvertex3f (x2, y1, -z1); glvertex3f (x2, y1, -z2); glvertex3f (x2, y2, -z1); glvertex3f (x2, y2, -z2); glend (); III. ALGORITMA/PROGRAM /* drawscene draws 4 triangles and a wire frame 49
18 * which represents the viewing volume. */ void drawscene (void) glmatrixmode (GL_PROJECTION); glloadidentity (); gluperspective (40.0, 4.0/3.0, 1.0, 100.0); glmatrixmode (GL_MODELVIEW); glloadidentity (); glulookat (7.5, 7.5, 12.5, 2.5, 2.5, -5.0, 0.0, 1.0, 0.0); glcolor3f (0.0, 1.0, 0.0); /* green triangle */ drawtriangle (2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -5.0); glcolor3f (1.0, 0.0, 0.0); /* red triangle */ drawtriangle (2.0, 7.0, 3.0, 7.0, 2.5, 8.0, -5.0); glcolor3f (1.0, 1.0, 0.0); /* yellow triangles */ drawtriangle (2.0, 2.0, 3.0, 2.0, 2.5, 3.0, 0.0); drawtriangle (2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -10.0); drawviewvolume (0.0, 5.0, 0.0, 5.0, 0.0, 10.0); /* processhits prints out the contents of the selection array */ void processhits (GLint hits, GLuint buffer[]) unsigned int i, j; GLuint names, *ptr; printf ("hits = %d\n", hits); ptr = (GLuint *) buffer; for (i = 0; i < hits; i++) /* for each hit */ names = *ptr; printf (" number of names for hit = %d\n", names); ptr++; printf(" z1 is %g;", (float) *ptr/0x7fffffff); ptr++; printf(" z2 is %g\n", (float) *ptr/0x7fffffff); ptr++; printf (" the name is "); for (j = 0; j < names; j++) /* for each name */ printf ("%d ", *ptr); ptr++; printf ("\n"); /* selectobjects "draws" the triangles in selection mode, * assigning names for the triangles. Note that the third * and fourth triangles share one name, so that if either * or both triangles intersects the viewing/clipping volume, * only one hit will be registered. */ #define BUFSIZE 512 void selectobjects(void) GLuint selectbuf[bufsize]; GLint hits; glselectbuffer (BUFSIZE, selectbuf); (void) glrendermode (GL_SELECT); glinitnames(); glpushname(0); glpushmatrix (); glmatrixmode (GL_PROJECTION); glloadidentity (); 50
19 glortho (0.0, 5.0, 0.0, 5.0, 0.0, 10.0); glmatrixmode (GL_MODELVIEW); glloadidentity (); glloadname(1); drawtriangle (2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -5.0); glloadname(2); drawtriangle (2.0, 7.0, 3.0, 7.0, 2.5, 8.0, -5.0); glloadname(3); drawtriangle (2.0, 2.0, 3.0, 2.0, 2.5, 3.0, 0.0); drawtriangle (2.0, 2.0, 3.0, 2.0, 2.5, 3.0, -10.0); glpopmatrix (); glfl ush (); hits = glrendermode (GL_RENDER); processhits (hits, selectbuf); void init (void) glenable(gl_depth_test); glshademodel(gl_flat); void display(void) glclearcolor (0.0, 0.0, 0.0, 0.0); glclear(gl_color_buffer_bit GL_D EPTH_BUFFER_BIT); drawscene (); selectobjects (); glflush(); void keyboard(unsigned char key, int x, int y) switch (key) case 27: exit(0); break; /* Main Loop */ int main(int argc, char** argv) glutinit(&argc, argv); glutinitdisplaymode (GLUT_SINGLE GLUT_RGB GLUT_DEPTH); glutinitwindowsize (200, 200); glutinitwindowposition (100, 100); glutcreatewindow (argv[0]); init(); glutdisplayfunc(display); glutkeyboardfunc(keyboard); glutmainloop(); return 0; IV. KESIMPULAN Komputer grafik ialah grafik yang dihasilkan oleh komputer. yang dimaksud grafik komputer 3D ialah dimana setiap titik yang membentuk suatu objek yang diproses dan mempunyai 3 sumbu koordinat. Proyeksi dapat diartikan sebagai suatu cara untuk menampilkan objek 3D pada suatu bidang 2D.Beragam bentuk proyeksi antara lain: Paralel(orthogonal) Perspektif Oblique 51
20 Cavalier Cabinet Axonometrik(Perspektif militer) Isometrik Diametrik DAFTAR PUSTAKA [1] Basuki, Achmad dan Nana Ramadijanti, Grafika Komputer: Teori danimplementasi, Andi Yogyakarta, [2] Hill, F.S, Computer Graphic Using OpenGl, Second Edition, Prentice Hall, [3] Kadir, Abdul, Pemrograman C++, Andi Yogyakarta, [4] Bambang wirawan, P aulus, Grafik Komputer dengan C, Jakarta : Penerbit Andi, 2003 [5] http :\\ [6] http :\\ [7] http :\\ Lahav 52
Topik bahasan: 1. Membuat objek mudah dan kompleks dengan jaring poligon 2. Merender jaring poligon sebagai wireframe dan atau pejal dengan OpenGL
 Grafika-5 Pemodelan 3D dengan Jaring Poligon Tujuan Materi: Setelah mempelajari bab ini, Anda diharapkan dapat menjelaskan secara ringkas bagaimana membentuk objek 3D dengan jaring poligon (polygon meshes)
Grafika-5 Pemodelan 3D dengan Jaring Poligon Tujuan Materi: Setelah mempelajari bab ini, Anda diharapkan dapat menjelaskan secara ringkas bagaimana membentuk objek 3D dengan jaring poligon (polygon meshes)
Tutorial 09. Lighting
 Tutorial 09. Lighting Visualisasi tentu saja tidak akan terjadi bila tidak ada cahaya. Pencahayaan merupakan esensi dari visualisasi dan merupakan topik yang sangat kompleks. Hingga tahap ini lingkungan
Tutorial 09. Lighting Visualisasi tentu saja tidak akan terjadi bila tidak ada cahaya. Pencahayaan merupakan esensi dari visualisasi dan merupakan topik yang sangat kompleks. Hingga tahap ini lingkungan
Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan
 A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan Perintah Arti Keterangan glvertex2i(x,y);
A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan Perintah Arti Keterangan glvertex2i(x,y);
LAMPIRAN SOURCE CODE
 DAFTAR PUSTAKA Anonim. www.opengl.org (diakses pada tanggal 01 Juli 2015). Fadlisyah, et al. 2007. Pengantar Grafika Komputer. Yogyakarta: Andi. Haemel, Nicholas, et al. 2011. OpenGL super bible : comprehensive
DAFTAR PUSTAKA Anonim. www.opengl.org (diakses pada tanggal 01 Juli 2015). Fadlisyah, et al. 2007. Pengantar Grafika Komputer. Yogyakarta: Andi. Haemel, Nicholas, et al. 2011. OpenGL super bible : comprehensive
Tabel 1 Perintah-perintah OpenGL yang telah dipraktekan
 No. : ST/EKA/PTI223/04 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL
No. : ST/EKA/PTI223/04 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Review Praktikum sebelumnya Sebelum ke modul selanjutnya, perhatikan sintak dibawah ini Tabel 1 Perintah-perintah OpenGL
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB. SHEET PRAKTIKUM GRAFIKA KOMPUTER
 No. : ST/EKA/PTI223/05 Revisi : 02 Senin 010409 Hal. 1 dari 8 hal. A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer.
No. : ST/EKA/PTI223/05 Revisi : 02 Senin 010409 Hal. 1 dari 8 hal. A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer.
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB. SHEET PRAKTIKUM GRAFIKA KOMPUTER
 No. : ST/EKA/PTI275/05 Revisi : 02 1 P a g e A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer. Bagian dari komputasi
No. : ST/EKA/PTI275/05 Revisi : 02 1 P a g e A. Pendahuluan OpenGL akan melakukan komputasi warna setiap pixel di display akhir, ditampilkan adegan itu dilakukan di frame buffer. Bagian dari komputasi
BAB IV IMPLEMENTASI DAN PENGUJIAN SISTEM
 BAB IV IMPLEMENTASI DAN PENGUJIAN SISTEM Pada bab ini akan dibahas implementasi bertujuan memastikan apakah aplikasi yang dibuat berjalan sesuai yang penulis harapakan. Sebelum program diimplementasikan
BAB IV IMPLEMENTASI DAN PENGUJIAN SISTEM Pada bab ini akan dibahas implementasi bertujuan memastikan apakah aplikasi yang dibuat berjalan sesuai yang penulis harapakan. Sebelum program diimplementasikan
Grafika Komputer. Evangs Mailoa
 Grafika Komputer Evangs Mailoa Kumpulan polygon atau permukaan yang secara bersama-sama membentuk kulit dari suatu obyek. Dinyatakan dengan daftar poligon-poligon yang disertai dengan arah dari permukaan
Grafika Komputer Evangs Mailoa Kumpulan polygon atau permukaan yang secara bersama-sama membentuk kulit dari suatu obyek. Dinyatakan dengan daftar poligon-poligon yang disertai dengan arah dari permukaan
Program 1 /* Menampilkan Bayangan sebuah obyek sumber file */
 No. : ST/EKA/PTI223/10 Revisi : 01 Senin 010509 Hal. 1 dari 5 hal. Pengantar Untuk menghasilkan gambar yang realistik perlu memodelkan pencerminan dan pembiasan maupun memunculkan bayangan karena pengaruh
No. : ST/EKA/PTI223/10 Revisi : 01 Senin 010509 Hal. 1 dari 5 hal. Pengantar Untuk menghasilkan gambar yang realistik perlu memodelkan pencerminan dan pembiasan maupun memunculkan bayangan karena pengaruh
PETEMUAN KE-3 PRIMITIVE DRAWING 2
 PETEMUAN KE-3 PRIMITIVE DRAWING 2 A.Tujuan 1. Dapat mengaplikasikan objek primitif dalam bentuk yang lain B. Dasar Teori Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam
PETEMUAN KE-3 PRIMITIVE DRAWING 2 A.Tujuan 1. Dapat mengaplikasikan objek primitif dalam bentuk yang lain B. Dasar Teori Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam
Tutorial 04 Modeling & Transformasi Proyeksi
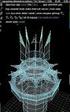 Tutorial 04 Modeling & Transformasi Proyeksi Secara substansi, Grafika Komputer adalah proses transformasi dari model 3D obyek berupa informasi geometri bentuk, informasi pose, warna, texture, dan pencahayaan
Tutorial 04 Modeling & Transformasi Proyeksi Secara substansi, Grafika Komputer adalah proses transformasi dari model 3D obyek berupa informasi geometri bentuk, informasi pose, warna, texture, dan pencahayaan
apa yang terjadi?. Kemudian lakukan pengantian beberapa bagian seperti sintak
 No. : ST/EKA/PTI223/02 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam praktikum hari ini lakukan penambahan
No. : ST/EKA/PTI223/02 Revisi : 02 Senin 010210 Hal. 1 dari 8 hal. A. Pendahuluan Dalam praktikum sebelumnya anda diminta membuat titik garis, dan sebagainya. Dalam praktikum hari ini lakukan penambahan
Gambar 1. Viewport pada layar
 No. : ST/EKA/PTI223/03 Revisi : 02 Hal. 1 dari 9 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi, balikan,
No. : ST/EKA/PTI223/03 Revisi : 02 Hal. 1 dari 9 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi, balikan,
Gambar 1. Viewport pada layar
 No. : ST/EKA/PTI223/03 Revisi : 03 Senin 010210 Hal. 1 dari 5 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi,
No. : ST/EKA/PTI223/03 Revisi : 03 Senin 010210 Hal. 1 dari 5 hal. A. Pendahuluan Transformasi adalah memindahkan objek tanpa merusak bentuk. Contoh transformasi adalah transisi, penskalaan, putaran/rotasi,
DAFTAR PUSTAKA. (diakses 1 maret 2016)
 DAFTAR PUSTAKA [1] http://www.surakarta.go.id/konten/bus-tingkat-werkudara# (diakses 28 februari 2016) [2] Anonim. www.opengl.org (diakses 1 maret 2016) [3] Haemel, Nicholas, et al. 2011. OpenGL super
DAFTAR PUSTAKA [1] http://www.surakarta.go.id/konten/bus-tingkat-werkudara# (diakses 28 februari 2016) [2] Anonim. www.opengl.org (diakses 1 maret 2016) [3] Haemel, Nicholas, et al. 2011. OpenGL super
PETEMUAN KE-5 TRANSFORMASI-PANDANGAN (Viewing)
 PETEMUAN KE-5 TRANSFORMASI-PANDANGAN (Viewing) A.Tujuan 1. Dapat menggambar objek 3D 2. Dapat mentransformasikan objek 3D 3. Dapat menggunkan glviewport,glmodelview, glprojection, glfrustum B. Dasar Teori
PETEMUAN KE-5 TRANSFORMASI-PANDANGAN (Viewing) A.Tujuan 1. Dapat menggambar objek 3D 2. Dapat mentransformasikan objek 3D 3. Dapat menggunkan glviewport,glmodelview, glprojection, glfrustum B. Dasar Teori
/*Bismillahirrohmanirrohim _Fatimah_Rombel 2_Projek_Akhir_Komgraf*/ #include <stdio.h> #include <stdlib.h> #include <string.
 /*Bismillahirrohmanirrohim.. 5302413025_Fatimah_Rombel 2_Projek_Akhir_Komgraf*/ #include #include #include #include "SOIL.h" #include float z_pos = -5.0f; float
/*Bismillahirrohmanirrohim.. 5302413025_Fatimah_Rombel 2_Projek_Akhir_Komgraf*/ #include #include #include #include "SOIL.h" #include float z_pos = -5.0f; float
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB. SHEET PRAKTIKUM GRAFIKA KOMPUTER
 No. : ST/EKA/PTI223/06 Revisi : 02 Senin 010509 Hal. 1 dari 9 hal. Pengantar Fog adalah pengaruh atmospheric yang ditambahkan objek, sehingga akan terjadi kekaburan pada obyek yang tergantung seberapa
No. : ST/EKA/PTI223/06 Revisi : 02 Senin 010509 Hal. 1 dari 9 hal. Pengantar Fog adalah pengaruh atmospheric yang ditambahkan objek, sehingga akan terjadi kekaburan pada obyek yang tergantung seberapa
BAB IV IMPLEMENTASI DAN PENGUJIAN
 BAB IV IMPLEMENTASI DAN PENGUJIAN 4.1 Implementasi Tahapan implementasi bertujuan untuk memastikan apakah aplikasi yang dibuat dapat bekerja secara efektif dan efisien sesuai dengan yang diharapkan. Sebelum
BAB IV IMPLEMENTASI DAN PENGUJIAN 4.1 Implementasi Tahapan implementasi bertujuan untuk memastikan apakah aplikasi yang dibuat dapat bekerja secara efektif dan efisien sesuai dengan yang diharapkan. Sebelum
Tutorial 06. Texture Mapping & Blending
 Tutorial 06. Texture Mapping & Blending Hingga tahap ini, geometric primitive digambar dengan warna solid atau warna hasil interpolasi warnawarna vertex-nya. Texture mapping memungkinkan untuk menaruh
Tutorial 06. Texture Mapping & Blending Hingga tahap ini, geometric primitive digambar dengan warna solid atau warna hasil interpolasi warnawarna vertex-nya. Texture mapping memungkinkan untuk menaruh
BAB II LINGKUNGAN PEMROGRAMAN GRAFIK DENGAN OPEN GL
 BAB II LINGKUNGAN PEMROGRAMAN GRAFIK DENGAN OPEN GL Pemrograman Grafis Pemrograman grafis adalah pemrograman yang digunakan untuk menghasilkan gambar pada komputer menggunakan library yang ada. Teknik-teknik
BAB II LINGKUNGAN PEMROGRAMAN GRAFIK DENGAN OPEN GL Pemrograman Grafis Pemrograman grafis adalah pemrograman yang digunakan untuk menghasilkan gambar pada komputer menggunakan library yang ada. Teknik-teknik
Gambar 1. Contoh tekstur makrostruktur
 No. : ST/EKA/PTI223/08 Revisi : 02 Senin 010510 Hal. 1 dari 14 hal. Pengantar Tekstur adalah tampilan permukaan (corak) dari suatu benda yang dapat dinilai dengan cara dilihat atau diraba. Pada prakteknya,
No. : ST/EKA/PTI223/08 Revisi : 02 Senin 010510 Hal. 1 dari 14 hal. Pengantar Tekstur adalah tampilan permukaan (corak) dari suatu benda yang dapat dinilai dengan cara dilihat atau diraba. Pada prakteknya,
PENGANTAR GRAFIKA KOMPUTER
 PENGANTAR GRAFIKA KOMPUTER Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Pengenalan grafika komputer
PENGANTAR GRAFIKA KOMPUTER Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Pengenalan grafika komputer
Praktikum Komputer Grafik [MODUL] Genap 2012/2013. Laboratorium Multimedia 1/35
![Praktikum Komputer Grafik [MODUL] Genap 2012/2013. Laboratorium Multimedia 1/35 Praktikum Komputer Grafik [MODUL] Genap 2012/2013. Laboratorium Multimedia 1/35](/thumbs/58/42599123.jpg) Praktikum Komputer Grafik [MODUL] Genap 2012/2013 1/35 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata Kuliah Prasyarat : - Dosen Penanggung Jawab
Praktikum Komputer Grafik [MODUL] Genap 2012/2013 1/35 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata Kuliah Prasyarat : - Dosen Penanggung Jawab
TRANSFORMASI. Tujuan transfomasi adalah:
 TRANSFORMASI Grafika komputer merupakan bidang yang menarik minat banyak orang. Salah sub bagian dari grafika komputer adalah pemodelan objek (object modelling). Dalam pemodelan objek dua dimensi (2D),didapati
TRANSFORMASI Grafika komputer merupakan bidang yang menarik minat banyak orang. Salah sub bagian dari grafika komputer adalah pemodelan objek (object modelling). Dalam pemodelan objek dua dimensi (2D),didapati
Praktikum Komputer Grafik [MODUL] Genap 2013/2014. Laboratorium Multimedia 1/47
![Praktikum Komputer Grafik [MODUL] Genap 2013/2014. Laboratorium Multimedia 1/47 Praktikum Komputer Grafik [MODUL] Genap 2013/2014. Laboratorium Multimedia 1/47](/thumbs/64/50791138.jpg) Praktikum Komputer Grafik [MODUL] Genap 2013/2014 1/47 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata Kuliah Prasyarat : - Dosen Penanggung Jawab
Praktikum Komputer Grafik [MODUL] Genap 2013/2014 1/47 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata Kuliah Prasyarat : - Dosen Penanggung Jawab
PEMBENTUKAN TRANSFORMASI OBJEK 2 DIMENSI DENGAN OPENGL
 PEMBENTUKAN TRANSFORMASI OBJEK 2 DIMENSI DENGAN OPENGL Ina Agustina, Fauziah Jurusan Sistem Informasi Universitas Nasional Jl. Sawo Manila No.61 Pasar Minggu E-Mail : [email protected], [email protected]
PEMBENTUKAN TRANSFORMASI OBJEK 2 DIMENSI DENGAN OPENGL Ina Agustina, Fauziah Jurusan Sistem Informasi Universitas Nasional Jl. Sawo Manila No.61 Pasar Minggu E-Mail : [email protected], [email protected]
Tutorial 08. Fog. mensimulasikan efek kabut membatasi ruang pandang pengguna agar komputasi grafis yang diperlukan dapat dibatasi.
 Tutorial 08. Fog Kabut/fog adalah salah satu fitur OpenGL lain yang sering digunakan pada banyak kesempatan. Kabut digunakan dalam banyak kesempatan, antara lain: mensimulasikan efek kabut membatasi ruang
Tutorial 08. Fog Kabut/fog adalah salah satu fitur OpenGL lain yang sering digunakan pada banyak kesempatan. Kabut digunakan dalam banyak kesempatan, antara lain: mensimulasikan efek kabut membatasi ruang
Laboratorium Teknologi Informasi & Aplikasi. Praktikum Komputer Grafik [MODUL] Genap 2014/2015. Lab TIA 1/58
![Laboratorium Teknologi Informasi & Aplikasi. Praktikum Komputer Grafik [MODUL] Genap 2014/2015. Lab TIA 1/58 Laboratorium Teknologi Informasi & Aplikasi. Praktikum Komputer Grafik [MODUL] Genap 2014/2015. Lab TIA 1/58](/thumbs/54/34559968.jpg) Laboratorium Teknologi Informasi & Aplikasi Praktikum Komputer Grafik [MODUL] Genap 2014/2015 1/58 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata
Laboratorium Teknologi Informasi & Aplikasi Praktikum Komputer Grafik [MODUL] Genap 2014/2015 1/58 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata
OPENGL DALAM MICROSOFT VISUAL STUDIO EXPRESS Created by: Gideon
 OPENGL DALAM MICROSOFT VISUAL STUDIO EXPRESS 2012 Created by: Gideon Tutorial Open GL untuk membuat garis dengan program Microsoft Visual Studio Express 2012 OpenGL dengan Microsoft Visual Express 2012
OPENGL DALAM MICROSOFT VISUAL STUDIO EXPRESS 2012 Created by: Gideon Tutorial Open GL untuk membuat garis dengan program Microsoft Visual Studio Express 2012 OpenGL dengan Microsoft Visual Express 2012
Modul 1 Primitif Drawing
 Modul 1 Primitif Drawing I. Tugas Pendahuluan 1. Jelaskan tentang OpenGL! 2. Jelaskan tenteng ouput primitif dalam grafika computer! II. Tujuan Mahasiswa mampu membuat dan memanfaatkan output primitif
Modul 1 Primitif Drawing I. Tugas Pendahuluan 1. Jelaskan tentang OpenGL! 2. Jelaskan tenteng ouput primitif dalam grafika computer! II. Tujuan Mahasiswa mampu membuat dan memanfaatkan output primitif
Pengenalan OpenGL. Sintax Perintah OpenGL. Library yang Berhubungan dengan OpenGL
 Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
Laboratorium Teknologi Informasi & Aplikasi. Praktikum Komputer Grafik [MODUL] Genap 2015/2016. Lab TIA 1/59
![Laboratorium Teknologi Informasi & Aplikasi. Praktikum Komputer Grafik [MODUL] Genap 2015/2016. Lab TIA 1/59 Laboratorium Teknologi Informasi & Aplikasi. Praktikum Komputer Grafik [MODUL] Genap 2015/2016. Lab TIA 1/59](/thumbs/54/33887896.jpg) Laboratorium Teknologi Informasi & Aplikasi Praktikum Komputer Grafik [MODUL] Genap 2015/2016 1/59 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata
Laboratorium Teknologi Informasi & Aplikasi Praktikum Komputer Grafik [MODUL] Genap 2015/2016 1/59 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TIF121 SKS : 1 Mata
PRIMITIVE DRAWING. Achmad Basuki Nana Ramadijanti
 PRIMITIVE DRAWING Achmad Basuki Nana Ramadijanti Materi Program Dasar dengan OpenGL Menggambar Titik Menggambar Garis Menggambar Polyline Menggambar Polygon Pewarnaan Struktur Dasar Program Grafik Dengan
PRIMITIVE DRAWING Achmad Basuki Nana Ramadijanti Materi Program Dasar dengan OpenGL Menggambar Titik Menggambar Garis Menggambar Polyline Menggambar Polygon Pewarnaan Struktur Dasar Program Grafik Dengan
Pengenalan OpenGL. Sintax Perintah OpenGL. Library yang Berhubungan dengan OpenGL
 Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
Pengenalan OpenGL OpenGL adalah suatu graphic library yang sebagian bersifat open source, dipakai pada banyak platform (windows, linux) dan dapat digunakan pada berbagai jenis compiler seperti C++ atau
ALGORITMA PERPOTONGAN OBJEK
 ALGORITMA PERPOTONGAN OBJEK Ina Agustina, Fauziah Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta 12520
ALGORITMA PERPOTONGAN OBJEK Ina Agustina, Fauziah Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta 12520
Transformasi Obyek (Lanjutan)
 Transformasi Obek (Lanjutan) Grafika Komputer Semester Ganjil 28 Teknik Informatika ITS Ann Yuniarti - 28 Kompetensi. Mampu memahami konsep transformasi 3D 2. Mampu mengimplementasikan konsep transformasi
Transformasi Obek (Lanjutan) Grafika Komputer Semester Ganjil 28 Teknik Informatika ITS Ann Yuniarti - 28 Kompetensi. Mampu memahami konsep transformasi 3D 2. Mampu mengimplementasikan konsep transformasi
PEMODELAN OBYEK DENGAN METODE KURVA PARAMETRIK
 PEMODELAN OBYEK DENGAN METODE KURVA PARAMETRIK Ina Agustina Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta
PEMODELAN OBYEK DENGAN METODE KURVA PARAMETRIK Ina Agustina Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta
BAB 2 DASAR TEORI. Pada bagian ini akan dibahas tentang teori dasar dari grafika komputer, yang
 BAB 2 DASAR TEORI 2.1 Teori Dasar Grafika Komputer Pada bagian ini akan dibahas tentang teori dasar dari grafika komputer, yang akan digunakan dalam pembahasan teknik environment mapping. 2.1.1 Sistem
BAB 2 DASAR TEORI 2.1 Teori Dasar Grafika Komputer Pada bagian ini akan dibahas tentang teori dasar dari grafika komputer, yang akan digunakan dalam pembahasan teknik environment mapping. 2.1.1 Sistem
Praktikum Komputer Grafik [MODUL] Ganjil 2012/2013. Laboratorium Multimedia 1/41
![Praktikum Komputer Grafik [MODUL] Ganjil 2012/2013. Laboratorium Multimedia 1/41 Praktikum Komputer Grafik [MODUL] Ganjil 2012/2013. Laboratorium Multimedia 1/41](/thumbs/54/33262563.jpg) Praktikum Komputer Grafik [MODUL] Ganjil 2012/2013 1/41 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TKC 111 SKS : 1 Mata Kuliah Prasyarat : - Dosen Penanggung Jawab
Praktikum Komputer Grafik [MODUL] Ganjil 2012/2013 1/41 KONTRAK PRAKTIKUM Nama Mata Kuliah : Praktikum Komputer Grafik Kode Mata Praktikum : TKC 111 SKS : 1 Mata Kuliah Prasyarat : - Dosen Penanggung Jawab
DIAN PRATIWI. ST, MTI
 DIAN PRATIWI. ST, MTI PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Diterbitkan melalui Nida Dwi Karya Publishing PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Oleh: Dian Pratiwi, ST, MTI Copyright 2015
DIAN PRATIWI. ST, MTI PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Diterbitkan melalui Nida Dwi Karya Publishing PEMROGRAMAN GRAFIKA KOMPUTER BERBASIS OPENGL Oleh: Dian Pratiwi, ST, MTI Copyright 2015
GRAFIK KOMPUTER & PENGOLAHAN CITRA
 GRAFIK KOMPUTER & PENGOLAHAN CITRA MEMBUAT GARIS MENGGUNAKAN OPENGL NAMA : ADRY FITRA AZHAR SIREGAR NPM : 10114361 KELAS : 3KA26 UNIVERSITAS GUNADARMA SISTEM INFORMASI PTA 2016 / 2017 PENGENALAN OPENGL
GRAFIK KOMPUTER & PENGOLAHAN CITRA MEMBUAT GARIS MENGGUNAKAN OPENGL NAMA : ADRY FITRA AZHAR SIREGAR NPM : 10114361 KELAS : 3KA26 UNIVERSITAS GUNADARMA SISTEM INFORMASI PTA 2016 / 2017 PENGENALAN OPENGL
Pengantar Kuliah: Grafika Komputer. By: Nana Ramadijanti
 Pengantar Kuliah: Grafika Komputer By: Nana Ramadijanti Tujuan Perkuliahan Mahasiswa dapat membuat program untuk membangun grafik 2D dan 3D menggunakan bahasa pemrograman C++ dan grafik library OpenGL.
Pengantar Kuliah: Grafika Komputer By: Nana Ramadijanti Tujuan Perkuliahan Mahasiswa dapat membuat program untuk membangun grafik 2D dan 3D menggunakan bahasa pemrograman C++ dan grafik library OpenGL.
MODUL 7 OBJEK 3D A. KOMPETENSI DASAR
 MODUL 7 OBJEK 3D A. KOMPETENSI DASAR Memahami Inisialisasi dunia 3D Memahami Object 3D (Wired). Memahami dasar menampilkan susunan objek 3D. B. ALOKASI WAKTU 4 js (4x50 menit) C. PETUNJUK Awali setiap
MODUL 7 OBJEK 3D A. KOMPETENSI DASAR Memahami Inisialisasi dunia 3D Memahami Object 3D (Wired). Memahami dasar menampilkan susunan objek 3D. B. ALOKASI WAKTU 4 js (4x50 menit) C. PETUNJUK Awali setiap
TUGAS PENGANTAR GRAFIK KOMPUTER DAN OLAH CITRA
 TUGAS PENGANTAR GRAFIK KOMPUTER DAN OLAH CITRA NAMA : HERU SANJAYA NPM : 39110387 KELAS : 2DB23 Gambar dibawah ini adalah tampilan awal Code Blocks. Setelah itu, pilih menu Settings Compiler and Debugger.
TUGAS PENGANTAR GRAFIK KOMPUTER DAN OLAH CITRA NAMA : HERU SANJAYA NPM : 39110387 KELAS : 2DB23 Gambar dibawah ini adalah tampilan awal Code Blocks. Setelah itu, pilih menu Settings Compiler and Debugger.
PAGI. SOAL PILIHAN GANDA : No
 PAGI SOAL PILIHAN GANDA : No. 1 35. 1. Salah satu contoh aplikasi Grafika Komputer adalah Virtual Reality. Yang dimaksud Virtual Reality adalah: a. lingkungan virtual seperti yang ada di dunia internet
PAGI SOAL PILIHAN GANDA : No. 1 35. 1. Salah satu contoh aplikasi Grafika Komputer adalah Virtual Reality. Yang dimaksud Virtual Reality adalah: a. lingkungan virtual seperti yang ada di dunia internet
Drawing, Viewport, dan Transformasi. Pertemuan - 02
 Drawing, Viewport, dan Transformasi Pertemuan - 02 Ruang Lingkup Definisi Drawing Viewport Transfomasi Definisi Bagian dari grafik komputer meliputi: 1. Citra (Imaging) : mempelajari cara pengambilan dan
Drawing, Viewport, dan Transformasi Pertemuan - 02 Ruang Lingkup Definisi Drawing Viewport Transfomasi Definisi Bagian dari grafik komputer meliputi: 1. Citra (Imaging) : mempelajari cara pengambilan dan
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB. SHEET PRAKTIKUM GRAFIKA KOMPUTER
 A. Pendahuluan Objek 3D pada open GL merupakan objek yang lebih hidup dibandingkan objek 2D. Namun permukaan objek 3D yang polos membuat 3D cenderung kurang menarik dan kaku. Untuk membuat objek yang lebih
A. Pendahuluan Objek 3D pada open GL merupakan objek yang lebih hidup dibandingkan objek 2D. Namun permukaan objek 3D yang polos membuat 3D cenderung kurang menarik dan kaku. Untuk membuat objek yang lebih
APLIKASI MENGUBAH POLARISASI FRAME GAMBAR 2 DIMENSI MENJADI 3 DIMENSI
 APLIKASI MENGUBAH POLARISASI FRAME GAMBAR 2 DIMENSI MENJADI 3 DIMENSI ABDUL ARDI 41507110115 PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS ILMU KOMPUTER UNIVERSITAS MERCU BUANA JAKARTA 2014 APLIKASI MENGUBAH
APLIKASI MENGUBAH POLARISASI FRAME GAMBAR 2 DIMENSI MENJADI 3 DIMENSI ABDUL ARDI 41507110115 PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS ILMU KOMPUTER UNIVERSITAS MERCU BUANA JAKARTA 2014 APLIKASI MENGUBAH
Viewing 3D. Tujuan: memberi kesan pada viewer bahwa ia melihat foto 3D dengan cara yg sama saat kita memotret obyek 3D ke film 2D.
 Komputer Grafik 1 Viewing 3D Tujuan: memberi kesan pada viewer bahwa ia melihat foto 3D dengan cara yg sama saat kita memotret obyek 3D ke film 2D. memproyeksikan obyek 3D ke bidang 2D 2 Pinhole Camera
Komputer Grafik 1 Viewing 3D Tujuan: memberi kesan pada viewer bahwa ia melihat foto 3D dengan cara yg sama saat kita memotret obyek 3D ke film 2D. memproyeksikan obyek 3D ke bidang 2D 2 Pinhole Camera
Pewarnaan dan Perputaran Polygon Untuk Objek Gambar Segi Tiga dan Segi Empat Menggunakan Program OPENGL 32
 Pewarnaan dan Perputaran Polygon Untuk Objek Gambar Segi Tiga dan Segi Empat Menggunakan Program OPENGL 32 Aqwam Rosadi Kardian, Bheta Agus Wardijono STMIK JAKARTA STI&K [email protected], [email protected]
Pewarnaan dan Perputaran Polygon Untuk Objek Gambar Segi Tiga dan Segi Empat Menggunakan Program OPENGL 32 Aqwam Rosadi Kardian, Bheta Agus Wardijono STMIK JAKARTA STI&K [email protected], [email protected]
LAPORAN PRAKTIKUM KOMPUTER GRAFIK
 LAPORAN PRAKTIKUM KOMPUTER GRAFIK KELAS TI4C SORE NAMA PRAKTIKAN Mulia Hamonangan Tambunan NOMOR TANGGAL TANDA TANGAN MAHASISWA KUMPUL PRAKTIKAN 1214370473 NAMA PENILAI TANGGAL KOREKSI NILAI TANDA TANGAN
LAPORAN PRAKTIKUM KOMPUTER GRAFIK KELAS TI4C SORE NAMA PRAKTIKAN Mulia Hamonangan Tambunan NOMOR TANGGAL TANDA TANGAN MAHASISWA KUMPUL PRAKTIKAN 1214370473 NAMA PENILAI TANGGAL KOREKSI NILAI TANDA TANGAN
FAKULTAS TEKNIK UNIVERSITAS NEGERI YOGYAKARTA LAB. SHEET PRAKTIKUM GRAFIKA KOMPUTER
 No. : ST/EKA/PTI223/10 Revisi : 03 Senin 170511 Hal. 1 dari 16 hal. Pengantar Media berasal dari bahasa latin yang merupakan bentuk jamak dari Medium yang secara harfiah berarti Perantara atau Pengantar
No. : ST/EKA/PTI223/10 Revisi : 03 Senin 170511 Hal. 1 dari 16 hal. Pengantar Media berasal dari bahasa latin yang merupakan bentuk jamak dari Medium yang secara harfiah berarti Perantara atau Pengantar
LAPORAN PRATIKUM KOMPUTER APLIKASI
 LAPORAN PRATIKUM KELAS TI VI SORE D KOMPUTER APLIKASI Nama Nomor Pratikan Mahasiswa Ayu MayaSari 1214370278 Tanggal Kumpul Tanda Tangan Pratikan Nama Penilai Tanggal Nilai Tanda Tangan Koreksi Dosen Universitas
LAPORAN PRATIKUM KELAS TI VI SORE D KOMPUTER APLIKASI Nama Nomor Pratikan Mahasiswa Ayu MayaSari 1214370278 Tanggal Kumpul Tanda Tangan Pratikan Nama Penilai Tanggal Nilai Tanda Tangan Koreksi Dosen Universitas
Primitive Drawing. Achmad Basuki Nana Ramadijanti
 Primitive Drawing Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Sistem Koordinat 2 Dimensi Menggambar
Primitive Drawing Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Sistem Koordinat 2 Dimensi Menggambar
BAB I PENGENALAN OPENGL
 BAB I PENGENALAN OPENGL A. TUJUAN a. Mampu melakukan konfigurasi Library opengl di Visual Studio 2008 b. Mampu memahami inisialisasi fungsi opengl c. Mampu membuat objek dasar dengan fungsi opengl B. MATERI
BAB I PENGENALAN OPENGL A. TUJUAN a. Mampu melakukan konfigurasi Library opengl di Visual Studio 2008 b. Mampu memahami inisialisasi fungsi opengl c. Mampu membuat objek dasar dengan fungsi opengl B. MATERI
Jurnal INFORMASI Vol.4 No.2 (1), November Chairuddin. Teknik Informatika, STMIK IM, Jl.Jakarta No.79 Bandung
 Jurnal INFORMASI Vol.4 No.2 (1), November 2011 1 PERGERAKAN DAN TEKNIK PENCAHAYAAN PADA OBJEK 3D Chairuddin Teknik Informatika, STMIK IM, Jl.Jakarta No.79 Bandung [email protected] Abstrak Grafik tiga
Jurnal INFORMASI Vol.4 No.2 (1), November 2011 1 PERGERAKAN DAN TEKNIK PENCAHAYAAN PADA OBJEK 3D Chairuddin Teknik Informatika, STMIK IM, Jl.Jakarta No.79 Bandung [email protected] Abstrak Grafik tiga
PEMINDAIAN OBYEK DENGAN ALGORITMA SCANLINE
 PEMINDAIAN OBYEK DENGAN ALGORITMA SCANLINE Ina Agustina Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta
PEMINDAIAN OBYEK DENGAN ALGORITMA SCANLINE Ina Agustina Jurusan Sistem Informasi, Fakultas Teknologi Komunikasi dan Informatika, Universitas Nasional Jl. Sawo Manila, Pejaten Pasar Minggu No.61, Jakarta
Sistem Multimedia. Image. Donny Reza, S.Kom
 Sistem Multimedia Image Donny Reza, S.Kom Image/Citra Image: representasi grafis dan visual dari suatu informasi yang dapat ditampilkan dalam layar komputer atau dicetak Berbagai bentuk image: Foto Gambar
Sistem Multimedia Image Donny Reza, S.Kom Image/Citra Image: representasi grafis dan visual dari suatu informasi yang dapat ditampilkan dalam layar komputer atau dicetak Berbagai bentuk image: Foto Gambar
Aplikasi AutoCAD. untuk Finishing. dan Rendering Desain
 Aplikasi AutoCAD untuk Finishing dan Rendering Desain Aplikasi AutoCAD untuk Finishing dan Rendering Desain Suparno Sastra M. PENERBIT PT ELEX MEDIA KOMPUTINDO Aplikasi AutoCAD untuk Finishing dan Rendering
Aplikasi AutoCAD untuk Finishing dan Rendering Desain Aplikasi AutoCAD untuk Finishing dan Rendering Desain Suparno Sastra M. PENERBIT PT ELEX MEDIA KOMPUTINDO Aplikasi AutoCAD untuk Finishing dan Rendering
PEMBUATAN MODUL AJAR GRAFIKA KOMPUTER BERBASIS WEB UNTUK OBYEK TIGA DIMENSI
 PEMBUATAN MODUL AJAR GRAFIKA KOMPUTER BERBASIS WEB UNTUK OBYEK TIGA DIMENSI Dwi Prihanto* Abstrak: Modul grafika komputer berbasis web adalah modul grafika yang dapat menggambarkan atau mensimulasikan
PEMBUATAN MODUL AJAR GRAFIKA KOMPUTER BERBASIS WEB UNTUK OBYEK TIGA DIMENSI Dwi Prihanto* Abstrak: Modul grafika komputer berbasis web adalah modul grafika yang dapat menggambarkan atau mensimulasikan
Grafika Komputer. Pendahuluan. Dr. Ahmad Sabri Universitas Gunadarma
 Grafika Komputer Pendahuluan Dr. Ahmad Sabri Universitas Gunadarma Ruang lingkup Perangkat Gambar Disiplin ilmu Grafik Komputer Gambar Grafik komputer adalah gambar yang dihasilkan oleh komputer. Natural
Grafika Komputer Pendahuluan Dr. Ahmad Sabri Universitas Gunadarma Ruang lingkup Perangkat Gambar Disiplin ilmu Grafik Komputer Gambar Grafik komputer adalah gambar yang dihasilkan oleh komputer. Natural
Grafik 3 Dimensi. Achmad Basuki Nana R Politeknik Elektronika Negeri Surabaya Surabaya 2009
 Grafik 3 Dimensi Achmad Basuki Nana R Politeknik Elektronika Negeri Surabaya Surabaya 29 Materi Sistem Koordinat 3D Definisi Obyek 3D Cara Menggambar Obyek 3D Konversi Vektor 3D menjadi Titik 2D Konversi
Grafik 3 Dimensi Achmad Basuki Nana R Politeknik Elektronika Negeri Surabaya Surabaya 29 Materi Sistem Koordinat 3D Definisi Obyek 3D Cara Menggambar Obyek 3D Konversi Vektor 3D menjadi Titik 2D Konversi
BAB 3 PERANCANGAN DAN PEMBUATAN. Engine akan dirancang agar memenuhi syarat maintainability, reusability dan
 13 BAB 3 PERANCANGAN DAN PEMBUATAN 3.1 Perancangan Engine Engine akan dirancang agar memenuhi syarat maintainability, reusability dan usability. Maintainability berarti kode program engine harus mudah
13 BAB 3 PERANCANGAN DAN PEMBUATAN 3.1 Perancangan Engine Engine akan dirancang agar memenuhi syarat maintainability, reusability dan usability. Maintainability berarti kode program engine harus mudah
ANALISA TEKNIK CUBE MAPPING BERBASIS OPENGL
 ANALISA TEKNIK CUBE MAPPING BERBASIS OPENGL Yohan Angjaya A11.2006.02722 Program Studi Ilmu Komputer Universitas Dian Nuswantoro Semarang ABSTRAK Tulisan ini berisi tentang analisa Cube Mapping berbasis
ANALISA TEKNIK CUBE MAPPING BERBASIS OPENGL Yohan Angjaya A11.2006.02722 Program Studi Ilmu Komputer Universitas Dian Nuswantoro Semarang ABSTRAK Tulisan ini berisi tentang analisa Cube Mapping berbasis
BAB III ANALISA DAN PERANCANGAN
 BAB III ANALISA DAN PERANCANGAN 3.1 Rancangan Awal Pemodelan Blender merupakan software grafis 3 Dimensi yang sangat baik. Tidak hanya menyediakan fasilitas untuk membuat object 3D dengan mudah tapi juga
BAB III ANALISA DAN PERANCANGAN 3.1 Rancangan Awal Pemodelan Blender merupakan software grafis 3 Dimensi yang sangat baik. Tidak hanya menyediakan fasilitas untuk membuat object 3D dengan mudah tapi juga
Modul 2 Primitive Objects
 Modul 2 Primitive Objects A. KOMPETENSI DASAR Memahami jenis-jenis primitive objects. Memahami dan dapat membuat objek primitif. Memahami penerapan Objek primitif menjadi bangun 2 dimensi dasar. Memahami
Modul 2 Primitive Objects A. KOMPETENSI DASAR Memahami jenis-jenis primitive objects. Memahami dan dapat membuat objek primitif. Memahami penerapan Objek primitif menjadi bangun 2 dimensi dasar. Memahami
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1 Grafika Komputer Grafika komputer atau dalam bahasa Inggris computer graphics dapat diartikan sebagai perangkat alat yang terdiri dari hardware dan software untuk membuat gambar,
BAB II LANDASAN TEORI 2.1 Grafika Komputer Grafika komputer atau dalam bahasa Inggris computer graphics dapat diartikan sebagai perangkat alat yang terdiri dari hardware dan software untuk membuat gambar,
Transformasi Geometri Sederhana. Farah Zakiyah Rahmanti 2014
 Transformasi Geometri Sederhana Farah Zakiyah Rahmanti 2014 Grafika Komputer TRANSFORMASI 2D Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut
Transformasi Geometri Sederhana Farah Zakiyah Rahmanti 2014 Grafika Komputer TRANSFORMASI 2D Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut
Grafika Komputer. Evangs Mailoa
 Grafika Komputer Evangs Mailoa Translasi Skala Rotasi/Putar Konsep yang terpenting dalam grafika komputer adalah Transformasi Affine. Pada dasarnya, transformasi ini adalah memindahkan objek tanpa merusak
Grafika Komputer Evangs Mailoa Translasi Skala Rotasi/Putar Konsep yang terpenting dalam grafika komputer adalah Transformasi Affine. Pada dasarnya, transformasi ini adalah memindahkan objek tanpa merusak
TRANFORMASI 2 DIMENSI
 TRANFORMASI 2 DIMENSI Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Struktur titik dan vektor Perubahan
TRANFORMASI 2 DIMENSI Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Struktur titik dan vektor Perubahan
Modul. Grafika Komputer. Disusun Oleh: Maya Amelia
 Modul Grafika Komputer Disusun Oleh: Maya Amelia Fakultas Ilmu Komputer Universitas Indo Global Mandiri 2012 DAFTAR ISI 1. PENGENALAN GRAFIKA KOMPUTER 1.1 Pengertian Grafika Komputer 1.2 Elemen-Elemen
Modul Grafika Komputer Disusun Oleh: Maya Amelia Fakultas Ilmu Komputer Universitas Indo Global Mandiri 2012 DAFTAR ISI 1. PENGENALAN GRAFIKA KOMPUTER 1.1 Pengertian Grafika Komputer 1.2 Elemen-Elemen
EC5130 Grafika Komputer dan Pemrograman GPU
 EC5130 Grafika Komputer dan Pemrograman GPU Suplemen Diktat Kuliah OpenGL Tutorial dengan GLUT: Fixed Pipeline Ary Setijadi Prihatmanto Sekolah Teknik Elektro & Informatika Institut Teknologi Bandung 2007
EC5130 Grafika Komputer dan Pemrograman GPU Suplemen Diktat Kuliah OpenGL Tutorial dengan GLUT: Fixed Pipeline Ary Setijadi Prihatmanto Sekolah Teknik Elektro & Informatika Institut Teknologi Bandung 2007
Perspektif mata burung : dilihat secara keseluruhan dari atas. Perspektif mata normal : dilihat secara keseluruhan dengan batas mata normal
 Pengertian Perspektif Menurut Leonardo da Vinci, perspektif adalah sesuatu yang alami yang menampilkan yang datar menjadi relative dan yang relative menjadi datar. Perspektif adalah suatu system matematikal
Pengertian Perspektif Menurut Leonardo da Vinci, perspektif adalah sesuatu yang alami yang menampilkan yang datar menjadi relative dan yang relative menjadi datar. Perspektif adalah suatu system matematikal
Animasi Objek 2 Dimensi GAMBAR BITMAP
 Animasi Objek 2 Dimensi `Animasi objek 2 Dimensi terdiri dari bitmap dan vektor.metode- metode ini menginterpretasikan input, menghitungnya dan menampilkannya pada output grafis seperti monitor.gambar
Animasi Objek 2 Dimensi `Animasi objek 2 Dimensi terdiri dari bitmap dan vektor.metode- metode ini menginterpretasikan input, menghitungnya dan menampilkannya pada output grafis seperti monitor.gambar
MENGGAMBAR PROYEKSI BENDA
 MENGGAMBAR PROYEKSI BENDA A. MENGGAMBAR PROYEKSI Proyeksi adalah ilmu yang mempelajari tentang cara menggambarkan penglihatan mata kita dari suatu benda tiga dimensi kedalam kertas gambar secara dua dimensi
MENGGAMBAR PROYEKSI BENDA A. MENGGAMBAR PROYEKSI Proyeksi adalah ilmu yang mempelajari tentang cara menggambarkan penglihatan mata kita dari suatu benda tiga dimensi kedalam kertas gambar secara dua dimensi
SISTEM PENJEJAK POSISI OBYEK BERBASIS UMPAN BALIK CITRA
 SISTEM PENJEJAK POSISI OBYEK BERBASIS UMPAN BALIK CITRA Syahrul 1, Andi Kurniawan 2 1,2 Jurusan Teknik Komputer, Fakultas Teknik dan Ilmu Komputer, Universitas Komputer Indonesia Jl. Dipati Ukur No.116,
SISTEM PENJEJAK POSISI OBYEK BERBASIS UMPAN BALIK CITRA Syahrul 1, Andi Kurniawan 2 1,2 Jurusan Teknik Komputer, Fakultas Teknik dan Ilmu Komputer, Universitas Komputer Indonesia Jl. Dipati Ukur No.116,
PEMBUATAN GENERATOR RULED SURFACE DAN ROTATIONAL OBJECT MENGGUNAKAN KURVA BEZIER DAN B-SPLINES
 PEMBUATAN GENERATOR RULED SURFACE DAN ROTATIONAL OBJECT MENGGUNAKAN KURVA BEZIER DAN B-SPLINES Liliana 1) Kartika Gunadi 2) Fricky Valiant 3) Jurusan Teknik Informatika, Fakultas Teknologi Industri, UK
PEMBUATAN GENERATOR RULED SURFACE DAN ROTATIONAL OBJECT MENGGUNAKAN KURVA BEZIER DAN B-SPLINES Liliana 1) Kartika Gunadi 2) Fricky Valiant 3) Jurusan Teknik Informatika, Fakultas Teknologi Industri, UK
Pendahuluan 9/7/2011. Overview. Deskripsi
 Pertemuan : I Dosen Pembina : Sriyani Violina Danang Junaedi Pendahuluan Overview Deskripsi Tujuan Instruksional Kaitan Materi Urutan Bahasan Penilaian Grade Referensi 2 Deskripsi Tujuan Instruksional
Pertemuan : I Dosen Pembina : Sriyani Violina Danang Junaedi Pendahuluan Overview Deskripsi Tujuan Instruksional Kaitan Materi Urutan Bahasan Penilaian Grade Referensi 2 Deskripsi Tujuan Instruksional
PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN
 PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN Rudy Adipranata 1, Liliana 2, Gunawan Iteh Fakultas Teknologi Industri, Jurusan Teknik Informatika, Universitas Kristen Petra Jl. Siwalankerto
PERANCANGAN DAN PEMBUATAN APLIKASI UNTUK MENDESAIN KARTU UCAPAN Rudy Adipranata 1, Liliana 2, Gunawan Iteh Fakultas Teknologi Industri, Jurusan Teknik Informatika, Universitas Kristen Petra Jl. Siwalankerto
Penerapan Transformasi Lanjar pada Proses Pengolahan Gambar
 Penerapan Transformasi Lanjar pada Proses Pengolahan Gambar Pratama Nugraha Damanik 13513001 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
Penerapan Transformasi Lanjar pada Proses Pengolahan Gambar Pratama Nugraha Damanik 13513001 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
RANCANG BANGUN APLIKASI PENGABURAN GAMBAR
 RANCANG BANGUN APLIKASI PENGABURAN GAMBAR Muhammad Sholeh 1, Avandi Badduring 2 1, 2 Teknik Informatika, Fakultas Teknologi Industri Institut Sains & Teknologi AKPRIND Yogyakarta Jl. Kalisahak 28 Komplek
RANCANG BANGUN APLIKASI PENGABURAN GAMBAR Muhammad Sholeh 1, Avandi Badduring 2 1, 2 Teknik Informatika, Fakultas Teknologi Industri Institut Sains & Teknologi AKPRIND Yogyakarta Jl. Kalisahak 28 Komplek
Pembuatan Simulasi Pergerakan Objek 3D (Tiga Dimensi) Menggunakan OpenGL
 1 Pembuatan Simulasi Pergerakan Objek 3D (Tiga Dimensi) Menggunakan OpenGL Deddy Suhardiman, S.T.G. Kaunang, Rizal Sengkey, Arthur M. Rumagit Jurusan Teknik Elektro-FT, UNSRAT, Manado-95115, Email: [email protected]
1 Pembuatan Simulasi Pergerakan Objek 3D (Tiga Dimensi) Menggunakan OpenGL Deddy Suhardiman, S.T.G. Kaunang, Rizal Sengkey, Arthur M. Rumagit Jurusan Teknik Elektro-FT, UNSRAT, Manado-95115, Email: [email protected]
Bab 4 SISTEM PROYEKSI 4.1. PENGERTIAN PROYEKSI GAMBAR PROYEKSI
 Bab 4 SISTEM PROYEKSI Materi : Pengertian proyeksi. Gambar proyeksi. Gambar pandangan tunggal. Gambar pandangan majemuk 4.1. PENGERTIAN PROYEKSI. Agar dapat menyatakan wujud suatu benda dalam bentuk gambar
Bab 4 SISTEM PROYEKSI Materi : Pengertian proyeksi. Gambar proyeksi. Gambar pandangan tunggal. Gambar pandangan majemuk 4.1. PENGERTIAN PROYEKSI. Agar dapat menyatakan wujud suatu benda dalam bentuk gambar
BAB I PENDAHULUAN 1.1 Latar Belakang
 BAB I PENDAHULUAN 1.1 Latar Belakang Objek tiga dimensi merupakan salah satu komponen multimedia yang memegang peranan sangat penting sebagai bentuk informasi visual. Objek tiga dimensi dibentuk oleh sekumpulan
BAB I PENDAHULUAN 1.1 Latar Belakang Objek tiga dimensi merupakan salah satu komponen multimedia yang memegang peranan sangat penting sebagai bentuk informasi visual. Objek tiga dimensi dibentuk oleh sekumpulan
Menggambar Garis dan Lingkaran dengan Algoritma Bresenham Teguh Susyanto 2)
 ISSN : 1693 1173 Menggambar Garis dan Lingkaran dengan Algoritma Bresenham Teguh Susyanto 2) Abstract In computer graphics, graphic depiction of the complex forms is actually composed of a group of primitive
ISSN : 1693 1173 Menggambar Garis dan Lingkaran dengan Algoritma Bresenham Teguh Susyanto 2) Abstract In computer graphics, graphic depiction of the complex forms is actually composed of a group of primitive
Computer Graphic. Output Primitif dan Algoritma Garis. Erwin Yudi Hidayat. Computer Graphics C Version 2 Ed by Donald Hearn
 Computer Graphic Output Primitif dan Algoritma Garis Erwin Yudi Hidayat [email protected] Computer Graphics C Version 2 Ed by Donald Hearn Addison Wesley is an imprint of [email protected] CG -
Computer Graphic Output Primitif dan Algoritma Garis Erwin Yudi Hidayat [email protected] Computer Graphics C Version 2 Ed by Donald Hearn Addison Wesley is an imprint of [email protected] CG -
OBYEK GRAFIK 2 DIMENSI
 OBYEK GRAFIK 2 DIMENSI Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Definisi Obyek Grafik 2-D PolyLine
OBYEK GRAFIK 2 DIMENSI Achmad Basuki Nana Ramadijanti Achmad Basuki, Nana Ramadijanti - Laboratorium Computer Vision Politeknik Elektronika Negeri Surabaya (PENS-ITS) Materi Definisi Obyek Grafik 2-D PolyLine
RANCANG BANGUN MODUL AJAR GRAFIKA KOMPUTER BERBASIS WEB
 RANCANG BANGUN MODUL AJAR GRAFIKA KOMPUTER BERBASIS WEB Juni Nurma Sari, Melvawati, dan Meilany Dewi Jurusan Teknik Komputer - Politeknik Caltex Riau Kampus Politeknik Caltex Riau, Jl. UmbanSari no 1,
RANCANG BANGUN MODUL AJAR GRAFIKA KOMPUTER BERBASIS WEB Juni Nurma Sari, Melvawati, dan Meilany Dewi Jurusan Teknik Komputer - Politeknik Caltex Riau Kampus Politeknik Caltex Riau, Jl. UmbanSari no 1,
PEMBUATAN PERANGKAT LUNAK UNTUK MEMVISUALISASIKAN BENDA TEMBUS PANDANG DENGAN METODE RAY TRACING
 PEMBUATAN PERANGKAT LUNAK UNTUK MEMVISUALISASIKAN BENDA TEMBUS PANDANG (Liliana) PEMBUATAN PERANGKAT LUNAK UNTUK MEMVISUALISASIKAN BENDA TEMBUS PANDANG DENGAN METODE RAY TRACING Liliana Fakultas Teknologi
PEMBUATAN PERANGKAT LUNAK UNTUK MEMVISUALISASIKAN BENDA TEMBUS PANDANG (Liliana) PEMBUATAN PERANGKAT LUNAK UNTUK MEMVISUALISASIKAN BENDA TEMBUS PANDANG DENGAN METODE RAY TRACING Liliana Fakultas Teknologi
Grafika Komputer Pertemuan Ke-13. Pada materi ini kita akan mempelajari proyeksi 3D. By: I Gusti Ngurah Suryantara, S.Kom., M.Kom
 Pada materi ini kita akan mempelajari proyeksi 3D. By: I Gusti Ngurah Suryantara, S.Kom., M.Kom BAB-12 PROEKSI 3D 12.1. PENDAHULUAN Proyeksi merupakan salah satu jenis transformasi, yaitu transforamsi
Pada materi ini kita akan mempelajari proyeksi 3D. By: I Gusti Ngurah Suryantara, S.Kom., M.Kom BAB-12 PROEKSI 3D 12.1. PENDAHULUAN Proyeksi merupakan salah satu jenis transformasi, yaitu transforamsi
Transformasi Geometri Sederhana
 Transformasi Geometri Sederhana Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut dengan manipulasi. Perubahan gambar dengan mengubah koordinat
Transformasi Geometri Sederhana Transformasi Dasar Pada Aplikasi Grafika diperlukan perubahan bentuk, ukuran dan posisi suatu gambar yang disebut dengan manipulasi. Perubahan gambar dengan mengubah koordinat
BAB III ANALISIS MASALAH DAN RANCANGAN PROGRAM
 BAB III ANALISIS MASALAH DAN RANCANGAN PROGRAM III.1. Analisis Masalah yang ingin penulis angkat dalam rancang bangun 3 dimensi simulasi pembuatan kapal selam berbasis multimedia adalah bagaimana merancang
BAB III ANALISIS MASALAH DAN RANCANGAN PROGRAM III.1. Analisis Masalah yang ingin penulis angkat dalam rancang bangun 3 dimensi simulasi pembuatan kapal selam berbasis multimedia adalah bagaimana merancang
4. VISUALISASI DAN GAMBAR SKET
 4. VISUALISASI DAN GAMBAR SKET Standar Kompetensi : Peserta didik dapat mengidentifikasi cara menggambar dengan cara: isometri, dimetri, trimetri, prespektif, gambar sket dengan menggunakan tangan, dan
4. VISUALISASI DAN GAMBAR SKET Standar Kompetensi : Peserta didik dapat mengidentifikasi cara menggambar dengan cara: isometri, dimetri, trimetri, prespektif, gambar sket dengan menggunakan tangan, dan
Gambar 1. Tampilan Layar Sebuah Program Animasi
 Menggambar Kotak (Ed. 2) 1/6 Lecture Notes Algoritma dan Pemrograman Menggambar Kotak Thompson Susabda Ngoen Di dalam penulisan program adakalanya kita perlu menggambar kotak (bingkai segi empat) di layar
Menggambar Kotak (Ed. 2) 1/6 Lecture Notes Algoritma dan Pemrograman Menggambar Kotak Thompson Susabda Ngoen Di dalam penulisan program adakalanya kita perlu menggambar kotak (bingkai segi empat) di layar
Modul 6 Interaksi dengan Keyboard dan Mouse
 Modul 6 Interaksi dengan Keyboard dan Mouse A. KOMPETENSI DASAR Memahami prinsip-prinsip deteksi input berupa interaksi dari keyboard. Membuat objek 2D yang dikendalikan dengan keyboard. Memahami prinsip-prinsip
Modul 6 Interaksi dengan Keyboard dan Mouse A. KOMPETENSI DASAR Memahami prinsip-prinsip deteksi input berupa interaksi dari keyboard. Membuat objek 2D yang dikendalikan dengan keyboard. Memahami prinsip-prinsip
IMPLEMENTASI OPEN GL32 UNTUK MEMANIPULASI GAMBAR SEGITIGA DAN SEGIEMPAT
 IMPLEMENTASI OPEN GL32 UNTUK MEMANIPULASI GAMBAR SEGITIGA DAN SEGIEMPAT Agung Slamet Riyadi, Universitas Gunadarma, Jl. Margonda Raya No. 100 Pondok Cina Depok Jawa Barat e-mail [email protected]
IMPLEMENTASI OPEN GL32 UNTUK MEMANIPULASI GAMBAR SEGITIGA DAN SEGIEMPAT Agung Slamet Riyadi, Universitas Gunadarma, Jl. Margonda Raya No. 100 Pondok Cina Depok Jawa Barat e-mail [email protected]
TIU: Mahasiswa mampu menghasilkan aplikasi Komputer Grafik sederhana. Pemrograman OpenGL API dasar 2 dimensi. Penggunaan aplikasi pengolah grafis 3D
 Matakuliah : Komputer Grafik Dosen : Yonathan Ferry Hendrawan ThAkad : 2013-2014 Semester : Genap (empat) Prodi : S1 Teknik Informatika KONTRAK KULIAH 1. Manfaat Matakuliah Dengan mengambil mata kuliah
Matakuliah : Komputer Grafik Dosen : Yonathan Ferry Hendrawan ThAkad : 2013-2014 Semester : Genap (empat) Prodi : S1 Teknik Informatika KONTRAK KULIAH 1. Manfaat Matakuliah Dengan mengambil mata kuliah
PROSES PEMBUATAN MODELING ARSITEKTUR 1. PENGATURAN BACKGROUND IMAGE
 PROSES PEMBUATAN MODELING ARSITEKTUR 1. PENGATURAN BACKGROUND IMAGE Untuk memunculkan tab Transform yang ada di sebelah kanan klik N pada keyboard.lalu scroll ke bawah dan cari option background image
PROSES PEMBUATAN MODELING ARSITEKTUR 1. PENGATURAN BACKGROUND IMAGE Untuk memunculkan tab Transform yang ada di sebelah kanan klik N pada keyboard.lalu scroll ke bawah dan cari option background image
