COMBINATORIAL GAME THEORY SERTA ANALISIS MENGENAI APLIKASINYA
|
|
|
- Liani Budiaman
- 7 tahun lalu
- Tontonan:
Transkripsi
1 Abstrak COMBINATORIAL GAME THEORY SERTA ANALISIS MENGENAI APLIKASINYA Arinta Primandini Auza NIM : Program Studi Teknik Informatika Sekolah Teknik Informatika dan Elektro Institut Teknologi Bandung Jl. Ganesha 10, Bandung if15021@students.if.itb.ac.id Makalah ini membahas mengenai salah satu teori dalam kombinatrika yaitu Combinatorial Game Theory beserta beberapa aplikasinya dalam strategi game. Teori ini merupakan teori yang mempelajari combinatorial game, yaitu permainan dengan dua orang pemain, dan juga strategi dalam permainan tersebut. Terdapat dua referensi utama mengenai combinatorial game. Salah satunya merupakan buku riset, On Numbers and Games oleh J.H. Conway, Academic Press, Buku ini memperkenalkan banyak dasar dari subjek. Sedangkan referensi lainnya adalah buku berjudul Winning Ways for your mathematical plays oleh Berlekamp, Conway and Guy, Akademik Press, Terdapat banyak sekali permainan yang menggunakan teori ini namun yang akan dibahas dalam makalah ini adalah Domineering dan Nim-game. Tiap permainan memiliki strategi yang berbeda untuk memenangkan permainan tersebut. Dalam Nim-game kita dapat mengetahui strategi untuk memenangkan permainan serta pemain mana yang memiliki strategi strategi tersebut. Variasi dari Nim-game sangatlah banyak dan beberapa akan dibahas pada makalah ini. 1. Pendahuluan Combinatorial Game Theory adalah salah satu teori matematika yang hanya mempelajari permainan dengan 2 pemain yang memiliki posisi dimana setiap pemain bermain bergantian untuk memperoleh kemenangan. Teori ini tidak mempelajari permainan tentang kesempatan seperti poker, tetapi mempelajari permainan dimana kedua pemain memiliki posisi yang umum dan juga himpunan langkah yang umum. Dalam aplikasinya, teori ini digunakan untuk menganalisis strategi dari game yang memiliki perfect information, yaitu hanya satu orang pemain yang melangkah tiap waktu dan masing-masing pemain mengetahui setiap tindakan dari pemain yang bergerak sebelum pemain tersebut pada setiap titik. Dengan teori ini kita dapat mengetahui langkah yang optimum dari kedua pemain hingga permainan selesai. Dalam teori matematika terdapat teori yang disebut game theory. Perlu diingat bahwa kedua teori ini berbeda. Game Theory digunakan pada teori ekonomi dan saat ini game theory mulai banyak digunakan di bidang akademik lainnya seperti biologi, psikologi, sosiologi, filosofi, dan lain-lain. Permainan yang dipelajari dalam game theory sebagian besar merupakan game yang memiliki imperfect information, sehingga tidak semua pemain mengetahui tindakan dari pemain lainnya. Selain itu pemain bermain secara bersama-sama, tidak bergiliran seperti pada combinatorial game theory. Hal inilah yang membedakan antara game theory dan combinatorial game theory. Permainan yang merupakan aplikasi dari Combinatorial Game Theory, yang disebut
2 juga sebagai Combinatorial game, memiliki persyaratan sebagai berikut : 1. Permainan memiliki tepat 2 pemain. 2. Pada umumnya pemain yang melakukan langkah terakhir menang ( beberapa permainan yang disebut misere form, dimana pemain yang melakukan langkah terakhir kalah). 3. Pemain bermain secara bergantian 4. Permainan memiliki akhir, tidak berlangsung terus menerus. 5. Dalam permainan tidak ada seri, hanya ada menang dan kalah. 6. Tidak ada informasi yang disembunyikan dari pemain (misalnya seperti pada poker). 7. Permainan tidak berdasarkan pada keberuntungan. dan memungkinkan untuk menempatkan X atau O pada setiap kotak, awal dari permainan Tic-Tac-Toe dapat direpresentasikan sebagai yang merupakan semua kemungkinan bagi pemain pertama untuk menempatkan X pada salah satu kotak. 2. Gambaran Singkat Gambar 2.2 Gambar 2.1 Mengenai gambaran singkat tentang teori ini, kita gunakan sebuah permainan yang disebut Tic-Tac-Toe. Masing-masing pemain kita sebut Left dan Right. Untuk memudahkan analisis, kita gunakan notasi {L R}. L merupakan langkah yang bisa diambil oleh pemain Left, dan R merupakan langkah yang dapat digunakan pemain Right. Jika kita melabeli masing-masing dari 9 kotak di atas dengan UL untuk Upper Left(kiri atas), CC untuk Cener Center (tengah tengah), LR untuk Lower Right (kanan bawah), dan seterusnya, Sementara itu saat salah satu pemain mengisi salah satu kotak, misalkan pemain left, pemain lainnya (right), yang akan mengisi kotak setelah pemain sebelumnya selesai, memiliki pilihan untuk mengisi kotak lainnya, selain yang diisi oleh pemain left. Maka misalkan untuk game Tic-Tac-Toe yang dilabeli XUL seperti pada gambar 2.2 dapat dinotasikan sebagai Dengan melanjutkan permainan, kemungkinan permainan akan berakhir seperti berikut : XUL_OUR_XCC_OCR_XLC_OLL_XCL_OUC = {{ } { }}
3 Sebuah struktur disebut collection of games jika dan dimana is the power set of, Gambar 2.3 Permainan di atas menggambarkan skenario dimana hanya ada satu langkah tersisa untuk setiap pemain, yaitu pada kotak LR pada bagian kanan bawah, dan jika salah satu pemain mengambil langkah tersebut, pemain tersebut akan memenangkan permainan. Lambang { } pada setiap list dari langkah pemain disebut zero game, yang sebenarnya dapat disingkat dengan lambang 0. Dalam zero game, tidak satupun dari pemain memiliki langkah yang valid, sehingga siapapun yang mengambil langkah saat zero game muncul akan secara otomatis kalah. Selain itu, permainan yang dilabeli "XUL_OUR_XCC_OCR_XLC_OLL_XCL_O UC" di atas juga mempunyai notasi yang jauh lebih sederhana yang disebut star game, yang juga dapat disingkat menjadi *. Dalam star game, satu-satunya langkah yang valid memimpin pemain menuju zero games, yang berarti siapapun yang memiliki giliran saat star game muncul akan otomatis memenangkan permainan. Tipe permainan lainnya, tidak terdapat pada permainan Tic-Tac-Toe, adalah loopy game. Pada loopy game, langkah yang valid yaitu permainan yang kemudian dapat menuju ke permainan awal. game. Permainan yang tidak memiliki langkah sepeti itu disebut nonloopy. 3. Definisi Formal dan Karena G ditetapkan secara unik oleh L(G) dan R(G), G sering kali dinotasikan sebagai. Elemen dari disebut games dan berdasarkan konvensi dinotasikan oleh huruf Latin G,H,K,... Pemain yang bermain dalam sebuah permainan yang hanya memiliki 2 orang pemain dinamakan Left and Right (kadangkadang dikenal sebagai blue and Red), dan serta berarti bahwa pemain Left (dan juga Right) diperbolehkan melangkah dari permainan G ke permainan H. Definisikan binary relation, (untuk successor) antara permainan oleh. Transitive closure dari dinotasikan oleh, untuk posisi. H adalah posisi dari G, dinotasikan, jika memungkinkan untuk mencapai H dari G lewat urutan langkah yang tidak kosong oleh Left dan Right.
4 disebut loopy jika ; selain itu merupakan nonloopy. Koleksi nonloopy dikatakan well-founded saat tidak ada deret tak hingga dengan. Jika terdapat sebuah elemen dari, dengan, maka kita menyebutnya sebagai zero element. Zero element, jika ada, merupakan elemen yang unik. Jika merupakan koleksi game dan maka permainan G 0 dapat dimainkan sebagai berikut : Pemain pertama, katakan Left, memilih sebuah elemen (jika ada). Kemudian Right memilih sebuah elemen. Setelah itu Left memilih sebuah elemen dan begitu seterusnya. Jika seorang pemain tidak dapat bergerak (yaitut saat himpunan atau kosong) maka, sesuai definisi, pemain tersebut telah kalah dalam permainan. Permainan G 0 dapat dimainkan dengan Right sebagai pemain pertama dengan menukar peran. 4. Beberapa contoh aplikasi dan Prinsip dari Combinatorial Game Theory dapat diaplikasikan pada permainan seperti catur, checkers, Go, Hex, dan Connect6, tetapi permainan-permainan tersebut terlalu rumit untuk diselesaikan dengan analisis komplit (walaupun teori ini telah mendapatkan kesuksesan dalam menganalisis akhir dari permainan Go). Dalam teks pendahuluan buku berjudul Winning Ways (karya E. R. Berlekamp, J. H. Conway, and R. K. Guy) diperkenalkan banyak permainan yang menggunakan teori ini. Game yang akan dibahas lebih lanjut pada makalah ini yaitu Domineering dan Nimgame. 4.1 Domineering Domineering (juga disebut Stop-Gate) adalah sebuah permainan matematika yang dimainkan pada selembar kertas graf, yaitu kertas yang dicetak dengan garis-garis yang membentuk grid, dengan desain yang ditentukan pemain. Sebagai contoh, permainan ini dapat dimainkan pada bujursangkar berukuran 6x6, checkerboard (papan berukuran 8 8 dan memiliki 64 persegi kemudian diwarnai warna terang dan gelap secara bergantian, biasanya merah dan hitam), polygon tak beraturan, atau kombinasi lainnya. Dua orang pemain dalam permainan ini memiliki sekumpulan domino yang akan ditempatkan pada grid secara bergiliran. Salah satu pemain meletakkan dominonya secara vertical, sedangkan pemain lainnya meletakkan domino secara horizontal. Seperti kebanyakan permainan dalam combinatorial game theory, pemain pertama yang tidak bisa melangkah akan kalah Beberapa contoh dasar a. Grid berukuran 1x1 Dengan mengesampingkan permainan dengan grid kosong, permainan paling sederhana adalah dengan menggunakan persegi berukuran 1x1. Dalam permainan ini jelas bahwa tak satupun dari pemain dapat melangkah. Oleh karena itu pemain kedua akan memenangkah permainan. Permainan dalam kondisi seperti ini disebut zero game. b. Baris Horizontal
5 Permainan ini dilakukan pada grid berukuran 2x1. Ada sebuah konvensi yang menyatakan sebuah permainan merupakan positif jika pemain Left yang memainkan pertandingan dan negative jika Right yang menang. Dalam kasus permainan baris horizontal ini, pemain Left tidak bisa melangkah, sementara Right dapat selalu meletakkan dominonya untuk menutupi semua grid, yang berarti merupakan zero game. Dengan demikian, permainan ini dapat dinotasikan dalam notasi surreal number sebagai { 0} = 1. Hal ini berlaku untuk sebanyak genap persegi dan juga ganjil. Misalkan untuk grid dengan ukuran 3x1 berikut. Permainan dengan grid berukuran 2x2 di atas adalah permainan yang lebih komplek. Jika Left yang melangkah pertama kali, maka akan menyisakan grid berukuran 1 2, yang berarti +1. Jika Right yang mulai pertama kali, ia dapat melangkah ke 1. Karena itu notasi surreal number dari game ini adalah {1 1}. Namun hal ini bukan merupakan surreal number, karena 1 > 1. Notasi untuk permainan ini adalah ±1, dan merupkan hot game, karena setiap pemain ingin melangkah di sini. Dalam kasus grid 2x2 ini maka pemain yang memiliki giliran pertama kali akan memenangkah permainan. Permainan ini juga merupakan { 0} = 1, karena sisa 1 persegi pada akhir permainan tidak dapat dimainkan. Dalam permainan dengan grid berukuran 4x1 di atas, Right dapat meletakkan dominonya pada 2 kotak paling kiri dan menyisakan kotak paling kanan juga menyisakan 1. Dia juga dapat meletakkan dominonya pada 2 kotak di tengah dan menyisakan 2 grid berukuran 1x1 yang berarti 0+0 = 0. Sehingga permainan ini dapat diekspresikan sebagai { 0, 1}. Dalam kasus ini dihitung sebagai -2. Grid di atas berukuran 2 3, yang merupakan grid yang lebih kompleks, tetapi kita tetap dapat menganalisisnya melalui variasi langkah yang untuk kedua pemain. Left dapat mengambil kolom kiri (atau secara ekivalen, kolom kanan), dan melangkah ke ±1, tetapi akan lebih baik jika ia meletakkan dominonya di tengah dan menyisakan 2 game yang terpisah, masing-masing bernilai +1. Karena itu langkah terbaik bagi Left adalah +2. Sedangkan Right memiliki 4 langkah yang berbeda, namun semuanya meninggalkan bentuk sebagai berikut : c. Kolom vertikal Kolom vertical juga dihitung dengan cara yang sama. Jika terdapat sebuah baris dengan 2n atau 2n+1 kotak, maka akan dihitung sebagai n. Sedangkan kolom yang berukuran seperti it akan dihitung sebagai +n. d. Grid yang lebih kompleks Permainan semacam ini bukan merupakan hot game (juga disebut cold game). Left dapat melangkah ke 1, Right dapat melangkah ke 0 or +1. Karena itu permainan ini adalah { 1 0,1} = { 1 0} = ½. Dalam permainan ini pemain pertama juga akan selalu dapat memenangkan permainan. 4.2 Nim- game Sejarah Nim
6 "Nim" adalah permainan strategi matematika yang dilakukan oleh 2 orang pemain dimana tiap pemain secara bergiliran memindahkan objek dari tumpukan yang berbeda. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap. Variasai dari Nim telah dimainkan sejak zaman dahulu. Permainan ini dikatakan berasal dari Cina (mirip dengan permainan Cina yang bernama Tsyanshidzi atau mengambil batu ), tetapi asal usulnya masih belum dapat dipastikan. Di Eropa permainan serupa Nim dimulai sejak awal abad ke-16. Teori mengenai permainan ini dikembangkan oleh Charles L Bouton dari Harvard University pada tahun Tetapi asal usul dari nama permainan ini masih belum dapat dijelaskan. Kemungkinan nama permainan ini dimabil dari diambil dari bahasa Jerman nimm! yang berarti ambil!, atau dari bahasa Inggris. Jika kita perhatikan kata NIM jika diputar 180 akan menghasilkan kata WIN. Nim biasanya dimainkan sebagai misere game, dimana pemain yang mengambil objek terakhir kalah. Nim juga dapat dimainkan secara normal, yaitu pemain yang mengambil objek terakhir menang. Hal ini dikatakan normal karena mengikuti konvensi, sedangkan Nim biasanya tidak mengikuti konvensi tersebut. Permainan normal Nim merupakan hal yang fundamental bagi Teorema Sprague Gundy, yang intinya mengatakan bahwa dalam permainan yang normal setiap impartial game, yaitu sebuah permainan dimana yang membedakan antara pemain 1 dan pemain 2 adalah bahwa pemain 1 mendapat giliran pertama, ekivalen dengan setumpuk Nim yang menghasilkan akibat yang sama dengan pada saat dimainkan dengan parallel dengan permainan normal impartial game lainnya Teori matematika Nim telah secara matematika dipecahkan untuk berbagai banyaknya tumpukan dan objek,. Telah ada sebuah metode untuk menentukan pemain mana yang akan menang dan strategi apa yang bisa digunakan untuk memenangkan permainan tersebut. Kunci dari teori permainan adalah binary digital sum dari ukuran tumpukan, yaitu jumlah dalam biner dengan mengabaikan semua kelebihan dari penjumlahan tiap digitnya. Operasi ini juga dikenal sebagai exclusive or (xor) atau penjumlahan vector dibagi GF(2). Dalam combinatorial game theory operasi ini biasanya dinamakan nimsum. Nim-sum dari x dan y ditulis sebagai x y untuk membedakan dengan penjumlahan biasa, x + y. Sebagai contoh perhitungan dengan tumpukan berukuran 3, 4, dan 5 adalah sebagai berikut : Biner Desimal Keterangan Tumpukan A Tumpukan B Tumpukan C Nim-Sum = = 2 Prosedur yang ekivalen dengan prosedur di atas, yang biasanya lebih mudah dilakukan, adalah untuk mengekspresikan ukuran tumpukan sebagai jumlah dari bilangan pangkat 2 yang berbeda, kemudian hapus semua pasangan bilangan yang sama dan jumlahkan semua yang tersisa : 3 = = Tumpukan A 4 = 4 = 4 Tumpukan B 5 = = Tumpukan C = 2 Sisa setelah menghapus 4 dan 1 Dalam permainan yang normal, strategi untuk memenangkan permainan adalah dengan menyelesaikan setiap langkah dengan Nimsum 0, yang biasanya selalu mungkin jika Nim-sum tidak nol sebelum langkah. Jika Nim-sum adalah 0, maka pemain berikutnya
7 akan kalah jika pemain lainnya tidak melakukan kesalahan. Untuk mengetahui langkah mana yang harus diambil, misalkan X adalah Nim-sum dari semua ukuran tumpukan. Ambil Nim-sum dari setiap ukuran tumpukan dengan X, dan cari tumpukan yang ukurannya berkurang. Strategi untuk menang adalah bermain dengan tumpukan tersebut dan mengurangi tumpukannya hingga sama dengan Nim-sum dari ukuran sebenarnya dengan X. Dalam contoh di atas, ambil Nimsum dari semua ukuran yaitu X = = 2. Nim-sum dari tumpukan A=3, B=4, dan C=5 dengan X=2 adalah A X = 3 2 = 1 B X = 4 2 = 6 C X = 5 2 = 7 Satu-satunya tumpukan yang berkurang adalah tumpukan A, sehingga langkah untuk menang adalah dengan mengurangi ukuran tumpukan A hingga 1, yaitu dengan memindahkan 2 objek. Sebagai contoh kasus khusus, jika hanya terdapat dua tumpukan yang tersisa, strategi untuk menang adalah dengan mengurangi banyaknya objek pada tumpukan yang lebih besar untuk membuaat kedua tumpukan berjumlah sama. Setelah itu, tidak masalah langkah apa yang lawan lakukan, kita dapat mengambil langkah yang sama pada tumpukan lainnya, sehingga pada akhirnya kita akan dapat mengambil objek terakhir. Jika dimainkan sebagai permainan misère, strategi Nim berbeda saat permainan normal meninggalkan tumpukan dengan ukuran 2 atau lebih besar. Dalam hal ini, langkah yang tepat adalah dengan meninggalkan sebanyak ganjil tumpukan dengan ukuran 1 (dalam permainan normal, langkah yang tepat adalah dengan meninggalkan sebanyak genap tumpukan berukuran 1). Dalam permainan misère dengan ukuran tumpukan 3, 4 and 5, strateginya adalah sebagai berikut : Misalkan kedua pemain tersebuat adalah X dan Y. A B C Nim-sum Keterangan =2 10 X mengambil 2 dari A, sehingga Nim-sum = 000, sehingga A akan menang =0 10 Y mengambil sebanyak 2 dari C =6 10 X mengambil sebanyak 2 dari B =0 10 Y mengambil 1 dari C =1 10 X mengambil 1 dari A =0 10 Y mengambil 1 dari C =3 10 Strategi permainan normal adalah X mengambil 1 dari B, meninggalkan sebanyak genap(2) tumpukan berukuran 1. Untuk misère, X mengambil semua objek di B, meninggalkan sebanyak ganjil(1) tumpukan berukuran =1 10 Y mengambil 1 dari C, dan kalah Bukti dari winning formula Strategi yang disebutkan di atas didemonstrasikan oleh C. Bouton. Teorema. Dalam sebuah permainan Nim normal, pemain pertama memiliki strategi untuk menang (winning strategy) jika dan hanya jika Nim-sum dari ukuran tumpukan adalah tidak nol. Sebaliknya, pemain kedua yang memiliki strategi untuk menang. Bukti: Perhatikan bahwa Nim-sum ( ) mematuhi hukum asosiasi dan komutatif dari operasi (+), dan juga memenuhi property x x = 0. Misalkan x 1,..., x n adalah ukuran dari tumpukan sebelum melakukan langkah apapun, dan y 1,..., y n merupakan ukuran setelah melangkah. Misalkan s = x 1... x n dan t = y 1... y n. Jika objek diambil pada tumpukan k, maka x i = y i untuk setiap i k, dan x k > y k. Dengan property dari yang disebutkan di atas, maka
8 t = 0 t = s s t = s (x 1... x n ) (y 1... y n ) = s (x 1 y 1 )... (x n y n ) = s (x k y k ) = s x k y k (*) t = s x k y k. Teorema ini kemudian dibuktikan dengan melalukan induksi pada panjang dari permainan dari 2 lemma berikut. Lemma 1. Jika s = 0, maka t 0 apapun langkah yang telah diambil. Bukti: Jika tidak terdapat langkah yang mungkin, maka lemma tersebut benar (dan pemain pertama kalah dalam permainan normal). Sebaliknya, langkah apapun yang diambil pada tumpukan k akan menghasilkan t = x k y k dari (*), yang tidak nol karena x k y k. Lemma 2. Jika s 0, adalah mungkin untuk mengambil langkah sehingga t = 0. Bukti: Misalkan d adalah posisi paling kiri dari bit tidak nol dalam representasi biner dari s, dan pilih k sedemikian sehingga bit ke-d dari x k juga tidak nol. Kemudian misalkan y k = s x k. Klaim bahwa y k < x k. Semua bit ke kiri dari d semua sama pada x k dan y k, bit d berkurang dari 1 menjadi 0 (dengan mengurangi nilainya dengan 2 k ), dan setiap perubahan dari digit yang tersisa akan berjumlah maksimal 2 k 1. Pemain pertama kemudian dapat melakukan langkah dengan mengambil x k y k objek dari tumpukan k, maka t = s x k y k = s x k (s x k ) = 0. Strategi dari permainan normal adalah dengan mengurangi ukurannya hingga 0 atau 1, meninggalkan sebanyak genap tumpukan dengan ukuran 1, dan strategi dari permainan misère adalah sebaliknya Variasi dari nim-game a. Normal Kayles Permainan ini diperkenalkan oleh H.E.Dudeney( ) dan dikenal sebagai "Kayles". Permainan : Sejumlah pin disusun pada baris yang terpisah. Langkah yang legal yaitu dengan menjatuhkan satu pin atau dua pin bersebelahan dari baris yang sama. Hal ini akan memecah baris menjadi 2 baris yang lebih kecil. Siapapun yang menjatuhkan pin terakhir akan memenangkan permainan. Permasalahan : Bagaimana memenangkan permainan ini? strategi untuk Analisis : Permainan yang dimainkan adalah dalam bentuk normal Nim. Dalam normal Nim, komponen adalah baris dan peraturan dari Nim menyatakan bahwa langkah yang dibolehkan yaitu dengan mengeliminasi komponen atau memindahkannya dengan yang lebih kecil. Dalam permainan Kayles ini, komponen juga berupa baris dan terdapat kesamaan prinsip mengenai perpindahan komponen. Kenyataan bahwa sebuah komponen dapat digantikan dengan beberapa (dua dalam kasus Kayles) tidak menjadi masalah karena beberapa baris dari Nim ekivalen dengan satu baris(tumpukan) Nim dengan value yang sama. Dengan demikian kita dapat menunjukkan bahwa sebuah baris- Kayles dengan panjang n ekivalen dengan beberapa baris-nim yang panjangnya dapat ditentukan. Mari kita tinjau baris-kayles yang pendek berikut : Dari sebuah baris-kayles dengan panjang 0, 1, atau 2, kita mempunyai langkah yang sama seperti pada sebuah baris-nim dengan panjang yang sama. Baris-baris pendek ini ekivalen untuk kedua permainan Sebuah baris-kayles dengan panjang 3 juga ekivalen dengan sebuah baris-nim dengan panjang 3. Walaupun kita tidak dapat menjatuhkan ketiga pin dari baris- Kayles tersebut, kita diperbolehkan untuk menjatuhkan pin yang berada di tengah dan
9 meninggalkan dua baris dengan satu pin yang terpisah. Hal ini ekivalen dengan baris-nim kosong. Berbeda halnya dengan baris-kayles berukuran 4. Dari baris-kayles berukuran 4, langkah yang diperbolehkan akan meninggalkan salah satu dari himpunan ukuran baris-kayles berikut : {3}, {2}, {1,2}, {1,1}, dengan Nim-value berturut-turut adalah 3, 2, 3 and 0. Bilangan 1 adalah bilangan bulat non negative terkecil yang tidak terdapat dalam list di atas. Karena itu, baris-kayles yang berukuran 4 ekivalen dengan baris-nim dengan ukuran 1. Secara umum, kita dapat melihat bahwa Nimvalue dari sebuah baris-kayles adalah nilai terkecil yang tidak diperoleh dari Nim-sum dari Nim-value dari dua baris-kayles yang diperoleh dari langkah yang diambil. Hal ini mempermudah perhitungan pada table berikut: Tabel 4.1 Nim ekivalen dengan Kayles untuk baris dengan panjang 20 Jika kita meneruskan table di atas, value akan berulang dengan periode 12. (hanya 14 kasus khusus yang tidak mengikuti pola periodic umum yaitu untuk baris-kayles berukuran 0, 3, 6, 9, 11, 15, 18, 21, 22, 28, 34, 39, 57, dan 70). b. Permainan Wythoff Permainan Wythoff dulu dikenal di Cina sebagai tsyan-shidzi. Kemudian diperkenalkan kembali oleh Willem Abraham Wythoff ( ), yang mempublikasikan analisisnya mengenai permainan ini pada tahun Setengah abad kemudian (sekitar 1960) salah satu matematikawan Rufus P. Isaacs dari Johns Hopkins University memberikan deskripsi lain dari permainan yang sama dalam langkah queen dalam catur yang hanya memperbolehkan langkah ke selatan dan atau ke barat. Permainan : Permainan ini dimainkan dengan dua tumpukan objek berdasarkan aturan permainan normal. Langkah yang diperbolehkan yaitu dengan memindahkan objek dari satu tumpukan atau banyak objek yang sama dari kedua tumpukan. Permasalahan : Bagaimana strategi untuk memenangkan permainan ini? Analisis : Saat seseorang bermain suatu permainan, tentunya ia ingin melangkah ke posisi yang aman. Berikut adalah table mengenai posisi aman atau zero position dari permainan Wythoff Tabel 4.2 Zero position dalam permainan Wythoff
10 Posisi aman atau zero position dari permainan ini adalah {0,0}, {1,2}, {3,5}, {4,7}, {6,10}, {8,13},... {u n,v n }, dimana u n dan v n adalah pasamgam zero ke-n dari deret yang dikenal sebagai lower dan upper dalam deret Wythoff, yang mempunyai ekspresi yang sangat sederhana : u n = n φ dan v n = n φ 2 = n + u n, dimana x merupakan bilangan bulat terbesar yang lebih kecil atau sama dengan x (dikenal pula sebagai floor dari x) dan φ adalah Golden Ratio (1+ 5)/2 = (sehingga φ 2 = 1 + φ ). Deret dimana urutan ke-n adalah n θ, untuk sebarang irrational number θ >0, dikenal sebagai Beatty sequence yang diasosiasikan dengan θ. Jika 1/α+1/β = 1, Beatty sequences yang diasosiasikan dengan α and β dikatakan complementary dan mempunyai property setiap bilangan bulat positif muncul sekali pada salah satu deret tapi tidak keduanya. c. Permainan Bachet Permainan : Terdapat n buah batu pada sebuah meja. Langkah yang diperbolehkan adalah memindahkan paling sedikit satu buah batu namun tidak lebih dari 3 buah batu. Pemenang adalah pemain yang mengambil batu terakhir. Permasalahan : Tentukan posisi kekalahan (losing position). Analisis : Himpunan dari L (losing position) adalah semua kelipatan dari k+1. Misalkan kedua pemain yang bermain adalah X dan Y. Tentu saja jika n bukan merupakan kelipatan dari k+1. salah satu pemain, katakan X, selalu dapat menuju kelipatan dari k+1. Sedangkan Y tidak dapat menuju kelipatan dari k+1, karena dia hanya bisa mengambil paling banyak k buah batu. Maka dia akan menuju ke suatu bilangan yang bukan merupakan kelipatan dari k+1. Dengan demikian X akan bisa mengambil sejumlah batu sehingga jumlah batu yang diambil X ditambah jumlah batu yang diambil Y sama dengan k+1. Pada akhirnya X akan mencapai 0 yang juga merupakan kelipatan dari k+1. d. Permainan kecil lainnya Beberapa permainan Nim dapat diselesaikan dengan menggunakan strategi yang sederhana. Mari kita tinjau beberapa permainan berikut. Permainan 1 : Terdapat sebuah batu di paling ujung papan catur berukuran n x n. A dan B secara bergantian memindahkan batu tersebut ke segala arah (atas, bawah, kiri, kanan. Mereka tidak boleh memindahkan batu ke kotak yang telah mereka kunjungi. Pemain yang kalah adalah yang tidak dapat melangkah. Permasalahan : a.. Siapa yang menang jika n genap? b. Bagaimana jika n ganjil? c. Siapa yang menang jika batu pertama kali diletakkan di sebelah persegi paling ujung? Analisis : a. Untuk n genap, kita selalu dapat mempartisi papan menjadi domino berukuran 2x1. A sebagai pemain pertama akan selalu bisa memindahkan batu. Jika batu ada pada salah satu persegi pada domino, dia akan melangkah pada sisi domino yang lainnya. Maka A akan menjadi pemain yang terakhir melangkah yang berarti A memenangkan permainan. b. Untuk n ganjil, kita dapat mempartisi papan dengan domino berukuran 2x1 kecuali sudut papan dimana batu pertama kali diletakkan. Dengan demikian B akan menang. c. Dalam kasus ini, A akan selalu menang. Untuk n genap, strateginya sama dengan yang disebutkan di (a). Sedangkan untuk n ganjil, kita mempartisi papan menjadi domino kecuali 1 kotak pada sudut papan. Lalu warnai papan secara bergantian(hitam, putih). Tanpa mengurangi keumuman, misalkan batu pertama kali diletakkan pada kotak yang berwarna hitam. Maka A akan melangkah ke kotak yang berwarna putih dan B ke kotak yang berwarna hitam. Sedangkan sudut dari
11 papan tersebut semuanya berwarna putih. Dengan demikian B tidak akan pernah mencapai sudut papan. Oleh karena itu, A memiliki strategi untuk menang dengan memindahkan batu ke kotak kedua dari domino. Permainan 2 : 98 titik diberikan pada sebuah lingkaran. Maria dan Jose secara bergantian menggambar garis di antara 2 dari titik-titik tersebut. Permainan berakhir saat setiap titik telah digunakan sebagai titik akhir paling sedikit satu akhir. Pemenang adalah yang menggambar garis terakhir. Permasalahan : Jika Jose menggambar pertama kali, siapa yang mempunyai strategi untuk memenangkan permainan? Analisis : Jose memiliki strategi untuk menang. Labeli titik-titik tersebut berdasarkan urutan digunakan sebagai titik akhir dari menggambar garis untuk pertama kali. A 1 merupakan titik pertama digunakan dan A 98 yang terakhir digunakan. Klaim bahwa pemain P 1 yang menggunakan A 96 pertama kali akan kalah. Jika P 1 menghubungkan A 96 A i, maka i 97. Sehingga pemain lainnya P 1 dapat menghubungkan A 97 A 98 dan memenangkan permainan. Karena terdapat C(95, 2) = 4465 (sebanyak ganjil) garis yang menghubungkan A 1,, A 95, Jose dapat memaksa Maria untuk menjadi yang pertama kali menggunakan A 96. Permainan 3 : Dua kumpulan korek api diletakkan di atas meja. Salah satunya terdiri dari korek api, lainnya terdiri dari korek api. Dua orang pemain secara bergantian memindahkan korek api dari kumpulan tersebut. Dalam setiap giliran, seorang pemain boleh mengambil k buah korek api dari satu kumpulan dan m dari kumpulan lainnya selama k 2 m Pemain yang mengambil korek api terakhir kalah. Permasalahan : Pemain mana yang akan menang secara optimal Analisis : Kita sebut posisi (a, b) dengan a korek api dari salah satu kumpulan dan b di kumpulan lainnya sebagai winning jika pemain yang memulai gilirannya dari posisi tersebut dapat memenangkan permainan. Sebaliknya kita katakana losing. Klaim bahwa pemain pertama menang. Anggap (2 100, ) merupakan posisi losing. Maka bagaimanapun pemain pertama melangkah, dia akan menginggalkan posisi winning; secara spesifik, ( i, i) adalah posisi winning untuk setiap i = 1,, Dari setiap posisi tersebut, pemain kedua dapat pindah pada korek api sebanyak (k i, m i ) dari kumpulan korek api tersebut untuk meninggalkan posisi losing lainnya yaitu (c i, d i ). Klaim bahwa 2002 subsequent posisi losing semuanya berbeda. Anggap (c i, d i ) = (c j, d j ) untuk suatu i < j, sehingga (k j, m j ) = (k i + 500(j - i), m i + 500(j - i )). Perhatikan bahwa k i - m i 1, atau pemain pertama dapat meninggalkan (c i, d i ) untuk pemain kedua. Maka k j 2 m j 2 = k i m i (k i + m i ) k 2 m 2 (k i + m i ) k 2 m > 1000 Kontradiksi! Lalu, untuk setiap 2002 posisi tersebut, k i m i 1000, maka berdasarkan Pigeonhole Principle dua di antara k i m i adalah sama. Maka dua di antara c i - d i juga sama dan satu posisi losing akan berpindah ke posisi losing yang berbeda, yang tidak mungkin terjadi. 5. Kesimpulan Dalam makalah ini penulis memperkenalkan salah satu teori dalam bidang kombinatorika mengenai Combinatorial games. Selain itu juga penulis telah memberi beberapa aplikasi menyangkut teori ini. Penulis juga memperkenalkan permainan yang bernama Domineering dan Nim-game juga menganalisis strategi dalam permainan Nim. Permainan-permainan tersebut pun memiliki
12 banyak sekali variasi yang bisa dimainkan dan bisa dianalisis. Combinatorial Game Theory telah banyak dipelajari dan digunakan dalam banyak permainan. Dengan makalah ini penulis berharap dapat memberi inspirasi bagi pembaca untuk lebih dekat dengan combinatorial games dan combinatorial games theory.
13 DAFTAR PUSTAKA [1] Engel, Arthur. (1998). Problem-Solving Strategies. Springer. [2] Wikipedia (2006). _game_theory. Tanggal akses : 1 Januari 2007 pukul [3] Tanggal akses : 3 Januari 2007 pukul [4] Mathematical Games. (2007) /games.htm. Tanggal akses : 3 Januari 2007 pukul [5] Tanggal akses: 2 Januari 2007 pukul 21:40. [6] Tanggal akses : 1 Januari 2007 pukul [7] Titu Andrescu and Zuming Feng. (1999). Mathematical Olympiads , Problems and Solutions From Around the World.
Combinatorial Game Theory, Game Tree, dan Intelegensia Buatan
 Combinatorial Game Theory, Game Tree, dan Intelegensia Buatan Ripandy Adha - 13507115 Jurusan Teknik Informatika ITB, Bandung 40116, email: if17115@students.if.itb.ac.id Abstract Makalah ini membahas tentang
Combinatorial Game Theory, Game Tree, dan Intelegensia Buatan Ripandy Adha - 13507115 Jurusan Teknik Informatika ITB, Bandung 40116, email: if17115@students.if.itb.ac.id Abstract Makalah ini membahas tentang
CHAPTER 5 INDUCTION AND RECURSION
 CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
CHAPTER 5 INDUCTION AND RECURSION
 CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
CHAPTER 5 INDUCTION AND RECURSION 5.1 MATHEMATICAL INDUCTION Jumlah n Bilangan Ganjil Positif 1 = 1 1 + 3 = 4 1 + 3 + 5 = 9 1 + 3 + 5 + 7 = 16 1 + 3 + 5 + 7 + 9 = 25 Tebakan: Jumlah dari n bilangan ganjil
Aplikasi Teori Graf dalam Permainan Kombinatorial
 Aplikasi Teori Graf dalam Permainan Kombinatorial Abraham Krisnanda Santoso 13510033 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Aplikasi Teori Graf dalam Permainan Kombinatorial Abraham Krisnanda Santoso 13510033 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Suatu Generalisasi Permainan Kombinatorik NIM dan Wythoff
 Suatu Generalisasi Permainan Kombinatorik NIM dan Wythoff Syamsurijal ), Loeky Haryanto ), Armin Lawi ) Departemen Matematika FMIPA Universitas Hasanuddin, Jalan Perintis Kemerdekaan KM. Makassar, Indonesia
Suatu Generalisasi Permainan Kombinatorik NIM dan Wythoff Syamsurijal ), Loeky Haryanto ), Armin Lawi ) Departemen Matematika FMIPA Universitas Hasanuddin, Jalan Perintis Kemerdekaan KM. Makassar, Indonesia
ALGORITMA GREEDY DALAM PERMAINAN DOTS AND BOXES
 ALGORITMA GREEDY DALAM PERMAINAN DOTS AND BOXES Danang Tri Massandy Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
ALGORITMA GREEDY DALAM PERMAINAN DOTS AND BOXES Danang Tri Massandy Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
STRATEGI PENYELESAIAN MASALAH (PROBLEM SOLVING STRATEGIES) EDDY HERMANTO
 STRATEGI PENYELESAIAN MASALAH (PROBLEM SOLVING STRATEGIES) EDDY HERMANTO Strategi Penyelesaian Masalah Beberapa Strategi Penyelesaian Masalah : 1. Membuat daftar Yang Teratur 2. Memisalkan Dengan Suatu
STRATEGI PENYELESAIAN MASALAH (PROBLEM SOLVING STRATEGIES) EDDY HERMANTO Strategi Penyelesaian Masalah Beberapa Strategi Penyelesaian Masalah : 1. Membuat daftar Yang Teratur 2. Memisalkan Dengan Suatu
Aplikasi Matematika Diskrit dalam Permainan Nonogram
 Aplikasi Matematika Diskrit dalam Permainan Nonogram Mahesa Gandakusuma (13513091) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Aplikasi Matematika Diskrit dalam Permainan Nonogram Mahesa Gandakusuma (13513091) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Teori Game dan Pembuatan Intelegensi Buatan
 Teori Game dan Pembuatan Intelegensi Buatan Adityo August-13506051 Program Studi Teknik Informatika, Institut Teknologi Bandung, Jl. Ganesha 10, Bandung, E-mail : if16051@students.if.itb.ac.id Abstract
Teori Game dan Pembuatan Intelegensi Buatan Adityo August-13506051 Program Studi Teknik Informatika, Institut Teknologi Bandung, Jl. Ganesha 10, Bandung, E-mail : if16051@students.if.itb.ac.id Abstract
APLIKASI TEORI BILANGAN DALAM PERMAINAN NIM
 PLIKSI TEORI ILNGN DLM PERMINN NIM (PPLICTION OF NUMER THEORY IN THE NIM GME) enny Yong 1, Caesar Stefanus 2, Vincent Hari 3 1 Universitas Katolik Parahyangan, benny_y@unpar.ac.id 2 evan0396@gmail.com
PLIKSI TEORI ILNGN DLM PERMINN NIM (PPLICTION OF NUMER THEORY IN THE NIM GME) enny Yong 1, Caesar Stefanus 2, Vincent Hari 3 1 Universitas Katolik Parahyangan, benny_y@unpar.ac.id 2 evan0396@gmail.com
Penggunaan Algoritma DFS dan BFS pada Permainan Three Piles of Stones
 Penggunaan Algoritma DFS dan BFS pada Permainan Three Piles of Stones Muharram Huda Widaseta NIM 13508033 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Penggunaan Algoritma DFS dan BFS pada Permainan Three Piles of Stones Muharram Huda Widaseta NIM 13508033 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
BNPC-HS 2010 BABAK PENYISIHAN (PILIHAN GANDA)
 1 Sejumlah burung akan menempati 4 buah sangkar. Setiap sangkar maksimal ditempati oleh 5 burung. Berapa jumlah burung yang diperlukan agar 3 sangkar pasti ditempati oleh minimal 3 ekor burung? A. 11 B.
1 Sejumlah burung akan menempati 4 buah sangkar. Setiap sangkar maksimal ditempati oleh 5 burung. Berapa jumlah burung yang diperlukan agar 3 sangkar pasti ditempati oleh minimal 3 ekor burung? A. 11 B.
Strategi Permainan Menggambar Tanpa Mengangkat Pena
 Strategi Permainan Menggambar Tanpa Mengangkat Pena Benardi Atmadja - 13510078 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Strategi Permainan Menggambar Tanpa Mengangkat Pena Benardi Atmadja - 13510078 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Menentukan Arah Pukulan Terbaik dalam Pertandingan Bulutangkis Kategori Tunggal dengan Teori Graf Terbalik
 Menentukan Arah Pukulan Terbaik dalam Pertandingan Bulutangkis Kategori Tunggal dengan Teori Graf Terbalik Jaisyalmatin Pribadi 13510084 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika
Menentukan Arah Pukulan Terbaik dalam Pertandingan Bulutangkis Kategori Tunggal dengan Teori Graf Terbalik Jaisyalmatin Pribadi 13510084 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika
Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem
 Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem Arie Tando (13510018) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Penerapan Pohon dengan Algoritma Branch and Bound dalam Menyelesaikan N-Queen Problem Arie Tando (13510018) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
SILABUS MATEMATIKA KEMENTERIAN
 SILABUS OLIMPIADE MATEMATIKA INTERNASIONAL UNTUK SELEKSI OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA, PROVINSI, DAN NASIONAL MATEMATIKA KEMENTERIAN Kementerian Pendidikan dan Kebudayaan Direktorat
SILABUS OLIMPIADE MATEMATIKA INTERNASIONAL UNTUK SELEKSI OLIMPIADE SAINS NASIONAL TINGKAT KABUPATEN/KOTA, PROVINSI, DAN NASIONAL MATEMATIKA KEMENTERIAN Kementerian Pendidikan dan Kebudayaan Direktorat
2 BILANGAN PRIMA. 2.1 Teorema Fundamental Aritmatika
 Bilangan prima telah dikenal sejak sekolah dasar, yaitu bilangan yang tidak mempunyai faktor selain dari 1 dan dirinya sendiri. Bilangan prima memegang peranan penting karena pada dasarnya konsep apapun
Bilangan prima telah dikenal sejak sekolah dasar, yaitu bilangan yang tidak mempunyai faktor selain dari 1 dan dirinya sendiri. Bilangan prima memegang peranan penting karena pada dasarnya konsep apapun
PANDUAN OLIMPIADE SAINS NASIONAL MATEMATIKA SMA/MA
 PANDUAN OLIMPIADE SAINS NASIONAL MATEMATIKA SMA/MA Seperti umumnya kompetisi matematika yang serius, Olimpiade Sains Nasional Matematika SMA/MA mengukur secara langsung tiga aspek berikut: pemecahan masalah
PANDUAN OLIMPIADE SAINS NASIONAL MATEMATIKA SMA/MA Seperti umumnya kompetisi matematika yang serius, Olimpiade Sains Nasional Matematika SMA/MA mengukur secara langsung tiga aspek berikut: pemecahan masalah
Aplikasi Teori Graf Pada Knight s Tour
 Aplikasi Teori Graf Pada Knight s Tour Adhika Aryantio - 13511061 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Aplikasi Teori Graf Pada Knight s Tour Adhika Aryantio - 13511061 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Matematika dalam Turnamen Bridge
 Matematika dalam Turnamen Bridge Nicky Irawan 1) 1) Jurusan Teknik Informatika ITB, Bandung 40135, email: if17078@students.if.itb.ac.id Abstract Makalah ini membahas mengenai aplikasi matematika atau struktur
Matematika dalam Turnamen Bridge Nicky Irawan 1) 1) Jurusan Teknik Informatika ITB, Bandung 40135, email: if17078@students.if.itb.ac.id Abstract Makalah ini membahas mengenai aplikasi matematika atau struktur
Algoritma Greedy dalam Artificial Intelligence Permainan Tic Tac Toe
 Algoritma Greedy dalam Artificial Intelligence Permainan Tic Tac Toe Alif Bhaskoro 13514016 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Algoritma Greedy dalam Artificial Intelligence Permainan Tic Tac Toe Alif Bhaskoro 13514016 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
BNPC-HS 2010 BABAK PENYISIHAN (PILIHAN GANDA)
 1 Sejumlah burung akan menempati 4 buah sangkar. Setiap sangkar maksimal ditempati oleh 5 burung. Berapa jumlah burung yang diperlukan agar 3 sangkar pasti ditempati oleh minimal 3 ekor burung? A. 11 B.
1 Sejumlah burung akan menempati 4 buah sangkar. Setiap sangkar maksimal ditempati oleh 5 burung. Berapa jumlah burung yang diperlukan agar 3 sangkar pasti ditempati oleh minimal 3 ekor burung? A. 11 B.
Mewarnai Tabel. Masukan. Keluaran. Batasan. Asia-Pacific Informatics Olympiad 2011 Bahasa Indonesia Version
 Mewarnai Tabel Sam dan saudara perempuannya, Sara, memiliki sebuah tabel berukuran n x m sel. Mereka ingin mewarnai semua sel tersebut dengan warna merah atau biru. Berdasarkan kepercayaan pribadi, mereka
Mewarnai Tabel Sam dan saudara perempuannya, Sara, memiliki sebuah tabel berukuran n x m sel. Mereka ingin mewarnai semua sel tersebut dengan warna merah atau biru. Berdasarkan kepercayaan pribadi, mereka
Penggunaan Algoritma Greedy untuk menyelesaikan Permainan Othello
 Penggunaan Algoritma Greedy untuk menyelesaikan Permainan Othello Annisa Muzdalifa - 13515090 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penggunaan Algoritma Greedy untuk menyelesaikan Permainan Othello Annisa Muzdalifa - 13515090 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
WORKSHOP PEMBIMBINGAN OLIMPIADE MATEMATIKA & SAINS BIDANG MATEMATIKA SMP
 WORKSHOP PEMBIMBINGAN OLIMPIADE MATEMATIKA & SAINS BIDANG MATEMATIKA SMP Ilham Rizkianto FMIPA Universitas Negeri Yogyakarta Ilham_rizkianto@uny.ac.id Wonosari, 9 Mei 2014 MASALAH KOMBINATORIK Mengecoh,
WORKSHOP PEMBIMBINGAN OLIMPIADE MATEMATIKA & SAINS BIDANG MATEMATIKA SMP Ilham Rizkianto FMIPA Universitas Negeri Yogyakarta Ilham_rizkianto@uny.ac.id Wonosari, 9 Mei 2014 MASALAH KOMBINATORIK Mengecoh,
TINJAUAN PUSTAKA. Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi
 II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
II. TINJAUAN PUSTAKA Pada bab ini akan dijelaskan beberapa konsep dasar teori graf dan dimensi partisi pada suatu graf sebagai landasan teori pada penelitian ini.. Konsep Dasar Graf Pada bagian ini akan
Implementasi Algoritma Greedy, BFS, Branch and Bound, dan Metode Heuristik dalam Permainan Reversi
 Implementasi Algoritma Greedy, BFS, Branch and Bound, dan Metode Heuristik dalam Permainan Reversi Gilang Julian Suherik - 13512045 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika
Implementasi Algoritma Greedy, BFS, Branch and Bound, dan Metode Heuristik dalam Permainan Reversi Gilang Julian Suherik - 13512045 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika
BAB 2 LANDASAN TEORI
 8 BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa konsep teori permainan pada permainan berstrategi murni dan campuran dari dua pemain yang akan digunakan sebagai landasan berpikir dalam melakukan
8 BAB 2 LANDASAN TEORI Pada bab ini akan dibahas beberapa konsep teori permainan pada permainan berstrategi murni dan campuran dari dua pemain yang akan digunakan sebagai landasan berpikir dalam melakukan
Matematika Rekreasi melalui Permainan Kartu
 Suska Journal of Mathematics Education Vol.2, No. 1, 2016, Hal. 31 40 Matematika Rekreasi melalui Permainan Kartu Benny Yong Program Studi Matematika, Universitas Katolik Parahyangan Email: benny_y@unpar.ac.id
Suska Journal of Mathematics Education Vol.2, No. 1, 2016, Hal. 31 40 Matematika Rekreasi melalui Permainan Kartu Benny Yong Program Studi Matematika, Universitas Katolik Parahyangan Email: benny_y@unpar.ac.id
PENCARIAN SOLUSI TTS ANGKA DENGAN ALGORITMA RUNUT BALIK BESERTA PENGEMBANGANNYA
 PENCARIAN SOLUSI TTS ANGKA DENGAN ALGORITMA RUNUT BALIK BESERTA PENGEMBANGANNYA Wahyu Fahmy Wisudawan Program Studi Teknik Informatika Institut Teknologi Bandung, NIM: 506 Jl. Dago Asri 4 No. 4, Bandung
PENCARIAN SOLUSI TTS ANGKA DENGAN ALGORITMA RUNUT BALIK BESERTA PENGEMBANGANNYA Wahyu Fahmy Wisudawan Program Studi Teknik Informatika Institut Teknologi Bandung, NIM: 506 Jl. Dago Asri 4 No. 4, Bandung
Algoritma Greedy pada Board Game Saboteur
 Algoritma Greedy pada Board Game Saboteur Lathifah Nurrahmah - 13515046 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Algoritma Greedy pada Board Game Saboteur Lathifah Nurrahmah - 13515046 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Aplikasi Graf Dalam Permainan Catur
 Aplikasi Graf Dalam Permainan Catur Sahat Nicholas Simangunsong - 13509095 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Aplikasi Graf Dalam Permainan Catur Sahat Nicholas Simangunsong - 13509095 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Penerapan Algoritma Greedy dalam Pembuatan Artificial Intelligence Permainan Reversi
 Penerapan Algoritma Greedy dalam Pembuatan Artificial Intelligence Permainan Reversi Zacki Zulfikar Fauzi / 13515147 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Penerapan Algoritma Greedy dalam Pembuatan Artificial Intelligence Permainan Reversi Zacki Zulfikar Fauzi / 13515147 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
TINJAUAN PUSTAKA. Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada
 II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
II. TINJAUAN PUSTAKA Pada bagian ini akan diberikan konsep dasar graf dan bilangan kromatik lokasi pada suatu graf sebagai landasan teori penelitian ini. 2. Konsep Dasar Graf Teori dasar mengenai graf
Penggunaan Algoritma Greedy Untuk Menyelesaikan Permainan Cluedo
 Penggunaan Algoritma Greedy Untuk Menyelesaikan Permainan Cluedo Adriano Milyardi - 13509010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penggunaan Algoritma Greedy Untuk Menyelesaikan Permainan Cluedo Adriano Milyardi - 13509010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
APLIKASI ALGORITMA GREEDY DALAM PERMAINAN CAPSA BANTING
 APLIKASI ALGORITMA GREEDY DALAM PERMAINAN CAPSA BANTING Sanrio Hernanto Mahasiswa Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha No 10
APLIKASI ALGORITMA GREEDY DALAM PERMAINAN CAPSA BANTING Sanrio Hernanto Mahasiswa Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha No 10
INDUKSI MATEMATIS Drs. C. Jacob, M.Pd Pengantar Apakah suatu formula untuk jumlah dari n bilangan bulat positif ganjil
 INDUKSI MATEMATIS Drs. C. Jacob, M.Pd Email: cjacob@upi.edu 3. Pengantar Apakah suatu formula untuk jumlah dari n bilangan bulat positif ganjil pertama? Jumlah dari n bilangan bulat ganjil positif pertama
INDUKSI MATEMATIS Drs. C. Jacob, M.Pd Email: cjacob@upi.edu 3. Pengantar Apakah suatu formula untuk jumlah dari n bilangan bulat positif ganjil pertama? Jumlah dari n bilangan bulat ganjil positif pertama
INVARIAN DAN MONOVARIAN
 1 olimpiadematematika.wordpress.com INVARIAN DAN MONOVARIAN Invarian adalah sebuah prinsip yang sangat berguna dalam pemecahan berbagai masalah. Secara harafiah, arti dari invarian adalah tidak berubah
1 olimpiadematematika.wordpress.com INVARIAN DAN MONOVARIAN Invarian adalah sebuah prinsip yang sangat berguna dalam pemecahan berbagai masalah. Secara harafiah, arti dari invarian adalah tidak berubah
Partisi Maksimum pada Poligon
 Partisi Maksimum pada Poligon Muhammad Nassirudin - 13511044 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Partisi Maksimum pada Poligon Muhammad Nassirudin - 13511044 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Penerapan Algoritma Greedy dalam Permainan Connect 4
 Penerapan Algoritma Greedy dalam Permainan Connect 4 Muhammad Hasby (13509054) 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Penerapan Algoritma Greedy dalam Permainan Connect 4 Muhammad Hasby (13509054) 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
BACKWARD INDUCTION (4) N = 4. Kemungkinan langkah awal pemain pertama: 1, 2, atau 3 keping. 03 Juli 2012 Tugas Akhir KI091391
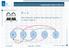 BACKWARD INDUCTION (4) N = 4 Kemungkinan langkah awal pemain pertama: 1, 2, atau 3 keping. 0 1 2 3 4 12 BACKWARD INDUCTION (5) Algoritma Backward Induction 1. Tentukan jumlah keping yang akan dihitung.
BACKWARD INDUCTION (4) N = 4 Kemungkinan langkah awal pemain pertama: 1, 2, atau 3 keping. 0 1 2 3 4 12 BACKWARD INDUCTION (5) Algoritma Backward Induction 1. Tentukan jumlah keping yang akan dihitung.
Bab 1 PENDAHULUAN. 1.1 Latar Belakang Masalah
 Bab 1 PENDAHULUAN 1.1 Latar Belakang Masalah Teori graf merupakan pokok bahasan yang memiliki banyak terapan sampai saat ini. Graf di gunakan untuk merepresentasikan objek objek diskrit dan hubungan antara
Bab 1 PENDAHULUAN 1.1 Latar Belakang Masalah Teori graf merupakan pokok bahasan yang memiliki banyak terapan sampai saat ini. Graf di gunakan untuk merepresentasikan objek objek diskrit dan hubungan antara
Strategi Algoritma Penyelesaian Puzzle Hanjie
 Strategi Algoritma Penyelesaian Puzzle Hanjie Whilda Chaq 13511601 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Strategi Algoritma Penyelesaian Puzzle Hanjie Whilda Chaq 13511601 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Menyelesaikan Kakuro Puzzle dengan Kombinatorial
 Menyelesaikan Kakuro Puzzle dengan Kombinatorial Muhammad Farhan Majid (13514029) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Menyelesaikan Kakuro Puzzle dengan Kombinatorial Muhammad Farhan Majid (13514029) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Pembuktian Cayley s Formula dengan Prüfer Sequence
 Pembuktian Cayley s Formula dengan Prüfer Sequence Muntaha Ilmi (13512048) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Pembuktian Cayley s Formula dengan Prüfer Sequence Muntaha Ilmi (13512048) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Aplikasi Teori Graf Pada Knight s Tour
 Aplikasi Teori Graf Pada Knight s Tour Fahmi Mumtaz 1) 1) Jurusan Teknik Informatika ITB, Bandung, NIM : 13506045 email: if16045@students.if..itb.ac.id Abstract Makalah ini membahas tentang aplikasi dari
Aplikasi Teori Graf Pada Knight s Tour Fahmi Mumtaz 1) 1) Jurusan Teknik Informatika ITB, Bandung, NIM : 13506045 email: if16045@students.if..itb.ac.id Abstract Makalah ini membahas tentang aplikasi dari
Penerapan Prinsip Greedy dalam Permainan Kartu Hearts
 Penerapan Prinsip Greedy dalam Permainan Kartu Hearts Adrian Edbert Luman Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha 10, Bandung e-mail:
Penerapan Prinsip Greedy dalam Permainan Kartu Hearts Adrian Edbert Luman Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha 10, Bandung e-mail:
Penerapan Algoritma Greedy Pada Permainan Kartu Truf
 Penerapan Algoritma Greedy Pada Permainan Kartu Truf Nikolaus Indra - 13508039 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Penerapan Algoritma Greedy Pada Permainan Kartu Truf Nikolaus Indra - 13508039 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Pemanfaatan Pohon dalam Realisasi Algoritma Backtracking untuk Memecahkan N-Queens Problem
 Pemanfaatan Pohon dalam Realisasi Algoritma Backtracking untuk Memecahkan N-Queens Problem Halida Astatin (13507049) Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika, Institut Teknologi
Pemanfaatan Pohon dalam Realisasi Algoritma Backtracking untuk Memecahkan N-Queens Problem Halida Astatin (13507049) Program Studi Teknik Informatika, Sekolah Teknik Elektro dan Informatika, Institut Teknologi
Implementasi Pemrograman Dinamis dalam Pencarian Solusi Permainan Menara Hanoi
 Implementasi Pemrograman Dinamis dalam Pencarian Solusi Permainan Menara Hanoi Jonathan Ery Pradana / 13508007 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
Implementasi Pemrograman Dinamis dalam Pencarian Solusi Permainan Menara Hanoi Jonathan Ery Pradana / 13508007 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi
KOMBINATORIKA. Berapa banyak cara menyusun sebuah bilangan yang terdiri dari empat buah angka yang tidak mengandung angka yang berulang?
 P a g e 1 KOMBINATORIKA Beberapa prinsip penting dalam menyelesaikan masalah kombinatorika yaitu permutasi dan kombinasi, prinsip inklusi-eksklusi, koefisien binomial, prinsip sarang merpati (pigeon hole
P a g e 1 KOMBINATORIKA Beberapa prinsip penting dalam menyelesaikan masalah kombinatorika yaitu permutasi dan kombinasi, prinsip inklusi-eksklusi, koefisien binomial, prinsip sarang merpati (pigeon hole
3. Graph Euler dan Graph Hamilton
 3. Graph Euler dan Graph Hamilton Oleh : Ade Nurhopipah Pokok Bahasan : 1. Masalah Exploring dan Travelling 2. Graph Euler 3. Graph Hamilton Sumber : Aldous, Joan M.,Wilson, Robin J. 2004. Graph and Applications.
3. Graph Euler dan Graph Hamilton Oleh : Ade Nurhopipah Pokok Bahasan : 1. Masalah Exploring dan Travelling 2. Graph Euler 3. Graph Hamilton Sumber : Aldous, Joan M.,Wilson, Robin J. 2004. Graph and Applications.
TEKNIK MEMBILANG. b T U V W
 TEKNIK MEMBILANG Berikut ini teknik-teknik (cara-cara) membilang atau menghitung banyaknya anggota ruang sampel dari suatu eksperimen tanpa harus mendaftar seluruh anggota ruang sampel tersebut. A. Prinsip
TEKNIK MEMBILANG Berikut ini teknik-teknik (cara-cara) membilang atau menghitung banyaknya anggota ruang sampel dari suatu eksperimen tanpa harus mendaftar seluruh anggota ruang sampel tersebut. A. Prinsip
BAB III PELABELAN KOMBINASI
 1 BAB III PELABELAN KOMBINASI 3.1 Konsep Pelabelan Kombinasi Pelabelan kombinasi dari suatu graf dengan titik dan sisi,, graf G, disebut graf kombinasi jika terdapat fungsi bijektif dari ( himpunan titik
1 BAB III PELABELAN KOMBINASI 3.1 Konsep Pelabelan Kombinasi Pelabelan kombinasi dari suatu graf dengan titik dan sisi,, graf G, disebut graf kombinasi jika terdapat fungsi bijektif dari ( himpunan titik
PELUANG DISKRIT PERMAINAN KARTU BLACKJACK
 PELUANG DISKRIT PERMAINAN KARTU BLACKJACK Haryus Aminul Akbar-13507016 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung E-Mail: if17016@students.if.itb.ac.id
PELUANG DISKRIT PERMAINAN KARTU BLACKJACK Haryus Aminul Akbar-13507016 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung E-Mail: if17016@students.if.itb.ac.id
Penerapan Algoritma Greedy dalam Permainan Othello
 Penerapan Algoritma Greedy dalam Permainan Othello Fabrian Oktavino H - 13510053 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Penerapan Algoritma Greedy dalam Permainan Othello Fabrian Oktavino H - 13510053 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Penerapan Algoritma Greedy dan Breadth First Search pada Permainan Kartu Sevens
 Penerapan Algoritma Greedy dan Breadth First Search pada Permainan Kartu Sevens Kharis Isriyanto 13514064 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Penerapan Algoritma Greedy dan Breadth First Search pada Permainan Kartu Sevens Kharis Isriyanto 13514064 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
IMPLEMENTASI ALGORITMA GREEDY PADA PERMAINAN OTHELLO
 IMPLEMENTASI ALGORITMA GREEDY PADA PERMAINAN OTHELLO Nur Fajriah Rachmah NIM 13506091 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha nomor
IMPLEMENTASI ALGORITMA GREEDY PADA PERMAINAN OTHELLO Nur Fajriah Rachmah NIM 13506091 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha nomor
Aplikasi Teori Graf dalam Permainan Instant Insanity
 Aplikasi Teori Graf dalam Permainan Instant Insanity Aurelia 13512099 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
Aplikasi Teori Graf dalam Permainan Instant Insanity Aurelia 13512099 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia
APLIKASI TEORI PELUANG PADA SALAH SATU GAME ONLINE
 APLIKASI TEORI PELUANG PADA SALAH SATU GAME ONLINE Restu Banowati 18209023 Program Studi Sistem dan Teknologi Informasi Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
APLIKASI TEORI PELUANG PADA SALAH SATU GAME ONLINE Restu Banowati 18209023 Program Studi Sistem dan Teknologi Informasi Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
LOMBA MATEMATIKA NASIONAL KE-26
 LOMBA MATEMATIKA NASIONAL KE-26 Babak Penyisihan Tingkat SMP Minggu, 8 November HIMPUNAN MAHASISWA MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS GADJAH MADA SEKIP UTARA UNIT III
LOMBA MATEMATIKA NASIONAL KE-26 Babak Penyisihan Tingkat SMP Minggu, 8 November HIMPUNAN MAHASISWA MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS GADJAH MADA SEKIP UTARA UNIT III
Studi Digital Watermarking Citra Bitmap dalam Mode Warna Hue Saturation Lightness
 Studi Digital Watermarking Citra Bitmap dalam Mode Warna Hue Saturation Lightness Evan 13506089 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : if16089@students.if.itb.ac.id
Studi Digital Watermarking Citra Bitmap dalam Mode Warna Hue Saturation Lightness Evan 13506089 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung E-mail : if16089@students.if.itb.ac.id
G a a = e = a a. b. Berdasarkan Contoh 1.2 bagian b diperoleh himpunan semua bilangan bulat Z. merupakan grup terhadap penjumlahan bilangan.
 2. Grup Definisi 1.3 Suatu grup < G, > adalah himpunan tak-kosong G bersama-sama dengan operasi biner pada G sehingga memenuhi aksioma- aksioma berikut: a. operasi biner bersifat asosiatif, yaitu a, b,
2. Grup Definisi 1.3 Suatu grup < G, > adalah himpunan tak-kosong G bersama-sama dengan operasi biner pada G sehingga memenuhi aksioma- aksioma berikut: a. operasi biner bersifat asosiatif, yaitu a, b,
PERANAN INDUKSI MATEMATIKA DALAM PEMBUKTIAN MATEMATIKA
 PERANAN INDUKSI MATEMATIKA DALAM PEMBUKTIAN MATEMATIKA Riani Rilanda NIM : 13505051 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung e-mail : if15051@students.if.itb.ac.id
PERANAN INDUKSI MATEMATIKA DALAM PEMBUKTIAN MATEMATIKA Riani Rilanda NIM : 13505051 Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha 10, Bandung e-mail : if15051@students.if.itb.ac.id
Studi Tentang Kombinatorial dan Peluang Diskrit Serta Beberapa Aplikasinya
 Studi Tentang Kombinatorial dan Peluang Diskrit Serta Beberapa Aplikasinya Hanif Eridaputra (13510091) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Studi Tentang Kombinatorial dan Peluang Diskrit Serta Beberapa Aplikasinya Hanif Eridaputra (13510091) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Pembahasan OSN Matematika SMA Tahun 2013 Seleksi Tingkat Provinsi. Tutur Widodo. Bagian Pertama : Soal Isian Singkat
 Pembahasan OSN Matematika SMA Tahun 013 Seleksi Tingkat Provinsi Tutur Widodo Bagian Pertama : Soal Isian Singkat 1. Diberikan tiga lingkaran dengan radius r =, yang saling bersinggungan. Total luas dari
Pembahasan OSN Matematika SMA Tahun 013 Seleksi Tingkat Provinsi Tutur Widodo Bagian Pertama : Soal Isian Singkat 1. Diberikan tiga lingkaran dengan radius r =, yang saling bersinggungan. Total luas dari
SOAL-JAWAB MATEMATIKA PENCACAHAN
 SOAL-JAWAB MATEMATIKA PENCACAHAN Soal 1 Tersedia angka-angka 1, 2, 3, 7, 8, 9. a) Dari angka-angka tersebut disusun bilangan terdiri dari tiga angka berbeda. Berapa banyaknya bilangan yang dapat disusun?
SOAL-JAWAB MATEMATIKA PENCACAHAN Soal 1 Tersedia angka-angka 1, 2, 3, 7, 8, 9. a) Dari angka-angka tersebut disusun bilangan terdiri dari tiga angka berbeda. Berapa banyaknya bilangan yang dapat disusun?
Combinatorics dan Counting
 CHAPTER 6 COUNTING Combinatorics dan Counting Kombinatorik Ilmu yang mempelajari pengaturan obyek Bagian penting dari Matematika Diskrit Mulai dipelajari di abad 17 Enumerasi Penghitungan obyek dengan
CHAPTER 6 COUNTING Combinatorics dan Counting Kombinatorik Ilmu yang mempelajari pengaturan obyek Bagian penting dari Matematika Diskrit Mulai dipelajari di abad 17 Enumerasi Penghitungan obyek dengan
Aplikasi Algoritma MiniMax pada Beberapa Permainan Papan
 Aplikasi Algoritma MiniMax pada Beberapa Permainan Papan Gaudensius Dimas Prasetyo Suprapto - 13514059 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
Aplikasi Algoritma MiniMax pada Beberapa Permainan Papan Gaudensius Dimas Prasetyo Suprapto - 13514059 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung,
PENERAPAN TEORI KOMBINATORIAL DAN PELUANG DISKRIT DALAM PERMAINAN POKER
 PENERAPAN TEORI KOMBINATORIAL DAN PELUANG DISKRIT DALAM PERMAINAN POKER Irma Juniati - 13506088 Jurusan Teknik Informatika ITB, Bandung 40116, email: if16088@students.if.itb.ac.id Abstrak Makalah ini membahas
PENERAPAN TEORI KOMBINATORIAL DAN PELUANG DISKRIT DALAM PERMAINAN POKER Irma Juniati - 13506088 Jurusan Teknik Informatika ITB, Bandung 40116, email: if16088@students.if.itb.ac.id Abstrak Makalah ini membahas
OLIMPIADE SAINS NASIONAL VII
 SOAL SESI 2 OLIMPIADE SAINS NASIONAL VII BIDANG INFORMATIKA 10 AGUSTUS 2008 MAKASSAR, SULAWESI SELATAN Selamat Bekerja, Berkompetisi, Jadilah Yang Terbaik! Kartu 1 Nama Program: kartu1.pas / C / CPP Pak
SOAL SESI 2 OLIMPIADE SAINS NASIONAL VII BIDANG INFORMATIKA 10 AGUSTUS 2008 MAKASSAR, SULAWESI SELATAN Selamat Bekerja, Berkompetisi, Jadilah Yang Terbaik! Kartu 1 Nama Program: kartu1.pas / C / CPP Pak
BAB III ANALISA DAN PERANCANGAN
 BAB III ANALISA DAN PERANCANGAN III.1. Analisis Masalah Strategi di belakang Minimax algoritma adalah komputer berasumsi bahwa kedua pemain akan main sejauh kemampuan mereka. Maka, jika lawan mempunyai
BAB III ANALISA DAN PERANCANGAN III.1. Analisis Masalah Strategi di belakang Minimax algoritma adalah komputer berasumsi bahwa kedua pemain akan main sejauh kemampuan mereka. Maka, jika lawan mempunyai
ALGORITMA MINIMAX DALAM PERMAINAN CHECKERS
 ALGORITMA MINIMAX DALAM PERMAINAN CHECKERS Nadhira Ayuningtyas (13506048) Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha No. 10 Bandung e-mail: if16048@students.if.itb.ac.id ABSTRAK
ALGORITMA MINIMAX DALAM PERMAINAN CHECKERS Nadhira Ayuningtyas (13506048) Program Studi Teknik Informatika, Institut Teknologi Bandung Jl. Ganesha No. 10 Bandung e-mail: if16048@students.if.itb.ac.id ABSTRAK
MATEMATIKA DISKRIT. Logika
 MATEMATIKA DISKRIT Logika SILABUS KULIAH 1. Logika 2. Himpunan 3. Matriks, Relasi dan Fungsi 4. Induksi Matematika 5. Algoritma dan Bilangan Bulat 6. Aljabar Boolean 7. Graf 8. Pohon REFERENSI Rinaldi
MATEMATIKA DISKRIT Logika SILABUS KULIAH 1. Logika 2. Himpunan 3. Matriks, Relasi dan Fungsi 4. Induksi Matematika 5. Algoritma dan Bilangan Bulat 6. Aljabar Boolean 7. Graf 8. Pohon REFERENSI Rinaldi
PENGGUNAAN ALGORITMA BACKTRACKING DALAM PENCARIAN KOEFISIEN ROOK POLYNOMIAL
 PENGGUNAAN ALGORITMA BACKTRACKING DALAM PENCARIAN KOEFISIEN ROOK POLYNOMIAL Arinta Primandini Auza 13505021 Program Studi Teknik Informatika Institut Teknologi Bandung Alamat : Jl Ganeca 10 Bandung e-mail:
PENGGUNAAN ALGORITMA BACKTRACKING DALAM PENCARIAN KOEFISIEN ROOK POLYNOMIAL Arinta Primandini Auza 13505021 Program Studi Teknik Informatika Institut Teknologi Bandung Alamat : Jl Ganeca 10 Bandung e-mail:
APLIKASI GAME TIC TAC TOE 6X6 BERBASIS ANDROID MENGGUNAKAN ALGORITMA MINIMAX DAN HEURISTIC EVALUATION
 APLIKASI GAME TIC TAC TOE 6X6 BERBASIS ANDROID MENGGUNAKAN ALGORITMA MINIMAX DAN HEURISTIC EVALUATION Ever Jayadi1), Muhammad Aziz Fatchur Rachman2), Muhammad Yuliansyah3) 1), 2), 3) Teknik Informatika
APLIKASI GAME TIC TAC TOE 6X6 BERBASIS ANDROID MENGGUNAKAN ALGORITMA MINIMAX DAN HEURISTIC EVALUATION Ever Jayadi1), Muhammad Aziz Fatchur Rachman2), Muhammad Yuliansyah3) 1), 2), 3) Teknik Informatika
I. PENDAHULUAN. Aljabar dapat didefinisikan sebagai manipulasi dari simbol-simbol. Secara historis
 1 I. PENDAHULUAN 1.2 Latar Belakang dan Masalah Aljabar dapat didefinisikan sebagai manipulasi dari simbol-simbol. Secara historis aljabar dibagi menjadi dua periode waktu, dengan batas waktu sekitar tahun
1 I. PENDAHULUAN 1.2 Latar Belakang dan Masalah Aljabar dapat didefinisikan sebagai manipulasi dari simbol-simbol. Secara historis aljabar dibagi menjadi dua periode waktu, dengan batas waktu sekitar tahun
Penerapan Kombinatorial dalam Permainan Sudoku
 Penerapan Kombinatorial dalam Permainan Sudoku Dendy Suprihady /13514070 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Penerapan Kombinatorial dalam Permainan Sudoku Dendy Suprihady /13514070 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Aplikasi Kombinatorial dan Peluang Diskrit dalam Permainan Dadu Cee-Lo
 Aplikasi Kombinatorial dan Peluang Diskrit dalam Permainan Dadu Cee-Lo Hendy - 13507011 Jurusan Teknik Informatika, ITB, Bandung 40116, email: if17011@students.if.itb.ac.id Abstract Makalah ini membahas
Aplikasi Kombinatorial dan Peluang Diskrit dalam Permainan Dadu Cee-Lo Hendy - 13507011 Jurusan Teknik Informatika, ITB, Bandung 40116, email: if17011@students.if.itb.ac.id Abstract Makalah ini membahas
Penerapan Algoritma A-star (A*) Untuk Menyelesaikan Masalah Maze
 Penerapan Algoritma A-star (A*) Untuk Menyelesaikan Masalah Maze Hapsari Tilawah - 13509027 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penerapan Algoritma A-star (A*) Untuk Menyelesaikan Masalah Maze Hapsari Tilawah - 13509027 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Analisa Dan Implementasi Teorema Sprague-Grundy Pada Penyelesaian Variasi Game Nim
 JURNAL TEKNIK POMITS Vol. 1, No. 1, (2012) 1-6 1 Analisa Dan Implementasi Teorema Sprague-Grundy Pada Penyelesaian Variasi Game Nim Halimah Winajma, Yudhi Purwananto, S.Kom, M.Kom, dan Rully Soelaiman,
JURNAL TEKNIK POMITS Vol. 1, No. 1, (2012) 1-6 1 Analisa Dan Implementasi Teorema Sprague-Grundy Pada Penyelesaian Variasi Game Nim Halimah Winajma, Yudhi Purwananto, S.Kom, M.Kom, dan Rully Soelaiman,
Penerapan Algoritma A* Sebagai Algoritma Pencari Jalan Dalam Game
 ABSTRAK Penerapan Algoritma A* Sebagai Algoritma Pencari Jalan Dalam Game Makalah ini membahas tentang bagaimana suatu entitas di dalam game mampu mencari jalan terpendek dari titik koordinatnya sekarang
ABSTRAK Penerapan Algoritma A* Sebagai Algoritma Pencari Jalan Dalam Game Makalah ini membahas tentang bagaimana suatu entitas di dalam game mampu mencari jalan terpendek dari titik koordinatnya sekarang
Aplikasi Graf dalam Permasalahan Knight s Tour
 Aplikasi Graf dalam Permasalahan Knight s Tour Rizka Irawan Ardiyanto - 13506012 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganesha 10, Bandung Email: if16012@students.if.itb.ac.id
Aplikasi Graf dalam Permasalahan Knight s Tour Rizka Irawan Ardiyanto - 13506012 Program Studi Teknik Informatika, Institut Teknologi Bandung Jalan Ganesha 10, Bandung Email: if16012@students.if.itb.ac.id
SELEKSI OLIMPIADE TINGKAT PROVINSI 2013 TIM OLIMPIADE MATEMATIKA INDONESIA 2014
 SELEKSI OLIMPIADE TINGKAT PROVINSI 2013 TIM OLIMPIADE MATEMATIKA INDONESIA 2014 Waktu : 210 Menit KEMENTERIAN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT
SELEKSI OLIMPIADE TINGKAT PROVINSI 2013 TIM OLIMPIADE MATEMATIKA INDONESIA 2014 Waktu : 210 Menit KEMENTERIAN PENDIDIKAN NASIONAL DIREKTORAT JENDERAL MANAJEMEN PENDIDIKAN DASAR DAN MENENGAH DIREKTORAT
Bilangan Kromatik Dominasi pada Graf-Graf Hasil Operasi Korona
 A-88 JURNAL SAINS DAN SENI ITS Vol. 5 No. 2 (2016) 2337-3520 (2301-928X Print) Bilangan Kromatik Dominasi pada Graf-Graf Hasil Operasi Korona Muh. Alwan Hadi, Dr. Darmaji, S.Si., M.T., Drs. Suhud Wahyudi,
A-88 JURNAL SAINS DAN SENI ITS Vol. 5 No. 2 (2016) 2337-3520 (2301-928X Print) Bilangan Kromatik Dominasi pada Graf-Graf Hasil Operasi Korona Muh. Alwan Hadi, Dr. Darmaji, S.Si., M.T., Drs. Suhud Wahyudi,
Menghitung Besarnya Kemungkinan Kemenangan pada Permainan Kasino dengan Memanfaatkan Kombinatorial
 Menghitung Besarnya Kemungkinan Kemenangan pada Permainan Kasino dengan Memanfaatkan Kombinatorial Frilla Amanda 13510068 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut
Menghitung Besarnya Kemungkinan Kemenangan pada Permainan Kasino dengan Memanfaatkan Kombinatorial Frilla Amanda 13510068 1 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut
INFORMATIKA/KOMPUTER. Hari 0 (Sesi Latihan) 1. Empek-empek 2. Gunting Kertas 3. Matriks Biner
 Hak Cipta Dilindungi Undang-undang OLIMPIADE SAINS NASIONAL 2016 DESKRIPSI SOAL INFORMATIKA/KOMPUTER Hari 0 (Sesi Latihan) 1. Empek-empek 2. Gunting Kertas 3. Matriks Biner Waktu: 2 Jam Hari 0 / Soal 1
Hak Cipta Dilindungi Undang-undang OLIMPIADE SAINS NASIONAL 2016 DESKRIPSI SOAL INFORMATIKA/KOMPUTER Hari 0 (Sesi Latihan) 1. Empek-empek 2. Gunting Kertas 3. Matriks Biner Waktu: 2 Jam Hari 0 / Soal 1
LOGIKA PERMAINAN UNO KARTU
 LOGIKA PERMAINAN UNO KARTU Shirley (13508094) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha no 10 Bandung e-mail: if18094@students.if.itb.ac.id
LOGIKA PERMAINAN UNO KARTU Shirley (13508094) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung Jalan Ganesha no 10 Bandung e-mail: if18094@students.if.itb.ac.id
Bab 1. Bilangan Bulat. Standar Kompetensi. 1. Memahami sifat-sifat operasi hitung bilangan dan pengunaannya dalam pemecahan masalah.
 Bab 1 Bilangan Bulat Standar Kompetensi 1. Memahami sifat-sifat operasi hitung bilangan dan pengunaannya dalam pemecahan masalah. Kompetensi Dasar 1.1. Melakukan operasi hitung bilangan pecahan. 1.2. Menggunakan
Bab 1 Bilangan Bulat Standar Kompetensi 1. Memahami sifat-sifat operasi hitung bilangan dan pengunaannya dalam pemecahan masalah. Kompetensi Dasar 1.1. Melakukan operasi hitung bilangan pecahan. 1.2. Menggunakan
Aplikasi Teori Bilangan Bulat dalam Pembangkitan Bilangan Acak Semu
 Aplikasi Teori Bilangan Bulat dalam Pembangkitan Bilangan Acak Semu Ferdian Thung 13507127 Program Studi Teknik Informatika ITB, Jalan Ganesha 10 Bandung, Jawa Barat, email: if17127@students.if.itb.ac.id
Aplikasi Teori Bilangan Bulat dalam Pembangkitan Bilangan Acak Semu Ferdian Thung 13507127 Program Studi Teknik Informatika ITB, Jalan Ganesha 10 Bandung, Jawa Barat, email: if17127@students.if.itb.ac.id
Algoritma Backtracking Pada Permainan Peg Solitaire
 Algoritma Backtracking Pada Permainan Peg Solitaire Gilbran Imami, 13509072 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Algoritma Backtracking Pada Permainan Peg Solitaire Gilbran Imami, 13509072 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132,
Penggunaan Algoritma Runut-balik Pada Pencarian Solusi dalam Persoalan Magic Square
 Penggunaan Algoritma Runut-balik Pada Pencarian Solusi dalam Persoalan Magic Square Tahir Arazi NIM : 1350505 Program Studi Informatika, Sekolah Teknik Elektro dan Informatika, Institut Teknologi Bandung
Penggunaan Algoritma Runut-balik Pada Pencarian Solusi dalam Persoalan Magic Square Tahir Arazi NIM : 1350505 Program Studi Informatika, Sekolah Teknik Elektro dan Informatika, Institut Teknologi Bandung
Penyelesaian Game Lights Out dengan Algoritma Runut Balik
 Penyelesaian Game Lights Out dengan Algoritma Runut Balik Muhammad Aulia Firmansyah (13509039) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
Penyelesaian Game Lights Out dengan Algoritma Runut Balik Muhammad Aulia Firmansyah (13509039) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha
BAB IV TEORI PERMAINAN
 BAB IV TEORI PERMAINAN Teori permainan merupakan suatu model matematika yang digunakan dalam situasi konflik atau persaingan antara berbagai kepentingan yang saling berhadapan sebagai pesaing. Dalam permaian
BAB IV TEORI PERMAINAN Teori permainan merupakan suatu model matematika yang digunakan dalam situasi konflik atau persaingan antara berbagai kepentingan yang saling berhadapan sebagai pesaing. Dalam permaian
Algoritma Greedy dalam Strategi Permainan Centipede
 Algoritma Greedy dalam Strategi Permainan Centipede Roland Hartanto (13515107) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Algoritma Greedy dalam Strategi Permainan Centipede Roland Hartanto (13515107) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung
Variasi Pohon Pencarian Biner Seimbang
 Variasi Pohon Pencarian Biner Seimbang Tony 13516010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia buddy90_lost@yahoo.co.id
Variasi Pohon Pencarian Biner Seimbang Tony 13516010 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10 Bandung 40132, Indonesia buddy90_lost@yahoo.co.id
Penyelesaian Permasalahan Nonogram dengan Algoritma Runut Balik
 Penyelesaian Permasalahan Nonogram dengan Algoritma Runut Balik Hendra Hadhil Choiri (135 08 041) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Penyelesaian Permasalahan Nonogram dengan Algoritma Runut Balik Hendra Hadhil Choiri (135 08 041) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl.
Penggunaan Graf Semi-Hamilton untuk Memecahkan Puzzle The Hands of Time pada Permainan Final Fantasy XIII-2
 Penggunaan Graf Semi-Hamilton untuk Memecahkan Puzzle The Hands of Time pada Permainan Final Fantasy XIII-2 Michael - 13514108 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut
Penggunaan Graf Semi-Hamilton untuk Memecahkan Puzzle The Hands of Time pada Permainan Final Fantasy XIII-2 Michael - 13514108 Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut
Penerapan Algoritma Greedy Untuk Memenangkan Permainan Go
 Penerapan Algoritma Greedy Untuk Memenangkan Permainan Go Innani Yudho afi (13511054) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
Penerapan Algoritma Greedy Untuk Memenangkan Permainan Go Innani Yudho afi (13511054) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
RANGKUMAN MATERI FUNGSI KOMPOSISI DAN FUNGSI INVERS
 RANGKUMAN MATERI FUNGSI KOMPOSISI DAN FUNGSI INVERS Diajukan untuk Memenuhi Tugas Mata Kuliah Matematika Sekolah Dosen Pembina: Dr. Tatag Yuli Eko Siswono, M.Pd. Universitas Negeri Surabaya Oleh Siti Rohmawati
RANGKUMAN MATERI FUNGSI KOMPOSISI DAN FUNGSI INVERS Diajukan untuk Memenuhi Tugas Mata Kuliah Matematika Sekolah Dosen Pembina: Dr. Tatag Yuli Eko Siswono, M.Pd. Universitas Negeri Surabaya Oleh Siti Rohmawati
