Pengintegralan Fungsi Rasional
|
|
|
- Widya Hartanto
- 8 tahun lalu
- Tontonan:
Transkripsi
1 Pengintegralan Fungsi Rasional Ahmad Kamsyakawuni, M.Kom Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Jember 25 Maret 2014
2 Pengintegralan Fungsi Rasional 1 Pengintegralan Fungsi Rasional 2
3 Pengintegralan Fungsi Rasional 1 Pengintegralan Fungsi Rasional 2
4 Pengintegralan Fungsi Rasional Fungsi Rasional (FR) merupakan hasil bagi dua fungsi suku banyak (polinom). 1 Derajat pembilang kurang dari derajat penyebut (FR Sejati). f (x) = 2 (x + 1) 3 g(x) = 2x + 2 x 2 4x Derajat pembilang lebih dari derajat penyebut (FR Tidak Sejati). h(x) = x 5 + 2x 3 x + 1 x 3 + 5x
5 Pengintegralan Fungsi Rasional Fungsi Rasional (FR) merupakan hasil bagi dua fungsi suku banyak (polinom). 1 Derajat pembilang kurang dari derajat penyebut (FR Sejati). f (x) = 2 (x + 1) 3 g(x) = 2x + 2 x 2 4x Derajat pembilang lebih dari derajat penyebut (FR Tidak Sejati). h(x) = x 5 + 2x 3 x + 1 x 3 + 5x
6 Pengintegralan Fungsi Rasional Fungsi Rasional (FR) merupakan hasil bagi dua fungsi suku banyak (polinom). 1 Derajat pembilang kurang dari derajat penyebut (FR Sejati). f (x) = 2 (x + 1) 3 g(x) = 2x + 2 x 2 4x Derajat pembilang lebih dari derajat penyebut (FR Tidak Sejati). h(x) = x 5 + 2x 3 x + 1 x 3 + 5x
7 Pengintegralan Fungsi Rasional FR Tidak Sejati selalu dapat ditulis sebagai jumlah fungsi suku banyak dan FR sejati. h(x) = x 5 + 2x 3 x + 1 x 3 + 5x = x x + 1 x 3 + 5x
8 Pengintegralan Fungsi Rasional Tentukan 2 (x + 1) 3 dx = 2 (x + 1) 3 (x + 1) 2 d(x + 1) = 2 + C = 1 2 (x + 1) 2 + C Tentukan 2x + 2 x 2 4x + 8 dx Misal u = x 2 4x + 8; du = 2x 4
9 Pengintegralan Fungsi Rasional Tentukan 2 (x + 1) 3 dx = 2 (x + 1) 3 (x + 1) 2 d(x + 1) = 2 + C = 1 2 (x + 1) 2 + C Tentukan 2x + 2 x 2 4x + 8 dx Misal u = x 2 4x + 8; du = 2x 4
10 Pengintegralan Fungsi Rasional Tentukan 2 (x + 1) 3 dx = 2 (x + 1) 3 (x + 1) 2 d(x + 1) = 2 + C = 1 2 (x + 1) 2 + C Tentukan 2x + 2 x 2 4x + 8 dx Misal u = x 2 4x + 8; du = 2x 4
11 Pengintegralan Fungsi Rasional catatan: = 2x 4 x 2 4x + 8 dx + = ln x 2 4x C x 2 4x dx = 6 x 2 4x + 8 dx 1 x 2 4x dx 1 (x 2) 2 d(x 2) + 4 ( x 2 2x + 2 x 2 4x + 8 dx = ln x 2 4x tan 1 du a 2 + u 2 = 1 ( u ) a tan 1 + C = 1 ( x 2 a 2 tan ) + K ) + C
12 2 x (x + 1) + 3(x 1) = x + 1 (x 1)(x + 1) = 5x 1 (x 1)(x + 1) = 5x 1 x 2 1 Untuk keperluan yang kita pelajari adalah mengerjakan sebaliknya Contoh Jabarkan 3x 1, kemudian tentukan integralnya! x 2 x 6 3x 1 (x + 2)(x 3) = A x B x 3
13 2 x (x + 1) + 3(x 1) = x + 1 (x 1)(x + 1) = 5x 1 (x 1)(x + 1) = 5x 1 x 2 1 Untuk keperluan yang kita pelajari adalah mengerjakan sebaliknya Contoh Jabarkan 3x 1, kemudian tentukan integralnya! x 2 x 6 3x 1 (x + 2)(x 3) = A x B x 3
14 Penjabarannya 3x 1 = A(x 3) + B(x + 2) 3x 1 = Ax 3A + Bx + 2B 3x 1 = (A + B)x + ( 3A + 2B) A + B = 3 A = B + 3 3A + 2B = 1 3( B + 3) + 2B = 1 B = 8 5 ; A = = 7 5 3x 1 (x + 2)(x 3) = 7/5 x /5 x 3
15 Faktor Linear Berlainan Integralnya = = 3x 1 x 2 x 6 dx 3x 1 (x + 2)(x 3) dx 7/5 x + 2 dx + 8/5 x 3 dx = 7 5 ln x ln x 3 + C 5
16 Faktor Linear Berbeda Tentukan Jawab 5x + 3 (x 3 2x 2 3x) dx 5x + 3 (x 3 2x 2 3x) = 5x + 3 x(x + 1)(x 3) = A x + B x x + 3 = A(x + 1)(x 3) + Bx(x 3) + Cx(x + 1) C x 3 substitusikan x = 0; x = 1; x = 3 3 = A( 3) A = 1 2 = B(4) B = = C(12) C = 3 2
17 Faktor Linear Berbeda Tentukan Jawab 5x + 3 (x 3 2x 2 3x) dx 5x + 3 (x 3 2x 2 3x) = 5x + 3 x(x + 1)(x 3) = A x + B x x + 3 = A(x + 1)(x 3) + Bx(x 3) + Cx(x + 1) C x 3 substitusikan x = 0; x = 1; x = 3 3 = A( 3) A = 1 2 = B(4) B = = C(12) C = 3 2
18 Faktor Linear Berbeda 5x + 3 x 3 2x 2 3x dx 1 = x dx x + 1 dx x 3 = ln x 1 2 ln x ln x 3 +C 2
19 Faktor Linear Berulang Tentukan Jawab Penjabarannya x (x 3) 2 dx substitusi : x = 3; x = 0 3 = B 0 = A( 3) + B A = 1 x (x 3) 2 = A x 3 + B (x 3) 2 x = A(x 3) + B
20 Faktor Linear Berulang Tentukan Jawab Penjabarannya x (x 3) 2 dx substitusi : x = 3; x = 0 3 = B 0 = A( 3) + B A = 1 x (x 3) 2 = A x 3 + B (x 3) 2 x = A(x 3) + B
21 Faktor Linear Berulang Integralnya x (x 3) 2 dx = 1 x 3 dx (x 3) 2 dx = ln x 3 3 x 3 + C
22 Faktor Linear Berbeda dan Berulang Tentukan 3x 2 8x + 13 (x + 3)(x 1) 2 dx Jawab Penjabarannya 3x 2 8x + 13 (x + 3)(x 1) 2 = A x B (x 1) + C (x 1) 2 3x 2 8x + 13 = A(x 1) 2 + B(x 1)(x + 3) + C(x + 3)
23 Faktor Linear Berbeda dan Berulang Tentukan 3x 2 8x + 13 (x + 3)(x 1) 2 dx Jawab Penjabarannya 3x 2 8x + 13 (x + 3)(x 1) 2 = A x B (x 1) + C (x 1) 2 3x 2 8x + 13 = A(x 1) 2 + B(x 1)(x + 3) + C(x + 3)
24 Faktor Linear Berbeda dan Berulang Substitusikan : x = 1; x = 3; x = 0 8 = C(4) C = 2 64 = A(16) A = 4 13 = A + B( 3) + C(3) 13 = 4 + B( 3) + 6 B = 1 3x 2 8x + 13 (x + 3)(x 1) 2 dx = 4 dx x + 3 dx x = 4 ln x + 3 ln x 1 2 x 1 + C dx (x 1) 2
25 Faktor Linear Berbeda dan Berulang Substitusikan : x = 1; x = 3; x = 0 8 = C(4) C = 2 64 = A(16) A = 4 13 = A + B( 3) + C(3) 13 = 4 + B( 3) + 6 B = 1 3x 2 8x + 13 (x + 3)(x 1) 2 dx = 4 dx x + 3 dx x = 4 ln x + 3 ln x 1 2 x 1 + C dx (x 1) 2
26 Faktor Kuadrat yang Berbeda Tentukan 6x 2 3x + 1 (4x + 1)(x 2 + 1) dx Jawab Penjabarannya 6x 2 3x + 1 (4x + 1)(x 2 + 1) = A 4x Bx + C (x 2 + 1) 6x 2 3x + 1 = A(x 2 + 1) + (Bx + C)(4x + 1)
27 Faktor Kuadrat yang Berbeda Tentukan 6x 2 3x + 1 (4x + 1)(x 2 + 1) dx Jawab Penjabarannya 6x 2 3x + 1 (4x + 1)(x 2 + 1) = A 4x Bx + C (x 2 + 1) 6x 2 3x + 1 = A(x 2 + 1) + (Bx + C)(4x + 1)
28 Faktor Kuadrat yang Berbeda Substitusikan : x = 1 4 ; x = 0; x = = A( 17 6 ) A = 2 1 = 2 + C C = 1 4 = 4 + (B 1)(5) B = 1 6x 2 3x + 1 (4x + 1)(x 2 + 1) dx = 2 x 1 4x + 1 dx + x dx
29 Faktor Kuadrat yang Berbeda Substitusikan : x = 1 4 ; x = 0; x = = A( 17 6 ) A = 2 1 = 2 + C C = 1 4 = 4 + (B 1)(5) B = 1 6x 2 3x + 1 (4x + 1)(x 2 + 1) dx = 2 x 1 4x + 1 dx + x dx
30 Faktor Kuadrat yang Berbeda 6x 2 3x + 1 (4x + 1)(x 2 + 1) dx = 1 2 4dx 4x xdx x dx x = 1 2 ln 4x ln x tan 1 x + C du a 2 + u 2 = 1 a tan 1 ( u a ) + C
31 Faktor Kuadrat yang Berbeda 6x 2 3x + 1 (4x + 1)(x 2 + 1) dx = 1 2 4dx 4x xdx x dx x = 1 2 ln 4x ln x tan 1 x + C du a 2 + u 2 = 1 a tan 1 ( u a ) + C
32 Faktor Kuadrat Berulang Tentukan 6x 2 15x + 22 (x + 3)(x 2 + 2) 2 dx Jawab Penjabarannya 6x 2 15x + 22 (x + 3)(x 2 + 2) 2 = A x Bx + C x Dx + E (x 2 + 2) 2 6x 2 15x + 22 = A(x 2 + 2) 2 + (Bx + C)(x + 3)(x 2 + 2)+ (Dx + E)(x + 3)
33 Faktor Kuadrat Berulang Tentukan 6x 2 15x + 22 (x + 3)(x 2 + 2) 2 dx Jawab Penjabarannya 6x 2 15x + 22 (x + 3)(x 2 + 2) 2 = A x Bx + C x Dx + E (x 2 + 2) 2 6x 2 15x + 22 = A(x 2 + 2) 2 + (Bx + C)(x + 3)(x 2 + 2)+ (Dx + E)(x + 3)
34 Faktor Kuadrat Berulang substitusikan : x = 3; x = 0; x = 1; x = 2; x = 3 x = = A(121) A = 1 x = 0 22 = A(4) + C(6) + E(3) 18 = C(6) + E(3) E = 6 C(2) x = 1 13 = A(9) + B(12) + C(12) + D(4) + E(4) 4 = B(12) + C(12) + D(4) + E(4)...(1) x = 2 16 = A(36) + B(60) + C(30) + D(10) + E(5) 20 = B(60) + C(30) + D(10) + E(5)...(2) x = 3 31 = A(121) + B(198) + C(66) + D(18) + E(6) 90 = B(198) + C(66) + D(18) + E(6)...(3)
35 Faktor Kuadrat Berulang E = 6 + C(2)...(4) 1 = B(3) + C(3) + D + E 5 = B(3) + C + D...(5) 4 = B(12) + C(6) + D(2) + E 10 = B(12) + C(4) + D(2) 5 = B(6) + C(2) + D...(6) 15 = B(33)+C11)+D(3)+E 21 = B(33)+C(9)+D(3) 7 = B(11) + C(3) + D...(7) (5) dan (7) 5 = B(3) + C + D 7 = B(11) + C(3) + D 2 = B( 8) + C( 2)...(8)
36 Faktor Kuadrat Berulang E = 6 + C(2)...(4) 1 = B(3) + C(3) + D + E 5 = B(3) + C + D...(5) 4 = B(12) + C(6) + D(2) + E 10 = B(12) + C(4) + D(2) 5 = B(6) + C(2) + D...(6) 15 = B(33)+C11)+D(3)+E 21 = B(33)+C(9)+D(3) 7 = B(11) + C(3) + D...(7) (5) dan (7) 5 = B(3) + C + D 7 = B(11) + C(3) + D 2 = B( 8) + C( 2)...(8)
37 Faktor Kuadrat Berulang (6) dan (7) 5 = B(6) + C(2) + D 7 = B(11) + C(3) + D 2 = B( 8) + C( 2)...(9) (8) dan (9) 1 = B( 4) + C( 1) 2 = B( 5) + C( 1) B = 1 substitusi ke: (5), (6) dan (7) 2 = C + D...(10) 1 = C(2) + D...(11) 4 = C(3) + D...(12)
38 Faktor Kuadrat Berulang (6) dan (7) 5 = B(6) + C(2) + D 7 = B(11) + C(3) + D 2 = B( 8) + C( 2)...(9) (8) dan (9) 1 = B( 4) + C( 1) 2 = B( 5) + C( 1) B = 1 substitusi ke: (5), (6) dan (7) 2 = C + D...(10) 1 = C(2) + D...(11) 4 = C(3) + D...(12)
39 Faktor Kuadrat Berulang (6) dan (7) 5 = B(6) + C(2) + D 7 = B(11) + C(3) + D 2 = B( 8) + C( 2)...(9) (8) dan (9) 1 = B( 4) + C( 1) 2 = B( 5) + C( 1) B = 1 substitusi ke: (5), (6) dan (7) 2 = C + D...(10) 1 = C(2) + D...(11) 4 = C(3) + D...(12)
40 Faktor Kuadrat Berulang (10) dan (11) 2 = C + D 1 = C(2) + D 3 = C( 1) C = 3 substitusi ke pers (10) 2 = C + D D = 5 substitusi ke pers (4) E = 6 + C( 2) E = 0 sehingga diperoleh : A = 1; B = 1; C = 3; D = 5; E = 0
41 Faktor Kuadrat Berulang (10) dan (11) 2 = C + D 1 = C(2) + D 3 = C( 1) C = 3 substitusi ke pers (10) 2 = C + D D = 5 substitusi ke pers (4) E = 6 + C( 2) E = 0 sehingga diperoleh : A = 1; B = 1; C = 3; D = 5; E = 0
42 Faktor Kuadrat Berulang (10) dan (11) 2 = C + D 1 = C(2) + D 3 = C( 1) C = 3 substitusi ke pers (10) 2 = C + D D = 5 substitusi ke pers (4) E = 6 + C( 2) E = 0 sehingga diperoleh : A = 1; B = 1; C = 3; D = 5; E = 0
43 Faktor Kuadrat Berulang (10) dan (11) 2 = C + D 1 = C(2) + D 3 = C( 1) C = 3 substitusi ke pers (10) 2 = C + D D = 5 substitusi ke pers (4) E = 6 + C( 2) E = 0 sehingga diperoleh : A = 1; B = 1; C = 3; D = 5; E = 0
44 Faktor Kuadrat Berulang = 6x 2 15x + 22 (x + 3)(x 2 + 2) 2 = A x Bx + C x Dx + E (x 2 + 2) 2 6x 2 15x + 22 (x + 3)(x 2 + 2) 2 dx 1 x + 3 = x + 3 dx + x dx + 5x (x 2 + 2) 2 dx dx x x x dx x dx 5 2 2x (x 2 + 2) 2 dx = ln x ln(x 2 + 2) + 3 tan 1 ( x 5 ) (x 2 + 2) + C
45 Faktor Kuadrat Berulang catatan: = 1 a tan 1 ( u a ) + C du a 2 +u 2 Untuk faktor berbentuk (ax + b) k, penjabarannya: A 1 (ax + b) + A 2 (ax + b) 2 + A 3 (ax + b) A k (ax + b) k Untuk faktor berbentuk (ax 2 + bx + c) m, penjabarannya: B 1 x + C 1 (ax 2 + bx + c) + B 2 x + C 2 (ax 2 + bx + c) 2 + B 3 x + C 3 (ax 2 + bx + c) B mx + C m (ax 2 + bx + c) m
46 Pengintegralan Fungsi Rasional Latihan Soal x+3 x 2 9 dx 2x 2 +x 4 x 3 x 2 2x dx 2x 2 +x 8 dx x 3 +4x x 3 8x 2 1 (x+3)(x 2)(x 2 +1) dx x 3 4x (x 2 +1) 2 dx
47 Pengintegralan Fungsi Rasional Latihan Soal x+3 x 2 9 dx 2x 2 +x 4 x 3 x 2 2x dx 2x 2 +x 8 dx x 3 +4x x 3 8x 2 1 (x+3)(x 2)(x 2 +1) dx x 3 4x (x 2 +1) 2 dx
48 Pengintegralan Fungsi Rasional Latihan Soal x+3 x 2 9 dx 2x 2 +x 4 x 3 x 2 2x dx 2x 2 +x 8 dx x 3 +4x x 3 8x 2 1 (x+3)(x 2)(x 2 +1) dx x 3 4x (x 2 +1) 2 dx
49 Pengintegralan Fungsi Rasional Latihan Soal x+3 x 2 9 dx 2x 2 +x 4 x 3 x 2 2x dx 2x 2 +x 8 dx x 3 +4x x 3 8x 2 1 (x+3)(x 2)(x 2 +1) dx x 3 4x (x 2 +1) 2 dx
50 Pengintegralan Fungsi Rasional Latihan Soal x+3 x 2 9 dx 2x 2 +x 4 x 3 x 2 2x dx 2x 2 +x 8 dx x 3 +4x x 3 8x 2 1 (x+3)(x 2)(x 2 +1) dx x 3 4x (x 2 +1) 2 dx
51 Pengintegralan Fungsi Rasional Latihan Soal x+3 x 2 9 dx 2x 2 +x 4 x 3 x 2 2x dx 2x 2 +x 8 dx x 3 +4x x 3 8x 2 1 (x+3)(x 2)(x 2 +1) dx x 3 4x (x 2 +1) 2 dx
Kalkulus 2. Teknik Pengintegralan ke - 3. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
Kalkulus 2 Teknik Pengintegralan ke - 3 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 27 Daftar
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
SUKU BANYAK. A. Teorema Sisa 1) F(x) = (x b) H(x) + S, maka S = F(b) 2) F(x) = (ax b) H(x) + S, maka S = F( a
SUKU BANYAK A. Teorema Sisa 1) F(x) = (x b) H(x) + S, maka S = F(b) 2) F(x) = (ax b) H(x) + S, maka S = F( a b ) 3) F(x) : [(x a)(x b)], maka S(x) = (x a)s 2 + S 1, dengan S 2 adalah sisa pembagian pada
TEKNIK PENGINTEGRALAN
TEKNIK PENGINTEGRALAN Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 2 Topik Bahasan Pendahuluan 2 Manipulasi Integran 3 Integral Parsial 4 Dekomposisi
Teknik pengintegralan: Integral fungsi pecah rasional (bagian 1)
Teknik pengintegralan: Integral fungsi pecah rasional (bagian 1) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 07 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 07/02/2017 1 / 8 Pemeran-pemeran
STANDAR KOMPETENSI KOMPETENSI DASAR. Menggunakan aturan suku banyak dalam penyelesaian masalah
STANDAR KOMPETENSI Menggunakan aturan suku banyak dalam penyelesaian masalah KOMPETENSI DASAR Menggunakan teorema sisa dan teorema faktor dalam pemecahan masalah INDIKATOR Menentukan faktor, akar-akar
POLINOM (SUKU BANYAK) Menggunakan aturan suku banyak dalam penyelesaian masalah.
POLINOM (SUKU BANYAK) Standar Kompetensi: Menggunakan aturan suku banyak dalam penyelesaian masalah. Kompetensi Dasar: 1. Menggunakan algoritma pembagian suku banyak untuk menentukan hasil bagi dan sisa
Kalkulus 2. Teknik Pengintegralan ke - 2. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
Kalkulus 2 Teknik Pengintegralan ke - 2 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 24 Daftar
TEKNIK PENGINTEGRALAN
TEKNIK PENGINTEGRALAN KALKULUS S- Teknik Industri Outline Integral Parsial Integral Fungsi Trigonometri Substitusi Trigonometri Integral Fungsi Rasional . Integral Parsial Formula Integral Parsial : u
TEOREMA SISA 1. Nilai Sukubanyak Tugas 1
TEOREMA SISA 1. Nilai Sukubanyak Apa yang dimaksud sukubanyak (polinom)? Ingat kembali bentuk linear seperti 2x + 1 atau bentuk kuadrat 2x 2-3x + 5 dan juga bentuk pangkat tiga 2x 3 x 2 + x 7. Bentuk-bentuk
Teknik Pengintegralan
Jurusan Matematika 13 Nopember 2012 Review Rumus-rumus Integral yang Dikenal Pada beberapa subbab sebelumnya telah dijelaskan beberapa integral dari fungsi-fungsi tertentu. Berikut ini diberikan sebuah
Catatan Kuliah KALKULUS II BAB V. INTEGRAL
BAB V. INTEGRAL Anti-turunan dan Integral TakTentu Persamaan Diferensial Sederhana Notasi Sigma dan Luas Daerah di Bawah Kurva Integral Tentu Teorema Dasar Kalkulus Sifat-sifat Integral Tentu Lebih Lanjut
Hendra Gunawan. 4 September 2013
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 4 September 2013 Latihan (Kuliah yang Lalu) 1. Tentukan daerah asal dan daerah nilai fungsi 2 f(x) = 1 x. sudah dijawab 2. Gambar grafik fungsi
Teorema Faktor. Misalkan P (x) suatu polynomial, (x k) merupakan faktor dari P (x) jika dan hanya jika P (k) = 0
Teorema faktor adalah salah satu teorema pada submateri polynomial. Teorema ini cukup terkenal dan sangat berguna untuk menyelesaikan soal - soal baik level sekolah maupun soal level olimpiade. Berikut
RENCANA PELAKSANAAN PEMBELAJARAN
RENCANA PELAKSANAAN PEMBELAJARAN Mata Pelajaran : Matematika Kelas/ Semester: XI Program IPA/2 Alokasi Waktu: 8 jam Pelajaran (4 Pertemuan) A. Standar Kompetensi Menggunakan aturan sukubanyak dalam penyelesaian
Pecahan Parsial (Partial Fractions)
oki neswan (fmipa-itb) Pecahan Parsial (Partial Fractions) Diberikan fungsi rasional f (x) p(x) q(x) f (x) r(x) : Jika deg p deg q; maka r (x) ^p (x) q(x) ; dengan deg r < deg q: p (x) q (x) r (x) ^p (x)
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
SUKU BANYAK. Secara umum sukubanyak atau polinom dalam berderajat dapat ditulis dalam bentuk berikut:
SUKU BANYAK A. Pengertian Suku Banyak Secara umum sukubanyak atau polinom dalam berderajat dapat ditulis dalam bentuk berikut: Dinamakan suku banyak (polinom) dalam yang berderajat dengan bilangan cacah
A. Menyelesaikan Persamaan Kuadrat
Jurnal Materi Umum Persamaan Kuadrat Peta Konsep Fungsi Kuadrat Peta Konsep Daftar Hadir Materi A SoalLatihan PERSAMAAN DAN FUNGSI KUADRAT Kelas X, Semester A. Menyelesaikan Persamaan Kuadrat Menyelesaikan
PERSAMAAN KUADRAT. AC 0 P DAN Q SAMA TANDA. 2. DG. MELENGKAPKAN BENTUK KUADRAT ( KUADRAT SEMPURNA ) :
PERSAMAAN KUADRAT. AC 0 P DAN Q SAMA TANDA.. DG. MELENGKAPKAN BENTUK KUADRAT ( KUADRAT SEMPURNA ) : Bab 3 PERSAMAAN KUADRAT 1. Bentuk Umum : ax bx c 0, a 0, a, b, c Re al Menyelesaikan persamaan kuadrat
MA1201 KALKULUS 2A Do maths and you see the world
Catatan Kuliah MA20 KALKULUS 2A Do maths and you see the world disusun oleh Khreshna I.A. Syuhada, MSc. PhD. Kelompok Keilmuan STATISTIKA - FMIPA Institut Teknologi Bandung 203 Catatan kuliah ini ditulis
FUNGSI-FUNGSI INVERS
FUNGSI-FUNGSI INVERS Logaritma, Eksponen, Trigonometri Invers Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 49 Topik Bahasan Fungsi Satu ke Satu 2
log2 PEMBAHASAN SOAL TRY OUT = = 2 1 = 27 8 = 19 Jawaban : C = = = 2( 15 10) Jawaban : B . 4. log3 1 2 (1) .
TRY OUT AKBAR UN SMA 08 PEMBAHASAN SOAL TRY OUT. 9 6 4 8 7 Jawaban : C 4 4 = = = 7 8 4 = 9. 5 + = 0 5 = 0 5 = 5 0 = ( 5 0). log5 5 log8 log6 4 log log4 = log5 5 4 log log log6 log4 =. log5 5. 4. log log
SOLUSI UJIAN SEKOLAH SEKOLAH MENENGAH ATAS (SMA) DINAS PENDIDIKAN KOTA BEKASI TAHUN PELAJARAN 2013/ a 16. definit positif adalah...
SOLUSI UJIAN SEKOLAH SEKOLAH MENENGAH ATAS (SMA) DINAS PENDIDIKAN KOTA BEKASI TAHUN PELAJARAN /. Nilai a yang menyebabkan fungsi kuadrat f x a x ax a a a a a a Solusi: [Jawaban D] a a a. () D a a a a a
MBS - DTA. Sucipto UNTUK KALANGAN SENDIRI. SMK Muhammadiyah 3 Singosari
MBS - DTA Sucipto UNTUK KALANGAN SENDIRI SMK Muhammadiyah Singosari SERI : MBS-DTA FUNGSI STANDAR KOMPETENSI Siswa mampu memecahkan masalah yang berkaitan dengan fungsi, persamaan fungsi linear dan fungsi
Setelah kita mengetahui hasil dari masing-masing persamaan, kemudian kita kembali gabungkan kedua persamaan tersebut :
Kumpulan Soal-Soal Diferensial 1. Tentukan turunan pertama dari y = (3x-2) 4 +(4x-1) 3 adalah... Jawab: misalnya : f (x) = y = (3x-2) 4 misal U = (3x-2) du/dx = 3 dy/dx = n.u n-1. du/dx = 4. (3x-2) 4-1.3
Wardaya College. Tes Simulasi Ujian Nasional SMA Berbasis Komputer. Mata Pelajaran Matematika Tahun Ajaran 2017/2018
Tes Simulasi Ujian Nasional SMA Berbasis Komputer Mata Pelajaran Matematika Tahun Ajaran 07/08 -. Jika diketahui x = 8, y = 5 dan z = 8, maka nilai dari x y z adalah.... (a) 0 (b) 00 (c) 500 (d) 750 (e)
SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 2011/2012
SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPA TAHUN PELAJARAN 0/0. Akar-akar persamaan kuadrat x +ax - 40 adalah p dan q. Jika p - pq + q 8a, maka nilai a... A. -8 B. -4 C. 4 D. 6 E. 8 BAB III Persamaan
Soal dan Pembahasan Tentang Suku Banyak
Soal dan Pembahasan Tentang Suku Banyak Oleh : Fendi Alfi Fauzi 9 Maret 014 1. Nilai suku banyak untuk f (x) = x 3 x 3x + 5 untuk x = adalah... f ( ) = ( ) 3 ( ) 3 ( ) + 5 = 16 4 + 6 + 5 = 0 + 11 = 9.
BAB 2 PERSAMAAN DIFFERENSIAL BIASA
BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
BAB 5 TEOREMA SISA. Menggunakan aturan sukubanyak dalam penyelesaian masalah. Kompetensi Dasar
Standar Kompetensi BAB 5 TEOREMA SISA Menggunakan aturan sukubanyak dalam penyelesaian masalah. Kompetensi Dasar Menggunakan algoritma pembagian sukubanyak untuk menentukan hasil bagi dan sisa pembagian
Kalkulus 2. Teknik Pengintegralan ke - 1. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
BAB IV PERTIDAKSAMAAN. 1. Pertidaksamaan Kuadrat 2. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak
BAB IV PERTIDAKSAMAAN 1. Pertidaksamaan Kuadrat. Pertidaksamaan Bentuk Pecahan 3. Pertidaksamaan Bentuk Akar 4. Pertidaksamaan Nilai Mutlak 86 LEMBAR KERJA SISWA 1 Mata Pelajaran : Matematika Uraian Materi
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
INTISARI KALKULUS Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 010 Pengantar Kalkulus 1 & merupakan matakuliah wajib tingkat pertama bagi semua
TEKNIK-TEKNIK PENGINTEGRALAN
TEKNIK-TEKNIK PENGINTEGRALAN 1. Teknik Subtitusi Teorema : Misal g fungsi yang terdiferensialkan dan F suatu anti turunan dari f, jika u = g() maka f(g())g () d = f(u) du = F(u) + c = F(g()) + c sin. 1.
INTEGRAL TAK TENTU 1
INTEGRAL TAK TENTU 1 Rumus umum integral b a f (x) dx F(x) =lambang integral f(x) = integran (fungsi yg diintegralkan) a dan b = batas pengintegralan a = batas bawah b = batas atas dx = faktor pengintegral
Indikator : Menentukan penarikan kesimpulan dari beberapa premis. Modus Ponens Modus Tollens Silogisme
Indikator : Menentukan penarikan kesimpulan dari beberapa premis Modus Ponens Modus Tollens Silogisme p q p q p q p ~q q r q ~p p r Bentuk ekuivalen : p q ~q ~p p q ~p q Soal 1 : Diketahui premis : Premis
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN. DEPARTEMEN TEKNIK KIMIA Universitas Indonesia
KALKULUS BAB II FUNGSI, LIMIT, DAN KEKONTINUAN DEPARTEMEN TEKNIK KIMIA Universitas Indonesia BAB II. FUNGSI, LIMIT, DAN KEKONTINUAN Fungsi dan Operasi pada Fungsi Beberapa Fungsi Khusus Limit dan Limit
MODUL MATEMATIKA XI IPA SUKU BANYAK SMA SANTA ANGELA TAHUN PELAJARAN SEMSTER GENAP
MODUL MATEMATIKA XI IPA SUKU BANYAK SMA SANTA ANGELA TAHUN PELAJARAN 05 06 SEMSTER GENAP STANDAR KOMPETENSI 4. Menggunakan aturan sukubanyak dalam penyelesaian masalah. KOMPETENSI DASAR 4. Menggunakan
MA1201 KALKULUS 2A (Kelas 10) Bab 8: Bentuk Tak Tentu d
MA1201 KALKULUS 2A (Kelas 10) Bab 8: dan Do maths and you see the world ? Pengantar Bentuk tak tentu? Bentuk apa? Bentuk tak tentu yang dimaksud adalah bentuk limit dengan nilai seolah-olah : 0 0 ; ; 0
JADWAL UTS GENAP TAHUN AKADEMIK 2017/2018 PROGRAM STUDI S1. MANAJEMEN
HARI/TANGGAL : KAMIS, 29 MARET 2018 08.30-10.30 Lab. Pengantar Akuntansi I AX 28 C.0601 BX 27 08.30-10.30 Lab. Akuntansi Biaya AX 7 B.0606 BX 28 B.0606 CX 10 DX 38 B.0605 EX 45 B.0604 08.30-10.30 Sosiologi
JADWAL UJIAN TENGAH SEMESTER GENAP TAHUN AKADEMIK 2015/2016 PROGRAM STUDI S 1 MANAJEMEN
HARI/TANGGAL : SENIN, 4 APRIL 2016 WAKTU MATA KULIAH KLS JML RUANG 08.30-10.30 PENGANTAR BISNIS AX 17 B.0605 BX 20 B.0605 PENGANTAR EKONOMI MAKRO AX 48 C.0601 BX 49 CX 30 DX 48 B.0501 B.0503 EX 50 B.0503
PERSAMAAN KUADRAT. Persamaan. Sistem Persamaan Linear
Persamaan Sistem Persamaan Linear PENGERTIAN Definisi Persamaan kuadrat adalah kalimat matematika terbuka yang memuat hubungan sama dengan yang pangkat tertinggi dari variabelnya adalah 2. Bentuk umum
Jakarta,. Guru Mata Pelajaran Memeriksa / Mengetahui Kepala SMP NIP... NIP...
Kompetensi Dasar : 2.1 Mengenali bentuk aljabar dan unsur-unsurnya. 2.2 Melakukan operasi pada bentuk aljabar. Indikator : 1. Menentukan variabel, koefisien, konstanta, dan suku sejenis. 2. Menentukan
Mata Pelajaran Wajib. Disusun Oleh: Ngapiningsih
Mata Pelajaran Wajib Disusun Oleh: Ngapiningsih Disklaimer Daftar isi Disklaimer Powerpoint pembelajaran ini dibuat sebagai alternatif guna membantu Bapak/Ibu Guru melaksanakan pembelajaran. Materi powerpoint
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL Dra.Sri Rejeki Dwi Putranti, M.Kes. Fakultas Teknik - Universitaas Yos Soedarso Surabaya Email : riccayusticia@gmail.com Abstrak Hubungan antara Differensial dan
Kunci Jawaban Quis 1 (Bab 1,2 dan 3) tipe 1
Kunci Jawaban Quis (Bab,2 dan 3) tipe. Tentukan representasi deret Taylor dari f(x) = ln( + x) di sekitar a =. Tuliskan sampai turunan ke 5. Kemudian estimasilah ln(.2) dengan menggunakan deret Taylor
PTE 4109, Agribisnis UB
MATEMATIKA EKONOMI PTE 4109, Agribisnis UB 1 Materi ang dipelajari Pengertian dan Unsur- unsur Fungsi Jenis- jenis fungsi Penggambaran fungsi Linear Penggambaran fungsi non linear -Penggal -Simetri - Perpanjangan
LOGO MAM 4121 KALKULUS 1. Dr. Wuryansari Muharini K.
LOGO MAM 4121 KALKULUS 1 Dr. Wuryansari Muharini K. BAB I. PENDAHULUAN SISTEM BILANGAN REAL, NOTASI SELANG, dan NILAI MUTLAK PERTAKSAMAAN SISTEM KOORDINAT GRAFIK PERSAMAAN SEDERHANA www.themegallery.com
Catatan Kuliah MA1123 Kalkulus Elementer I
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Modul 05 Persamaan Linear dan Persamaan Linear Simultan
Modul 05 Persamaan Linear dan Persamaan Linear Simultan 5.1. Persamaan Linear Persamaan adalah pernyataan kesamaan antara dua ekspresi aljabar yang cocok untuk bilangan nilai variable tertentu atau variable
KETIDAKSAMAAN. A. Pengertian
A. Pengertian KETIDAKSAMAAN Ketidaksamaan dinotasikan dengan 1. < (lebih Kecil 2. ( lebih kecil atau sama dengan)) 3. > ( lebih besar) 4. ( lebih besar atau sama dengan) Tanda di atas digunakan untuk membuat
JADWAL UAS GENAP TAHUN AKADEMIK 2017/2018 PROGRAM STUDI S1. MANAJEMEN
JADWAL UAS GENAP TAHUN AKADEMIK 2017/2018 PROGRAM STUDI S1. MANAJEMEN HARI/TANGGAL : JUM'AT, 25 MEI 2018 JURUSAN : MANAJEMEN WAKTU MATA KULIAH KLS JML RUANG 08.30-10.30 Seminar Manajemen SDM AX 11 C.0601
matematika PEMINATAN Kelas X SISTEM PERTIDAKSAMAAN LINEAR DAN KUADRAT K13 A. Pertidaksamaan Linear B. Daerah Pertidaksamaan Linear
K13 Kelas matematika PEMINATAN SISTEM PERTIDAKSAMAAN LINEAR DAN KUADRAT Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi pertidaksamaan
Soal-Soal dan Pembahasan Matematika IPA SBMPTN/SNMPTN 2008
Soal-Soal dan Pebahasan Mateatika IPA SBMPTN/SNMPTN 008. Diketahui fungsi-fungsi f dan g dengan f(x) g(x) x - x untuk setiap bilangan real x. Jika g(), f ' () f(), dan g ' () f(), aka g ' () A. C. 0 E.
TUJUAN INSTRUKSIONAL KHUSUS
PREVIEW KALKULUS TUJUAN INSTRUKSIONAL KHUSUS Mahasiswa mampu: menyebutkan konsep-konsep utama dalam kalkulus dan contoh masalah-masalah yang memotivasi konsep tersebut; menjelaskan menyebutkan konsep-konsep
Persamaan Di erensial Orde-2
oki neswan FMIPA-ITB Persamaan Di erensial Orde- Persamaan diferensial orde-n adalah persamaan yang melibatkan x; y; dan turunan-turunan y; dengan yang paling tinggi adalah turunan ke-n: F x; y; y ; y
Kata Pengantar. Cirebon, oktober Penulis
Kata Pengantar Alhamdulillah, segala puji kita panjatkan kepada Allah SWT atas limpahan Taufiq dan Hidayah-Nya, sehingga penulis dapat menyelesaikan tugas program komputer ini dengan baik. Tugas ini membahas
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 2010/2011 Tanggal Ujian: 01 Juni 2011
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 00/0 Tanggal Ujian: 0 Juni 0. Diketahui vektor u = (a, -, -) dan v = (a, a, -). Jika vektor u tegak lurus pada v, maka nilai a adalah... A.
PREDIKSI UAN MATEMATIKA SESUAI KISI-KISI PEMERINTAH
PREDIKSI UAN MATEMATIKA SESUAI KISI-KISI PEMERINTAH. Apabila P dan q kalimat pernyataan, di mana ~p q kalimat bernilai salah, maka kalimat yang benar berikut ini, kecuali (d) p q (~p ~q) (~p ~q) ~ (~p
Suku Banyak. A. Pengertian Suku Banyak B. Menentukan Nilai Suku Banyak C. Pembagian Suku Banyak D. Teorema Sisa E. Teorema Faktor
Bab 5 Sumber: www.in.gr Setelah mempelajari bab ini, Anda harus mampu menggunakan konsep, sifat, dan aturan fungsi komposisi dalam pemecahan masalah; menggunakan konsep, sifat, dan aturan fungsi invers
Ujian Nasional. Tahun Pelajaran 2010/2011 IPA MATEMATIKA (D10) UTAMA. SMA / MA Program Studi
Ujian Nasional Tahun Pelajaran 00/0 UTAMA SMA / MA Program Studi IPA MATEMATIKA (D0) c Fendi Alfi Fauzi alfysta@yahoo.com Ujian Nasional Tahun Pelajaran 00/0 (Pelajaran Matematika) Tulisan ini bebas dibaca
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 2008/2009
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 008/009. Perhatikan premis premis berikut! - Jika saya giat belajar maka saya bisa meraih juara - Jika saya bisa meraih juara maka saya boleh
INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP
A. Soal dan Pembahasan. ( x ) dx... Jawaban : INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP ( x) dx x dx x C x C x x C. ( x 9) dx... x Jawaban : ( x 9) dx. (x x 9) dx x 9x C x x x. (x )(x + ) dx =.
SOAL PREDIKSI UJIAN NASIONAL MATEMATIKA IPA 2015
SOAL PREDIKSI UJIAN NASIONAL MATEMATIKA IPA 0 Paket Pilihlah jawaban yang paling tepat!. Diberikan premis-premis berikut!. Jika pengguna kendaraan bermotor bertambah banyak maka kemacetan di ruas jalan
Pembahasan Matematika IPA SNMPTN 2012 Kode 132
Tutur Widodo Pembahasan Matematika IPA SNMPTN 0 Pembahasan Matematika IPA SNMPTN 0 Kode Oleh Tutur Widodo. Lingkaran (x 6) + (y + ) = menyinggung garis x = di titik... (, 6) d. (, ) (, 6) e. (, ) c. (,
Materi Fungsi Linear Fungsi Variabel, koefisien, dan konstanta Variabel variabel bebas Koefisien Konstanta 1). Pengertian fungsi linier
Materi Fungsi Linear Admin 8:32:00 PM Duhh akhirnya nongol lagi... kali ini saya akan bahas mengenai pelajaran yang paling disukai oleh hampir seluruh warga dunia :v... MATEMATIKA, ya itu namanya. materi
Aturan dasar pengintegralan Integral fungsi rasional Integral parsial Integral trigonometri Substitusi yang merasionalkan Strategi pengintegralan
Aturan dasar pengintegralan Integral fungsi rasional Integral parsial Integral trigonometri Substitusi yang merasionalkan Strategi pengintegralan Kemampuan yang diinginkan: kejelian melihat bentuk soal
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 2010
Soal-Soal dan Pembahasan Matematika IPA SNMPTN. Diketahui a dan b adalah dua buah bilangan bulat positif yang memenuhi : Nilai ab (a+b) adalah.. A. 68 C. 68 E. 6 B. 8 D. 9 a b 6 a b 6 b a ab a+b ab 6 6
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
I N T E G R A L (Anti Turunan)
I N T E G R A L (Anti Turunan) I. Integral Tak Tentu A. Rumus Integral Bentuk Baku. Derifatif d/ X n = nx n- xn = Integral x n+ n. d/ cos x = - sin x sin x = - cos x. d/ sin x = cos x cos x = sin x 4.
fungsi rasional adalah rasio dari dua polinomial. Secara umum,
fungsi rasional adalah rasio dari dua polinomial. Secara umum, Fungsi Rasional Fungsi rasional adalah fungsi yang memiliki bentuk Dengan p dan d merupakan polinomial dan d(x) 0. Domain dari V(x) adalah
16. INTEGRAL. A. Integral Tak Tentu 1. dx = x + c 2. a dx = a dx = ax + c. 3. x n dx = + c. cos ax + c. 4. sin ax dx = 1 a. 5.
6. INTEGRAL A. Integral Tak Tentu. dx = x + c. a dx = a dx = ax + c. x n dx = n+ x n+ + c. sin ax dx = a cos ax + c 5. cos ax dx = a sin ax + c 6. sec ax dx = a tan ax + c 7. [ f(x) ± g(x) ] dx = f(x)
PROGRAM STUDI S1. MANAJEMEN
JADWAL UJIAN AKHIR SEMESTER GENAP TAHUN AKADEMIK 2016 / 2017 PROGRAM STUDI S1. MANAJEMEN HARI/TANGGAL : SENIN, 5 JUNI 2017 JURUSAN : MANAJEMEN WAKTU MATA KULIAH KLS JML RUANG 08.30-10.30 Lab. Pengantar
MADRASAH ALIYAH AL-MU AWANAH BEKASI SELATAN 2012
MODUL MATEMATIKA PERSIAPAN UJIAN NASIONAL 0 TAHUN AJARAN 0/0 MATERI PERSAMAAN KUADRAT DAN PERTIDAKSAMAAN KUADRAT UNTUK KALANGAN MA AL-MU AWANAH MADRASAH ALIYAH AL-MU AWANAH BEKASI SELATAN 0 Jalan RH. Umar
Pembahasan Matematika IPA SNMPTN 2012 Kode 483
Tutur Widodo Pembahasan Matematika IPA SNMPTN 0 Pembahasan Matematika IPA SNMPTN 0 Kode 8 Oleh Tutur Widodo. Di dalam kotak terdapat bola biru, 6 bola merah dan bola putih. Jika diambil 8 bola tanpa pengembalian,
Notasi turunan. Penggunaan turunan. 6. Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah.
Turunan fungsi adalah fungsi lain dari suatu fungsi sebelumnya misalkan fungsi f menjadi f' TURUNAN Notasi turunan y' atau f'(x) atau dy/dx fungsi naik Penggunaan turunan fungsi turun persamaan garis singgung
MA1201 MATEMATIKA 2A Hendra Gunawan
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2016/2017 27 Januari 2017 Bab Sebelumnya 7. Teknik Pengintegralan 7.1 Aturan Dasar Pengintegralan 7.2 Pengintegralan Parsial 7.3 Integral Trigonometrik
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1
Ringkasan Kalkulus 2, Untuk dipakai di ITB Deret Tak Hingga Pada bagian ini akan dibicarakan penjumlahan berbentuk a +a 2 + +a n + dengan a n R Sebelumnya akan dibahas terlebih dahulu pengertian barisan
Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika. F (x) = f(x) dx dan f (x) dinamakan integran.
4 INTEGRAL Definisi 4.0. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
TRY OUT MATEMATIKA PAKET 3B TAHUN 2010
. Perhatikan argumen berikut ini. p q. q r. r ~ s TRY OUT MATEMATIKA PAKET B TAHUN 00 Negasi kesimpulan yang sah dari argumen di atas adalah... A. p ~s B. p s C. p ~s D. p ~s E. p s. Diketahui npersamaan
MATEMATIKA EKONOMI 1 FUNGSI DAN GRAFIK. DOSEN Fitri Yulianti, SP, MSi.
MATEMATIKA EKONOMI 1 FUNGSI DAN GRAFIK DOSEN Fitri Yulianti, SP, MSi. Fungsi Fungsi merupakan hubungan antara dua variabel atau lebih. Variabel dibedakan : 1. Variabel bebas yaitu variabel yang besarannya
Teknik pengintegralan: Integral parsial (Integral by part)
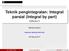Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
Aljabar Linear dan Matriks. Semester Pendek TA 2010/2011 S1 Teknik Informatika. Dosen Pengampu: Heri Sismoro, M.Kom.
1. Introduction Mata Kuliah: Aljabar Linear dan Matriks Semester Pendek TA 2010/2011 S1 Teknik Informatika Dosen Pengampu: Heri Sismoro, M.Kom. Sistem Persamaan Linear Sistem Linear m kali n : suatu himpunan
Regresi Linier. Metode Numerik POLITEKNIK ELEKTRONIKA NEGERI SURABAYA DEPARTEMEN TEKNIK INFORMATIKA DAN KOMPUTER PROGRAM STUDI TEKNIK INFORMATIKA
POLITEKNIK ELEKTRONIKA NEGERI SURABAYA DEPARTEMEN TEKNIK INFORMATIKA DAN KOMPUTER PROGRAM STUDI TEKNIK INFORMATIKA Regresi Linier Metode Numerik Zulhaydar Fairozal Akbar zfakbar@pens.ac.id 2017 TOPIK Pengenalan
FUNGSI DAN PERSAMAAN LINEAR. EvanRamdan
FUNGSI DAN PERSAMAAN LINEAR TEORI FUNGSI Fungsi yaitu hubungan matematis antara suatu variabel dengan variabel lainnya. Unsur-unsur pembentukan fungsi yaitu variabel (terikat dan bebas), koefisien dan
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO. Mohamad Sidiq
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO REFERENSI E-BOOK REFERENSI ONLINE SOS Mathematics http://www.sosmath.com/diffeq/diffeq.html Wolfram Research Math World http://mathworld.wolfram.com/ordinarydifferentialequation.h
Soal-Soal dan Pembahasan Ujian Nasional Matematika Tahun Pelajaran 2010/2011 Program Studi IPA
Soal-Soal dan Pembahasan Ujian Nasional Matematika Tahun Pelajaran 010/011 Program Studi IPA 1. Akar-akar persamaan 3x -1x + = 0 adalah α dan β. Persamaan Kuadrat baru yang akar-akarnya (α +) dan (β +)
Persamaan Diferensial Biasa
Persamaan Diferensial Biasa Titik Tetap dan Sistem Linear Toni Bakhtiar Departemen Matematika IPB Oktober 2012 Toni Bakhtiar (m@thipb) PDB Oktober 2012 1 / 31 Titik Tetap SPD Mandiri dan Titik Tetap Tinjau
Solusi: [Jawaban C] Solusi: [Jawaban ]
![Solusi: [Jawaban C] Solusi: [Jawaban ]](/thumbs/57/40367668.jpg "Solusi: [Jawaban C] Solusi: [Jawaban ]")
SOLUSI SMA/MA MATEMATIKA Program Studi IPA Kerjasama UNIVERSITAS GUNADARMA dengan Dinas Pendidikan Provinsi DKI Jakarta, Kota/Kabupaten BODETABEK, Tangerang Selatan, Karawang, Serang, Pandeglang, dan Cilegon
Berapakah nilai a? a. 25. d. 25 b. 15. e. 15 c. 10. Penyelesaian: Berarti bahwa 1, 3, 5, 7 dan 9 adalah akar-akar persamaan polinomial g(x) = 0.
KOMPETISI MATEMATIKA 07 TINGKAT SMA SE-SULUT SOLUSI BABAK SEMI FINAL Rabu, Februari 07 . Misalkan f(x) = x 5 + ax 4 + bx 3 + cx + dx + c dan f() = f(3) = f(5) = f(7) = f(9). Berapakah nilai a? a. 5 d.
β α α β SOAL MATEMATIKA UNTUK SMA istiyanto.com Mari Berbagi Ilmu Dengan Yang Lain A. Persamaan Kuadrat dan Fungsi Kuadrat
A. Persamaan Kuadrat dan Fungsi Kuadrat 1. Salah satu akar persamaan kuadrat ( a 1) x + (3a 1) x 3a = 0 adalah 1, maka akar lainnya adalah.... Nilai m yang memenuhi agar persamaan kuadrat ( m + 1) x +
A. DEFINISI DAN BENTUK UMUM SISTEM PERSAMAAN LINEAR KUADRAT
K-13 Kelas X matematika PEMINATAN SISTEM PERSAMAAN LINEAR KUADRAT TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi dan bentuk umum sistem
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 2008/2009
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 8/9. Perhatikan premis premis berikut! - Jika saya giat belajar maka saya bisa meraih juara - Jika saya bisa meraih juara maka saya boleh ikut
Jenis Jenis--jenis jenis fungsi dan fungsi linier Hafidh Munawir
Jenis-jenis fungsi dan fungsi linier Hafidh Munawir Diskripsi Mata Kuliah Memperkenalkan unsur-unsur fungsi ialah variabel bebas dan variabel terikat, koefisien, dan konstanta, yang saling berkaitan satu
Persamaan Diferensial
TKS 4003 Matematika II Persamaan Diferensial Linier Non Homogen Tk. 2 (Differential: Linier Non Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Solusi umum merupakan jumlah
1. Akar-akar persamaan 2x² + px - q² = 0 adalah p dan q, p - q = 6. Nilai pq =... A. 6 B. -2 C. -4 Kunci : E Penyelesaian : D. -6 E.
1. Akar-akar persamaan 2x² + px - q² = 0 adalah p dan q, p - q = 6. Nilai pq =... A. 6-2 -4 Kunci : E -6-8 2. Himpunan penyelesaian sistem persamaan Nilai 6x 0.y 0 =... A. 1 Kunci : C 6 36 3. Absis titik
Pembahasan Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) Tahun 2012
Pembahasan Seleksi Nasional Masuk Perguruan Tinggi Negeri (SNMPTN) Tahun 2012 Bidang Matematika Dasar Kode Paket 623 Oleh : Fendi Alfi Fauzi 1. Jika a dan b adalah bilangan bulat positif yang memenuhi
K13 Revisi Antiremed Kelas 11 Matematika
K1 Revisi Antiremed Kelas 11 Matematika Peminatan - Persiapan PTS Semester Genap Halaman 1 01. Grafik berikut ini yang menunjukkan grafik dari parabola x 2 = -12y adalah... (Catatan: Setiap kotak pada