BAB 1 PERSAMAAN DIFERENSIAL ORDER SATU
|
|
|
- Lanny Muljana
- 6 tahun lalu
- Tontonan:
Transkripsi
1 BAB PERSAAA DIFERESIAL ORDER SATU PEDAHULUA Persamaan Diferensial adalah salah satu cabang ilmu matematika ang banak digunakan dalam memahami permasalahan-permasalahan di bidang fisika dan teknik Persamaan Diferensial merupakan alat ang ampuh dalam menelesaikan berbagai macam masalah praktis ang sering muncul di dunia nata Pada pembahasan berikut, pertama akan diberikan pengertian Persamaan Diferensial, order dan derajat serta penelesaian Persamaan Diferensial Selanjutna dibahas berbagai teknik penelesaian Persamaan Diferensial order satu Tujuan Instruksional : Setelah mempelajari bab ini, saudara harus dapat embedakan Persamaan Diferensial Biasa dengan Persamaan Diferensial Parsial, serta membedakan order dan derajat Persamaan Diferensial engidentifikasi dan menentukan penelesaian Persamaan Diferensial dengan peubah terpisah, Persamaan Diferensial eksak, serta Persamaan Diferensial Linier order satu enentukan faktor integral dan mengubah Persamaan Diferensial menjadi Eksak engidentifikasi dan menentukan penelesaian Persamaan Diferensial tipe homogen, Riccati, dan Bernoulli ereduksi Persamaan Diferensial nonhomogen ke bentuk Persamaan Diferensial Homogen enentukan traektori ortogonal
2 PEGERTIA PERSAAA DIFERESIAL Pada kuliah kalkulus, kita telah belajar bagaimana menentukan derivatif d (turunan ' f '( dari suatu fungsi f ( isalna, jika d e cos, maka d d e sin ( Atau jika diberikan persamaan dalam bentuk g (, C dengan C konstanta, d kita dapat mendiferensialkan secara implisit untuk memperoleh isalkan d dipunai fungsi implisit 9 maka akan diperoleh d 0 d d d ( Persamaan ( dan ( di atas merupakan contoh persamaan diferensial Definisi : Suatu persamaan diferensial adalah suatu persamaan ang menatakan hubungan fungsi ang tidak diketahui beserta turunanna Jika hana ada satu peubah bebas, maka disebut Persamaan Diferensial Biasa (PDB, sebagai contoh adalah persamaan ( dan ( Contoh PDB laina adalah sebagai berikut :
3 d 4 e d d d sin d d d d 0 Sedangkan jika persamaan memuat dua lebih peubah bebas, maka disebut Persamaan Diferensial Parsial (PDP isalkan : v v v o t u u t u u u 0 z Pembahasan tentang PDP akan dibicarakan dalam bab tersendiri Bentuk Umum dan Order PDB Bentuk umum PDB order n adalah ( n ( n f (,, ', '',, ( ang menatakan adana keterkaitan antara peubah bebas dan peubah tak bebas beserta turunan-turunanna dalam bentuk persamaan ang identik nol Beberapa (n buku menulis persamaan ini dalam bentuk f (,, ', '',, 0 Order dari Persamaan diferensial adalah order tertinggi dari turunan ang ada dalam persamaan isalkan d sin d adalah persamaan diferensial order satu, sedangkan d 0 d merupakan persamaan diferensial order dua
4 Penelesaian PDB asalah kita selanjutna adalah bagaimana menemukan penelesaian PDB, aitu suatu fungsi ( ang memenuhi PDB tersebut Definisi : Suatu fungsi ( ang didefinisikan pada suatu interval disebut penelesaian PDB jika secara identik memenuhi persamaan ( pada interval ang diberikan Contoh : Fungsi d ke adalah penelesaian persamaan diferensial pada interval d d < <, karena ( ke ke Jadi jika disubstitusikan ke dalam d persamaan diperoleh ke ke, ang berlaku untuk semua Tidak semua penelesaian PDB dapat disajikan secara eksplisit seperti Contoh Beberapa kasus ditemukan penelesaian ang disajikan dalam bentuk implisit, seperti contoh berikut Contoh : Persamaan C, untuk suatu konstanta C > 0, merupakan penelesaian d bentuk implisit dari d Contoh : Persamaan e sin, merupakan penelesaian bentuk implisit dari asalah ilai Awal d d e e sin cos isalkan akan dicari penelesaian ( dari PDB order satu ' f (, (4
5 ang memenuhi ( 0 0 (5 Persamaan (5 disebut kondisi awal dari PDB order satu PDB (4 dengan kondisi awal (5 disebut asalah ilai Awal (A Penelesaian ang memenuhi kondisi awal ini disebut penelesaian khusus, sedangkan jika tidak diberikan kondisi awal dinamakan penelesaian umum, seperti Contoh Jadi pada penelesaian umum masih memuat konstanta sebarang C, sedangkan pada penelesaian khusus sudah tidak memuat konstanta sebarang Contoh 4 : Persamaan Latihan : adalah penelesaian khusus dari A ', ( 0 0 Tunjukkan bahwa fungsi ang diberikan merupakan penelesaian dari Persamaan diferensial ', Ce '' ' 0, ( c c e '' sec, sec 4 '' ' sin e, c e ( c sin e e 5 ', 4 6, (4 0 4
6 PERSAAA DIFERESIAL BIASA ORDER SATU Pada Bagian ini, kita akan membahas teknik-teknik penelesaian PDB order satu Untuk PDB order satu ang berbentuk ' f (, dimana f fungsi kontinu dari satu peubah bebas, maka kita dapat mengintegralkan secara langsung kedua ruas untuk memperoleh penelesaianna Selanjutna akan dicari penelesaian PDB order satu d ' f (, (6 d dimana f fungsi kontinu dari dua peubah bebas dan Penelesaian (6 tidak dapat diperoleh dengan mengintegralkan secara langsung Untuk memperoleh penelesaianna dapat dilakukan dengan pemisahan peubah, seperti dibahas dalam bagian berikut PD dengan Peubah terpisah Untuk mencari penelesaian umum dari persamaan (6, terlebih dahulu kita pisahkan peubah dan, sehingga kita peroleh fungsi f (, p( q( Persamaan (6 berubah menjadi dapat ditulis d d p( q( d p( d (7 q( d '( Dengan asumsi bahwa adalah fungsi dari, maka kita puna d, q( q( ( sehingga persamaan (7 menjadi '( d p( d q( (
7 Selanjutna dengan menuliskan u ( dan du ' (, maka dengan mengintegralkan kedua ruas kita peroleh penelesaian umum persamaan (7, aitu dengan C konstanta sebarang du C q( u p( d Berikut ini beberapa contoh PDB dengan peubah ang dapat dipisahkan (8 Contoh 5: d Selesaikan e cos d Penelesaian : Dengan melakukan pemisahan peubah diperoleh Integralkan kedua ruas e d cos d e sin C Sehingga kita peroleh Penelesaian umumna adalah ln( sin C Untuk mengecek kebenaran penelesaian ini, perhatikan bahwa Substitusikan ke PDB, kita peroleh Karena e ln( sin C ' (cos sin C ln( sin C (cos e sin C sin C cos, persamaan di atas terpenuhi untuk setiap sin C > 0 Dengan demikian adalah penelesaian PDB tersebut Contoh 6
8 d Selesaikan ( d Penelesaian : PDB dapat kita tulis dalam bentuk Pemisahan peubah memberikan Integralkan kedua ruas diperoleh d d d ( ( d ln C e C Dalam beberapa kasus akan kita jumpai persamaan diferensial dalam bentuk (, d (, d 0 (9 Contoh 7 : Selesaikan e d d 0 Penelesaian : Persamaan dapat kita bawa ke bentuk d e d Integralkan keuda ruas, diperoleh ( e C ( e C
9 Contoh 8 : d Selesaikan d Penelesaian PD d d Dapat ditulis dalam bentuk, d d d d Integralkan kedua ruas, diperoleh, Dalam hal ini d d c c, c, c c konstanta Jadi penelesaian umumna adalah [ c ] Contoh 9 : Selesaikan d dt t Penelesaian
10 PD dapat ditulis dalam bentuk d dt ( t ( t, d ( t dt Integralkan kedua ruas, diperoleh d t dt c ( 4, t t c, 4 4, dengan c 4 4c, t 4t c Latihan : Selesaikan soal berikut dengan pemisahan peubah d d ( d e d d ( d 4 e d ( d 5 cos d sin d 0 6 e d ( d 0 7 d sec( d d 0 8 d 9 d (ln 0 d ( d 0 d Selesaikan A berikut : d e d, ( 0 0, d e d ( dp t P Pte, P( 0 dt 5 t d ( dt 0, ( dp p p 4, p( dq q
11 Persamaan Diferensial Linier Order Satu Persamaan linier order satu adalah persamaan ang berbentuk d a ( a ( b( (0 d dimana a (, a(, dan b ( hana bergantung pada peubah bebas isalna, d Persamaan e 0 d d d ( dipisahkan Sedangkan persamaan dan peubah tidak dapat dipisah e d d,, d (sin tan d bukan persamaan linier, meskipun peubah dapat d ( bukan persamaan linier d Pada persamaan (0, diasumsikan bahwa a (, a(, dan b( kontinu pada suatu interval tertentu dengan a ( 0 aka persamaan dapat kita bawa ke bentuk d a ( b( d a( a( d P( Q( ( d ang merupakan Bentuk Standar PDB linier order satu Penelesaian PDB Linier Langkah-langkah penelesaian PDB Linier order satu adalah sebagai berikut : Langkah Tuliskan PDB dalam bentuk standar
12 Langkah Tentukan faktor integral d P( Q( d P( d ( e Langkah Kalikan Q ( dengan dan integralkan ( Q( d C Langkah 4 Tuliskan penelesaian umum ( ( Q( C ( Q( C ( Contoh 0 : Tentukan penelesaian umum dari Penelesaian d d Langkah Tulis persamaan dalam bentuk standar: Jadi P( dan Q ( d d Langkah Tentukan faktor integral P( d ( e e ln e d Langkah Kalikan Q ( dengan dan integralkan, sehigga diperoleh
13 ( Q( d d d ln C Langkah 4 Penelesaian umumna adalah ln C Contoh : ln C Selesaikan PD d cos sin d Penelesaian PD dapat dinatakan dalam d d sin cos cos d d tan sec Yang merupakan bentuk PD linier d d p( q(, dengan p( tan, q( sec Selanjutna diperoleh faktor integral e pd e tan d e ln sec sec Kalikan PD dengan faktor integral, diperoleh
14 d sec sec tan sec d d ( sec sec d Integralkan kedua ruas, sec sec d c Jadi penelesaian PD adalah,, Contoh : Selesaikan PD Penelesaian sec tan c tan sec d ( d c sin c cos sec Perhatikan bahwa PD memuat,jadi ini bkan PD linier, tetapi jika kita lihat sebagai fungsi, dan PD dapat kita tulis dalam bentuk Atau d d d d aka diperoleh bentuk PD linear dengan sebagai fungsi,
15 d d p( q( dengan p( d an q( Selanjutna dapat kita selesaikan dengan langkah-langkah seperti pada contoh sebelumna Faktor integralna adalah e p ( d e d ln e Kalikan PD dengan, d d Atau d d Dengan mengintegralkan kedua ruas diperoleh c, Jadi penelesaian PD adalah, ( c Ada dan tunggalna penelesaian PDB linier order satu ang memenuhi sarat awal tertentu diberikan dalam sifat berikut Sifat :
16 isalkan P( dan Q ( fungsi kontinu pada interval α < < β aka d terdapat satu dan hana satu fungsi ( ang memenuhi P( Q( d pada interval tersebut dengan kondisi awal 0, dimana < < β ( 0 α 0 Latihan : Selesaikan PDB linier order satu berikut d d e, > 0 e d d d π π d (tan cos, < < 4 ln d d d 5 d d ( d 6 e d Selesaikan A berikut d d 7 ln, > 0, ( 8 4, ( 0 d d d 9, ( 0 d 0 d ( cos d 0, ( 0 π Persamaan Diferensial Eksak Perhatikan kembali persamaan diferensial order satu ang dituliskan dalam bentuk diferensial (, d (, d 0 Definisi : Persamaan (, d (, d 0 dikatakan PD Eksak jika terdapat fungsi Q (, sedemikian sehingga Q (, dan Q (,
17 Dengan mengingat diferensial total dari fungsi Q (,, maka dari definisi di atas dapat disimpulkan bahwa persamaan (, d (, d 0 eksak jika dan hana jika Adapun langkah-langkah untuk menelesaikan PD Eksak adalah sebagai berikut Langkah Tuliskan PD dalam bentuk diferensial : (, d (, d 0 Langkah Tes ke-eksak-an PD; Apakah? Langkah Jika eksak, integralkan terhadap terhadap isal dipilih, maka : Q (, d g( Langkah 4 Turunkan Q terhadap dan samakan hasilna dengan ( d g' ( Langkah 5 Integralkan g '( untuk memperoleh g Langkah 6 Tuliskan penelesaian umum dalam bentuk implisit: Q (, C Langkah 7 Tentukan C jika diberikan kondisi awal tertentu Contoh : d Selesaikan PD, ( 0 d Penelesaian : Langkah Bentuk diferensial PD adalah : ( d ( d 0 Langkah PD ini eksak, karena
18 Langkah isal dipilih untuk diintegralkan, maka : Q(, d Q Langkah 4 Samakan dengan, maka : g( ( d g( g( dg 0 d g '( Langkah 5 Integralkan g '(, diperoleh : g ( Langkah 6 Penelesaian umum dalam bentuk implisit: C Langkah 7 Dengan kondisi awal ( 0, diperoleh C 9, sehingga penelesaian khususna adalah : 9 Contoh 4 : Selesaikan persamaan ( d ( d 0 Penelesaian : Akan kita selesaikan mengikuti langkah-langkah di atas, tanpa menuliskan masing-masing item Persamaan sudah dalam bentuk diferensial, selanjutna tes ke-eksak-an: ( (
19 Jadi persamaan tersebut eksak Selanjutna Q(, ( d g( g( Q Untuk memperoleh g (, gunakan fakta Jadi g' ( 4, Sehingga penelesaian umumna adalah Q g' ( g( C : Pada bagian sebelumna, kita mencari faktor integral ( e P( d untuk menelesaikan persamaan diferensial linier order satu dalam bentuk standar Ternata faktor integral d P( Q( d P( d ( e akan membawa persamaan diferensial d linier order satu P( Q( menjadi PD eksak (Tunjukkan! d Secara umum suatu faktor integral adalah faktor (, ang membawa persamaan diferensial tidak eksak menjadi persamaan diferensial eksak Contoh 5 :
20 Tunjukkan bahwa d ( e d 0 tidak eksak, tetapi dengan mengalikan dengan faktor PD tersebut menjadi eksak Kemudian selesaikan Penelesaian : Tes ke-eksak-an, kita punai ( e dan ( Jadi persamaan tidak eksak Dengan mengalikan dengan faktor integral diperoleh d ( e d 0 Persamaan menjadi eksak, karena Selanjutna kita punai dan Jadi g '( 0 sehingga g ( C ( e ( Q(, e e e g( Q g'( Dengan demikian penelesaian umumna adalah e e e C enemukan faktor integral Seperti terlihat pada contoh, faktor integral adalah suatu fungsi ang jika dikalikan dengan PD non eksak, maka PD tersebut menjadi PD eksak Bagaimana menemukan foaktor integral tersebut akan dijelaskan sebagai berikut: isal (, d (, d 0 PD non eksak dan (, faktor integral, maka d d 0 adalah PD eksak, sehingga
21 Ada beberapa kasus, aitu (i, ( ( ( Faktor integral hana merupakan fungsi saja Pada kasus ini dipunai 0 d e d d ln Jadi jika menghasilkan fungsi saja maka ( (ii, ( ( ( Faktor integral hana merupakan fungsi saja Pada kasus ini dipunai secara sama akan dipunai
22 (iii Jika Jadi jika d e menghasilkan fungsi saja, maka ( menghasilkan fungsi, maka ( (iv Jika menghasilkan fungsi (, maka ( (v Jika (vi Jika menghasilkan fungsi ( -, maka ( menghasilkan fungsi (, maka ( Jadi untuk mencari faktor integral kita harus menghitung terlebih dahulu, kemudian kita tentukan pembagina ( pembagina apa sehingga diperoleh fungsi ang mandiri Contoh 6: Tunjukkan faktor integral dari PD d ( e d 0 sehingga menjadi PD eksak Penelesaian: Pada contoh 5 telah ditunjukkan bahwa PD ini tidak eksak, kemudian dengan mengalikan PD dengan, PD menjadi eksak ( Jadi adalah faktor integral Disini kita akan mengetahui dari mana itu didapat
23 (, ( e dan, ( ( e dan ( Sehingga diperoleh dan fungsi dari saja aka faktor integralna adalah e d e d e ln ( Contoh 7 : Tentukan solusi umum PD 0 ( (4 d d Penelesaian : 4, ( dan, ( dan 4 Sehingga diperoleh Selanjutna kita pilih pembagina, aitu, sehingga diperoleh ( ( ( ( ( ( ( fungsi dari ( saja
24 Selanjutna misalkan z z z z z Integralkan, diperoleh z z ln ln Faktor integralna adalah PD menjadi 0 ( ( (4 ( d d 0 4 ( 6 (4 d d Bukti bahwa PD ini eksak: 6 4, ( , ( Jadi terbukti Eksak Solusi PD adalah (, ( g d Q ( 6 (4 g d ( 4 g 4, ( '( 4 g Q Diperoleh ( ' g ( g Dengan demikian penelesaian umum PD adalah
25 4 C Latihan : Selesaikan PD eksak berikut d d 4, ( 0 d d ( e d ( e d 0, ( 0 5 ( e e d ( e d 0 d cos 4 d sin 6 ( sin d ( sin d 0 7 Tentukan (, sehingga ( d (, d 0 eksak 8 Tentukan (, sehingga (, d ( sin ln e d 0 eksak Tunjukkan bahwa PD berikut adalah non eksak, kemudian tentukan faktor integralna sehigga PD tersebut menjadi eksak dan selesaikan 9 d ( d 0 0 ( d ( d 0 ( d ( d 0 ( d ( d 0
26 4 PERSAAA HOOGE, PERSAAA BEROULLI, DA PERSAAA RICCATI Pada bagian ini, kita akan menelesaikan tiga tipe persamaan diferensial tidak linier, aitu persamaan homogen, persamaan Bernoulli, dan persamaan Riccati Teknik penelesaian ketiga tipe PD tersebut menggunakan substitusi ang mengubah PD tersebut menjadi linier ang dapat diselesaikan dengan metode ang telah kita pelajari sebelumna 4 Persamaan Homogen d Suatu persamaan diferensial f (, dikatakan homogen jika fungsi d f (, dapat dinatakan dalam fungsi dari, aitu f (, g Jadi akan kita punai ang dengan substitusi dipisah d d g ( ( v akan menjadi persamaan dengan peubah dapat dv d g( v v Sebagai contoh, persamaan-persamaan d, d d cos d d 4 d (, merupakan persamaan homogen, sedangkan persamaan
27 d d bukan tipe persamaan homogen, karena tidak dapat dinatakan dalam fungsi saja Contoh 8 : Selesaikan Penelesaian : d ( d 0, > 0 Persamaan ini tidak dapat dipisah, tidak linier, dan juga tidak eksak Secara langsung tidak terlihat bahwa ini adalah PD homogen, tetapi dengan membagi persamaan dengan, kita peroleh d ( d 0 Substitusi v, menjadi d d dv v v d v v d dv v Kemudian integralkan, kita peroleh penelesaian umum Karena > 0, maka ln( v ln C v ln C
28 dengan C C e C C Catatan : - Suatu fungsi F disebut fungsi homogen berderajat n jika n F( λ, λ λ F(, - PD (, d (, d 0 disebut PD homogen jika (, dan (, merupakan fungsi-fungsi homogen berderajat sama Contoh 9 Selesaikan d d Penelesaian PD ini adalah PD homogen, karena f (, dan merupakan fungsi homogen berderajad PD dapat ditulis dalam bentuk d d dv v v, where v, d v g (, dv v ( v v v d v v diperoleh, ( v d dv c v ( v Dengan c adalah konstanta integrasi, dapat ditulis sebagai
29 v v v dv d c ln v ln ( v ln ln A, Dimana A adalah konstanta, sedemikian sehingga c ln A v Jadi diperoleh ln ln A v v v A Selanjutna, natakan v sebagai, diperoleh penlesaian umum PD A or A Contoh 0 : Selesaikan PD Penlesaian ( d d 0 d PD dapat ditulis dalam bentuk, ang merupakan PD d homogen Substitusi v, diperoleh ( v d v ( vd dv 0 (since d vd dv ( v v d vdv 0 d v 0 ( v dv Integralkan, diperoleh v d dv c, c konstanta ( v v ln dv c, ( v v Untuk menentukan integral, ( v dv substitusi v t, seingga dv dt dan diperoleh t ln dt c t
30 t t ln dt dt c t ln ln ( t c v ln ln ( v c (Karena (v t Persaman terakhir dapat ditulis sebagai ln ( v c Selanjutna mengingat v v, diperoleh penelesaian umum PD ln c 4 Persamaan Bernoulli Persamaan Bernoulli berbentuk d n P( Q( d Untuk n 0,, dapat dibuktikan bahwa dengan substitusi PD linier tingkat satu dengan penelesaian umum berbentuk ze (n dz ( n P( z ( n Q( d P( d (n P( d ( n e Q( d C n ( n P( d ( n e n P( d ( e Q( d C z ( n akan diperoleh Contoh Selesaikan persamaan Penelesaian d d e PD dapat ditulis dalam entuk d
31 d d e Yang merupakan PD bentuk d d P( Q( n dengan P(, Q( e and n Untuk meneelesaikan PD ini, pertama bagi persamaan dengan, sehigga diperoleh d d Subtitusi z aka, jadi, diperoleh d d dz ( d dz d d d e d d dz z e d dz d 4z e ang merupakan PD Linier order satu Faktor integral dari PD linier ini adalah diperoleh e dz d 4ze d d sehingga diperoleh ze ( ze e e e e e d c 4 d e e
32 Atau ze e c z e e ce e ce Selanjutna dengan mengingat z, diperoleh penelesaian umum PD e ce e c e dimana c c Contoh : d Selesaikan d Penelesaian : Dengan substitusi υ diperoleh dυ d Sehingga Penelesaian umumna adalah υ e ( e C 4 Persamaan Riccati Persamaan Riccati berbentuk d P( Q( d R( (4 Jika adalah fungsi ang memenuhi persamaan Riccati, dapat dibuktikan bahwa dengan substitusi akan diperoleh PD linier tingkat satu u
33 du d [ ( Q( P( ] u Q( dengan penelesaian umum berbentuk [ Q( P( ] ue ( d ( Q( P( e Q( d C [ ( Q( P( ] d ( Q( P( e e Q( d C Contoh : d Selesaikan, > 0 d Penelesaian : Jika, maka dengan substitusi Sehingga penelesaian umumna adalah diperoleh u du u d C Latihan 4 Selesaikan PD homogen berikut d d ( d d d ( 4 ( d ( d 0 d d d 5 e 6 ln ln d d d 7 cos, > 0 d 8 d d 0
34 Selesaikan PD Bernoulli berikut d d 9 0 d d d d, > 0 e d d d d ( d 0 4 e 0, > 0 d Selesaikan Persamaan Riccati berikut d d 5,, > 0 6 0, d d d 7 (,, > 0 d 5 PD O HOOGE BETUK KHUSUS DA TRAYEKTORI ORTOGOAL Pada bagian ini dibahas tentang Persamaan diferensial non homogen ang dapat direduksi menjadi persamaan homogen serta tentang traektori orthogonal 5 PD on Homogen Bentuk Khusus Bagian ini membahas PD non homogen bentuk ( a b c d ( p q r d 0 (5 a b c Kasus, k, (k konstanta p q r aka persamaan (5 menjadi ( kp kq kr d ( p q r d 0 kd d 0 sehingga penelesaianna dengan mudah dapat diselesaikan Kasus, a b c k p q r
35 PD ( menjadi ( kp kq c d ( p q r d 0 ( k( p q c d ( p q r d 0 Kemudian gunakan substitusi u p q Contoh 4 : Selesaikan PD ( d ( d 0 Penelesaian : PD dapat ditulis dalam bentuk ( d (( d 0 isal z d d dz d dz d diperoleh ( z d (z ( dz d 0 ( z d (z dz (z d 0 ( z z d (z dz 0 zd ( z dz 0 (z d dz 0 z Selanjutna penelesaian umum diperoleh dengan mengintegralkan, (z 0 z d dz dz z d dz z ln z C ( ln( C ln( C ln( C dapat ditulis ln( C Contoh 5 C
36 Selesaikan ( d (4 6 d 0 Penelesaian Substitusikan u, diperoleh Sehingga penelsaianna adalah Kasus, a p b q c r u d du 0 u ln( C PD (5 dapat diselesaikan melalui dua cara, aitu Pertama, mengubah variabel u dan v variabel u k v l k dan l dapat dicari dengan substitusi persamaan ak bl c 0 pk ql r 0 Dengan mengubah variabel ini PD ( akan menjadi PD homogen Cara kedua adalah dengan substitusi u a b c v p q r sehingga PD (5 menjadi PD homogen dalam u dan v Contoh 6 : Tentukan solusi umum PD ( 4 d ( d 0 Penelesaian: isal u 4 du d d v dv d d Ini adalah Sistem Persamaan Linier dalam peubah d dan d Diperoleh dv du d dan dv du d
37 PD menjadi ud vd 0 dv du dv du u v 0 u ( dv du v( dv du 0 ( u v du ( u v dv 0 ini adalah bentuk PD tipe homogen Selanjutna, misalkan PD menjadi ( u uz du ( u uz( zdu udz 0 ( u ( z du u( z zdu u v z v uz dv zdu udz u ( z dz 0 ( z z du u( z dz 0 ini adalah PD dengan peubah dapat dipisah du u du u ( z ( z z ( z dz ( z dz z integralkan, diperoleh lnu ln( z z C ln u ln( z u ( z z C 0 0, z ln C v v u C u u v uv u C ( ( ( 4 ( 4 C Atau 8 4 C Contoh 7: Tentukan penelesaian umum PD ( d ( d 0
38 Penelesaian: isal u, du d d Diperoleh v, dv d d du dv d dan 5 Sehingga PD menjadi du dv d 5 du dv du dv ud vd 0 u v isal PD menjadi udu udv vdu vdv 0 ( u v du (u v dv 0 PD tipe homogen dalam u dan v u z u zv du zdv vdz v ( zv v( zdv vdz (zv v dv 0 v ( z z z dv v ( z 4z dv v( z dz 0 dv ( z dz v ( z 4z Integralkan, diperoleh ln v ln z 4z C Atau ln v ln z Diperoleh 0 4z ln C ( z dz 0 u u v ( z 4z C v 4 C v v Jadi penelesaian umumna adalah u 4 uv v C u 4 uv v C dengan u dan v
39 Contoh 8: Selesaikan PD ( d (4 6 d 0 Penelesaian : Dengan cara pertama u k v l Diperoleh k dan l, sehingga PD menjadi u u du 4 dv 0 v v ang merupakan tipe PD homogen Akhirna diperoleh penelesaian umum berbentuk Silahkan coba dengan cara kedua! 5 ( 9 C( Latihan 5 : Selesaikan PD berikut ( d (6 d 0 ( 4 d ( d 0 ( 4 d ( d 0 4 ( d ( d 0 5 Traektori Ortogonal Dalam atematika terapan, seringkali dijumpai permasalahan untuk mendapatkan keluarga kurva ang tegak lurus terhadap suatu keluarga kurva ang diberikan asalah ini disebut Traektori Ortogonal Pengertian dari ortogonal / tegak lurus dari dua keluarga kurva adalah pada titik potongna kedua garis singgung kurva saling tegak lurus isal diberikan keluarga kurva F (, C dengan C merupakan parameter aka untuk mendapatkan traektori ortogonal dilakukan langkah sebagai berikut : (i Turunkan F (, C secara implisit terhadap, diperoleh
40 (ii d d f (, enggunakan fakta bahwa gradien dari garis garis singgung traektori ortogonal fungsi tersebut adalah d d f (, (iii Persamaan kurva traektori adalah penelesaian PD pada (ii Contoh 9 : Tentukan traetori ortogonal dari k Penelesaian : Dari k diperoleh d d k f (, Gradien dari traektori adalah k Persamaan traektori adalah penelesaian dari PD d d f (,, aitu C Contoh 0: Tentukan traektori orthogonal dari Penelesaian : Turunkan, Diperoleh d d 0 d d Traektori orthogonal merupakan penelesaian dari PD d d d d 0 Integralkan, diperoleh: c
41 C Latihan 5 : Tentukan traektori ortogonal dari keluarga kurva ang diberikan berikut C C C 4 C 5 - C 6 C 7 4 C 8 4 C 9 C
PERSAMAAN DIFFERENSIAL ORDE I. Nurdinintya Athari
 PERSAMAAN DIFFERENSIAL ORDE I Nurdininta Athari Definisi PERSAMAAN DIFERENSIAL Persamaan diferensial adalah suatu persamaan ang memuat satu atau lebih turunan fungsi ang tidak diketahui. Jika persamaan
PERSAMAAN DIFFERENSIAL ORDE I Nurdininta Athari Definisi PERSAMAAN DIFERENSIAL Persamaan diferensial adalah suatu persamaan ang memuat satu atau lebih turunan fungsi ang tidak diketahui. Jika persamaan
Persamaan Diferensial Orde Satu
 Modul Persamaan Diferensial Orde Satu P PENDAHULUAN Prof. SM. Nababan, Ph. ersamaan Diferensial (PD) adalah salah satu cabang matematika ang banak digunakan untuk menjelaskan masalah-masalah fisis. Masalahmasalah
Modul Persamaan Diferensial Orde Satu P PENDAHULUAN Prof. SM. Nababan, Ph. ersamaan Diferensial (PD) adalah salah satu cabang matematika ang banak digunakan untuk menjelaskan masalah-masalah fisis. Masalahmasalah
BAB II PERSAMAAN TINGKAT SATU DERAJAT SATU
 BAB II PERSAAA TIGKAT SATU DERAJAT SATU Standar Kompetensi Setelah mempelajari pokok bahasan ini diharapkan mahasiswa dapat memahami ara-ara menentukan selesaian umum persamaan diferensial tingkat satu
BAB II PERSAAA TIGKAT SATU DERAJAT SATU Standar Kompetensi Setelah mempelajari pokok bahasan ini diharapkan mahasiswa dapat memahami ara-ara menentukan selesaian umum persamaan diferensial tingkat satu
Adalah : hubungan antara variabel bebas x, variabel
 Adalah : hubungan antara variabel bebas, variabel Bentuk Umum : bebas dan turunanna. d d F(,,, n d,..., ) n Persamaan differensial (PD) menatakan hubungan dinamik, maksudna hubungan tersebut memuat besaran
Adalah : hubungan antara variabel bebas, variabel Bentuk Umum : bebas dan turunanna. d d F(,,, n d,..., ) n Persamaan differensial (PD) menatakan hubungan dinamik, maksudna hubungan tersebut memuat besaran
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
! " #" # $# % " "& " # ' ( ) #
 ! "#"# $#%""&"#'# "*# *" " " #,#" " "# * # ""- # # "! " #" # $#%""&"# '# #" &# '&$'# # "'/0& " # #'"# ## # # #"""--* # #* #"* "'# #* 0 # # ***0" #""# ** #""# " #,#"##' ##' #*"#"#"'#"" #"#" ## # # "*###
! "#"# $#%""&"#'# "*# *" " " #,#" " "# * # ""- # # "! " #" # $#%""&"# '# #" &# '&$'# # "'/0& " # #'"# ## # # #"""--* # #* #"* "'# #* 0 # # ***0" #""# ** #""# " #,#"##' ##' #*"#"#"'#"" #"#" ## # # "*###
BAB VIII PERSAMAAN DIFERENSIAL (PD)
 BAB VIII PERSAMAAN DIFERENSIAL (PD) Banak masalah dalam kehidupan sehari-hari ang dapat dimodelkan dalam persamaan diferensial. Untuk menelesaikan masalah tersebut kita perlu menelesaikan pula persamaan
BAB VIII PERSAMAAN DIFERENSIAL (PD) Banak masalah dalam kehidupan sehari-hari ang dapat dimodelkan dalam persamaan diferensial. Untuk menelesaikan masalah tersebut kita perlu menelesaikan pula persamaan
BAB 2 LANDASAN TEORI
 6 BAB LANDASAN TEORI Pada bab ini akan dibahas beberapa konsep dasar ang akan digunakan sebagai landasan berpikir seperti beberapa teorema dan definisi ang berkaitan dengan penelitian ini. Dengan begitu
6 BAB LANDASAN TEORI Pada bab ini akan dibahas beberapa konsep dasar ang akan digunakan sebagai landasan berpikir seperti beberapa teorema dan definisi ang berkaitan dengan penelitian ini. Dengan begitu
Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui.
 1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika. F (x) = f(x) dx dan f (x) dinamakan integran.
 4 INTEGRAL Definisi 4.0. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
4 INTEGRAL Definisi 4.0. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
MODUL MATEMATIKA II. Oleh: Dr. Eng. LILYA SUSANTI
 MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
MODUL MATEMATIKA II Oleh: Dr. Eng. LILYA SUSANTI DEPARTEMEN RISET TEKNOLOGI DAN PENDIDIKAN TINGGI UNIVERSITAS BRAWIJAYA FAKULTAS TEKNIK JURUSAN TEKNIK SIPIL KATA PENGANTAR Puji sukur kehadirat Allah SWT
Fungsi Peubah Banyak. Modul 1 PENDAHULUAN
 Modul 1 Fungsi Peubah Banak Prof. Dr. Bambang Soedijono PENDAHULUAN D alam modul ini dibahas masalah Fungsi Peubah Banak. Dengan sendirina para pengguna modul ini dituntut telah menguasai pengertian mengenai
Modul 1 Fungsi Peubah Banak Prof. Dr. Bambang Soedijono PENDAHULUAN D alam modul ini dibahas masalah Fungsi Peubah Banak. Dengan sendirina para pengguna modul ini dituntut telah menguasai pengertian mengenai
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL
 Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
Solusi Analitis Persamaan-persamaan Diferensial Orde-1 dengan Metode Analitis Persamaan Diferensial dengan konfigurasi VARIABEL TERPISAH
 Solusi Analitis Persamaan-persamaan Diferensial Orde- dengan Metode Analitis.. Persamaan Diferensial dengan konfigurasi VARIABEL TERPISAH a. Bentuk Umum: f ( ) g( ), f dan g fungsi sembarang. b. Metode
Solusi Analitis Persamaan-persamaan Diferensial Orde- dengan Metode Analitis.. Persamaan Diferensial dengan konfigurasi VARIABEL TERPISAH a. Bentuk Umum: f ( ) g( ), f dan g fungsi sembarang. b. Metode
DIKTAT. Persamaan Diferensial
 Diktat Persamaan Diferensial; Dwi Lestari, M.S. 3 DIKTAT Persamaan Diferensial Disusun oleh: Dwi Lestari, M.S email: dwilestari@un.a.id JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN
Diktat Persamaan Diferensial; Dwi Lestari, M.S. 3 DIKTAT Persamaan Diferensial Disusun oleh: Dwi Lestari, M.S email: dwilestari@un.a.id JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN
perpindahan, kita peroleh persamaan differensial berikut :
 1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
Matematika Teknik I. Prasyarat : Kalkulus I, Kalkulus II, Aljabar Vektor & Kompleks
 Kode Mata Kuliah : TE 318 SKS : 3 Matematika Teknik I Prasarat : Kalkulus I, Kalkulus II, Aljabar Vektor & Kompleks Tujuan : Mahasiswa memahami permasalahan teknik dalam bentuk PD atau integral, serta
Kode Mata Kuliah : TE 318 SKS : 3 Matematika Teknik I Prasarat : Kalkulus I, Kalkulus II, Aljabar Vektor & Kompleks Tujuan : Mahasiswa memahami permasalahan teknik dalam bentuk PD atau integral, serta
Kuliah PD. Gaya yang bekerj a pada suatu massa sama dengan laju perubahan momentum terhadap waktu.
 Kuliah PD Pertemuan ke-1: Motivasi: 1. Mekanika A. Hukum Newton ke-: Gaya yang bekerj a pada suatu massa sama dengan laju perubahan momentum terhadap waktu. Misalkan F: gaya, m: massa benda, a: percepatan,
Kuliah PD Pertemuan ke-1: Motivasi: 1. Mekanika A. Hukum Newton ke-: Gaya yang bekerj a pada suatu massa sama dengan laju perubahan momentum terhadap waktu. Misalkan F: gaya, m: massa benda, a: percepatan,
dy = f(x,y) = p(x) q(y), dx dy = p(x) dx,
 5. Persamaan Diferensian Dengan Variabel Terpisah Persamaan diferensial berbentuk y = f(), dengan f suatu fungsi kontinu pada suatu interval real, dapat dicari penyelesaiannya dengan cara mengintegralkan
5. Persamaan Diferensian Dengan Variabel Terpisah Persamaan diferensial berbentuk y = f(), dengan f suatu fungsi kontinu pada suatu interval real, dapat dicari penyelesaiannya dengan cara mengintegralkan
digunakan untuk menyelesaikan integral seperti 3
 Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Sudaryatno Sudirham. Integral dan Persamaan Diferensial
 Sudaratno Sudirham Integral dan Persamaan Diferensial Bahan Kuliah Terbuka dalam format pdf tersedia di www.buku-e.lipi.go.id dalam format pps beranimasi tersedia di www.ee-cafe.org Bahasan akan mencakup
Sudaratno Sudirham Integral dan Persamaan Diferensial Bahan Kuliah Terbuka dalam format pdf tersedia di www.buku-e.lipi.go.id dalam format pps beranimasi tersedia di www.ee-cafe.org Bahasan akan mencakup
Nurdinintya Athari PERSAMAAN DIFFERENSIAL ORDE 2
 Nurdininta Athari PERSAMAAN DIFFERENSIAL ORDE 2 2 PDB ORDE II Bentuk umum : + p() + g() = r() p(), g() disebut koefisien jika r() = 0, maka Persamaan Differensial diatas disebut homogen, sebalikna disebut
Nurdininta Athari PERSAMAAN DIFFERENSIAL ORDE 2 2 PDB ORDE II Bentuk umum : + p() + g() = r() p(), g() disebut koefisien jika r() = 0, maka Persamaan Differensial diatas disebut homogen, sebalikna disebut
TURUNAN. Ide awal turunan: Garis singgung. Kemiringan garis singgung di titik P: lim. Definisi
 TURUNAN Ide awal turunan: Garis singgung Tali busur c +, f c + Garis singgung c, f c c P h c+h f c + f c Kemiringan garis singgung di titik P: f c + f c lim Definisi Turunan fungsi f adalah fungsi lain
TURUNAN Ide awal turunan: Garis singgung Tali busur c +, f c + Garis singgung c, f c c P h c+h f c + f c Kemiringan garis singgung di titik P: f c + f c lim Definisi Turunan fungsi f adalah fungsi lain
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: = f(x, y) M(x, y) + N(x, y) = 0 Penyelesaian PDB orde satu dengan integrasi secara langsung Jika
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: = f(x, y) M(x, y) + N(x, y) = 0 Penyelesaian PDB orde satu dengan integrasi secara langsung Jika
TURUNAN FUNGSI IKA ARFIANI, S.T.
 TURUNAN FUNGSI IKA ARFIANI, S.T. DEFINISI TURUNAN Turunan dari ( terhadap dideinisikan dengan: d d ' ' ( lim h 0 ( h-( h RUMUS DASAR TURUNAN ' n n n k k ' 0 k ' u' nu u n n '( ( '( ( '( ( '( ( 0 '( ( n
TURUNAN FUNGSI IKA ARFIANI, S.T. DEFINISI TURUNAN Turunan dari ( terhadap dideinisikan dengan: d d ' ' ( lim h 0 ( h-( h RUMUS DASAR TURUNAN ' n n n k k ' 0 k ' u' nu u n n '( ( '( ( '( ( '( ( 0 '( ( n
BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx +
 BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx + N(x y) = 0 (2.1) 2.1.1 PDB Eksak
BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx + N(x y) = 0 (2.1) 2.1.1 PDB Eksak
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO. Mohamad Sidiq
 MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO REFERENSI E-BOOK REFERENSI ONLINE SOS Mathematics http://www.sosmath.com/diffeq/diffeq.html Wolfram Research Math World http://mathworld.wolfram.com/ordinarydifferentialequation.h
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO REFERENSI E-BOOK REFERENSI ONLINE SOS Mathematics http://www.sosmath.com/diffeq/diffeq.html Wolfram Research Math World http://mathworld.wolfram.com/ordinarydifferentialequation.h
Pecahan Parsial (Partial Fractions)
 oki neswan (fmipa-itb) Pecahan Parsial (Partial Fractions) Diberikan fungsi rasional f (x) p(x) q(x) f (x) r(x) : Jika deg p deg q; maka r (x) ^p (x) q(x) ; dengan deg r < deg q: p (x) q (x) r (x) ^p (x)
oki neswan (fmipa-itb) Pecahan Parsial (Partial Fractions) Diberikan fungsi rasional f (x) p(x) q(x) f (x) r(x) : Jika deg p deg q; maka r (x) ^p (x) q(x) ; dengan deg r < deg q: p (x) q (x) r (x) ^p (x)
Diferensial dan Integral
 Open Course Diferensial dan Integral Oleh: Sudaratno Sudirham Pengantar Setelah kita mempelajari fungsi dan grafik, ang merupakan bagian pertama dari kalkulus, berikut ini kita akan membahas bagian kedua
Open Course Diferensial dan Integral Oleh: Sudaratno Sudirham Pengantar Setelah kita mempelajari fungsi dan grafik, ang merupakan bagian pertama dari kalkulus, berikut ini kita akan membahas bagian kedua
BAB: TEKNIK PENGINTEGRALAN Topik: Metode Substitusi
 BAB: TEKNIK PENGINTEGRALAN Topik: Metode Substitusi Kompetensi yang diukur adalah kemampuan mahasiswa menghitung integral fungsi dengan metode substitusi.. UAS Kalkulus Semester Pendek no. b (kriteria:
BAB: TEKNIK PENGINTEGRALAN Topik: Metode Substitusi Kompetensi yang diukur adalah kemampuan mahasiswa menghitung integral fungsi dengan metode substitusi.. UAS Kalkulus Semester Pendek no. b (kriteria:
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
Suatu persamaan diferensial biasa orde n adalah persamaan bentuk :
 PERSAMAAN DIFERENSIAL BIASA PERSAMAAN DIFERENSIAL Suatu persamaan iferensial biasa ore n aalah persamaan bentuk : F n, ', '', ''',......, 0 Yang menatakan hubungan antara, fungsi () an turunanna ', '',
PERSAMAAN DIFERENSIAL BIASA PERSAMAAN DIFERENSIAL Suatu persamaan iferensial biasa ore n aalah persamaan bentuk : F n, ', '', ''',......, 0 Yang menatakan hubungan antara, fungsi () an turunanna ', '',
TURUNAN FUNGSI IKA ARFIANI, S.T.
 TURUNAN FUNGSI IKA ARFIANI, S.T. DEFINISI TURUNAN Turunan dari ( terhadap dideinisikan dengan: d d ( lim h 0 ( h-( h RUMUS DASAR TURUNAN n n n k k 0 k u nu u n n ( ( ( ( ( ( ( ( 0 ( ( n n n c RUMUS JUMLAH
TURUNAN FUNGSI IKA ARFIANI, S.T. DEFINISI TURUNAN Turunan dari ( terhadap dideinisikan dengan: d d ( lim h 0 ( h-( h RUMUS DASAR TURUNAN n n n k k 0 k u nu u n n ( ( ( ( ( ( ( ( 0 ( ( n n n c RUMUS JUMLAH
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
 MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
TURUNAN DALAM RUANG DIMENSI-n
 TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
TURUNAN DALAM RUANG DIMENSI-n A. Fungsi Dua Variabel atau Lebih Dalam subbab ini, fungsi dua variabel atau lebih dikaji dari tiga sudut pandang: secara verbal (melalui uraian dalam kata-kata) secara aljabar
4. TURUNAN. MA1114 Kalkulus I 1
 4. TURUNAN MA4 Kalkulus I 4. Konsep Turunan 4.. Turunan di satu titik Pendauluan dua masala dalam satu tema a. Garis Singgung Kemiringan tali busur PQ adala : m PQ Jika, maka tali busur PQ akan beruba
4. TURUNAN MA4 Kalkulus I 4. Konsep Turunan 4.. Turunan di satu titik Pendauluan dua masala dalam satu tema a. Garis Singgung Kemiringan tali busur PQ adala : m PQ Jika, maka tali busur PQ akan beruba
BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I
 BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I. Pengertian PD, Orde (tingkat), & Derajat (Pangkat) Persamaan diferensial adalah suatu persamaan yang memuat derivatifderivatif (turunan) sekurang-kurangnya derivatif
BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I. Pengertian PD, Orde (tingkat), & Derajat (Pangkat) Persamaan diferensial adalah suatu persamaan yang memuat derivatifderivatif (turunan) sekurang-kurangnya derivatif
PERSAMAAN DIFERENSIAL (PD)
 PERSAMAAN DIFERENSIAL (PD) A. PENGERTIAN Persamaan yang mengandung variabel dan beberapa fungsi turunan terhadap variabel tersebut. CONTOH : + 5 5 0 disebut PD orde I + 6 + 7 0 disebut PD orde II B. PEMBENTUKAN
PERSAMAAN DIFERENSIAL (PD) A. PENGERTIAN Persamaan yang mengandung variabel dan beberapa fungsi turunan terhadap variabel tersebut. CONTOH : + 5 5 0 disebut PD orde I + 6 + 7 0 disebut PD orde II B. PEMBENTUKAN
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
 MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
Pemodelan Teknik Kimia Bebarapa Contoh Aplikasi Persamaan Diferensial (oleh: Prof. Dr. Ir. Setijo Bismo, DEA.)
 Pemodelan Teknik Kimia - 206 Bebarapa Contoh Aplikasi Persamaan Diferensial (oleh: Prof. Dr. Ir. Setijo Bismo, DEA.) Contoh #: Kepedulian terhadap Iklan Suatu produk sereal baru (diberi nama Oat Puff )
Pemodelan Teknik Kimia - 206 Bebarapa Contoh Aplikasi Persamaan Diferensial (oleh: Prof. Dr. Ir. Setijo Bismo, DEA.) Contoh #: Kepedulian terhadap Iklan Suatu produk sereal baru (diberi nama Oat Puff )
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
PENDAHULUAN KALKULUS
 . BILANGAN REAL PENDAHULUAN KALKULUS Ada beberapa jenis bilangan ang telah kita kenal ketika di bangku sekolah. Bilangan-bilangan tersebut adalah bilangan asli, bulat, cacah, rasional, irrasional. Tahu
. BILANGAN REAL PENDAHULUAN KALKULUS Ada beberapa jenis bilangan ang telah kita kenal ketika di bangku sekolah. Bilangan-bilangan tersebut adalah bilangan asli, bulat, cacah, rasional, irrasional. Tahu
Bagian 2 Turunan Parsial
 Bagian Turunan Parsial Bagian Turunan Parsial mempelajari bagaimana teknik dierensiasi diterapkan untuk ungsi dengan dua variabel atau lebih. Teknik dierensiasi ini tidak hana akan diterapkan untuk ungsi-ungsi
Bagian Turunan Parsial Bagian Turunan Parsial mempelajari bagaimana teknik dierensiasi diterapkan untuk ungsi dengan dua variabel atau lebih. Teknik dierensiasi ini tidak hana akan diterapkan untuk ungsi-ungsi
Sistem Persamaan Linier FTI-UY
 BAB V Sistem Persamaan Linier Salah satu hal penting dalam aljabar linear dan dalam banak masalah matematika terapan adalah menelesaikan suatu sistem persamaan linear. Representasi Sistem Persamaan Linear
BAB V Sistem Persamaan Linier Salah satu hal penting dalam aljabar linear dan dalam banak masalah matematika terapan adalah menelesaikan suatu sistem persamaan linear. Representasi Sistem Persamaan Linear
MATEMATIKA BISNIS BAB 2 FUNGSI LINIER
 MATEMATIKA BISNIS BAB FUNGSI LINIER Hikmah Agustin, S.P.,MM DEFINISI FUNGSI Fungsi adalah hubungan matematis antara suatu variabel dengan variabel lainna. Unsur-unsur pembentukan fungsi : 1. Variabel Variabel
MATEMATIKA BISNIS BAB FUNGSI LINIER Hikmah Agustin, S.P.,MM DEFINISI FUNGSI Fungsi adalah hubungan matematis antara suatu variabel dengan variabel lainna. Unsur-unsur pembentukan fungsi : 1. Variabel Variabel
Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika. F (x) = f(x) dx dan f (x) dinamakan integran.
 4 INTEGRAL Definisi 4. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
4 INTEGRAL Definisi 4. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
BAB I PENGERTIAN DASAR
 BAB I PENGERTIAN DASAR Kompetensi Dasar: Menjelaskan pengertian dan klasifikasi dari persamaan diferensial serta beberapa hal yang terkait. Indikator: a. Menjelaskankan pengertian persamaan diferensial.
BAB I PENGERTIAN DASAR Kompetensi Dasar: Menjelaskan pengertian dan klasifikasi dari persamaan diferensial serta beberapa hal yang terkait. Indikator: a. Menjelaskankan pengertian persamaan diferensial.
MATEMATIKA 3 Turunan Parsial. -Irma Wulandari-
 MATEMATIKA 3 Turunan Parsial -Irma Wulandari- Pengertian Turunan Parsial T = (,) Rata-rata perubahan suhu pelat T per satuan panjang dalam arah sumbu, sejauh, untuk koordinat tetap ; (, ) (, ) Rata-rata
MATEMATIKA 3 Turunan Parsial -Irma Wulandari- Pengertian Turunan Parsial T = (,) Rata-rata perubahan suhu pelat T per satuan panjang dalam arah sumbu, sejauh, untuk koordinat tetap ; (, ) (, ) Rata-rata
Sudaryatno Sudirham. Studi Mandiri. Diferensiasi. Darpublic
 Sudaratno Sudirham Studi Mandiri Diferensiasi ii Darpublic BAB Turunan Fungsi-Fungsi () (Fungsi Perkalian Fungsi, Fungsi Pangkat Dari Fungsi, Fungsi Rasional, Fungsi Implisit).1. Fungsi Yang Merupakan
Sudaratno Sudirham Studi Mandiri Diferensiasi ii Darpublic BAB Turunan Fungsi-Fungsi () (Fungsi Perkalian Fungsi, Fungsi Pangkat Dari Fungsi, Fungsi Rasional, Fungsi Implisit).1. Fungsi Yang Merupakan
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: Penyelesaian PDB orde satu dengan integrasi secara langsung Jika PDB dapat disusun dalam bentuk,
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: Penyelesaian PDB orde satu dengan integrasi secara langsung Jika PDB dapat disusun dalam bentuk,
TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 2016/2017
 A. Pengantar Persamaan Diferensial TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 016/017 1. Tentukan hasil turunan dari fungsi sebagai berikut: a. f() = c e b. f() = c cos k + c sin k c.
A. Pengantar Persamaan Diferensial TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 016/017 1. Tentukan hasil turunan dari fungsi sebagai berikut: a. f() = c e b. f() = c cos k + c sin k c.
BAB I PENDAHULUAN. Kompetensi
 BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL
 BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
Jurusan Matematika FMIPA-IPB
 Jurusan Matematika FMIPA-IPB Ujian Kedua Semester Pendek T.A 4/5 KALKULUS/KALKULUS Jum at, Agustus 4 (Waktu : jam) SETIAP SOAL BERNILAI. Tentukan (a) + (b) p 4 + 5. Periksa apakah Teorema Nilai Rata-rata
Jurusan Matematika FMIPA-IPB Ujian Kedua Semester Pendek T.A 4/5 KALKULUS/KALKULUS Jum at, Agustus 4 (Waktu : jam) SETIAP SOAL BERNILAI. Tentukan (a) + (b) p 4 + 5. Periksa apakah Teorema Nilai Rata-rata
Fungsi dan Grafik Diferensial dan Integral
 Sudaratno Sudirham Studi Mandiri Fungsi dan Grafik Diferensial dan Integral i Darpublic Hak cipta pada penulis, 010 SUDIRHAM, SUDARYATNO Fungsi dan Grafik, Diferensial dan Integral Oleh: Sudaratmo Sudirham
Sudaratno Sudirham Studi Mandiri Fungsi dan Grafik Diferensial dan Integral i Darpublic Hak cipta pada penulis, 010 SUDIRHAM, SUDARYATNO Fungsi dan Grafik, Diferensial dan Integral Oleh: Sudaratmo Sudirham
Hendra Gunawan. 23 April 2014
 MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 23 April 2014 Kuliah ang Lalu 13.11 Integral Lipat Dua atas Persegi Panjang 13.2 Integral Berulang 13.3 33Integral Lipat Dua atas Daerah Bukan
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 23 April 2014 Kuliah ang Lalu 13.11 Integral Lipat Dua atas Persegi Panjang 13.2 Integral Berulang 13.3 33Integral Lipat Dua atas Daerah Bukan
BAB I PENDAHULUAN. Kompetensi
 BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
yang tak terdefinisikan dalam arti keberadaannya tidak perlu didefinisikan. yang sejajar dengan garis yang diberikan tersebut.
 3 Gariis Lurus Dalam geometri aksiomatik/euclide konsep garis merupakan salah satu unsur ang tak terdefinisikan dalam arti keberadaanna tidak perlu didefinisikan. Karakteristik suatu garis diberikan pada
3 Gariis Lurus Dalam geometri aksiomatik/euclide konsep garis merupakan salah satu unsur ang tak terdefinisikan dalam arti keberadaanna tidak perlu didefinisikan. Karakteristik suatu garis diberikan pada
KAJIAN MODEL EPIDEMIK SIR DETERMINISTIK DAN STOKASTIK PADA WAKTU DISKRIT. Oleh: Arisma Yuni Hardiningsih
 KAJIAN MODEL EPIDEMIK SIR DETERMINISTIK DAN STOKASTIK PADA WAKTU DISKRIT Oleh: Arisma Yuni Hardiningsih 126 1 5 Dosen Pembimbing: Dra. Laksmi Prita Wardhani, M.Si Jurusan Matematika Fakultas Matematika
KAJIAN MODEL EPIDEMIK SIR DETERMINISTIK DAN STOKASTIK PADA WAKTU DISKRIT Oleh: Arisma Yuni Hardiningsih 126 1 5 Dosen Pembimbing: Dra. Laksmi Prita Wardhani, M.Si Jurusan Matematika Fakultas Matematika
11. Turunan Perkalian Fungsi, Pangkat Dari Fungsi, Fungsi Rasional, Fungsi Implisit
 Darpublic Nopember 01.darpublic.com 11. Turunan erkalian Fungsi, angkat Dari Fungsi, Fungsi Rasional, Fungsi Implisit 11.1. Fungsi Yang Merupakan erkalian Dua Fungsi Misalkan kita memiliki dua fungsi,
Darpublic Nopember 01.darpublic.com 11. Turunan erkalian Fungsi, angkat Dari Fungsi, Fungsi Rasional, Fungsi Implisit 11.1. Fungsi Yang Merupakan erkalian Dua Fungsi Misalkan kita memiliki dua fungsi,
Pada integral diatas, dalam mencari penyelesaiannya, pertama diintegralkan terlebih dahulu terhadap x kemudian diintegralkan lagi terhadap y.
 PENDAHULUAN Pada bagian ini akan dibahas perluasan integral tertentu ke bentuk integral lipat dua dari fungsi dua peubah Akan dibahas bentukbentuk integral lipat dalam koordinat kartesius koordinat kutub
PENDAHULUAN Pada bagian ini akan dibahas perluasan integral tertentu ke bentuk integral lipat dua dari fungsi dua peubah Akan dibahas bentukbentuk integral lipat dalam koordinat kartesius koordinat kutub
Unit 2 KONSEP DASAR ALJABAR. Clara Ika Sari Pendahuluan
 Unit KONSEP DASAR ALJABAR Clara Ika Sari Pendahuluan P ada unit ini kita akan mempelajari beberapa konsep dasar dalam aljabar seperti persamaan dan pertidaksamaan ang berbentuk linear dan kuadrat, serta
Unit KONSEP DASAR ALJABAR Clara Ika Sari Pendahuluan P ada unit ini kita akan mempelajari beberapa konsep dasar dalam aljabar seperti persamaan dan pertidaksamaan ang berbentuk linear dan kuadrat, serta
disebut Persamaan Diferensial Parsial (PDP).
 Persamaan Diferensial Febrizal, MT Pendahuluan Persamaandiferensial i merupakan persamaan yang berkaitan dengan turunan dari suatu fungsi atau memuat suku suku dari fungsi tersebut dan atau turunannya.
Persamaan Diferensial Febrizal, MT Pendahuluan Persamaandiferensial i merupakan persamaan yang berkaitan dengan turunan dari suatu fungsi atau memuat suku suku dari fungsi tersebut dan atau turunannya.
INTEGRAL PARSIAL DENGAN TEKNIK TURIN. Mintarjo SMK Negeri 2 Gedangsari Gunungkidul
 INTEGRAL PARSIAL DENGAN TEKNIK TURIN Mintarjo SMK Negeri Gedangsari Gunungkidul email : tarjamint@gmailcom Abstrak Matematika merupakan ilmu pengetahuan yang memiliki sifat universal Salah satu cabang
INTEGRAL PARSIAL DENGAN TEKNIK TURIN Mintarjo SMK Negeri Gedangsari Gunungkidul email : tarjamint@gmailcom Abstrak Matematika merupakan ilmu pengetahuan yang memiliki sifat universal Salah satu cabang
Tinjauan Tentang Fungsi Harmonik. Oleh : Atmini Dhoruri Jurusan Pendidikan Matematika FMIPA UNY ABSTRAK
 Tinjauan Tentang Fungsi Harmonik Oleh : Atmini Dhoruri Jurusan Pendidikan Matematika FMIPA UNY ABSTRAK Tujuan penulisan ini untuk mengkaji tentang pengertian fungsi harmonik, fungsi harmonik konjugat pada
Tinjauan Tentang Fungsi Harmonik Oleh : Atmini Dhoruri Jurusan Pendidikan Matematika FMIPA UNY ABSTRAK Tujuan penulisan ini untuk mengkaji tentang pengertian fungsi harmonik, fungsi harmonik konjugat pada
TINJAUAN PUSTAKA. Jika y = f(x) dengan f(x) adalah suatu fungsi yang terdiferensialkan terhadap
 II. TINJAUAN PUSTAKA 2.1 Diferensial Jika y = f(x) dengan f(x) adalah suatu fungsi yang terdiferensialkan terhadap variabel bebas x, maka dy adalah diferensial dari variabel tak bebas (terikat) y, yang
II. TINJAUAN PUSTAKA 2.1 Diferensial Jika y = f(x) dengan f(x) adalah suatu fungsi yang terdiferensialkan terhadap variabel bebas x, maka dy adalah diferensial dari variabel tak bebas (terikat) y, yang
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL
 BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA
 PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
Ilustrasi Permukaan ruang dalam bentuk fungsi eksplisit dan implisit.
 Koko Martono FMIPA - ITB 77 Fungsi dua peubah, permukaan ruang, dan kurva ketinggian Fungsi dua peubah mempunai aturan = f (,) dengan daerah asal dan daerah nilai D f = {(,) : f (,) } dan R f = { : = f
Koko Martono FMIPA - ITB 77 Fungsi dua peubah, permukaan ruang, dan kurva ketinggian Fungsi dua peubah mempunai aturan = f (,) dengan daerah asal dan daerah nilai D f = {(,) : f (,) } dan R f = { : = f
Respect, Professionalism, & Entrepreneurship. Mata Kuliah : Mekanika Bahan Kode : TSP 205. Analisis Penampang. Pertemuan 4, 5, 6
 Mata Kuliah : Mekanika Bahan Kode : TSP 05 SKS : SKS nalisis Penampang Pertemuan 4, 5, 6 TU : Mahasiswa dapat menghitung properti dasar penampang, seperti luas, momen statis, momen inersia TK : Mahasiswa
Mata Kuliah : Mekanika Bahan Kode : TSP 05 SKS : SKS nalisis Penampang Pertemuan 4, 5, 6 TU : Mahasiswa dapat menghitung properti dasar penampang, seperti luas, momen statis, momen inersia TK : Mahasiswa
Bab. Persamaan Garis Lurus. Pengertian Persamaan Garis Lurus Gradien Menentukan Persamaan Garis lurus
 Bab Sumb er: Scien ce Enclopedia, 997 Persamaan Garis Lurus Dalam suatu perlombaan balap sepeda, seorang pembalap mengauh sepedana dengan kecepatan tetap. Setiap 5 detik, pembalap tersebut menempuh jarak
Bab Sumb er: Scien ce Enclopedia, 997 Persamaan Garis Lurus Dalam suatu perlombaan balap sepeda, seorang pembalap mengauh sepedana dengan kecepatan tetap. Setiap 5 detik, pembalap tersebut menempuh jarak
TEKNIK-TEKNIK PENGINTEGRALAN
 TEKNIK-TEKNIK PENGINTEGRALAN 1. Teknik Subtitusi Teorema : Misal g fungsi yang terdiferensialkan dan F suatu anti turunan dari f, jika u = g() maka f(g())g () d = f(u) du = F(u) + c = F(g()) + c sin. 1.
TEKNIK-TEKNIK PENGINTEGRALAN 1. Teknik Subtitusi Teorema : Misal g fungsi yang terdiferensialkan dan F suatu anti turunan dari f, jika u = g() maka f(g())g () d = f(u) du = F(u) + c = F(g()) + c sin. 1.
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde II
 Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL
 HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL Dra.Sri Rejeki Dwi Putranti, M.Kes. Fakultas Teknik - Universitaas Yos Soedarso Surabaya Email : riccayusticia@gmail.com Abstrak Hubungan antara Differensial dan
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL Dra.Sri Rejeki Dwi Putranti, M.Kes. Fakultas Teknik - Universitaas Yos Soedarso Surabaya Email : riccayusticia@gmail.com Abstrak Hubungan antara Differensial dan
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II
 Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II [MA4] PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II [MA4] PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU
 MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
SOLUSI PERSAMAAN DIFFERENSIAL
 SOLUSI PERSAMAAN DIFFERENSIAL PENGERTIAN SOLUSI. Solusi dari suatu persamaan differensial adalah persamaan yang memuat variabelvariabel dari persamaan differensial dan memenuhi persamaan differensial yang
SOLUSI PERSAMAAN DIFFERENSIAL PENGERTIAN SOLUSI. Solusi dari suatu persamaan differensial adalah persamaan yang memuat variabelvariabel dari persamaan differensial dan memenuhi persamaan differensial yang
BAB PDB Linier Order Satu
 BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
4.1 Konsep Turunan. lim. m PQ Turunan di satu titik. Pendahuluan ( dua masalah dalam satu tema )
 4. TURUNAN 4. Konsep Turunan 4.. Turunan di satu titik Pendauluan dua masala dalam satu tema a. Garis Singgung Kemiringan tali busur PQ adala : m PQ Jika, maka tali busur PQ akan beruba menjadi garis ggung
4. TURUNAN 4. Konsep Turunan 4.. Turunan di satu titik Pendauluan dua masala dalam satu tema a. Garis Singgung Kemiringan tali busur PQ adala : m PQ Jika, maka tali busur PQ akan beruba menjadi garis ggung
Teknik pengintegralan: Integral parsial (Integral by part)
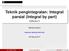 Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
I. PENDAHULUAN. kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini
 1 I. PENDAHULUAN 1.1 Latar Belakang dan Masalah Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus mengalami kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini mengalami
1 I. PENDAHULUAN 1.1 Latar Belakang dan Masalah Perkembangan ilmu pengetahuan dan teknologi sampai saat ini terus mengalami kemajuan. Salah satunya adalah cabang ilmu matematika yang sampai saat ini mengalami
IDENTIFIKASI KESALAHAN MENYELESAIKAN KALKULUS LANJUT MAHASISWA PROGRAM STUDI PENDIDIKAN MATEMATIKA UNIVERSITAS MUHAMMADIYAH PURWOREJO
 IDENTIFIKASI KESALAHAN MENYELESAIKAN KALKULUS LANJUT MAHASISWA PROGRAM STUDI PENDIDIKAN MATEMATIKA UNIVERSITAS MUHAMMADIYAH PURWOREJO Erni Puji Astuti Program Studi Pendidikan Matematika Universitas Muhammadiah
IDENTIFIKASI KESALAHAN MENYELESAIKAN KALKULUS LANJUT MAHASISWA PROGRAM STUDI PENDIDIKAN MATEMATIKA UNIVERSITAS MUHAMMADIYAH PURWOREJO Erni Puji Astuti Program Studi Pendidikan Matematika Universitas Muhammadiah
yang tak terdefinisikan dalam arti keberadaannya tidak perlu didefinisikan.
 3 Gariis Lurus Dalam geometri aksiomatik/euclide konsep garis merupakan salah satu unsur ang tak terdefinisikan dalam arti keberadaanna tidak perlu didefinisikan. Karakteristik suatu garis diberikan pada
3 Gariis Lurus Dalam geometri aksiomatik/euclide konsep garis merupakan salah satu unsur ang tak terdefinisikan dalam arti keberadaanna tidak perlu didefinisikan. Karakteristik suatu garis diberikan pada
TEKNIK PENGINTEGRALAN
 TEKNIK PENGINTEGRALAN Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 2 Topik Bahasan Pendahuluan 2 Manipulasi Integran 3 Integral Parsial 4 Dekomposisi
TEKNIK PENGINTEGRALAN Departemen Matematika FMIPA IPB Bogor, 202 (Departemen Matematika FMIPA IPB) Kalkulus I Bogor, 202 / 2 Topik Bahasan Pendahuluan 2 Manipulasi Integran 3 Integral Parsial 4 Dekomposisi
Persamaan Diferensial: Pengertian, Asal Mula dan Penyelesaian
 Modul 1 Persamaan Diferensial: Pengertian, Asal Mula dan Penyelesaian Drs. Sardjono, S.U. M PENDAHULUAN odul 1 ini berisi uraian tentang persamaan diferensial, yang mencakup pengertian-pengertian dalam
Modul 1 Persamaan Diferensial: Pengertian, Asal Mula dan Penyelesaian Drs. Sardjono, S.U. M PENDAHULUAN odul 1 ini berisi uraian tentang persamaan diferensial, yang mencakup pengertian-pengertian dalam
Kalkulus 2. Teknik Pengintegralan ke - 1. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
 Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
BAB II PERSAMAAN DIFERENSIAL BIASA (PDB) ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL BIASA (PDB) ORDE SATU Tujuan Instruksional: Mampu memahami dan menyelesaikan PD orde-1 dg integrasi langsung, pemisahan variael. Mampu memahami dan menyelesaikan Persamaan
BAB II PERSAMAAN DIFERENSIAL BIASA (PDB) ORDE SATU Tujuan Instruksional: Mampu memahami dan menyelesaikan PD orde-1 dg integrasi langsung, pemisahan variael. Mampu memahami dan menyelesaikan Persamaan
TURUNAN FUNGSI. dy (y atau f (x) atau ) dx. Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :
 TURUNAN FUNGSI dy (y atau f () atau ) d Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :. ( a + b) = ( a + ab + b ). ( a b) = ( a ab + b ) m n m n. a = a 4. a m = a m m m.
TURUNAN FUNGSI dy (y atau f () atau ) d Hal-hal yang perlu diingat untuk menyelesaikan turunan fungsi aljabar adalah :. ( a + b) = ( a + ab + b ). ( a b) = ( a ab + b ) m n m n. a = a 4. a m = a m m m.
16. INTEGRAL. A. Integral Tak Tentu 1. dx = x + c 2. a dx = a dx = ax + c. 3. x n dx = + c. cos ax + c. 4. sin ax dx = 1 a. 5.
 6. INTEGRAL A. Integral Tak Tentu. dx = x + c. a dx = a dx = ax + c. x n dx = n+ x n+ + c. sin ax dx = a cos ax + c 5. cos ax dx = a sin ax + c 6. sec ax dx = a tan ax + c 7. [ f(x) ± g(x) ] dx = f(x)
6. INTEGRAL A. Integral Tak Tentu. dx = x + c. a dx = a dx = ax + c. x n dx = n+ x n+ + c. sin ax dx = a cos ax + c 5. cos ax dx = a sin ax + c 6. sec ax dx = a tan ax + c 7. [ f(x) ± g(x) ] dx = f(x)
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Linier Non Homogen Tk. 2 (Differential: Linier Non Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Solusi umum merupakan jumlah
TKS 4003 Matematika II Persamaan Diferensial Linier Non Homogen Tk. 2 (Differential: Linier Non Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Solusi umum merupakan jumlah
BAB II PERSAMAAN DIFERENSIAL ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
2 Akar Persamaan NonLinear
 2 Akar Persamaan NonLinear Beberapa metoda untuk mencari akar ang telah dikenal adalah dengan memfaktorkan atau dengan cara Horner Sebagai contoh, untuk mencari akar dari persamaan 2 6 = 0 ruas kiri difaktorkan
2 Akar Persamaan NonLinear Beberapa metoda untuk mencari akar ang telah dikenal adalah dengan memfaktorkan atau dengan cara Horner Sebagai contoh, untuk mencari akar dari persamaan 2 6 = 0 ruas kiri difaktorkan
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde I
 Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
Univrsitas Indonusa Esa Unggul Fakultas Ilmu Komputr Tknik Informatika Prsamaan Difrnsial Ord I Dfinisi Prsamaan Difrnsial Prsamaan difrnsial adalah suatu prsamaan ang mmuat satu atau lbih turunan fungsi
TURUNAN. Bogor, Departemen Matematika FMIPA-IPB. (Departemen Matematika FMIPA-IPB) Kalkulus: Turunan Bogor, / 50
 TURUNAN Departemen Matematika FMIPA-IPB Bogor, 2012 (Departemen Matematika FMIPA-IPB) Kalkulus: Turunan Bogor, 2012 1 / 50 Topik Bahasan 1 Pendahuluan 2 Turunan Fungsi 3 Tafsiran Lain Turunan 4 Kaitan
TURUNAN Departemen Matematika FMIPA-IPB Bogor, 2012 (Departemen Matematika FMIPA-IPB) Kalkulus: Turunan Bogor, 2012 1 / 50 Topik Bahasan 1 Pendahuluan 2 Turunan Fungsi 3 Tafsiran Lain Turunan 4 Kaitan
Pertemuan Minggu ke Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai
 Pertemuan Minggu ke-10 1. Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai 1. Keterdiferensialan Pada fungsi satu peubah, keterdiferensialan f di x berarti keujudan derivatif f (x).
Pertemuan Minggu ke-10 1. Keterdiferensialan 2. Derivatif berarah dan gradien 3. Aturan rantai 1. Keterdiferensialan Pada fungsi satu peubah, keterdiferensialan f di x berarti keujudan derivatif f (x).
integral = 2 . Setiap fungsi ini memiliki turunan ( ) = adalah ( ) = 6 2.
 integral 13.1 PENGERTIAN INTEGRAL Untuk itu, coba tentukan turunan fungsi berikut. Perhatikan bahwa fungsi ini memiliki bentuk umum 6 2. Jadi, turunan fungsi = 2 =2 3. Setiap fungsi ini memiliki turunan
integral 13.1 PENGERTIAN INTEGRAL Untuk itu, coba tentukan turunan fungsi berikut. Perhatikan bahwa fungsi ini memiliki bentuk umum 6 2. Jadi, turunan fungsi = 2 =2 3. Setiap fungsi ini memiliki turunan
Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif INTEGRASI FUNGSI. 0 a b X A. b A = f (X) dx a. Penyusun : Martubi, M.Pd., M.T.
 Kode Modul MAT. TKF 20-03 Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif INTEGRASI FUNGSI Y Y = f (X) 0 a b X A b A = f (X) dx a Penyusun : Martubi, M.Pd., M.T. Sistem Perencanaan Penyusunan Program
Kode Modul MAT. TKF 20-03 Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif INTEGRASI FUNGSI Y Y = f (X) 0 a b X A b A = f (X) dx a Penyusun : Martubi, M.Pd., M.T. Sistem Perencanaan Penyusunan Program
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Fungsi Dua Peubah
 Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Fungsi Dua Peubah [MA114] Sistem Koordinat Kuadran II Kuadran I P(,) z P(,,z) Kuadran III Kuadran IV R (Bidang) Oktan 1 R 3 (Ruang) 7/6/007
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Fungsi Dua Peubah [MA114] Sistem Koordinat Kuadran II Kuadran I P(,) z P(,,z) Kuadran III Kuadran IV R (Bidang) Oktan 1 R 3 (Ruang) 7/6/007
TURUNAN FUNGSI (DIFERENSIAL)
 TURUNAN FUNGSI (DIFERENSIAL) A. Pengertian Derivatif (turunan) suatu fungsi. Perhatikan grafik fungsi f( (pengertian secara geometri) ang melalui garis singgung. f( f( f(+ Q [( +, f ( + ] f( P (, f ( )
TURUNAN FUNGSI (DIFERENSIAL) A. Pengertian Derivatif (turunan) suatu fungsi. Perhatikan grafik fungsi f( (pengertian secara geometri) ang melalui garis singgung. f( f( f(+ Q [( +, f ( + ] f( P (, f ( )
