Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II
|
|
|
- Ridwan Hardja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II [MA4]
2 PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan Differensial diatas disebut homogen, sebaliknya disebut non homogen. Persamaan Differensial Biasa linier orde dua homogen dengan koefisien konstan, memiliki bentuk umum : y + ay + by = 0 dimana a, b merupakan konstanta sebarang.
3 Solusi Homogen Diketahui y + ay + by = 0 Misalkan y=e rx Persamaannya berubah menjadi r + ar + b = 0, sebuah persamaan kuadrat. Jadi kemungkinan akarnya ada 3 yaitu:. Akar real berbeda (r,r ; dimana r r ) Memiliki solusi basis y = e r x dan y = e r x dan mempunyai solusi umum y = C e r x + C e r x 3
4 Solusi Homogen. Akar real kembar (r,r ; dimana r = r =r ) Memiliki solusi basis y = e r x dan y =x e r x dan mempunyai solusi umum y = C e r x + C x e r x 3.Akar kompleks kojugate (r = u + wi, r = u wi) Memiliki solusi basis y = e ux cos wx; dan y = e ux sin wx dan mempunyai solusi umum y = e ux ( C cos wx + C sin wx ) 4
5 Contoh soal. y + 5y + 6y = 0 Persamaan karakteristiknya: ( r + ) ( r + 3 ) = 0 r = - atau r = -3 maka solusinya : y = C e - x + C e -3x. y + 6y + 9y = 0 Persamaan karakteristiknya: ( r + 3 ) ( r + 3 ) = 0 r = r = -3 maka solusinya : y = C e -3x + C x e -3x 3. y + 4y = 0 Persamaan karakteristiknya: r + 4 = 0 ± 4..4 r = = ± i maka solusinya : y = C cos x + C sin x 5
6 Latihan. y 3y -4y=0. y 9y=0 3. y + 4y=0 4. y +y =0 5. y 4y + 4y=0 6. y + 3y 4y=0 7. y + 9y= 0 8. y + y =0 9. y 4y=0, y=4, y =0 bila x=0 0. y 5y + 6y=0, y=, y =0 bila x=0 6
7 Persamaan Differensial non homogen Bentuk umum: dengan r(x) 0 y + p(x)y + g(x)y = r(x) Solusi total : y = y h + y p Dimana y h = solusi P D homogen y p = solusi P D non homogen Menentukan y p. Metode koefisien tak tentu. Metode variasi parameter 7
8 Metode koefisien tak tentu pilihlah y p yang serupa dengan r(x), lalu substitusikan ke dalam persamaan. r(x) = e mx r(x) y p = A e mx y p r(x) = X n y p = A n X n + A n- X n- +.+A X + A 0 r(x) = sin wx y p = A cos wx + B sin wx r(x) =cos wx y p = A cos wx + B sin wx r(x) = e ux sin wx y p = e ux (A cos wx + B sin wx ) R(x) =e ux cos wx y p = e ux (A cos wx + B sin wx ) Ctt: Solusi Parsial tidak boleh muncul pada solusi homogennya. Jika hal ini terjadi, kalikan solusi khususnya dengan faktor x atau x sehingga tidak memuat lagi solusi homogennya. 8
9 Contoh. y 3y + y = e -x Jawab: Persamaan karakteristiknya: r 3r + = 0 (r )(r ) = 0 Sehingga didapat r = dan r = Jadi solusi homogennya adalah y h = C e x + C e x Untuk y p dipilih y p = A e -x y p =-A e -x y p = A e -x KemudianmasukankePD diatas: A e -x + 3 A e -x + A e -x = e -x 6 A e -x = e -x A = /6 Jadi solusi umum PD di atas adalah y = C e x + C e x + /6 e -x 9
10 Contoh. y 3y + y = cos x Jawab: Persamaan karakteristiknya: r 3 r + = 0 (r ) (r ) = 0 Sehingga didapat r = dan r = Jadi solusi homogennya adalah y h = C e x + C e x Untuk y p dipilih y p = A cos x + B sin x y p = -A sinx + B cos x KemudianmasukankePD diatas: y p = -A cosx B sin x (-A cos x B sin x) 3(-A sin x + B cos x)+(a cos x +B sin x)= cos x (-A-3B+A) cos x + (-B+3A+B) sin x= cos x (-3B + A) cos x + (3A+B) sin x= cos x -3B + A = dan 3A+B= 0 0
11 Contoh (no. Lanjutan) Didapat A = /0 dan B = -3/0 Jadi solusi umum PD di atas adalah y = C e x + C e x + (/0) cos x (3/0) sin x 3. y 3y + y = e -x + cos x Jawab: Dari contoh dan didapat, solusi umumnya adalah y = C e x + C e x + (/6) e -x + (/0) cos x (3/0) sin x
12 Contoh 4. y 3y + y = e x, y(0)=, y (0)=- Jawab: Persamaan karakteristiknya: r 3 r + = 0 (r )(r ) = 0 Sehingga didapat r = dan r = Jadi solusi homogennya adalah y h = C e x + C e x Untuk y p dipilih y p = A x e x y p = A e x + A x e x KemudianmasukankePD diatas: y p = A e x + A x e x Ae x +Axe x 3(Ae x + Axe x ) + Axe x = e x -A e x = e x A = - Jadi solusi umum PD di atas adalah y = C e x + C e x xe x
13 Contoh Kita punya y(0)= dan y (0)=- y = C e x + C e x x e x =C +C y = C e x + C e x e x xe x Didapat C =-, dan C = 0=C +C Jadi solusi khusus PD di atas adalah y = e x + e x x e x 3
14 Latihan. y 3y -4y=3x +. y 9y=x+ 3. y 3y 4y=e x 4. y + 4y= sin x 5. y 3y -4y=e -x 6. y + 4y= cos x 7. y +y =3x + 8. y 4y + 4y=e x 9. y + 3y 4y=3x + 0. y + 9y= sin 3x+e x. y + y =e x + 3x. y 4y=4 sinx, y=4, y =0 bila x=0 3. y 5y + 6y=e x, y=, y =0 bila x=0 4
15 Metode Variasi Parameter Metode ini digunakan untuk memecahkan persamaanpersamaan yang tidak dapat diselesaikan dengan menggunakan metode koefisien tak tentu. Persamaan Differensial orde dua non homogen y + a y + b y = r(x) memiliki solusi total : y = y h + y p misal y p = u y + v y dimana u = u(x) ; v = v(x) maka y p = u y + u y + v y + v y pilih u dan v sehingga : u y + v y = 0.(*) 5
16 Metode Variasi Parameter y p = u y + v y y p = u y + u y + v y + vy Substitusikan y p, y p, y p ke dalam persamaan awal sehingga di dapatkan : u y + u y + v y + vy + a (u y + v y )+ b ( u y + v y ) = r(x) u ( y + a y + b y ) + v ( y + a y + b y ) + u y + v y = r (x) u y + v y = r (x).(**) 6
17 Metode Variasi Parameter Eleminasi (*) dan (**) di peroleh : u y + v y = 0 u y + v y = r (x) dengan aturan cramer diperoleh 0 r(x) y' y r(x) ' = u = dx y y W y ' y y u Keterangan: W = ' y y y' y' y y' r(x) y r(x) ' = v = dx y y W y ' y 0 v ' 7
18 Contoh. y + y = tan x Jawab: Persamaan karakteristiknya: r + = 0 r = ± i Jadi solusi homogennya adalah y h = C cos x + C sin x Untuk y p dipilih y p = u y + v y dengan y = cos x y = sin x y = - sin x y = cos x W= y y y y =cos x+sin x = Sehingga diperoleh sin x tan x sin u = dx = x dx cos x = cos x dx cos x (sec = x cos x) dx 8
19 Contoh (Lanjutan) + = sec x dx cos x dx = ln sec x + tan x + sin x Sedangkan, cos x tan x v = dx = sin x dx = cos x Jadi solusi non homogen didapat y p = = ( ln sec x + tan x ) cos x + sin x cos x sin x cos x ( ln sec x + tan x ) cos x Jadi solusi umum dari persamaan diferensial di atas y = C cos x + C sin x + ( ln sec x tan x ) cos x 9
20 Contoh. y +9y = sec 3x Jawab: Persamaan karakteristiknya: r + 9 = 0 r = ± 3 i Jadi solusi homogennya adalah y h = C cos 3x + C sin 3x Untuk y p dipilih y p = u y + v y dengan y = cos 3x y = sin 3x y = -3 sin 3x y = 3 cos 3x W= y y y y =3cos 3x+3 sin 3x =3 Sehingga diperoleh sin 3xsec 3x u = dx = 3 sec3x tan 3x dx 3 = 9 sec 3x 0
21 Contoh (Lanjutan) Sedangkan, cos 3xsec 3x v = dx = sec 3x dx = ln sec3x + tan 3x Jadi solusi non homogen didapat y p = sec3x cos3x + ( ln sec3x + tan 3x ) sin 3x 9 9 y p = + ( ln sec3x + tan 3x ) sin 3x 9 9 Jadi solusi umum dari persamaan diferensial di atas y = C cos3x + C sin 3x ( ln sec3x tan 3x ) sin x
22 Latihan. y + y = cosec x cot x. y + y = cot x x e 3. y 3 y + y = x e + x e 4. y + 4 y + 4 y = x 5. y + 4 y = 3 cosec x 6. y + 4 y = 3 cosec x 7. 4 y + y = sec (x/) x e 8. y y + y = + x
23 Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Penggunaan PD Orde II [MA4]
24 Penerapan dalam Rangkaian Listrik Perhatikan suatu rangkaian (gambar samping) dengan sebuah tahanan (R ohm), dan sebuah kumparan (L Henry) dan sebuah kapasitor (C farad) dalam rangkaian seri dengan sumber gaya elektromotif yang menyediakan suatu voltase E(t) volt pada saat t. Hukum Kirchhoff untuk kasus ini, muatan Q pada kapasitor, diukur dalam coulomb, memenuhi d Q dq L + R + Q = dt dt C E() t 4
25 Arus (Lanjutan) I = dq dt, diukur dalam ampere, memenuhi persamaan yang diperoleh dengan pendiferensialan persamaan di atas terhadap t, yaitu L d I dt + R di dt + C I = E' () t 5
26 Contoh Tentukan muatan Q dan arus I sebagai fungsi dari waktu t dari suatu rangkaian RLC dengan R = 6 ohm, L = 0,0 henry, C = x 0-4 farad dan E = Volt dengan diasumsikan saat awal arus dan muatannya adalah nol (pada waktu saklar S ditutup) Jawab Dari hukum kirchhoff, tentang rangkaian RLC didapat 0,0 Q" + 6 Q' Q = Atau bisa disederhanakan Q" Q' Q = 600 6
27 Contoh Persamaan karakteristiknya adalah r r = 0 Diperoleh akar akar persamaannya : Solusi homogen : Q r = 400 ± 300i ( C 300t + C sin t) 400 t Qh = e cos 300 Dengan menggunakan metode koefisien tak tentu, dengan mengambil Q p = A, di dapat 3 =,4 x 0 Q p Jadi solusi umumnya adalah ( C cos 300t + C sin 300t ) t =,4 x 0 + e 7
28 Rangkaian RLC Dengan memasukkan syarat awal Q(0) =0 dan I(0)=0 maka diperoleh C =,4 x 0 Q = dan Jadi solusi khususnya adalah C = 3, x 0 (,4 cos 300t + 3, sin 300t ) [ e ] 400 t,4 Dengan pendiferensialan diperoleh I( t) = Q'( t) = e 400t sin300t 3 8
29 Latihan. Hitunglah kuat arus yang mengalir dalam suatu rangkaian RLC dengan nilai R = 00 ohm, L = 0, henry, C = 0-3 farad yang dihubungkan dengan sumber tegangan E(t) = 55 sin 377 t dengan diasumsikan pada saat awal arus dan muatannya adalah nol.. Tentukan muatan Q sebagai fungsi dari waktu t yang mengalir dalam suatu rangkaian RC dengan R = 0 6 ohm, C = 0-6 farad dan sumber tegangannya konstan dengan E = Volt dan diasumsikan saat awal muatannya adalah nol. 9
30 Latihan 3. Hitunglah muatan dan kuat arus I yang mengalir dalam suatu rangkaian RLC dengan nilai R = 000 ohm, L = 3,5 henry, C = x 0-6 farad yang dihubungkan dengan sumber tegangan E(t) = 0 sin 377t dengan diasumsikan pada saat awal arus dan muatannya adalah nol. 4. Tentukan kuat arus I sebagai fungsi dari waktu t yang mengalir dalam suatu rangkaian LC dengan L = 0 - Henry, C = 0-7 farad dan sumber tegangannya konstan dengan E = 0 Volt dan diasumsikan saat awal muatan dan arusnya adalah nol. 30
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde II
 Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
Nurdinintya Athari PERSAMAAN DIFFERENSIAL ORDE 2
 Nurdininta Athari PERSAMAAN DIFFERENSIAL ORDE 2 2 PDB ORDE II Bentuk umum : + p() + g() = r() p(), g() disebut koefisien jika r() = 0, maka Persamaan Differensial diatas disebut homogen, sebalikna disebut
Nurdininta Athari PERSAMAAN DIFFERENSIAL ORDE 2 2 PDB ORDE II Bentuk umum : + p() + g() = r() p(), g() disebut koefisien jika r() = 0, maka Persamaan Differensial diatas disebut homogen, sebalikna disebut
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO. Mohamad Sidiq
 MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO REFERENSI E-BOOK REFERENSI ONLINE SOS Mathematics http://www.sosmath.com/diffeq/diffeq.html Wolfram Research Math World http://mathworld.wolfram.com/ordinarydifferentialequation.h
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO REFERENSI E-BOOK REFERENSI ONLINE SOS Mathematics http://www.sosmath.com/diffeq/diffeq.html Wolfram Research Math World http://mathworld.wolfram.com/ordinarydifferentialequation.h
PERSAMAAN DIFERENSIAL LINIER NON HOMOGEN
 LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui.
 1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
Hendra Gunawan. 25 April 2014
 MA101 MATEMATIKA A Hendra Gunawan Semester II, 013/014 5 April 014 Kuliah yang Lalu 15.11 Persamaan Diferensial Linear Orde, Homogen 15. Persamaan Diferensial Linear Orde, Tak Homogen 15.3 Penggunaan Persamaan
MA101 MATEMATIKA A Hendra Gunawan Semester II, 013/014 5 April 014 Kuliah yang Lalu 15.11 Persamaan Diferensial Linear Orde, Homogen 15. Persamaan Diferensial Linear Orde, Tak Homogen 15.3 Penggunaan Persamaan
BAB I PENDAHULUAN. Kompetensi
 BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: = f(x, y) M(x, y) + N(x, y) = 0 Penyelesaian PDB orde satu dengan integrasi secara langsung Jika
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: = f(x, y) M(x, y) + N(x, y) = 0 Penyelesaian PDB orde satu dengan integrasi secara langsung Jika
BAB I PENDAHULUAN. Kompetensi
 BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
BAB I PENDAHULUAN Kompetensi Mahasiswa diharapkan 1. Memiliki kesadaran tentang manfaat yang diperoleh dalam mempelajari materi kuliah persamaan diferensial. 2. Memahami konsep-konsep penting dalam persamaan
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: Penyelesaian PDB orde satu dengan integrasi secara langsung Jika PDB dapat disusun dalam bentuk,
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: Penyelesaian PDB orde satu dengan integrasi secara langsung Jika PDB dapat disusun dalam bentuk,
PERSAMAAN DIFFERENSIAL LINIER
 PERSAMAAN DIFFERENSIAL LINIER Persamaan Differensial Linier Pengertian : Suatu persamaan differensial orde satu dikatakan linier jika persamaan tersebut dapat dituliskan sbb: y + p x y = r(x) (1) linier
PERSAMAAN DIFFERENSIAL LINIER Persamaan Differensial Linier Pengertian : Suatu persamaan differensial orde satu dikatakan linier jika persamaan tersebut dapat dituliskan sbb: y + p x y = r(x) (1) linier
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Linier Homogen Tk. 2 (Differential: Linier Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya PD linier homogen orde 2 Bentuk
TKS 4003 Matematika II Persamaan Diferensial Linier Homogen Tk. 2 (Differential: Linier Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya PD linier homogen orde 2 Bentuk
BAB IV PERSAMAAN TAKHOMOGEN
 BAB IV PERSAMAAN TAKHOMOGEN Kompetensi Mahasiswa mampu 1. Menentukan selesaian khusus PD tak homogen dengan metode koefisien tak tentu 2. Menentukan selesaian khusus PD tak homogen dengan metode variasi
BAB IV PERSAMAAN TAKHOMOGEN Kompetensi Mahasiswa mampu 1. Menentukan selesaian khusus PD tak homogen dengan metode koefisien tak tentu 2. Menentukan selesaian khusus PD tak homogen dengan metode variasi
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Linier Non Homogen Tk. 2 (Differential: Linier Non Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Solusi umum merupakan jumlah
TKS 4003 Matematika II Persamaan Diferensial Linier Non Homogen Tk. 2 (Differential: Linier Non Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Solusi umum merupakan jumlah
PEMBENTUKAN MODEL RANGKAIAN LISTRIK
 PEMBENTUKAN MODEL RANGKAIAN LISTRIK Pada sub bab ini akan membahas tentang sistem listrik. Pembahasan ini berperan sebagai suatu contoh yang mengesankan dari kenyataan penting, bahwa sistem fisis yang
PEMBENTUKAN MODEL RANGKAIAN LISTRIK Pada sub bab ini akan membahas tentang sistem listrik. Pembahasan ini berperan sebagai suatu contoh yang mengesankan dari kenyataan penting, bahwa sistem fisis yang
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE DUA
 MATERI MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE DUA 1 Tujuan 1. Dapat menyelesaikan persamaan diferensial orde dua.. Dapat menyelesaikan suatu Sistem Linier dengan menggunakan metode Eliminasi atau
MATERI MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE DUA 1 Tujuan 1. Dapat menyelesaikan persamaan diferensial orde dua.. Dapat menyelesaikan suatu Sistem Linier dengan menggunakan metode Eliminasi atau
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 2 - II
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE - II.Persamaan Homogen dengan Koefisien Konstan Suatu persamaan linier homogen y + ay + by = 0 (1) mempunyai koefisien a dan b adalah konstan. Persamaan ini mempunyai
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE - II.Persamaan Homogen dengan Koefisien Konstan Suatu persamaan linier homogen y + ay + by = 0 (1) mempunyai koefisien a dan b adalah konstan. Persamaan ini mempunyai
Persamaan Di erensial Orde-2
 oki neswan FMIPA-ITB Persamaan Di erensial Orde- Persamaan diferensial orde-n adalah persamaan yang melibatkan x; y; dan turunan-turunan y; dengan yang paling tinggi adalah turunan ke-n: F x; y; y ; y
oki neswan FMIPA-ITB Persamaan Di erensial Orde- Persamaan diferensial orde-n adalah persamaan yang melibatkan x; y; dan turunan-turunan y; dengan yang paling tinggi adalah turunan ke-n: F x; y; y ; y
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU
 MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
PERSAMAAN DIFFERENSIAL ORDE I. Nurdinintya Athari
 PERSAMAAN DIFFERENSIAL ORDE I Nurdininta Athari Definisi PERSAMAAN DIFERENSIAL Persamaan diferensial adalah suatu persamaan ang memuat satu atau lebih turunan fungsi ang tidak diketahui. Jika persamaan
PERSAMAAN DIFFERENSIAL ORDE I Nurdininta Athari Definisi PERSAMAAN DIFERENSIAL Persamaan diferensial adalah suatu persamaan ang memuat satu atau lebih turunan fungsi ang tidak diketahui. Jika persamaan
INTEGRAL TAK TENTU 1
 INTEGRAL TAK TENTU 1 Rumus umum integral b a f (x) dx F(x) =lambang integral f(x) = integran (fungsi yg diintegralkan) a dan b = batas pengintegralan a = batas bawah b = batas atas dx = faktor pengintegral
INTEGRAL TAK TENTU 1 Rumus umum integral b a f (x) dx F(x) =lambang integral f(x) = integran (fungsi yg diintegralkan) a dan b = batas pengintegralan a = batas bawah b = batas atas dx = faktor pengintegral
PD Orde 2 Lecture 3. Rudy Dikairono
 PD Orde Lecture 3 Rudy Dikairono Today s Outline PD Orde Linear Homogen PD Orde Linear Tak Homogen Metode koefisien tak tentu Metode variasi parameter Beberapa Pengelompokan Persamaan Diferensial Order
PD Orde Lecture 3 Rudy Dikairono Today s Outline PD Orde Linear Homogen PD Orde Linear Tak Homogen Metode koefisien tak tentu Metode variasi parameter Beberapa Pengelompokan Persamaan Diferensial Order
TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 2016/2017
 A. Pengantar Persamaan Diferensial TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 016/017 1. Tentukan hasil turunan dari fungsi sebagai berikut: a. f() = c e b. f() = c cos k + c sin k c.
A. Pengantar Persamaan Diferensial TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 016/017 1. Tentukan hasil turunan dari fungsi sebagai berikut: a. f() = c e b. f() = c cos k + c sin k c.
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL
 HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL Dra.Sri Rejeki Dwi Putranti, M.Kes. Fakultas Teknik - Universitaas Yos Soedarso Surabaya Email : riccayusticia@gmail.com Abstrak Hubungan antara Differensial dan
HUBUNGAN ANTARA DIFFERENSIAL DAN INTEGRAL Dra.Sri Rejeki Dwi Putranti, M.Kes. Fakultas Teknik - Universitaas Yos Soedarso Surabaya Email : riccayusticia@gmail.com Abstrak Hubungan antara Differensial dan
BAB 2 PERSAMAAN DIFFERENSIAL BIASA
 BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
PENYELESAIAN MODEL RANGKAIAN LISTRIK RL DAN RC SERI Oleh: 1 Ir. SIGIT KUSMARYANTO, M.Eng.
 PENYELESAIAN MODEL RANGKAIAN LISTRIK RL DAN RC SERI Oleh: 1 Ir. SIGIT KUSMARYANTO, M.Eng. 1 Teknik Elektro, http://sigitkus@ub.ac.id Pengantar: Modul ini menjelaskan pemodelan rangkaian listrik RL dan
PENYELESAIAN MODEL RANGKAIAN LISTRIK RL DAN RC SERI Oleh: 1 Ir. SIGIT KUSMARYANTO, M.Eng. 1 Teknik Elektro, http://sigitkus@ub.ac.id Pengantar: Modul ini menjelaskan pemodelan rangkaian listrik RL dan
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA
 PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
perpindahan, kita peroleh persamaan differensial berikut :
 1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
BAB PDB Linier Order Satu
 BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
Ringkasan Kalkulus 2, Untuk dipakai di ITB 1. Integral Lipat Dua Atas Daerah Persegipanjang
 ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x, y) pada = {(x, y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
ingkasan Kalkulus 2, Untuk dipakai di ITB 1 Integral Lipat Dua Atas Daerah Persegipanjang Perhatikan fungsi z = f(x, y) pada = {(x, y) : a x b, c y d} Bentuk partisi P atas daerah berupa n buah persegipanjang
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Linier Homogen & Non Homogen Tk. n (Differential: Linier Homogen & Non Homogen Orde n) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
TKS 4003 Matematika II Persamaan Diferensial Linier Homogen & Non Homogen Tk. n (Differential: Linier Homogen & Non Homogen Orde n) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
K13 Revisi Antiremed Kelas 12 Fisika
 K13 Revisi Antiremed Kelas 12 Fisika Listrik Arus Bolak-balik - Soal Doc. Name: RK13AR12FIS0401 Version: 2016-12 halaman 1 01. Suatu sumber tegangan bolak-balik menghasilkan tegangan sesuai dengan fungsi
K13 Revisi Antiremed Kelas 12 Fisika Listrik Arus Bolak-balik - Soal Doc. Name: RK13AR12FIS0401 Version: 2016-12 halaman 1 01. Suatu sumber tegangan bolak-balik menghasilkan tegangan sesuai dengan fungsi
Hendra Gunawan. 23 April 2014
 MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 23 April 2014 Kuliah ang Lalu 13.11 Integral Lipat Dua atas Persegi Panjang 13.2 Integral Berulang 13.3 33Integral Lipat Dua atas Daerah Bukan
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 23 April 2014 Kuliah ang Lalu 13.11 Integral Lipat Dua atas Persegi Panjang 13.2 Integral Berulang 13.3 33Integral Lipat Dua atas Daerah Bukan
Antiremed Kelas 12 Fisika
 Antiremed Kelas 12 Fisika Listrik Arus Bolak Balik - Latihan Soal Doc. Name: AR12FIS0699 Version: 2011-12 halaman 1 01. Suatu sumber tegangan bolak-balik menghasilkan tegangan sesuai dengan fungsi: v =140
Antiremed Kelas 12 Fisika Listrik Arus Bolak Balik - Latihan Soal Doc. Name: AR12FIS0699 Version: 2011-12 halaman 1 01. Suatu sumber tegangan bolak-balik menghasilkan tegangan sesuai dengan fungsi: v =140
Bab 7 Persamaan Differensial Non-homogen
 Bab 7 Persamaan Differensial Non-homogen Persamaan Differensial Orde- Non Homogen Bentuk hukum : d y dy + p( ) + Q( ) y R( ) (*) Dimana, P(), Q(), dan R() dapat juga berwujud suatu leoust Solusinya : y
Bab 7 Persamaan Differensial Non-homogen Persamaan Differensial Orde- Non Homogen Bentuk hukum : d y dy + p( ) + Q( ) y R( ) (*) Dimana, P(), Q(), dan R() dapat juga berwujud suatu leoust Solusinya : y
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL
 Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
 MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
TEKNIK PENGINTEGRALAN
 TEKNIK PENGINTEGRALAN KALKULUS S- Teknik Industri Outline Integral Parsial Integral Fungsi Trigonometri Substitusi Trigonometri Integral Fungsi Rasional . Integral Parsial Formula Integral Parsial : u
TEKNIK PENGINTEGRALAN KALKULUS S- Teknik Industri Outline Integral Parsial Integral Fungsi Trigonometri Substitusi Trigonometri Integral Fungsi Rasional . Integral Parsial Formula Integral Parsial : u
MODUL MATEMATIKA TEKNIK
 MODUL MATEMATIKA TEKNIK Disusun oleh: Dwi Lestari, M.Sc email: dwilestari@uny.ac.id JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA 2011 Linear
MODUL MATEMATIKA TEKNIK Disusun oleh: Dwi Lestari, M.Sc email: dwilestari@uny.ac.id JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA 2011 Linear
DERET FOURIER. n = bilangan asli (1,2,3,4,5,.) L = pertemuan titik. Bilangan-bilangan untuk,,,, disebut koefisien fourier dari f(x) dalam (-L,L)
 DERET FOURIER Bila f adalah fungsi periodic yang berperioda p, maka f adalah fungsi periodic. Berperiode n, dimana n adalah bilangan asli positif (+). Untuk setiap bilangan asli positif fungsi yang didefinisikan
DERET FOURIER Bila f adalah fungsi periodic yang berperioda p, maka f adalah fungsi periodic. Berperiode n, dimana n adalah bilangan asli positif (+). Untuk setiap bilangan asli positif fungsi yang didefinisikan
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
RANGKAIAN ARUS BOLAK-BALIK.
 Arus Bolak-balik RANGKAIAN ARUS BOLAK-BALIK. Dalam pembahasan yang terdahulu telah diketahui bahwa generator arus bolakbalik sebagai sumber tenaga listrik yang mempunyai GGL : E E sinω t Persamaan di atas
Arus Bolak-balik RANGKAIAN ARUS BOLAK-BALIK. Dalam pembahasan yang terdahulu telah diketahui bahwa generator arus bolakbalik sebagai sumber tenaga listrik yang mempunyai GGL : E E sinω t Persamaan di atas
Jl. Ir. M. Putuhena, Kampus Unpatti, Poka-Ambon 2 ABSTRAK
 Jurnal Barekeng Vol. 8 No. 1 Hal. 39 43 (2014) APLIKASI METODE RUNGE KUTTA ORDE EMPAT PADA PENYELESAIAN RANGKAIAN LISTRIK RLC Application of Fourth Order Runge Kutta methods on Completion of the Electrical
Jurnal Barekeng Vol. 8 No. 1 Hal. 39 43 (2014) APLIKASI METODE RUNGE KUTTA ORDE EMPAT PADA PENYELESAIAN RANGKAIAN LISTRIK RLC Application of Fourth Order Runge Kutta methods on Completion of the Electrical
BAB 2 TINJAUAN PUSTAKA
 5 BAB 2 TINJAUAN PUSTAKA 2.1 Persamaan Diferensial Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen, suatu variabel dependen, dan satu atau lebih turunan dari
5 BAB 2 TINJAUAN PUSTAKA 2.1 Persamaan Diferensial Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen, suatu variabel dependen, dan satu atau lebih turunan dari
Bab 7 Persamaan Differensial Orde-2 Non Homogen
 Metode Matematika Astronomi- Bab 7 Persamaan Differensial Orde- Non Homogen 7. Persamaan Differensial Orde- Homogen 0 Bentuk Umum a b cy ab, dan c konstanta, persamaan ini dapat juga ditulis sebagai :
Metode Matematika Astronomi- Bab 7 Persamaan Differensial Orde- Non Homogen 7. Persamaan Differensial Orde- Homogen 0 Bentuk Umum a b cy ab, dan c konstanta, persamaan ini dapat juga ditulis sebagai :
BAB III PD LINIER HOMOGEN
 BAB III PD LINIER HOMOGEN Kompetensi Mahasiswa diharapkan. Mampu menentukan selesaian umum dari PD linier homogen orde dua dengan jenis akarakar karakteristik yang berbeda-beda. Memahami pengertian kebebaslinieran
BAB III PD LINIER HOMOGEN Kompetensi Mahasiswa diharapkan. Mampu menentukan selesaian umum dari PD linier homogen orde dua dengan jenis akarakar karakteristik yang berbeda-beda. Memahami pengertian kebebaslinieran
16. INTEGRAL. A. Integral Tak Tentu 1. dx = x + c 2. a dx = a dx = ax + c. 3. x n dx = + c. cos ax + c. 4. sin ax dx = 1 a. 5.
 6. INTEGRAL A. Integral Tak Tentu. dx = x + c. a dx = a dx = ax + c. x n dx = n+ x n+ + c. sin ax dx = a cos ax + c 5. cos ax dx = a sin ax + c 6. sec ax dx = a tan ax + c 7. [ f(x) ± g(x) ] dx = f(x)
6. INTEGRAL A. Integral Tak Tentu. dx = x + c. a dx = a dx = ax + c. x n dx = n+ x n+ + c. sin ax dx = a cos ax + c 5. cos ax dx = a sin ax + c 6. sec ax dx = a tan ax + c 7. [ f(x) ± g(x) ] dx = f(x)
BAB III PERSAMAAN DIFERENSIAL LINIER
 BAB III PERSAMAAN DIFERENSIAL LINIER Bentuk umum PD orde-n adalah PD yang tidak dapat dinyatakan dalam bentuk di atas dikatakan tidak linier. Contoh: Jika F(x) pada persamaan (3.1) sama dengan nol maka
BAB III PERSAMAAN DIFERENSIAL LINIER Bentuk umum PD orde-n adalah PD yang tidak dapat dinyatakan dalam bentuk di atas dikatakan tidak linier. Contoh: Jika F(x) pada persamaan (3.1) sama dengan nol maka
Kalkulus 2. Teknik Pengintegralan ke - 1. Tim Pengajar Kalkulus ITK. Institut Teknologi Kalimantan. Januari 2018
 Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
Kalkulus 2 Teknik Pengintegralan ke - 1 Tim Pengajar Kalkulus ITK Institut Teknologi Kalimantan Januari 2018 Tim Pengajar Kalkulus ITK (Institut Teknologi Kalimantan) Kalkulus 2 Januari 2018 1 / 36 Daftar
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegral
 MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
MA1201 KALKULUS 2A (Kelas 10) Bab 7: Teknik Pengintegralan Do maths and you see the world Integral atau Anti-turunan? Integral atau pengintegral adalah salah satu konsep (penting) dalam matematika disamping
4. Dibawah ini persamaan diferensial ordo dua berderajat satu adalah
 Pilihlah jawaban yang benar dengan cara mencakra huruf didepan jawaban yang saudara anggap benar pada lembar jawaban 1. Dibawah ini bentuk persamaan diferensial biasa linier homogen adalah a. y + xy =
Pilihlah jawaban yang benar dengan cara mencakra huruf didepan jawaban yang saudara anggap benar pada lembar jawaban 1. Dibawah ini bentuk persamaan diferensial biasa linier homogen adalah a. y + xy =
Untai Elektrik I. Untai Orde Tinggi & Frekuensi Kompleks. Dr. Iwan Setyawan. Fakultas Teknik Universitas Kristen Satya Wacana. Untai 1. I.
 Untai Elektrik I Untai Orde Tinggi & Frekuensi Kompleks Dr. Iwan Setyawan Fakultas Teknik Universitas Kristen Satya Wacana Pada bagian sebelumnya, dibahas untai RC dan RL dengan hanya satu elemen penyimpan
Untai Elektrik I Untai Orde Tinggi & Frekuensi Kompleks Dr. Iwan Setyawan Fakultas Teknik Universitas Kristen Satya Wacana Pada bagian sebelumnya, dibahas untai RC dan RL dengan hanya satu elemen penyimpan
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
Pertemuan Kesatu. Matematika III. Oleh Mohammad Edy Nurtamam, S.Pd., M.Si. Page 1.
 Pertemuan Kesatu Matematika III Oleh Mohammad Edy Nurtamam, S.Pd., M.Si Page 1 Materi 1. Persamaan Diferensial Orde I Pengenalan bentuk dasar Pers. Diff. Orde I. Definisi Derajat,Orde. Konsep Pemisahan
Pertemuan Kesatu Matematika III Oleh Mohammad Edy Nurtamam, S.Pd., M.Si Page 1 Materi 1. Persamaan Diferensial Orde I Pengenalan bentuk dasar Pers. Diff. Orde I. Definisi Derajat,Orde. Konsep Pemisahan
PENYELESAIAN MODEL RANGKAIAN LISTRIK ORDE-2 Oleh: Ir. Sigit Kusmaryanto, M.Eng
 PENYELESAIAN MODEL RANGKAIAN LISTRIK ORDE-2 Oleh: Ir. Sigit Kusmaryanto, M.Eng Dua fenomena fisik berbeda (yaitu: sistem gerak benda pada pegas dan rangkaian listrik) menghasilkan model persamaan matematika
PENYELESAIAN MODEL RANGKAIAN LISTRIK ORDE-2 Oleh: Ir. Sigit Kusmaryanto, M.Eng Dua fenomena fisik berbeda (yaitu: sistem gerak benda pada pegas dan rangkaian listrik) menghasilkan model persamaan matematika
BAB I PENGERTIAN DASAR
 BAB I PENGERTIAN DASAR Kompetensi Dasar: Menjelaskan pengertian dan klasifikasi dari persamaan diferensial serta beberapa hal yang terkait. Indikator: a. Menjelaskankan pengertian persamaan diferensial.
BAB I PENGERTIAN DASAR Kompetensi Dasar: Menjelaskan pengertian dan klasifikasi dari persamaan diferensial serta beberapa hal yang terkait. Indikator: a. Menjelaskankan pengertian persamaan diferensial.
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL
 BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
Sudaryatno Sudirham. Integral dan Persamaan Diferensial
 Sudaratno Sudirham Integral dan Persamaan Diferensial Bahan Kuliah Terbuka dalam format pdf tersedia di www.buku-e.lipi.go.id dalam format pps beranimasi tersedia di www.ee-cafe.org Bahasan akan mencakup
Sudaratno Sudirham Integral dan Persamaan Diferensial Bahan Kuliah Terbuka dalam format pdf tersedia di www.buku-e.lipi.go.id dalam format pps beranimasi tersedia di www.ee-cafe.org Bahasan akan mencakup
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL
 BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
Persamaan Differensial Biasa
 Bab 7 cakul fi5080 by khbasar; sem1 2010-2011 Persamaan Differensial Biasa Dalam banyak persoalan fisika, suatu topik sering dinyatakan dalam bentuk perubahan (laju perubahan). Telah disinggung sebelumnya
Bab 7 cakul fi5080 by khbasar; sem1 2010-2011 Persamaan Differensial Biasa Dalam banyak persoalan fisika, suatu topik sering dinyatakan dalam bentuk perubahan (laju perubahan). Telah disinggung sebelumnya
INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP
 A. Soal dan Pembahasan. ( x ) dx... Jawaban : INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP ( x) dx x dx x C x C x x C. ( x 9) dx... x Jawaban : ( x 9) dx. (x x 9) dx x 9x C x x x. (x )(x + ) dx =.
A. Soal dan Pembahasan. ( x ) dx... Jawaban : INTEGRAL (ANTI DIFERENSIAL) Tito Adi Dewanto S.TP ( x) dx x dx x C x C x x C. ( x 9) dx... x Jawaban : ( x 9) dx. (x x 9) dx x 9x C x x x. (x )(x + ) dx =.
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
MODUL FISIKA. TEGANGAN DAN ARUS BOLAK-BALIK (AC) DISUSUN OLEH : NENIH, S.Pd SMA ISLAM PB. SOEDIRMAN
 MODUL ISIKA TEGANGAN DAN ARUS BOLAK-BALIK (AC) DISUSUN OLEH : NENIH, S.Pd SMA ISLAM PB. SOEDIRMAN TEGANGAN DAN ARUS BOLAK-BALIK (AC) 1. SUMBER TEGANGAN DAN ARUS BOLAK-BALIK Sumber tegangan bolak-balik
MODUL ISIKA TEGANGAN DAN ARUS BOLAK-BALIK (AC) DISUSUN OLEH : NENIH, S.Pd SMA ISLAM PB. SOEDIRMAN TEGANGAN DAN ARUS BOLAK-BALIK (AC) 1. SUMBER TEGANGAN DAN ARUS BOLAK-BALIK Sumber tegangan bolak-balik
Gambar 3. (a) Diagram fasor arus (b) Diagram fasor tegangan
 RANGKAIAN ARUS BOLAK-BALIK Arus bolak-balik atau Alternating Current (AC) yaitu arus listrik yang besar dan arahnya yang selalu berubah-ubah secara periodik. 1. Sumber Arus Bolak-balik Sumber arus bolak-balik
RANGKAIAN ARUS BOLAK-BALIK Arus bolak-balik atau Alternating Current (AC) yaitu arus listrik yang besar dan arahnya yang selalu berubah-ubah secara periodik. 1. Sumber Arus Bolak-balik Sumber arus bolak-balik
Keep running VEKTOR. 3/8/2007 Fisika I 1
 VEKTOR 3/8/007 Fisika I 1 BAB I : VEKTOR Besaran vektor adalah besaran yang terdiri dari dua variabel, yaitu besar dan arah. Sebagai contoh dari besaran vektor adalah perpindahan. Sebuah besaran vektor
VEKTOR 3/8/007 Fisika I 1 BAB I : VEKTOR Besaran vektor adalah besaran yang terdiri dari dua variabel, yaitu besar dan arah. Sebagai contoh dari besaran vektor adalah perpindahan. Sebuah besaran vektor
integral = 2 . Setiap fungsi ini memiliki turunan ( ) = adalah ( ) = 6 2.
 integral 13.1 PENGERTIAN INTEGRAL Untuk itu, coba tentukan turunan fungsi berikut. Perhatikan bahwa fungsi ini memiliki bentuk umum 6 2. Jadi, turunan fungsi = 2 =2 3. Setiap fungsi ini memiliki turunan
integral 13.1 PENGERTIAN INTEGRAL Untuk itu, coba tentukan turunan fungsi berikut. Perhatikan bahwa fungsi ini memiliki bentuk umum 6 2. Jadi, turunan fungsi = 2 =2 3. Setiap fungsi ini memiliki turunan
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
 INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
INTISARI KALKULUS 2 Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 200 Pengantar Kalkulus & 2 merupakan matakuliah wajib tingkat pertama bagi semua
E = = (1,80 x 10 5 N/C )( 4π )(0,50 m) 2 = 5,652 x 10 5 Nm 2 /C
 PERTEMUAN KE 5 1. Fluks listrik melalui sebuah bola Sebuah muatan titik positif q = 5,0 μc dikelilingi oleh sebuah bola dengan jari-jari 0,50 m yang berpusat pada muatan itu. Berapa fluks listrik yang
PERTEMUAN KE 5 1. Fluks listrik melalui sebuah bola Sebuah muatan titik positif q = 5,0 μc dikelilingi oleh sebuah bola dengan jari-jari 0,50 m yang berpusat pada muatan itu. Berapa fluks listrik yang
Persamaan Diferensial Biasa
 Darmawijoyo Persamaan Diferensial Biasa Suatu Pengantar FKIP-UNSRI Untuk istriku tercinta Nelly Efrina dan anak-anakku tersayang, Yaya, Haris, dan Oji. Pendahuluan Buku Persamaan Diferensial Suatu Pengantar
Darmawijoyo Persamaan Diferensial Biasa Suatu Pengantar FKIP-UNSRI Untuk istriku tercinta Nelly Efrina dan anak-anakku tersayang, Yaya, Haris, dan Oji. Pendahuluan Buku Persamaan Diferensial Suatu Pengantar
Teknik pengintegralan: Integral parsial (Integral by part)
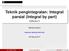 Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
Teknik pengintegralan: Integral parsial (Integral by part) Kalkulus 2 Nanang Susyanto Departemen Matematika FMIPA UGM 06 Februari 2017 NS (FMIPA UGM) Teknik pengintegralan 06/02/2017 1 / 14 Mari mengingat
Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb
 Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XII Differensial e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 PENDAHULUAN Persamaan diferensial
Mata Kuliah :: Matematika Rekayasa Lanjut Kode MK : TKS 8105 Pengampu : Achfas Zacoeb Sesi XII Differensial e-mail : zacoeb@ub.ac.id www.zacoeb.lecture.ub.ac.id Hp. 081233978339 PENDAHULUAN Persamaan diferensial
R +1 R= UR V+1 R= ( ) R +1 R= ( )
 Penyelesaian Model Rangkaian Listrik orde-2 Dua fenomena fisik berbeda (yaitu: sistem gerak benda pada pegas dan rangkaian listrik) menghasilkan model persamaan matematika dan solusi yang sama. Perilaku
Penyelesaian Model Rangkaian Listrik orde-2 Dua fenomena fisik berbeda (yaitu: sistem gerak benda pada pegas dan rangkaian listrik) menghasilkan model persamaan matematika dan solusi yang sama. Perilaku
MASALAH SYARAT BATAS (MSB)
 Program Studi Pendidikan Matematika FKIP Unmuh Ponorogo PENDAHULUAN MODEL KABEL MENGGANTUNG DEFINISI MSB Persamaan diferensial (PD) dikatakan berdimensi 1 jika domainnya berupa himpunan bagian pada R 1.
Program Studi Pendidikan Matematika FKIP Unmuh Ponorogo PENDAHULUAN MODEL KABEL MENGGANTUNG DEFINISI MSB Persamaan diferensial (PD) dikatakan berdimensi 1 jika domainnya berupa himpunan bagian pada R 1.
Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika. F (x) = f(x) dx dan f (x) dinamakan integran.
 4 INTEGRAL Definisi 4. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
4 INTEGRAL Definisi 4. Fungsi F disebut anti turunan (integral tak tentu) dari fungsi f pada himpunan D jika untuk setiap D. F () f() Fungsi integral tak tentu f dinotasikan dengan f ( ) d dan f () dinamakan
Penerapan Bilangan Kompleks pada Rangkaian RLC
 Penerapan Bilangan Kompleks pada Rangkaian RLC Hishshah Ghassani - 354056 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 0 Bandung 403, Indonesia
Penerapan Bilangan Kompleks pada Rangkaian RLC Hishshah Ghassani - 354056 Program Studi Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 0 Bandung 403, Indonesia
BAB 2 PDB Linier Order Satu 2
 BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2 BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua 4 BAB 5 Aplikasi PDB Order Dua 5 BAB 6 Sistem PDB 6 BAB 7 PDB Nonlinier dan Kesetimbangan 7
BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2 BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua 4 BAB 5 Aplikasi PDB Order Dua 5 BAB 6 Sistem PDB 6 BAB 7 PDB Nonlinier dan Kesetimbangan 7
e. muatan listrik menghasilkan medan listrik dari... a. Faraday d. Lenz b. Maxwell e. Hertz c. Biot-Savart
 1. Hipotesis tentang gejala kelistrikan dan ke-magnetan yang disusun Maxwell ialah... a. perubahan medan listrik akan menghasilkan medan magnet b. di sekitar muatan listrik terdapatat medan listrik c.
1. Hipotesis tentang gejala kelistrikan dan ke-magnetan yang disusun Maxwell ialah... a. perubahan medan listrik akan menghasilkan medan magnet b. di sekitar muatan listrik terdapatat medan listrik c.
Persamaan Diferensial Parsial CNH3C3
 Persamaan Diferensial Parsial CNH3C3 Week 5: Separasi Variabel untuk Persamaan Panas Orde Satu - Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Review
Persamaan Diferensial Parsial CNH3C3 Week 5: Separasi Variabel untuk Persamaan Panas Orde Satu - Tim Ilmu Komputasi Coordinator contact: Dr. Putu Harry Gunawan phgunawan@telkomuniversity.ac.id 1 Review
Metode Koefisien Tak Tentu untuk Penyelesaian PD Linier Homogen Tak Homogen orde-2 Matematika Teknik I_SIGIT KUSMARYANTO
 Metode Koefisien Tak Tentu untuk Penyelesaian Persamaan Diferensial Linier Tak Homogen orde-2 Solusi PD pada PD Linier Tak Homogen ditentukan dari solusi umum PD Linier Homogen dan PD Linier Tak Homogen.
Metode Koefisien Tak Tentu untuk Penyelesaian Persamaan Diferensial Linier Tak Homogen orde-2 Solusi PD pada PD Linier Tak Homogen ditentukan dari solusi umum PD Linier Homogen dan PD Linier Tak Homogen.
Rangkaian Arus Bolak Balik. Rudi Susanto
 Rangkaian Arus Bolak Balik Rudi Susanto Arus Searah Arahnya selalu sama setiap waktu Besar arus bisa berubah Arus Bolak-Balik Arah arus berubah secara bergantian Arus Bolak-Balik Sinusoidal Arus Bolak-Balik
Rangkaian Arus Bolak Balik Rudi Susanto Arus Searah Arahnya selalu sama setiap waktu Besar arus bisa berubah Arus Bolak-Balik Arah arus berubah secara bergantian Arus Bolak-Balik Sinusoidal Arus Bolak-Balik
BAB II PERSAMAAN DIFERENSIAL BIASA
 BAB II PERSAMAAN DIFERENSIAL BIASA Tujuan Pembelajaran Umum: 1 Mahasiswa mampu memahami konsep dasar persamaan diferensial 2 Mahasiswa mampu menggunakan konsep dasar persamaan diferensial untuk menyelesaikan
BAB II PERSAMAAN DIFERENSIAL BIASA Tujuan Pembelajaran Umum: 1 Mahasiswa mampu memahami konsep dasar persamaan diferensial 2 Mahasiswa mampu menggunakan konsep dasar persamaan diferensial untuk menyelesaikan
BAB 7 INDUKSI ELEKTROMAGNET
 BAB 7 INDUKSI ELEKTROMAGNET Induksi Elektromagnetik Hasil Yang harus anda capai Menerapkan konsep kelistrikan dan kemagnetan berbagai penyelesaian masalah dan produk teknologi Setelah mempelajari Bab ini
BAB 7 INDUKSI ELEKTROMAGNET Induksi Elektromagnetik Hasil Yang harus anda capai Menerapkan konsep kelistrikan dan kemagnetan berbagai penyelesaian masalah dan produk teknologi Setelah mempelajari Bab ini
INTISARI KALKULUS 2. Penyusun: Drs. Warsoma Djohan M.Si. Open Source. Not For Commercial Use
 INTISARI KALKULUS Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 010 Pengantar Kalkulus 1 & merupakan matakuliah wajib tingkat pertama bagi semua
INTISARI KALKULUS Penyusun: Drs. Warsoma Djohan M.Si. Program Studi Matematika - FMIPA Institut Teknologi Bandung Januari 010 Pengantar Kalkulus 1 & merupakan matakuliah wajib tingkat pertama bagi semua
BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx +
 BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx + N(x y) = 0 (2.1) 2.1.1 PDB Eksak
BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx + N(x y) = 0 (2.1) 2.1.1 PDB Eksak
digunakan untuk menyelesaikan integral seperti 3
 Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Bab Teknik Pengintegralan BAB TEKNIK PENGINTEGRALAN Rumus-rumus dasar integral tak tertentu yang diberikan pada bab hanya dapat digunakan untuk mengevaluasi integral dari fungsi sederhana dan tidak dapat
Persamaan Diferensial
 Orde Satu Jurusan Matematika FMIPA-Unud Senin, 18 Desember 2017 Orde Satu Daftar Isi 1 Pendahuluan 2 Orde Satu Apakah Itu? Solusi Pemisahan Variabel Masalah Gerak 3 4 Orde Satu Pendahuluan Dalam subbab
Orde Satu Jurusan Matematika FMIPA-Unud Senin, 18 Desember 2017 Orde Satu Daftar Isi 1 Pendahuluan 2 Orde Satu Apakah Itu? Solusi Pemisahan Variabel Masalah Gerak 3 4 Orde Satu Pendahuluan Dalam subbab
Rangkaian Listrik Arus dan Tegangan AC Sinusoidal dan Phasor
 Rangkaian Listrik Arus dan Tegangan AC Sinusoidal dan Phasor Alexander Sadiku edited by Agus Virgono Ir. MT. & Randy E. Saputra Prodi S1-Sistem Komputer Fakultas Teknik Elektro Universitas Telkom - 2016
Rangkaian Listrik Arus dan Tegangan AC Sinusoidal dan Phasor Alexander Sadiku edited by Agus Virgono Ir. MT. & Randy E. Saputra Prodi S1-Sistem Komputer Fakultas Teknik Elektro Universitas Telkom - 2016
Rangkaian Listrik II
 Rangkaian Listrik II OLEH : Ir. Rachman Hasibuan dan Naemah Mubarakah,ST file:///d /E-Learning/Rangkaian%20listrik%20II/Bahan%20Buku/Rangkaian%20Listrik.htm (1 of 216)5/8/2007 3:26:21 PM Departemen Teknik
Rangkaian Listrik II OLEH : Ir. Rachman Hasibuan dan Naemah Mubarakah,ST file:///d /E-Learning/Rangkaian%20listrik%20II/Bahan%20Buku/Rangkaian%20Listrik.htm (1 of 216)5/8/2007 3:26:21 PM Departemen Teknik
HAMBATAN & ARUS LISTRIK MINGGU KE-6 2 X PERTEMUAN
 HAMBATAN & ARUS LISTRIK MINGGU KE-6 2 X PERTEMUAN Arus: Aliran muatan Arus rata-rata I av : Muatan ΔQ yang mengalir melalui luas A dalam waktu Δt Arus sesaat : limit Δt 0 darii av Satuan arus: Coulomb/sekon
HAMBATAN & ARUS LISTRIK MINGGU KE-6 2 X PERTEMUAN Arus: Aliran muatan Arus rata-rata I av : Muatan ΔQ yang mengalir melalui luas A dalam waktu Δt Arus sesaat : limit Δt 0 darii av Satuan arus: Coulomb/sekon
Pecahan Parsial (Partial Fractions)
 oki neswan (fmipa-itb) Pecahan Parsial (Partial Fractions) Diberikan fungsi rasional f (x) p(x) q(x) f (x) r(x) : Jika deg p deg q; maka r (x) ^p (x) q(x) ; dengan deg r < deg q: p (x) q (x) r (x) ^p (x)
oki neswan (fmipa-itb) Pecahan Parsial (Partial Fractions) Diberikan fungsi rasional f (x) p(x) q(x) f (x) r(x) : Jika deg p deg q; maka r (x) ^p (x) q(x) ; dengan deg r < deg q: p (x) q (x) r (x) ^p (x)
BAB II PERSAMAAN DIFERENSIAL ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
ARUS BOLAK-BALIK Pertemuan 13/14 Fisika 2
 ARUS BOLAK-BALIK Pertemuan 13/14 Fisika 2 Arus bolak-balik adalah arus yang arahnya berubah secara bergantian. Bentuk arus bolakbalik yang paling sederhana adalah arus sinusoidal. Tegangan yang mengalir
ARUS BOLAK-BALIK Pertemuan 13/14 Fisika 2 Arus bolak-balik adalah arus yang arahnya berubah secara bergantian. Bentuk arus bolakbalik yang paling sederhana adalah arus sinusoidal. Tegangan yang mengalir
II. TINJAUAN PUSTAKA. Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada ( ) ( ) ( )
 II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
II. TINJAUAN PUSTAKA 2.1 Definisi Turunan Turunan fungsi f adalah fungsi lain f (dibaca f aksen ) yang nilainya pada sebarang bilangan c adalah asalkan limit ini ada. Jika limit ini memang ada, maka dikatakan
Bab 16. LIMIT dan TURUNAN. Motivasi. Limit Fungsi. Fungsi Turunan. Matematika SMK, Bab 16: Limit dan Turunan 1/35
 Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Bab 16 Grafik LIMIT dan TURUNAN Matematika SMK, Bab 16: Limit dan 1/35 Grafik Pada dasarnya, konsep limit dikembangkan untuk mengerjakan perhitungan matematis yang melibatkan: nilai sangat kecil; Matematika
Analisis Rangkaian Listrik Di Kawasan Waktu
 Sudaryatno Sudirham nalisis Rangkaian Listrik Di Kawasan Waktu 2 Sudaryatno Sudirham, nalisis Rangkaian Listrik (1) BB 6 Hukum-Hukum Dasar Pekerjaan analisis pada suatu rangkaian linier yang parameternya
Sudaryatno Sudirham nalisis Rangkaian Listrik Di Kawasan Waktu 2 Sudaryatno Sudirham, nalisis Rangkaian Listrik (1) BB 6 Hukum-Hukum Dasar Pekerjaan analisis pada suatu rangkaian linier yang parameternya
Kalkulus Diferensial week 09. W. Rofianto, ST, MSi
 Kalkulus Diferensial week 09 W. Rofianto, ST, MSi Tingkat Perubahan Rata-rata Jakarta Km 0 jam Bandung Km 140 Kecepatan rata-rata s t 140Km jam 70Km / jam Konsep Diferensiasi Bentuk y/ disebut difference
Kalkulus Diferensial week 09 W. Rofianto, ST, MSi Tingkat Perubahan Rata-rata Jakarta Km 0 jam Bandung Km 140 Kecepatan rata-rata s t 140Km jam 70Km / jam Konsep Diferensiasi Bentuk y/ disebut difference
Diferensial dan Integral
 Open Course Diferensial dan Integral Oleh: Sudaratno Sudirham Pengantar Setelah kita mempelajari fungsi dan grafik, ang merupakan bagian pertama dari kalkulus, berikut ini kita akan membahas bagian kedua
Open Course Diferensial dan Integral Oleh: Sudaratno Sudirham Pengantar Setelah kita mempelajari fungsi dan grafik, ang merupakan bagian pertama dari kalkulus, berikut ini kita akan membahas bagian kedua
BAB VI PENYELESAIAN DERET UNTUK PERSAMAAN DIFERENSIAL
 BAB VI PENYELESAIAN DERET UNTUK PERSAMAAN DIFERENSIAL Bila persamaan diferensial linear homogen memiliki koefisien constant maka persamaan tersebut dapat diselesaikan dengan metoda aljabar (seperti yang
BAB VI PENYELESAIAN DERET UNTUK PERSAMAAN DIFERENSIAL Bila persamaan diferensial linear homogen memiliki koefisien constant maka persamaan tersebut dapat diselesaikan dengan metoda aljabar (seperti yang
MENGGUNAKAN METODE TRANSFORMASI LAPLACE. Kristo Dantes Lingga 1, Abil Mansyur 2.
 STUDI PENYELESAIAN PERSAMAAN DIFERENSIAL MENGGUNAKAN METODE TRANSFORMASI LAPLACE Kristo Dantes Lingga 1, Abil Mansyur 2 1 Mahasiswa Program Studi Matematika, FMIPA, Universitas Negeri Medan e-mail: krizhto.lingga@gmail.com
STUDI PENYELESAIAN PERSAMAAN DIFERENSIAL MENGGUNAKAN METODE TRANSFORMASI LAPLACE Kristo Dantes Lingga 1, Abil Mansyur 2 1 Mahasiswa Program Studi Matematika, FMIPA, Universitas Negeri Medan e-mail: krizhto.lingga@gmail.com
