KUNCI JAWABAN BAB 1 SISTEM BILANGAN REAL

SMK N 1 Demak Jurusan Multimedia Kelas X Semester 1

SOAL LATIHAN ULANGAN SEMESTER GASAL KELAS X MM BAB SISTEM BILANGAN REAL Himpunan-Himpunan Bilangan pada Sistem Bilangan Real. Bilangan-bilangan berikut adalah irasional, kecuali... 4 7. Bilangan-bilangan

Silabus. - Membedakan berbagai jenis bilangan yang ada. Tugas individu, tugas kelompok, kuis.

Silabus Nama Sekolah : SMK Mata Pelajaran : MATEMATIKA Kelas / Program : X / AKUNTANSI DAN PENJUALAN Semester : GANJIL Sandar Kompetensi: 1. Memecahkan masalah berkaitan dengan konsep operasi bilangan

KATA PENGANTAR. Penulis

KATA PENGANTAR Puji syukur pada Allah SWT yang telah memberikan rahmat begitu besar pada kita semua, sehingga, buku matematika SMK untuk kelas X Kelompok Penjualan dan Akuntansi Sekolah Menengah Kejuruan

Contoh : Gambarlah daerah x + y 0. Jika daerah tersebut dibatasi untuk nilai-nilai x 0, dan y 0, maka diperoleh gambar seperti berikut.

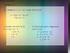Setelah mempelajari materi pada kompetensi dasar ini, kalian diharapkan dapat: menjelaskan pengertian program linier, menggambar grafik himpunan penyelesaian pertidaksamaan linier, dan menggambar grafik

RENCANA PELAKSANAAN PEMBELAJARAN NO: 1

RENCANA PELAKSANAAN PEMBELAJARAN NO: 1 Materi Pokok : Integral Pertemuan Ke- : 1 dan Alokasi Waktu : x pertemuan (4 x 45 menit) Standar Kompetensi : Menggunakan konsep integral dalam pemecahan masalah

PROGRAM LINIER. Sumber: Art & Gallery

4 PROGRAM LINIER Sumber: Art & Gallery 114 Matematika X SMK Kelompok: Penjualan dan Akuntansi Standar kompetensi program linier terdiri atas empat kompetensi dasar. Dalam penyajian pada buku ini setiap

Pilihlah jawaban yang paling tepat! 1. Ordo dari matriks A = adalah. A. 2 x 3 B. 2 x 2 C. 3 x 1 D. 3 x 2 E. 3 x 3

Pilihlah jawaban yang paling tepat!. Ordo dari matriks A = 7 A. x B. x C. x D. x x adalah.. Berikut ini yang termasuk Matriks identitas adalah... A. 7 B. 7 C. D. a b. Diketahui A = dan B = b A. B. C. D..

ULANGAN SEMESTER GENAP TAHUN PELAJARAN 2009/2010. Hari, Tanggal : Senin, 17 Mei 2010 Waktu : WIB (120 menit)

PEMERINTAH KABUPATEN DEMAK DINAS PENDIDIKAN PEMUDA DAN OLAHRAGA SMK NEGERI 1 DEMAK Jalan Sultan Trenggono No. 87 Telp/Fax : (0291) 685519 Demak (Email : smk1dmk@yahoo.com) ULANGAN SEMESTER GENAP TAHUN

Xpedia Matematika Dasar

Xpedia Matematika Dasar Soal Program Linear Doc. Name: XPMATDAS0999 Doc. Version : 01-09 halaman 1 01. Nilai z = 3x + y maksimum pada x = a dan y = b. Jika x = a dan y = b juga memenuhi pertidaksamaan

Silabus. Tugas individu, tugas kelompok, kuis.

Silabus Nama Sekolah : SMK Mata Pelajaran : MATEMATIKA Kelas / Program : X / TEKNOLOGI, KESEHATAN, DAN PERTANIAN Semester : GANJIL Sandar Kompetensi: 1. Memecahkan masalah berkaitan dengan konsep operasi

a 2 e. 7 p 7 q 7 r 7 3. a. 8p 3 c. (2 14 m 3 n 2 ) e. a 10 b c a. Uji Kompetensi a. a c. x 3. a. 29 c. 2

Kunci Jawaban Uji Kompetensi 1.1 1. a. {, 1,0,1,,3,4} BAB I Bilangan Riil Uji Kompetensi 1. 1. a. asosiatif b. memiliki elemen penting 3. 10 Uji Kompetensi 1.3 1. a. 1 4 e. 1 35 15 c. 1 8 1 1 c. 1 4 5.

SOAL TRY OUT UN MATEMATIKA 2013 PROGRAM IPS. Berilah tanda silang (x) pada huruf A, B, C, D atau E di depan jawaban yang benar!

SOAL TRY OUT UN MATEMATIKA 0 PROGRAM IPS Berilah tanda silang (x) pada huruf A, B, C, D atau E di depan jawaban yang benar!. Ingkaran dari pernyataan Diana lulus ujian nasional dan kuliah di luar negeri

SOAL PENJAJAKAN UN MATEMATIKA 2012 PROVINSI DIY

SOAL PENJAJAKAN UN MATEMATIKA 0 PROVINSI DIY. Suatu proyek akan selesai dalam waktu 0 hari oleh 0 orang pekerja. Tambahan pekerja yang dibutuhkan agar proyek tersebut selesai dalam waktu 90 hari adalah.

1. Bentuk sederhana dari adalah. a. 3 b. 3 3 c. 4 3 d. 5 3 e adalah. a b c d e.

1. Bentuk sederhana dari 2 8 75 + 12 a. 3 b. 3 3 c. 3 d. 5 3 e. 15 3 2. Bentuk sederhana dari a. 2 6 b. 2 6 2 c. 2 6 d. 6 8 e. 6 8 3. Bentuk sederhana dari.... 2 a. b 8 b. c 8 c. a 16 d. b 16 e. a 10 b

UN SMK PSP 2015 Matematika

UN SMK PSP 201 Matematika Soal Doc. Name: UNSMKPSP201MAT999 Doc. Version : 2016-0 halaman 1 01. Sebuah mobil menghabiskan 8 liter bensin untuk menempuh jarak 20 km, apabila mobil tersebut menghabiskan

MATEMATIKA DASAR 16. Jika maka Jawab : E 17. Diketahui premis-premis sebagai berikut : 1) Jika maka 2) atau Jika adalah peubah pada himpunan bilangan real, nilai yang memenuhi agar kesimpulan dari kedua

B. y = 1 x 2 1 UN-SMK-TEK Jika A = 2 0

UN-SMK-TEK-04-0 Jarak kota A ke kota B pada peta 0 cm. Jika skala peta : 0.000, maka jarak kedua kota sebenarnya adalah..., km km 0 km.00 km.000 km UN-SMK-TEK-04-0 Hasil perkalian dari (4a) - (a) =...

PROGRAM LINEAR. LA - WB (Lembar Aktivitas Warga Belajar) MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XII

LA - WB (Lembar Aktivitas Warga Belajar) PROGRAM LINEAR Oleh: Hj. ITA YULIANA, S.Pd, M.Pd MATEMATIKA PAKET C TINGKAT VI DERAJAT MAHIR 2 SETARA KELAS XII Created By Ita Yuliana 9 Program Linear Kompetensi

Matematika SMA/MA IPA. Nama : No. Peserta : , dan z = 10, maka nilai dari 12 A. 36 B. 25 C D. 1 9 E Jika log 3.

Nama : No. Peserta :. Jika x =, y =, dan z = 0, maka nilai dari x y z =. x yz A. 6 B. 5 C. 6 D. 9 E.. Jika log A. ab+a+b a+ B. b+a+ a+ C. a+b+ a+ D. ab+a+ a+ E. ab+a+ a+ = a dan log 5 = b, maka log 60.

2. FUNGSI KUADRAT. , D = b 2 4ac

. FUNGSI KUADRAT A. Persamaan Kuadrat 1) Bentuk umum persamaan kuadrat : ax + bx + c =, a ) Akar akar persamaan kuadrat dapat dicari dengan memfaktorkan ataupun dengan rumus: x 1, b D, D = b 4ac a 3) Jumlah,

M. PRAHASTOMI M. S. SISTEM PERSAMAAN LINEAR. A. a = 2 dan b = 4 B. a = 2 dan b = 4 C. a = 2 dan b = 4 D. E. a = 2

SISTEM PERSAMAAN LINEAR M. PRAHASTOMI M. S. 0. MD-8-8 B C G E F A D H 6 7 8 6 Jika gradien garis AB = m, gradien garis CD = m, gradien garis EF = m dan gradien garis GH = m, maka... () m = () m = 0 ()

SILABUS. Kegiatan Pembelajaran Teknik. Tugas individu.

SILABUS NAMA SEKOLAH : MATA PELAJARAN : Matematika KELAS : X STANDAR KOMPETENSI : Memecahkan masalah berkaitan dengan konsep operasi bilangan real. KODE KOMPETENSI : ALOKASI WAKTU : 57 x 45 Kompetensi

Matematika SMA IPS MATA PELAJARAN. Mata Pelajaran : Matematika Jenjang : SMA/MA Program Studi : IPS

Mata Pelajaran : Matematika Jenjang : SMA/MA Program Studi : IPS MATA PELAJARAN WAKTU PELAKSANAAN Hari/Tanggal : Jum at, 6 Januari 8 Jam :. 9. ( menit) PETUNJUK UMUM. Periksalah Naskah Soal yang Anda terima

adalah. 1. Bentuk sederhana dari A. 5 B. 5 C. 25 D. 20 E Bentuk sederhana dari ToT MATEMATIKA PARIWISATA

1. Bentuk sederhana dari 10 a c b A. 0 a b 2 a b 2 c c 6 2 adalah. 20 a c b B. 10 a c b C. 2 0 0 20 a b c D. 20 10 a b c E. 0 0 2 2. Bentuk sederhana dari 6 12 2 27 7 adalah... A. 12 B. C. 2 D. 8 E.. Bentuk

UN SMK PSP 2014 Matematika

UN SMK PSP 014 Matematika Soal Doc. Name: UNSMKPSP014MAT999 Doc. Version : 016-03 halaman 1 01. Nilai dari -50-5 5 5 (E) 50 1 3 3 6 4 15 64 81... ab c 0. Bentuk sederhana dari 3 adalah... a bc 10 a b c

UN SMA IPS 2012 Matematika

UN SMA IPS 01 Matematika Kode Soal A Doc. Name: UNSMAIPS01MATA Doc. Version : 01-1 halaman 1 01. Ingkaran pernyataan Pada hari Senin siswa SMAN memakai sepatu hitam dan atribut lengkap adalah. Pada hari

6. Jika 2 log 3 = a dan 3 log 5 = b, maka 15 log 20 = a. 2. c. a. e

Page of. Negasi dari pernyataan Matematika tidak mengasyikkan atau adalah a. Matematika mengasyikkan atau Matematika mengasikkan atau tidak c. Matematika mengasikkan dan tidak Matematika tidak mengasikkan

UTAMA SMA/MA PROGRAM STUDI IPS MATEMATIKA. Soal ini merupakan hasil ketik ulang tanpa merubah isi konten

DOKUMEN M4THLAB www.m4th-lab.net UJIAN NASIONAL TAHUN PELAJARAN 016/017 UTAMA SMA/MA PROGRAM STUDI IPS MATEMATIKA Selasa, 11 April 017 (10.0-1.0) X - m + - : M4TH-LAB BALITBANG Badan Standar Nasional Pendidikan

2. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT

2. PERSAMAAN, PERTIDAKSAMAAN DAN FUNGSI KUADRAT A. Persamaan Kuadrat 1) Bentuk umum persamaan kuadrat : ax 2 + bx + c =, a 2) Nilai determinan persamaan kuadrat : D = b 2 4ac 3) Akar-akar persamaan kuadrat

Sistem Bilangan 06. UN-SMK-BIS adalah... Jika a = 4, b = 5 maka nilai dari

Sistem Bilangan 0. UN-SMK-PERT-0-0 Bentuk sederhana dari ( ) =... 7 8 9 8 0. UN-SMK-TEK-0-0 Hasil perkalian dari (a) - (a) =... a a a a a 0. UN-SMK-PERT-0-0 Bentuk sederhana dari 0. UN-SMK-TEK-0-0 6 6.

SOAL ToT MATEMATIKA TEKNIK 2018

1. Nilai dari =... A. 4 B. 6 C. 1 D. 12 E. 18 2. Bentuk sederhana dari ( ) =... A. a 5. b 8. c 4 B. a 5. b 2. c 4 C. a 6. b 8. c 4 D. a 6. b 8. c 4 E. a 6. b 2. c 4 3. Bentuk sederhana dari A. B. C. D.

UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA

A TROUT UJIAN NASIONAL DINAS PENDIDIKAN DKI JAKARTA SMA/MA TAHUN PELAJARAN 0/05 MATEMATIKA IPS Hasil Kerja Sama dengan Mata Pelajaran : Matematika IPS Jenjang : SMA/MA MATA PELAJARAN Hari, tanggal : Selasa,

Soal Soal Latihan UKK

Sal Sal Latihan UKK. Jika p q 6 ; p dan q bilangan bulat, maka nilai p + q A. E.. Himpunan penyelesaian dari persamaan () A. E.. Diketahui bahwa. Maka nilai... A. E. 7 6. Diketahui bahwa dan merupakan

2. Hasil dari =. a. 4 3 b. 2 3 c. 3 d. 3 2 e adalah. 3. Bentuk sederhana pecahan. a. 4 ( ) b. d. ( ) c.

1. Untuk menempuh jarak 80 km diperlukan 16 liter bensin. Jika bensin yang diperlukan 12 liter, maka jarak yang dapat ditempuh adalah. a. 171 km b. 300 km c. 360 km 00 km e. 60 km 2. Hasil dari 8 3 12

Program Linear. Bab I

Program Linear 1 Bab I Program Linear Sumber: Ensiklopedia Pelajar, 1999 Motivasi Setiap pedagang, pengusaha, atau orang yang berkecimpung di bidang usaha pasti menginginkan keuntungan sebanyak-banyaknya

a. 30 orang b. 25 orang c. 15 orang d. 12 orang e. 10 orang

1. Perbandingan siswa laki-laki dan siswa perempuan pada suatu kelas adalah 3 : 5. Jika jumlah siswa kelas tersebut adalah 40 orang,maka banyak perempuan kelas tersebut a. 30 orang b. 25 orang c. 15 orang

PAKET 05 MATEMATIKA NON TEKNIK UJI COBA UJIAN NASIONAL SMK. Tahun Pelajaran 2014 / 2015

UJI COBA UJIAN NASIONAL SMK Tahun Pelajaran 01 / 015 MATEMATIKA NON TEKNIK KELOMPOKPARIWISATA, SENI DAN KERAJINAN, PEKERJAAN SOSIAL TEKNOLOGI KERUMAHTANGGAAN, DAN ADMINISTRASI PERKANTORAN (UTAMA) 1 MATA

UJI COBA UJIAN NASIONAL SMK. Tahun Pelajaran 2014 / 2015 PAKET 01 MATEMATIKA NON TEKNIK KELOMPOK AKUNTANSI DAN PENJUALAN (UTAMA)

UJI COBA UJIAN NASIONAL SMK Tahun Pelajaran 04 / 0 PAKET 0 MATEMATIKA NON TEKNIK KELOMPOK AKUNTANSI DAN PENJUALAN (UTAMA) A Mata Pelajaran Kelompok : MATEMATIKA : Akuntansi dan Penjualan MATA PELAJARAN

SOAL PREDIKSI UJIAN NASIONAL MATEMATIKA IPS TAHUN 2015

SOAL PREDIKSI UJIAN NASIONAL MATEMATIKA IPS TAHUN 05 PAKET Pilihan Ganda: Pilihlah satu jawaban ang paling tepat.. Ingkaran dari pernataan Jika air sungai meluap, maka kota kebanjiran dan semua warga kota

2009 ACADEMY QU IDMATHCIREBON

NASKAH UJIAN NASIONAL TAHUN PELAJARAN 2008/2009 Jenjang Sekolah : SMA/MA Hari/Tanggal : Rabu/22 April 2009 Program Studi : IPS Waktu : 08.00 10.00 Petunjuk: Pilihlah satu jawababan yang tepat! 1. Diketahui:

SISTEM BILANGAN RIIL

SISTEM BILANGAN RIIL Sumber: Art & Gallery Matematika X SMK Kelompok: Penjualan dan Akuntansi Standar kompetensi sistem bilangan riil terdiri atas empat kompetensi dasar. Dalam penyajian pada buku ini,

SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPS TAHUN PELAJARAN 2011/2012

SOAL-SOAL dan PEMBAHASAN UN MATEMATIKA SMA/MA IPS TAHUN PELAJARAN 2011/2012 1. Ingkaran pernyataan: Petani panen beras atau harga beras murah. A. Petani panen beras dan harga beras mahal B. Petani panen

K13 Revisi Antiremed Kelas 11 Matematika Wajib

K13 Revisi Antiremed Kelas 11 Matematika Wajib Program Linier - Latihan Soal Doc. Name: RK13AR11MATWJB0401 Version : 2016-10 halaman 1 01. Nilai z = 3x + 2y maksimum pada x = a dan y = b. Jika x = a dan

BAB 3 PROGRAM LINEAR 1. MODEL MATEMATIKA

BAB 3 PROGRAM LINEAR 1. MODEL MATEMATIKA Masalah 1.1 Sekelompok tani transmigran mendapatkan 10 hektar tanah yang dapat ditanami padi, jagung, dan palawija lain. Karena keterbatasan sumber daya petani

MATEMATIKA DASAR TAHUN 1981

MATEMATIKA DASAR TAHUN 98 MD-8-0 Jika A = {bilangan asli} dan B = {bilangan prima} maka A B adalah himpunan... bilangan asli bilangan cacah bilangan bulat bilangan prima kosong MD-8-0 Pada diagram Venn

PEMERINTAH KABUPATEN SUKOHARJO DINAS PENDIDIKAN SMA KABUPATEN SUKOHARJO Sekretariat : Jl. Jend. Sudirman No.197 Sukoharjo Telp.

PEMERINTAH KABUPATEN SUKOHARJO DINAS PENDIDIKAN SMA KABUPATEN SUKOHARJO Sekretariat : Jl. Jend. Sudirman No.9 Sukoharjo Telp. 0-590 55 TR OUT UJIAN NASIONAL TAHAP TAHUN PELAJARAN 0/0 Mata Pelajaran : MATEMATIKA

PEMERINTAH KABUPATEN SUKOHARJO DINAS PENDIDIKAN SMA KABUPATEN SUKOHARJO Sekretariat : Jl. Jend. Sudirman No.197 Sukoharjo Telp.

PEMERINTAH KABUPATEN SUKOHARJO DINAS PENDIDIKAN SMA KABUPATEN SUKOHARJO Sekretariat : Jl. Jend. Sudirman No.97 Sukoharjo Telp. 07-59 575 TR OUT UJIAN NASIONAL TAHAP TAHUN PELAJARAN 0/0 Mata Pelajaran :

CONTOH SOAL UAN PROGRAM LINIER

1. Luas daerah parkir 1.760 m 2. Luas rata rata untuk mobil kecil 4 m 2 dan mobil besar 20 m 2. Daya tampung maksimum hanya 200 kendaraan, biaya parkir mobil kecil Rp 1.000,00/jam dan mobil besar Rp 2.000,00/jam.

3. Diberikan sistem persamaan linier: . Nilai dari x 4y dari sistem. persamaan tersebut adalah... A. 6 B. 5 C. 2 D. -2 E adalah...

. Sebuah perkebunan seluas 7 Ha memperkejakan 0 orang untuk memetik buah dalam waktu 8 jam. Jika pihak perkebunan ingin mempercepat pemetikan menjadi 7 jam, maka diperlukan tambahan tenaga sebanyak....

Antiremed Kelas 11 Matematika

Antiremed Kelas Matematika Persiapan UTS Doc. Name: KARMATWJB0UTS Version: 04-0 halaman 0. Nilai maksimum dari 0 + 8 untuk dan y yang memenuhi + y 0, + y 48, 0 0 dan 0 y 48 adalah. (A) 408 (B) 456 (C)

MATEMATIKA. Sesi MATRIKS CONTOH SOAL A. MATRIKS SATUAN (MATRIKS IDENTITAS)

MATEMATIKA KELAS XII - KURIKULUM GABUNGAN 10 Sesi N MATRIKS A. MATRIKS SATUAN (MATRIKS IDENTITAS) Masih ingat angka 1 kan, setiap bilangan yang dikali satu apakah berubah? Tentunya tidak. Matriks satuan

muhammadamien.wordpress.com

1. 2. Gradien garis singgung di setiap titik dapat dinyatakan sebagai 34 maka nilai minimumnya 1 3 5 7 9. Jika nilai maksimum 3. Jika maka 4. 5. 1 3 4 5 6 1 6. 7. Luas daerah yang dibatasi oleh parabola

02. Nilai maksimum dari 20x + 8y untuk x dan y yang memenuhi x + y 20, 2x + y 48, 0 x 20 dan 0 y 48 adalah. (A) 408 (B) 456 (C) 464 (D) 480 (E) 488

01. Nilai z = 3x + 2y maksimum pada x = a dan y = b. Jika x = a dan y = b juga memenuhi pertidaksamaan: -2x + y 0 x - 2y 0 dan x + 2y 8, maka a + b =. (A) 2 (B) 1 (C) 2 (D) (E) 6 02. Nilai maksimum dari

6. Perhatikan grafik berikut! Y x

1. Jika Jarak sebenarnya antara kota Surakarta dan kota Semarang adalah 125 km, maka jarak kedua kota pada peta dengan skala 1 : 2.000.000 adalah. a. 62,5 cm b. 25 cm c. 6,25 cm d. 2,5 cm e. 0,625 cm 2.

1. Fungsi Objektif z = ax + by

Nilai Optimum Suatu Fungsi Objektif, Program Linear, Fungsi Objektif, Cara Menentukan, Contoh Soal, Rumus, Pembahasan, Metode Uji Titik Sudut, Metode Garis Selidik, Matematika Nilai Optimum Suatu Fungsi

TAHUN PELAJARAN 2003/2004 SMK. Matematika Teknik Industri (E3-1) PAKET 1 (UTAMA) SELASA, 11 MEI 2004 Pukul

0-04 E--P9-0-4 DOKUMEN NEGARA SANGAT RAHASIA UJIAN NASIONAL TAHUN PELAJARAN 00/004 SMK Matematika Teknik Industri (E-) PAKET (UTAMA) SELASA, MEI 004 Pukul 07.0 09.0 DEPARTEMEN PENDIDIKAN NASIONAL Hak Cipta

Gambar 1.1 Mesin dan SDM perusahaan

BAB I PROGRAM LINEAR Tujuan Pembelajaran Setelah mempelajari materi bab ini, Anda diharapkan dapat: 1. menyelesaikan sistem pertidaksamaan linear dua variabel, 2. merancang model matematika dari masalah

UN SMA 2013 PRE Matematika IPS

UN SMA 201 PRE Matematika IPS Kode Soal Doc. Name: UNSMA2014PREMATIPS999 Doc. Version : 2014-01 halaman 1 01. (1) Jika jalan basah maka hari hujan (2) Jika hari tidak hujan maka jalan tidak basah () Jika

ULANGAN UMUM MADRASAH ALIYAH SEMESTER GANJIL TAHUN PELAJARAN MATEMATIKA XII BAHASA

ULANGAN UMUM MADRASAH ALIYAH SEMESTER GANJIL TAHUN PELAJARAN 29-21 MATEMATIKA XII BAHASA Hari / tanggal :... Desember 29 Waktu : 12 menit Pilih salah satu jawaban ang benar dengan memberi tanda silang

Model Matematika. Persamaan atau pertidaksamaan Matematika Tujuan

Kehidupan Nyata Bisa Disajikan Bahasa Matematika Diperlukan Alat Bantu Model Matematika Menggunakan Persamaan atau pertidaksamaan Matematika Tujuan Penyelesaian masalah Kemampuan yang akan dibahas Menentukan

2.1 Soal Matematika Dasar UM UGM c. 1 d d. 3a + b. e. 3a + b. e. b + a b a

Soal - Soal UM UGM. Soal Matematika Dasar UM UGM 00. Jika x = 3 maka + 3 log 4 x =... a. b. c. d. e.. Jika x+y log = a dan x y log 8 = b dengan 0 < y < x maka 4 log (x y ) =... a. a + 3b ab b. a + b ab

12. Diketahui segitiga ABC dengan AC = 5 cm, AB = 7 cm, dan BCA = 120. Keliling segitiga ABC =...

1 1. Diketahui: Premis 1 : Jika hari hujan maka tanah basah. Premis : Tanah tidak basah. Ingkaran dari penarikan kesimpulan yang sah dari premis-premis di atas adalah.... Agar F(x) = (p - ) x² - (p - 3)

6 FUNGSI LINEAR DAN FUNGSI

6 FUNGSI LINEAR DAN FUNGSI KUADRAT 5.1. Fungsi Linear Pada Bab 5 telah dijelaskan bahwa fungsi linear merupakan fungsi yang variabel bebasnya paling tinggi berpangkat satu. Bentuk umum fungsi linear adalah

h t t p : / / m a t e m a t r i c k. b l o g s p o t. c o m

1. Dalam permasalahan program linear dikenal dua istilah, yaitu : a. Fungsi Kendala/ pembatas, berupa pertidaksamaan pertidaksamaan linear ax by 0; ax by p; ax by 0; ax by 0 b. Fungsi/ bentuk objektif,

UM UGM 2017 Matematika Dasar

UM UGM 07 Matematika Dasar Soal UTUL UGM - Matematika Dasar 07 (Kode Soal 84) Halaman 0. Tujuh bilangan membentuk barisan aritmetika. Jika jumlah tiga bilangan pertama sama dengan 33 dan jumlah tiga bilangan

BOCORAN UJIAN NASIONAL TAHUN PELAJARAN 2015/2016 UTAMA SMA/MA PROGRAM STUDI IPA. MATEMATIKA Selasa, 5 April 2016 ( )

BOCORAN UJIAN NASIONAL TAHUN PELAJARAN 0/06 UTAMA SMA/MA PROGRAM STUDI IPA MATEMATIKA Selasa, April 06 (07.0 09.0) BALITBANG PAK ANANG KEMENTARIAN PAK ANANG DAN KEBUDAYAAN Mata Pelajaran Jenjang Program

matematika WAJIB Kelas X PERTIDAKSAMAAN LINEAR SATU VARIABEL K-13 A. PENDAHULUAN

K-1 Kelas X matematika WAJIB PERTIDAKSAMAAN LINEAR SATU VARIABEL TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi pertidaksamaan linear

Matriks Jawab:

Matriks A. Operasi Matriks 1) Penjumlahan Matriks Jika A dan B adalah sembarang Matriks yang berordo sama, maka penjumlahan Matriks A dengan Matriks B adalah Matriks yang diperoleh dengan cara menjumlahkan

SOAL ToT MATEMATIKA BISNIS-MANAJEMEN adalah...

SOAL ToT MATEMATIKA BISNIS-MANAJEMEN 08. Bentuk sederhana dari 0 0 3 0 3 8 0 4 0 3 5 8 adalah.... Nilai dari log 6 3 log 4 log6 log 48 adalah... 7 3 3 3. Jika diketahui log 5 = a dan log 3 = b maka nilai

Hak Cipta 2014 Penerbit Erlangga

00-00-008-0 Hak Cipta 0 Penerbit Erlangga Berilah tanda silang (X) pada huruf A, B, C, D, atau E pada jawaban yang benar!. Diketahui premis-premis: () Jika beberapa daerah dilanda banjir, maka beberapa

PEMERINTAH KABUPATEN SUKOHARJO DINAS PENDIDIKAN SMA KABUPATEN SUKOHARJO Sekretariat : Jl. Jend. Sudirman No.197 Sukoharjo Telp.

PEMERINTAH KABUPATEN SUKOHARJO DINAS PENDIDIKAN SMA KABUPATEN SUKOHARJO Sekretariat : Jl. Jend. Sudirman No.97 Sukoharjo Telp. 07-90 7 TRY OUT UJIAN NASIONAL TAHAP TAHUN PELAJARAN 0/0 Mata Pelajaran :

10 Soal dan Pembahasan Permasalahan Program Linear

10 Soal dan Pembahasan Permasalahan Program Linear 1. BAYU FURNITURE memproduksi 2 jenis produk yaitu meja dan kursi yang harus diproses melalui perakitan dan finishing. Proses perakitan memiliki 60 jam

E-learning matematika, GRATIS

1 Penusun Editor : Rifan Nadhifi, S.Si. ; Imam Indra Gunawan, S.Si. : Drs. Keto Susanto, M.Si. M.T. ; Istijab, S.H. M.Hum. Imam Indra Gunawan, S.Si. A. Sistem Pertidaksamaan Linear Pertidaksamaan linear

RENCANA PELAKSANAAN PEMBELAJARAN NO. 01/2

RENCANA PELAKSANAAN PEMBELAJARAN NO. 01/2 Nama Sekolah : SMK Diponegoro Lebaksiu Mata Pelajaran : Matematika Kelas / Semester : X / 2 Alokasi Waktu : 4 x 45 menit (1 x pertemuan) Standar Kompetensi Kompetensi

matematika PEMINATAN Kelas X PERSAMAAN KUADRAT K-13 A. BENTUK UMUM PERSAMAAN KUADRAT

K-13 Kelas X matematika PEMINATAN PERSAMAAN KUADRAT TUJUAN PEMBELAJARAN Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi dan bentuk umum persamaan kuadrat..

PERSAMAAN KUADRAT. Persamaan. Sistem Persamaan Linear

Persamaan Sistem Persamaan Linear PENGERTIAN Definisi Persamaan kuadrat adalah kalimat matematika terbuka yang memuat hubungan sama dengan yang pangkat tertinggi dari variabelnya adalah 2. Bentuk umum

BAB 4 MATRIK ( ) ( ) ( ) ( ) ( ) ( )

BAB MATRIK. Operasi Penjumlahan Pada Matriks Dan Sifat-Sifatnya Masalah. Dua orang bersaudara laki-laki dan perempuan membuka dua cabang toko kue di Padang dan di Medan. Toko kue itu menyediakan jenis

a. 16 b. 24 c. 30 d. 36 e Nilai maksimum fungsi sasaran Z = 6x + 8y dari system pertidaksamaan 4x + 2y 60, 2x

1. Luas daerah parkir 1.760 m 2. Luas rata rata untuk mobil kecil 4 m 2 dan mobil besar 20 m 2. Daya tampung maksimum hanya 200 kendaraan, biaya parkir mobil kecil Rp. 1.000,00/jam dan mobil besar Rp.

PAKET 3. Paket : 3. Jumlah Soal : 40 soal Kompetensi : 1. Program Linear 3. Vektor 2. Matriks 4. Logika Compile By : Syaiful Hamzah Nasution

PAKET 3 Jumlah Soal : 40 soal Kompetensi : 1. Program Linear 3. Vektor 2. Matriks 4. Logika Compile By : Syaiful Hamzah Nasution No Soal Jawaban 1 Nilai maksimum f(x, y) = 2x + 3y yang memenuhi system

TAHUN PELAJARAN 2003/2004 SMK. Matematika Teknik Pertanian (E3-2) PAKET 1 (UTAMA) SELASA, 11 MEI 2004 Pukul

0-0 E--P9-0- DOKUMEN NEGARA SANGAT RAHASIA UJIAN NASIONAL TAHUN PELAJARAN 00/00 SMK Matematika Teknik Pertanian (E-) PAKET (UTAMA) SELASA, MEI 00 Pukul 07.0 09.0 DEPARTEMEN PENDIDIKAN NASIONAL Hak Cipta

Pembahasan Soal SBMPTN 2014 SELEKSI BERSAMA MASUK PERGURUAN TINGGI NEGERI. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS.

Pembahasan Soal SBMPTN 2014 SELEKSI BERSAMA MASUK PERGURUAN TINGGI NEGERI Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika Dasar Disusun Oleh : Pak Anang (http://pak-anang.blogspot.com) Kumpulan

PERTIDAKSAMAAN RASIONAL. Tujuan Pembelajaran

Kurikulum 1 Kelas matematika PEMINATAN PERTIDAKSAMAAN RASIONAL Tujuan Pembelajaran Setelah mempelajari materi ini, kamu diharapkan memiliki kemampuan berikut. 1. Memahami definisi pertidaksamaan rasional..

Prediksi 1 UN SMA IPS Matematika

Prediksi UN SMA IPS Matematika Kode Soal Doc. Version : 0-06 halaman 0. () Jika jalan basah maka hari hujan () Jika hari tidak hujan maka jalan tidak basah () Jika jalan tidak basah maka hari tidak hujan

MATA PELAJARAN PELAKSANAAN PETUNJUK UMUM

MATA PELAJARAN Mata Pelajaran Jenjang Program Studi : MATEMATIKA : SMA/MA : IPA PELAKSANAAN Hari/Tanggal Jam : Isi sesuai waktu anda latihan : Isi sesuai waktu anda latihan PETUNJUK UMUM. Isikan identitas

Contoh Kasus Program Linier K A S U S M A K S I M A S I D A N K A S U S M I N I M A S I

Contoh Kasus Program Linier K A S U S M A K S I M A S I D A N K A S U S M I N I M A S I Kasus maksimasi Seorang pengrajin menghasilkan satu tipe meja dan satu tipe kursi. Proses yang dikerjakan hanya merakit

4. Bentuk sederhana dari : a b

PAKET A. Pernyataan yang setara dengan Jika cuaca buruk, maka semua penerbangan ditunda adalah. A. Jika beberapa penerbangan tidak ditunda, maka cuaca baik. B. Jika semua penerbangan ditunda, maka cuaca

Program Linear B A B. A. Sistem Pertidaksamaan Linear Dua Variabel. B. Model Matematika. C. Nilai Optimum Suatu Fungsi Objektif

Program Linear Program Linear B A B 2 A. Sistem Pertidaksamaan Linear Dua Variabel B. Model Matematika C. Nilai Optimum Suatu Fungsi Objektif Sumber: http://blontankpoer.blogsome.com Dalam dunia usaha,

UN SMA 2014 Matematika IPS

UN SMA 04 Matematika IPS Kode Soal Doc. Name: UNSMA04MATIPS999 Doc. Version : 0-0 halaman 0. Negasi dari pernyataan Semua bilangan rasional adalah bilangan real dan prima adalah... Tidak ada bilangan rasional

PENGEMBANGAN SILABUS TAHUN PELAJARAN 2012/2013

PENGEMBANGAN SILABUS TAHUN PELAJARAN 01/013 NAMA SEKOLAH : SMK DIPONEGORO LEBAKSIU MATA PELAJARAN : MATEMATIKA KELAS / SEMESTER : X / 1 STANDAR KOMPETENSI : MEMECAHKAN MASALAH BERKAITAN DENGAN KONSEP OPERASI

A. 100 B. 25 C. 20 D. 10 E Bentuk sederhana dari pecahan bentuk akar. adalah. A B C D

, PEMERINTAH KABUPATEN KENDAL DINAS PENDIDIKAN PEMUDA DAN OLAH RAGA SMK NEGERI KENDAL Alamat : Jl. Boja - Limbangan KM Salamsari, Boja, Kendal Telp.(9) 88 Fax. (9) e-mail : smktelukendal@yahoo.com. Pak

PEMBAHASAN UN 2009/2010

PEMBAHASAN UN 009/00. Konsep: Operasi Bilangan Real (Perbandingan Berbalik Nilai) Suatu pekerjaan dikerjakan orang dapat selesai 0 hari. Pekerjaan akan diselesaikan dalam waktu hari. Pekerja Hari 0 y y

m, selalu di atas sumbu x, batas batas nilai m yang memenuhi grafik fungsi tersebut adalah.

. Di berikan premis sebagai berikut : Premis : Jika terjadi hujan lebat atau mendapat air kiriman maka Jakarta banjir Premis : Jalan menjadi macet dan aktivitas kerja terhambat jika Jakarta banjir Kesimpulan

PR ONLINE MATA UJIAN: MATEMATIKA IPS (KODE S09)

PR ONLINE MATA UJIAN: MATEMATIKA IPS (KODE S09) 1. Luas daerah yang dibatasi oleh kurva y = x + x + 5, sumbu x, dan 0 x 1... satuan luas (A) (C) (E) 5 (B) 0 (D) 5 1. Diketahui segitiga ABC, siku-siku di

RENCANA PELAKSANAAN PEMBELAJARAN (RPP)

RENCANA PELAKSANAAN PEMBELAJARAN (RPP) Nama Sekolah : SMK Mata Pelajaran : Matematika Kelas / Program : X (Sepuluh) / Akuntansi dan Penjualan Semester : Ganjil Standar Kompetensi : 1. Memecahkan masalah

yos3prens.wordpress.com

yosprens.wordpress.com Before anything else, preparation is the key to success. Alexander Graham Bell Mata Pelajaran Jenjang Program Studi : Matematika : SMA/MA : IPA Hari/Tanggal Jam :... :.... Isilah

SMA 74 JAKARTA LATIHAN SOAL UN MATEMATIKA JURUSAN IPS TAHUN 2012

SMA 74 JAKARTA LATIHAN SOAL UN MATEMATIKA JURUSAN IPS TAHUN 0. Negasi dari semua siswa rajin belajar untuk menghadapi UN, adalah... A. tidak semua siswa rajin belajar untuk menghadapi UN B. semua siswa

Matematika Proyek Perintis I Tahun 1980

Matematika Proyek Perintis I Tahun 980 MA-80-0 Di antara lima hubungan di bawah ini, yang benar adalah Jika B C dan B C, maka A C Jika A B dan C B, maka A C Jika B A dan C B, maka A C Jika A C dan C B,

TO MGMP MATEMATIKA BAHASA PAKET A HAL 1

MATEMATIKA SMA BAHASA PAKET A 1. Bentuk sederhana dari( 4x 8 y 3 16x 6 y 5) 1 =. A. ( y 2x )2 B. ( 2x y )2 C. ( x 2y )2 D. ( 1 2xy )2 E. (2xy) 2 2. Hasil dari 5 2 5+2 =. A. 4 5 + 9 B. 4 5 C. 9 4 5 D. 9

MATEMATIKA DASAR TAHUN 1987

MATEMATIKA DASAR TAHUN 987 MD-87-0 Garis singgung pada kurva y di titik potong nya dengan sumbu yang absisnya positif mempunyai gradien 0 MD-87-0 Titik potong garis y + dengan parabola y + ialah P (5,

SOAL PREDIKSI VI. I. Pilihlah jawaban yang paling benar!

SOAL PREDIKSI VI I. Pilihlah jawaban yang paling benar! 1. Kiki melakukan perjalanan Surabaya Solo mengendarai sepeda motor dengan kecepatan rata-rata 80 km/jam dalam waktu 2 jam. Jika kecepatannya menjadi