TRANSLASI BANGUN RUANG BERSISI DATAR PADA RUANG BERDIMENSI TIGA
|
|
|
- Hartanti Atmadja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 TRANSLASI BANGUN RUANG BERSISI DATAR PADA RUANG BERDIMENSI TIGA Skripsi disusun sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Mohammad Yusuf Guntari JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI SEMARANG 2015
2 ii
3 iii
4 MOTTO DAN PERSEMBAHAN MOTTO: 1. Karena sesungguhnya sesudah kesulitan itu ada kemudahan (QS. Alam Nasyrah: 5) 2. Maka nikmat Tuhan kamu yang manakah yang kamu dustakan? (QS. Ar- Rahman) 3. Musuh terbesarmu adalah dirimu sendiri PERSEMBAHAN: a. Untuk Bapak dan Ibuku, serta Adikku Avinda Esti Saraswati b. Untuk semua keluarga besarku, khususnya Mbak Navy dan Mas Nova c. Untuk Abah Kiai Masrokhan d. Untuk Kange dan Mbake Santri PPDAW e. Untuk Sahabat Proxima 2010 iv
5 PRAKATA Puji Syukur kehadirat Allah SWT atas segala rahmat dan hidayah-nya sehingga penulis dapat menyelesaikan skripsi ini yang berjudul Translasi Bangun Ruang Bersisi Datar Pada Ruang Berdimensi Tiga. Shalawat serta salam tercurahkan kepada Nabi Agung Muhammad SAW. Penulis sangat berterima kasih atas bantuan, bimbingan, dan dukungan dari berbagai pihak dalam proses penyusunan skripsi ini. Oleh karena itu, penulis menyampaikan ucapan terima kasih kepada: 1. Prof. Dr. Fathur Rokhman, M.Hum., Rektor Universitas Negeri Semarang. 2. Prof. Dr. Wiyanto, M.Si., Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang. 3. Drs. Arief Agoestanto, M.Si., Ketua Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Semarang. 4. Drs. Suhito, M.Pd., Dosen Pembimbing yang telah memberikan bimbingan, arahan, dan saran kepada penulis selama penyusunan skripsi. 5. Tri Sri Noor Asih, S.Si, M.Si, Dosen Wali yang telah memberikan arahan dan motivasi selama penulis menuntut ilmu di Universitas Negeri Semarang. 6. Bapak dan Ibu Dosen Jurusan Matematika yang telah mengajarkan ilmunya dalam perkuliahan. 7. Bapak, Ibu, dan Adikku, yang telah memberikan doa, semangat dan kasih sayangnya kepada penulis. v
6 8. Abah Kiai Masrokhan, pengasuh PP. Durotu Aswaja yang telah memberikan doa dan bimbingannya, serta mengajarkan ilmunya kepada penulis. 9. Keluarga besar Pondok Pesantren Durrotu Ahlissunnah Waljama ah yang telah memberikan berbagai pengalaman baru kepada penulis. 10. Sahabat PROXIMA Program Studi Matematika angkatan 2010 atas kebersamaannya, perjuangan kita baru akan dimulai. 11. Seluruh pihak yang turut membantu penyelesaian skripsi yang tidak dapat penulis sebutkan satu persatu. Akhir kata penulis mengharapkan kritik dan saran dari pembaca agar skripsi ini menjadi lebih baik. Semoga skripsi ini dapat memberikan manfaat bagi pembaca dan menambah referensi pustaka matematika. Semarang, 14 Juli 2015 Penulis vi
7 ABSTRAK Guntari, M. Y Translasi Bangun Ruang Bersisi Datar Pada Ruang Berdimensi Tiga. Skripsi, Jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Negeri Semarang. Drs. Suhito, M.Pd. Kata kunci: translasi, bangun ruang, sisi datar, dimensi tiga. Translasi geometri adalah suatu transformasi yang memetakan titik ke titik lainnya pada ruang. Bangun ruang yang dibahas adalah bangun ruang yang dibatasi oleh bidang datar. Suatu bangun ruang bersisi datar ditentukan titik sudutnya, kemudian satu per satu bidang yang membatasinya dicari persamaan bidangnya, setelah itu persamaan bidang tersebut ditranslasikan. Permasalahan yang diangkat dalam skripsi ini adalah bagaimana menyatakan hasil translasi bangun ruang bersisi datar pada ruang berdimensi tiga. Tujuan dari penelitian ini adalah untuk mengetahui rumus umum dan sifat translasi pada sehingga dapat dinyatakan hasil translasi pada bangun ruang bersisi datar khususnya pada bangun ruang prisma dan limas. Metode yang digunakan pada penulisan skripsi ini adalah studi pustaka. Hasil dari studi pustaka ini digunakan untuk mengumpulkan referensi yang diperlukan dalam menyusun skripsi. Hasil dari translasi di memiliki sifat-sifat mempertahankan besar sudut dan kesejajaran antara dua garis sehingga hasil translasi garis akan berupa garis lagi dan mempertahankan besar sudut dan kesejajaran antara dua bidang sehingga hasil translasi bidang akan berupa bidang lagi. Pada dasarnya mentranslasikan bangun ruang bersisi datar di adalah mentranslasikan setiap titik pada bangun ruang tersebut. Rumus umum mentranslasikan bangun ruang ada tiga, yaitu rumus translasi titik, garis, dan bidang sebagai berikut: ( ) ( ) ( ) Hasil dari translasi bangun ruang ini akan kongruen dengan bangun ruang aslinya. vii
8 DAFTAR ISI Halaman HALAMAN JUDUL... PERNYATAAN KEASLIAN TULISAN... i ii HALAMAN PENGESAHAN... iii MOTTO DAN PERSEMBAHAN... iv PRAKATA... v ABSTRAK... vii DAFTAR ISI... viii DAFTAR GAMBAR... x BAB 1. PENDAHULUAN Latar Belakang Rumusan Masalah Batasan Masalah Tujuan Penelitian Manfaat Penelitian Sistematika Penulisan TINJAUAN PUSTAKA Fungsi dan Transformasi Translasi Isometri viii
9 2.4 Isometri Bidang METODE PENELITIAN Identifikasi Masalah Perumusan Masalah Studi Pustaka Pemecahan Masalah Penarikan Simpulan HASIL DAN PEMBAHASAN Ruang Euclid Translasi di Translasi di merupakan Isometri Translasi Bangun Ruang di PENUTUP Simpulan Saran DAFTAR PUSTAKA ix
10 DAFTAR GAMBAR Gambar Halaman 2.1 Definisi keekivalenan Ketunggalan titik Refleksi pada dua garis sejajar Translasi merupakan dua kali refleksi Translasi merupakan dua kali setengah putaran Isometri garis Isometri mempertahankan besar sudut Isometri mempertahankan kesejajaran garis Translasi garis Translasi mempertahankan besar sudut antara dua garis Translasi mempertahankan kesejajaran garis Translasi bidang Translasi mempertahankan besar sudut antara dua bidang Translasi mempertahankan kesejajaran bidang Hasil translasi prisma Hasil translasi limas x
11 BAB 1 PENDAHULUAN 1.1 Latar Belakang Geometri merupakan salah satu cabang dari ilmu matematika terapan yang telah ada selama ini. Menurut Wallace dan West (1992: 1) The word geometry comes from the Greek words meaning earth measure, which when taken literally imply that geometry involves measuring earthly things. Geometri dalam perkembangannya mempunyai beberapa disiplin ilmu, salah satunya adalah geometri transformasi. Geometri transformasi merupakan ilmu geometri yang mempelajari tentang jenis-jenis transformasi. Transformasi yang dimaksud adalah suatu fungsi bijektif yang memetakan titik pada ruang ke titik lainnya pada ruang itu juga, atau biasa disebut transformasi geometri. Pada ruang berdimensi tiga, geometri transformasi merupakan ilmu yang sulit dipahami karena membutuhkan imajinasi ruang agar bisa membayangkan objek yang sedang dibicarakan. Oleh karena itu perlu adanya pengembangan konsep geometri transformasi yang lebih luas agar lebih mudah dipahami dan dipelajari. Jenis-jenis transformasi pada geometri ada empat, yaitu translasi (pergeseran), dilatasi (perkalian), refleksi (pencerminan) dan rotasi (perputaran). Pada skripsi ini akan 1
12 2 dibahas konsep translasi bangun ruang pada ruang berdimensi tiga yang mana banyak sekali contohnya pada kehidupan sehari-hari. Oleh karena itu diperlukan pembuktian secara matematis agar pemahaman tentang objek geometri yang ditranslasikan ini tidak berhenti pada melihat dan membayangkan bangun ruangnya saja. Pada dasarnya mentranslasikan sebuah bangun ruang haruslah dengan cara mentranslasikan semua himpunan titik-titik yang ada pada bangun ruang tersebut. Hal tersebut tidak mungkin dilakukan karena himpunan titik-titik suatu bangun ruang jumlahnya yang tak terhingga itu tidak mungkin ditranslasikan satu per satu. Oleh karena itu cukup titik-titik tertentu saja yang ditranslasikan, misalnya dengan mentransalsikan titiktitik sudut bangun ruang tersebut. Ada dua cara lain yang bisa dilakukan, yaitu dengan mentranslasikan setiap garis yang membentuk suatu bangun ruang dan mentranslasikan setiap bidang yang membatasi bangun ruang tersebut. Persamaan garis dan bidang yang akan ditranslasikan diperoleh dari titik-titik sudut yang membentuk bangun ruang tersebut. Pada skripsi ini akan dibahas cara mentranslasikan bangun ruang dengan mentranslasikan setiap bidang datar yang membatasi suatu bangun ruang. Persamaan umum bidang ditanslasikan, bagaimana hasilnya?
13 3 1.2 Rumusan Masalah Berdasarkan latar belakang di atas maka dapat ditarik suatu permasalahan Bagaimana menyatakan hasil translasi bangun ruang bersisi datar pada ruang berdimensi tiga?. 1.3 Batasan Masalah Dalam skripsi ini, hasil geometri transformasi yang dikaji penulis menitikberatkan pada hasil translasi dari bangun ruang yang dibatasi oleh bidang bersisi datar saja, khususnya pada bangun ruang prisma dan limas. 1.4 Tujuan Penelitian Tujuan yang dapat diambil dari rumusan masalah diatas adalah sebagai berikut: 1. Mengetahui definisi Ruang Euclid. 2. Mengetahui rumus umum translasi titik, garis, dan bidang pada. 3. Mengetahui sifat-sifat translasi pada. 4. Mengetahui hasil translasi suatu bangun ruang bersisi datar pada. 1.5 Manfaat Penulisan Adapun manfaat dari penelitian ini adalah sebagai berikut: 1. Bagi Penulis a. Dapat menambah pengetahuan penulis di bidang ilmu geometri.
14 4 b. Dapat mengaplikasikan dan mengembangkan materi yang sudah diperoleh di bangku kuliah. 2. Bagi Pembaca a. Sebagai sumber referensi yang berkaitan dengan ilmu geometri, khususnya tentang translasi pada geometri transformasi. b. Menambah pengetahuan tentang ilmu geometri. 1.6 Sistematika Penulisan Skripsi ini terdiri atas beberapa bagian yang masing-masing diuraikan sebagai berikut: 1. Bagian awal skripsi, terdiri dari halaman judul, halaman pengesahan, pernyataan, motto, persembahan, kata pengantar, abstrak, daftar isi, dan daftar gambar. 2. Bangian isi, merupakan bagian yang pokok dalam skripsi yang terdiri dari lima bab sebagai berikut: Bab 1 : Pendahuluan berisi tentang latar belakang, rumusan masalah, batasan masalah, tujuan penelitian, manfaat penulisan, dan sistematika penulisan. Bab 2 : Tinjauan pustaka berisi tentang teori-teori yang mendukung dan berkaitan dengan permasalahan skripsi sehingga dapat dijadikan sebagai teori penunjang yang menjadi dasar-dasar disusunnya skripsi ini.
15 5 Bab 3 : Metode penelitian berisi tentang langkah atau proses penelitian. Bab ini meliputi identifikasi masalah, rumusan masalah, studi pustaka, pemecahan masalah, dan penarikan simpulan. Bab 4 : Hasil dan pembahasan berisi tentang hasil penelitian dan pembahasan mengenai translasi bangun ruang bersisi datar pada ruang berdimensi tiga ( ). Bab 5 : Penutup berisi tentang simpulan dari pembahasan dan saransaran yang berkaitan dengan simpulan sehingga dapat dikembangkan lagi lebih luas dan bermanfaat bagi pembaca. 3. Bagian akhir, merupakan bagian yang terdiri atas daftar pustaka yang bertujuan untuk memberikan informasi tentang semua buku, sumber, dan literatur lainnya yang digunakan dalam penulisan skripsi ini yang dijadikan penulis sebagai acuan penulisan skripsi.
16 BAB 2 TINJAUAN PUSTAKA 2.1 Fungsi dan Transformasi Pengertian fungsi dan jenis-jenis fungsi sangat diperlukan sebelum dibahas materi transformasi. Oleh karena itu, terlebih dahulu pengertian fungsi dan jenis-jenis fungsi harus dipahami dengan baik Pengertian Fungsi Pengertian fungsi menurut Varberg, Purcell, dan Rigdon (2008: 29) adalah sebagai berikut: Sebuah fungsi adalah suatu aturan korespondensi yang menghubungkan tiap objek dalam satu himpunan, yang disebut daerah asal (domain), dengan sebuah nilai tunggal dari suatu himpunan kedua. Himpunan nilai yang diperoleh secara demikian disebut daerah hasil (range) fungsi tersebut Jenis-jenis Fungsi a. Fungsi surjektif, fungsi yang bersifat. b. Fungsi injektif, fungsi yang bersifat. c. Fungsi bijektif, fungsi bijektif adalah fungsi yang bersifat surjektif dan injektif. 6
17 Pengertian Transformasi Suatu transformasi adalah suatu fungsi bijektif yang daerah asalnya sama dengan daerah hasilnya. Misalkan jika daerah asalnya ruang maka daerah hasilnya juga ruang. Contoh: Andaikan. Ada padanan dengan daerah asal dan daerah hasil juga. Jadi yang didefinisikan sebagai berikut: (1) (2) Jika maka dengan titik tengah ruas. Selidiki apakah padanan tersebut suatu transformasi? Jawab: Untuk mengetahui apakah padanan suatu tranformasi, maka harus dibuktikan bahwa padanan adalah fungsi bijektif. i) Akan dibuktikan padanan adalah fungsi Ambil titik sebarang... Ini berarti. Jadi padanan adalah fungsi.
18 8 ii) Akan dibuktikan surjektif. Ambil sebarang... Ini berarti. Jadi surjektif. iii) Akan dibuktikan injektif. Ambil dua titik,, dan dengan,, dan tidak kolinear (segaris). Andaikan. Oleh karena dan maka dan memiliki dua titik sekutu yaitu dan. Ini berarti garis dan berhimpit sehingga mengakibatkan. Ini berlawanan dengan,, dan tidak kolinear. Jadi pengandaian salah, haruslah. Diperoleh. Jadi injektif. Dari uraian di atas diperoleh simpulan bahwa padanan adalah suatu transformasi.
19 Komposisi Transformasi Andaikan dan dua buah transformasi dengan dan, maka komposisi transformasi dari dan yang ditulis didefinisikan sebagai:,. Teorema: Komposisi transformasi adalah transformasi. Bukti: Jika dan masing-masing suatu transformasi, maka komposit akan dibuktikan juga suatu transformasi. Untuk ini harus kita buktikan dua hal yaitu: 1) Akan dibuktikan surjektif. Ambil sebarang. Oleh karena transformasi berarti surjektif. Maka untuk setiap. Karena transformasi berarti juga surjektif. Maka pada terdapat sehingga. Jadi. Ini berarti. Jadi surjektif. 2) Akan dibuktikan injektif. Ambil dan sebarang. Jika maka.
20 10 Oleh karena injektif maka dan injektif maka. Jadi injektif. Karena bijektif, maka suatu transformasi Transformasi Identitas Suatu transformasi dinamakan transformasi identitas jika transformasi tersebut memetakan setiap titik pada bidang terhadap dirinya sendiri. Transformasi identitas dilambangkan dengan huruf. Jadi. Contoh: Jika sebuah garis dan refleks pada garis, maka. Dapat ditulis juga. Jadi adalah suatu transformasi yang memetakan setiap titik pada dirinya. Transformasi demikian dinamakan transformasi identitas. 2.2 Translasi Translasi sangat erat kaitannya dengan ruas garis berarah, karena translasi adalah suatu transformasi yang ditransformasikan oleh ruas garis berarah. Oleh karena itu sebelum membahas materi translasi, akan dibahas materi ruas garis berarah terlebih dahulu.
21 Definisi dan Sifat-sifat Ruas Garis Berarah Suatu ruas garis berarah adalah sebuah ruas garis yang salah satu ujungnya dinamakan titik pangkal dan ujung lainnya dinamakan titik akhir. Misalkan dan dua titik sebarang, merupakan ruas garis berarah dengan titik pangkal dan titik akhir, ditulis. Definisi: Jika dengan titik tengah maka (Rawuh, 1994: 90). B D P A C Gambar 2.1 Definisi keekivalenan Teorema 1 Andaikan dan dua ruas garis berarah yang tidak segaris maka segiempat sebuah jajargenjang jika dan hanya jika. Bukti: Ditentukan dan dua ruas garis berarah yang tidak segaris. ( ) Akan ditunjukkan jika jajargenjang maka. Andaikan jajargenjang.
22 12 Maka diagonal-diagonal dan berpotongan membagi sama panjang, misalkan di titik. Diperoleh, dengan titik tengah maupun. Jadi. ( ) Akan dibuktikan jika maka jajargenjang. Andaikan. Diperoleh dengan titik tengah maupun. Sehingga diagonal-diagonal dan segiempat berpotongan membagi sama panjang di. Jadi segiempat sebuah jajargenjang. Akibat: Jika maka dan dan sejajar atau segaris. Teorema 2 Jika diketahui ruas garis berarah,, dan maka berlaku: 1). (sifat refleksi) 2) Jika maka. (sifat simetrik) 3) Jika dan maka. (sifat transitif) Bukti: 1) Akan dibuktikan. Misalkan adalah titik tengah, maka.
23 13 Jadi. 2) Akan dibuktikan jika maka. Jika maka segiempat sebuah jajargenjang, dengan diagonal-diagonal dan membagi sama panjang di. Ini berarti titik tengah, akibatnya. Jika dengan titik tengah maka. Jadi. 3) Akan dibuktikan jika dan maka. Jika dengan titik tengah, maka. Jika maka segiempat jika jajargenjang sehingga. Jika maka. Jika dengan titik tengah, maka. Jika maka segiempat jika jajargenjang sehingga. Jika maka. Diperoleh dan. Karena dan maka sebuah jajargenjang. Jika jajargenjang maka. Jadi.
24 14 Teorema 3 Jika ditentukan sebuah titik dan sebuah garis berarah, maka ada titik tunggal sehingga. Bukti: Gambar 2.2 Ketunggalan titik Andaikan titik tengah, maka. Diperoleh. Akan dibuktikan tunggal. Andaikan, maka. Oleh karena peta dari oleh tunggal, maka. Jadi. Akibat: 1) Jika,, dan adalah titik-titik yang diketahui maka titik adalah titik tunggal sehingga. 2) Jika dengan maka.
25 15 Definisi: Misalkan adalah ruas garis berarah dan adalah bilangan riil. 1) Jika maka adalah suatu ruas garis berarah dengan (sinar ). 2) Jika maka dengan pada sinar yang berlawanan dengan dan Translasi Pengertian translasi menurut Hvidsten (2005: 193) adalah An isometry that is made up of two reflections, where the lines of reflection are parallel, or identical, is called a translation. Referensi buku pada umumnya mendefinisikan bahwa suatu transformasi merupakan suatu translasi, (ditulis ), diperoleh. Teorema 1 Andaikan dan adalah dua garis sejajar. Jika ada dua titik dan maka dengan dan. Bukti: Misalnya garis sebagai sumbu- dan garis di sumbu- positif. (lihat gambar)
26 16 Gambar 2.3 Refleksi pada dua garis sejajar Andaikan dan. Jika titik tengah, maka harus dibuktikan. Andaikan persamaan adalah. Jika dan, maka garis memotong di sebuah titik dengan sebagai titik tengah. Jadi sedangkan. Jadi [ ] Jadi Oleh karena titik tengah, maka ( ) Sedangkan ( * + * + )
27 17 atau. Dengan demikian maka. Teorema 2 Jika maka. Bukti: Ambil sebarang. Misal dan. Jadi dan. Karena maka. Ini berarti sehingga. Jadi. Teorema 3 Andaikan dan dua garis yang sejajar dan ruas garis berarah yang tegak lurus pada dan dengan dan. Jika maka. Bukti: Ambil sebarang titik. Jika dan maka harus dibuktikan bahwa. (lihat gambar)
28 18 Gambar 2.4 Translasi adalah dua kali refleksi Menurut definisi translasi. Oleh karena, maka. Karena,, maka. Jadi adalah titik tengah sehingga. Menurut teorema 1, maka. Ini berarti. Jadi. Karena sebarang, maka. Akibat: 1) Jika,, dan adalah garis-garis yang tegak lurus yang berturutturut melalui, ( adalah titik tengah ), dan maka.
29 19 2) Setiap translasi adalah isometri langsung Teorema 4 Jika sebuah translasi maka. Bukti: Oleh karena himpunan isometri-isometri merupakan subgrup dari grup transformasi-transformasi, maka setiap translasi memiliki balikan. Diperoleh. Sedangkan. Sehingga. Jadi Komposisi Translasi Di atas dijelaskan bahwa suatu translasi dapat dinyatakan dalam bentuk komposisi dari dua refleksi. Pada bagian ini akan diperlihatkan bahwa setiap translasi dapat diuraikan sebagai komposisi dua setengah putaran. Komposisi dari dua translasi akan berbentuk translasi juga.
30 20 Teorema 1 Jika sebuah translasi sedangkan dan adalah dua titik sehingga maka. Bukti: Andaikan, di, dan di. Gambar 2.5 Translasi adalah dua kali setengah putaran Diketahui bahwa maka. Jadi. Jadi. Teorema 2 Komposit suatu translasi dan suatu setengah putaran adalah suatu setengah putaran. Bukti: Jika suatu translasi dan suatu setengah putaran maka dengan titik tengah sedemikian hingga.
31 21 Jadi. Jadi. Akibat: Jika,, dan masing-masing adalah setengah putaran, maka dengan sebuah titik sehingga. Bukti: Kita peroleh berturut-turut. Jadi. Andaikan maka. Jadi sehingga. Teorema 3 Komposit dua translasi adalah translasi. Bukti: Misalkan dan dua buah translasi. Andaikan dan dua buah titik sehingga dan. Ambil titik sebarang. Diperoleh dan. Jadi Ini berarti translasi membawa titik ke titik..
32 22 Teorema 4 Jika sebuah translasi yang ditentukan oleh titik-titik dan dan transformasi didefinisikan untuk setiap titik sebagai, maka. Bukti: Untuk. Andaikan, maka. Sehingga. Jadi. Ini berarti. 2.3 Isometri Telah dijelaskan bahwa suatu translasi pada sebuah garis adalah suatu transformasi yang mengawetkan jarak atau juga dinamakan suatu isometri. Definisi isometri menurut Susanta (1990: 23) adalah sebagai berikut: Transformasi adalah suatu isometri bila dan hanya bila untuk setiap pasang titik dan dipenuhi dengan dan Isometri Langsung dan Isometri Lawan Suatu transformasi dikatakan mengawetkan suatu orientasi, jika setiap tiga ganda titik tak segaris, orientasinya sama dengan
33 23 ganda tiga titik dengan,, dan. Sedangkan suatu transformasi dikatakan membalik suatu orientasi, jika setiap tiga ganda titik tak segaris, orientasinya tidak sama dengan ganda tiga titik dengan,, dan. Jadi suatu transformasi dinamakan isometri langsung, jika transformasi itu mengawetkan orientasi, dan dinamakan isometri lawan jika transformasi itu mengubah orientasi Teorema-teorema dalam Isometri Teorema 1 Suatu isometri garis adalah kolineasi. Bukti: Gambar 2.6 Isometri garis Ambil sebarang dan. Maka,, dan. Tarik garis melalui dan, sebut. Akan dibuktikan. (i) Akan dibuktikan.
34 24 Ambil sebarang. Andaikan artinya. Karena transformasi maka. isometri maka,, dan. Diperoleh. Ini berarti segaris pada dan juga. Jadi jika maka. Jadi. (ii) Akan dibuktikan. Ambil, maka. Andaikan artinya dan. isometri maka,, dan. Diperoleh. Ini berarti segaris yaitu garis yang melalui dan. Oleh karena garis yang melalui dan, maka. Jadi jika maka. Jadi. Dari uraian di atas diperoleh dan. Jadi. Terbukti bahwa isometri garis akan berupa garis juga. Teorema 2 Isometri mempertahankan besar sudut antara dua garis.
35 25 Bukti: Ambil sebarang. Gambar 2.7 Isometri mempertahankan besar sudut Maka,, dan. Karena isometri maka,, dan. Menurut teorema 1, maka,, dan berupa garis juga. Oleh karena maka. Karena,, dan maka. Jadi. Terbukti bahwa isometri mempertahankan besar sudut antara dua garis. Teorema 3 Isometri mempertahankan kesejajaran dua garis. Bukti: Ambil sebarang dua garis sejajar, misal garis dan garis. Maka dan.
36 26 Gambar 2.8 Isometri mempertahankan kesejajaran garis Andaikan. Maka dan berpotongan di sebuah titik, misal titik. Jadi dan. Karena transformasi maka dengan dan. Ini berarti dan berpotongan di titik. Bertentangan dengan yang diketahui bahwa. Jadi pengandaian salah. Jadi haruslah. Terbukti bahwa isometri mempertahankan kesejajaran dua garis. Akibat: Isometri adalah suatu kolineasi yang mempertahankan keantaraan (jarak), ruas garis, sinar garis, sudut, besar sudut, ketegaklurusan, dan kesejajaran. (Susanta, 1990: 25) Translasi merupakan Isometri Translasi merupakan suatu transformasi oleh garis berarah. Selanjutnya akan dibuktikan teorema bahwa translasi merupakan isometri.
37 27 Teorema. Translasi merupakan suatu isometri Bukti: Misalkan suatu geseran. Diberikan dua titik dan. Diperoleh dan. Ini berarti dan. Diperoleh. Akan dibuktikan. (i) Jika,, dan tidak segaris maka jajargenjang. sehingga. Jadi. (ii) Jika,, dan segaris maka akan terletak pada garis yang sama.. Jadi. Jadi terbukti bahwa translasi merupakan suatu isometri. Akibat: Translasi merupakan suatu kolineasi dan mempertahankan arah garis. 2.4 Isometri Bidang Jika diketahui dua titik dan di, maka merupakan isometri yang memetakan ke. Selain translasi tersebut juga
38 28 dengan adalah sumbu, sehingga. Dan juga, jika titik tengah. Teorema Ketunggalan Isometri Diketahui tiga titik yang tidak kolinear,, dan. Jika ada tiga titik lain,, dan maka terdapat dengan tunggal isometri yang memetakan ke, ke, dan ke. Bukti: Andaikan ada 2 isometri dan sehingga. dan isometri maka. Oleh karena,, dan tidak kolinear maka,, dan juga tidak kolinear. Andaikan dan maka. Jadi di sumbu. Analog untuk dan juga di sumbu. Jadi,, dan kolinear. Ini berlawanan dengan yang diketahui yaitu,, dan tidak kolinear. Jadi haruslah. Ini berarti. Bahwa tidak selalu ada isometri dapat kita lihat bila.
39 BAB 3 METODE PENELITIAN 3.1 Identifikasi Masalah Identifikasi masalah dimulai dengan studi pustaka. Studi pustaka merupakan penelaah sumber pustaka yang relevan berupa buku-buku yang berhubungan dengan translasi bangun ruang bersisi datar pada ruang berdimensi tiga (R 3 ). Kemudian hasil dari studi pustaka ini digunakan untuk mengumpulkan referensi yang diperlukan dalam menyusun skripsi. Setelah sumber pustaka terkumpul, dilanjutkan dengan penelaah isi sumber pustaka tersebut. Dengan melakukan telaah pustaka dari berbagai buku referensi yang ada dan konsultasi dengan dosen pembimbing, masalah tersebut menghasilkan gagasan untuk menuliskannya dalam bentuk skripsi. 3.2 Perumusan Masalah Perumusan masalah dinyatakan dalam bentuk pernyataan yang singkat dan jelas sehingga mudah untuk dipahami. Tahap ini dimaksud untuk memperjelas permasalahan yang telah ditemukan yaitu dengan 29
40 30 merumuskan Bagaimana menyatakan hasil translasi bangun ruang bersisi datar pada ruang berdimensi tiga ( )?. Dalam hal ini penulis membatasi pada bangun ruang prisma dan limas. 3.3 Studi Pustaka Dalam langkah ini dilakukan kajian sumber-sumber pustaka dengan cara mengumpulkan data atau informasi yang berkaitan dengan masalah translasi bangun ruang khususnya pada bangun ruang bersisi datar, mengumpulkan konsep pendukung yang diperlukan dalam menyelesaikan masalah tersebut. Sehingga didapatkan suatu ide mengenai bahan dasar pengembangan upaya pemecahan masalah. 3.4 Pemecahan Masalah Pada tahap ini, dilakukan analisis terhadap permasalahan yang sudah dirumuskan dengan didasari teori dan argumentasi yang tepat. Pemecahan masalah ini meliputi penjelasan tema yang telah ditetapkan dan pembahasan mengenai masalah yang telah diungkapkan sebelumnya secara lengkap dengan landasan teori dan referensi yang ada serta konsultasi dengan dosen pembimbing. Dalam proses pemecahan masalah ini, dilakukan analisa dan pemecahan masalah yaitu dengan langkahlangkah sebagai berikut:
41 31 1. Mengkaji definisi ruang euclid 2. Mengkaji rumus umum dari translasi titik, garis dan bidang. 3. Membuktikan sifat-sifat translasi di 4. Menggunakan rumus-rumus umum yang diperoleh untuk menyatakan hasil translasi bangun ruang bersisi datar pada ruang berdimensi tiga ( ). 3.5 Penarikan Simpulan Hasil dari pembahasan ini dituangkan dalam bentuk simpulan akhir yang menyimpulkan secara umum pemecahan masalah tersebut. Simpulan ini dijadikan sebagai hasil kajian akhir dan merupakan hasil akhir dari proses penulisan skripsi.
42 BAB 5 PENUTUP 5.1 Simpulan Diilhami dari definisi dan Ruang Euclid, diperoleh definisi Ruang Euclid sebagai berikut: Definisi Ruang Euclid Fungsi dari dengan rumus disebut inner product, dot product, atau scalar product pada. Ruang vektor yang dilengkapi dengan inner product disebut ruang euclide, dengan { }. Suatu translasi di merupakan isometri yang mempunyai sifatsifat sebagai berikut: a. Translasi garis akan berupa garis lagi b. Translasi mempertahankan besar sudut antara dua garis c. Translasi mempertahankan kesejajaran antara dua garis d. Translasi bidang akan berupa bidang lagi e. Translasi mempertahankan besar sudut antara dua bidang f. Translasi mempertahankan kesejajaran antara dua bidang 64
43 65 Rumus umum dalam mentranslasikan bangun ruang ada 3 cara, yaitu: a. Rumus umum translasi titik dalam matriks ( ) ( ) ( ) b. Rumus umum translasi garis c. Rumus umum translasi bidang { } 5.2 Saran Pada skripsi ini hanya dibahas tentang transformasi translasi di ruang berdimensi tiga. Objek yang digambarkan hanya untuk memperjelas objek yang dibahas sehingga lebih mudah dipahami. Perluasan objek pembahasan tidak hanya pada bangun ruang bersisi datar, tetapi juga pada bangun ruang bersisi lengkung. Ruang dimensi yang digunakan juga dapat diperluas menjadi ruang berdimensi-.
44 DAFTAR PUSTAKA Anton, Howard Aljabar Linear Elementer (5 th ed.). Translated by Silaban, P. dan Susila, I. N. Jakarta: Erlangga. Drooyan, Irving Analytic Geometry. Canada: John Wiley & Sons, Inc. Hvidsten, Michael Geometry With Geometry Explorer. New York: The McGraw-Hill Companies, Inc. Kurnianto, Y. S Geometri Euclid R n. Skripsi. Yogyakarta: Universitas Gadjah Mada. Kusni dan Suhito Geometri Transformasi. Semarang: Universitas Negeri Semarang. Mujahid, Muhammad Bidang Rata Dan Garis Lurus. Tersedia di [diakses 13/09/14]. Mulyati, Sri Geometri Euclid. Malang: JICA. Purcell, E. J. dan D. Varberg Kalkulus Dan Geometri Analitis (5 th ed.). Jilid 1 dan 2. Translated by Susila, I. N. et al. Jakarta: Erlangga. Rawuh Geometri Transformasi. Bandung: Depdikbud. Sriwasito, Putut Bidang Dan Garis. Semarang: Universitas Diponegoro. 66
45 67 Susanta, B Geometri Transformasi. Jogjakarta: Universitas Gadjah Mada. Varberg, D. et al Kalkulus Edisi Kesembilan. Jilid 1 dan 2. Translated by Susila, I. N. Jakarta: Erlangga. Wallace, E. C. and S. F. West Roads to Geometry. America: Prentice-Hall, Inc.
46 68
47 69
TRANSFORMASI. Dosen Pengampu Mata Kuliah. HERDIAN, S.Pd., M.Pd. Disusun Oleh : Kelompok 1. Hayatun Nupus Rina Ariyani
 TRANSFORMASI Makalah ini disusun sebagai tugas mata kuliah Geometri Transformasi Dosen Pengampu Mata Kuliah HERDIAN, S.Pd., M.Pd. Disusun Oleh : Kelompok 1 Hayatun Nupus 08030121 Rina Ariyani 08030057
TRANSFORMASI Makalah ini disusun sebagai tugas mata kuliah Geometri Transformasi Dosen Pengampu Mata Kuliah HERDIAN, S.Pd., M.Pd. Disusun Oleh : Kelompok 1 Hayatun Nupus 08030121 Rina Ariyani 08030057
1 P E N D A H U L U A N
 1 P E N D A H U L U A N Pemetaan (fungsi) f dari himpunan A ke himpunan B adalah suatu hubuungan yang memasangkan setiap unsur di A dengan tepat satu unsur di B. Jika a A dan pasangannya b B, maka ditulis
1 P E N D A H U L U A N Pemetaan (fungsi) f dari himpunan A ke himpunan B adalah suatu hubuungan yang memasangkan setiap unsur di A dengan tepat satu unsur di B. Jika a A dan pasangannya b B, maka ditulis
Matematika Semester IV
 F U N G S I KOMPETENSI DASAR Mendeskripsikan perbedaan konsep relasi dan fungsi Menerapkan konsep fungsi linear Menggambar fungsi kuadrat Menerapkan konsep fungsi kuadrat Menerapkan konsep fungsi trigonometri
F U N G S I KOMPETENSI DASAR Mendeskripsikan perbedaan konsep relasi dan fungsi Menerapkan konsep fungsi linear Menggambar fungsi kuadrat Menerapkan konsep fungsi kuadrat Menerapkan konsep fungsi trigonometri
MAKALAH OLEH KELOMPOK I NAMA : 1. SHINTA JULIANTY 2. SITI HERLIZA 3. FATMALIZA 4. SUPRA ANTONI 5. JUNIANTY
 MAKALAH OLEH KELOMPOK I NAMA : 1. SHINTA JULIANTY 2. SITI HERLIZA 3. FATMALIZA 4. SUPRA ANTONI 5. JUNIANTY PROGRAM STUDI MATA KULIAH DOSEN PENGAMPU : PENDIDIKAN MATEMATIKA : GEOMETRI TRANSFORMASI : FADLI,
MAKALAH OLEH KELOMPOK I NAMA : 1. SHINTA JULIANTY 2. SITI HERLIZA 3. FATMALIZA 4. SUPRA ANTONI 5. JUNIANTY PROGRAM STUDI MATA KULIAH DOSEN PENGAMPU : PENDIDIKAN MATEMATIKA : GEOMETRI TRANSFORMASI : FADLI,
GEOMETRI TRANSFORMASI SETENGAH PUTARAN
 GEOMETRI TRANSFORMASI SETENGAH PUTARAN Disusun Oleh : Kelompok Empat (V1 A) 1. Purna Irawan (4007178 ) 2. Sudarsono (4007028 p) 3. Mellyza Vemi R. (4007217 ) 4. Kristina Nainggolan (4007013 ) 5. Desi Kartini
GEOMETRI TRANSFORMASI SETENGAH PUTARAN Disusun Oleh : Kelompok Empat (V1 A) 1. Purna Irawan (4007178 ) 2. Sudarsono (4007028 p) 3. Mellyza Vemi R. (4007217 ) 4. Kristina Nainggolan (4007013 ) 5. Desi Kartini
MENUNJUKKAN SIFAT SIFAT AFFINITAS PERSPEKTIF DENGAN MENGGUNAKAN PROGRAM CABRI. Oleh Sugiyono Jurusan Pendidikan Matematika FMIPA UNY ABSTRAK
 MENUNJUKKAN SIFAT SIFAT AFFINITAS PERSPEKTIF DENGAN MENGGUNAKAN PROGRAM CABRI Oleh Sugiyono Jurusan Pendidikan Matematika FMIPA UNY ABSTRAK Misalkan s suatu garis dalam bidang (Euclides), α menyatakan
MENUNJUKKAN SIFAT SIFAT AFFINITAS PERSPEKTIF DENGAN MENGGUNAKAN PROGRAM CABRI Oleh Sugiyono Jurusan Pendidikan Matematika FMIPA UNY ABSTRAK Misalkan s suatu garis dalam bidang (Euclides), α menyatakan
ISOMETRI TERHADAP GEOMETRI INSIDENSI TERURUT
 Prosiding Semirata FMIPA Universitas Lampung, 2013 ISOMETRI TERHADAP GEOMETRI INSIDENSI TERURUT Damay Lisdiana, Muslim Ansori, Amanto Jurusan Matematika FMIPA Universitas Lampung Email: peace_ay@yahoo.com
Prosiding Semirata FMIPA Universitas Lampung, 2013 ISOMETRI TERHADAP GEOMETRI INSIDENSI TERURUT Damay Lisdiana, Muslim Ansori, Amanto Jurusan Matematika FMIPA Universitas Lampung Email: peace_ay@yahoo.com
M A K A L A H GEOMETRI TRANFORMASI ( TRANFORMASI BALIKAN )
 M A K A L A H GEOMETRI TRANFORMASI ( TRANFORMASI BALIKAN ) D I S U S U N O L E H : 1. NOPITA SARI ( 4007213 ) 2. MULYATI ( 4007152 ) 3. ROHIM ( 4007142 ) 4. RUSMINI ( 4007222 ) 5. MARYANA ( ) 6. ARY WIJAYA
M A K A L A H GEOMETRI TRANFORMASI ( TRANFORMASI BALIKAN ) D I S U S U N O L E H : 1. NOPITA SARI ( 4007213 ) 2. MULYATI ( 4007152 ) 3. ROHIM ( 4007142 ) 4. RUSMINI ( 4007222 ) 5. MARYANA ( ) 6. ARY WIJAYA
1 Mengapa Perlu Belajar Geometri Daftar Pustaka... 1
 Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
MENUNJUKKAN SIFAT SIFAT AFFINITAS PERSPEKTIF DENGAN MENGGUNAKAN PROGRAM CABRI
 Prosiding Seminar Nasional Penelitian, Pendidikan dan Penerapan MIPA Fakultas MIPA, Universitas Negeri Yogyakarta, 16 Mei 2009 MENUNJUKKAN SIFAT SIFAT AFFINITAS PERSPEKTIF DENGAN MENGGUNAKAN PROGRAM CABRI
Prosiding Seminar Nasional Penelitian, Pendidikan dan Penerapan MIPA Fakultas MIPA, Universitas Negeri Yogyakarta, 16 Mei 2009 MENUNJUKKAN SIFAT SIFAT AFFINITAS PERSPEKTIF DENGAN MENGGUNAKAN PROGRAM CABRI
Relasi, Fungsi, dan Transformasi
 Modul 1 Relasi, Fungsi, dan Transformasi Drs. Ame Rasmedi S. Dr. Darhim, M.Si. M PENDAHULUAN odul ini merupakan modul pertama pada mata kuliah Geometri Transformasi. Modul ini akan membahas pengertian
Modul 1 Relasi, Fungsi, dan Transformasi Drs. Ame Rasmedi S. Dr. Darhim, M.Si. M PENDAHULUAN odul ini merupakan modul pertama pada mata kuliah Geometri Transformasi. Modul ini akan membahas pengertian
GEOMETRI TRANSFORMASI MATERI
 GEOMETRI TRANSFORMASI MATERI TRANSFORMASI BALIKAN DISUSUN OLEH : KELOMPOK IV 1. Retno Fitria Pratiwi ( 2010 121 179 ) 2. Nanda Wahyuni Pritama ( 2010 121 140 ) 3. Verawati (2010 121 173 ) KELAS : 5 D Dosen
GEOMETRI TRANSFORMASI MATERI TRANSFORMASI BALIKAN DISUSUN OLEH : KELOMPOK IV 1. Retno Fitria Pratiwi ( 2010 121 179 ) 2. Nanda Wahyuni Pritama ( 2010 121 140 ) 3. Verawati (2010 121 173 ) KELAS : 5 D Dosen
France title. Handy of transformation of Geometry. Tangkas Geometri Transformasi
 France title Handy of transformation of Geometry Tangkas Geometri Transformasi i TANGKAS GEOMETRI TRANSFORMASI Meyta Dwi Kurniasih Isnaini Handayani Pendidikan Matematika Fakultas Pendidikan dan Ilmu Pendidikan
France title Handy of transformation of Geometry Tangkas Geometri Transformasi i TANGKAS GEOMETRI TRANSFORMASI Meyta Dwi Kurniasih Isnaini Handayani Pendidikan Matematika Fakultas Pendidikan dan Ilmu Pendidikan
SILABUS MATAKULIAH. : Setelah mengikuti matakuliah ini mahasiswa diharapkan dapat memiliki pengetahuan dan pemahaman mengenai
 SILABUS MATAKULIAH Matakuliah Program Studi : Geometri Transformasi : Pendidikan Matematika Kode Matakuliah : 011-032513 Bobot Semester Mata Kuliah Prasyarat Standar Kompetensi : 3 SKS : VI : Aljabar Linier
SILABUS MATAKULIAH Matakuliah Program Studi : Geometri Transformasi : Pendidikan Matematika Kode Matakuliah : 011-032513 Bobot Semester Mata Kuliah Prasyarat Standar Kompetensi : 3 SKS : VI : Aljabar Linier
OLEH : PROGRAM STUDI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN ILMU SEKOLAH TINNGI KEGURUAN DAN ILMU PENDIDIKAN
 OLEH : 1. ASRIA HIRDA YANTI ( 4007014 ) 2. ANNIE RACHMAWATI ( 4006116 ) 3. RUPITA FITRIANI ( 4007036 ) 4. PERA HIJA TERISTIANA ( 4007001 ) 5. HARTATI SUSANTI ( 4007166 ) PROGRAM STUDI PENDIDIKAN MATEMATIKA
OLEH : 1. ASRIA HIRDA YANTI ( 4007014 ) 2. ANNIE RACHMAWATI ( 4006116 ) 3. RUPITA FITRIANI ( 4007036 ) 4. PERA HIJA TERISTIANA ( 4007001 ) 5. HARTATI SUSANTI ( 4007166 ) PROGRAM STUDI PENDIDIKAN MATEMATIKA
Janos meninggalkan sekolahnya pada saat kelas 4. Ia
 4 PENGENLN GEOMETRI FFINE Janos olyai dilahirkan pada tanggal 15 Desember 1802 di Koloszvar, sekarang luj, bagian dari Romania Transylvania. Orang tua dari Janos olyai adalah Farkas Wolfgang olyai dan
4 PENGENLN GEOMETRI FFINE Janos olyai dilahirkan pada tanggal 15 Desember 1802 di Koloszvar, sekarang luj, bagian dari Romania Transylvania. Orang tua dari Janos olyai adalah Farkas Wolfgang olyai dan
TUGAS MATA KULIAH GEOMETRI TRANSFORMASI
 TUGAS MATA KULIAH GEOMETRI TRANSFORMASI Dosen Pengampu HERDIAN, S.Pd., M.Pd. Disusun Oleh : Kelompok 3 Nama : NPM : 1. Ahmad Muslim 08030007 2. Ivo ayu Septiana 08030159 3. Elsa Fitriana 08030200 SEKOLAH
TUGAS MATA KULIAH GEOMETRI TRANSFORMASI Dosen Pengampu HERDIAN, S.Pd., M.Pd. Disusun Oleh : Kelompok 3 Nama : NPM : 1. Ahmad Muslim 08030007 2. Ivo ayu Septiana 08030159 3. Elsa Fitriana 08030200 SEKOLAH
II. TINJAUAN PUSTAKA. sebuah geometri selain aksioma diperlukan juga unsur-unsur tak terdefinisi. Untuk. 2. Himpunan titik-titik yang dinamakan garis.
 5 II. TINJAUAN PUSTAKA 2.1 Geometri Insidensi Suatu geometri dibentuk berdasarkan aksioma yang berlaku dalam geometrigeometri tersebut. Geometri insidensi didasari oleh aksioma insidensi. Di dalam sebuah
5 II. TINJAUAN PUSTAKA 2.1 Geometri Insidensi Suatu geometri dibentuk berdasarkan aksioma yang berlaku dalam geometrigeometri tersebut. Geometri insidensi didasari oleh aksioma insidensi. Di dalam sebuah
TRANSFORMASI. 1) T(A) = A 2) Apabila P A, maka T(P) = Q dengan Q titik tengah garis. Selidiki apakah
 TRNSFORMSI Suatu transformasi pada suatu bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga. Fungsi yang bijektif adalah sebuah fungsi yang bersifat : juga V.
TRNSFORMSI Suatu transformasi pada suatu bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga. Fungsi yang bijektif adalah sebuah fungsi yang bersifat : juga V.
GESERAN atau TRANSLASI
 GESERAN atau TRANSLASI Makalah ini disusun untuk memenuhi Tugas Geometri Transformasi Dosen Pembimbing : Havid Risyanto, S.Si., M.Sc. D I S U S U N O L E H 1. AMILIA 1111050031 2. HAIRUDIN 1111050153 3.
GESERAN atau TRANSLASI Makalah ini disusun untuk memenuhi Tugas Geometri Transformasi Dosen Pembimbing : Havid Risyanto, S.Si., M.Sc. D I S U S U N O L E H 1. AMILIA 1111050031 2. HAIRUDIN 1111050153 3.
TRANSFORMASI. Suatu transfornmasi pada bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga.
 1 TRANSFORMASI Suatu transfornmasi pada bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga. Sebuah fungsi yang bijektif adalah sebuah fungsi yang bersifat: 1.
1 TRANSFORMASI Suatu transfornmasi pada bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga. Sebuah fungsi yang bijektif adalah sebuah fungsi yang bersifat: 1.
UKURAN RUAS-RUAS GARIS PADA SEGITIGA SKRIPSI
 UKURAN RUAS-RUAS GARIS PADA SEGITIGA SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana
UKURAN RUAS-RUAS GARIS PADA SEGITIGA SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana
MA Analisis dan Aljabar Teori=4 Praktikum=0 II (angka. 17 Juli
 INSTITUT TEKNOLOGI KALIMANTAN JURUSAN MATEMATIKA DAN TEKNOLOGI INFORMASI PROGRAM STUDI MATEMATIKA SILABUS MATA KULIAH KODE Rumpun MK BOBOT (sks) SEMESTER Tgl Penyusunan Aljabar Linear ELementer MA Analisis
INSTITUT TEKNOLOGI KALIMANTAN JURUSAN MATEMATIKA DAN TEKNOLOGI INFORMASI PROGRAM STUDI MATEMATIKA SILABUS MATA KULIAH KODE Rumpun MK BOBOT (sks) SEMESTER Tgl Penyusunan Aljabar Linear ELementer MA Analisis
Materi Aljabar Linear Lanjut
 Materi Aljabar Linear Lanjut TRANSFORMASI LINIER DARI R n KE R m ; GEOMETRI TRANSFORMASI LINIER DARI R 2 KE R 2 Disusun oleh: Dwi Lestari, M.Sc email: dwilestari@uny.ac.id JURUSAN PENDIDIKAN MATEMATIKA
Materi Aljabar Linear Lanjut TRANSFORMASI LINIER DARI R n KE R m ; GEOMETRI TRANSFORMASI LINIER DARI R 2 KE R 2 Disusun oleh: Dwi Lestari, M.Sc email: dwilestari@uny.ac.id JURUSAN PENDIDIKAN MATEMATIKA
Bilangan Real. Modul 1 PENDAHULUAN
 Modul 1 Bilangan Real S PENDAHULUAN Drs. Soemoenar emesta pembicaraan Kalkulus adalah himpunan bilangan real. Jadi jika akan belajar kalkulus harus paham terlebih dahulu tentang bilangan real. Bagaimanakah
Modul 1 Bilangan Real S PENDAHULUAN Drs. Soemoenar emesta pembicaraan Kalkulus adalah himpunan bilangan real. Jadi jika akan belajar kalkulus harus paham terlebih dahulu tentang bilangan real. Bagaimanakah
Hand-Out Geometri Transformasi. Bab I. Pendahuluan
 Hand-Out Geometri Transformasi Bab I. Pendahuluan 1.1 Vektor dalam R 2 Misalkan u = (x 1,y 1 ), v = (x 2,y 2 ) dan w = (x 3,y 3 ) serta k skalar (bilangan real) Definisi 1. : Penjumlahan vektor u + v =
Hand-Out Geometri Transformasi Bab I. Pendahuluan 1.1 Vektor dalam R 2 Misalkan u = (x 1,y 1 ), v = (x 2,y 2 ) dan w = (x 3,y 3 ) serta k skalar (bilangan real) Definisi 1. : Penjumlahan vektor u + v =
DERET KOMPOSISI DARI SUATU MODUL
 DERET KOMPOSISI DARI SUATU MODUL SKRIPSI Oleh : ANI NURHAYATI J2A 006 001 PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS DIPONEGORO SEMARANG 2010
DERET KOMPOSISI DARI SUATU MODUL SKRIPSI Oleh : ANI NURHAYATI J2A 006 001 PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS DIPONEGORO SEMARANG 2010
BAB II TINJAUAN PUSTAKA. tegak, perlu diketahui tentang materi-materi sebagai berikut.
 BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
BAB II TINJAUAN PUSTAKA Sebelum pembahasan mengenai irisan bidang datar dengan tabung lingkaran tegak, perlu diketahui tentang materi-materi sebagai berikut. A. Matriks Matriks adalah himpunan skalar (bilangan
TRANSFORMASI DAN PENCERMINAN
 TRANSFORMASI DAN PENCERMINAN DISUSUN OLEH: KELOMPOK 1 (SATU) 1.AISYAH (4007005) 2.WIWIN AGUSTINA (4007018) 3.MARTINI (4007024) 4.TUKIJO (4007009) Dosen Pengampu : Fadli, S.Si, M.Pd. SEKOLAH TINGGI KEGURUAN
TRANSFORMASI DAN PENCERMINAN DISUSUN OLEH: KELOMPOK 1 (SATU) 1.AISYAH (4007005) 2.WIWIN AGUSTINA (4007018) 3.MARTINI (4007024) 4.TUKIJO (4007009) Dosen Pengampu : Fadli, S.Si, M.Pd. SEKOLAH TINGGI KEGURUAN
SISTEM SCHREIER PADA FREE GROUP. Skripsi untuk memenuhi sebagian persyaratan mencapai derajat Sarjana S-1. Program Studi Matematika
 SISTEM SCHREIER PADA FREE GROUP Skripsi untuk memenuhi sebagian persyaratan mencapai derajat Sarjana S-1 Program Studi Matematika diajukan oleh Yulianita 05610008 Kepada PROGRAM STUDI MATEMATIKA FAKULTAS
SISTEM SCHREIER PADA FREE GROUP Skripsi untuk memenuhi sebagian persyaratan mencapai derajat Sarjana S-1 Program Studi Matematika diajukan oleh Yulianita 05610008 Kepada PROGRAM STUDI MATEMATIKA FAKULTAS
BAB I PENDAHULUAN Latar Belakang Masalah
 BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ruang vektor adalah suatu grup abelian yang dilengkapi dengan operasi pergandaan skalar atas suatu lapangan. Suatu ruang vektor dapat dikawankan dengan ruang
BAB I PENDAHULUAN 1.1. Latar Belakang Masalah Ruang vektor adalah suatu grup abelian yang dilengkapi dengan operasi pergandaan skalar atas suatu lapangan. Suatu ruang vektor dapat dikawankan dengan ruang
MODUL PEMBELAJARAN ANALISIS VARIABEL KOMPLEKS 2/22/2012 IKIP BUDI UTOMO MALANG ALFIANI ATHMA PUTRI ROSYADI
 MODUL PEMBELAJARAN ANALISIS VARIABEL KOMPLEKS 2/22/2012 IKIP BUDI UTOMO MALANG ALFIANI ATHMA PUTRI ROSYADI IDENTITAS MAHASISWA NAMA NPM KELOMPOK : : : DAFTAR ISI Kata Pengantar Daftar Isi BAB I Bilangan
MODUL PEMBELAJARAN ANALISIS VARIABEL KOMPLEKS 2/22/2012 IKIP BUDI UTOMO MALANG ALFIANI ATHMA PUTRI ROSYADI IDENTITAS MAHASISWA NAMA NPM KELOMPOK : : : DAFTAR ISI Kata Pengantar Daftar Isi BAB I Bilangan
SEKOLAH TINGGI KEGURUAN DAN ILMUPENDIDIKAN PERSATUAN GURU REPUBLIK INDONESIA STKIP PGRI LUBUKLINGGAU
 MATERI : TRANSFORMASI BALIKAN (VI.C) Disusun Oleh: 1. KARMILA 2. NURMALINA 3. DWINDA JANUARTI 4. YUYUN MARNITA 5. ROVELI 6. MIKA MARDASARI 7. IKA NURSINTA 8. LISA MAYANI SEKOLAH TINGGI KEGURUAN DAN ILMUPENDIDIKAN
MATERI : TRANSFORMASI BALIKAN (VI.C) Disusun Oleh: 1. KARMILA 2. NURMALINA 3. DWINDA JANUARTI 4. YUYUN MARNITA 5. ROVELI 6. MIKA MARDASARI 7. IKA NURSINTA 8. LISA MAYANI SEKOLAH TINGGI KEGURUAN DAN ILMUPENDIDIKAN
Catatan Kuliah MA1123 Kalkulus Elementer I
 Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
Catatan Kuliah MA1123 Kalkulus Elementer I Oleh Hendra Gunawan, Ph.D. Departemen Matematika ITB Sasaran Belajar Setelah mempelajari materi Kalkulus Elementer I, mahasiswa diharapkan memiliki (terutama):
r = 4 5 Ê Á 3. a. A ' (10,5) 5 A', Á Ë Á Ë B',
 Kunci Jawaban Bab 1 Logika Matematika I. 1. c 9. a 3. d 11. a 5. e 13. b 7. a 15. c II. 1. a. Benar b. Benar c. Benar 3. Kucing bukan ikan 5. Jika 6 bilangan komposit maka 6 bilangan rasional Bab 2 Relasi
Kunci Jawaban Bab 1 Logika Matematika I. 1. c 9. a 3. d 11. a 5. e 13. b 7. a 15. c II. 1. a. Benar b. Benar c. Benar 3. Kucing bukan ikan 5. Jika 6 bilangan komposit maka 6 bilangan rasional Bab 2 Relasi
TRANSFORMASI BALIKAN
 TRANSFORMASI BALIKAN Disusun Oleh : Nama : Dodi Sunhaji (4007017) Esty Gustina (4007199) Indah Sri (4007015) Warnitik (4007009) Oryza Sativa Kelas : VIA Prodi : Matematika Mata Kuliah : Geometri Transformasi
TRANSFORMASI BALIKAN Disusun Oleh : Nama : Dodi Sunhaji (4007017) Esty Gustina (4007199) Indah Sri (4007015) Warnitik (4007009) Oryza Sativa Kelas : VIA Prodi : Matematika Mata Kuliah : Geometri Transformasi
ISOMETRI & HASIL KALI TRANSFORMASI
 ISOMETRI & HASIL KALI TRANSFORMASI MATA KULIAH : GEOMETRI TRANNSFORMMASI DISUSUN OLEH : 1. ASMERI : 4007118 2. NITA FITRIA.N : 4007501 SEMESTER / KELAS : VI (ENAM). C PRODI : PEND. MATEMATIKA DOSEN PEMBIMBING
ISOMETRI & HASIL KALI TRANSFORMASI MATA KULIAH : GEOMETRI TRANNSFORMMASI DISUSUN OLEH : 1. ASMERI : 4007118 2. NITA FITRIA.N : 4007501 SEMESTER / KELAS : VI (ENAM). C PRODI : PEND. MATEMATIKA DOSEN PEMBIMBING
REFLEKSI DAN AKSIOMA CERMIN PADA BIDANG POINCARÉ
 REFLEKSI DAN AKSIOMA CERMIN PADA BIDANG POINCARÉ Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika Oleh : Chintia Rudiyanto NIM :
REFLEKSI DAN AKSIOMA CERMIN PADA BIDANG POINCARÉ Skripsi Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Pendidikan Program Studi Pendidikan Matematika Oleh : Chintia Rudiyanto NIM :
Modul ini adalah modul ke-7 dalam mata kuliah Matematika. Isi modul ini
 PENDAHULUAN Modul ini adalah modul ke-7 dalam mata kuliah Matematika. Isi modul ini membahas tentang transformasi. Modul ini terdiri dari 2 kegiatan belajar. Pada kegiatan belajar 1 akan dibahas mengenai
PENDAHULUAN Modul ini adalah modul ke-7 dalam mata kuliah Matematika. Isi modul ini membahas tentang transformasi. Modul ini terdiri dari 2 kegiatan belajar. Pada kegiatan belajar 1 akan dibahas mengenai
Candi Gebang Permai Blok R/6 Yogyakarta Telp. : ; Fax. :
 ii Aljabar Linear Kata Pengantar iii iv Aljabar Linear ALJABAR LINEAR Oleh : Setiadji Edisi Pertama Cetakan Pertama, 2008 Hak Cipta 2008 pada penulis, Hak Cipta dilindungi undang-undang. Dilarang memperbanyak
ii Aljabar Linear Kata Pengantar iii iv Aljabar Linear ALJABAR LINEAR Oleh : Setiadji Edisi Pertama Cetakan Pertama, 2008 Hak Cipta 2008 pada penulis, Hak Cipta dilindungi undang-undang. Dilarang memperbanyak
MATERI : GESERAN (TRANSLASI) KELOMPOK 6 (VI.E)
 MATERI : GESERAN (TRANSLASI) KELOMPOK 6 (VI.E) Disusun Oleh: 1. ARI SUKA LESMANA 2. YULAIMA SUPRIHATIN 3. HERVI MARDIANA SEKOLAH TINGGI KEGURUAN DAN ILMUPENDIDIKAN PERSATUAN GURU REPUBLIK INDONESIA STKIP
MATERI : GESERAN (TRANSLASI) KELOMPOK 6 (VI.E) Disusun Oleh: 1. ARI SUKA LESMANA 2. YULAIMA SUPRIHATIN 3. HERVI MARDIANA SEKOLAH TINGGI KEGURUAN DAN ILMUPENDIDIKAN PERSATUAN GURU REPUBLIK INDONESIA STKIP
MAKALAH GEOMETRI TRANSFORMASI TRANSFORMASI
 MAKALAH GEOMETRI TRANSFORMASI TRANSFORMASI DOSEN PENGAMPU MATA KULIAH HERDIAN, S.Pd., M.Pd. DISUSUN OLEH : NAMA NPM 1. UMI SULISTIYOWATI 08 030 089 2. NURSITI LAILA 08 030 092 3. RATNA LISTIAWATI 08 030
MAKALAH GEOMETRI TRANSFORMASI TRANSFORMASI DOSEN PENGAMPU MATA KULIAH HERDIAN, S.Pd., M.Pd. DISUSUN OLEH : NAMA NPM 1. UMI SULISTIYOWATI 08 030 089 2. NURSITI LAILA 08 030 092 3. RATNA LISTIAWATI 08 030
II. LANDASAN TEORI. Dalam bab ini akan didiskusikan unsur tak terdefinisi, aksioma-aksioma, istilahistilah,
 3 II. LANDASAN TEORI Dalam bab ini akan didiskusikan unsur tak terdefinisi, aksioma-aksioma, istilahistilah, definisi-definisi dan teorema-teorema yang berhubungan dengan penelitian ini. 2.1 Geometri Insidensi
3 II. LANDASAN TEORI Dalam bab ini akan didiskusikan unsur tak terdefinisi, aksioma-aksioma, istilahistilah, definisi-definisi dan teorema-teorema yang berhubungan dengan penelitian ini. 2.1 Geometri Insidensi
PROGRAM STUDI : PENDIDIKAN MATEMATIKA
 MAKALAH OLEH KELOMPOK DUA NAMA : GIYATNI ( 40077 ) SEPTI PRATIWI ( 400796 ) 3HARI YADI (400763 ) PROGRAM STUDI : PENDIDIKAN MATEMATIKA MATA KULIAH : GEOMETRI TRANSFORMASI DOSEN PENGAMPU : PADLI MPd SEKOLAH
MAKALAH OLEH KELOMPOK DUA NAMA : GIYATNI ( 40077 ) SEPTI PRATIWI ( 400796 ) 3HARI YADI (400763 ) PROGRAM STUDI : PENDIDIKAN MATEMATIKA MATA KULIAH : GEOMETRI TRANSFORMASI DOSEN PENGAMPU : PADLI MPd SEKOLAH
Himpunan dan Fungsi. Modul 1 PENDAHULUAN
 Modul 1 Himpunan dan Fungsi Dr Rizky Rosjanuardi P PENDAHULUAN ada modul ini dibahas konsep himpunan dan fungsi Pada Kegiatan Belajar 1 dibahas konsep-konsep dasar dan sifat dari himpunan, sedangkan pada
Modul 1 Himpunan dan Fungsi Dr Rizky Rosjanuardi P PENDAHULUAN ada modul ini dibahas konsep himpunan dan fungsi Pada Kegiatan Belajar 1 dibahas konsep-konsep dasar dan sifat dari himpunan, sedangkan pada
TEORI GRUP SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS
 TEORI GRUP SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta
TEORI GRUP SUMANANG MUHTAR GOZALI KBK ALJABAR & ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta
MIDDLE PADA BEBERAPA GRAF KHUSUS
 PELABELAN DAN PEMBENTUKAN GRAF MIDDLE PADA BEBERAPA GRAF KHUSUS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Meliana Deta Anggraeni 4111409019
PELABELAN DAN PEMBENTUKAN GRAF MIDDLE PADA BEBERAPA GRAF KHUSUS skripsi disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains Program Studi Matematika oleh Meliana Deta Anggraeni 4111409019
REFLEKSI TERHADAP LINGKARAN SKRIPSI
 REFLEKSI TERHADAP LINGKARAN SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta Untuk Memenuhi Sebagian Persyaratan Guna Memperoleh Gelar Sarjana Sains Disusun
REFLEKSI TERHADAP LINGKARAN SKRIPSI Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta Untuk Memenuhi Sebagian Persyaratan Guna Memperoleh Gelar Sarjana Sains Disusun
BAB V GEOMETRI DAN TRANSFORMASI
 BAB V GEOMETRI DAN TRANSFORMASI Pernahkah anda mengamati proses pekerjaan pembangunan sebuah rumah? Semua tahap pekerjaan tersebut, mulai dari perancangan hingga finishing, tidak terlepas dari penerapan
BAB V GEOMETRI DAN TRANSFORMASI Pernahkah anda mengamati proses pekerjaan pembangunan sebuah rumah? Semua tahap pekerjaan tersebut, mulai dari perancangan hingga finishing, tidak terlepas dari penerapan
SILABUS MATAKULIAH. Revisi : 2 Tanggal Berlaku : September Indikator Pokok Bahasan/Materi Strategi Pembelajaran
 SILABUS MATAKULIAH Revisi : 2 Tanggal Berlaku : September 2014 A. Identitas 1. Nama Matakuliah : A11. 54101 / Kalkulus I 2. Program Studi : Teknik Informatika-S1 3. Fakultas : Ilmu Komputer 4. Bobot sks
SILABUS MATAKULIAH Revisi : 2 Tanggal Berlaku : September 2014 A. Identitas 1. Nama Matakuliah : A11. 54101 / Kalkulus I 2. Program Studi : Teknik Informatika-S1 3. Fakultas : Ilmu Komputer 4. Bobot sks
GEOMETRI ANALITIK RUANG. Dr. Susanto, MPd
 GEOMETRI ANALITIK RUANG Dr. Susanto, MPd PROGRAM STUDI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN IPA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS JEMBER TAHUN 2012 KATA PENGANTAR Puji
GEOMETRI ANALITIK RUANG Dr. Susanto, MPd PROGRAM STUDI PENDIDIKAN MATEMATIKA JURUSAN PENDIDIKAN MATEMATIKA DAN IPA FAKULTAS KEGURUAN DAN ILMU PENDIDIKAN UNIVERSITAS JEMBER TAHUN 2012 KATA PENGANTAR Puji
BAB II KAJIAN PUSTAKA. glide/refleksi geser, grup simetri, frieze group, graphical user interface (GUI) dijelaskan mengenai operasi biner.
 BAB II KAJIAN PUSTAKA Secara umum, pada bab ini membahas mengenai kajian teori yang digunakan dalam penelitian yaitu, grup, transformasi, translasi, refleksi, rotasi, glide/refleksi geser, grup simetri,
BAB II KAJIAN PUSTAKA Secara umum, pada bab ini membahas mengenai kajian teori yang digunakan dalam penelitian yaitu, grup, transformasi, translasi, refleksi, rotasi, glide/refleksi geser, grup simetri,
Hubungan Kekongruenan Dalam Geometri Terhingga
 Prosiding Semirata FMIPA Universitas Lampung, 2013 Hubungan Kekongruenan Dalam Geometri Terhingga Lina Ardila Sari, Suharsono, Muslim Ansori Jurusan Matematika FMIPA Universitas Lampung Alamat Email :
Prosiding Semirata FMIPA Universitas Lampung, 2013 Hubungan Kekongruenan Dalam Geometri Terhingga Lina Ardila Sari, Suharsono, Muslim Ansori Jurusan Matematika FMIPA Universitas Lampung Alamat Email :
PENYELESAIAN SISTEM PERSAMAAN LINIER KOMPLEKS MENGGUNAKAN METODE ITERASI GAUSS-SEIDEL TUGAS AKHIR
 PENYELESAIAN SISTEM PERSAMAAN LINIER KOMPLEKS MENGGUNAKAN METODE ITERASI GAUSS-SEIDEL TUGAS AKHIR Diajukan sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains pada Jurusan Matematika Oleh :
PENYELESAIAN SISTEM PERSAMAAN LINIER KOMPLEKS MENGGUNAKAN METODE ITERASI GAUSS-SEIDEL TUGAS AKHIR Diajukan sebagai Salah Satu Syarat untuk Memperoleh Gelar Sarjana Sains pada Jurusan Matematika Oleh :
BAB II KAJIAN PUSTAKA
 BAB II KAJIAN PUSTAKA Pada Bab II ini akan diuraikan berbagai konsep dasar yang digunakan pada bagian pembahasan. Pada bab II ini akan dibahas pengenalan Geometri Non- Euclid, Geometri Insidensi, Geometri
BAB II KAJIAN PUSTAKA Pada Bab II ini akan diuraikan berbagai konsep dasar yang digunakan pada bagian pembahasan. Pada bab II ini akan dibahas pengenalan Geometri Non- Euclid, Geometri Insidensi, Geometri
TUGAS GEOMETRI TRANSFORMASI GRUP
 TUGAS GEOMETRI TRANSFORMASI GRUP KELOMPOK 8 1. I WAYAN AGUS PUTRAWAN (2008.V.1.0093) 2. I KADEK DWIJAYAPUTRA (2008.V.1.0094) 3. I KETUT DIARTA (2008.V.1.0123) 4. AGUS EKA SURYA KENCANA (2008.V.1.0043)
TUGAS GEOMETRI TRANSFORMASI GRUP KELOMPOK 8 1. I WAYAN AGUS PUTRAWAN (2008.V.1.0093) 2. I KADEK DWIJAYAPUTRA (2008.V.1.0094) 3. I KETUT DIARTA (2008.V.1.0123) 4. AGUS EKA SURYA KENCANA (2008.V.1.0043)
DAFTAR ISI. HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN...
 DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
DAFTAR ISI HALAMAN JUDUL... i HALAMAN PERSETUJUAN... II HALAMAN PENGESAHAN... III KATA PENGANTAR... IV DAFTAR ISI... V BAB I PENDAHULUAN... 1 A. LATAR BELAKANG MASALAH... 1 B. PEMBATASAN MASALAH... 2 C.
FUNGSI KOMPOSISI DAN FUNGSI INVERS
 FUNGSI KOMPOSISI DAN FUNGSI INVERS Jika A dan B adalah dua himpunan yang tidak kosong, fungsi f dari A ke B; f : A B atau A f B adalah cara pengawanan anggota A dengan anggota B yang memenuhi aturan setiap
FUNGSI KOMPOSISI DAN FUNGSI INVERS Jika A dan B adalah dua himpunan yang tidak kosong, fungsi f dari A ke B; f : A B atau A f B adalah cara pengawanan anggota A dengan anggota B yang memenuhi aturan setiap
STANDAR KOMPETENSI. 5. Menggunakan konsep matriks, vektor, dan transformasi dalam pemecahan masalah KOMPETENSI DASAR
 STANDAR KOMPETENSI 5. Menggunakan konsep matriks, vektor, dan transformasi dalam pemecahan masalah KOMPETENSI DASAR 5.1 Menggunakan sifat-sifat dan operasi matriks untuk menunjukkan bahwa suatu matriks
STANDAR KOMPETENSI 5. Menggunakan konsep matriks, vektor, dan transformasi dalam pemecahan masalah KOMPETENSI DASAR 5.1 Menggunakan sifat-sifat dan operasi matriks untuk menunjukkan bahwa suatu matriks
RUAS GARIS BERARAH. Andaikan sekarang ada 2 ruas garis berarah AB dan CD. Dalam
 RUAS GARIS BERARAH 9.1 Definisi dan Sifat-sifat ang Sederhana Untuk melajutkan penelidikan tentang isometri diperlukan pengertian tentang ruas garis berarah sebagai berikut: Definisi: Suatu ruas garis
RUAS GARIS BERARAH 9.1 Definisi dan Sifat-sifat ang Sederhana Untuk melajutkan penelidikan tentang isometri diperlukan pengertian tentang ruas garis berarah sebagai berikut: Definisi: Suatu ruas garis
APLIKASI GRUP KRISTALOGRAFI UNTUK PEMBENTUKAN MOTIF BATIK YANG DIIMPLEMENTASIKAN DENGAN GRAPHICAL USER INTERFACE (GUI) TUGAS AKHIR SKRIPSI
 APLIKASI GRUP KRISTALOGRAFI UNTUK PEMBENTUKAN MOTIF BATIK YANG DIIMPLEMENTASIKAN DENGAN GRAPHICAL USER INTERFACE (GUI) TUGAS AKHIR SKRIPSI Diajukan Kepada Fakultas Matematika dan Ilmu Pengetahuan Alam
APLIKASI GRUP KRISTALOGRAFI UNTUK PEMBENTUKAN MOTIF BATIK YANG DIIMPLEMENTASIKAN DENGAN GRAPHICAL USER INTERFACE (GUI) TUGAS AKHIR SKRIPSI Diajukan Kepada Fakultas Matematika dan Ilmu Pengetahuan Alam
PENERAPAN GEOMETRI TRANSFORMASI PADA MOTIF BATIK LAMPUNG
 PENERAPAN GEOMETRI TRANSFORMASI PADA MOTIF BATIK LAMPUNG Abi Fadila STKIP Muhammadiya Pringsewu Jl. Makam KH. Ghalib No.112 Telp. (0729)24002 Pringsewu Lampung 35373 E-mail: fadilaabi@gmail.com Abstrak
PENERAPAN GEOMETRI TRANSFORMASI PADA MOTIF BATIK LAMPUNG Abi Fadila STKIP Muhammadiya Pringsewu Jl. Makam KH. Ghalib No.112 Telp. (0729)24002 Pringsewu Lampung 35373 E-mail: fadilaabi@gmail.com Abstrak
Tentang. Isometri dan Refleksi
 TUGS II GEOMETRI TRNSFORMSI Tentang Isometri dan Refleksi Oleh : EVI MEG PUTRI : 42. 35I Dosen Pembimbing : NDI SUSNTO S. Si M.Sc TDRIS MTEMTIK FKULTS TRBIYH INSTITUT GM ISLM NEGERI (IIN) IMM BONJOLPDNG
TUGS II GEOMETRI TRNSFORMSI Tentang Isometri dan Refleksi Oleh : EVI MEG PUTRI : 42. 35I Dosen Pembimbing : NDI SUSNTO S. Si M.Sc TDRIS MTEMTIK FKULTS TRBIYH INSTITUT GM ISLM NEGERI (IIN) IMM BONJOLPDNG
II. TINJAUAN PUSTAKA
 II. TINJAUAN PUSTAKA 2.1 Angin Angin adalah gerakan udara dari daerah yang bertekanan tinggi ke daerah yang bertekanan rendah. Kekuatan angin berlebihan dapat dikontrol menggunakan sistem manual atau otomatik.
II. TINJAUAN PUSTAKA 2.1 Angin Angin adalah gerakan udara dari daerah yang bertekanan tinggi ke daerah yang bertekanan rendah. Kekuatan angin berlebihan dapat dikontrol menggunakan sistem manual atau otomatik.
MATRIKS & TRANSFORMASI LINIER
 MATRIKS & TRANSFORMASI LINIER Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 082334051324 Daftar Referensi : 1. Kreyzig Erwin, Advance Engineering Mathematic, Edisi ke-7, John wiley,1993 2. Spiegel, Murray R, Advanced
MATRIKS & TRANSFORMASI LINIER Oleh : SRI ESTI TRISNO SAMI, ST, MMSI 082334051324 Daftar Referensi : 1. Kreyzig Erwin, Advance Engineering Mathematic, Edisi ke-7, John wiley,1993 2. Spiegel, Murray R, Advanced
WARP PADA SEBUAH SEGITIGA
 Jurnal Matematika UNAND Vol. 3 No. 3 Hal. 26 33 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND WARP PADA SEBUAH SEGITIGA ABDUL ZAKY, MAHDHIVAN SYAFWAN Program Studi Matematika, Fakultas Matematika dan
Jurnal Matematika UNAND Vol. 3 No. 3 Hal. 26 33 ISSN : 2303 2910 c Jurusan Matematika FMIPA UNAND WARP PADA SEBUAH SEGITIGA ABDUL ZAKY, MAHDHIVAN SYAFWAN Program Studi Matematika, Fakultas Matematika dan
FUNGSI KOMPLEKS TRANSFORMASI PANGKAT. Makalah Untuk Memenuhi Tugas Mata Kuliah Fungsi Kompleks. yang diampuh Oleh Ibu Indriati N.H.
 FUNGSI KOMPLEKS TRANSFORMASI PANGKAT Makalah Untuk Memenuhi Tugas Mata Kuliah Fungsi Kompleks yang diampuh Oleh Ibu Indriati N.H Kelompok 6:. Amalia Ananingtyas (309324753) 2. Pratiwi Dwi Warih S (3093247506)
FUNGSI KOMPLEKS TRANSFORMASI PANGKAT Makalah Untuk Memenuhi Tugas Mata Kuliah Fungsi Kompleks yang diampuh Oleh Ibu Indriati N.H Kelompok 6:. Amalia Ananingtyas (309324753) 2. Pratiwi Dwi Warih S (3093247506)
SURVEI POLA GRUP KRISTALOGRAFI BIDANG RAGAM BATIK TRADISIONAL
 JMA, VOL. 11, NO. 2, DESEMBER, 2012, -- 1 SURVEI POLA GRUP KRISTALOGRAFI BIDANG RAGAM BATIK TRADISIONAL A.D.GARNADI, S. GURITMAN, A. KUSNANTO, F. HANUM Departemen Matematika Fakultas Matematika dan Ilmu
JMA, VOL. 11, NO. 2, DESEMBER, 2012, -- 1 SURVEI POLA GRUP KRISTALOGRAFI BIDANG RAGAM BATIK TRADISIONAL A.D.GARNADI, S. GURITMAN, A. KUSNANTO, F. HANUM Departemen Matematika Fakultas Matematika dan Ilmu
SILABUS. Mengenal matriks persegi. Melakukan operasi aljabar atas dua matriks. Mengenal invers matriks persegi.
 SILABUS Nama Sekolah Mata Pelajaran Kelas / Program Semester : SMA NEGERI 2 LAHAT : MATEMATIKA : XII / IPA : GANJIL STANDAR KOMPETENSI: 3. Menggunakan konsep matriks, vektor, dan transformasi dalam pemecahan
SILABUS Nama Sekolah Mata Pelajaran Kelas / Program Semester : SMA NEGERI 2 LAHAT : MATEMATIKA : XII / IPA : GANJIL STANDAR KOMPETENSI: 3. Menggunakan konsep matriks, vektor, dan transformasi dalam pemecahan
TUGAS GEOMETRI TRANSFORMASI. Tentang. Isometri dan Sifat-sifat Isometri. Oleh : EVI MEGA PUTRI : I. Dosen Pembimbing :
 TUGAS GEOMETRI TRANSFORMASI Tentang Isometri dan Sifat-sifat Isometri Oleh : EVI MEGA PUTRI : 412. 35I Dosen Pembimbing : ANDI SUSANTO, S. Si, M.Sc TADRIS MATEMATIKA A FAKULTAS TARBIYAH INSTITUT AGAMA
TUGAS GEOMETRI TRANSFORMASI Tentang Isometri dan Sifat-sifat Isometri Oleh : EVI MEGA PUTRI : 412. 35I Dosen Pembimbing : ANDI SUSANTO, S. Si, M.Sc TADRIS MATEMATIKA A FAKULTAS TARBIYAH INSTITUT AGAMA
APLIKASI KRIPTOGRAFI HILL CIPHER DENGAN MATRIKS m n
 1 APLIKASI KRIPTOGRAFI HILL CIPHER DENGAN MATRIKS m n SKRIPSI Diajukan untuk Memenuhi Sebagian Syarat Mencapai Derajat Sarjana S-1 Oleh : LILIS DWI HENDRAWATI 0601060012 PROGRAM STUDI PENDIDIKAN MATEMATIKA
1 APLIKASI KRIPTOGRAFI HILL CIPHER DENGAN MATRIKS m n SKRIPSI Diajukan untuk Memenuhi Sebagian Syarat Mencapai Derajat Sarjana S-1 Oleh : LILIS DWI HENDRAWATI 0601060012 PROGRAM STUDI PENDIDIKAN MATEMATIKA
MATEMATIKA DASAR PENDIDIKAN BIOLOGI UPI 0LEH: UPI 0716
 MATEMATIKA DASAR PENDIDIKAN BIOLOGI UPI 0LEH: UPI 0716 N0 TOPIK FUNGSI 2.1 DEFINISI FUNGSI 2.2 DAERAH DEFINISI DAN DAERAH HASIL 2.3 JENIS-JENIS FUNGSI 2.4 OPERASI ALJABAR FUNGSI 2.5 FUNGSI GENAP, GANJIL,
MATEMATIKA DASAR PENDIDIKAN BIOLOGI UPI 0LEH: UPI 0716 N0 TOPIK FUNGSI 2.1 DEFINISI FUNGSI 2.2 DAERAH DEFINISI DAN DAERAH HASIL 2.3 JENIS-JENIS FUNGSI 2.4 OPERASI ALJABAR FUNGSI 2.5 FUNGSI GENAP, GANJIL,
TRANSFORMASI BILINEAR
 TRANSFORMASI BILINEAR Di susun untuk memenuhi tugas matakuliah Fungsi Kompleks yang dibimbing oleh Ibu Indriati Nurul H. KELOMPOK 7 Anggota: Maharani Kusuma Arumsari (40931413115) Andrie Kurniawan (40931417687)
TRANSFORMASI BILINEAR Di susun untuk memenuhi tugas matakuliah Fungsi Kompleks yang dibimbing oleh Ibu Indriati Nurul H. KELOMPOK 7 Anggota: Maharani Kusuma Arumsari (40931413115) Andrie Kurniawan (40931417687)
Vektor-Vektor. Ruang Berdimensi-2. Ruang Berdimensi-3
 Vektor-Vektor dalam Ruang Berdimensi-2 dan Ruang Berdimensi-3 Disusun oleh: Achmad Fachrurozi Albert Martin Sulistio Iffatul Mardhiyah Rifki Kosasih Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan
Vektor-Vektor dalam Ruang Berdimensi-2 dan Ruang Berdimensi-3 Disusun oleh: Achmad Fachrurozi Albert Martin Sulistio Iffatul Mardhiyah Rifki Kosasih Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan
APLIKASI MATRIKS DALAM GEOMETRI
 APLIKASI MATRIKS DALAM GEOMETRI Diajukan untuk memenuhi salah satu tugas mata Kuliah Dosen Pembina: Drs. Darwing Paduppai, M.Pd O l e h: KELOMPOK VI Kelas A ANDI RUSDI 06507010 Hj. KHADIJAH 06507003 BAMBANG
APLIKASI MATRIKS DALAM GEOMETRI Diajukan untuk memenuhi salah satu tugas mata Kuliah Dosen Pembina: Drs. Darwing Paduppai, M.Pd O l e h: KELOMPOK VI Kelas A ANDI RUSDI 06507010 Hj. KHADIJAH 06507003 BAMBANG
Geometri Dimensi Dua
 Geometri Dimensi Dua Materi Pelatihan Guru SMK Model Seni/Pariwisata/Bisnis Manajemen Yogyakarta, 28 November 23 Desember 2010 Oleh Dr. Ali Mahmudi JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN
Geometri Dimensi Dua Materi Pelatihan Guru SMK Model Seni/Pariwisata/Bisnis Manajemen Yogyakarta, 28 November 23 Desember 2010 Oleh Dr. Ali Mahmudi JURUSAN PENDIDIKAN MATEMATIKA FAKULTAS MATEMATIKA DAN
GEOMETRI. Transformasi & Analitik Ruang UNIVERSITAS HASANUDDIN. M Saleh AF. Geometri Transformasi Dan Analitik Ruang LKPP.
 GEOMETRI Transformasi & Analitik Ruang D M M Refleksi M Saleh AF LKPP UNIVERSITAS HASANUDDIN BAB II TRANSFORMASI GEOMETRI DI A. Pendahuluan Salam hangat dan sejahtera bagi para pembelajar Kreatif! Bab
GEOMETRI Transformasi & Analitik Ruang D M M Refleksi M Saleh AF LKPP UNIVERSITAS HASANUDDIN BAB II TRANSFORMASI GEOMETRI DI A. Pendahuluan Salam hangat dan sejahtera bagi para pembelajar Kreatif! Bab
IKIP BUDI UTOMO MALANG. Analytic Geometry TEXT BOOK. Alfiani Athma Putri Rosyadi, M.Pd
 IKIP BUDI UTOMO MALANG Analytic Geometry TEXT BOOK Alfiani Athma Putri Rosyadi, M.Pd 2012 DAFTAR ISI 1 VEKTOR 1.1 Vektor Pada Bidang... 4 1.2 Vektor Pada Ruang... 6 1.3 Operasi Vektor.. 8 1.4 Perkalian
IKIP BUDI UTOMO MALANG Analytic Geometry TEXT BOOK Alfiani Athma Putri Rosyadi, M.Pd 2012 DAFTAR ISI 1 VEKTOR 1.1 Vektor Pada Bidang... 4 1.2 Vektor Pada Ruang... 6 1.3 Operasi Vektor.. 8 1.4 Perkalian
KAJIAN TEORI PENYELESAIAN MASALAH JARAK DAN SUDUT PADA BANGUN RUANG DIMENSI TIGA MENGGUNAKAN PENDEKATAN VEKTOR
 KAJIAN TEORI PENYELESAIAN MASALAH JARAK DAN SUDUT PADA BANGUN RUANG DIMENSI TIGA MENGGUNAKAN PENDEKATAN VEKTOR Andi Pujo Rahadi FKIP Universitas Advent Indonesia Abstrak Materi utama dalam bab Geometri
KAJIAN TEORI PENYELESAIAN MASALAH JARAK DAN SUDUT PADA BANGUN RUANG DIMENSI TIGA MENGGUNAKAN PENDEKATAN VEKTOR Andi Pujo Rahadi FKIP Universitas Advent Indonesia Abstrak Materi utama dalam bab Geometri
GEOMETRI AFFINE A. PENDAHULUAN
 1 GEOMETRI FFINE. PENDHULUN Euclides telah mengumpulkan materinya dari beberapa sumber, maka tidak mengherankan bahwa geometri Euclides dapat diambil sarinya berupa dua geometri yang berlainan dalam dasar
1 GEOMETRI FFINE. PENDHULUN Euclides telah mengumpulkan materinya dari beberapa sumber, maka tidak mengherankan bahwa geometri Euclides dapat diambil sarinya berupa dua geometri yang berlainan dalam dasar
VEKTOR. Gambar 1.1 Gambar 1.2 Gambar 1.3. Liduina Asih Primandari, S.Si., M.Si.
 VEKTOR 1 A. Definisi vektor Beberapa besaran Fisika dapat dinyatakan dengan sebuah bilangan dan sebuah satuan untuk menyatakan nilai besaran tersebut. Misal, massa, waktu, suhu, dan lain lain. Namun, ada
VEKTOR 1 A. Definisi vektor Beberapa besaran Fisika dapat dinyatakan dengan sebuah bilangan dan sebuah satuan untuk menyatakan nilai besaran tersebut. Misal, massa, waktu, suhu, dan lain lain. Namun, ada
Silabus. 1 Sistem Bilangan Real. 2 Fungsi Real. 3 Limit dan Kekontinuan. Kalkulus 1. Arrival Rince Putri. Sistem Bilangan Real.
 Silabus 1 2 3 Referensi E. J. Purcell, D. Varberg, and S. E. Rigdon, Kalkulus, Jilid 1 Edisi Kedelapan, Erlangga, 2003. Penilaian 1 Ujian Tengah Semester (UTS) : 30 2 Ujian Akhir Semester (UAS) : 20 3
Silabus 1 2 3 Referensi E. J. Purcell, D. Varberg, and S. E. Rigdon, Kalkulus, Jilid 1 Edisi Kedelapan, Erlangga, 2003. Penilaian 1 Ujian Tengah Semester (UTS) : 30 2 Ujian Akhir Semester (UAS) : 20 3
GLOSSARIUM. A Akar kuadrat
 A Akar kuadrat GLOSSARIUM Akar kuadrat adalah salah satu dari dua faktor yang sama dari suatu bilangan. Contoh: 9 = 3 karena 3 2 = 9 Anggota Himpunan Suatu objek dalam suatu himpunan B Belahketupat Bentuk
A Akar kuadrat GLOSSARIUM Akar kuadrat adalah salah satu dari dua faktor yang sama dari suatu bilangan. Contoh: 9 = 3 karena 3 2 = 9 Anggota Himpunan Suatu objek dalam suatu himpunan B Belahketupat Bentuk
IKIP BUDI UTOMO MALANG GEOMETRI HAND OUT 2
 IKIP BUDI UTOMO MALANG GEOMETRI HAND OUT 2 ALFIANI ATHMA PUTRI ROSYADI, M.Pd 4/14/2012 KUMPULAN DEFINISI DAN AKSIOMA DALAM GEOMETRI Nama Definisi 2.1 Definisi 2.2 Definisi 2.3 Definisi 2.4 Definisi 2.5
IKIP BUDI UTOMO MALANG GEOMETRI HAND OUT 2 ALFIANI ATHMA PUTRI ROSYADI, M.Pd 4/14/2012 KUMPULAN DEFINISI DAN AKSIOMA DALAM GEOMETRI Nama Definisi 2.1 Definisi 2.2 Definisi 2.3 Definisi 2.4 Definisi 2.5
terlatih dalam konsistensi dan keteraturan pola pikir dan prilaku terampil dalam membuat konstruksi ilmiah maupun konstruksi geometri.
 Kata Pengantar Buku ini dirancang berdasarkan pengalaman penulis setelah mengajar matakuliah Geometri selama kurang lebih 23 tahun dan pengalaman menulis buku ajar matematika Dasar dan Logika Matematika.
Kata Pengantar Buku ini dirancang berdasarkan pengalaman penulis setelah mengajar matakuliah Geometri selama kurang lebih 23 tahun dan pengalaman menulis buku ajar matematika Dasar dan Logika Matematika.
MODUL MATEMATIKA SMA IPA Kelas 11
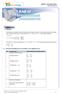 SMA IPA Kelas DEFINISI Transformasi merupakan pemetaan titik, garis atau bidang ke titik, garis atau bidang lain pada bidang yang sama. Misalkan transformasi T memetakan titik P (, y) ke titik P(, y) dan
SMA IPA Kelas DEFINISI Transformasi merupakan pemetaan titik, garis atau bidang ke titik, garis atau bidang lain pada bidang yang sama. Misalkan transformasi T memetakan titik P (, y) ke titik P(, y) dan
15. KOMPETENSI INTI DAN KOMPETENSI DASAR MATEMATIKA SMP/MTs
 15. KOMPETENSI INTI DAN MATEMATIKA SMP/MTs KELAS: VII Tujuan kurikulum mencakup empat kompetensi, yaitu (1) kompetensi sikap spiritual, (2) sikap sosial, (3) pengetahuan, dan (4) keterampilan. Kompetensi
15. KOMPETENSI INTI DAN MATEMATIKA SMP/MTs KELAS: VII Tujuan kurikulum mencakup empat kompetensi, yaitu (1) kompetensi sikap spiritual, (2) sikap sosial, (3) pengetahuan, dan (4) keterampilan. Kompetensi
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI A. Titik, Garis, dan Bidang Pada geometri, tepatnya pada sistem aksioma, terdapat istilah tak terdefinisi. Istilah tak terdefinisi adalah istilah dasar yang digunakan dalam membangun
BAB II LANDASAN TEORI A. Titik, Garis, dan Bidang Pada geometri, tepatnya pada sistem aksioma, terdapat istilah tak terdefinisi. Istilah tak terdefinisi adalah istilah dasar yang digunakan dalam membangun
SKRIPSI Untuk memenuhi sebagian persyaratan Guna mencapai derajat Sarjana S-1 Pendidikan Matematika. Diajukan oleh : NOVIANA RAHMAWATI A
 PENERAPAN MODEL PEMBELAJARAN INSTRUKSI LANGSUNG UNTUK MENINGKATKAN KEAKTIFAN BELAJAR MATEMATIKA (PTK bagi Siswa Kelas VIII Semester Genap di SMP IT Nur Hidayah Surakarta Tahun Ajaran 2010/2011) SKRIPSI
PENERAPAN MODEL PEMBELAJARAN INSTRUKSI LANGSUNG UNTUK MENINGKATKAN KEAKTIFAN BELAJAR MATEMATIKA (PTK bagi Siswa Kelas VIII Semester Genap di SMP IT Nur Hidayah Surakarta Tahun Ajaran 2010/2011) SKRIPSI
SIFAT-SIFAT TOPOLOGI RUANG LINEAR. Nila Kurniasih Program Studi Pendidikan Matematika Jalan KHA Dahlan 3 Purworejo. Abstrak
 SIFAT-SIFAT TOPOLOGI RUANG LINEAR Nila Kurniasih Program Studi Pendidikan Matematika Jalan KHA Dahlan 3 Purworejo Abstrak Penulisan ini bertujuan menyelidiki sifat-sifat yang berlaku di dalam topologi
SIFAT-SIFAT TOPOLOGI RUANG LINEAR Nila Kurniasih Program Studi Pendidikan Matematika Jalan KHA Dahlan 3 Purworejo Abstrak Penulisan ini bertujuan menyelidiki sifat-sifat yang berlaku di dalam topologi
Komposisi fungsi dan invers fungsi. Syarat agar suatu fungsi mempunyai invers. Grafik fungsi invers
 Komposisi fungsi dan invers fungsi mempelajari Fungsi komposisi menentukan Fungsi invers terdiri dari Syarat dan aturan fungsi yang dapat dikomposisikan Nilai fungsi komposisi dan pembentuknya Syarat agar
Komposisi fungsi dan invers fungsi mempelajari Fungsi komposisi menentukan Fungsi invers terdiri dari Syarat dan aturan fungsi yang dapat dikomposisikan Nilai fungsi komposisi dan pembentuknya Syarat agar
BAB III PEMBAHASAN. Pada bab pembahasan ini akan dibahas mengenai Geometri Hiperbolik yang
 BAB III PEMBAHASAN Pada bab pembahasan ini akan dibahas mengenai Geometri Hiperbolik yang didasarkan kepada enam postulat pada Geometri Netral dan Postulat Kesejajaran Hiperbolik. Akan dibahas sifat-sifat
BAB III PEMBAHASAN Pada bab pembahasan ini akan dibahas mengenai Geometri Hiperbolik yang didasarkan kepada enam postulat pada Geometri Netral dan Postulat Kesejajaran Hiperbolik. Akan dibahas sifat-sifat
2. Memahami dan mampu menyelesaikan Permasalahan yang berkaitan dengan vektor di Ruang Tiga, yaitu Persamaan Bidang
 TUJUAN EMBELAJARAN Agar pembaca memahami tentang Sistem Koordinat Kartesian beserta fungsinya yaitu titik, jarak dua titik, persamaan bola serta Vektor dalam ruang dimensi tiga beserta aplikasinya yaitu
TUJUAN EMBELAJARAN Agar pembaca memahami tentang Sistem Koordinat Kartesian beserta fungsinya yaitu titik, jarak dua titik, persamaan bola serta Vektor dalam ruang dimensi tiga beserta aplikasinya yaitu
PENERAPAN AKAD MUDHARABAH DALAM APLIKASI PRODUK SIMPANAN BERJANGKA (DEPOSITO) DI KSP GIRI MURIA GROUP CABANG DAWE KUDUS
 PENERAPAN AKAD MUDHARABAH DALAM APLIKASI PRODUK SIMPANAN BERJANGKA (DEPOSITO) DI KSP GIRI MURIA GROUP CABANG DAWE KUDUS TUGAS AKHIR Diajukan Untuk Memenuhi Tugas Akhir dan Melengkapi Syarat Guna Memperoleh
PENERAPAN AKAD MUDHARABAH DALAM APLIKASI PRODUK SIMPANAN BERJANGKA (DEPOSITO) DI KSP GIRI MURIA GROUP CABANG DAWE KUDUS TUGAS AKHIR Diajukan Untuk Memenuhi Tugas Akhir dan Melengkapi Syarat Guna Memperoleh
BESARAN VEKTOR. Gb. 1.1 Vektor dan vektor
 BAB 1 BESARAN VEKTOR Tujuan Pembelajaran 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahkan vektor secara grafis dan dengan vektor komponen 3. Melakukan
BAB 1 BESARAN VEKTOR Tujuan Pembelajaran 1. Menjelaskan definisi vektor, dan representasinya dalam sistem koordinat cartesius 2. Menjumlahkan vektor secara grafis dan dengan vektor komponen 3. Melakukan
TRANSFORMASI MOBIUS 1. Sangadji *
 Transformasi Mobius (Sangadji) TRANSFORMASI MOBIUS 1 Sangadji * ABSTRAK TRANSFORMASI MOBIUS. Transformasi Mobius atau bilinear, sudah lama dikenal. Topik ini muncul pada beberapa bidang, misalnya pada
Transformasi Mobius (Sangadji) TRANSFORMASI MOBIUS 1 Sangadji * ABSTRAK TRANSFORMASI MOBIUS. Transformasi Mobius atau bilinear, sudah lama dikenal. Topik ini muncul pada beberapa bidang, misalnya pada
BENTUK NORMAL JORDAN UNTUK MENENTUKAN INVERS MOORE PENROSE
 i BENTUK NORMAL JORDAN UNTUK MENENTUKAN INVERS MOORE PENROSE SKRIPSI Diajukan untuk Memenuhi sebagian Syarat untuk Memperoleh Gelar Sarjana Strata 1 (S1) Oleh Riyan Emmy Trihastuti 0901060006 PROGRAM STUDI
i BENTUK NORMAL JORDAN UNTUK MENENTUKAN INVERS MOORE PENROSE SKRIPSI Diajukan untuk Memenuhi sebagian Syarat untuk Memperoleh Gelar Sarjana Strata 1 (S1) Oleh Riyan Emmy Trihastuti 0901060006 PROGRAM STUDI
D. GEOMETRI 2. URAIAN MATERI
 D. GEOMETRI 1. TUJUAN Setelah mempelajari modul ini diharapkan peserta diklat memahami dan dapat menjelaskan unsur-unsur geometri, hubungan titik, garis dan bidang; sudut; melukis bangun geometri; segibanyak;
D. GEOMETRI 1. TUJUAN Setelah mempelajari modul ini diharapkan peserta diklat memahami dan dapat menjelaskan unsur-unsur geometri, hubungan titik, garis dan bidang; sudut; melukis bangun geometri; segibanyak;
FUNGTOR KOVARIAN PADA KATEGORI. Soleh Munawir dan Y.D. Sumanto
 FUNGTOR KOVARIAN PADA KATEGORI Soleh Munawir YD Sumanto Program Studi Matematika Jurusan Matematika Fakultas Sains Matematika Universitas Diponegoro Jalan Prof H Soedarto, SH Tembalang Semarang 50275 e-mail
FUNGTOR KOVARIAN PADA KATEGORI Soleh Munawir YD Sumanto Program Studi Matematika Jurusan Matematika Fakultas Sains Matematika Universitas Diponegoro Jalan Prof H Soedarto, SH Tembalang Semarang 50275 e-mail
ANALISIS REAL 1 SUMANANG MUHTAR GOZALI KBK ANALISIS
 ANALISIS REAL 1 SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta salam
ANALISIS REAL 1 SUMANANG MUHTAR GOZALI KBK ANALISIS UNIVERSITAS PENDIDIKAN INDONESIA BANDUNG 2010 2 KATA PENGANTAR Bismillahirrahmanirrahim Segala puji bagi Allah Rabb semesta alam. Shalawat serta salam
