BAB II DASAR TEORI II.1 Sistem referensi koordinat
|
|
|
- Yuliani Indradjaja
- 7 tahun lalu
- Tontonan:
Transkripsi
1 BAB II DASAR TEORI Pada bab II ini akan dibahas dasar teori mengenai sistem referensi koordinat, sistem koordinat dan proyeksi peta, yang terkait dengan masalah penentuan posisi geodetik. Selain itu akan dibahas juga mengenai algoritma penentuan posisi geodetik di sistem koordinat proyeksi dan sistem koordinat toposentrik. II. Sistem referensi koordinat Sistem referensi koordinat adalah sistem (termasuk teori, konsep, deskripsi fisis dan geometris, serta standar dan parameter) yang digunakan dalam pendefinisian koordinat dari suatu atau beberapa titik dalam ruang. Sistem referensi digunakan sebagai acuan untuk menyatakan nilai suatu titik [Abidin, 00]. Realisasi praktis dari sistem referensi adalah kerangka referensi. Kerangka referensi digunakan untuk pendeskripsian secara kuantitatif posisi dan pergerakan titik titik. Kerangka referensi biasanya direalisasikan dengan melakukan pengamatan-pengamatan geodetik, dan umumnya direpresentasikan dengan menggunakan suatu set koordinat dari sekumpulan titik maupun objek [Abidin, 00]. Berikut merupakan jenis-jenis sistem referensi yang biasa dipakai dalam pendeskripsian posisi :. CIS (Conventional Inertial System) ialah sistem referansi koordinat yang biasa digunakan untuk pendeskripsian posisi dan pergerakan satelit. Sifatnya geosentrik dan terikat langit.. CTS (Conventional Terestrial System) ialah sistem referansi koordinat yang biasa digunakan untuk menyatakan posisi di permukaan bumi. Sifatnya geosentrik dan terikat bumi. Salah satu realisasi dari CTS adalah WGS 84 (World Geodetic System 84). WGS 84 adalah sistem yang saat ini digunakan oleh sistem navigasi GPS. WGS 84 pada prinsipnya adalah sistem koordinat CTS yang didefinisikan, direalisasikan dan dipantau oleh NIMA (National Imaery and Mapping) Amerika Serikat. Berikut merupakan parameter WGS 84 : b = 3575,34; f = /98,57353; 5
2 e = 0, Dengan memanfaatkan teknologi GPS dalam melakukan penentuan posisi, maka secara tidak langsung posisi titik-titik yang ditentukan nilainya tersebut akan berada pada satu sistem referensi WGS 84. II. Sistem koordinat Sistem koordinat merupakan suatu sistem yang digunakan untuk merepresentasikan nilai suatu titik. Sistem koordinat didefinisikan dengan menspesifikasikan tiga parameter berikut [Abidin, 00].:. Lokasi titik nol dari sistem koordinat (Geosentrik atau Toposentrik). Orientasi dari sumbu-sumbu koordinat (Terikat ke bumi atau ke langit) 3. Besaran yang digunakan untuk menyatakan posisi suatu titik dalam sistem koordinat tersebut (Jarak atau sudut jarak) Berikutnya akan dijelaskan mengenai beberapa jenis sistem koordinat : II.. Sistem Koordinat Geodetik Sistem koordinat geodetik mengacu pada ellipsoid referensi tertentu yang dipakai untuk mendekati model permukaan bumi dimana nilainya bergantung pada ukuran, bentuk dan orientasi ellipsoid. Lokasi titik nol dari sistem koordinat geodetik berada pada pusat ellipsoid. Orientasi dari sumbu-sumbu koordinat geodetik terikat ke bumi. Posisi suatu titik dalam sistem koordinat geodetik dinyatakan dalam basaran sudut dan jarak, seperti yang di jelaskan sebagai berikut : ϕ (Lintang ) = sudut yang dibentuk oleh normal ellipsoid yang melalui titik tersebut dengan bidang ekuator, yang nilainya berkisar o o 90 ϕ 90. λ (Bujur) = sudut yang dibentuk antara meridian suatu titik, pusat ellipsoid dan meridian referensi (yaitu meridian yang melalui Greenwich), yang nilainya berkisar 0 o λ 80 o E dan 80 0 o o W λ. h (Tinggi) = tinggi suatu titik di atas ellipsoid(h) dihitung sepanjang normal ellipsoid yang melalui titik tersebut.
3 II.. Sistem Koordinat Geosentrik Serupa dengan sistem koordinat geodetik, posisi suatu titik dalam sistem koordinat geosentrik orientasi sumbu-sumbu koordinatnya terikat ke bumi. Lokasi titik nol dari sistem koordinat geosentrik berada pada pusat ellipsoid. Sistem koordinat geosentrik ditetapkan relatif terhadap tiga sumbu koordinat X,Y,Z dengan ketentuan sebagai berikut : Sumbu Z adalah garis dalam arah kutub menengah (Conventional International Origin). Sumbu X adalah arah perpotongan meridian Greenwich atau meridian nol CZM (Conventional Zero Meridian) yang ditetapkan oleh BIH (Berau International de l Heureu) dan bidang ekuator. Sumbu Y adalah garis pada bidang ekuator yang tegak lurus terhadap sumbu X dan Z yang sesuai dengan sistem tangan kanan. Besaran yang digunakan untuk menyatakan posisi suatu titik dalam sistem koordinat geosentrik adalah jarak (meter). Gambar.II. berikut ini menjelaskan hubungan antara sistem koordinat geosentrik dan geodetik : Gambar.II. Sistem koordinat geodetik dan geosentrik. [Kosasih Prijatna, 005]. Seperti yang ditunjukan pada gambar di atas, bahwa titik Q yang berada di permukaan bumi dapat direpresentasikan dalam sistem koordinat geodetik dan sistem koordinat geosentrik. Kedua sistem koordinat terebut, titik pusat sistem koordinatnya terletak pada pusat ellipsoid referensi, sehingga sistem koordinat geodetik dan geosentrik dapat dihubungkan antara satu dengan yang lain. Konversi koordinat geodetik ke koordinat geosentrik dapat dilakukan dengan menggunakan persamaan berikut ini [Seeber,993]: 7
4 X ( N + h) cos ϕ cos λ Y = ( N + h) cos ϕ sin λ Z (( e ) N + h) sin ϕ N = e a b = a Dimana : a e sin ϕ (.) N = Jari jari irisan normal a dan b = setengah sumbu panjang dan pendek ellipsoid e = eksentrisitas pertama Sedangkan konversi koordinat geosentrik ke geodetik, dapat dilakukan menggunakan berbagai macam cara, diantaranya metode Bowring sebagai berikut [Bowring,97] : p = h X θ = arctan ϕ = arctan λ = arctan + Y Za pb Z Y X p = N cos ϕ + e' b sin θ 3 p e a cos θ 3 (.) Dimana : ϕ,λ,h = Lintang, bujur dan tinggi geodetik X,Y,Z = Nilai koordinat geosentrik II..3 Sistem Koordinat Toposentrik Selain sistem koordinat geodetik dan geosentrik terdapat pula sistem koordinat toposentrik. Sistem koordinat toposentrik merupakan sistem koordinat yang bersifat lokal, dengan n (northing) mengacu ke utara geodetik, e (east), u (up) tegak lurus n dan titik nolnya mengacu pada garis gaya berat bumi. Seperti yang terlihat pada gambar.ii., dengan memanfaatkan data sudut jurusan (α ), sudut miring (m), dan jarak ruang (d), maka dapat dihitung nilai koordinat toposentrik menggunakan persamaan (.3). 8
5 z North Normal Ellipsoid Pemukaan bumi d m α East Pemukaan bumi h λ K ϕ K Ellipsoid meridian y x Gambar.II.. Sistem koordinat toposentrik Persamaan untuk menghitung koordinat toposentrik : n = d cos( m ) cos( α ) e = d cos( m ) sin( α ) (.3) u = d sin(m ) Konversi koordinat toposentrik ke koordinat geodetik dapat dilakukan menggunakan minimal dua koordinat toposentrik (misalnya: titik dan titik ). Konversi koordinat ini dilakukan dengan cara mengasumsikan salah satu kordinat toposentrik bernilai nol relatif terhadap salah satu koordinat geodetik yang diketahui nilainya. Dibawah ini akan dijelaskan mengenai tahapan konversi koordinat toposentrik ke koordinat geodetik :. Mencari delta koordinat geosentrik titik dan titik Δx Δy Δz n = R ( ϕ, λ ) e (.4) u Dimana : ( ϕ, λ ) Δx Delta Δy Δz sinϕ cosλ sinϕ sinλ cosϕ R = sin λ cosλ 0 (.5) cosϕ cosλ cosϕ sin λ sinϕ, digunakan untuk mencari nilai koordinat geosentrik titik.. Konversi koordinat geodetik titik ke koordinat geosentrik menggunakan persamaan (.) 9
6 3. Jumlahkan delta koordinat geosentrik titik dan titik dengan koordinat geosentrik titik. x y z Δx = Δy Δz x + y z (.) 3. Konversikan koordinat geosentrik titik dan titik ke koordinat geodetik menggunakan metode bowring pada persamaan (.) Konversi koordinat geodetik ke koordinat toposentrik juga dapat dilakukan dengan cara mengasumsikan salah satu koordinat geodetik berada relatif terhadap nol sistem koordinat toposentrik (misalnya : titik bernilai (0,0,0)). Konversi koordinat geodetik titik dan titik ke koordinat geosentrik menggunakan persamaan (.). Hitung delta koordinat geosentrik titik dan titik : Δx Δy Δz x = y z x - y z 3. Hitung koordinat toposentrik titik : n e u (.7) Δx = R ( ϕ, λ ) Δy (.8) Δz Dari penjelasan diatas, maka dapat dikatakan bahwa sistem koordinat geodetik dan toposentrik memiliki keterkaitan erat. Selain dapat dilakukan konversi koordinat satu sama lain, keterkaitan lainnya adalah n(north) pada sistem toposentrik mengacu pada utara geodetik dan u(up) yang tegak lurus n(north) titik nolnya mengacu pada garis gaya berat bumi, maka penentuan posisi geodetik yang dilakukan di sistem koordinat toposentrik pun dapat dilakukan dengan sederhana. II.3 Proyeksi peta Proyeksi peta merupakan model matematik untuk mengkonversi posisi tiga-dimensi suatu titik di permukaan bumi ke representasi posisi dua-dimensi di bidang peta (bidang datar) [Kosasih Prijatna,005].Gambar berikut ini merupakan ilustrasinya : 0
7 Pada meridian sentral, faktor skala = (tidak ada distorsi), perbesaran sepanjang meridian akan menjadi lebih besar bila meridian-meridian tersebut makin jauh ke Barat atau ke Timur dari meridian tengah. Perbesaran sepanjang paralel akan menjadi lebih besar jika lingkaran-lingkaran paralel tersebut mendekati ekuator. Dengan adanya distorsi yang makin membesar menjauhi meridian sentral, maka pada proyeksi TM diusahakan suatu cara untuk memperkecil distorsi tersebut, yaitu dengan cara membagi daerah- ϕ, λ,h konversi x, y Gambar.II.3. Konversi ke bidang datar [Kosasih Prijatna,005]. Dalam melakukan konversi posisi geodetik di permukaan bumi ke bidang proyeksi akan menghasilkan distorsi. Setiap model proyeksi peta mempunyai kelemahan dan kelebihan. Apabila satu atau dua jenis distorsi diminimalkan, maka distorsi lainnya akan membesar. Sehingga pemilihan model proyeksi peta disesuaikan dengan kebutuhan. Pemilihan model proyeksi peta biasanya didasarkan pada : Posisi daerah, bentuk dan ukuran daerah yang akan dipetakan. Kegunaan peta bersangkutan. Pekerjaan pemetaan untuk keperluan pembuatan peta dasar Indonesia saat ini menggunakan Transverse Mercator (TM). Proyeksi Transverse Mercator adalah proyeksi silinder transversal yang bersifat konform. Pada proyeksi ini secara geometris silindernya menyinggung bola bumi pada sebuah meridian yang disebut meridian sentral (meridian tengah). Gambar.II.4 Proyeksi Transverse Mercator [Kosasih Prijatna, 005].
8 daerah dalam zone-zone (daerah pada permukaan bumi yang dibatasi oleh dua buah meridian) yang sempit dan lebar zone yang lebih kecil. Untuk memperkecil distorsi pada bidang proyeksi TM maka digunakanlah sistem proyeksi UTM. Sistem proyeksi UTM sebenarnya merupakan bidang proyeksi TM yang dibagi tiap zonanya sebesar derajat, dengan ketentuan yang sifatnya universal. Sistem grid dan proyeksi ini dapat digunakan baik untuk pekerjaan pemetaan topografi, referensi untuk citra satelit dan aplikasi lainnya yang memerlukan ketelitian untuk penentuan posisi. Di Indonesia sistem proyeksi UTM digunakan oleh instansi Bakosurtanal, biasanya untuk keperluan pemetaan skala sedang. Selain sistem proyeksi UTM digunakan pula sistem proyeksi TM3. Serupa halnya dengan sistem proyeksi UTM, sistem proyeksi TM3 pun merupakan sistem proyeksi UTM yang dibagi tiap zonanya menjadi lebih kecil dari derajat menjadi 3 derajat setiap zonanya, sehingga distorsi yang dihasilkan akan semakin kecil. Di Indonesia sistem proyeksi TM3 digunakan oleh instansi BPN, biasanya untuk keperluan peta skala besar dalam pendaftaran tanah (penjelasan lebih lengkap mengenai sistem proyeksi terdapat pada Bab Lampiran). II.3. Penghitungan koordinat bidang proyeksi Penghitungan koordinat di bidang proyeksi, baik untuk proyeksi UTM ataupun TM3 dapat dilakukan dengan menggunakan rumus-rumus trigonometri di bidang datar sebagai berikut : x = x + y = y + d sinα d cosα Dimana : d = Jarak proyeksi α = Sudut jurusan di bidang proyeksi (.9) II.4 Model hitungan penentuan posisi geodetik di sistem koordinat proyeksi Penentuan posisi geodetik dua dimensi dapat dihitung dengan memanfaatkan sistem koordinat proyeksi sebagai bidang perantara hitungan. Berikut ini adalah algoritma hitungan koordinat geodetik di sistem koordinat proyeksi :
9 Koordinat geodetik min titik hasil pengamatan GPS Data sudut horizontal dan jarak ruang Konversi koordinat Reduksi ke bidang Proyeksi Koordinat proyeksi (D) Data di bidang Proyeksi Proses hitungan Koordinat Proyeksi (D) Konversi koordinat Koordinat Geodetik Gambar.II.5 Penghitungan koordinat keodetik di sistem koordinat proyeksi Dalam penelitian tugas akhir ini, digunakan sistem proyeksi UTM dan TM3 sebagai bidang perantara hitungan.untuk melakukan penghitungan koordinat geodetik di sistem koordinat proyeksi, langkah pertama yang dilakukan adalah terlebih dahulu melakukan reduksi data sudut horizontal dan jarak ruang hasil pengukuran terestris menggunakan Total Station di permukaan bumi ke bidang ellipsoid, kemudian data sudut horizontal dan jarak di bidang ellipsoid tersebut direduksi lagi ke bidang proyeksi. Lebih jauh mengenai proses reduksi, akan dijelaskan sebagai berikut : II.4. Reduksi data ukuran di permukaan bumi Proses reduksi data sudut horizontal dan jarak di permukaan bumi ke bidang proyeksi atau bidang datar dilakukan agar data tersebut dapat digunakan untuk melakukan penentuan posisi geodetik yang dihitung di sistem koordinat Proyeksi (sistem koordinat bidang datar).adapun prosedur reduksi data ukuran tersebut adalah sebagai berikut : Data, sudut horizontal dan jarak di permukaan bumi Reduksi ke Bidang Ellipsoid Reduksi ke Bidang Proyeksi Gambar.II. Proses reduksi data sudut horizontal dan jarak 3
10 II.4..a Reduksi sudut horizontal dan jarak di prmukaan bumi ke bidang Ellipsoid. Dalam melakukan reduksi sudut horizontal dan jarak dipermukaan bumi ke bidang ellipsoid, perlu dipertimbangkan efek geometrik dan gravimetrik. Adapun dua efek geometrik tersebut adalah skew normal correction dan irisan normal geodesik, sedangkan efek gravimetrik tersebut adalah koreksi efek defleksi vertikal. Berikut akan dibahas mengenai efek geometrik dan gravimetrik yang di perhitungkan dalam proses reduksi sudut horizontal dan jarak :. Komponen reduksi di bidang ellipsoid Efek Geometrik δh = Skew-Normal Correction Untuk posisi target bidik di atas ellipsoid, titik target dan proyeksinya di atas permukaan ellipsoid tidak terletak pada bidang normal yang sama apabila dilihat dari alat theodolit maka perlu dipertimbangkan skew normal correction. Berikut ini merupakan persamaan untuk mencari skew normal correction [Krakiwsky, 973] : h δh = ρ e sinα cosα cos ϕ M m (.0) M + M M m = Dimana : h = tinggi geodetik titik P α = asimut sisi P-P ρ = 80/pi*300 φ = lintang geodetik titik P Pemukaan bumi P P Pemukaan bumi P P δh ' α α Permukaan ellipsoid referensi s Garis normal di P P P Garis normal di P Sumbu putar ellipsoid referensi n Gambar.II.7 Skew-Normal correction n 4
11 M dan M masing-masing adalah radius lengkung meridian pada titik P dan P 0 Efek skew normal correction akan terlihat signifikan saat ϕ = 45 dan h = 00atau000,efek skew normal correction ( δ h" ) akan bernilai = 0,008 dan 0,05. δg = Koreksi Irisan Normal-Geodesik Saat melakukan pengukuran arah ke titik target seharusnya adalah arah garis geodesik, bukannya arah irisan normal, maka untuk melakukan reduksi ukuran yang berhubungan dengan sudut perlu dilakukan koreksi irisan normal geodesik. Berikut ini merupakan persamaan untuk mencari koreksi irisan normal geodesik [Krakiwsky, 973]: e s δg = ρ ϕ + ϕ ϕ m = N + N N m = cos ϕ m sin α N m (.) Dimana : α = asimut sisi P-P S = jarak di bidang ellipsoid ϕ m = lintang rata-rata titik dan P δ Normal to ellipsoid Geodesik Normal section P Δ δ Gambar.II.8 Normal geodesik N dan N masing-masing adalah radius lengkung vertikal utama pada titik P dan P Normal section akan terlihat signifikan saat δ h" = 0, α = 45 dan s = 00 km, 00 km dan 50 km, yaitu akan bernilai δg 0, 0,0 dan 0,00. 5
12 Efek Gravimetrik δθ = Koreksi Efek Defleksi Vertikal θ B id a n g P Terrain M e r id ia n Gambar.II.9 Koreksi efek defleksi vertikal Ketika mengukur sudut horizontal, sumbu vertikal Total Station harus berimpit dengan arah vektor gaya berat. Agar sudut horizontal mengacu pada ellipsoid referensi, maka sudut horizontal tersebut harus dikoreksi dengan efek defleksi vertikal. Berikut merupakan persamaan untuk mencari efek defleksi vertikal [Krakiwsky, 973]: : δθ = ( ξ sinα η cosα ) cot z (.) ξ,η = komponen defleksi vertikal di P z = sudut zenit dari titik P ke P 0 Defleksi vertikal akan terlihat signifikan saatθ = 0, bernilai -3. α ' α Plumbline P P Normal to ellipsoid Terrain Δh P 0 Z = 80, defleksi vertikal akan. Reduksi pada sudut horizontal dan jarak ke bidang elllipsoid Efek geometrik dan gravimetrik seperti yang dijelaskan diatas merupakan komponen yang perlu diperhitungkan dalam melakukan reduksi jarak dan sudut horizontal hasil ukuran di permukaan bumi. Berikut ini akan dibahas mengenai komponen-komponen reduksi yang diterapkan dalam upaya melakukan reduksi ukuran jarak dan sudut horizontal di permukaan bumi ke bidang ellipsoid : Reduksi Sudut Horizontal Pada ukuran sudut horizontal dilakukan koreksi defleksi vertikal, skew normal corection dan koreksi normal geodesik. Adapun proses koreksi tersebut dilakukan sebagai berikut : β β u u u 3 = α3 α u 3 = β3 + δh3 δh + δg3 δg + δθ3 δθ u β3 = sudut horisontal ( ) ( ) ( ) ukuran (.3)
13 Reduksi Jarak Ruang Reduksi jarak ruang d ke jarak dipermukaan ellipsoid S dapat dilakukan sebagai berikut : jika S S θ = =, maka jarak di bidang ellipsoid adalah : R h + R R S = (.4) d d R + h θ S R h Dimana : d = jarak di permukaan bumi h = tinggi di permukaan ellipsoid S = jarak di bidang ellipsoid R = radius Euler θ = sudut yang dibentuk jarak ke pusat ellipsoid Gambar.II.0 Reduksi jarak ruang II.4..b Reduksi sudut horizontal dan jarak di bidang Ellipsoid ke bidang Proyeksi Reduksi sudut horizontal dan jarak ke bidang proyeksi dilakukan setelah data sudut horizontal dan jarak telah direduksi ke bidang ellipsoid. Berikut ini merupakan proses reduksi yang akan dilakukan :. Reduksi Sudut horizontal di Bidang Ellipsoid ke Bidang Proyeksi Y Jika a 3 merupakan sudut horizontal ukuran, t T (T-t) sementara ( T t) merupakan perbedaan antara grid azimuth proyeksi jarak geodesik T dan grid azimuth garis singgung jarak geodesik t, lalu serupa halnya a3 a*3 (T-t)3 Gambar.II. Reduksi pada sudut horizontal 3 X dengan ( T t) 3, maka dapat dirumuskan : a (.5) 3 = a 3 + ( T t) + ( T t) 3 Yang merupakan persamaan untuk melakukan reduksi sudut horizontal ellipsoid ke bidang proyeksi. Berikut ini merupakan persamaan matematis untuk mencari koreksi T minus t Proyeksi TM,UTM dan TM3 [Krakiwsky, 973] : 7
14 Sudut antara proyeksi Geodesik dengan tali busur (TM) : ( y y)(x + x ) ( y y)( x ( T t) = (.a); ( T t) = R m R m R m = MN Sedangkan ntuk UTM dan TM3: + x ) (.b) ( T t) ( y = y )(x Rm k 0 + x ) (.c); ( T t) Rmk0 UTM : k0= ; TM30: k0= ; ( y = y )( x + x ) (.d). Reduksi Jarak Bidang Ellipsoid ke Bidang Proyeksi Karena bidang ellipsoid berbeda dengan bidang proyeksi maka jarak di bidang ellipsoid (jarak geodesik) juga memiliki panjang yang berbeda dengan jarak proyeksi. Berikut ini merupakan persamaan yang digunakan untuk mereduksi jarak geodesik ke jarak proyeksi. [Krakiwsky, 973] : Y d m = S (.7) d S X Gambar.II. Reduksi pada jarak Dimana : m = faktor skala garis; d = jarak di proyeksi; S = jarak geodesik; dalam hal ini m adalah faktor skala garis, berikut persamaannya : d 4 m = ( ( + + )) S k k k3 (.8) k = masing masing adalah faktor skala titik, yang dihitung menggunakan, k, k3 persamaan berikut : cos ϕ k i = k0 ( + Δλ...) (.9) Dimana : Δλ = λ Dapat diartikan bahwa, faktor skala titik merupakan perbandingan perbedaan jarak di peta dengan perbedaan jarak di elipsoid, sedangkan faktor skala garis adalah fungsi dari tiga faktor skala titik, titik di awal, di tengah, dan di akhir garis. Dengan kata lain faktor λ 0 8
15 skala garis adalah rata-rata skala garis yang digunakan untuk melihat perbedaan atara panjang garis geodesik dengan panjang garis proyeksi geodesik. II.4. Penghitungan koordinat geodetik Setelah proses reduksi dilakukan pada sudut horizontal dan jarak, maka sudut horizontal dan jarak tersebut kini telah berada pada bidang proyeksi/datar, sehingga penghitungan koordinat di bidang proyeksi/datar dapat dilakukan. Sebelum dilakukan penghitungan koordinat, langkah pertama yang dilakukan adalah melakukan konversi koordinat geodetik minimal dua titik hasil pengamatan GPS ke dalam sistem koordinat proyeksi UTM dan TM3. Sistem proyeksi UTM dan sebenarnya merupakan sistem proyeksi TM yang dibagi menjadi zona-zona kecil. Proses konversi koordinat ini dapat dilakukan dengan cara mengkonversikan koordinat geodetik ke sistem koordinat TM terlebih dahulu, kemudian selanjutnya dapat diketahui dalam sistem koordinat UTM dan TM3 dengan mendefinisikan meridian sentral, faktor perbesaran dan koordinat semu masingmasing sistem proyeksi. Konversi koordinat ini dapat dilakukan menggunakan persamaan berikut [Krakiwsky, 973]: Konversi Koordinat Geodetik ke Koordinat Proyeksi TM 3 3 Δλ cos ϕ x = N ( Δλ cosϕ + ( t + η ) + 5 Δ cos 5 λ ϕ (5 8t + t 4η 58t η + 3η + 4η 4η t 4η t ) cos 7 Δλ ϕ 4 ( 479t + 79t t ) f ( q) Δλ Δλ 3 4 y = N ( + sinϕ cosϕ + sinϕ cos ϕ(5 t + 9η + 4η ) + N 4 λ sinϕ cosϕ ( 58t + t + 70η 330t η + 445η + 34η 80η t Δλ η t 9η t ) + sinϕ cos ϕ(385 3t + 543t t )) 4030 dimana : Δ 8 f ( q) = ϕ 0 Mdϕ t = tanϕ + 88η (.0) Setelah dilakukan konversi koordinat geodetik ke koordinat proyeksi UTM dan TM3, selanjutnya dapat ditentukan sudut jurusan masing-masing dari minimal dua titik hasil pengamatan GPS menggunakan persamaan berikut : 9
16 Δx α = tan ( ) (.) Δy Untuk mendapatkan sudut jurusan titik-titik lainnya, dapat dilakukan penghitungan cara geometris menggunakan sudut horizontal yang telah direduksi ke bidang proyeksi. Setelah didapat sudut jurusan di semua titik yang akan ditentukan nilai koordinatnya, selanjutnya dilakukan penghitungan koordinat proyeksi UTM dan TM3 menggunakan rumus-rumus trigonometri di bidang datar seperti pada persamaan (.9). Untuk mendapatkan koordinat geodetik sebagai hasil akhir, selanjutnya dilakukan konversi koordinat proyeksi UTM dan TM3 hasil hitungan diatas ke dalam sistem koordinat geodetik. Konversi koordinat proyeksi UTM dan TM3 ke koordinat geodetik juga dilakukan dengan menggunakan sistem proyeksi TM sebagai bidang perantara. Berikut ini merupakan persaamaan matematis yang dapat digunakan untuk melakukan konversi koordinat proyeksi TM ke koordinat geodetik [Krakiwsky, 973]: Konversi Koordinat Proyeksi TM ke Koordinat Geodetik x x 3 Δ λ = secϕ ( ( ) ( + t + η ) + N N x ( ) (5 + η t η tη t η tη tη ) 0 N x 7 4 ( ) (+ t t + t ) 5040 N 4 tx tx 4 ϕ = ϕ + (5 + 3t + η 4η 9η t ) 3 M N 4M N tx ( 90t + 4η + 45t 5tη 3η + 00η tη 90tη M N tx 4 88η + 5t η + 84tη 9tη ) + ( t t + 575t M N (.) dimana : ϕ = lintang kaki (foot point), yang dihitung secara iteratif menggunkan Metode Newton- Rapshon. Penjelasan lebih rinci dapat dilihat di Krakiwsky(973). ) 0
17 II.5 Model hitungan penentuan posisi di sistem koordinat toposentrik Selain di sistem koordinat proyeksi, penentuan koordinat geodetik dengan memanfaatkan data kombinasi metode GPS dn Total Station juga dapat dilakukan di sistem koordinat toposentrik..gambar.iii.0 di berikut merupakan algoritma penghitungan koordinat geodetik di sistem koordinat toposentrik : Koordinat geodetik min titik hasil pengamatan GPS Konversi koordinat Koordinat toposentrik Data sudut miring, sudut horizontal dan jarak ruang Proses hitungan Koordinat Toposentrik Konversi koordinat Koordinat Geodetik Gambar.II.3 Penghitungan koordinat geodetik di sistem koordinat toposentrik Penentuan koordinat geodetik di sistem koordinat toposentrik dapat dilakukan dengan mengkombinasikan data hasil pengamatan GPS untuk mendapatkan minimal dua koordinat awal sebagai acuan dan data hasil pengukuran terestris menggunakan instrument Total Station untuk mendapatkan data jarak, sudut horizontal dan sudut vertikal. Langkah pertama yang dilakukan adalah melakukan konversi koordinat geodetik hasil pengukuran menggunakan GPS ke dalam sistem koordinat toposentrik. Konversi koordinat geodetik ke koordinat toposentrik dilakukan dengan cara mengasumsikan salah
18 satu koordinat geodetik berada relatif terhadap nol sistem koordinat toposentrik (misalnya : titik bernilai (0,0,0) dan titik (n,e,u)). Berikut ini tahapan konversi koordinat geodetik ke koordinat toposentrik :. Konversi koordinat geodetik titik dan titik ke koordinat geosentrik menggunakan persamaan (.). Hitung delta geosentrik titik dan titik menggunakan persamaan (.7) : 3. Menghitung koordinat toposentrik titik dua menggunakan persamaan (.8) : Setelah dilakukan konversi koordinat, selanjutnya koordinat toposentrik tersebut dapat digunakan untuk mencari sudut jurusan sebagai berikut : e α = tan ( ) (.3) n Untuk mendapatkan sudut jurusan titik-titik lainnya, dapat dilakukan penghitungan cara geometris menggunakan sudut horizontal hasil pengukuran Total Station. Lalu penghitungan koordinat toposentrik dapat dilakukan dengan mengkombinasikan data sudut jurusan (α ) dengan data sudut horizontal, sudut miring dan jarak hasil pengukuran terestris menggunakan instrumen Total Station, adapun penghitungannya dapat dilakukan dengan menggunakan persamaan (.3). Setelah dilakukan penghitungan, selanjutnya koordinat toposentrik tersebut dikonversi ke dalam sistem koordinat geodetik. Konversi koordinat toposentrik ke sistem koordinat geodetik dapat dilakukan dengan berbagai macam cara, salah satunya adalah menggunakan metode Bowring seperti pada persamaan (.).
Bab II TEORI DASAR. Suatu batas daerah dikatakan jelas dan tegas jika memenuhi kriteria sebagai berikut:
 Bab II TEORI DASAR 2.1 Batas Daerah A. Konsep Batas Daerah batas daerah adalah garis pemisah wilayah penyelenggaraan kewenangan suatu daerah dengan daerah lain. Batas daerah administrasi adalah wilayah
Bab II TEORI DASAR 2.1 Batas Daerah A. Konsep Batas Daerah batas daerah adalah garis pemisah wilayah penyelenggaraan kewenangan suatu daerah dengan daerah lain. Batas daerah administrasi adalah wilayah
SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521
 SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 Sistem Koordinat Parameter SistemKoordinat Koordinat Kartesian Koordinat Polar Sistem Koordinat Geosentrik Sistem Koordinat Toposentrik Sistem Koordinat
SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 Sistem Koordinat Parameter SistemKoordinat Koordinat Kartesian Koordinat Polar Sistem Koordinat Geosentrik Sistem Koordinat Toposentrik Sistem Koordinat
DAFTAR PUSTAKA. 1. Abidin, Hasanuddin Z.(2001). Geodesi satelit. Jakarta : Pradnya Paramita.
 DAFTAR PUSTAKA 1. Abidin, Hasanuddin Z.(2001). Geodesi satelit. Jakarta : Pradnya Paramita. 2. Abidin, Hasanuddin Z.(2002). Survey Dengan GPS. Cetakan Kedua. Jakarta : Pradnya Paramita. 3. Krakiwsky, E.J.
DAFTAR PUSTAKA 1. Abidin, Hasanuddin Z.(2001). Geodesi satelit. Jakarta : Pradnya Paramita. 2. Abidin, Hasanuddin Z.(2002). Survey Dengan GPS. Cetakan Kedua. Jakarta : Pradnya Paramita. 3. Krakiwsky, E.J.
SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521
 SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 Sistem Koordinat Parameter SistemKoordinat Koordinat Kartesian Koordinat Polar Sistem Koordinat
SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 SISTEM KOORDINAT SISTEM TRANSFORMASI KOORDINAT RG091521 Sistem Koordinat Parameter SistemKoordinat Koordinat Kartesian Koordinat Polar Sistem Koordinat
By. Y. Morsa Said RAMBE
 By. Y. Morsa Said RAMBE Sistem Koordinat Sistem koordinat adalah sekumpulan aturan yang menentukan bagaimana koordinatkoordinat yang bersangkutan merepresentasikan titik-titik. Jenis sistem koordinat:
By. Y. Morsa Said RAMBE Sistem Koordinat Sistem koordinat adalah sekumpulan aturan yang menentukan bagaimana koordinatkoordinat yang bersangkutan merepresentasikan titik-titik. Jenis sistem koordinat:
BAB IV ANALISIS PENELITIAN
 BAB IV ANALISIS PENELITIAN Pada bab IV ini akan dibahas mengenai analisis pelaksanaan penelitian sarta hasil yang diperoleh dari pelaksanaan penelitian yang dilakukan pada bab III. Analisis dilakukan terhadap
BAB IV ANALISIS PENELITIAN Pada bab IV ini akan dibahas mengenai analisis pelaksanaan penelitian sarta hasil yang diperoleh dari pelaksanaan penelitian yang dilakukan pada bab III. Analisis dilakukan terhadap
Materi : Bab IV. PROYEKSI PETA Pengajar : Ira Mutiara A, ST
 PENDIDIKAN DAN PELATIHAN (DIKLAT) TEKNIS PENGUKURAN DAN PEMETAAN KOTA Surabaya, 9 24 Agustus 2004 Materi : Bab IV. PROYEKSI PETA Pengajar : Ira Mutiara A, ST FAKULTAS TEKNIK SIPIL DAN PERENCANAAN INSTITUT
PENDIDIKAN DAN PELATIHAN (DIKLAT) TEKNIS PENGUKURAN DAN PEMETAAN KOTA Surabaya, 9 24 Agustus 2004 Materi : Bab IV. PROYEKSI PETA Pengajar : Ira Mutiara A, ST FAKULTAS TEKNIK SIPIL DAN PERENCANAAN INSTITUT
Mengapa proyeksi di Indonesia menggunakan WGS 84?
 Nama : Muhamad Aidil Fitriyadi NPM : 150210070005 Mengapa proyeksi di Indonesia menggunakan WGS 84? Jenis proyeksi yang sering di gunakan di Indonesia adalah WGS-84 (World Geodetic System) dan UTM (Universal
Nama : Muhamad Aidil Fitriyadi NPM : 150210070005 Mengapa proyeksi di Indonesia menggunakan WGS 84? Jenis proyeksi yang sering di gunakan di Indonesia adalah WGS-84 (World Geodetic System) dan UTM (Universal
BAB III PELAKSANAAN PENELITIAN
 BAB III PELAKSANAAN PENELITIAN Pada BAB III ini akan dibahas mengenai pengukuran kombinasi metode GPS dan Total Station beserta data yang dihasilkan dari pengukuran GPS dan pengukuran Total Station pada
BAB III PELAKSANAAN PENELITIAN Pada BAB III ini akan dibahas mengenai pengukuran kombinasi metode GPS dan Total Station beserta data yang dihasilkan dari pengukuran GPS dan pengukuran Total Station pada
Modul 13. Proyeksi Peta MODUL KULIAH ILMU UKUR TANAH JURUSAN TEKNIK SIPIL POLIBAN. Modul Pengertian Proyeksi Peta
 MODUL KULIAH Modul 13-1 Modul 13 Proyeksi Peta 13.1 Pengertian Proyeksi Peta Persoalan ditemui dalam upaya menggambarkan garis yang nampak lurus pada muka lengkungan bumi ke bidang datar peta. Bila cakupan
MODUL KULIAH Modul 13-1 Modul 13 Proyeksi Peta 13.1 Pengertian Proyeksi Peta Persoalan ditemui dalam upaya menggambarkan garis yang nampak lurus pada muka lengkungan bumi ke bidang datar peta. Bila cakupan
BENTUK BUMI DAN BIDANG REFERENSI
 BENTUK BUMI DAN BIDANG REFERENSI Geoid dan ellipsoida merupakan bidang 2 yang sangat penting didalam Geodesi. Karena masing 2 bidang tersebut merupakan bentuk bumi dalam pengertian fisik dan dalarn pengertian
BENTUK BUMI DAN BIDANG REFERENSI Geoid dan ellipsoida merupakan bidang 2 yang sangat penting didalam Geodesi. Karena masing 2 bidang tersebut merupakan bentuk bumi dalam pengertian fisik dan dalarn pengertian
PROYEKSI PETA DAN SKALA PETA
 PROYEKSI PETA DAN SKALA PETA Proyeksi Peta dan Skala Peta 1. Pengertian Proyeksi peta ialah cara pemindahan lintang/ bujur yang terdapat pada lengkung permukaan bumi ke bidang datar. Ada beberapa ketentuan
PROYEKSI PETA DAN SKALA PETA Proyeksi Peta dan Skala Peta 1. Pengertian Proyeksi peta ialah cara pemindahan lintang/ bujur yang terdapat pada lengkung permukaan bumi ke bidang datar. Ada beberapa ketentuan
GEODESI DASAR DAN PEMETAAN
 GEODESI DASAR DAN PEMETAAN KONSEP TAHAPAN PEMETAAN 2 PENGOLAHAN DATA PENYAJIAN DATA PENGUMPULAN DATA PETA MUKA BUMI FENOMENA MUKA BUMI INTERPRETASI PETA 1 Sistem Perolehan Data 3 Pengukuran terestrial
GEODESI DASAR DAN PEMETAAN KONSEP TAHAPAN PEMETAAN 2 PENGOLAHAN DATA PENYAJIAN DATA PENGUMPULAN DATA PETA MUKA BUMI FENOMENA MUKA BUMI INTERPRETASI PETA 1 Sistem Perolehan Data 3 Pengukuran terestrial
Proyeksi Peta. Tujuan
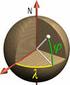 Arna fariza Politeknik elektronika negeri surabaya Tujuan Setelah menyelesaikan bab ini, anda diharapkan dapat: Memahami tentang bentuk permukaan bumi Memahami proyeksi dari peta bumi (3D) ke peta topografi
Arna fariza Politeknik elektronika negeri surabaya Tujuan Setelah menyelesaikan bab ini, anda diharapkan dapat: Memahami tentang bentuk permukaan bumi Memahami proyeksi dari peta bumi (3D) ke peta topografi
Sistem Proyeksi Peta. Arif Basofi PENS 2012
 Sistem Proyeksi Peta Arif Basofi PENS 2012 Tujuan Sistem Proyeksi Peta Jenis Proyeksi Peta Pemilihan Proyeksi Peta UTM (Universal Transverse Mercator) Sistem Proyeksi Peta Bentuk bumi berupa ruang 3D yg
Sistem Proyeksi Peta Arif Basofi PENS 2012 Tujuan Sistem Proyeksi Peta Jenis Proyeksi Peta Pemilihan Proyeksi Peta UTM (Universal Transverse Mercator) Sistem Proyeksi Peta Bentuk bumi berupa ruang 3D yg
SURVEYING (CIV 104) PERTEMUAN 2 : SISTEM SATUAN, ARAH DAN MENENTUKAN POSISI DALAM SURVEYING
 SURVEYING (CIV 104) PERTEMUAN 2 : SISTEM SATUAN, ARAH DAN MENENTUKAN POSISI DALAM SURVEYING UNIVERSITAS PEMBANGUNAN JAYA Jl. Boulevard Bintaro Sektor 7, Bintaro Jaya Tangerang Selatan 15224 Sistem satuan
SURVEYING (CIV 104) PERTEMUAN 2 : SISTEM SATUAN, ARAH DAN MENENTUKAN POSISI DALAM SURVEYING UNIVERSITAS PEMBANGUNAN JAYA Jl. Boulevard Bintaro Sektor 7, Bintaro Jaya Tangerang Selatan 15224 Sistem satuan
Sistem Proyeksi Peta. Arif Basofi PENS 2015
 Sistem Proyeksi Peta Arif Basofi PENS 2015 Contents 1 Proyeksi Peta 2 Jenis Proyeksi Peta 3 Pemilihan Proyeksi Peta 4 Sistem Proyeksi Peta Indonesia Proyeksi Peta Peta : representasi dua-dimesional dari
Sistem Proyeksi Peta Arif Basofi PENS 2015 Contents 1 Proyeksi Peta 2 Jenis Proyeksi Peta 3 Pemilihan Proyeksi Peta 4 Sistem Proyeksi Peta Indonesia Proyeksi Peta Peta : representasi dua-dimesional dari
Bab ini memperkenalkan mengenai proyeksi silinder secara umum dan macam proyeksi silinder yang dipakai di Indonesia.
 BAB 7 PENDAHULUAN Diskripsi singkat : Proyeksi Silinder bila bidang proyeksinya adalah silinder, artinya semua titik di atas permukaan bumi diproyeksikan pada bidang silinder yang kemudian didatarkan.
BAB 7 PENDAHULUAN Diskripsi singkat : Proyeksi Silinder bila bidang proyeksinya adalah silinder, artinya semua titik di atas permukaan bumi diproyeksikan pada bidang silinder yang kemudian didatarkan.
K NSEP E P D A D SA S R
 Mata Kuliah : Sistem Informasi Geografis (SIG) Perikanan. Kode MK : M10A.125 SKS :2 (1-1) KONSEP DASAR DATA GEOSPASIAL OLEH SYAWALUDIN A. HRP, SPi, MSc SISTEM KOORDINAT DATA SPASIAL SUB POKOK BAHASAN 1
Mata Kuliah : Sistem Informasi Geografis (SIG) Perikanan. Kode MK : M10A.125 SKS :2 (1-1) KONSEP DASAR DATA GEOSPASIAL OLEH SYAWALUDIN A. HRP, SPi, MSc SISTEM KOORDINAT DATA SPASIAL SUB POKOK BAHASAN 1
Datum Geodetik & Sistem Koordinat Maju terus
 Datum Geodetik & Sistem Koordinat Maju terus 31/03/2015 8:34 Susunan Lapisan Bumi Inside eartth Datum geodetik atau referensi permukaan atau georeferensi adalah parameter sebagai acuan untuk mendefinisikan
Datum Geodetik & Sistem Koordinat Maju terus 31/03/2015 8:34 Susunan Lapisan Bumi Inside eartth Datum geodetik atau referensi permukaan atau georeferensi adalah parameter sebagai acuan untuk mendefinisikan
BAB II TINJAUAN PUSTAKA
 BAB II TINJAUAN PUSTAKA Pada bab ini diuraikan hasil tinjauan pustaka tentang definisi, konsep, dan teori-teori yang terkait dengan penelitian ini. Adapun pustaka yang dipakai adalah konsep perambatan
BAB II TINJAUAN PUSTAKA Pada bab ini diuraikan hasil tinjauan pustaka tentang definisi, konsep, dan teori-teori yang terkait dengan penelitian ini. Adapun pustaka yang dipakai adalah konsep perambatan
REKONSTRUKSI/RESTORASI REKONSTRUKSI/RESTORASI. Minggu 9: TAHAPAN ANALISIS CITRA. 1. Rekonstruksi (Destripe) SLC (Scan Line Corrector) off
 Minggu 9: TAHAPAN ANALISIS CITRA REKONSTRUKSI/KOREKSI Rekonstruksi/Restorasi Koreksi geometri Mosaik Koreksi radiometri/koreksi topografi TRANSFORMASI Penajaman citra Transformasi spasial/geometri : merubah
Minggu 9: TAHAPAN ANALISIS CITRA REKONSTRUKSI/KOREKSI Rekonstruksi/Restorasi Koreksi geometri Mosaik Koreksi radiometri/koreksi topografi TRANSFORMASI Penajaman citra Transformasi spasial/geometri : merubah
CORPORATE SOCIAL RESPONSIBLE
 CORPORATE SOCIAL RESPONSIBLE LAPORAN PENENTUAN ARAH KIBLAT MASJID SYUHADA PERUMAHAN BEJI PERMAI, DEPOK PT. Mahakarya Geo Survey DAFTAR ISI DAFTAR ISI... 1 DAFTAR GAMBAR... 2 DAFTAR TABEL... 2 1. PENDAHULUAN...
CORPORATE SOCIAL RESPONSIBLE LAPORAN PENENTUAN ARAH KIBLAT MASJID SYUHADA PERUMAHAN BEJI PERMAI, DEPOK PT. Mahakarya Geo Survey DAFTAR ISI DAFTAR ISI... 1 DAFTAR GAMBAR... 2 DAFTAR TABEL... 2 1. PENDAHULUAN...
BAB I Pengertian Sistem Informasi Geografis
 BAB I KONSEP SISTEM INFORMASI GEOGRAFIS 1.1. Pengertian Sistem Informasi Geografis Sistem Informasi Geografis (Geographic Information System/GIS) yang selanjutnya akan disebut SIG merupakan sistem informasi
BAB I KONSEP SISTEM INFORMASI GEOGRAFIS 1.1. Pengertian Sistem Informasi Geografis Sistem Informasi Geografis (Geographic Information System/GIS) yang selanjutnya akan disebut SIG merupakan sistem informasi
BEBERAPA PEMIKIRAN TENTANG SISTEM DAN KERANGKA REFERENSI KOORDINAT UNTUK DKI JAKARTA. Hasanuddin Z. Abidin
 BEBERAPA PEMIKIRAN TENTANG SISTEM DAN KERANGKA REFERENSI KOORDINAT UNTUK DKI JAKARTA Hasanuddin Z. Abidin Jurusan Teknik Geodesi, Institut Teknologi Bandung Jl. Ganesha 10, Bandung 40132 e-mail : hzabidin@gd.itb.ac.id
BEBERAPA PEMIKIRAN TENTANG SISTEM DAN KERANGKA REFERENSI KOORDINAT UNTUK DKI JAKARTA Hasanuddin Z. Abidin Jurusan Teknik Geodesi, Institut Teknologi Bandung Jl. Ganesha 10, Bandung 40132 e-mail : hzabidin@gd.itb.ac.id
Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY
 SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
SISTEM-SISTEM KOORDINAT Dr. Ramadoni Syahputra Jurusan Teknik Elektro FT UMY Sistem Koordinat Kartesian Dalam sistem koordinat Kartesian, terdapat tiga sumbu koordinat yaitu sumbu x, y, dan z. Suatu titik
KONSEP GEODESI UNTUK DATA SPASIAL
 BAB VI KONSEP GEODESI UNTUK DATA SPASIAL 6.1. PENDAHULUAN Objek memiliki properties geometric (seperti jalan, sungai, batas-batas pulau, dll) yang disebut sebagai objek spasial, dalam SIG objek-objek tersebut
BAB VI KONSEP GEODESI UNTUK DATA SPASIAL 6.1. PENDAHULUAN Objek memiliki properties geometric (seperti jalan, sungai, batas-batas pulau, dll) yang disebut sebagai objek spasial, dalam SIG objek-objek tersebut
Pertemuan 3. Penentuan posisi titik horizontal dan vertikal
 Pertemuan 3 Penentuan posisi titik horizontal dan vertikal Koordinat 3D Koordinat 3D Koordinat 3D Pernyataan lintang Pernyataan bujur dan Tinggi λ (Bujur) = sudut yang dibentuk antara meridian suatu titik,
Pertemuan 3 Penentuan posisi titik horizontal dan vertikal Koordinat 3D Koordinat 3D Koordinat 3D Pernyataan lintang Pernyataan bujur dan Tinggi λ (Bujur) = sudut yang dibentuk antara meridian suatu titik,
Bab IV ANALISIS. 4.1 Hasil Revisi Analisis hasil revisi Permendagri no 1 tahun 2006 terdiri dari 2 pasal, sebagai berikut:
 Bab IV ANALISIS Analisis dilakukan terhadap hasil revisi dari Permendagri no 1 tahun 2006 beserta lampirannya berdasarkan kaidah-kaidah keilmuan Geodesi, adapun analalisis yang diberikan sebagai berikut:
Bab IV ANALISIS Analisis dilakukan terhadap hasil revisi dari Permendagri no 1 tahun 2006 beserta lampirannya berdasarkan kaidah-kaidah keilmuan Geodesi, adapun analalisis yang diberikan sebagai berikut:
Jadi huruf B yang memiliki garis kontur yang renggang menunjukkan kemiringan/daerahnya landai.
 SMA/MA IPS kelas 10 - GEOGRAFI IPS BAB 8. SUPLEMEN PENGINDRAAN JAUH, PEMETAAN, DAN SISTEM INFORMASI GEOGRAFI (SIG)LATIHAN SOAL 8.2 1. Kemiringan lereng kontur huruf B seperti pada gambar mempunyai http://www.primemobile.co.id/assets/uploads/materi/8.2.1.jpg
SMA/MA IPS kelas 10 - GEOGRAFI IPS BAB 8. SUPLEMEN PENGINDRAAN JAUH, PEMETAAN, DAN SISTEM INFORMASI GEOGRAFI (SIG)LATIHAN SOAL 8.2 1. Kemiringan lereng kontur huruf B seperti pada gambar mempunyai http://www.primemobile.co.id/assets/uploads/materi/8.2.1.jpg
BAB I PENDAHULUAN I.1.
 BAB I PENDAHULUAN I.1. Latar Belakang Sistem proyeksi peta merupakan bagian yang penting dalam sebuah peta karena pemilihan sistem proyeksi peta berpengaruh pada ketelitian koordinat setiap titik di peta.
BAB I PENDAHULUAN I.1. Latar Belakang Sistem proyeksi peta merupakan bagian yang penting dalam sebuah peta karena pemilihan sistem proyeksi peta berpengaruh pada ketelitian koordinat setiap titik di peta.
MAKALAH SISTEM TRANSFORMASI KOORDINAT 2 DIMENSI DISUSUN OLEH : HERA RATNAWATI 16/395027/TK/44319
 MAKALAH SISTEM TRANSFORMASI KOORDINAT DIMENSI DISUSUN OLEH : HERA RATNAWATI 16/9507/TK/19 DEPARTEMEN TEKNIK GEODESI FAKULTAS TEKNIK UNIVERSITAS GADJAH MADA 017 1 KATA PENGANTAR Puji dan syukur kehadirat
MAKALAH SISTEM TRANSFORMASI KOORDINAT DIMENSI DISUSUN OLEH : HERA RATNAWATI 16/9507/TK/19 DEPARTEMEN TEKNIK GEODESI FAKULTAS TEKNIK UNIVERSITAS GADJAH MADA 017 1 KATA PENGANTAR Puji dan syukur kehadirat
LENGKUNG MENDATAR LENGKUNG SEDERHANA LENGKUNG DGN TITIK PERANTARA LENGKUNG DGN PERANTARA KOORDINAT LENGKUNG SEPEREMPAT BAGIAN
 LENGKUNG MENDATAR LENGKUNG SEDERHANA LENGKUNG DGN TITIK PERANTARA LENGKUNG DGN PERANTARA KOORDINAT LENGKUNG SEPEREMPAT BAGIAN LENGKUNG MENDATAR LENGKUNG SEDERHANA LENGKUNG DGN TITIK PERANTARA LENGKUNG
LENGKUNG MENDATAR LENGKUNG SEDERHANA LENGKUNG DGN TITIK PERANTARA LENGKUNG DGN PERANTARA KOORDINAT LENGKUNG SEPEREMPAT BAGIAN LENGKUNG MENDATAR LENGKUNG SEDERHANA LENGKUNG DGN TITIK PERANTARA LENGKUNG
METODE PENGUKURAN TRIANGULASI
 METODE PENGUKURAN TRIANGULASI Triangulasi adalah proses mencari koordinat dari sebuah titik dengan cara menghitung panjang sisi segitiga yang berhadapan dengan titik tersebut, dan ukuran kedua sudut antara
METODE PENGUKURAN TRIANGULASI Triangulasi adalah proses mencari koordinat dari sebuah titik dengan cara menghitung panjang sisi segitiga yang berhadapan dengan titik tersebut, dan ukuran kedua sudut antara
BAB V TINJAUAN MENGENAI DATA AIRBORNE LIDAR
 51 BAB V TINJAUAN MENGENAI DATA AIRBORNE LIDAR 5.1 Data Airborne LIDAR Data yang dihasilkan dari suatu survey airborne LIDAR dapat dibagi menjadi tiga karena terdapat tiga instrumen yang bekerja secara
51 BAB V TINJAUAN MENGENAI DATA AIRBORNE LIDAR 5.1 Data Airborne LIDAR Data yang dihasilkan dari suatu survey airborne LIDAR dapat dibagi menjadi tiga karena terdapat tiga instrumen yang bekerja secara
TUGAS 1 ASISTENSI GEODESI SATELIT. Sistem Koordinat CIS dan CTS
 TUGAS 1 ASISTENSI GEODESI SATELIT KELAS A Sistem Koordinat CIS dan CTS Oleh : Enira Suryaningsih (3513100036) Dosen : JURUSAN TEKNIK GEOMATIKA FAKULTAS TEKNIK SIPIL DAN PERENCANAAN INSTITUT TEKNOLOGI SEPULUH
TUGAS 1 ASISTENSI GEODESI SATELIT KELAS A Sistem Koordinat CIS dan CTS Oleh : Enira Suryaningsih (3513100036) Dosen : JURUSAN TEKNIK GEOMATIKA FAKULTAS TEKNIK SIPIL DAN PERENCANAAN INSTITUT TEKNOLOGI SEPULUH
Can be accessed on:
 Pertemuan 5 Pembuatan Peta Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Pendahuluan Pada umumnya peta adalah sarana guna memperoleh gambaran data ilmiah yang terdapat di atas permukaan
Pertemuan 5 Pembuatan Peta Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Pendahuluan Pada umumnya peta adalah sarana guna memperoleh gambaran data ilmiah yang terdapat di atas permukaan
Koordinat Kartesius, Koordinat Tabung & Koordinat Bola. Tim Kalkulus II
 Koordinat Kartesius, Koordinat Tabung & Koordinat Bola Tim Kalkulus II Koordinat Kartesius Sistem Koordinat 2 Dimensi Sistem koordinat kartesian dua dimensi merupakan sistem koordinat yang terdiri dari
Koordinat Kartesius, Koordinat Tabung & Koordinat Bola Tim Kalkulus II Koordinat Kartesius Sistem Koordinat 2 Dimensi Sistem koordinat kartesian dua dimensi merupakan sistem koordinat yang terdiri dari
Konsep Geodesi untuk Data Spasial. by: Ahmad Syauqi Ahsan
 Konsep Geodesi untuk Data Spasial by: Ahmad Syauqi Ahsan Geodesi Menurut definisi klasik dari F.R. Helmert, Geodesi adalah sebuah sains dalam pengukuran dan pemetaan permukaan bumi. Pembahasan tentang
Konsep Geodesi untuk Data Spasial by: Ahmad Syauqi Ahsan Geodesi Menurut definisi klasik dari F.R. Helmert, Geodesi adalah sebuah sains dalam pengukuran dan pemetaan permukaan bumi. Pembahasan tentang
SISTEM INFORMASI SUMBER DAYA LAHAN
 16/09/2012 DATA Data adalah komponen yang amat penting dalam GIS SISTEM INFORMASI SUMBER DAYA LAHAN Kelas Agrotreknologi (2 0 sks) Dwi Priyo Ariyanto Data geografik dan tabulasi data yang berhubungan akan
16/09/2012 DATA Data adalah komponen yang amat penting dalam GIS SISTEM INFORMASI SUMBER DAYA LAHAN Kelas Agrotreknologi (2 0 sks) Dwi Priyo Ariyanto Data geografik dan tabulasi data yang berhubungan akan
Datum dan Ellipsoida Referensi
 Datum dan Ellipsoida Referensi RG141227 - Sistem Koordinat dan Transformasi Semester Gasal 2016/2017 Ira M Anjasmara PhD Jurusan Teknik Geomatika Datum Geodetik Datum Geodetik adalah parameter yang mendefinisikan
Datum dan Ellipsoida Referensi RG141227 - Sistem Koordinat dan Transformasi Semester Gasal 2016/2017 Ira M Anjasmara PhD Jurusan Teknik Geomatika Datum Geodetik Datum Geodetik adalah parameter yang mendefinisikan
Gambar 1. prinsip proyeksi dari bidang lengkung muka bumi ke bidang datar kertas
 MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
TATA KOORDINAT BENDA LANGIT. Kelompok 6 : 1. Siti Nur Khotimah ( ) 2. Winda Yulia Sari ( ) 3. Yoga Pratama ( )
 TATA KOORDINAT BENDA LANGIT Kelompok 6 : 1. Siti Nur Khotimah (4201412051) 2. Winda Yulia Sari (4201412094) 3. Yoga Pratama (42014120) 1 bintang-bintang nampak beredar dilangit karena bumi berotasi. Jika
TATA KOORDINAT BENDA LANGIT Kelompok 6 : 1. Siti Nur Khotimah (4201412051) 2. Winda Yulia Sari (4201412094) 3. Yoga Pratama (42014120) 1 bintang-bintang nampak beredar dilangit karena bumi berotasi. Jika
BAB III PELAKSANAAN PENELITIAN
 BAB III PELAKSANAAN PENELITIAN Pada bab ini akan dijelaskan mengenai alat dan bahan yang digunakan dalam penelitian ini serta tahapan-tahapan yang dilakukan dalam mengklasifikasi tata guna lahan dari hasil
BAB III PELAKSANAAN PENELITIAN Pada bab ini akan dijelaskan mengenai alat dan bahan yang digunakan dalam penelitian ini serta tahapan-tahapan yang dilakukan dalam mengklasifikasi tata guna lahan dari hasil
Desain Sistem Proyeksi Distorsi Minimum Untuk Pengintegrasian Berbagai Skala Peta Dalam Upaya Mewujudkan Satu Peta Indonesia Raya
 Dalam Upaya Mewujudkan Satu Peta Indonesia Raya Ringkasan Sistem Koordinat Planimetrik Nasional (SKPN), selama ini lebih dikenal sebagai sistem proyeksi transverse mercator yaitu TM6 atau Universal Transverse
Dalam Upaya Mewujudkan Satu Peta Indonesia Raya Ringkasan Sistem Koordinat Planimetrik Nasional (SKPN), selama ini lebih dikenal sebagai sistem proyeksi transverse mercator yaitu TM6 atau Universal Transverse
ILMU UKUR TANAH 2 PENENTUAN POSISI
 ILMU UKUR TANAH 2 PENENTUAN POSISI Oleh: Andri Oktriansyah JURUSAN SURVEI DAN PEMETAAN UNIVERSITAS INDO GLOBAL MANDIRI PALEMBANG 2017 1. Penentuan Posisi Penentuan posisi titik dikelompokkan dalam dua
ILMU UKUR TANAH 2 PENENTUAN POSISI Oleh: Andri Oktriansyah JURUSAN SURVEI DAN PEMETAAN UNIVERSITAS INDO GLOBAL MANDIRI PALEMBANG 2017 1. Penentuan Posisi Penentuan posisi titik dikelompokkan dalam dua
LAPORAN PRAKTIKUM SIG ACARA II TRANSFORMASI PROYEKSI DAN DIGITASI ON SCREEN
 LAPORAN PRAKTIKUM SIG ACARA II TRANSFORMASI PROYEKSI DAN DIGITASI ON SCREEN Disusun oleh : NAMA : NUR SIDIK NIM : 11405244001 HARI : Kamis, 13 MARET 2014 JAM : 08.00 10.00 JURUSAN PENDIDIKAN GEOGRAFI FAKULTAS
LAPORAN PRAKTIKUM SIG ACARA II TRANSFORMASI PROYEKSI DAN DIGITASI ON SCREEN Disusun oleh : NAMA : NUR SIDIK NIM : 11405244001 HARI : Kamis, 13 MARET 2014 JAM : 08.00 10.00 JURUSAN PENDIDIKAN GEOGRAFI FAKULTAS
BAB I SISTEM KOORDINAT
 BAB I SISTEM KOORDINAT 1.1 Sistem Koordinat Sistem koordinat adalah suatu cara ang digunakan untuk menentukan letak suatu titik pada bidang ( R ) atau ruang ( R ). Beberapa macam sistem koordinat ang kita
BAB I SISTEM KOORDINAT 1.1 Sistem Koordinat Sistem koordinat adalah suatu cara ang digunakan untuk menentukan letak suatu titik pada bidang ( R ) atau ruang ( R ). Beberapa macam sistem koordinat ang kita
PERATURAN KEPALA BADAN INFORMASI GEOSPASIAL NOMOR 15 TAHUN 2013 /2001 TENTANG SISTEM REFERENSI GEOSPASIAL INDONESIA 2013
 PERATURAN KEPALA BADAN INFORMASI GEOSPASIAL NOMOR 15 TAHUN 2013 /2001 TENTANG SISTEM REFERENSI GEOSPASIAL INDONESIA 2013 DENGAN RAHMAT TUHAN YANG MAHA ESA KEPALA BADAN INFORMASI GEOSPASIAL, Menimbang :
PERATURAN KEPALA BADAN INFORMASI GEOSPASIAL NOMOR 15 TAHUN 2013 /2001 TENTANG SISTEM REFERENSI GEOSPASIAL INDONESIA 2013 DENGAN RAHMAT TUHAN YANG MAHA ESA KEPALA BADAN INFORMASI GEOSPASIAL, Menimbang :
BAB 2 DASAR TEORI. 2.1 Tinjauan Umum Teknologi Pemetaan Tiga Dimensi
 BB 2 DSR TEORI 2.1 Tinjauan Umum Teknologi Pemetaan Tiga Dimensi Pemetaan objek tiga dimensi diperlukan untuk perencanaan, konstruksi, rekonstruksi, ataupun manajemen asset. Suatu objek tiga dimensi merupakan
BB 2 DSR TEORI 2.1 Tinjauan Umum Teknologi Pemetaan Tiga Dimensi Pemetaan objek tiga dimensi diperlukan untuk perencanaan, konstruksi, rekonstruksi, ataupun manajemen asset. Suatu objek tiga dimensi merupakan
BAB III APLIKASI PEMANFAATAN BAND YANG BERBEDA PADA INSAR
 BAB III APLIKASI PEMANFAATAN BAND YANG BERBEDA PADA INSAR III.1 Model Tinggi Digital (Digital Terrain Model-DTM) Model Tinggi Digital (Digital Terrain Model-DTM) atau sering juga disebut DEM, merupakan
BAB III APLIKASI PEMANFAATAN BAND YANG BERBEDA PADA INSAR III.1 Model Tinggi Digital (Digital Terrain Model-DTM) Model Tinggi Digital (Digital Terrain Model-DTM) atau sering juga disebut DEM, merupakan
MODUL 3 REGISTER DAN DIGITASI PETA
 MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
MODUL 3 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
Home : tedyagungc.wordpress.com
 Email : tedyagungc@gmail.com Home : tedyagungc.wordpress.com Subagyo 2003, Permukaan bumi merupakan suatu bidang lengkung yang tidak beraturan, sehingga hubungan geometris antara titik satu dengan titik
Email : tedyagungc@gmail.com Home : tedyagungc.wordpress.com Subagyo 2003, Permukaan bumi merupakan suatu bidang lengkung yang tidak beraturan, sehingga hubungan geometris antara titik satu dengan titik
BAB III PENGOLAHAN DATA Proses Pengolahan Data LIDAR Proses pengolahan data LIDAR secara umum dapat dilihat pada skema 3.1 di bawah ini.
 BAB III PENGOLAHAN DATA 3.1. Pengolahan Data LIDAR 3.1.1. Proses Pengolahan Data LIDAR Proses pengolahan data LIDAR secara umum dapat dilihat pada skema 3.1 di bawah ini. Sistem LIDAR Jarak Laser Posisi
BAB III PENGOLAHAN DATA 3.1. Pengolahan Data LIDAR 3.1.1. Proses Pengolahan Data LIDAR Proses pengolahan data LIDAR secara umum dapat dilihat pada skema 3.1 di bawah ini. Sistem LIDAR Jarak Laser Posisi
MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB
 MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB A. Gerak Semu Benda Langit Bumi kita berputar seperti gasing. Ketika Bumi berputar pada sumbu putarnya maka hal ini dinamakan
MENGENAL GERAK LANGIT DAN TATA KOORDINAT BENDA LANGIT BY AMBOINA ASTRONOMY CLUB A. Gerak Semu Benda Langit Bumi kita berputar seperti gasing. Ketika Bumi berputar pada sumbu putarnya maka hal ini dinamakan
ACARA I. Pengenalan Sistem Proyeksi Peta Kartografis
 ACARA I I. Judul Pengenalan Sistem Proyeksi Peta Kartografis II. Tujuan 1. Melatih mahasiswa untuk memahami pengertian proyeksi peta secara umum. 2. Melatih mahasiswa untuk mengenali dan memahami beberapa
ACARA I I. Judul Pengenalan Sistem Proyeksi Peta Kartografis II. Tujuan 1. Melatih mahasiswa untuk memahami pengertian proyeksi peta secara umum. 2. Melatih mahasiswa untuk mengenali dan memahami beberapa
BAB I PENDAHULUAN I.1. Latar Belakang
 1 BAB I PENDAHULUAN I.1. Latar Belakang Geodesi merupakan ilmu yang mempelajari pengukuran bentuk dan ukuran bumi termasuk medan gayaberat bumi. Bentuk bumi tidak teratur menyebabkan penentuan bentuk dan
1 BAB I PENDAHULUAN I.1. Latar Belakang Geodesi merupakan ilmu yang mempelajari pengukuran bentuk dan ukuran bumi termasuk medan gayaberat bumi. Bentuk bumi tidak teratur menyebabkan penentuan bentuk dan
SISTEM KOORDINAT GEOGRAFIK
 SISTEM KOORDINAT GEOGRAFIK Oleh: Ir. Djawahir, M.Sc Untuk mengidentifikasi posisi titik di bumi atau yang terkait dengan bumi, dikembangkanlah Sistem Koordinat Geografik dengan mendefinisikan bentuk bumi
SISTEM KOORDINAT GEOGRAFIK Oleh: Ir. Djawahir, M.Sc Untuk mengidentifikasi posisi titik di bumi atau yang terkait dengan bumi, dikembangkanlah Sistem Koordinat Geografik dengan mendefinisikan bentuk bumi
PENGENALAN GPS & PENGGUNAANNYA
 PENGENALAN GPS & PENGGUNAANNYA PENGENALAN GPS & PENGGUNAANNYA SISTIM GPS SISTEM KOORDINAT PENGGUNAAN GPS SISTIM GPS GPS Apakah itu? Singkatan : Global Positioning System Dikembangkan oleh DEPHAN A.S. yang
PENGENALAN GPS & PENGGUNAANNYA PENGENALAN GPS & PENGGUNAANNYA SISTIM GPS SISTEM KOORDINAT PENGGUNAAN GPS SISTIM GPS GPS Apakah itu? Singkatan : Global Positioning System Dikembangkan oleh DEPHAN A.S. yang
BAB I PENDAHULUAN. A.Latar Belakang. B. Tujuan Praktikum
 BAB I PENDAHULUAN A.Latar Belakang Pengukuran merupakan penentuan besaran, dimensi, atau kapasitas, biasanya terhadap suatu standar atau satuan pengukuran atau dapat dikatakan juga bahwa pengukuran adalah
BAB I PENDAHULUAN A.Latar Belakang Pengukuran merupakan penentuan besaran, dimensi, atau kapasitas, biasanya terhadap suatu standar atau satuan pengukuran atau dapat dikatakan juga bahwa pengukuran adalah
Transformasi Datum dan Koordinat
 Transformasi Datum dan Koordinat Sistem Transformasi Koordinat RG091521 Lecture 6 Semester 1, 2013 Jurusan Pendahuluan Hubungan antara satu sistem koordinat dengan sistem lainnya diformulasikan dalam bentuk
Transformasi Datum dan Koordinat Sistem Transformasi Koordinat RG091521 Lecture 6 Semester 1, 2013 Jurusan Pendahuluan Hubungan antara satu sistem koordinat dengan sistem lainnya diformulasikan dalam bentuk
BAB 2 KONSEP PENGOLAHAN DATA SIDE SCAN SONAR
 BAB 2 KONSEP PENGOLAHAN DATA SIDE SCAN SONAR Pengolahan data side scan sonar terdiri dari dua tahap, yaitu tahap real-time processing dan kemudian dilanjutkan dengan tahap post-processing. Tujuan realtime
BAB 2 KONSEP PENGOLAHAN DATA SIDE SCAN SONAR Pengolahan data side scan sonar terdiri dari dua tahap, yaitu tahap real-time processing dan kemudian dilanjutkan dengan tahap post-processing. Tujuan realtime
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI A. Kerangka Dasar Pemetaan Tahap awal sebelum melakukan suatu pengukuran adalah dengan melakukan penentuan titik-titik kerangka dasar pemetaan pada daerah atau areal yang akan dilakukan
BAB II LANDASAN TEORI A. Kerangka Dasar Pemetaan Tahap awal sebelum melakukan suatu pengukuran adalah dengan melakukan penentuan titik-titik kerangka dasar pemetaan pada daerah atau areal yang akan dilakukan
BAB III METODOLOGI PENELITIAN
 BAB III METODOLOGI PENELITIAN 3.1 Persiapan Tahap persiapan merupakan tahapan penting dalam penelitian ini. Proses persiapan data ini berpengaruh pada hasil akhir penelitian. Persiapan yang dilakukan meliputi
BAB III METODOLOGI PENELITIAN 3.1 Persiapan Tahap persiapan merupakan tahapan penting dalam penelitian ini. Proses persiapan data ini berpengaruh pada hasil akhir penelitian. Persiapan yang dilakukan meliputi
BAB I PENDAHULUAN I.1. Latar Belakang
 BAB I PENDAHULUAN I.1. Latar Belakang Bendungan adalah suatu bangunan penampung air yang dibentuk dari berbagai batuan, tanah dan juga beton. Bendungan dibangun untuk menahan laju air, sehingga menjadi
BAB I PENDAHULUAN I.1. Latar Belakang Bendungan adalah suatu bangunan penampung air yang dibentuk dari berbagai batuan, tanah dan juga beton. Bendungan dibangun untuk menahan laju air, sehingga menjadi
3. ORBIT KEPLERIAN. AS 2201 Mekanika Benda Langit. Monday, February 17,
 3. ORBIT KEPLERIAN AS 2201 Mekanika Benda Langit 1 3.1 PENDAHULUAN Mekanika Newton pada mulanya dimanfaatkan untuk menentukan gerak orbit benda dalam Tatasurya. Misalkan Matahari bermassa M pada titik
3. ORBIT KEPLERIAN AS 2201 Mekanika Benda Langit 1 3.1 PENDAHULUAN Mekanika Newton pada mulanya dimanfaatkan untuk menentukan gerak orbit benda dalam Tatasurya. Misalkan Matahari bermassa M pada titik
PENGENALAN GPS & PENGGUNAANNYA
 PENGENALAN GPS & PENGGUNAANNYA PENGENALAN GPS & PENGGUNAANNYA 1. SISTIM GPS 2. PENGANTAR TANTANG PETA 3. PENGGUNAAN GPS SISTIM GPS GPS Apakah itu? Dikembangkan oleh DEPHAN A.S. yang boleh dimanfaatkan
PENGENALAN GPS & PENGGUNAANNYA PENGENALAN GPS & PENGGUNAANNYA 1. SISTIM GPS 2. PENGANTAR TANTANG PETA 3. PENGGUNAAN GPS SISTIM GPS GPS Apakah itu? Dikembangkan oleh DEPHAN A.S. yang boleh dimanfaatkan
MODUL 2 REGISTER DAN DIGITASI PETA
 MODUL 2 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
MODUL 2 REGISTER DAN DIGITASI PETA A. Tujuan Praktikum - Praktikan memahami dan mampu melakukan register peta raster pada MapInfo - Praktikan mampu melakukan digitasi peta dengan MapInfo B. Tools MapInfo
BAB 2 LANDASAN TEORITIS PERMASALAHAN
 BAB LANDASAN TEORITIS PERMASALAHAN. PRINSIP DASAR GRAVITASI Gaya tarik-menarik antara dua buah partikel sebanding dengan perkalian massa kedua partikel tersebut dan berbanding terbalik dengan kuadrat jarak
BAB LANDASAN TEORITIS PERMASALAHAN. PRINSIP DASAR GRAVITASI Gaya tarik-menarik antara dua buah partikel sebanding dengan perkalian massa kedua partikel tersebut dan berbanding terbalik dengan kuadrat jarak
Kinematika Gerak KINEMATIKA GERAK. Sumber:
 Kinematika Gerak B a b B a b 1 KINEMATIKA GERAK Sumber: www.jatim.go.id Jika kalian belajar fisika maka kalian akan sering mempelajari tentang gerak. Fenomena tentang gerak memang sangat menarik. Coba
Kinematika Gerak B a b B a b 1 KINEMATIKA GERAK Sumber: www.jatim.go.id Jika kalian belajar fisika maka kalian akan sering mempelajari tentang gerak. Fenomena tentang gerak memang sangat menarik. Coba
BAB IV PENGOLAHAN DATA DAN ANALISIS
 BAB IV PENGOLAHAN DATA DAN ANALISIS IV.1. PENGOLAHAN DATA Dalam proses pemodelan gempa ini digunakan GMT (The Generic Mapping Tools) untuk menggambarkan dan menganalisis arah vektor GPS dan sebaran gempa,
BAB IV PENGOLAHAN DATA DAN ANALISIS IV.1. PENGOLAHAN DATA Dalam proses pemodelan gempa ini digunakan GMT (The Generic Mapping Tools) untuk menggambarkan dan menganalisis arah vektor GPS dan sebaran gempa,
PENERAPAN NAVSTAR GPS UNTUK PEMETAAN TOPOGRAFI
 PENERAPAN NAVSTAR GPS UNTUK PEMETAAN TOPOGRAFI Muh. Altin Massinai Lab. Fisika Bumi dan Lautan Program Studi Geofisika FMIPA Universitas Hasanuddin Makassar Abstract A research have been done about topography
PENERAPAN NAVSTAR GPS UNTUK PEMETAAN TOPOGRAFI Muh. Altin Massinai Lab. Fisika Bumi dan Lautan Program Studi Geofisika FMIPA Universitas Hasanuddin Makassar Abstract A research have been done about topography
BAB I PENDAHULUAN. I.1. Latar Belakang
 BAB I PENDAHULUAN I.1. Latar Belakang Undang-Undang Nomor 4 Tahun 2011 tentang Informasi Geospasial mengamanahkan Peta Rupa Bumi Indonesia sebagai Peta Dasar diselenggarakan mulai pada skala 1 : 1.000.000
BAB I PENDAHULUAN I.1. Latar Belakang Undang-Undang Nomor 4 Tahun 2011 tentang Informasi Geospasial mengamanahkan Peta Rupa Bumi Indonesia sebagai Peta Dasar diselenggarakan mulai pada skala 1 : 1.000.000
KINEMATIKA GERAK 1 PERSAMAAN GERAK
 KINEMATIKA GERAK 1 PERSAMAAN GERAK Posisi titik materi dapat dinyatakan dengan sebuah VEKTOR, baik pada suatu bidang datar maupun dalam bidang ruang. Vektor yang dipergunakan untuk menentukan posisi disebut
KINEMATIKA GERAK 1 PERSAMAAN GERAK Posisi titik materi dapat dinyatakan dengan sebuah VEKTOR, baik pada suatu bidang datar maupun dalam bidang ruang. Vektor yang dipergunakan untuk menentukan posisi disebut
BAB 3 DINAMIKA GERAK LURUS
 BAB 3 DINAMIKA GERAK LURUS A. TUJUAN PEMBELAJARAN 1. Menerapkan Hukum I Newton untuk menganalisis gaya-gaya pada benda 2. Menerapkan Hukum II Newton untuk menganalisis gerak objek 3. Menentukan pasangan
BAB 3 DINAMIKA GERAK LURUS A. TUJUAN PEMBELAJARAN 1. Menerapkan Hukum I Newton untuk menganalisis gaya-gaya pada benda 2. Menerapkan Hukum II Newton untuk menganalisis gerak objek 3. Menentukan pasangan
Proyeksi Stereografi. Proyeksi Stereografi
 Proyeksi Stereografi Proyeksi Stereografi Proyeksi Stereografi merupakan salah satu aplikasi dalam geometri yang bisa diartikan sebagai sebuah pemetaan khusus (fungsi) yang memproyeksikan sebuah bola (sphere)
Proyeksi Stereografi Proyeksi Stereografi Proyeksi Stereografi merupakan salah satu aplikasi dalam geometri yang bisa diartikan sebagai sebuah pemetaan khusus (fungsi) yang memproyeksikan sebuah bola (sphere)
a menunjukkan jumlah satuan skala relatif terhadap nol pada sumbu X Gambar 1
 1. Koordinat Cartesius Sistem koordinat Cartesius terdiri dari dua garis yang saling tegak lurus yang disebut sumbu Sumbu horizontal disebut sumbu X dan sumbu vertikal disebut sumbu Y Tiap sumbu mempunyai
1. Koordinat Cartesius Sistem koordinat Cartesius terdiri dari dua garis yang saling tegak lurus yang disebut sumbu Sumbu horizontal disebut sumbu X dan sumbu vertikal disebut sumbu Y Tiap sumbu mempunyai
SIFAT DAN FORMAT DATA TITIK GEOARKINDO 2016
 SIFAT DAN FORMAT DATA TITIK GEOARKINDO 2016 DATA TITIK Merupakan salah satu jenis data vektor selain garis dan polygon, Dapat digunakan untuk merepresentasikan lokasi seperti Bangunan, Struktur, Situs,
SIFAT DAN FORMAT DATA TITIK GEOARKINDO 2016 DATA TITIK Merupakan salah satu jenis data vektor selain garis dan polygon, Dapat digunakan untuk merepresentasikan lokasi seperti Bangunan, Struktur, Situs,
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI 2.1. PETA 2.1.1. Pengertian peta Peta merupakan suatu representasi konvensional (miniatur) dari unsur-unsur (fatures) fisik (alamiah dan buatan manusia) dari sebagian atau keseluruhan
BAB II LANDASAN TEORI 2.1. PETA 2.1.1. Pengertian peta Peta merupakan suatu representasi konvensional (miniatur) dari unsur-unsur (fatures) fisik (alamiah dan buatan manusia) dari sebagian atau keseluruhan
BAB II DASAR TEORI 2.1 Populasi Penduduk 2.2 Basis Data
 BAB II DASAR TEORI 2.1 Populasi Penduduk Populasi adalah sekelompok orang, benda, atau hal yang menjadi sumber pengambilan sampel; sekumpulan yang memenuhi syarat-syarat tertentu yang berkaitan dengan
BAB II DASAR TEORI 2.1 Populasi Penduduk Populasi adalah sekelompok orang, benda, atau hal yang menjadi sumber pengambilan sampel; sekumpulan yang memenuhi syarat-syarat tertentu yang berkaitan dengan
PENGENALAN GPS & PENGGUNAANNYA Oleh : Winardi & Abdullah S.
 Coral Reef Rehabilitation and Management Program (COREMAP) (Program Rehabilitasi dan Pengelolaan Terumbu Karang) Jl. Raden Saleh, 43 jakarta 10330 Phone : 62.021.3143080 Fax. 62.021.327958 E-mail : Coremap@indosat.net.id
Coral Reef Rehabilitation and Management Program (COREMAP) (Program Rehabilitasi dan Pengelolaan Terumbu Karang) Jl. Raden Saleh, 43 jakarta 10330 Phone : 62.021.3143080 Fax. 62.021.327958 E-mail : Coremap@indosat.net.id
PENENTUAN POSISI DENGAN GPS UNTUK SURVEI TERUMBU KARANG. Winardi Puslit Oseanografi - LIPI
 PENENTUAN POSISI DENGAN GPS UNTUK SURVEI TERUMBU KARANG Winardi Puslit Oseanografi - LIPI Sekilas GPS dan Kegunaannya GPS adalah singkatan dari Global Positioning System yang merupakan sistem untuk menentukan
PENENTUAN POSISI DENGAN GPS UNTUK SURVEI TERUMBU KARANG Winardi Puslit Oseanografi - LIPI Sekilas GPS dan Kegunaannya GPS adalah singkatan dari Global Positioning System yang merupakan sistem untuk menentukan
Sistem Geodetik Global 1984 (WGS 1984 ) Dalam Menentukan Nilai Gravitasi Normal (G n )
 Proseding Seminar Geoteknologi Kontribusi Ilmu Kebumian Dalam Pembangunan BerkelanjutanBandung 3 Desember 2007 ISBN : 978-979-799-255-5 Sistem Geodetik Global 1984 (WGS 1984 ) Dalam Menentukan Nilai Gravitasi
Proseding Seminar Geoteknologi Kontribusi Ilmu Kebumian Dalam Pembangunan BerkelanjutanBandung 3 Desember 2007 ISBN : 978-979-799-255-5 Sistem Geodetik Global 1984 (WGS 1984 ) Dalam Menentukan Nilai Gravitasi
BAB IV ANALISIS FORMULA PENENTUAN ARAH KIBLAT DENGAN THEODOLIT DALAM BUKU EPHEMERIS HISAB RUKYAT 2013
 BAB IV ANALISIS FORMULA PENENTUAN ARAH KIBLAT DENGAN THEODOLIT DALAM BUKU EPHEMERIS HISAB RUKYAT 2013 A. Konsep Penentuan Arah Kiblat Dengan Theodolit Dalam Buku Ephemeris Hisab Rukyat 2013 Konsep penentuan
BAB IV ANALISIS FORMULA PENENTUAN ARAH KIBLAT DENGAN THEODOLIT DALAM BUKU EPHEMERIS HISAB RUKYAT 2013 A. Konsep Penentuan Arah Kiblat Dengan Theodolit Dalam Buku Ephemeris Hisab Rukyat 2013 Konsep penentuan
KINEMATIKA. A. Teori Dasar. Besaran besaran dalam kinematika
 KINEMATIKA A. Teori Dasar Besaran besaran dalam kinematika Vektor Posisi : adalah vektor yang menyatakan posisi suatu titik dalam koordinat. Pangkalnya di titik pusat koordinat, sedangkan ujungnya pada
KINEMATIKA A. Teori Dasar Besaran besaran dalam kinematika Vektor Posisi : adalah vektor yang menyatakan posisi suatu titik dalam koordinat. Pangkalnya di titik pusat koordinat, sedangkan ujungnya pada
Bab 7 Sistem Koordinat
 Bab 7 Sistem Koordinat 7.1 Proyeksi Peta Peta adalah gambaran sebagian atau seluruh muka bumi baik yang terletak di atas maupun di bawah permukaan dan disajikan pada bidang datar pada skala dan proyeksi
Bab 7 Sistem Koordinat 7.1 Proyeksi Peta Peta adalah gambaran sebagian atau seluruh muka bumi baik yang terletak di atas maupun di bawah permukaan dan disajikan pada bidang datar pada skala dan proyeksi
APA ITU ILMU UKUR TANAH?
 APA ITU ILMU UKUR TANAH? Merupakan ilmu, seni dan teknologi untuk menyajikan bentuk permukaan bumi baik unsur alam maupun unsur buatan manusia pada bidang yang dianggap datar. ILMU UKUR TANAH (DEFINISI)
APA ITU ILMU UKUR TANAH? Merupakan ilmu, seni dan teknologi untuk menyajikan bentuk permukaan bumi baik unsur alam maupun unsur buatan manusia pada bidang yang dianggap datar. ILMU UKUR TANAH (DEFINISI)
 Pertemuan 1. Membuat Sudut Siku-Siku. Pengukuran Guna Pembuatan Peta dengan Alat-alatalat Sederhana Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Email: haryono_putro@gunadarma.ac.id
Pertemuan 1. Membuat Sudut Siku-Siku. Pengukuran Guna Pembuatan Peta dengan Alat-alatalat Sederhana Can be accessed on: http://haryono_putro.staff.gunadarma.ac.id/ Email: haryono_putro@gunadarma.ac.id
MENGGAMBAR BATAS DESA PADA PETA
 MENGGAMBAR BATAS DESA PADA PETA Edisi : I Tahun 2003 KERJASAMA ANTARA DEPARTEMEN DALAM NEGERI DENGAN BADAN KOORDINASI SURVEI DAN PEMETAAAN NASIONAL Cibogo, April 2003 MENGGAMBAR BATAS DESA PADA PETA Oleh:
MENGGAMBAR BATAS DESA PADA PETA Edisi : I Tahun 2003 KERJASAMA ANTARA DEPARTEMEN DALAM NEGERI DENGAN BADAN KOORDINASI SURVEI DAN PEMETAAAN NASIONAL Cibogo, April 2003 MENGGAMBAR BATAS DESA PADA PETA Oleh:
Bab II Tinjauan Pustaka
 11 Bab II Tinjauan Pustaka II.1. Penelitian Terdahulu Beberapa penelitian terdahulu mengenai penerapan teknologi penginderaan jauh citra resolusi tinggi sebagai media untuk memetakan suatu daerah antara
11 Bab II Tinjauan Pustaka II.1. Penelitian Terdahulu Beberapa penelitian terdahulu mengenai penerapan teknologi penginderaan jauh citra resolusi tinggi sebagai media untuk memetakan suatu daerah antara
BAB II LANDASAN TEORI
 BAB II LANDASAN TEORI A. Alat Ukur GPS GPS (Global Positioning System) adalah sistem radio navigasi menggunakan satelit yang dimiliki dan dikelola oleh Amerika Serikat, untuk menentukan posisi, kecepatan
BAB II LANDASAN TEORI A. Alat Ukur GPS GPS (Global Positioning System) adalah sistem radio navigasi menggunakan satelit yang dimiliki dan dikelola oleh Amerika Serikat, untuk menentukan posisi, kecepatan
I. RENCANA KEGIATAN PEMBELAJARAN MINGGUAN (RKPM) MINGGU 6
 I. RENCANA KEGIATAN PEMBELAJARAN MINGGUAN (RKPM) MINGGU 6 A. TUJUAN AJAR: Dapat menjelaskan Peta laut, Basepoint (Titik Pangkal), dan Baseline (Garis Pangkal) untuk delimiasi batas maritim. B.POKOK BAHASAN/SUB
I. RENCANA KEGIATAN PEMBELAJARAN MINGGUAN (RKPM) MINGGU 6 A. TUJUAN AJAR: Dapat menjelaskan Peta laut, Basepoint (Titik Pangkal), dan Baseline (Garis Pangkal) untuk delimiasi batas maritim. B.POKOK BAHASAN/SUB
BAB I PENDAHULUAN I.1. Latar Belakang
 BAB I PENDAHULUAN I.1. Latar Belakang Bangsa Indonesia pada dasarnya secara filosofis memandang tanah sesuai dengan Pasal 33 ayat(3) UUD 1945 dan Undang-Undang No.5 Tahun 1960 tentang Peraturan Dasar Pokok
BAB I PENDAHULUAN I.1. Latar Belakang Bangsa Indonesia pada dasarnya secara filosofis memandang tanah sesuai dengan Pasal 33 ayat(3) UUD 1945 dan Undang-Undang No.5 Tahun 1960 tentang Peraturan Dasar Pokok
Nur Meita Indah Mufidah
 Pengantar GIS (Gographical Information System) Nur Meita Indah Mufidah Meita153@gmail.com Lisensi Dokumen: Copyright 2003-2006 IlmuKomputer.Com Seluruh dokumen di IlmuKomputer.Com dapat digunakan, dimodifikasi
Pengantar GIS (Gographical Information System) Nur Meita Indah Mufidah Meita153@gmail.com Lisensi Dokumen: Copyright 2003-2006 IlmuKomputer.Com Seluruh dokumen di IlmuKomputer.Com dapat digunakan, dimodifikasi
BAB II PENENTUAN BATAS LAUT DAERAH
 BAB II PENENTUAN BATAS LAUT DAERAH 2.1 Dasar Hukum Penetapan Batas Laut Daerah Agar pelaksanaan penetapan batas laut berhasil dilakukan dengan baik, maka kegiatan tersebut harus mengacu kepada peraturan
BAB II PENENTUAN BATAS LAUT DAERAH 2.1 Dasar Hukum Penetapan Batas Laut Daerah Agar pelaksanaan penetapan batas laut berhasil dilakukan dengan baik, maka kegiatan tersebut harus mengacu kepada peraturan
BAB IV HASIL DAN PEMBAHASAN
 BAB IV HASIL DAN PEMBAHASAN 4.1. Hasil Pengecekan Kualitas Data Observasi Dengan TEQC Kualitas dari data observasi dapat ditunjukkan dengan melihat besar kecilnya nilai moving average dari multipath untuk
BAB IV HASIL DAN PEMBAHASAN 4.1. Hasil Pengecekan Kualitas Data Observasi Dengan TEQC Kualitas dari data observasi dapat ditunjukkan dengan melihat besar kecilnya nilai moving average dari multipath untuk
BAB III TEORI DASAR (3.1-1) dimana F : Gaya antara dua partikel bermassa m 1 dan m 2. r : jarak antara dua partikel
 BAB III TEORI DASAR 3.1 PRINSIP DASAR GRAVITASI 3.1.1 Hukum Newton Prinsip dasar yang digunakan dalam metoda gayaberat ini adalah hukum Newton yang menyatakan bahwa gaya tarik menarik dua titik massa m
BAB III TEORI DASAR 3.1 PRINSIP DASAR GRAVITASI 3.1.1 Hukum Newton Prinsip dasar yang digunakan dalam metoda gayaberat ini adalah hukum Newton yang menyatakan bahwa gaya tarik menarik dua titik massa m
METODE PENENTUAN ARAH KIBLAT DENGAN TEODOLIT
 METODE PENENTUAN ARAH KIBLAT DENGAN TEODOLIT (Pendekatan Sistem Koordinat Geografik dan Ellipsoid) Oleh : Akhmad Syaikhu A. PERSIAPAN Untuk melakukan pengukuran arah kiblat suatu tempat atau kota dengan
METODE PENENTUAN ARAH KIBLAT DENGAN TEODOLIT (Pendekatan Sistem Koordinat Geografik dan Ellipsoid) Oleh : Akhmad Syaikhu A. PERSIAPAN Untuk melakukan pengukuran arah kiblat suatu tempat atau kota dengan
BAB III PROSES GENERALISASI GARIS PANTAI DALAM PETA KEWENANGAN DAERAH DI WILAYAH LAUT MENGGUNAKAN ALGORITMA DOUGLAS-PEUCKER
 BAB III PROSES GENERALISASI GARIS PANTAI DALAM PETA KEWENANGAN DAERAH DI WILAYAH LAUT MENGGUNAKAN ALGORITMA DOUGLAS-PEUCKER III.1 Peta Dasar Peta yang digunakan untuk menentukan garis batas adalah peta
BAB III PROSES GENERALISASI GARIS PANTAI DALAM PETA KEWENANGAN DAERAH DI WILAYAH LAUT MENGGUNAKAN ALGORITMA DOUGLAS-PEUCKER III.1 Peta Dasar Peta yang digunakan untuk menentukan garis batas adalah peta
KLASIFIKASI PENGUKURAN DAN UNSUR PETA
 PERPETAAN - 2 KLASIFIKASI PENGUKURAN DAN UNSUR PETA Pemetaan dimana seluruh data yg digunakan diperoleh dengan melakukan pengukuran-pengukuran dilapangan disebut : Pemetaan secara terestris Pemetaan Extra
PERPETAAN - 2 KLASIFIKASI PENGUKURAN DAN UNSUR PETA Pemetaan dimana seluruh data yg digunakan diperoleh dengan melakukan pengukuran-pengukuran dilapangan disebut : Pemetaan secara terestris Pemetaan Extra
