BAB II PERSAMAAN DIFERENSIAL BIASA (PDB) ORDE SATU
|
|
|
- Liana Susman
- 7 tahun lalu
- Tontonan:
Transkripsi
1 BAB II PERSAMAAN DIFERENSIAL BIASA (PDB) ORDE SATU Tujuan Instruksional: Mampu memahami dan menyelesaikan PD orde-1 dg integrasi langsung, pemisahan variael. Mampu memahami dan menyelesaikan Persamaan Diferensial Linier Homogen orde satu. Mampu memahami dan menyelesaikan Persamaan Bernaoulli. Mampu memahami dan menyelesaikan PD Eksak dan Tak-eksak. PDB orde satu dapat dinyatakan dalam entuk = (, ) atau dalam entuk (, ) + (, ) = Penyelesaian PDB Orde Satu dgn Integrasi Langsung Jika PDB dapat disusun dalam entuk = (), maka persamaan terseut dapat diselesaikan dengan integrasi langsung. Contoh maka = = ( ) = Penyelesaian menggunakan program MATLAB seagai erikut: >> y=dsolve('dy= 3*x^2-6*x+5','x')
2 y= x^3-3*x^2+5*x+c1 Contoh: Maka sehingga = = = Penyelesaian menggunakan program MATLAB seagai erikut: >> y=dsolve('x*dy= 5*x^3 + 4','x') y=5/3*x^3+4*log(x)+c1 Nilai c tidak dapat ditentukan kecuali jika dalam persamaan di atas dieri keterangan syarat (seuah nilai y untuk x tertentu). Solusi dengan nilai konstanta semarang atau c diseut solusi umum/primitif, sedangkan solusi diseut khusus jika nilai c dapat dihitung. Contoh: Tentukan solusi khusus persamaan erikut jika y=3 untuk x=0: = 4 Penyelesaian = 4 = 4 maka = 4 = 4 + dengan mengetahui y=3 untuk x=0 dapat dihitung nilai c yaitu sehingga solusi khusus adalah: = = 4 + ; = 7 = 4 = Penyelesaian menggunakan program MATLAB seagai erikut: >> y=dsolve('exp(x)*dy=4','y(0)=3','x') y=-4*exp(-x)+7
3 Latihan Soal: Tentukan penyelesaian PD erikut: 1. = 2. = = = sin + cos 5. = sin 6. = e+ sin + cos Tentukan solusi PD dengan masalah nilai awal seagai erikut: 7. = ; (0) = 1 8. = ; (0) = 4 9. = ; (0) = = cos ; (0) = = 4 sin ; (0) = = e+ sin + cos ; (0) = Penyelesaian PDB Orde Satu Dengan Pemisahan Variael Jika persamaan diferensial erentuk = (, ), yaitu persamaan yang ruas kanannya dapat dinyatakan seagai perkalian atau pemagian fungsi x dan fungsi y, maka penyelesaian PD dengan cara memisahkan variaelnya sehingga faktor y isa kita kumpulkan dengan dy dan faktor x dengan dx. Contoh: Selesaikan PD erikut (1) = (1 + )(1 + )
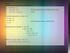
4 Pisahkan erdasarkan variaelnya untuk mendapatkan 1 = (1 + ) (1 + ) jika kita integrasikan kedua ruas menjadi: 1 = (1 + ) (1 + ) (1 + ) = Penyelesaian menggunakan program MATLAB seagai erikut: >> y=dsolve('dy = (1+x)*(1+y)') y=c3*exp(t*(x + 1)) 1 (2) = 0 dengan memisahkan variaelnya diperoleh: 9 = 4 selanjutnya tiap ruas diintegralkan dan didapatkan solusi: 9 2 = = = 9 =./ kurva f(x,y)=2x 2 +9/2y 2 -c y x Gamar 1 Keluarga Kurva =
5 Program MATLAB untuk Gamar 3 seagai erikut: clear all; clc; syms x y c fx='(2*x^2)+(9/2*y^2)-c' for c=-11:11 ezplot(eval(fx)) axis square axis equal hold on grid on end title('kurva f(x,y)=2x^2+9/2y^2-c') Latihan Soal: Selesaikan persamaan diferensial erikut dengan memisahkan variaelvariaelnya: 1. 2 = = 3. 2 = = = = = (:; )(:; 2) 8. 2 = (1 + ) 9. 2 = 2 :; = 2( + ) 11. ( + 2) + ( + 1) = ( + 1) + ( + 1) = 0
6 2.3 Persamaan Homogen sustitusi y=vx Tinjau persamaan diferensial = Persamaan di atas tidak dapat diselesaikan dengan cara memisahkan variaelnya. Dalam hal ini kita lakukan sustitusi y =vx, dengan v adalah fungsi x. Sehingga penyelesaiannya: dari y = vx dideferensialkan menjadi = < + < sehingga Persamaan sekarang menjadi: = 1 + 3< 2 < + < = 1 + 3< 2 < = 1 + 3< < = 1 + < < < = 1 kedua ruas diintegrasikan menjadi: < < = 1 sustitusi v=y/x didapatkan Latihan Soal: 2(1 + <) = + (1 + <) =. (1 + ) =. atau ( + ) =. Selesaikan persamaan diferensial erikut dengan sustitusi y=vx (=) ( 3 ) + 2 = 0 (>) A = 0 () 2 + = 0 () = + 2 :;( )
7 2.4 Persamaan Diferensial Linier dalam entuk CD CE + FD = G Untuk PD yang erentuk CD + FD = G dengan P dan Q fungsi x atau CE konstanta penyelesaianny dapat diperoleh dengan mengalikan kedua ruas dengan faktor integrasi Contoh, selesaikan PD Penyelesaian: H I = dari persamaan diperoleh P = -1 dan Q = x faktor integrasinya H I = jika kedua ruas persamaan dikalikan dengan maka: ( ) = (). =. J K =. L H I. M = H I. = H I. N sehingga penyelesaiannya ( ) =.. =. + =. + = 1 + / dari contoh di atas jika faktor integrasi H I = P, maka PD linier orde satu isa dinyatakan dalam entuk (P. ) = P. N dengan entuk di atas, penyelesaiannya menjadi: P. = PN + =Q=R. H I = H I. N + Latihan soal: Selesaikan PD linier erikut: = 0
8 = 3 3. = 4. + = sin 5. + = = = = = cos + ;S = = :; + ;S = ( + 2 ) = Tentukan Solusi PD untuk masalah nilai awal erikut: 14. = 1 ; (0) = = ; (10) = = ; (1) = = ; (0) = (1 + ) + = 0 ; (0) = 1
9 2.5 Persamaan Bernoulli erentuk CD CE + FD = G DT PD yang erentuk + U = N V dengan P dan Q fungsi x atau konstanta diselesaikan dengan cara: Pertama, memagi kedua ruas dengan V sehingga persamaan menjadi V + U 4V = N Kedua, misalkanlah W = 4V sehingga W = (4V ) supaya suku pertama didapat X didapat: W = (1 ) V maka persamaan pertama dikalikan (1-n) V (1 ) + (1 )U 4V = (1 )N W + U 4. W = N 4 (UY ZSS[) dengan P1 dan Q1 fungsi x atau konstanta. Persamaan terakhir dapat diselesaikan dengan faktor integrasi. Setelah diperoleh penyelesaian untuk z, dengn sustitusi W = 4V kita dapatkan y. contoh: selesaikan PD erikut: penyelesaian kedua ruas diagi menjadi + =. + 4 = misalkan = 4V, n=2 sehingga W = 4 dan X supaya suku pertama didapat X = maka persamaan dikali -1, diperoleh: 4 = W W = UY ZSS[ faktor integral H I dimana P = 4 maka
10 H I = H 4 = \V = \V]^ = 1 entuk umum penyelesaian PD linier didapat: P. = H I. N + sehingga 4. W = H 4. ( ) + X = + W = karena W = 4 maka 4 = = ( ) 4 Latihan soal: Selesaiakan PD Bernoulli erikut: 1. + = =. _ = ( 1) 2.6 Persamaan Diferensial Eksak PDB dalam entuk: (, ) + (, ) = 0 dikatakan eksak jika terdapat fungsi Q(x,y), sedemikian sehingga `a = (, ) ` dan `a = (, ). Dengan mengingat diferensial total dari fungsi Q(x, y), maka ` disimpulkan ahwa persamaan (, ) + (, ) = 0 eksak jika dan hanya jika: = Langkah-langkah untuk menyelesaikan PD Eksak adalah seagai erikut: Langkah 1. Tuliskan PD dalam entuk diferensial : Langkah 2. Uji ke-eksak-an PD: (, ) + (, ) = 0 =
11 Langkah 3. Jika eksak, integralkan M terhadap x atau N terhadap y. Misal dipilih M, maka : N(, ) = (, ) + c() Langkah 4. Turunkan Q terhadap y dan samakan hasilnya dengan N(x,y) (, ) = / (, )0 + c2 () Langkah 5. Integralkan g'( y) untuk memperoleh g(y) Langkah 6. Tuliskan penyelesaian umum dalam entuk implisit: Q(x, y) = C. Langkah 7. Tentukan C jika dierikan kondisi awal tertentu. Contoh: Selesaikan PDB Penyelesaian: = 3, y(0)=3 Langkah 1. Bentuk diferensial PD adalah : Langkah 2. Uji ke- eksak-an PD ini: ( 2) + ( 2) = 0 = 2 ; = 2 Langkah 3. Misal dipilih M untuk diintegralkan, maka : N(, ) = (, ) + c() = ( 2) + c() = c() Langkah 4. Menyamakan turunan Q(x,y) terhadap y dengan N(x,y): / c()0 = c 2 () = 2 c 2 () = Langkah 5. Integralkan g'( y), diperoleh :
12 c() = 1 3 Langkah 6. Penyelesaian umum dalam entuk implisit Q(x,y)=c: = Langkah 7. Dengan kondisi awal y(0) = 3, diperoleh C = 9, sehingga Latihan soal: penyelesaian khususnya adalah : = 9 Uji ke-eksakan persamaan diferensial erikut dan selesaikan: 1. = = , (0) = 3 3. (9 + 1) (4 ) = 0 4. = cos sin 5. ( ) ( + ) = 0 6. ( ;S 2;S) + ( :; + 2:;) = 0 7. ( 2) ( 2 + 1) = 0 8. Tentukan N(x,y)sehingga ( + ) + (, ) = 0 eksak! 9. Tentukan M(x,y) shg (, ) + ( sin + ln ) = 0 eksak! 2.7 Persamaan Diferensial Tak-Eksak Jika suatu PD orde satu erentuk mempunyai sifat: (, ) + (, ) = 0 maka PD terseut diseut PD Tak-Eksak. Suatu PD tak eksak dapat diuah ke PD eksak dengan mengalikan persamaan dengan suatu faktor yang tepat, yang diseut faktor pengintegralan (integrating factor). Pada agian seelumnya,
13 kita mengenal faktor integral: P() = H I() persamaan diferensial linier order satu dalam entuk: CD + F(E)D = G(E) CE untuk menyelesaikan Faktor integral P() = H I() akan memawa persamaan diferensial linier order satu erentuk + U() = N() menjadi PD eksak. Secara umum suatu faktor integral adalah faktor µ(x, y) dapat menguah persamaan diferensial tidak eksak menjadi persamaan diferensial eksak. Contoh: Tunjukkan ahwa x dy + (2y xex )dx = 0 tidak eksak, tetapi dengan mengalikan dengan faktor µ = x PD terseut menjadi eksak. Kemudian selesaikan! Penyelesaian : Uji ke-eksak-an, (2 ) = 2 = () = 1 Jadi PD adalah tidak eksak. Dengan mengalikan faktor integral x diperoleh: + (2 ) = 0 UY f;=f = (2 ) = 2 ; = ( ) = 2 dari langkah-langkah penyelesaian PD eksak, maka: jika diketahui: maka jadi solusi PD adalah: N(, ) = c() N(, ) = (, ) + c 2 () = c 2 () = 0 c() = 0 N(, ) = =
14 2.8 Menentukan Faktor Itegrasi Jika (, ) + (, ) = 0 PD tak eksak dan P(, ) faktor integrasi, maka P(, )(, ) + P(, )(, ) = 0 adalah PD eksak, sehingga ada eerapa kasus, yaitu: P = P atau P + P = P + P / 0 P = P P / P P 0 P = / 0 (1) (, ) = P(), faktor integrasi hanya fungsi x, maka: / P P 0 P = / 0 P A / 0 = P P 1 / P P = 0 / 0 P = `h / P = H `i ` ` 0 i
15 @ jk jl jm jn A Sehingga jika i menghasilkan fungsi x saja maka P(, ) = P(). (2) P(, ) = P(), faktor integrasi hanya fungsi y, dengan analisis spt (1) maka: `h / P = H `i ` ` 0 h Sehingga jk jl jm jn A h menghasilkan fungsi y, maka P(, ) = P(). (3) P(, ) = P(), jika (4) P(, ) = P( + ), jika (5) P(, ) = P( ), jika (6) P(, ) = P( + ), jk jl jm jn A menghasilkan fungsi jk jl jm jn A jk jl jm jn A i8h menghasilkan fungsi + menghasilkan jk jl jm jn A i8h menghasilkan fungsi + Kesimpulan: Faktor integrasi ditentukan dengan menghitung `h ` `i ` kemudian memaginya sehingga diperoleh fungsi yang mandiri. Contoh: Uji ke-eksakan Persamaan Diferensial + (2 ) = 0 Tentukan faktor integral-nya dan erikan solusi PD-nya! Penyelesaian: (, ) = (2 ) dan (, ) = = (2 ) = 2 ; = 1 o=s Faktor integrasi: (UY Q=ff;=f)
16 = 2 1 = 1 P = H4 = dari sini seperti contoh seelumnya dapat ditunjukkan dengan mengalikan x pada persamaan dihasilkan PD eksak. Dan solusi PD seperti diahas pada contoh seelumnya didapatkan: Latihan soal: = Tunjukkan ahwa PD erikut takeksak, kemudian tentukan faktor integrasi serta uji ke-eksakannya, selanjutnya dapatkan solusi umum PD! (3 + 2 ) = 0 2. (3 2) + ( 1 ) = 0 3. ( ) + ( + + 1) = 0 4. ( 2 ) (1 ) = 0
17
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: Penyelesaian PDB orde satu dengan integrasi secara langsung Jika PDB dapat disusun dalam bentuk,
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: Penyelesaian PDB orde satu dengan integrasi secara langsung Jika PDB dapat disusun dalam bentuk,
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: = f(x, y) M(x, y) + N(x, y) = 0 Penyelesaian PDB orde satu dengan integrasi secara langsung Jika
BAB II PERSAMAAN DIFERENSIAL BIASA(PDB) ORDE SATU PDB orde satu dapat dinyatakan dalam: atau dalam bentuk: = f(x, y) M(x, y) + N(x, y) = 0 Penyelesaian PDB orde satu dengan integrasi secara langsung Jika
PENGANTAR Ketua Jurusan Teknik Elektro Fakultas Teknik UB
 PENGANTAR Ketua Jurusan Teknik Elektro Fakultas Teknik UB Proses pembelajaran melalui transfer ilmu pengetahuan dan teknologi merupakan faktor penting dalam mewujudkan keberhasilan mahasiswa untuk memahami
PENGANTAR Ketua Jurusan Teknik Elektro Fakultas Teknik UB Proses pembelajaran melalui transfer ilmu pengetahuan dan teknologi merupakan faktor penting dalam mewujudkan keberhasilan mahasiswa untuk memahami
PERSAMAAN DIFERENSIAL (PD)
 PERSAMAAN DIFERENSIAL (PD) A. PENGERTIAN Persamaan yang mengandung variabel dan beberapa fungsi turunan terhadap variabel tersebut. CONTOH : + 5 5 0 disebut PD orde I + 6 + 7 0 disebut PD orde II B. PEMBENTUKAN
PERSAMAAN DIFERENSIAL (PD) A. PENGERTIAN Persamaan yang mengandung variabel dan beberapa fungsi turunan terhadap variabel tersebut. CONTOH : + 5 5 0 disebut PD orde I + 6 + 7 0 disebut PD orde II B. PEMBENTUKAN
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL
 BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
BAB I KONSEP DASAR PERSAMAAN DIFERENSIAL Tujuan Instruksional: Mampu memahami definisi Persamaan Diferensial Mampu memahami klasifikasi Persamaan Diferensial Mampu memahami bentuk bentuk solusi Persamaan
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA
 PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
PERSAMAAN DIFERENSIAL I PERSAMAAN DIFERENSIAL BIASA Persamaan Diferensial Biasa 1. PDB Tingkat Satu (PDB) 1.1. Persamaan diferensial 1.2. Metode pemisahan peubah dan PD koefisien fungsi homogen 1.3. Persamaan
7.1. Residu dan kutub Pada bagian sebelumnya telah kita pelajari bahwa suatu titik z 0 disebut titik singular dari f (z)
 BAB 7 RESIDU DAN PENGGUNAAN 7 idu dan kutu Pada agian seelumnya telah kita pelajari ahwa suatu titik diseut titik singular dari f () ila f () gagal analitik di tetapi analitik pada suatu titik dari setiap
BAB 7 RESIDU DAN PENGGUNAAN 7 idu dan kutu Pada agian seelumnya telah kita pelajari ahwa suatu titik diseut titik singular dari f () ila f () gagal analitik di tetapi analitik pada suatu titik dari setiap
7.1. Residu dan kutub Pada bagian sebelumnya telah kita pelajari bahwa suatu titik z 0 disebut titik singular dari f (z)
 Ba 7 Residu dan Penggunaannya BAB 7 RESIDU DAN PENGGUNAAN 7 Residu dan kutu Pada agian seelumnya telah kita pelajari ahwa suatu titik diseut titik singular dari f () ila f () gagal analitik di tetapi analitik
Ba 7 Residu dan Penggunaannya BAB 7 RESIDU DAN PENGGUNAAN 7 Residu dan kutu Pada agian seelumnya telah kita pelajari ahwa suatu titik diseut titik singular dari f () ila f () gagal analitik di tetapi analitik
KONSEP DASAR PERSAMAAN DIFERENSIAL
 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu fungsi (dasar). Sebagai
PERSAMAAN DIFFERENSIAL ORDE I. Nurdinintya Athari
 PERSAMAAN DIFFERENSIAL ORDE I Nurdininta Athari Definisi PERSAMAAN DIFERENSIAL Persamaan diferensial adalah suatu persamaan ang memuat satu atau lebih turunan fungsi ang tidak diketahui. Jika persamaan
PERSAMAAN DIFFERENSIAL ORDE I Nurdininta Athari Definisi PERSAMAAN DIFERENSIAL Persamaan diferensial adalah suatu persamaan ang memuat satu atau lebih turunan fungsi ang tidak diketahui. Jika persamaan
BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I
 BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I. Pengertian PD, Orde (tingkat), & Derajat (Pangkat) Persamaan diferensial adalah suatu persamaan yang memuat derivatifderivatif (turunan) sekurang-kurangnya derivatif
BAB I PERSAMAAN DIFERENSIAL LINIER ORDE I. Pengertian PD, Orde (tingkat), & Derajat (Pangkat) Persamaan diferensial adalah suatu persamaan yang memuat derivatifderivatif (turunan) sekurang-kurangnya derivatif
Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui.
 1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
1 Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan fungsi yang tidak diketahui. Jika persamaan diferensial memiliki satu peubah tak bebas maka disebut Persamaan Diferensial
disebut Persamaan Diferensial Parsial (PDP).
 Persamaan Diferensial Febrizal, MT Pendahuluan Persamaandiferensial i merupakan persamaan yang berkaitan dengan turunan dari suatu fungsi atau memuat suku suku dari fungsi tersebut dan atau turunannya.
Persamaan Diferensial Febrizal, MT Pendahuluan Persamaandiferensial i merupakan persamaan yang berkaitan dengan turunan dari suatu fungsi atau memuat suku suku dari fungsi tersebut dan atau turunannya.
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL
 Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
Pertemuan 1 dan 2 KONSEP DASAR PERSAMAAN DIFERENSIAL A. PENGERTIAN PERSAMAAN DIFERENSIAL Dalam pelajaran kalkulus, kita telah berkenalan dan mengkaji berbagai macam metode untuk mendiferensialkan suatu
BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx +
 BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx + N(x y) = 0 (2.1) 2.1.1 PDB Eksak
BAB 1 Konsep Dasar 1 BAB 2 PDB Linier Order Satu 2.1 PDB Linier Order Satu Homogen PDB order satu dapat dinyatakan dalam atau dalam bentuk derivatif = f(x y) dx M(x y)dx + N(x y) = 0 (2.1) 2.1.1 PDB Eksak
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU
 MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
MATERI 2 MATEMATIKA TEKNIK 1 PERSAMAAN DIFERENSIAL ORDE SATU 1 Persamaan diferensial orde satu Persamaan diferensial menyatakan hubungan dinamik antara variabel bebas dan variabel tak bebas, maksudnya
Bab 3 PERUMUSAN MODEL KINEMATIK DDMR
 Ba 3 PERUMUSAN MODEL KINEMATIK DDMR Model kinematika diperlukan dalam menganalisis pergerakan suatu root moil. Model kinematik merupakan analisis pergerakan sistem yang direpresentasikan secara matematis
Ba 3 PERUMUSAN MODEL KINEMATIK DDMR Model kinematika diperlukan dalam menganalisis pergerakan suatu root moil. Model kinematik merupakan analisis pergerakan sistem yang direpresentasikan secara matematis
PERSAMAAN DIFERENSIAL LINIER NON HOMOGEN
 LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - I 1. Pendahuluan Pengertian Persamaan Diferensial Metoda Penyelesaian -contoh Aplikasi 1 1.1. Pengertian Persamaan Differensial Secara Garis Besar Persamaan
Adalah : hubungan antara variabel bebas x, variabel
 Adalah : hubungan antara variabel bebas, variabel Bentuk Umum : bebas dan turunanna. d d F(,,, n d,..., ) n Persamaan differensial (PD) menatakan hubungan dinamik, maksudna hubungan tersebut memuat besaran
Adalah : hubungan antara variabel bebas, variabel Bentuk Umum : bebas dan turunanna. d d F(,,, n d,..., ) n Persamaan differensial (PD) menatakan hubungan dinamik, maksudna hubungan tersebut memuat besaran
BAB 2 PERSAMAAN DIFFERENSIAL BIASA
 BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
BAB 2 BIASA 2.1. KONSEP DASAR Persamaan Diferensial (PD) Biasa adalah persamaan yang mengandung satu atau beberapa penurunan y (varibel terikat) terhadap x (variabel bebas) yang tidak spesifik dan ditentukan
BAB I PERSAMAAN DIFERENSIAL BIASA ORDE SATU
 BAB I PERSAMAAN DIFERENSIAL BIASA ORDE SATU Definisi: Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen x, suatu variabel dependen y, dan satu atau lebih turunan
BAB I PERSAMAAN DIFERENSIAL BIASA ORDE SATU Definisi: Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen x, suatu variabel dependen y, dan satu atau lebih turunan
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO. Mohamad Sidiq
 MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO REFERENSI E-BOOK REFERENSI ONLINE SOS Mathematics http://www.sosmath.com/diffeq/diffeq.html Wolfram Research Math World http://mathworld.wolfram.com/ordinarydifferentialequation.h
MATEMATIKA TEKNIK 2 S1-TEKNIK ELEKTRO REFERENSI E-BOOK REFERENSI ONLINE SOS Mathematics http://www.sosmath.com/diffeq/diffeq.html Wolfram Research Math World http://mathworld.wolfram.com/ordinarydifferentialequation.h
TRIGONOMETRI. Bab. Di unduh dari : Bukupaket.com. Aturan sinus Aturan kosinus Luas segitiga A. KOMPETENSI DASAR DAN PENGALAMAN BELAJAR
 a 6 TRIGONOMETRI A. KOMPETENSI DASAR DAN PENGALAMAN ELAJAR Kompetensi Dasar 1. Menghayati pola hidup disiplin, kritis, ertanggungjawa, konsisten dan jujur serta menerapkannya dalam kehidupan sehari hari..
a 6 TRIGONOMETRI A. KOMPETENSI DASAR DAN PENGALAMAN ELAJAR Kompetensi Dasar 1. Menghayati pola hidup disiplin, kritis, ertanggungjawa, konsisten dan jujur serta menerapkannya dalam kehidupan sehari hari..
1. SISTEM TERTUTUP HOMOGEN
 BAB II . SISEM EUU HOMOGEN Sistem tertutup adalah sistem yang tidak ada transfer massa antara sistem dan sekeliling W Sistem n out = 0 dn i = 0 (2.) i =, 2, 3,... n in = 0 Q idak ada perpindahan internal
BAB II . SISEM EUU HOMOGEN Sistem tertutup adalah sistem yang tidak ada transfer massa antara sistem dan sekeliling W Sistem n out = 0 dn i = 0 (2.) i =, 2, 3,... n in = 0 Q idak ada perpindahan internal
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL
 BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB I DASAR-DASAR PEMODELAN MATEMATIKA DENGAN PERSAMAAN DIFERENSIAL Pendahuluan Persamaan diferensial adalah persamaan yang memuat diferensial Kita akan membahas tentang Persamaan Diferensial Biasa yaitu
BAB VI DEFLEKSI BALOK
 VI DEFEKSI OK.. Pendahuluan Semua alok akan terdefleksi (atau melentur) dari kedudukannya apaila tereani. Dalam struktur angunan, seperti : alok dan plat lantai tidak oleh melentur terlalu erleihan untuk
VI DEFEKSI OK.. Pendahuluan Semua alok akan terdefleksi (atau melentur) dari kedudukannya apaila tereani. Dalam struktur angunan, seperti : alok dan plat lantai tidak oleh melentur terlalu erleihan untuk
COURSE NOTE : Sistem Persamaan Liniear
 COURSE NOTE : Sistem Persamaan Liniear PERSAMAAN LINIEAR Secara umum kita mendefinisikan persamaan liniear dalam n variale x 1 x x n seagai erikut : dengan a1 a... an adalah konstanta real. a1x 1 ax ax...
COURSE NOTE : Sistem Persamaan Liniear PERSAMAAN LINIEAR Secara umum kita mendefinisikan persamaan liniear dalam n variale x 1 x x n seagai erikut : dengan a1 a... an adalah konstanta real. a1x 1 ax ax...
4. Dibawah ini persamaan diferensial ordo dua berderajat satu adalah
 Pilihlah jawaban yang benar dengan cara mencakra huruf didepan jawaban yang saudara anggap benar pada lembar jawaban 1. Dibawah ini bentuk persamaan diferensial biasa linier homogen adalah a. y + xy =
Pilihlah jawaban yang benar dengan cara mencakra huruf didepan jawaban yang saudara anggap benar pada lembar jawaban 1. Dibawah ini bentuk persamaan diferensial biasa linier homogen adalah a. y + xy =
BAB 1 PERSAMAAN DIFERENSIAL ORDER SATU
 BAB PERSAAA DIFERESIAL ORDER SATU PEDAHULUA Persamaan Diferensial adalah salah satu cabang ilmu matematika ang banak digunakan dalam memahami permasalahan-permasalahan di bidang fisika dan teknik Persamaan
BAB PERSAAA DIFERESIAL ORDER SATU PEDAHULUA Persamaan Diferensial adalah salah satu cabang ilmu matematika ang banak digunakan dalam memahami permasalahan-permasalahan di bidang fisika dan teknik Persamaan
E-LEARNING MATEMATIKA
 MODUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYADIN EKO RAHARJO, M.PD. NIP. 9705 00 00 Penulisan Modul e Learning ini diiayai oleh dana DIPA BLU UNY TA 00 Sesuai dengan Surat Perjanjian Pelaksanaan
MODUL E-LEARNING E-LEARNING MATEMATIKA Oleh : NURYADIN EKO RAHARJO, M.PD. NIP. 9705 00 00 Penulisan Modul e Learning ini diiayai oleh dana DIPA BLU UNY TA 00 Sesuai dengan Surat Perjanjian Pelaksanaan
PERSAMAAN DIFFERENSIAL LINIER
 PERSAMAAN DIFFERENSIAL LINIER Persamaan Differensial Linier Pengertian : Suatu persamaan differensial orde satu dikatakan linier jika persamaan tersebut dapat dituliskan sbb: y + p x y = r(x) (1) linier
PERSAMAAN DIFFERENSIAL LINIER Persamaan Differensial Linier Pengertian : Suatu persamaan differensial orde satu dikatakan linier jika persamaan tersebut dapat dituliskan sbb: y + p x y = r(x) (1) linier
1). Definisi Relasi Relasi dari dua himpunan A dan B adalah pemasangan anggota-anggota A dengan anggota B.
 Bayangkan suatu fungsi seagai seuah mesin, misalnya mesin hitung. Ia mengamil suatu ilangan (masukan), maka fungsi memproses ilangan yang masuk dan hasil produksinya diseut keluaran. x Masukan Fungsi f
Bayangkan suatu fungsi seagai seuah mesin, misalnya mesin hitung. Ia mengamil suatu ilangan (masukan), maka fungsi memproses ilangan yang masuk dan hasil produksinya diseut keluaran. x Masukan Fungsi f
Persamaan Differensial Biasa
 Bab 7 cakul fi5080 by khbasar; sem1 2010-2011 Persamaan Differensial Biasa Dalam banyak persoalan fisika, suatu topik sering dinyatakan dalam bentuk perubahan (laju perubahan). Telah disinggung sebelumnya
Bab 7 cakul fi5080 by khbasar; sem1 2010-2011 Persamaan Differensial Biasa Dalam banyak persoalan fisika, suatu topik sering dinyatakan dalam bentuk perubahan (laju perubahan). Telah disinggung sebelumnya
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Jurusan Matematika FMIPA-IPB
 Jurusan Matematika FMIPA-IPB Ujian Kedua Semester Pendek T.A 4/5 KALKULUS/KALKULUS Jum at, Agustus 4 (Waktu : jam) SETIAP SOAL BERNILAI. Tentukan (a) + (b) p 4 + 5. Periksa apakah Teorema Nilai Rata-rata
Jurusan Matematika FMIPA-IPB Ujian Kedua Semester Pendek T.A 4/5 KALKULUS/KALKULUS Jum at, Agustus 4 (Waktu : jam) SETIAP SOAL BERNILAI. Tentukan (a) + (b) p 4 + 5. Periksa apakah Teorema Nilai Rata-rata
Metode Simpleks Diperbaiki (Revised Simplex Method) Materi Bahasan
 /7/ Metode Simpleks Diperaiki (Revised Simple Method) Kuliah TI Penelitian Operasional I Materi ahasan Dasar-dasar aljaar dari metode simpleks Metode simpleks yang diperaiki TI Penelitian Operasional I
/7/ Metode Simpleks Diperaiki (Revised Simple Method) Kuliah TI Penelitian Operasional I Materi ahasan Dasar-dasar aljaar dari metode simpleks Metode simpleks yang diperaiki TI Penelitian Operasional I
PERSAMAAN DIFERENSIAL ORDE SATU
 Kode Modul MTL. OTO 207-02 Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif PERSAMAAN DIFERENSIAL ORDE SATU i L C d i V i = L ----- d t Penyusun : Martubi, M.Pd., M.T. Sistem Perencanaan Penyusunan
Kode Modul MTL. OTO 207-02 Fakultas Teknik UNY Jurusan Pendidikan Teknik Otomotif PERSAMAAN DIFERENSIAL ORDE SATU i L C d i V i = L ----- d t Penyusun : Martubi, M.Pd., M.T. Sistem Perencanaan Penyusunan
BAB II PERSAMAAN DIFERENSIAL ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
PENYELESAIAN MODEL RANGKAIAN LISTRIK RL DAN RC SERI Oleh: 1 Ir. SIGIT KUSMARYANTO, M.Eng.
 PENYELESAIAN MODEL RANGKAIAN LISTRIK RL DAN RC SERI Oleh: 1 Ir. SIGIT KUSMARYANTO, M.Eng. 1 Teknik Elektro, http://sigitkus@ub.ac.id Pengantar: Modul ini menjelaskan pemodelan rangkaian listrik RL dan
PENYELESAIAN MODEL RANGKAIAN LISTRIK RL DAN RC SERI Oleh: 1 Ir. SIGIT KUSMARYANTO, M.Eng. 1 Teknik Elektro, http://sigitkus@ub.ac.id Pengantar: Modul ini menjelaskan pemodelan rangkaian listrik RL dan
Bab III Model Difusi Oksigen di Jaringan dengan Laju Konsumsi Konstan
 Ba III Model Difusi Oksigen di Jaringan dengan Laju Konsumsi Konstan Pada a ini, akan diahas penyearan oksigen di pemuluh kapiler dan jaringan, dimana sel-sel di jaringan diasumsikan mengkonsumsi oksigen
Ba III Model Difusi Oksigen di Jaringan dengan Laju Konsumsi Konstan Pada a ini, akan diahas penyearan oksigen di pemuluh kapiler dan jaringan, dimana sel-sel di jaringan diasumsikan mengkonsumsi oksigen
perpindahan, kita peroleh persamaan differensial berikut :
 1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
1.1 Pengertian Persamaan Differensial Banyak sekali masalah terapan (dalam ilmu teknik, ilmu fisika, biologi, kimia, sosial, dan lain-lain), yang telah dirumuskan dengan model matematika dalam bentuk persamaan
PERSAMAAN DAN PERTIDAKSAMAAN
 PERSAMAAN DAN PERTIDAKSAMAAN Sumer: Art & Gallery 44 Matematika X SMK Kelompok: Penjualan dan Akuntansi Standar kompetensi persamaan dan pertidaksamaan linier dan kuadrat terdiri atas tiga kompetensi dasar.
PERSAMAAN DAN PERTIDAKSAMAAN Sumer: Art & Gallery 44 Matematika X SMK Kelompok: Penjualan dan Akuntansi Standar kompetensi persamaan dan pertidaksamaan linier dan kuadrat terdiri atas tiga kompetensi dasar.
Persamaan Diferensial
 Orde Satu Jurusan Matematika FMIPA-Unud Senin, 18 Desember 2017 Orde Satu Daftar Isi 1 Pendahuluan 2 Orde Satu Apakah Itu? Solusi Pemisahan Variabel Masalah Gerak 3 4 Orde Satu Pendahuluan Dalam subbab
Orde Satu Jurusan Matematika FMIPA-Unud Senin, 18 Desember 2017 Orde Satu Daftar Isi 1 Pendahuluan 2 Orde Satu Apakah Itu? Solusi Pemisahan Variabel Masalah Gerak 3 4 Orde Satu Pendahuluan Dalam subbab
PERSAMAAN DIFERENSIAL BIASA ORDE SATU
 PERSAMAAN DIFERENSIAL BIASA ORDE SATU Definisi: Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen x, suatu variabel dependen y, dan satu atau lebih turunan y terhadap
PERSAMAAN DIFERENSIAL BIASA ORDE SATU Definisi: Persamaan diferensial adalah suatu hubungan yang terdapat antara suatu variabel independen x, suatu variabel dependen y, dan satu atau lebih turunan y terhadap
PENGANTAR MATEMATIKA TEKNIK 1. By : Suthami A
 PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
PENGANTAR MATEMATIKA TEKNIK 1 By : Suthami A MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK 1??? MATEMATIKA TEKNIK Matematika sebagai ilmu dasar yang digunakan sebagai alat pemecahan masalah di bidang keteknikan
Aplikasi Geometri pada Permainan Dinamis Non- Kooperatif Skalar Waktu tak Berhingga
 Seminar Nasional eknologi Informasi, Komunikasi dan Industri (SNIKI) 7 ISSN :85-99 Pekanaru, Novemer 5 Aplikasi Geometri pada Permainan Dinamis Non- Kooperatif Skalar Waktu tak Berhingga Nilwan Andiraja
Seminar Nasional eknologi Informasi, Komunikasi dan Industri (SNIKI) 7 ISSN :85-99 Pekanaru, Novemer 5 Aplikasi Geometri pada Permainan Dinamis Non- Kooperatif Skalar Waktu tak Berhingga Nilwan Andiraja
BAB 1 PENDAHULUAN. Masalah kependudukan di Indonesia merupakan masalah penting yang perlu
 BAB 1 PENDAHULUAN 1.1 Latar Belakang Masalah kependudukan di Indonesia merupakan masalah penting yang perlu mendapat perhatian dan pemahasan serius dari pemerintah dan ahli kependudukan. Bila para ahli
BAB 1 PENDAHULUAN 1.1 Latar Belakang Masalah kependudukan di Indonesia merupakan masalah penting yang perlu mendapat perhatian dan pemahasan serius dari pemerintah dan ahli kependudukan. Bila para ahli
LAJU PERTUMBUHAN BAKTERI S. Aerous MELALUI PENDEKATAN PERSAMAAN DIFERENSIAL
 LAJU PERTUMBUHAN BAKTERI S. Aerous MELALUI PENDEKATAN PERSAMAAN DIFERENSIAL Nurdeni 1, Witri Lestari 2, dan Seruni 3 1 Program Studi Pendidikan Matematika, FTMIPA, Universitas Indraprasta PGRI [Email:
LAJU PERTUMBUHAN BAKTERI S. Aerous MELALUI PENDEKATAN PERSAMAAN DIFERENSIAL Nurdeni 1, Witri Lestari 2, dan Seruni 3 1 Program Studi Pendidikan Matematika, FTMIPA, Universitas Indraprasta PGRI [Email:
BAB II FUNGSI, PERSAMAAN DAN PERTIDAKSAMAAN KUADRAT
 BAB II FUNGSI, PERSAMAAN DAN PERTIDAKSAMAAN KUADRAT Standar kompetensi:. Memecahkan masalah yang erkaitan dengan fungsi, persamaan dan pertidaksamaan kuadrat Kompetensi Dasar:. Memahami konsep fungsi.
BAB II FUNGSI, PERSAMAAN DAN PERTIDAKSAMAAN KUADRAT Standar kompetensi:. Memecahkan masalah yang erkaitan dengan fungsi, persamaan dan pertidaksamaan kuadrat Kompetensi Dasar:. Memahami konsep fungsi.
BAB PDB Linier Order Satu
 BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
BAB II PERSAMAAN DIFERENSIAL ORDE SATU
 BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
BAB II PERSAMAAN DIFERENSIAL ORDE SATU Kompetensi Mahasiswa diharapkan: 1. Mengenali bentuk PD orde satu dengan variabel terpisah dan tak terpisah.. Dapat mengubah bentuk PD tak terpisah menjadi terpisah
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Linier Non Homogen Tk. 2 (Differential: Linier Non Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Solusi umum merupakan jumlah
TKS 4003 Matematika II Persamaan Diferensial Linier Non Homogen Tk. 2 (Differential: Linier Non Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Solusi umum merupakan jumlah
Pertemuan Kesatu. Matematika III. Oleh Mohammad Edy Nurtamam, S.Pd., M.Si. Page 1.
 Pertemuan Kesatu Matematika III Oleh Mohammad Edy Nurtamam, S.Pd., M.Si Page 1 Materi 1. Persamaan Diferensial Orde I Pengenalan bentuk dasar Pers. Diff. Orde I. Definisi Derajat,Orde. Konsep Pemisahan
Pertemuan Kesatu Matematika III Oleh Mohammad Edy Nurtamam, S.Pd., M.Si Page 1 Materi 1. Persamaan Diferensial Orde I Pengenalan bentuk dasar Pers. Diff. Orde I. Definisi Derajat,Orde. Konsep Pemisahan
dy = f(x,y) = p(x) q(y), dx dy = p(x) dx,
 5. Persamaan Diferensian Dengan Variabel Terpisah Persamaan diferensial berbentuk y = f(), dengan f suatu fungsi kontinu pada suatu interval real, dapat dicari penyelesaiannya dengan cara mengintegralkan
5. Persamaan Diferensian Dengan Variabel Terpisah Persamaan diferensial berbentuk y = f(), dengan f suatu fungsi kontinu pada suatu interval real, dapat dicari penyelesaiannya dengan cara mengintegralkan
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Linier Homogen Tk. 2 (Differential: Linier Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya PD linier homogen orde 2 Bentuk
TKS 4003 Matematika II Persamaan Diferensial Linier Homogen Tk. 2 (Differential: Linier Homogen Orde 2) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya PD linier homogen orde 2 Bentuk
PERSAMAAN FUNGSI KUADRAT-1
 PERSAMAAN FUNGSI KUADRAT- Mata Pelajaran K e l a s Nomor Modul : Matematika : X (Sepuluh) : MAT.X.0 Penulis Pengkaji Materi Pengkaji Media : Drs. Suyanto : Dra.Wardani Rahayu, M.Si. : Drs. Soekiman DAFTAR
PERSAMAAN FUNGSI KUADRAT- Mata Pelajaran K e l a s Nomor Modul : Matematika : X (Sepuluh) : MAT.X.0 Penulis Pengkaji Materi Pengkaji Media : Drs. Suyanto : Dra.Wardani Rahayu, M.Si. : Drs. Soekiman DAFTAR
Metode Koefisien Tak Tentu untuk Penyelesaian PD Linier Homogen Tak Homogen orde-2 Matematika Teknik I_SIGIT KUSMARYANTO
 Metode Koefisien Tak Tentu untuk Penyelesaian Persamaan Diferensial Linier Tak Homogen orde-2 Solusi PD pada PD Linier Tak Homogen ditentukan dari solusi umum PD Linier Homogen dan PD Linier Tak Homogen.
Metode Koefisien Tak Tentu untuk Penyelesaian Persamaan Diferensial Linier Tak Homogen orde-2 Solusi PD pada PD Linier Tak Homogen ditentukan dari solusi umum PD Linier Homogen dan PD Linier Tak Homogen.
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Linier Homogen & Non Homogen Tk. n (Differential: Linier Homogen & Non Homogen Orde n) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
TKS 4003 Matematika II Persamaan Diferensial Linier Homogen & Non Homogen Tk. n (Differential: Linier Homogen & Non Homogen Orde n) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
METODE SIMPLEKS PRIMAL MENGGUNAKAN WORKING BASIS
 JURNAL MATEMATIKA DAN KOMPUTER Vol 6 No 3, 167-178, Desemer 2003, ISSN : 1410-8518 METODE SIMPLEKS PRIMAL MENGGUNAKAN WORKING BASIS Sunarsih dan Ahmad Khairul Ramdani Jurusan Matematika FMIPA UNDIP ABSTRAK
JURNAL MATEMATIKA DAN KOMPUTER Vol 6 No 3, 167-178, Desemer 2003, ISSN : 1410-8518 METODE SIMPLEKS PRIMAL MENGGUNAKAN WORKING BASIS Sunarsih dan Ahmad Khairul Ramdani Jurusan Matematika FMIPA UNDIP ABSTRAK
Pengantar Metode Perturbasi Bab 4. Ekspansi Asimtotik pada Persamaan Diferensial Biasa
 Pengantar Metode Perturbasi Bab 4. Ekspansi Asimtotik pada Persamaan Diferensial Biasa Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas PAM 454 KAPITA SELEKTA MATEMATIKA TERAPAN II Semester
Pengantar Metode Perturbasi Bab 4. Ekspansi Asimtotik pada Persamaan Diferensial Biasa Mahdhivan Syafwan Jurusan Matematika FMIPA Universitas Andalas PAM 454 KAPITA SELEKTA MATEMATIKA TERAPAN II Semester
PENYELESAIAN MODEL RANGKAIAN LISTRIK ORDE-2 Oleh: Ir. Sigit Kusmaryanto, M.Eng
 PENYELESAIAN MODEL RANGKAIAN LISTRIK ORDE-2 Oleh: Ir. Sigit Kusmaryanto, M.Eng Dua fenomena fisik berbeda (yaitu: sistem gerak benda pada pegas dan rangkaian listrik) menghasilkan model persamaan matematika
PENYELESAIAN MODEL RANGKAIAN LISTRIK ORDE-2 Oleh: Ir. Sigit Kusmaryanto, M.Eng Dua fenomena fisik berbeda (yaitu: sistem gerak benda pada pegas dan rangkaian listrik) menghasilkan model persamaan matematika
METODE SIMPLEKS PRIMAL MENGGUNAKAN WORKING BASIS
 JURNAL MATEMATIKA DAN KOMPUTER Vol 6 No 3, 118-177, Desemer 2003, ISSN : 1410-8518 METODE SIMPLEKS PRIMAL MENGGUNAKAN WORKING BASIS Sunarsih dan Ahmad Khairul Ramdani Jurusan Matematika FMIPA UNDIP ABSTRAK
JURNAL MATEMATIKA DAN KOMPUTER Vol 6 No 3, 118-177, Desemer 2003, ISSN : 1410-8518 METODE SIMPLEKS PRIMAL MENGGUNAKAN WORKING BASIS Sunarsih dan Ahmad Khairul Ramdani Jurusan Matematika FMIPA UNDIP ABSTRAK
4. Mononom dan Polinom
 Darpulic www.darpulic.com 4. Mononom dan Polinom Sudaratno Sudirham Mononom adalah pernataan tunggal ang erentuk k n, dengan k adalah tetapan dan n adalah ilangan ulat termasuk nol. Fungsi polinom merupakan
Darpulic www.darpulic.com 4. Mononom dan Polinom Sudaratno Sudirham Mononom adalah pernataan tunggal ang erentuk k n, dengan k adalah tetapan dan n adalah ilangan ulat termasuk nol. Fungsi polinom merupakan
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - II
 PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - II c. Metoda Persamaan Differensial Pasti (Exact) Pada kalkulus bahwa jika suatu fungsi u(x,y) mempunyai turunan parsial yang sifatnya kontinyu, turunan pasti
PENYELESAIAN PERSAMAAN DIFFERENSIAL ORDE 1 - II c. Metoda Persamaan Differensial Pasti (Exact) Pada kalkulus bahwa jika suatu fungsi u(x,y) mempunyai turunan parsial yang sifatnya kontinyu, turunan pasti
Bab 2 Bentuk Aljabar. A. Pengertian Bentuk Aljabar. B. Suku-suku Sejenis. C. Penjumlahan dan Pengurangan. Contoh Soal dan Pembahasan:
 Moh. Fatkoer Rohman 6 Ba Bentuk Aljaar Pengertian Bentuk Aljaar Bentuk aljaar adalah entuk matematika ang didalamna memuat variael atau konstanta. Perhatikan entuk-entuk aljaar erikut! ) ) 4 ) Bentuk aljaar
Moh. Fatkoer Rohman 6 Ba Bentuk Aljaar Pengertian Bentuk Aljaar Bentuk aljaar adalah entuk matematika ang didalamna memuat variael atau konstanta. Perhatikan entuk-entuk aljaar erikut! ) ) 4 ) Bentuk aljaar
Solusi Analitis Persamaan-persamaan Diferensial Orde-1 dengan Metode Analitis Persamaan Diferensial dengan konfigurasi VARIABEL TERPISAH
 Solusi Analitis Persamaan-persamaan Diferensial Orde- dengan Metode Analitis.. Persamaan Diferensial dengan konfigurasi VARIABEL TERPISAH a. Bentuk Umum: f ( ) g( ), f dan g fungsi sembarang. b. Metode
Solusi Analitis Persamaan-persamaan Diferensial Orde- dengan Metode Analitis.. Persamaan Diferensial dengan konfigurasi VARIABEL TERPISAH a. Bentuk Umum: f ( ) g( ), f dan g fungsi sembarang. b. Metode
b. Titik potong grafik dengan sumbu y, dengan mengambil x = 0
 B.3 Fungsi Kuadrat a. Tujuan Setelah mempelajari uraian kompetensi dasar ini, anda dapat: Menentukan titik potong grafik fungsi dengan sumu koordinat, sumu simetri dan nilai ekstrim suatu fungsi Menggamar
B.3 Fungsi Kuadrat a. Tujuan Setelah mempelajari uraian kompetensi dasar ini, anda dapat: Menentukan titik potong grafik fungsi dengan sumu koordinat, sumu simetri dan nilai ekstrim suatu fungsi Menggamar
PDB ORDE SATU PADA KURVA TRAYEKTORI ORTOGONAL Oleh: 1 Ir. Sigit Kusmaryanto, M.Eng
 PDB ORDE SATU PADA KURVA TRAYEKTORI ORTOGONAL Oleh: 1 Ir. Sigit Kusmaryanto, M.Eng 1 Teknik Elektro UB, http://sigitkus@ub.ac.id Pengantar: Modul ini mempelajari penerapan Persamaan Diferensial orde satu
PDB ORDE SATU PADA KURVA TRAYEKTORI ORTOGONAL Oleh: 1 Ir. Sigit Kusmaryanto, M.Eng 1 Teknik Elektro UB, http://sigitkus@ub.ac.id Pengantar: Modul ini mempelajari penerapan Persamaan Diferensial orde satu
6. 2 Menerapkan konsep fungsi linier Menggambarkan fungsi kuadrat Menerapkan konsep fungsi kuadrat
 Sumer: Art and Gallery Standar Kompetensi 6. Memecahkan masalah yang erkaitan dengan fungsi, persamaan fungsi linier dan fungsi kuadrat Kompetensi Dasar 6. Mendeskripsikan peredaan konsep relasi dan fungsi
Sumer: Art and Gallery Standar Kompetensi 6. Memecahkan masalah yang erkaitan dengan fungsi, persamaan fungsi linier dan fungsi kuadrat Kompetensi Dasar 6. Mendeskripsikan peredaan konsep relasi dan fungsi
KALKULUS MULTIVARIABEL II
 Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Pada Bidang Bentuk Vektor dari KALKULUS MULTIVARIABEL II (Minggu ke-9) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Pada Bidang Bentuk Vektor dari 1 Definisi Daerah Sederhana x 2 Pada Bidang
Persamaan Diferensial Orde Satu
 Modul Persamaan Diferensial Orde Satu P PENDAHULUAN Prof. SM. Nababan, Ph. ersamaan Diferensial (PD) adalah salah satu cabang matematika ang banak digunakan untuk menjelaskan masalah-masalah fisis. Masalahmasalah
Modul Persamaan Diferensial Orde Satu P PENDAHULUAN Prof. SM. Nababan, Ph. ersamaan Diferensial (PD) adalah salah satu cabang matematika ang banak digunakan untuk menjelaskan masalah-masalah fisis. Masalahmasalah
BAB IV PERSAMAAN TAKHOMOGEN
 BAB IV PERSAMAAN TAKHOMOGEN Kompetensi Mahasiswa mampu 1. Menentukan selesaian khusus PD tak homogen dengan metode koefisien tak tentu 2. Menentukan selesaian khusus PD tak homogen dengan metode variasi
BAB IV PERSAMAAN TAKHOMOGEN Kompetensi Mahasiswa mampu 1. Menentukan selesaian khusus PD tak homogen dengan metode koefisien tak tentu 2. Menentukan selesaian khusus PD tak homogen dengan metode variasi
UN SMA 2015 Matematika IPA
 UN SMA 05 Matematika IPA Soal Doc. Name: UNSMA05MATIPA Doc. Version : 05- halaman 0. Ani rajin elajar maka naik kelas. Ani dapat hadiah atau tidak naik kelas. Ani rajin elajar. Kesimpulan yang sah adalah
UN SMA 05 Matematika IPA Soal Doc. Name: UNSMA05MATIPA Doc. Version : 05- halaman 0. Ani rajin elajar maka naik kelas. Ani dapat hadiah atau tidak naik kelas. Ani rajin elajar. Kesimpulan yang sah adalah
BAB I PENGERTIAN DASAR
 BAB I PENGERTIAN DASAR Kompetensi Dasar: Menjelaskan pengertian dan klasifikasi dari persamaan diferensial serta beberapa hal yang terkait. Indikator: a. Menjelaskankan pengertian persamaan diferensial.
BAB I PENGERTIAN DASAR Kompetensi Dasar: Menjelaskan pengertian dan klasifikasi dari persamaan diferensial serta beberapa hal yang terkait. Indikator: a. Menjelaskankan pengertian persamaan diferensial.
TEORI BAHASA DAN AUTOMATA
 MODUL V TEORI BAHASA DAN AUTOMATA Tujuan : Mahasiswa memahami NFA dengan e-move, dapat malakukan ekivalensi ke NFA tanpa e-move dan operasi gaungan/konkatenasi. Materi : NFA dengan e-move Ekivalensi NFA
MODUL V TEORI BAHASA DAN AUTOMATA Tujuan : Mahasiswa memahami NFA dengan e-move, dapat malakukan ekivalensi ke NFA tanpa e-move dan operasi gaungan/konkatenasi. Materi : NFA dengan e-move Ekivalensi NFA
Persamaan Diferensial
 TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
TKS 4003 Matematika II Persamaan Diferensial Konsep Dasar dan Pembentukan (Differential : Basic Concepts and Establishment ) Dr. AZ Jurusan Teknik Sipil Fakultas Teknik Universitas Brawijaya Pendahuluan
UN SMA IPA 2010 Matematika
 UN SMA IPA 00 Matematika Kode Soal P0 Doc. Name: UNSMAIPA00MATP0 Doc. Version : 0-0 halaman 0. Akar-akar persamaan kuadrat x² + (a - ) x + =0 adalah α dan β. Jika a > 0 maka nilai a =. 8 x 0. Diketahui
UN SMA IPA 00 Matematika Kode Soal P0 Doc. Name: UNSMAIPA00MATP0 Doc. Version : 0-0 halaman 0. Akar-akar persamaan kuadrat x² + (a - ) x + =0 adalah α dan β. Jika a > 0 maka nilai a =. 8 x 0. Diketahui
Matematika Teknik I. Prasyarat : Kalkulus I, Kalkulus II, Aljabar Vektor & Kompleks
 Kode Mata Kuliah : TE 318 SKS : 3 Matematika Teknik I Prasarat : Kalkulus I, Kalkulus II, Aljabar Vektor & Kompleks Tujuan : Mahasiswa memahami permasalahan teknik dalam bentuk PD atau integral, serta
Kode Mata Kuliah : TE 318 SKS : 3 Matematika Teknik I Prasarat : Kalkulus I, Kalkulus II, Aljabar Vektor & Kompleks Tujuan : Mahasiswa memahami permasalahan teknik dalam bentuk PD atau integral, serta
TEOREMA GREEN UNTUK MENYELESAIKAN PERHITUNGAN INTEGRAL GARIS
 TEOEMA GEEN UNTUK MENYELESAIKAN PEHITUNGAN INTEGAL GAIS Prasetio Budi Darmono Jurusan Pendidikan Matematika FKIP Universitas Muhammadiah Purworejo Astrak Integral merupakan operasi kealikan dari turunan.
TEOEMA GEEN UNTUK MENYELESAIKAN PEHITUNGAN INTEGAL GAIS Prasetio Budi Darmono Jurusan Pendidikan Matematika FKIP Universitas Muhammadiah Purworejo Astrak Integral merupakan operasi kealikan dari turunan.
Hendra Gunawan. 16 Oktober 2013
 MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 16 Oktober 2013 Latihan (Kuliah yang Lalu) 1. Diketahui g(x) = x 3 /3, x є [ 2,2]. Hitung nilai rata rata g pada [ 2,2] dan tentukan c є ( 2,2)
MA1101 MATEMATIKA 1A Hendra Gunawan Semester I, 2013/2014 16 Oktober 2013 Latihan (Kuliah yang Lalu) 1. Diketahui g(x) = x 3 /3, x є [ 2,2]. Hitung nilai rata rata g pada [ 2,2] dan tentukan c є ( 2,2)
PRAKTIKUM 13 PENYELESAIAN PERSAMAAN ALJABAR
 PRAKTIKUM 13 PENYELESAIAN PERSAMAAN ALJABAR Dalam bab ini kita akan menggunakan Matlab untuk menyelesaikan persamaan aljabar. Kita akan mulai dengan menyelesaikan persamaan sederhana (persamaan dengan
PRAKTIKUM 13 PENYELESAIAN PERSAMAAN ALJABAR Dalam bab ini kita akan menggunakan Matlab untuk menyelesaikan persamaan aljabar. Kita akan mulai dengan menyelesaikan persamaan sederhana (persamaan dengan
BAB 1. KONSEP DASAR. d y ; 3x = d3 y ; y = 3 d y ; x = @u @z 5 6. d y = 7 y x Dalam bahan ajar ini pemba
 BAB 1 Konsep Dasar 1.1 Klasikasi Persamaan Difrensial Pada umumnya dikenal dua jenis persamaan difrensial yaitu Persamaan Difrensial Biasa (PDB) dan Persamaan Difrensial Parsial (PDP). Untuk mengetahui
BAB 1 Konsep Dasar 1.1 Klasikasi Persamaan Difrensial Pada umumnya dikenal dua jenis persamaan difrensial yaitu Persamaan Difrensial Biasa (PDB) dan Persamaan Difrensial Parsial (PDP). Untuk mengetahui
Hendra Gunawan. 26 Februari 2014
 MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 26 Februari 2014 9.6 Deret Pangkat Kuliah yang Lalu Menentukan selang kekonvergenan deret pangkat 9.7 Operasi pada Deret Pangkat Mlkk Melakukan
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2013/2014 26 Februari 2014 9.6 Deret Pangkat Kuliah yang Lalu Menentukan selang kekonvergenan deret pangkat 9.7 Operasi pada Deret Pangkat Mlkk Melakukan
Persamaan Difusi. Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M. Jamhuri. April 7, UIN Malang. M. Jamhuri Persamaan Difusi
 Persamaan Difusi Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M Jamhuri UIN Malang April 7, 2013 Penurunan Persamaan Difusi Misalkan u(x, t) menyatakan konsentrasi dari zat pada posisi
Persamaan Difusi Penurunan, Solusi Analitik, Solusi Numerik (Beda Hingga, RBF) M Jamhuri UIN Malang April 7, 2013 Penurunan Persamaan Difusi Misalkan u(x, t) menyatakan konsentrasi dari zat pada posisi
Kalkulus Multivariabel I
 dan Fungsi Implisit dan Fungsi Implisit Statistika FMIPA Universitas Islam Indonesia dan Fungsi Implisit Ingat kembali aturan rantai pada fungsi satu peubah! Jika y = f (x(t)), di mana baik f maupun t
dan Fungsi Implisit dan Fungsi Implisit Statistika FMIPA Universitas Islam Indonesia dan Fungsi Implisit Ingat kembali aturan rantai pada fungsi satu peubah! Jika y = f (x(t)), di mana baik f maupun t
Desain Filter Respon Impuls TakTerbatas (Infinite Impulse Response/IIR)
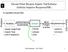 Prolem 8 Desain Filter Respon Impuls TakTeratas (Infinite Impulse Response/IIR) 8. Spesifikasi Desain Filter Analisa respon magnitude respon fasa performance constraints Desain FIR/IIR sutype G(z) Fungsi
Prolem 8 Desain Filter Respon Impuls TakTeratas (Infinite Impulse Response/IIR) 8. Spesifikasi Desain Filter Analisa respon magnitude respon fasa performance constraints Desain FIR/IIR sutype G(z) Fungsi
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II
 Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II [MA4] PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan
Program Perkuliahan Dasar Umum Sekolah Tinggi Teknologi Telkom Persamaan Diferensial Orde II [MA4] PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka Persamaan
RUNGE-KUTTA ORDE EMPAT
 RUNGE-KUTTA ORDE EMPAT Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: supri@fisika.ui.ac.id atau supri9@gmail.com December 30, 00 Pada saat membahas metode Euler
RUNGE-KUTTA ORDE EMPAT Dr. Eng. Supriyanto, M.Sc Lab. Komputer, Departemen Fisika, Universitas Indonesia email: supri@fisika.ui.ac.id atau supri9@gmail.com December 30, 00 Pada saat membahas metode Euler
BAB VIII PERSAMAAN DIFERENSIAL (PD)
 BAB VIII PERSAMAAN DIFERENSIAL (PD) Banak masalah dalam kehidupan sehari-hari ang dapat dimodelkan dalam persamaan diferensial. Untuk menelesaikan masalah tersebut kita perlu menelesaikan pula persamaan
BAB VIII PERSAMAAN DIFERENSIAL (PD) Banak masalah dalam kehidupan sehari-hari ang dapat dimodelkan dalam persamaan diferensial. Untuk menelesaikan masalah tersebut kita perlu menelesaikan pula persamaan
Pemodelan Teknik Kimia Bebarapa Contoh Aplikasi Persamaan Diferensial (oleh: Prof. Dr. Ir. Setijo Bismo, DEA.)
 Pemodelan Teknik Kimia - 206 Bebarapa Contoh Aplikasi Persamaan Diferensial (oleh: Prof. Dr. Ir. Setijo Bismo, DEA.) Contoh #: Kepedulian terhadap Iklan Suatu produk sereal baru (diberi nama Oat Puff )
Pemodelan Teknik Kimia - 206 Bebarapa Contoh Aplikasi Persamaan Diferensial (oleh: Prof. Dr. Ir. Setijo Bismo, DEA.) Contoh #: Kepedulian terhadap Iklan Suatu produk sereal baru (diberi nama Oat Puff )
Konstruksi Rangka Batang
 Konstruksi Rangka atang Salah satu sistem konstruksi ringan yang mempunyai kemampuan esar, yaitu erupa suatu Rangka atang. Rangka atang merupakan suatu konstruksi yang terdiri dari sejumlah atang atang
Konstruksi Rangka atang Salah satu sistem konstruksi ringan yang mempunyai kemampuan esar, yaitu erupa suatu Rangka atang. Rangka atang merupakan suatu konstruksi yang terdiri dari sejumlah atang atang
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika. Persamaan Diferensial Orde II
 Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
Universitas Indonusa Esa Unggul Fakultas Ilmu Komputer Teknik Informatika Persamaan Diferensial Orde II PDB Orde II Bentuk umum : y + p(x)y + g(x)y = r(x) p(x), g(x) disebut koefisien jika r(x) = 0, maka
BAB XIV V E K T O R Pengertian Vektor adalah besaran yang mempunyai arah. Tafsiran geometri sebuah vektor dilukiskan sebagai panah.
 XIV V E K T O R 4. engertian adalah esaran yang mempunyai arah. Tafsiran geometri seuah vektor dilukiskan seagai panah. dengan titik pangkal (a x, a y, a z ) dan titik ujung ( x, y, z ) dinotasikan dengan.
XIV V E K T O R 4. engertian adalah esaran yang mempunyai arah. Tafsiran geometri seuah vektor dilukiskan seagai panah. dengan titik pangkal (a x, a y, a z ) dan titik ujung ( x, y, z ) dinotasikan dengan.
matematika K-13 PEMBAGIAN HORNER DAN TEOREMA SISA K e l a s
 i K- ateatika K e l a s XI PEMBAGIAN HORNER DAN TEOREMA SISA Tujuan Peelajaran Setelah epelajari ateri ini, kau diharapkan eiliki keapuan erikut.. Menguasai konsep peagian suku anyak dengan etode Horner..
i K- ateatika K e l a s XI PEMBAGIAN HORNER DAN TEOREMA SISA Tujuan Peelajaran Setelah epelajari ateri ini, kau diharapkan eiliki keapuan erikut.. Menguasai konsep peagian suku anyak dengan etode Horner..
Message Authentication Code (MAC) Pembangkit Bilangan Acak Semu
 Bahan Kuliah ke-21 IF5054 Kriptografi Message Authentication Code (MAC) Pemangkit Bilangan Acak Semu Disusun oleh: Ir. Rinaldi Munir, M.T. Departemen Teknik Informatika Institut Teknologi Bandung 2004
Bahan Kuliah ke-21 IF5054 Kriptografi Message Authentication Code (MAC) Pemangkit Bilangan Acak Semu Disusun oleh: Ir. Rinaldi Munir, M.T. Departemen Teknik Informatika Institut Teknologi Bandung 2004
TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 2016/2017
 A. Pengantar Persamaan Diferensial TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 016/017 1. Tentukan hasil turunan dari fungsi sebagai berikut: a. f() = c e b. f() = c cos k + c sin k c.
A. Pengantar Persamaan Diferensial TUGAS MANDIRI KULIAH PERSAMAAN DIFERENSIAL BIASA Tahun Ajaran 016/017 1. Tentukan hasil turunan dari fungsi sebagai berikut: a. f() = c e b. f() = c cos k + c sin k c.
Analisis Kestabilan Titik Keseimbangan Model Perilaku Jumlah Pelaku Narkoba dengan Faktor Rehabilitasi
 Vol. 7 No. 6-7 Januari Analisis Kestailan Titik Keseimangan Model Perilaku Jumlah Pelaku Narkoa dengan Faktor ehailitasi Syamsuddin Toaha Astrak Tulisan ini memahas suatu model laju eruahan jumlah elaku
Vol. 7 No. 6-7 Januari Analisis Kestailan Titik Keseimangan Model Perilaku Jumlah Pelaku Narkoa dengan Faktor ehailitasi Syamsuddin Toaha Astrak Tulisan ini memahas suatu model laju eruahan jumlah elaku
BERBAGAI MODEL MATEMATIKA BERBENTUK PERSAMAAN DIFERENSIAL BIASA TINGKAT SATU
 BERBAGAI MODEL MATEMATIKA BERBENTUK PERSAMAAN DIFERENSIAL BIASA TINGKAT SATU Budiyono Jurusan Pendidikan Matematika FKIP Universitas Muhammadiyah Purworejo Abstrak Untuk mengetahui peranan matematika dalam
BERBAGAI MODEL MATEMATIKA BERBENTUK PERSAMAAN DIFERENSIAL BIASA TINGKAT SATU Budiyono Jurusan Pendidikan Matematika FKIP Universitas Muhammadiyah Purworejo Abstrak Untuk mengetahui peranan matematika dalam
Nurdinintya Athari PERSAMAAN DIFFERENSIAL ORDE 2
 Nurdininta Athari PERSAMAAN DIFFERENSIAL ORDE 2 2 PDB ORDE II Bentuk umum : + p() + g() = r() p(), g() disebut koefisien jika r() = 0, maka Persamaan Differensial diatas disebut homogen, sebalikna disebut
Nurdininta Athari PERSAMAAN DIFFERENSIAL ORDE 2 2 PDB ORDE II Bentuk umum : + p() + g() = r() p(), g() disebut koefisien jika r() = 0, maka Persamaan Differensial diatas disebut homogen, sebalikna disebut
