1+ 1 1! xt + 1 2! (xt)2 +...=e tx. g(t) =g 1 t + g 2 t , g 1 0. G x (t) :=e xg(t). G x (t) =p 0 (x)+ p 1(x) 1! t + p 2(x) p k (x) k!
|
|
|
- Widya Yuwono
- 5 tahun lalu
- Tontonan:
Transkripsi
1 GAZETA MATEMATIC SERIA A REVIST DE CULTUR MATEMATIC ANUL XXVCIV) Nr. 3 / 2007 Metoda fuc iilor geeratoare II) de Liviu I. Nicolaescu urmare di um rul 2/2007 ) Abstract We survey, from a moder poit of view, but relyig oly o high-school mathematics, some classical applicatios of the very versatile method of geeratig fuctios. Key words: geeratig fuctios, fiite differece equatios, recurrece relatios, Stirlig, Catala ad Beroulli umbers, Lagrage iversio formula, traslatio ivariat differetial operators, Beroulli ad Laguerre polyomials, Euler- MacLauri formula M.S.C.: 05A5, B73, 3F25, 3J05, 30B0 5. iruri de polioame Î aceast sec iue ii iem descrierea uui formalism moder care se ascude î spatele multor probleme di combiatoric. Îtr-o form sau alta, aceste trucuri erau cuoscute marilor clasici precum Euler, Lagrage, Gauss, Cauchy. Î cele ce urmeaz vom covei c gradul poliomului trivial p =0este. Defii ia 5.. a) U ir bazic de polioame este u ir de polioame p x) R[x], 0 cu proprietatea c gradp x) =, petru orice 0. irul bazic se ume te ormalizat dac p 0 x) =, p 0) = 0, petru orice. b) U ir biomial este u ir bazic ormalizat {p x)} 0 cu proprietatea c ) p x + y) = p k x)p k y), 5.) k petru orice 0, x,y R. 59
2 c) Dat fiid u ir bazic {p x)} 0, defiim fuc ia lui geeratoare pri P x t) :=Fg exp p x); t) = p x)t.! 0 Aceast serie poate fi gâdit î dou moduri: fie ca o serie de puteri ai c rui coeficie i sut polioame, fie ca o familie de serii de puteri parametrizat de variabila x. Exemplul 5.2. a) Formula biomului lui Newto e spue c irul de polioame,x,x 2,... este u ir biomial. Fuc ia lui geeratoare este +! xt + 2! xt)2 +...=e tx. b) S presupuem c gt) R[[t]] este o serie f-iversabil, Petru x R fixat, form m seria formal gt) =g t + g 2 t , g 0. G x t) :=e xgt). Atuci G x t) admite o dezvoltare de forma G x t) =p 0 x)+ p x)! ude {p x)} 0 este u ir bazic ormalizat. S observ m c Pe de alt parte, = 0 G x t)g y t) =e x+y)t = 0 G x t)g y t) = k 0 t + p 2x) t , 2! p k x) t k) k! j 0 p x + y) t.! p j y) t j) = j! ) p k x)p k y t = ) ) t p k x)p k y) k! k)! k!. 0 k+j= Rezult c irul de polioame {p x)} 0 este u ir biomial. S observ m c situa ia b) co ie ca u caz special situa ia a). Petru a vedea acest lucru cosider m seria M x t) = x t! =ext. 0 Rezult c dac alegem gt) de forma cea mai simpl posibil, gt) = t, ob iem irul biomial fudametal {x } 0. 60
3 c) Petru orice, defiim [x] := xx ) x +). Petru uiformitate, defiim [x] 0 =. S observ m c irul {[x] } 0 este u ir bazic ormalizat. Vom ar ta pri dou metode diferite c irul {[x] } 0 este u ir biomial. Prima metod este pri iduc ie. Trebuie s demostr m idetitatea [x + y] = ) [x] k [y] k, k petru orice x, y R i petru orice Z 0. Dac fix m x arbitrar, este suficiet s demostr m c aceast idetitate este valabil petru orice y îtreg eegativ. Vom ar ta pri iduc ie dup y c idetitatea de mai sus este valabil petru orice. Câd y =0afirma ia este trivial. Petru pasul iductiv s observ m c petru orice um r real z are loc idetitatea petru orice. Pri urmare, [x+y+)] =[x+y] +[x+y] = = ) [x] k [y] k + k [z +] [z] = [z], ) [x] k [y] k + k ) k [x] k [y] k = k = ) [x] k [y +] k. k ) [x] k [y] k = k ) ) [x] k [y]k + k[y] k k Cealalt metod de demostra ie folose te fuc ia geeratoare a acestui ir, aume S x t) = t [x]!. 0 Coform Exerci iului.0), petru x fixat, seria S x t) este coverget câd t <, iar suma ei este fuc ia t + t) x. Dac scriem + t) x =e x log+t), observ m c e afl m exact î situa ia descris î exemplul b), ude gt) =log+t) =t + t2 2 + t Aceasta arat di ou c irul {[x] } 0 este biomial. 6
4 Exemplul 5.2.b) e arat c dac Fg exp p x); t) are forma P x t) =e xst), st) R[[t]], st) =O), [t ]st) 0, atuci irul {p x)} 0 este biomial. Î cele ce urmeaz, dorim s producem alte criterii de recuoa tere ale irurilor biomiale. Defii ia 5.3. a) U operator admisibil este o aplica ie care satisface urm toarele codi ii: L este liiar, adic, petru orice λ, µ R, p, q R[x]. petru orice p R[x], iile L : R[x] R[x], R[x] p Lp Lλp + µq) =λlp + µlq, gradlp gradp. b) U operator difere ial este u operator admisibil L care satisface codi- L =0 i gradlp =gradp, petru orice p R[x], gradp >0. Vom ota cu Op mul imea operatorilor admisibili i cu DiffOp mul imea operatorilor difere iali. Compuerea a doi operatori admisibili S, T este u operator admisibil S T. Petru a simplifica ota ia, vom scrie ST î loc de S T. De asemeea, vom folosi ota ia S k := S } S S {{}. k ori Defiim Op := { T Op : gradtp=gradp, p R[x] }. Exemplul 5.4. a) Operatorul este u operator difere ial. b) Operatorul D x : R[x] R[x], D x p = dp dx :R[x] R[x], p)x) =px +) px) este operator difere ial. c) Petru u um r real h, defiim E h : R[x] R[x], pri egalitatea E h p)x) =px + h). 62
5 E h este u operator admisibil umit operatorul de trasla ie cu h. S observ m c =E, ude este aplica ia idetic R[x] R[x]. d) Operatorul lui Beroulli B : R[x] R[x], p x+ x pt)dt este u operator admisibil care p streaz gradul, adic B Op. e) Dat fiid u operator difere ial L, i o serie formal de puteri ut) = 0 u t, putem forma operatorul admisibil ul) = 0 u L, a c rui ac iue pe u poliom p este dat de ul)p = u 0 p + u Lp + + u L p +. S observam c suma de mai sus este fiit, petru c L p =0,petru orice >gradp. De exemplu, are loc egalitatea E h = e hdx. 5.2) Petru a vedea acest lucru, folosim formula lui Taylor care spue c E h p)x) =px + h) = 0 h! p) x) = h h )! D xp)x) =! D x px). 0 0 Î particular, rezult c =e Dx. 5.3) Exerci iul 5.5. Ar ta i c dac L DiffOp, iar u, v R[[t]], atuci ul)vl) =u v)l) i ul) =0 u =0. Propozi ia 5.6. Orice operator T Op este iversabil, iar iversul lui este u operator admisibil, care p streaz gradul. Demostra ie. S observ m mai îtâi c T este ijectiv. Îtr-adev r, dac Tp = Tq, atuci Tp q) =0, 63
6 de ude gradp q) = grad0 =, deci p q =0. S ot m cu R[x] mul imea polioamelor de grad mai mic sau egal cu. Este clar c T : R[x] R[x] i vom ar ta c aplica ia T : R[x] R[x] este surjectiv. Cosider m matricea A =a ij ) 0 i,j, defiit de egalit ile S observ m c dac Tx j = a ij x i, j =0,...,. i=0 qx) =q 0 + q x + + q x, atuci ude Tq = p p x, p 0 p. p = A q 0 q. q. 5.4) Privim egalitatea 5.4) ca pe u sistem liiar, î care ecuoscutele sut coeficie ii q i. Arezolva ecua ia Tq = p, p R[x], î care ecuoscuta este poliomul q R[x], revie la a rezolva sistemul liiar 5.4). Deoarece T este ijectiv, deducem c sistemul de mai sus, î care p j =0, are doar solu ia trivial q i =0. Rezult c det A 0, adic matricea A este iversabil. Pri urmare, petru orice poliom p R[x] exist u sigur poliom q R[x], astfel îcât Tq = p. Exemplul 5.7. a) Operatorul de trasla ie E h p streaz gradul, E h Op i, pri urmare, este bijectiv. Iversul lui este operatorul E h. b) Operatorul lui Beroulli p streaz gradul i pri urmare este iversabil. S observ m c D x B = i deci putem scrie formal B = D. Egalitatea de mai sus ar trebui pus ître ghilimele fiidc operatorul de derivare D u este iversabil. 64
7 S presupuem c {p x)} 0 este u ir bazic. Acestui ir îi asociem o aplica ie R = R {p} : R[x] R[x], descris astfel: R a 0 + a x a x ) = a 0 p 0 + a p x)+...+ a p x). Este evidet c R este u operator admisibil. Îl vom umi reperul asociat irului bazic {p x)} 0. S observ m c Rx )=p x), petru orice 0 i, pri urmare, gradrq =gradq, 5.5) petru orice q R[x], q 0. Rezult c R Op. Folosid Propozi ia 5.6) deducem urm torul rezultat: Corolarul 5.8. Reperul R asociat uui ir basic {p x)} 0 este bijectiv, iar iversul lui este u operator admisibil R,care satisface codi iile petru orice 0 i R p = x, petru orice q R[x]. Corolarul 5.9. Fie {p } 0 u ir bazic. descompue uic sub forma gradr q =gradq, 5.6) qx) =q 0 p 0 x)+q p x)+...+ q p x), Orice poliom q de grad se petru orice x R, ude q 0,...,q sut umere reale. Demostra ie. Poliomul Rqx) admite o descompuere uic de forma Rqx) = q k x k. Pri urmare qx) =R Rqx))= q k Rx k )= q k p k x). S presupuem c p = {p x)} 0 i q = {q x)} 0 sut dou iruri bazice cu repere R p i respectiv R q. Atuci avem u operator liiar S observ m c T q/p : R[x] R[x], T p/q := R p R q. T q/p p = R q R p p )=R q x )=q. 65
8 Vom spue c T q/p este operatorul de trazi ie de la p la q. Acestui operator îi asociem matricea ifiit Aq, p) =a ij ) 0 i,j, defiit de egalit ile q j = i a ij p i. Aceasta este o matrice triughiular superior, adic are forma a 00 a 0 a 02 0 a a 2 A = 0 0 a a j=0 Vom spue c Aq, p) este matricea trazi iei de la p la q. Aceast matrice este iversabil, iar iversa ei este matricea trazi iei de la q la p. S observ m c operatorul reper asociat irului {p } 0 este exact operatorul de trazi ie de la irul caoic {x } 0 la irul {p x)} 0. Exemplul 5.0. a) S cosider m irurile bazice { p x) =x ) } { 0 i q x) =x }. Di formula biomului lui Newto, ob iem 0 x = +x ) ) ) = x ) m m m=0 i deducem c matricea trazi iei de la p la q este dat de ) ) ) ) ) 2 0 ) A = ) Recuoa tem mai sus triughiul lui Pascal. U irdeumere reale se poate gâdi ca o matrice ifiit cu o sigur liie X =[x 0,x ] Prodususl Y = XA este o matrice ifiit cu o sigur liie Y =[y 0,y, ], 66
9 ude y = ) x k, k petru orice 0. Petru a calcula matricea ivers a lui A folosim di ou formula lui Newto ) x ) = ) k x k k i deducem c matricea ivers a lui A este ) ) ) ) ) ) ) B = A ) ) = ) Rezult c i deci 3.5b).) X =XA)A = YB x = ) ) k y k. k Rezult de aici formula de iversiue biomial compara i cu Exercitiul y = petru orice 0, ceeaceesteechivalet cu x = ) x k, k ) ) k y k, 5.7) k petru orice 0. Exerci iul 5.. Cosider m dou iruri de umere reale {x } 0 i {y } 0. Form m seriilor lor geeratoare de tip expoe ial xt) = 0 x t! i yt) = 0 y t!. 67
10 Ar ta i c y = ) x k, 0 yt) =e t xt) k i deduce i de aici formula de iversiue biomial. Defii ia 5.2. Dat fiid u ir bazic { p x)} 0 cu reper R, defiim L : R[x] R[x], L := RD x R i îl vom umi operatorul fudametal al irului {p x)} 0. Propozi ia 5.3. Fie u ir bazic ormalizat {p x)} 0 cu operator fudametal L. Atuci au loc urm toarele: a) L este u operator difere ial care satisface Lp = p, 5.8) petru orice. b) Dac L este u operator difere ial care satisface 5.8), atuci L = L. Demostra ie. a) Fie p u poliom de grad. Atuci Lp) =RD x R p). Di 5.6) deducem c gradr p = i, pri urmare, Folosid 5.5), deducem c gradd x R p)=. gradlp =gradrd x R p)= ), rela ie care arat c L este operator difere ial. S observ m acum c Lp = RD x R p )=RD x )x )=Rx = p x). b) Fie L u operator difere ial care satisface 5.8). Defiim S = R LR. Atuci Sx = R Lp )=R p )=x. Aceasta arat c petru orice q R[x]. Cu alte cuvite Sq = D x q, R LR = D x, de ude L = RD x R = L. 68
11 Exemplul 5.4. Operatorul fudametal al irului {x } 0 este operatorul obi uit de derivare D x. Deoarece [x] =[x +] [x] = [x], deducem c operatorul fudametal al irului {[x] } 0 este. Propozi ia 5.5. Orice operator difere ial L este operatorul fudametal al uui uic ir bazic ormalizat. Demostra ie. Vom costrui iductiv u astfel de ir. Uicitatea va rezulta imediat di metoda de costruc ie. Vrem s costruim u ir bazic ormalizat {p x)} 0, astfel îcât Lp = p, oricare ar fi. p 0 este uic determiat petru c p 0 =. Presupuem c am determiat p 0,...,p i dorim s -l g sim pe p. Observ m c p 0,p,...,p formeaz o baz a spa iului R [x] costâd di polioame de grad. C ut m p sub forma p x) =ax + c p x)+...+ c p x)+c 0. Deoarece dorim ca p 0) = 0 i deja tim c p k 0) = 0, petru k, deducem c c 0 =0. Poliomul Lx ) are gradul i deci admite o descompuere de forma Lx )=l 0 + l p x)+ + l p x), ude l 0. Coeficie ii l i trebuiesc gâdi i ca fiid cuoscu i, petru c operatorul L este cuoscut. Dorim s determiam um rul a i coefice ii c k î fuc ie de umerele l i. Deducem c Rezult p x) =Lp x) =alx )+ kc k p k x) = = al p x)+ al k + kc k )p k x). a =, c k = al k = l k, l k kl petru orice k =,...,. Propozi iile 5.3 i 5..5 implic existe a uei bijec ii operatori difere iali iruri bazice ormalizate. Aceast bijec ie va juca u rol fudametal î cele ce urmeaz. S cosider m u ir bazic ormalizat {p x)} 0 cu operatorul de referi R i operator fudametal L. S observ m c petru orice 0 <k. L k p m =[m] k p m k, 69
12 Î particular, deducem c L k p m ) x=0 = {!, k = m 0, k m. Pri urmare p m x) = k 0 L k p m ) x=0 p k x). k! Dac îmul im egalitatea de mai sus cu o costat q m i apoi sum m dup m =0,...,, ob iem q 0 p 0 x)+ + q p x) = L k q 0 p 0 x)+ + q p x)) ) x=0 p k x). k! k 0 S ot m Deducem qx) :=q 0 p 0 x)+ + q p x). L k q k p k x) =qx) = qx) ) x=0 p k x). k! k 0 k 0 Di Corolarul 5.9., g sim c L k qx) ) x=0 q k =. k! Corolarul 5.6. Fie {p x)} 0 u ir bazic ormalizat cu operatorul fudametal L. Atuci, petru orice poliom qx) de grad, are loc descompuerea qx) = A k q)p k x), A k q) := k! L k q ) x=0 p k. Î particular, dac q = {q x)} 0 este u ir bazic, atuci matricea de trazi ie de la p la q este descris de umerele a k = A k q )= k! L k q ) x=0. Rezultatul de mai sus pue î evide o aplica ie S : R[x] R, dat de px) =p0). Aceast aplica ie se ume te aplica ia de specializare î 0. Mai geeral, petru orice a R, defiim S a : R[x] R, dat de petru orice p R[x]. S a p := pa), 70
13 S a se ume te aplica ia de specializare î a. Cocluzia Corolarului 5.6 se poate rescrie sub forma qx) = k! SLk q)p k x), 5.9) k 0 petru orice q R[x]. Remarca 5.7. Putem folosi ultima egalitate petru a reformula costruc ia irul bazic ormalizat {p } 0 asociat uui operator difere ial L descris î Propozi ia 5.5. Mai exact, avem p 0 = i, folosid 5.9), deducem formula iductiv +)! SL+ x + )p + x) =x + k! SLk x + )p k x). Reamitim c expresiile SL k x k ) sut umere reale care se ob i calculâd valoarea î x =0a poliomului L k x + ) care are gradul + k. Exemplul 5.8 [Numerele Stirlig de tipul 2]. S cosider m irul bazic ormalizat {[x] } 0. Atuci, petru orice îtreg eegativ, are loc descompuerea petru orice x R. Numerele x = S k, )=! S k, [x] k, d k dx k [x] se umesc umerele Stirlig de tipul 2. Matricea S =S k, ) 0 k, este matricea trazi iei de la irul bazic {[x] } 0 la irul bazic {x } 0. Numerele Stirlig de tipul 2 sut umere îtregi pozitive care au o iterpretare combiatoric foarte iteresat. S cosider m o mul ime fiit N, de cardial N =, iomul ime fiit R, de cardial R = r. Not m cu R N mul imea tuturor fuc iilor f : N R. Dup cum este bie cuoscut, R N = r. Petru orice submul ime K R, ot m cu SurN,K) mul imea surjec iilor N K. Cardialul mul imii SurN,K) depide doar de cardialul a lui N i de cardialul k amul imii K. S ot m Vrem s ar t m c Îtr-adev r, avem r = R N = K R ) x=0 c k, := SurN,K), := N, k := K. SurN,K) = c k, = k!s k,. K R, k= K c k, = ) r c k, = k [r] k k! c k,. 7
14 Pri urmare, au loc egalit ile S k, [r] k = r = petru orice, r Z,, r. De aici rezult egalitatea k!s k, = SurN,K), c k, k! [r] k, ude = N, k = K. Acum putem oferi o iterpretare combiatoric a umerelor S k,. S presupuem c avem bile diferite i vrem s le distribuim î k cutii idetice astfel îcât fiecare cutie co ie cel pu i o bil. Afirm m c um rul acestor distribu ii este exact S k,. Etichet m bilele cu umerele {, 2,...,} i cutiile cu umerele {, 2,...,k}. S observ m c fiec rei surjec ii f : {, 2,...,} {,...,k} îi corespude o distribu ie de bile cu propriet ile dorite: bila i se duce î cutia fi). Pe de alt parte, dou surjec ii f,g : {, 2,...,} {,...,k} coduc la aceea i distribu ie de bile dac putem ob ie g di f pritr-o re-etichetare a cutiilor, adic dac exist o permutare λ : {, 2...,k} {, 2...,k}, astfel îcât, g = λ f. Deoarece exist k! re-etichet ri, deducem ca um r de distribu ii a bile disticte î k cutii idetice astfel îcât ici o cutie s u fie goal, este egal cu k! SurN,K) = S k,, = N, k = K. Exerci iul 5.9. Folosid formula de iversiue biomial 5.7), ar ta i c umerele Stirlig de tipul 2 satisfac egalitatea S,k = k! ) k ) k j j. j j=0 Exerci iul S form m seriile formale de puteri S k t) = k S k, t, k.! a) Folosid defii ia combiatoric a umerelor Stirlig de tipul 2 ar ta i c S k, = ks k, + S k, 72
15 i apoi deduce i c S k t) = k! et ), petru orice k. b) Demostra i egalitatea de mai sus folosid fuc ia geeratoare a irului biomial {[x] } Operatori ivaria i la trasla ii Î aceast sec iue vom ivestiga leg tura strâs ditre irurile biomiale i o clas special de operatori difere iali. Defii ia 6.. U operator admisibil T Op se ume te ivariat la trasla ii dac E h T = TE h, petru orice h R, ude reamitim c E h este operatorul de trasla ie descris astfel: E h p)x) =px + h), petru orice p R[x]. Vom ota cu Op iv mul imea operatorilor admisibili ivaria i la trasla ii, iar cu DiffOp iv mul imea operatorilor difere iali ivaria i la trasla ii. S aaliz m pu i codi ia de ivaria la trasla ii. Dac T Op, iar p R[x]], atuci petru orice um r real h deducem di formula lui Taylor c E h p)x) =px + h) = 0 h! D xpx), i pri urmare TE h p)x) = 0 h! T D x p)x). Î mod asem tor deducem E h Tp)x) = 0 h! D xtp)x). Rezult c T este ivariat la trasla ii dac i umai dac 0 h! T D x p)x) = h! D x Tp)x), 6.) 0 petru orice h R, p R[x]. Di egalitatea de mai sus deducem c dac operatorul T comut cu D x, i.e., TD x = D x T, atuci T este ivariat la trasla ii. Exemplul 6.2. Operatorii D x i sut operatori difere iali ivaria i la trasla ii. Operatorul Beroulli B este, de asemeea, u operator ivariat la trasla ii. 73
16 Exerci iul 6.3. a) Ar ta i c dac S, T Op iv, iar c R, atuci cs, S + T, ST Op iv. Deduce i c mul imea Op iv cu opera iile de aduare i compuere este u iel cu uitate. b) Ar ta i c dac L DiffOp iv, atuci, petru orice serie formal ut) =u 0 + u t +... R[[t]], operatorul admisibil ul) este ivariat la trasla ii. Î particular, operatorii de forma ud x ) sut ivaria i la trasla ii. c) Ar ta i c T Op este ivariat la trasla ii dac i umai dac T comut cu D. Idica ie: Folosi i idetitatea D x p = lim h E h )p, oricare ar fi p R[x].) Urm torul rezultat ar t de ce sutem iteresa i î operatori ivaria i la trasla ii. Teorema 6.4. S presupuem c {p x)} 0 este u ir bazic ormalizat cu operator fudametal L. Atuci urm toarele afirma ii sut echivalete: a) L este ivariat la trasla ii. b) {p x)} 0 este ir biomial. Demostra ie. a) = b). Avem ) p x + y) = p k x)p k y), k petru orice 0, x, y R. S observ m c h 0 p x + y) =E y p )x). Acum folosim idetitatea 5.9) î care qx) =E y p )x) i deducem p x + y) =E y p )x) = k 0 k! SLk E y p )p k x). Deoarece L este ivariat la trasla ii, deducem c L k E y urmare, p x + y) = k! SE yl k p )p k x). k 0 = E y L k i, pri Reamitidu-e c L este operatorul fudametal al irului {p x)} 0, deducem c L k p =[] k p k. Pe de alt parte, petru orice poliom p, are loc egalitatea Deducem p x + y) = k 0 SE y p)=s y p = py). [] k k! S yp k )p k x) = ) p k x)p k y). k k 0 b) = a). tim deci c {p } 0 este u ir biomial i trebuie s ar t m c petru orice poliom q are loc egalitatea E y Lq = LE y q, 6.2) 74
17 petru orice y R. Deoarece orice poliom q se scrie ca o combia ie liiar î polioamele p, qx) = 0 q p x), petru orice x R, este suficiet s verific m egalitatea 6.2) doar î cazul special câd qx) este egal cu uul di polioamle bazice p x). Î acest caz avem ) E y Lp )x) =E y p )x) =p x + y) = p k x)p k y). k Pe de alt parte, E y p )x) =p x + y) = ) p k x)p k y). k Î egalitatea de mai sus y este fixat, iar umerele p k y) trebuie gâdite ca fiid costate. Deducem = LE y p )x) = k ) p k y)lp k )x) = k k ) p k y)p k x) = ) ) p k x)p k y) = p k x)p k y) =E y Lp )x). k k S presupuem c L este u operator difere ial ivariat la trasla ii, iar {p x)} 0 este irul bazic asociat. Atuci {p } 0 este ir biomial i, pri urmare, satisface egalit ile p x + h) = ) p k x)p k h) = k k! Lk p )x)p k h). k 0 k 0 Dac fix m h, putem rescrie egalitatea de mai sus sub forma E h p = k 0 p k h) L k p, k! petru orice 0. Orice poliom p se scrie ca o combia ie liiar fiit p = 0 c p. Deducem E h p = E h 0 c p = 0 c E h p = 0 c k 0 p k h) ) L k p = k! 75
18 = k 0 p k h) k! L k ) c p = 0 k 0 p k h) L k p. k! Am ob iut astfel urm torul rezultat. Propozi ia 6.5 [Formula lui Taylor geeralizat ]. S presupuem c L este u operator difere ial ivariat la trasla ii, iar {p x)} 0 este irul biomial asociat lui L. Atuci are loc egalitatea E h p = k 0 p k h) L k p, k! petru orice p R[x]. S presupuem c L DiffOp iv. Exerci iul 5.5 arat c operatorii de forma ul), u R[[t]], sut operatori admisibili ivaria i la trasla ii. Rezultatul care urmeaz va ar ta c ace tia sut to i operatorii admisibili ivaria i la trasla ii. Teorema 6.6. Fie L DiffOp iv. Aplica ia Q L : R[[t]] Op iv, descris astfel: R[[t]] u Q L u = ul) Op iv, este u izomorfism de iele. Demostra ie. Exerci iul 5.5 arat c Q L este u morfism ijectiv de iele. Vom ar ta c este u morfism surjectiv. Reamitim c S : R[x] R este aplica ia de specializare î 0, Sp = p0). Not m cu {l x)} 0 irul biomial asociat lui L. S presupuem c U Op iv. Form m irul de umere reale u := SUl =Ul ) x=0. Not m cu ut) fuc ia geeratoare de tip expoe ial a acestui ir, aume Vom ar ta c ut) :=Fg exp u ; t) = 0 U = 0 u! L = 0 u! t. Ul ) x=0 L. 6.3)! S ot m cu T operatorul di partea dreapt a egalit ii de mai sus. Vom ar ta c au loc egalit ile Ul ) x=h =Tl ) x=h, petru orice 0, h R. Ultima egalitate se poate rescrie sub forma SE h Ll = SE h Tl, petru orice 0, h R. Di defii ia irului u, deducem c egalitatea de mai sus are loc petru h =0, deoarece L m l =0, 76
19 petru orice m m i L l ) x=0 =!. Aceasta implic faptul c, petru orice poliom p, avem ceea ce este echivalet cu SUp = STp, SU = ST. Pri urmare, petru orice um r real h, are loc egalitatea SUE h =SU) E h =ST ) E h = STE h. Deoarece U si T sut ivaria i la trasla ii deducem c UE h = E h U i TE h = E h. Pri urmare, SE h U = SE h T, de ude SE h Ul = SE h Ul, petru orice 0 i petru orice h R. Remarca 6.7. Morfismul Q L se mai ume te i morfismul de cuatizare. Iversul lui se ume te morfismul simbol. Petru orice operator T Op iv, seria formal Q L T ) se ume te simbolul operatorului T relativ la L. Vom folosi ota ia Σ T/L t) :=Q L T. Seria formal Σ T/L este uic determiat de codi ia T =Σ T/L L). Exerci iul 6.8. S presupuem c P, Q DiffOp iv, R Op iv. Ar ta i c Σ R/Q Σ Q/B =Σ R/P R[[t]], i Σ Q/P t) =Σ P/Q t). Reamitim ca ultima egalitate îseam c Σ Q/P Σ P/Q t) =Σ P/Q t) Σ Q/P = t R[[t]]. Defii ia 6.9. Petru orice T Op iv, defiim σ T t) R[[t]] pri egalitatea σ T t) :=Σ T/Dx t), ude D x este operatorul obi uit de difere iere. Vom spue c σ T t) este simbolul complet) al operatorului T. Exerci iul 6.0. Ar ta i c petru orice S, T Op iv au loc egalit ile σ S+T t) =σ S t)+σ T t), i σ ST t) =σ S t) σ T t). 77
20 Exerci iul 6.. a) S observ m mai îtâi c σ Dx t) =t. Folosid egalit ile 5.2) i 5.3), E h = e hdx i =e Dx, deducem c σ Eh t) =e ht i σ t) =e t. b) Operatorul lui Beroulli B, defiit de Bp)x) := x+ x ps)ds, satisface egalitatea i, pri urmare, D x B)px) =px +) px) = p)x) D x B = σ DxB = σ = σ B t) = et. t Operatorul lui Beroulli este iversabil, iar iversul lui are simbolul σ B t) = t e t. t Fuc ia e t joac u rol remarcabil î matematic petru c este implicat î multe ditre cele mai profude descoperiri de la Newto pâ î prezet. c) Defiim L : R[x] R[x], Lpx) = 0 e s px + s)ds, petru orice p R[x]. Operatorul lui Laguerre Lag : R[x] R[x] este defiit de egalitatea Lagp)x) = D x Lp. S observ m c Lp este îtr-adev r u poliom atuci câd p este poliom. Petru a vedea acest lucru este suficiet s studiem cazurile particulare px) =x. Î aceast situa ie deducem Lp)x) = 0 e s x + s) ds = ) x k k 0 e s s k ds. Dac ot m I k = 0 e s s k ds 78
21 deducem, itegrâd pri p r i, I k = e s s k ) s= +k s=0 0 e s s k = ki k. Observâd c I 0 =, deducem I k = k! i, pri urmare, Lx )= ) x k k!= k [] k x k. Î particular, deducem c L Op i deci este iversabil. Este clar ivariat la trasla ii. Vrem s -i calcul m simbolul. S observ m c D x Lp)x) = 0 =e s px + s) e s dp s= s=0 x + s)ds = dx 0 0 e s dp x + s)ds = ds e s px + s)ds = px)+lx). Putem rescrie cocluzia calculului de mai sus sub forma D x L)p = p + Lp, petru orice p R[x] D x )L =. Dac ot m lt) =σ L t), deducem t )lt) = lt) = t. Di egalitatea Lag = D x L deducem c operatorul lui Laguerre este u operator difere ial ivariat la trasla ii al c rui simbol este σ Lag t) = σ Dx t)lt) = Putem rescrie ultima egalitate sub forma Lag = D x D x ). t t. S presupuem c Q, R DiffOp iv. Not m cu {q x)} 0 irul biomial asociat lui Q i cu {r x)} 0 irul biomial asociat lui Q. Dorim s g sim o metod coveabil de exprimare a polioamelor r î fuc ie de polioamele q i operatorul Q. S ot m ft) :=Σ R/Q t) R[[t]] i gt) :=Σ Q/R t) R[[t]]. 79
22 u w w u u w w u Pri urmare R = fq), Q = gr) i g = f. S cosider m operatorul T Q/R : R[x] R[x] de trazi ie de la irul {r } 0 la irul {q } 0, adic operatorul admisibil defiit de egalit ile T Q/R r = q, petru orice 0. T Q/R este bijectiv, iar iversul lui este descris de petru orice 0. Are loc egalitatea Îtr-adev r, petru orice 0, avem T Q/R = T R/Q T Q/R q = r, Q = T Q/R RT Q/R = T Q/RRT R/Q. T Q/R RT Q/R q = T Q/R Rr = T Q/R r )=T Q/R r = q = Qq. S cosider m u alt operator S DiffOp iv al c rui ir biomial asociat este {s s)} 0. Not m p := T Q/R s, petru orice 0 i defiim P = T Q/R ST Q/R. Teorema 6.2. a) Operatorul P = T Q/R ST Q/R este u operator difere ial ivariat la trasla ii, iar {p x)} 0 este irul biomial asociat lui P. b) Defiim ht) :=Σ S/R t), adic adic i Atuci S = hr). P = hq), Σ P/Q t) =Σ S/R t), Σ P/S t) =Σ S/R Σ Q/R Σ S/R. Cocluzia b) a teoremei de mai sus se poate ilustra î diagrama urm toare T S/R {r } {s } R Σ S/R S T Q,R T P/S =T Q,R = Σ Q/R {q } {p } Q Σ P/Q =Σ S/R P 80
23 Demostra ie. S ot m p =0. Petru a aerisi prezetarea vom scrie T î loc de T Q/R. Împ r im demostra ia î trei pa i. Pasul. irul p ) 0 este u ir bazic asociat lui P, adic petru orice 0. Îtr-adev r, au loc egalit ile Pp = p, Pp = T ST p = T Ss = T s )=T s = p. Pasul 2. irul p este ormalizat. S observ m c, pri defii ie, irurile {q } 0, {r } 0 i {s } 0 sut ormalizate. Pri urmare q 0 = r 0 = s 0 =. Rezult c p 0 = T s 0 = T r 0 = q 0 =. Fie. Atuci, coform Corolarului 5.9, poliomul q se descompue ca o combia ie liiar petru orice x R. Deoarece s x) =c 0 p x)+c p x)+ + c p x), q 0) = p k 0) = 0, petru orice k,, deducem c 0 =0. Pri urmare, i deci p = Cs = T c p + + c p )=c q + + c q, p 0) = 0, petru orice. Aceasta arat c {p x)} 0 este irul bazic ormalizat asociat lui P. Pasul 3. P = hs). Î particular P DiffOp iv. Di egalitatea Q = T RT, deducem c, petru orice k, are loc egalitatea T R k T =CRC ) CRC ) = Q k. }{{} k Rezult c, petru orice poliom ut) R[t], are loc egalitatea S cosider m acum seria formal CuR)C = uq). ht) =h t + h 2 t
24 Not m Atuci h t) =h t + + h t R[t]. T h R)T = h Q). Dac qx) R[x] este u poliom de grad, atuci Q N q =0=R N q, petru orice N >. Î particular, deoarece gradp = gradc p, petru orice p R[x], deducem c hq)q = h Q)q = T h R)T p)=t hr)t q, petru orice q R[x], gradp. Ultima egalitate se poate rescrie astfel: hq) =T hr)t. Reamitidu-e c hr) =S, deducem Rezult c Folosid Exerci iul 6.8, deducem hq) =T ST = P. Σ P/Q t) =ht) =Σ S/R t). Σ P/S =Σ P/Q Σ Q/R Σ R/S =Σ S/R Σ Q/R Σ S/R. Dac aplic m teorema de mai sus î cazul particular câd S = Q, ob iem urm torul rezultat: Corolarul 6.3. S presupuem c R, Q DiffOp iv, {r x)} 0 este irul biomial asociat lui R, iar {q } 0 este irul biomial asociat lui Q. S ot m ft) :=Σ R/Q t), adic R = fq). Atuci irul bazic {p x) =T Q/R q } 0 este irul biomial asociat operatorului P = f Q). Demostra ie. Di Teorema 6.2, deducem Σ P/Q =Σ Q/R Σ Q/R Σ Q/R =Σ Q/R = f. Folosid egalitatea 5.9) petru irul biomial {p x)} 0 di corolarul de mai sus, deducem c, petru orice poliom q R[x], avem o descompuere de forma qx) = k! P k q) x=0 p k. Î particular, dac alegem q = q, deducem q = k! P k q ) x=0 p k 82
25 i deci r = T Q/R q = T R/Q k 0 = k 0 ) k! P k q ) x=0 p k = k 0 k! P k q ) x=0 T Q/R p k = k! P k q ) x=0 q k = f Q) k ) q k! q x=0 k. k 0 Am ob iut astfel urm torul rezultat fudametal. Teorema 6.4. S presupuem c Q, R DiffOp iv. Not m cu {q x)} 0 irul bazic asociat lui Q i cu {r x)} 0 irul biomial asociat lui R. Dac ft) =Σ R/Q t), adic R = fq), atuci r = k 0 f Q) k ) q k! q x=0 k, petru orice 0. Remarca 6.5. a) Î teorema de mai sus s observ m c um rul real f Q) k q ) x=0 q k este egal cu! îmul it cu coeficietul lui t î seria f t), adic k! f Q) k q =![t] f t) ) k. Dac ot m gt) =f t) deducem c matricea de trazi ie de la irul {q x)} 0 la irul {r x)} 0 este dat de A k =! k! [t ]gt) k. Rezult c A k t) := 0 A k t! = k! gt)k. Cu alte cuvite, A k t), fuc ia geeratoare de tip expoe ial a umerelor de pe liia k a matricei de trazi ie este egal cu seria formal k! gt)k. b) S scriem ft) sub forma t ht), ht) =h 0 + h t + R[[t]], h 0 0. Atuci, di formula de iversiue a lui Lagrage, deducem [t] gt) k = k [t k ]ht) k,,k 0. 83
26 Rezult )! A k = k )! [t k ]ht) k )! A k = = k )! [t k ]ht) k = k )! [t ]tht)) k. Îmul id ultima egalitate cu t i apoi sumâd dup, deducem A k t Putem rescrie acest lucru sub forma )! = k ) tk ht) k. td t A k t) = Dac e reamitim c ft) = t k+ D t A k t) = k ) tk ht) k. t, deducem c tht) = t2 ht) ft) t ) k. k )! ft) i, pri urmare, Î aplica ii, u caz particular al Teoremei 6.4 este foarte util. Corolarul 6.6. S presupuem c R DiffOp iv. Not m cu {r x)} 0 irul biomial asociat lui R i cu σt) R[[t]] simbolul lui R, adic R = σd x ). Dac ot m cu µ x) moomul µ x) =x, atuci r x) = k 0 k! σ D x ) k µ ) x=0 µ k x). Demostra ie. Î Teorema 6.4, alegem Q = D x. Atuci Q x) =x = µ x) i ft) =Σ R/Dx t) =σ R t) =σt). Corolarul 6.7. S presupuem c P DiffOp iv, iar {p x)} 0 este irul biomial asociat lui P. Dac σt) este simbolul lui P, adic P = σd x ), iar gt) =σ t), atuci p x) t! = exgt). 0 Demostra ie. S ot m cu G operatorul G = gd x ) DiffOp iv Σ G/Dx t) =gt). 84
27 Folosid Corolarul 6.6, deducem p x) = G k x x k ) x=0 k! = G k x x k ) x=0 k!. Petru h R cosider m operatorul k 0 Q h : R[x] R[x], Q h p = 0 p h) Dx! p. S observ m c Q h este u operator admisibil ivariat la trasla ii al c rui simbol este Σ Qh /D x t) = p h) t!. 0 Pe de alt parte Q h = p h) Dx = G k x h k ) ) x=0! k!! D x = 0 0 k 0 k 0 h k k! 0 G k x ) ) x=0 Dx.! Deoarece {x } 0 este irul biomial asociat lui D x, deducem, di 6.3), c Pri urmare, Q h = k 0 G k = 0 Folosid Exerci iul 6.8, deducem 0 G k x ) x=0 D! x. h k k! Gk = e hg = Σ Qh /Gt) =e ht. p h) t! =Σ Q h /D x =Σ Qh /G Σ G/Dx t) =e hgt). 7. Exemple S ilustr m rezultatele ob iute pe câteva situa ii celebre. Exerci iul 7.. [Polioamele lui Laguerre]. Ca s vedem cum fuc ioeaz Corolarul 6.6 îl aplic m îtr-o situa ie cocret, dar cu multe aplica ii î matematic. S presupuem c R este operatorul lui Laguerre R = Lag = D x D x ) S ot m cu {l x)} 0 sirul biomial asociat operatorului lui Laguerre. Dorim s d m o descriere mai explicit a acestor polioame folosid Corolarul 85
28 Simbolul operatoratorului Lag este st) =tt ). Petru a afla iversa compozi ioal a seriei s rezolv m ecua ia s = tt ), î care ecuoscuta este t. Ajugem la cocluzia surpriz toare t = ss ). Cu alte cuvite Deducem l x) = k 0 s t) =st). k! Lagk µ ) x=0 x k i µ x) =x. Petru a calcula Lagµ ) x=0 putem folosi fie calculele di Exemplul 6., fie putem proceda direct, folosid formula Lag = D D) = Lag k = D k D) k = ) k D ) j + k k D j. j j 0 i deci Coeficietul lui D î aceast serie este ) ) ) k = ) k k k ) ) Lag k µ ) x=0 = ) k D µ ) x=0 = ) k!. k k Pri urmare l x) =! ) x ) k k k k!. Deoarece l 0) = 0, petru orice >0, deducem c poliomul l + x) se scrie ca u produs l + x) =xl x), ude gradl =. Mai exact L x) =! ) x) k. k k! 86
29 De exemplu L 0 x) =, L x) = x), L 2 x) =2 4x + x 2 ). Polioamele L x) au multe aplica ii î matematic. Au ap rut mai îtâi î fizica matematic, dar î ultimile deceii i-au f cut apari ia i î combiatoric. S me io m o astfel de aplica ie surpriz toare. Probabil cititorul a auzit deja de problema derajametelor, dar petru orice evetualitate o reamitim. S presupuem c avem bile, umerotate cu umerele,..., i cutii umerotate cu umerele,... Problema clasic a derajametelor îtreab î câte moduri putem distribui bilele, ua pe cutie, îcât iciua di bile s u fie situat îtr-o cutie cu acela i um r ca i bila. R spusul la acest îtrebare se g se te pri metoda icluderii-excluderi i deducem c um rul de derajamete este D =! ) k. k! Putem cosidera o situa ie mult mai sofisticat. S presupuem c avem o parti ie a mul imii {,...,} î k submul imi evide {,...,} = F F k, F i F j, petru orice i j. Not m f i := F i. Not m cu Df,...,f k ) um rul de permut ri ϕ ale mul imii {,...,} cu proprietatea c u exist i {,...,} îcât i i ϕi) se afla î aceea i mul ime a parti iei. Puem aceast problem îtr-u mod mai amuzat. S presupuem c la o petrecere particip k familii F,...,F k i î total sut persoae. Fiecare di persoae î i scrie umele pe o bucat de hârtie pe care apoi o pue îtr-o cutie. Urmeaz o tragere la sor i î care fiecare persoa extrage u ume di cutie. Atuci Df,...,f k ) este um rul de posibilt i de trageri la sor i cu proprietatea c ici ua ditre persoae u a extras umele uei persoae di familia sa. Problema clasic a derajametelor corespude cazului special câd k =, f i =. U rezultat di 976 datorat matematicieilor S. Eve i J. Gillis ofer u r spus surpriz tor, aume: Df,...,f k )= ) Este u or de verificat c îtr-adev r 0 e x L f x) L fk x)dx. ) k! k! = e x x ) dx. 0 Demostra ia cazului geeral este bazat tot pe pricipiul icluderii-excluderii, dar ecesit mai mult igeiozitate petru a formula rezultatul fial îtr-o form a a de elegat. 87
30 La foarte scurt timp dup ce Eve i Gillis au demostrat acest fapt, D. M. Jackso a dat o demostra ie foarte scurt bazat pe rezultatele di Exerci iul 2.9. Cititorul are acum toate cuo tii ele ecesare demostr rii acestui rezultat curios. Exerci iul 7.2. Ar ta i c l x) =xe x D xe x x ), petru orice 0. Exerci iul 7.3. [Polioame Beroulli]. Polioamele lui Beroulli {β x)} 0 formeaz u ir bazic foarte special care u este ormalizat, dar al c rui operator fudametal este D x, adic Dβ x) =β x), 7.) petru orice. Î plus, aceste polioame satisfac ecua iile cu difere e β )x) =D x x ), 7.2) petru orice. S ar t m ca aceste dou codi ii de mai sus defiesc uic irul bazic {β x)} 0. S e reamitim c operatorul lui Beroulli B satisface DB = BD =. Aplicâd operatorul B ambelor p r i ale egalit ii 7.) ob iem BDβ = Bβ. Pe de alt parte, folosid 7.2), ob iem BDβ = β = x i deducem x = Bβ, petru orice, ceea ce implic β = B x ), petru orice 0. S ot m b := β 0). Numerele b se umesc umerele lui Beroulli. S observ m c D k x β =[] k β k. 88
31 Di formula lui Taylor deducem c, petru orice, are loc egalitatea β x) = Dxβ k )0) xk k! = [] k β k 0) xk k! = ) b k x k. 7.3) k Aceast egalitate e arat ca polioamle lui Beroulli sut uic determiate de umerele lui Beroulli. S ot m cu bt) fuc ia geeratoare de tip expoe ial a umerelor lui Beroulli, adic bt) = t b!. 0 Atuci egalitatea 7.3) se poate reformula compact sub forma bt)e tx = 0 β x) t!. 7.4) Not m seria di partea dreapt cu β x t). S e reamitim c β x +) β x) =x, petru orice 0. Pri urmare t! β x x +) β x)) = tx )!, petru orice. Sumâd aceste egalit i dup, deducem de ude β x+ t) β x t) =te tx. Pe de alt parte, folosid 7.4), ob iem egalitatea Pri urmare De aici rezult β x+ t) β x t) =bt) e tx+) e tx ). te tx = bt) e tx+) e tx ) =e tx bt)e t ), t = bt)e t ). bt) = t e t. Trebuie s comet m pu i ultima egalitate. Seria formal e t u areivers multiplicativ. S observ m îs c putem scrie e t =t + t 2! t! +...)=t 0 t +)!. 89
32 t Seria are ivers multiplicativ i atuci defiim +)! 0 t e t = 0 t +)! Petru a face calcule cocrete este îs mult mai util s folosim egalitatea t = bt)e t ), care coduce la urm toarele rela ii de recure b 0 =, ) b k =0, k. petru orice. Mai explicit de ude rezult c ) b + ) b b = ) b ) b 0 =0, ) )b 0, petru orice. Iat câteva valori petru umerele lui Beroulli: b 2k+ =0, petru orice k, b Iat i câteva polioame Beroulli: β 2 x) =x 2 x + 6, β 3 x) =x x2 + 2 x, β 4 x) =x 4 2x 3 + x 2 30, β 5 x) =x x x3 6 x, β 6 x) =x 6 3 x x4 2 x
33 Polioamele Beroulli apar î surpiz tor de multe situa ii î matematic. Vrem s me ioam aici câteva aplica ii elemetare. Di egalitatea petru orice x R, k, deducem β k+ x +) β k+ x) =k +)x k, β k ) β k 0) = k + ) k +2 k + + ) k ), adic j k = βk+ ) β k+ 0) ). 7.5) k + j= Mai geeral, are loc egalitatea petru orice h R. De exemplu h + j) k = βk+ h + ) β k+ h), ), 7.6) k + j= ) 5 = ), petru orice 2. Exemplul de mai sus este u caz special al formulei de sumare Euler-MacLauri. S presupuem c p este u poliom. S ot m q := Bp qx) = x+ x pt)dt. Î particular, qx + j) = Rezult c x+j+ x+j qx + j) = j=0 0 pt)dt. pt)dt. Dac acum scriem px) =B q)x), ob iem qx + j) = j=0 x+j x B q)t)dt. 7.7) 9
34 Î fie, dac poliomul q este derivata uui poliom f, adic q = Df atuci B Df = DB deoarece B este ivariat la trasla ii i deci comut cu D. Di formula Leibiz-Newto, ob iem celebra formul de sumare Euler-MacLauri: D x fx + j) = j=0 k 0 b ) k k! Dk f)x + ) k 0 =B f)x + ) B f)x). b ) k k! Dk f)x) = 7.8) Probabil c ar trebui s explic m de ce egalitatea de mai sus este uluitoare. Suma di partea stâg a egalit ii depide de comportarea global a poliomului f pe îtreg itervalul [x, x + ]. Pe de alt parte, suma di partea dreapt depide doar de comportarea local a lui f doar î veci tatea a dou pucte, aume x i x +. Exerci iul 7.4. S cosider m seria formal de puteri ut) = t u! cu 0 proprietatea c u 0 0. Not m cu P operatorul P = ud) Op iv i cu p x) polioamele P x ). Ar ta i c p x) t! = ut)etx. 0 Exerci iul 7.5. a) Ar ta i c petru orice i orice x R i β x) = ) β x), b 2k+ =0, petru orice k. b) Demostra i formula lui Raabe j=0 j ) β k x + = k β kx), petru orice k,. c) Ar ta i c ) ) β k = b k 2 2 k. d) Ar ta i c, petru orice x 0, ), au loc iegalit ile 2 ) k β 2k x) > 0, ) k β 2k x) b 2k ) > 0. e) Ar ta i c petru orice k 0. ) k+ b 2k > 0, 92
35 Exerci iul 7.6. S defiim fuc iile Beroulli periodice β x) =β x x ), ude x este partea îtreg a um rului real x. S presupuem c f : R R este o fuc ie ifiit difere iabil. a) Ar ta i, pri iduc ie dup, c f0) = m j=0 0 ft)dt + = b ) k f k ) ) f k ) 0) + ) β t)f ) t)dt. k!! 0 b) Ar ta i c, petru orice îtregi pozitivi m,, are loc egalitatea fj) = m 0 ft)dt + b ) k f k ) m) f k ) 0) + ) k!! m 0 β t)f ) t)dt. Idica ie: Folosi i partea a) petru fuc iile f j t) = ft + j), ude j =0,...,m. Exerci iul 7.7. a) Ar ta i c, petru orice k, are loc egalitatea 0 β 2k t)dt =0. b) Ar ta i c, petru orice îtregi k, m, au loc egalit ile 0 β 2k t)si2mπt)dt =0 i A k,m := c) S cosider m fuc iile 0 β 2k t)cos2πmt)dt = )k+ 2k)! 2πm) 2k. i Ar ta i c m f m t) = A k,m cos 2πjt j= m C m t) = cos2πjt). j=0 0 C m t)dt = 93
36 i b 2k = β 2k 0) = lim m f m0). Idica ie. Scrie i difere a b 2k f m 0) sub forma b 2k f m 0) = 0 β 2k 0)dt 0 β 2k t)c m t)dt = 0 C m t) β2k 0) β 2k t) ) dt. Bibliografie [] Eciclopedia electroic a irurilor de umere îtregi, se poate cosulta gratuit pe Iteret la adresa jas/sequeces/idex.html?laguage=romaia. [2] M. Aiger, Combiatorial Aalysis, Spriger-Verlag, 979. [3] G.M. Fihtehol, Curs de Calcul Difere ial i Itegral, vol.ii, Editura Tehic, Bucure ti, 964. [4] R. Staley, Eumerative Combiatorics. vol.i, Cambridge Uiversity Press, 986 [5] H. S. Wilf, Geeratig fuctioology se poate cosulta gratuit pe Iteret la adresa wilf/dowldgf.html) Departmet of Mathematics Uiversity of Notre Dame Notre Dame, IN icolaescu.@d.edu licolae/ Despre formula lui Taylor i calculul uor limite de Maria Tetiva Abstract The aim of this article is the calculate some limits usig Taylor series. Establishig the order of covergece of some sequeces could be cosidered the startig poit of this work. Some short presetatio of fuctio series ad Taylor series is icluded. Key words: Taylor formula, limits, Taylor series. M.S.C.: 26A03, 26A06, 26A24.. Itroducere. S cosider m, petru îceput, umerele reale pozitive a,a 2,...,a p ude p 2 este u um r atural) i fuc ia h : R R + defiit pri hx) = a x + a x ) ax x p, dac x 0 p p a a 2...a p, dac x =0. 94
37 Dup cum se tie, fuc ia h este cotiu pe R, cotiuitatea î origie a x stabilidu-se pri calculul limitei,,de tip + a x a x ) x p lim, care este x 0 p egal cu p a a 2...a p, deci cu valoarea fuc iei î 0. Cotiuitatea pe R {0} rezult di faptul c fuc ia se exprim pri opera ii elemetare cu fuc ii elemetare, i î acela i fel e d m seama c ea este idefiit derivabil pe R {0}; sepueîmod firesc problema: este fuc ia h derivabil î origie? R spusul la aceast îtrebare este afirmativ i ar t m acest lucru î cotiuare. Deoarece fuc ia este derivabil î veci tatea origiii i cotiu î origie se poate utiliza corolarul teoremei lui Lagrage, coform c ruia, dac exist i este fiit limita derivatei lim h x), atuci fuc ia este derivabil î 0, avâd derivata x 0 î 0 egal cu aceast limit. Avem: h h x) x) = a x + ax ax p x a x l a + a x 2 l a a x p l a p) a x + a x ) a x ax + p l ax ax p p x 2, petru orice x 0. Se poate calcula limita primului raport di aceast expresie, p a a 2...a p petru x 0 aume, ea este ), iar petru cea de-a doua frac ie folosim p regula lui l'hospital e afl m î cazul 0 0 ). Derivata um r torului este p a x k l a k + x i, deoarece avem p p ) a x k l2 a k a x k l a k l lim x 0 = lim x 0 2 = x x p a x k p p ) a x k l 2 a k a x k l a k l p p ) a x k l2 a k a x k l a k l p p p a x k p p a x k 2x p p p ) a x k l2 a k a x k 2 l a k l p p a x k a x k = ) x p a x k l a k p = a x k = 95
38 p ) p ) 2 = p p ) p l 2 a k l a k l 2 a k l a k l 2 2 p a a 2...a p =, 2p rezult c aceasta este i limita celui de al doilea raport di expresia derivatei h x). Atuci avem p ) p ) 2 p l 2 a k l a k h 0) = lim x 0 h x) = 2p 2 p a a 2...a p. S mai observ m c, dac folosim defii ia derivatei, am ob iut rela ia lim x 0 care coduce i la p p = h 0) = a x k x p a a 2...a p x p ) p ) 2 p l 2 a k l a k hx) h0) = lim = x 0 x 2p 2 p a a 2...a p, lim a + a ) a ) p p p a a 2...a p = h 0), adic stabile te ordiul de coverge al irului cu termeul geeral a + a x = ) a ) p = h p care are, la fel ca i fuc ia h î origie, limita p a a 2...a p ). Dup felul î care am calculat derivata fuc iei h se observ c aceasta este cotiu chiar i î origie) i, cum am ar tat mai sus, h este derivabil pe R {0} h are derivate de orice ordi pe R {0}); îtrebarea atural care se pue acum este dac fuc ia h este derivabil î origie deci dac h este de dou ori derivabil î 0). Problema care se ive te este, evidet, aceea a calculelor care devi tot mai epl cute ici î prima faz u au fost tocmai simple), de aceea se impue g sirea uei alte metode petru ivestigarea derivabilit ii lui h i, evetual, mai departe); remarc m, totu i, c datorit cotiuit ii derivatei îtâi putem calcula h 0) = = lim h x). Petru a putea cotiua aceast discu ie s facem îtâi o paratez x 0 mai lug, referitoare la formula pomeit î titlu precum i alte chestiui îrudite cu aceasta. 96
39 2. Formula lui Taylor se eu, de obicei, îtr-o form asem toare cu cea care urmeaz a se vedea [2], [3]). Teorema. Formula lui Taylor) Fie I u iterval i f o fuc ie defiit i de + ori derivabil pe I fiid u um r atural). Atuci, petru orice a, b I, a b, exist c I, cupris ître a i b ceea ce îseam c a<c<bsau b<c<a, î fuc ie de ordiea care exist ître a i b), astfel îcât f b) =f a)+ f a)! b a)+ + f ) a)! b a) + f +) c) +)! b a) +. Se observ c, petru =0, teorema devie biecuoscuta teorem a cre terilor fiite a lui Lagrage. Demostra ia se bazeaz pe urm toarea Lem. Fie F, G dou fuc ii defiite pe itervalul I, u um r atural i a, b I. Presupuem c F i G sut de + ori derivabile pe I, c F k) a) = = G k) a) =0,petru k =0,,..., i c G +) u se auleaz î itervalul a, b) sau b, a)). Atuci exist c I, cupris ître a i b astfel îcât F b) G b) = F +) c) G +) c). Demostra ie. Vom presupue, petru fixarea ideilor, c a<bcazul b<a tratâdu-se la fel). Mai îtâi observ m c fuc ia G i toate derivatele salepâ la cea de ordiul iclusiv u seauleaz î itervalul a, b]; demostr m acest fapt petru G, petru derivate efiid ici o deosebire ese ial. Îtr-adev r, dac exist u puct α a, b] astfel îcât G α) =0, atuci avâd i G a) =0), coform teoremei lui Rolle, exist α a, α), astfel îcât G α )=0. Apoi, petru c i G a) =0, iar i aplicâd teorema lui Rolle, rezult existe a uui α 2 a, α ), astfel îcât G α 2 )=0; cotiu m î acela i fel i ob iem pâ la urm u α + a, α ) a, b), astfel îcât G +) α + )=0, deci o cotrazicere a ipotezei c G +) useauleaz î itervalul a, b). Demostra ia lemei se bazeaz pe aplicarea repetat a teoremei lui Cauchy. Mai îtâi, exist c a, b) astfel îcât F b) F b) F a) = G b) G b) G a) = F c ) G c ) ; apoi aplic m teorema lui Cauchy derivatelor fuc iilor i g sim c exist c 2 a, c ) a, b), astfel îcât F c ) G c ) = F c ) F a) G c ) G a) = F c 2 ) G c 2 ).a.m.d. Î fial se ob i c k, k =, 2,...,+, astfel îcât, c k+ a, c k ), petru k =, 2,..., i F b) G b) = F c ) G c ) =...= F +) c + ) G +) c + ) i demostra ia se îcheie cu c = c +. 97
40 pri Demostra ia teoremei. Aplic m lema fuc iilor F, G : I R defiite F x) =f x) f a) f a)! petru orice x I. Se verific u or codi iile petru k =0,,..., ; de asemeea, i x a) f ) a)! G x) =x a) +, F k) a) =G k) a) =0, F +) x) =f +) x) G +) x) = +)! 0, x a), petru orice x I. Atuci, coform lemei, exist c a, b) sau c b, a)), astfel îcât egalitate care se dovede te echivalet cu f b) = f k) a) k! F b) G b) = F +) c) G +) c), i formula lui Taylor este demostrat. Vom scrie aceast formul î forma f x) = f k) a) k! ude a<c<xsau x<c<a, sau î forma ude b a) k + f +) c) +)! x a) k + f +) c) +)! f x) =T f,a)x)+r f,a)x), T f,a)x) = f k) a) k! x a) k b a) + x a) +, se ume te poliomul Taylor de grad asociat fuc iei f î puctul a, iarr f,a)x) este restul de ordi î formula lui Taylor; dac u exist pericol de cofuzie, vom ota simplu T = T f,a), respectiv R = R f,a). Teorema demostrat de oi ofer o exprimare a restului, aume ea arat c exist petru a fixat i x î itervalul I) c = c x, cupris ître a i x, astfel îcât R f,a)x) = f +) c x ) +)! x a) + ; 98
41 aceasta este forma lui Lagrage a restului formulei lui Taylor de ordiul sigura pe care o vom folosi î aceast lucrare). Exist i alte forme ale restului, petru care se poate cosulta [2]. Mai amitim aici doar forma itegral a restului: dac derivata de ordiul + a fuc iei f este cotiu pe I, atuci restul de ordi poate fi pus î forma R = cu alte cuvite are loc egalitatea f x) = x a f k) a) k! x t) f +) t)dt,! x x a) k + a x t) f +) t)dt.! O prim coseci a teoremei este formula,,exact a lui Taylor, care, de i u va fi folosit î aceast lucrare, este util î eum rate aplica ii. Corolarul. Dac f este o fuc ie poliomial de grad, atuci are loc egalitatea: f x) =f a)+ f a)! x a)+ f a) 2! x a) f ) a)! x a), petru orice umere reale a i x. Petru demostra ie este suficiet s observ m c derivata de ordiul + a fuc iei f este idetic ul pe R, deci restul formulei lui Taylor este, de asemeea, ul. Mai remarc m c, fiid o egalitate de fuc ii poliomiale pe R, formula este, de fapt, valabil chiar petru a i x umere complexe. Corolarul 2. Fie f o fuc ie de + ori derivabil pe itervalul I i a u puct iterior itervalului. a) Dac f +) este m rgiit îtr-o veci tate a lui a, atuci f x) T x) lim x a x a) =0. b) Dac derivata de ordiul + a fuc iei f este cotiu î puctul a, atuci f x) T x) lim x a x a) + = f +) a). +)! Demostra ie. a) Di formula lui Taylor se poate scrie, petru x I, x a f x) T x) x a) = f +) c x ) x a), +)! deci, dac presupuem c f +) x) M petru orice x V I V fiid o veci tate a lui a), vom avea f x) T x) x a) M x a, +)! 99
42 oricare ar fi x a, suficiet de apropiat de a; di aceast iegalitate cocluzia rezult imediat. b) La fel ca mai sus, putem rescrie formula lui Taylor î forma petru x I, x a. Avem, di ipotez, f x) T x) x a) + = f +) c x ), +)! lim f +) x) =f +) a); x a c x di formul este cupris ître a i x, de aceea, dac x a, atuci i c x a. Atuci lim x a f +) c x )=f +) a) i di formula de mai sus rezult i cocluzia, aume f x) T x) lim x a x a) + = f +) a). +)! De exemplu, deoarece fuc ia expoe ial x e x este idefiit derivabil pe R i toate derivatele sale au valoarea î origie, ob iem formula e x x x2 x lim 2!! x 0 x + = +)! am ales a =0, dar o formul asem toare u ese ial diferit se poate scrie petru orice a R). S mai remarc m u lucru, aume c, dac derivata de ordi + a fuc iei f este m rgiit î veci tatea puctului a, s zicem, ca mai sus, c f +) x) M petru x I, cu x a <α, α>0 fiid fixat, atuci se poate deduce, di formula lui Taylor, iegalitatea: f x) T x) <M α+ +)!, valabil petru orice x I, x a <α. Dac ar fi posibil g sirea uei costate M care s fie idepedet de m car petru u iterval mic a α, a + α) î jurul lui a), deoarece lim α + =0, aceasta coduce la cocluzia c fuc ia f +)! poate fi aproximat, î veci tatea lui a, cu polioamele sale Taylor, aproximarea fiid cu atât mai bu cu cât este mai mare, adic am avea f x) = lim T x) petru x a α, a + α) I. Acest fapt poate s u fie adev rat; de pild, se poate ar ta c petru fuc ia f : R R, defiit pri f x) =e x 2 dac x 0 i f 0) = 0, exist derivate de orice ordi î origie, toate egale cu 0. Desigur, aceasta îseam c poliomul Taylor de orice grad asociat fuc iei f î origie este 200
43 idetic ul, astfel c egalitatea f x) = lim T f,0) x) are loc umai petru x =0 x 0 u ipetru x îtr-u iterval edegeerat care co ie origiea, deoarece f este eul î toate puctele diferite de 0). Î sec iuea care urmeaz preciz m î al i termei formula f x) = lim T f,a)x) i ar t m care este ideea care e-a codus la scrierea acestui articol. 3. Serii umerice i serii de fuc ii. Serii Taylor. Î mod obi uit o serie umeric se defie te ca fiid o pereche de iruri de umere reale a ), S ) ), ude, petru orice, avem S = a + a a ; S ) se ume te irul sumelor par iale ale seriei. Nota ia folosit petru o serie este a sau a desigur c irul a ) poate fi idexat i cu 0, ude = 0 poate fi orice um r atural u eap rat, ceea ce se va reflecta i î ota ia seriei). Coverge a uei serii este î direct leg tur cu coverge a irului sumelor par iale: dac irul S ) este coverget i are limita S, atuci seria a se zice i ea coverget i se scrie a = S. Faptul c a = sau ) îseam c lim S = respectiv lim S = ). Î geeral, dac irul sumelor par iale are limita S R {, } se mai spue c seria are suma S; dac S ) u are limit seria u are sum. Î fie, seria se ume te diverget dac irul sumelor par iale este diverget o serie cu suma ifiit este diverget ). De exemplu, avem =, deoarece 2 lim ) 2 = lim ) 2 = i, mai geeral, q = q q, dac q, ) seria q se ume te seria geometric i este coverget petru q, )). De asemeea se verific u or c seria geometric are suma, dac q i u are ici u fel de sum î cazul q, ]. O alt serie celebr este seria armoic ; aceasta este seria i are suma. Seria armoic geeralizat, s ude s este u um r real fixat) este coverget dac i umai dac s>. Î particular, o celebr i frumoas ) formul a lui Euler afirm c 2 = π2 a se vedea [], ude mai sut demostrate i 6 alte formule asem toare). O serie u trebuie s fie privit, simplist, ca fiid,,o sum ifiit terme c ruia, de altfel, u-i acord m ici u ses); dac scriem S = a sau, ueori, se mai folose te i scrierea S = a + a 2 + ) trebuie s î elegem c 20
1, 1 PENANGKAPAN IKAN DENGAN PURSE SEINE
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N A N G K A P A N I K A N D E N G A N P U R S E S E I N E P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N A N G K A P A
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N A N G K A P A N I K A N D E N G A N P U R S E S E I N E P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N A N G K A P A
USAHA PEMBUATAN GULA AREN
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) G U L A A R E N ( G u l a S e m u t d a n C e t a k ) P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) G U L A A R E N ( G u l a S
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) G U L A A R E N ( G u l a S e m u t d a n C e t a k ) P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) G U L A A R E N ( G u l a S
1 0 0 m 2 BUDIDAYA PEMBESARAN IKAN NILA
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A R A N I K A N N I L A P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A R A N I K A N N I L A P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A
5 S u k u B u n g a 1 5 %
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) U S A H A A B O N I K A N P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) U S A H A A B O N I K A N B A N K I N D O N E S I A K A
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) U S A H A A B O N I K A N P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) U S A H A A B O N I K A N B A N K I N D O N E S I A K A
USAHA BUDIDAYA CABAI MERAH
 P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) U S A H A B U D I D A Y A C A B A I M E R A H P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P
P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) U S A H A B U D I D A Y A C A B A I M E R A H P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P
USAHA PENANGKAPAN IKAN PELAGIS DENGAN ALAT TANGKAP GILLNET
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N A N G K A P A N I K A N P E L A G I S D E N G A N A L A T T A N G K A P G I L L N E T P O L A P E M B I A Y A A N U S A H A K E C I L (
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N A N G K A P A N I K A N P E L A G I S D E N G A N A L A T T A N G K A P G I L L N E T P O L A P E M B I A Y A A N U S A H A K E C I L (
P r o f i l U s a h. a A s p e k P a s a r P e r m i n t a a n H a r g a...
 P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) I N D U S T R I S O H U N P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H
P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) I N D U S T R I S O H U N P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H
USAHA KONVEKSI PAKAIAN JADI
 P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) U S A H A K O N V E K S I P A K A I A N J A D I P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H (
P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) U S A H A K O N V E K S I P A K A I A N J A D I P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H (
6 S u k u B u n g a 1 5 % 16,57 % 4,84 tahun PENGOLAHAN IKAN BERBASIS FISH JELLY PRODUCT
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N G O L A H A N I K A N B E R B A S I S F I S H J E L L Y P R O D U C T ( O T A K -O T A K d a n K A K I N A G A ) P O L A P E M B I A Y
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) P E N G O L A H A N I K A N B E R B A S I S F I S H J E L L Y P R O D U C T ( O T A K -O T A K d a n K A K I N A G A ) P O L A P E M B I A Y
m 2 BUDIDAYA PEMBESARAN IKAN LELE
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A R A N I K A N L E L E P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A R A N I K A N L E L E P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) B U D I D A Y A P E M B E S A
BAB VI KESIMPULAN DAN SARAN
 59 BAB VI KESIMPULAN DAN SARAN 6.1. Kesimpulan Berdasarkan hasil data survai dan analisis yang dilakukan pada lahan parkir Rumah Sakit Umum Daerah RAA Soewondo Pati selama 3 hari dapat diambil kesimpulan
59 BAB VI KESIMPULAN DAN SARAN 6.1. Kesimpulan Berdasarkan hasil data survai dan analisis yang dilakukan pada lahan parkir Rumah Sakit Umum Daerah RAA Soewondo Pati selama 3 hari dapat diambil kesimpulan
0,8 9 0,9 4 1,2 4 7,1 6 %
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) E M P I N G M E L I N J O P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) E M P I N G M E L I N J O B A N K I N D O N E S I A K A
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) E M P I N G M E L I N J O P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) E M P I N G M E L I N J O B A N K I N D O N E S I A K A
SOAL-JAWAB MATEMATIKA PEMINATAN DIMENSI TIGA. Sebuah kubus ABCD.EFGH memiliki panjang rusuk 4 cm. P adalah titik tengah CD. Tentukan panjang EP!
 SOAL-JAWAB MATEMATIKA PEMINATAN DIMENSI TIGA Soal Sebuah kubus ABCD.EFGH memiliki panjang rusuk 4 cm. P adalah titik tengah CD. Tentukan panjang EP! Lihat gambar! Panjang EP didapat dengan rumus Pythagoras
SOAL-JAWAB MATEMATIKA PEMINATAN DIMENSI TIGA Soal Sebuah kubus ABCD.EFGH memiliki panjang rusuk 4 cm. P adalah titik tengah CD. Tentukan panjang EP! Lihat gambar! Panjang EP didapat dengan rumus Pythagoras
HASIL KALI TRANSFORMASI
 Definisi : Andaikan F dan G dua transformasi, denan F : V V G : V V HASIL KALI TRANSFORMASI Maka komposisi dari F dan G yan ditulis sebaai Go F didefinisikan sebaai: (Go F) (P) = G[F(P)], P V Teorema :
Definisi : Andaikan F dan G dua transformasi, denan F : V V G : V V HASIL KALI TRANSFORMASI Maka komposisi dari F dan G yan ditulis sebaai Go F didefinisikan sebaai: (Go F) (P) = G[F(P)], P V Teorema :
Soal Ujian 2 Persamaan Differensial Parsial
 Soal Uian 2 Persamaan Differensial Parsial M. Jamhuri April 15, 2013 1 Buktikan bahwa ux,t) = πˆ 1 x e θ2 dθ merupakan solusi persamaan difusi u t = u xx untuk setiap x R,t > 0. Untuk x 0 tunukkan bahwa
Soal Uian 2 Persamaan Differensial Parsial M. Jamhuri April 15, 2013 1 Buktikan bahwa ux,t) = πˆ 1 x e θ2 dθ merupakan solusi persamaan difusi u t = u xx untuk setiap x R,t > 0. Untuk x 0 tunukkan bahwa
Program Kerja TFPPED KBI Semarang 1
 U P A Y A M E N G G E R A K K A N P E R E K O N O M I A N D A E R A H M E L A L U I F A S I L I T A S I P E R C E P A T A N P E M B E R D A Y A A N E K O N O M I D A E R A H ( F P P E D ) S E K T O R P
U P A Y A M E N G G E R A K K A N P E R E K O N O M I A N D A E R A H M E L A L U I F A S I L I T A S I P E R C E P A T A N P E M B E R D A Y A A N E K O N O M I D A E R A H ( F P P E D ) S E K T O R P
KEMENTERIAN KESEHATAN RENIA KL TAHUN SEKRETARIAT IENDERAL 4 APRIL 2014 I '-I. "l I t t I
 KMRA KHAA RA K AHU 01 '- KRARA DRA 4 APR 0. -l "l . UMUM 1. Keee/e. U 0. M U 4. e. Ke P. P 7. Pe [u Rup,l 1. Rup Pe. Pep. Pep. PH u PD RMUR R CAA KRA KM'RA/MBAA (RA- K) AHU AARA 01 KMRA KHAA eke leel 04.01.01.
KMRA KHAA RA K AHU 01 '- KRARA DRA 4 APR 0. -l "l . UMUM 1. Keee/e. U 0. M U 4. e. Ke P. P 7. Pe [u Rup,l 1. Rup Pe. Pep. Pep. PH u PD RMUR R CAA KRA KM'RA/MBAA (RA- K) AHU AARA 01 KMRA KHAA eke leel 04.01.01.
BAB VI KESIMPULAN DAN SARAN. Permasalahan yang sering terjadi di kawasan perkotaan adalah kurangnya
 79 BAB VI KESIMPULAN DAN SARAN 6.1. Kesimpulan Permasalahan yang sering terjadi di kawasan perkotaan adalah kurangnya fasilitas parkir di luar badan jalan, baik berupa taman parkir atau gedung parkir sehingga
79 BAB VI KESIMPULAN DAN SARAN 6.1. Kesimpulan Permasalahan yang sering terjadi di kawasan perkotaan adalah kurangnya fasilitas parkir di luar badan jalan, baik berupa taman parkir atau gedung parkir sehingga
Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas
 Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Slide II Toni Bakhtiar Departemen Matematika IPB February 2012 TBK (IPB) Kalkulus Variasi February 2012 1 / 37 Masalah Brachystochrone
Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Slide II Toni Bakhtiar Departemen Matematika IPB February 2012 TBK (IPB) Kalkulus Variasi February 2012 1 / 37 Masalah Brachystochrone
Jabatan : Kepala Biro Pemerintahan Setda Provinsi Bali. Jabatan : Plt. Direktur Jenderal Bina Administrasi Kewilayahan. Jakarta, Februari 2016
 KMTRA DALAM R RPUBLK DOSA PRAA KRA TAHU 201 BRO PMRTAHA SKRTARAT DARAH PROVS BAL Dalam ranka mewujudkan manajemen pemerintahan yan efektif, transparan, dan akuntabel serta berrientasi pada hasil, kami
KMTRA DALAM R RPUBLK DOSA PRAA KRA TAHU 201 BRO PMRTAHA SKRTARAT DARAH PROVS BAL Dalam ranka mewujudkan manajemen pemerintahan yan efektif, transparan, dan akuntabel serta berrientasi pada hasil, kami
Kalkulus Variasi. Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas. Toni Bakhtiar. Departemen Matematika IPB
 Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum
Kalkulus Variasi Masalah Kalkulus Variasi, Fungsional Objektif, Variasi, Syarat Perlu Optimalitas Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum
Hand-Out Geometri Transformasi. Bab I. Pendahuluan
 Hand-Out Geometri Transformasi Bab I. Pendahuluan 1.1 Vektor dalam R 2 Misalkan u = (x 1,y 1 ), v = (x 2,y 2 ) dan w = (x 3,y 3 ) serta k skalar (bilangan real) Definisi 1. : Penjumlahan vektor u + v =
Hand-Out Geometri Transformasi Bab I. Pendahuluan 1.1 Vektor dalam R 2 Misalkan u = (x 1,y 1 ), v = (x 2,y 2 ) dan w = (x 3,y 3 ) serta k skalar (bilangan real) Definisi 1. : Penjumlahan vektor u + v =
Data Survey Kendaraan Yang Keluar Areal Parkir
 LAMPIRAN E.2-1 Data Survey Kendaraan Yang Keluar Areal Parkir Lokasi Survey : Areal Parkir Bagian Depan Jenis Kendaraan : Sepeda Motor Hari/Tanggal : Senin, 10 Juli 2006 Surveyor : Heri Plat Kendaraan
LAMPIRAN E.2-1 Data Survey Kendaraan Yang Keluar Areal Parkir Lokasi Survey : Areal Parkir Bagian Depan Jenis Kendaraan : Sepeda Motor Hari/Tanggal : Senin, 10 Juli 2006 Surveyor : Heri Plat Kendaraan
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 2008/2009
 SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 008/009. Perhatikan premis premis berikut! - Jika saya giat belajar maka saya bisa meraih juara - Jika saya bisa meraih juara maka saya boleh
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 008/009. Perhatikan premis premis berikut! - Jika saya giat belajar maka saya bisa meraih juara - Jika saya bisa meraih juara maka saya boleh
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 2008/2009
 SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 8/9. Perhatikan premis premis berikut! - Jika saya giat belajar maka saya bisa meraih juara - Jika saya bisa meraih juara maka saya boleh ikut
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 8/9. Perhatikan premis premis berikut! - Jika saya giat belajar maka saya bisa meraih juara - Jika saya bisa meraih juara maka saya boleh ikut
CONTOH SOAL MATEMATIKA SMP SATU ATAP: 1. Hasil dari (3 + (-4)) (5 + 3) adalah... A. 8 B. -7 C. -8 D Hasil dari adalah... A.
 CONTOH SOAL MATEMATIKA SMP SATU ATAP: 1. Hasil dari (3 + (-4)) (5 + 3) adalah... A. 8 B. -7 C. -8 D. -15 2. Hasil dari 12+13-14 adalah... A. 320 B. 512 C. 712 D. 1 E. 3. Ibu membeli 24 permen yang akan
CONTOH SOAL MATEMATIKA SMP SATU ATAP: 1. Hasil dari (3 + (-4)) (5 + 3) adalah... A. 8 B. -7 C. -8 D. -15 2. Hasil dari 12+13-14 adalah... A. 320 B. 512 C. 712 D. 1 E. 3. Ibu membeli 24 permen yang akan
DAFTAR SISA PANJAR YANG TELAH DIKEMBALIKAN KEPADA PENGGUGAT/PEMOHON BULAN JANUARI TAHUN 2012 OLEH PENGADILAN AGAMA LEBONG
 BULAN JANUARI TAHUN 2012 OLEH PENGADILAN AGAMA LEBONG Mengetahui, Lebong, 31 Januari 2012 BULAN FEBRUARITAHUN 2012 OLEH PENGADILAN AGAMA LEBONG 1. 0001/Pdt.G/2012/PA.Lbg RA Bin N X RPW BINTI SU Rp. 690.000,-
BULAN JANUARI TAHUN 2012 OLEH PENGADILAN AGAMA LEBONG Mengetahui, Lebong, 31 Januari 2012 BULAN FEBRUARITAHUN 2012 OLEH PENGADILAN AGAMA LEBONG 1. 0001/Pdt.G/2012/PA.Lbg RA Bin N X RPW BINTI SU Rp. 690.000,-
Pembahasan Soal SIMAK UI 2012 SELEKSI MASUK UNIVERSITAS INDONESIA. Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS. Matematika IPA
 Pembahasan Soal SIMAK UI 0 SELEKSI MASUK UNIVERSITAS INDONESIA Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA Disusun Oleh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pembahasan
Pembahasan Soal SIMAK UI 0 SELEKSI MASUK UNIVERSITAS INDONESIA Disertai TRIK SUPERKILAT dan LOGIKA PRAKTIS Matematika IPA Disusun Oleh : Pak Anang Kumpulan SMART SOLUTION dan TRIK SUPERKILAT Pembahasan
A s p e k P a s a r P e r m i n t a a n... 9
 P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) U S A H A K E R U P U K I K A N P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R
P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R I A H ) U S A H A K E R U P U K I K A N P O L A P E M B I A Y A A N U S A H A K E C I L S Y A R I A H ( P P U K -S Y A R
s\ fr Eni fzto v3z t ei* Et\^ fr 6 6-E iep EI :EeBEs eee **c 1Eg r: HH* E3s , E eeee =*s ehe *ts *EE9E5 d. xo 9<E =E tr6 2<fi {vr :..
 P b Q b 0 4. u 1.. xe 9< B r ee ** ( uy 3 H A3 HH* 3 P 3 r; 3 / * r.9< ^O ; u; 9 Oru B: ; :. T ' ' ^\n \^ r \ r. (. (5? n _$ 9 y.,. u,. r :.. 9 x p O (5..., e Q *95 0 ^ { u 1 1e. x 9< r eh * U, \ {R e*
P b Q b 0 4. u 1.. xe 9< B r ee ** ( uy 3 H A3 HH* 3 P 3 r; 3 / * r.9< ^O ; u; 9 Oru B: ; :. T ' ' ^\n \^ r \ r. (. (5? n _$ 9 y.,. u,. r :.. 9 x p O (5..., e Q *95 0 ^ { u 1 1e. x 9< r eh * U, \ {R e*
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 2010/2011 Tanggal Ujian: 01 Juni 2011
 Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 00/0 Tanggal Ujian: 0 Juni 0. Diketahui vektor u = (a, -, -) dan v = (a, a, -). Jika vektor u tegak lurus pada v, maka nilai a adalah... A.
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 00/0 Tanggal Ujian: 0 Juni 0. Diketahui vektor u = (a, -, -) dan v = (a, a, -). Jika vektor u tegak lurus pada v, maka nilai a adalah... A.
PENGGUNAAN METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN PADA KALKULUS VARIASI ABSTRACT
 PENGGUNAAN METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN PADA KALKULUS VARIASI Febrian Lisnan, Asmara Karma 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
PENGGUNAAN METODE DEKOMPOSISI ADOMIAN UNTUK MENYELESAIKAN PERMASALAHAN PADA KALKULUS VARIASI Febrian Lisnan, Asmara Karma 2 Mahasiswa Program Studi S Matematika 2 Dosen Jurusan Matematika Fakultas Matematika
Sistem Koordinat Kartesian Tegak Lurus dan Persamaan Garis Lurus
 Modul 1 Sistem Koordinat Kartesian Tegak Lurus dan Persamaan Garis Lurus Drs. Sukirman, M.Pd. D alam Modul Pertama ini, kita akan membahas tentang Sistem Koordinat Kartesian Tegak Lurus dan Persamaan Garis
Modul 1 Sistem Koordinat Kartesian Tegak Lurus dan Persamaan Garis Lurus Drs. Sukirman, M.Pd. D alam Modul Pertama ini, kita akan membahas tentang Sistem Koordinat Kartesian Tegak Lurus dan Persamaan Garis
Dasar Sistem Pengaturan - Transformasi Laplace. Transformasi Laplace bilateral atau dua sisi dari sinyal bernilai riil x(t) didefinisikan sebagai :
 Defiisi Trasformasi Laplace Trasformasi Laplace Bilateral Trasformasi Laplace bilateral atau dua sisi dari siyal berilai riil x(t) didefiisika sebagai : X B x(t)e Operasi trasformasi Laplace bilateral
Defiisi Trasformasi Laplace Trasformasi Laplace Bilateral Trasformasi Laplace bilateral atau dua sisi dari siyal berilai riil x(t) didefiisika sebagai : X B x(t)e Operasi trasformasi Laplace bilateral
A. C O B O L R e se rv e d W o rd s
 P e m rop a m rja n T e rstru lctu r 1 (C O B O L ) A. C O B O L R e se rv e d W o rd s R ese rv ed W o rd s, m e ry p a fc a rn :: - k ata y a n g te la h d id e fin is ik a n - y a n g m e m ilik i art!
P e m rop a m rja n T e rstru lctu r 1 (C O B O L ) A. C O B O L R e se rv e d W o rd s R ese rv ed W o rd s, m e ry p a fc a rn :: - k ata y a n g te la h d id e fin is ik a n - y a n g m e m ilik i art!
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 2010/2011
 Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 00/0 Tanggal Ujian: 0 Juni 0. Diketahui vektor u (a, -, -) dan v (a, a, -). Jika vektor u tegak lurus pada v, maka nilai a adalah... A. -
Soal-Soal dan Pembahasan SNMPTN Matematika IPA Tahun Pelajaran 00/0 Tanggal Ujian: 0 Juni 0. Diketahui vektor u (a, -, -) dan v (a, a, -). Jika vektor u tegak lurus pada v, maka nilai a adalah... A. -
R p ,-
 P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) F U R N I T U R E K A Y U P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) F U R N I T U R E K A Y U B A N K I N D O N E S I A K A
P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) F U R N I T U R E K A Y U P O L A P E M B I A Y A A N U S A H A K E C I L ( P P U K ) F U R N I T U R E K A Y U B A N K I N D O N E S I A K A
BAB II LANDASAN TEORI. Untuk menghitung nilai cadangan asuransi secara umum, maka dibutuhkan
 5 BAB II LANDASAN TEORI Untuk menghitung nilai cadangan asuransi secara umum, maka dibutuhkan beberapa teori dasar yang dapat menyederhanakan permasalahan dan mempermudah proses perhitungan dan analisis
5 BAB II LANDASAN TEORI Untuk menghitung nilai cadangan asuransi secara umum, maka dibutuhkan beberapa teori dasar yang dapat menyederhanakan permasalahan dan mempermudah proses perhitungan dan analisis
disesuaikan dengan soal yaitu 2 atau 3 )
 SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 6/7. Bentuk sederhana dari ( + ) ( 5 ) adalah. A. C. 8 E. 8 + 5 B. + 5 D. 8 + ( + ) ( 5 ) ( + ) (. 5 ) ( + ) ( 5 ) + + 5 - + 8 8 - Jawabannya
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 6/7. Bentuk sederhana dari ( + ) ( 5 ) adalah. A. C. 8 E. 8 + 5 B. + 5 D. 8 + ( + ) ( 5 ) ( + ) (. 5 ) ( + ) ( 5 ) + + 5 - + 8 8 - Jawabannya
BAB PDB Linier Order Satu
 BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
BAB 1 Konsep Dasar 1 BAB PDB Linier Order Satu BAB 3 Aplikasi PDB Order Satu 3 BAB 4 PDB Linier Order Dua Untuk memulai pembahasan ini terlebih dahulu akan ditinjau beberapa teorema tentang konsep umum
Analisis Riil II: Diferensiasi
 Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Definisi Turunan Definisi dan Teorema Aturan Rantai Fungsi Invers Definisi (Turunan) Misalkan I R sebuah interval, f : I R, dan c I. Bilangan riil L dikatakan turunan dari f di c jika diberikan sebarang
Vektor dan Operasi Dasarnya
 Modul 1 Vektor dan Operasi Dasarnya Drs. Sukirman, M.Pd. D PENDAHULUAN alam modul ini disajikan pengertian vektor, aljabar vektor dan aplikasinya dalam geometri. Aljabar vektor membicarakan penjumlahan
Modul 1 Vektor dan Operasi Dasarnya Drs. Sukirman, M.Pd. D PENDAHULUAN alam modul ini disajikan pengertian vektor, aljabar vektor dan aplikasinya dalam geometri. Aljabar vektor membicarakan penjumlahan
Ruang Vektor Real. Modul 1 PENDAHULUAN
 Modul Ruang Vektor Real Drs. R.J. Pamuntjak, M.Sc. P PENDAHULUAN ada bagian pertama Modul 5 Aljabar Linear Elementer I sudah kita bahas sepuluh sifat untuk R dan R 3 mengenai penjumlahan dan perkalian
Modul Ruang Vektor Real Drs. R.J. Pamuntjak, M.Sc. P PENDAHULUAN ada bagian pertama Modul 5 Aljabar Linear Elementer I sudah kita bahas sepuluh sifat untuk R dan R 3 mengenai penjumlahan dan perkalian
Persamaan Di erensial Orde-2
 oki neswan FMIPA-ITB Persamaan Di erensial Orde- Persamaan diferensial orde-n adalah persamaan yang melibatkan x; y; dan turunan-turunan y; dengan yang paling tinggi adalah turunan ke-n: F x; y; y ; y
oki neswan FMIPA-ITB Persamaan Di erensial Orde- Persamaan diferensial orde-n adalah persamaan yang melibatkan x; y; dan turunan-turunan y; dengan yang paling tinggi adalah turunan ke-n: F x; y; y ; y
Beberapa Pertidaksamaan Tipe Ostrowski
 Beberapa Pertidaksamaan Tipe Ostrowski Rani Fransiska Departemen Marematika, FMIPA UI, Kampus UI Depok 1644 ranifransiska@uiacid Abstrak Pertidaksamaan Ostrowski adalah suatu pertidaksamaan integral untuk
Beberapa Pertidaksamaan Tipe Ostrowski Rani Fransiska Departemen Marematika, FMIPA UI, Kampus UI Depok 1644 ranifransiska@uiacid Abstrak Pertidaksamaan Ostrowski adalah suatu pertidaksamaan integral untuk
Page 1
 SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 6/7. Bentuk sederhana dari ( + ) ( 5 ) adalah. A. C. 8 E. 8 + 5 B. + 5 D. 8 + ( + ) ( 5 ) ( + ) (. 5 ) ( + ) ( 5 ) + + 5 - + 8 8 - Jawabannya
SOAL DAN PEMBAHASAN UJIAN NASIONAL SMA/MA IPA TAHUN PELAJARAN 6/7. Bentuk sederhana dari ( + ) ( 5 ) adalah. A. C. 8 E. 8 + 5 B. + 5 D. 8 + ( + ) ( 5 ) ( + ) (. 5 ) ( + ) ( 5 ) + + 5 - + 8 8 - Jawabannya
PERSAMAAN DIFERENSIAL LINIER NON HOMOGEN
 LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
LINIER NON HOMOGEN Contoh PD linier non homogen orde 2. Bentuk umum persamaan PD Linier Non Homogen Orde 2, adalah sebagai berikut : y + f(x) y + g(x) y = r(x) ( 2-35) Solusi umum y(x) akan didapatkan
Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak
 4 Lingkaran 4.1. Persamaan Lingkaran Bentuk Baku. Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak tetap dari suatu titik tetap. Titik tetap dari lingkaran disebut pusat lingkaran,
4 Lingkaran 4.1. Persamaan Lingkaran Bentuk Baku. Lingkaran adalah tempat kedudukan titik-titik pada bidang yang berjarak tetap dari suatu titik tetap. Titik tetap dari lingkaran disebut pusat lingkaran,
Teori kendali. Oleh: Ari suparwanto
 Teori kendali Oleh: Ari suparwanto Minggu Ke-1 Permasalahan oleh : Ari Suparwanto Permasalahan Diberikan sistem dan sinyal referensi. Masalah kendali adalah menentukan sinyal kendali sehingga output sistem
Teori kendali Oleh: Ari suparwanto Minggu Ke-1 Permasalahan oleh : Ari Suparwanto Permasalahan Diberikan sistem dan sinyal referensi. Masalah kendali adalah menentukan sinyal kendali sehingga output sistem
Barisan dan Deret Agus Yodi Gunawan
 Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Barisan dan Deret Agus Yodi Gunawan Barisan. Definisi. Barisan tak hingga adalah suatu fungsi dengan daerah asalnya himpunan bilangan bulat positif dan daerah kawannya himpunan bilangan real. Notasi untuk
Kalkulus Variasi. Persamaan Euler, Masalah Kalkulus Variasi Berkendala, Syarat Batas. Toni Bakhtiar. Departemen Matematika IPB.
 Kalkulus Variasi Persamaan Euler, Masalah Kalkulus Variasi Berkendala, Syarat Batas Toni Bakhtiar Departemen Matematika IPB Februari 214 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 214 1
Kalkulus Variasi Persamaan Euler, Masalah Kalkulus Variasi Berkendala, Syarat Batas Toni Bakhtiar Departemen Matematika IPB Februari 214 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 214 1
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 204 CALON TIM OLIMPIADE MATEMATIKA INDONESIA 205 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Disusun oleh : Olimpiade Matematika Tk Kabupaten/Kota
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 204 CALON TIM OLIMPIADE MATEMATIKA INDONESIA 205 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Disusun oleh : Olimpiade Matematika Tk Kabupaten/Kota
OSN MATEMATIKA SMA Hari 1 Soal 1. Buktikan bahwa untuk sebarang bilangan asli a dan b, bilangan. n = F P B(a, b) + KP K(a, b) a b
 OSN MATEMATIKA SMA Hari 1 Soal 1. Buktikan bahwa untuk sebarang bilangan asli a dan b, bilangan adalah bilangan bulat genap tak negatif. n = F P B(a, b + KP K(a, b a b Solusi. Misalkan d = F P B(a, b,
OSN MATEMATIKA SMA Hari 1 Soal 1. Buktikan bahwa untuk sebarang bilangan asli a dan b, bilangan adalah bilangan bulat genap tak negatif. n = F P B(a, b + KP K(a, b a b Solusi. Misalkan d = F P B(a, b,
Variabel Banyak Bernilai Real 1 / 1
 Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Fungsi Variabel Banyak Bernilai Real Turunan Parsial dan Turunan Wono Setya Budhi KK Analisis dan Geometri, FMIPA ITB Variabel Banyak Bernilai Real 1 / 1 Turunan Parsial dan Turunan Usaha pertama untuk
Bab 2 Distribusi Survival dan Tabel Mortalitas
 Bab 2 Distribusi Survival dan Tabel Mortalitas 2.1 Distribusi Survival Meninggalnya seseorang merupakan sesuatu yang pasti terjadi namun kapan terjadinya tidak dapat diprediksi. Karena itu, ketahanan hidup
Bab 2 Distribusi Survival dan Tabel Mortalitas 2.1 Distribusi Survival Meninggalnya seseorang merupakan sesuatu yang pasti terjadi namun kapan terjadinya tidak dapat diprediksi. Karena itu, ketahanan hidup
FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU ABSTRACT
 FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU Syofia Deswita 1, Syamsudhuha 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
FORMULA PENGGANTI METODE KOEFISIEN TAK TENTU Syofia Deswita 1, Syamsudhuha 2, Agusni 2 1 Mahasiswa Program Studi S1 Matematika 2 Dosen Jurusan Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas
BAB IV VEKTOR. Latihan Kompetensi Siswa 1. c Q. R a 8. E. 0. A. Evaluasi Pengertian atau Ingatan. 1. C. PR 2. D. 2QR 3. E B.
 B IV VEKTOR E C Q P Lhn Koeens Ssw A Els Pengern Ingn A AP BQ CR R B C PR D QR E BC CD DA AA AA D E CD BA DC CD BA B BF B OB CE EB BC BC A O geser Jd CE EB BC OB A D B C BC OB B Els Pehn dn Pengsn Mer
B IV VEKTOR E C Q P Lhn Koeens Ssw A Els Pengern Ingn A AP BQ CR R B C PR D QR E BC CD DA AA AA D E CD BA DC CD BA B BF B OB CE EB BC BC A O geser Jd CE EB BC OB A D B C BC OB B Els Pehn dn Pengsn Mer
SISTEM DINAMIK KONTINU LINEAR. Oleh: 1. Meirdania Fitri T 2. Siti Khairun Nisa 3. Grahani Ayu Deca F. 4. Fira Fitriah 5.
 SISTEM DINAMIK KONTINU LINEAR Oleh: 1. Meirdania Fitri T 2. Siti Khairun Nisa 3. Grahani Ayu Deca F. 4. Fira Fitriah 5. Lisa Risfana Sari Sistem Dinamik D Sistem dinamik adalah sistem yang dapat diketahui
SISTEM DINAMIK KONTINU LINEAR Oleh: 1. Meirdania Fitri T 2. Siti Khairun Nisa 3. Grahani Ayu Deca F. 4. Fira Fitriah 5. Lisa Risfana Sari Sistem Dinamik D Sistem dinamik adalah sistem yang dapat diketahui
TEOREMA VIETA DAN JUMLAH NEWTON. 1. Pengenalan
 TEOREMA VIETA DAN JUMLAH NEWTON TUTUR WIDODO. Pengenalan Sebelum berbicara banyak tentang Teorema Vieta dan Identitas Newton, terlebih dahulu saya beri penjelasan singkat mengenai polinomial. Di sekolah
TEOREMA VIETA DAN JUMLAH NEWTON TUTUR WIDODO. Pengenalan Sebelum berbicara banyak tentang Teorema Vieta dan Identitas Newton, terlebih dahulu saya beri penjelasan singkat mengenai polinomial. Di sekolah
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 015 CALON TIM OLIMPIADE MATEMATIKA INDONESIA 016 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Disusun oleh : 1. 015 = 5 13 31 Banyaknya faktor
SELEKSI OLIMPIADE TINGKAT KABUPATEN/KOTA 015 CALON TIM OLIMPIADE MATEMATIKA INDONESIA 016 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL Bidang Matematika Disusun oleh : 1. 015 = 5 13 31 Banyaknya faktor
RANCANGAN PERATURAN KEPALA BADAN PENGAWAS TENAGA NUKLIR NOMOR... TAHUN 2012 TENTANG TINGKAT KLIERENS
 KEPALA BADAN PENGAWAS TENAGA NUKLIR REPUBLIK INDONESIA RANCANGAN PERATURAN KEPALA BADAN PENGAWAS TENAGA NUKLIR NOMOR... TAHUN 2012 TENTANG TINGKAT KLIERENS DENGAN RAHMAT TUHAN YANG MAHA ESA KEPALA BADAN
KEPALA BADAN PENGAWAS TENAGA NUKLIR REPUBLIK INDONESIA RANCANGAN PERATURAN KEPALA BADAN PENGAWAS TENAGA NUKLIR NOMOR... TAHUN 2012 TENTANG TINGKAT KLIERENS DENGAN RAHMAT TUHAN YANG MAHA ESA KEPALA BADAN
JARAK DUA TITIK KEGIATAN BELAJAR 2
 1 KEGIATAN BELAJAR 2 JARAK DUA TITIK Setelah mempelajari kegiatan belajar 2 ini, mahasiswa diharapkan mampu: 1. menghitung jarak dua titik di bidang, 2. menghitung jarak dua titik di ruang, 3. menentukan
1 KEGIATAN BELAJAR 2 JARAK DUA TITIK Setelah mempelajari kegiatan belajar 2 ini, mahasiswa diharapkan mampu: 1. menghitung jarak dua titik di bidang, 2. menghitung jarak dua titik di ruang, 3. menentukan
MA1201 MATEMATIKA 2A Hendra Gunawan
 MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2016/2017 8 Maret 2017 Kuliah yang Lalu 10.1-2 Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1
MA1201 MATEMATIKA 2A Hendra Gunawan Semester II, 2016/2017 8 Maret 2017 Kuliah yang Lalu 10.1-2 Parabola, Elips, dan Hiperbola 10.4 Persamaan Parametrik Kurva di Bidang 10.5 Sistem Koordinat Polar 11.1
b = dan a b= 22. Jika sudut antara a dan b adalah a, maka
 1. Jika vektor p = i + 4j + 9k, q = 2i + 5 j 3k, p = 3i + j 2k dan, a = p 2q + 3r maka panjang vektor a =... 2. Diketahui vektor a 4i 5 j 3k = + dan titik ( 2, 1,3) P. Jika panjang PQ sama dengan panjang
1. Jika vektor p = i + 4j + 9k, q = 2i + 5 j 3k, p = 3i + j 2k dan, a = p 2q + 3r maka panjang vektor a =... 2. Diketahui vektor a 4i 5 j 3k = + dan titik ( 2, 1,3) P. Jika panjang PQ sama dengan panjang
1 Mengapa Perlu Belajar Geometri Daftar Pustaka... 1
 Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
Daftar Isi 1 Mengapa Perlu Belajar Geometri 1 1.1 Daftar Pustaka.................................... 1 2 Ruang Euclid 3 2.1 Geometri Euclid.................................... 8 2.2 Pencerminan dan Transformasi
Persamaan Diferensial Biasa
 Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Persamaan Diferensial Biasa Pendahuluan, Persamaan Diferensial Orde-1 Toni Bakhtiar Departemen Matematika IPB September 2012 Toni Bakhtiar (m@thipb) PDB September 2012 1 / 37 Pendahuluan Konsep Dasar Beberapa
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 2012 Tanggal Ujian: 13 Juni 2012
 Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6, 4 ). ( -1, 4 ) E. ( 5, 4 ) B. ( 6, 4) D. ( 1, 4 )
Soal-Soal dan Pembahasan Matematika IPA SNMPTN 01 Tanggal Ujian: 13 Juni 01 1. Lingkaran (x + 6) + (y + 1) 5 menyinggung garis y 4 di titik... A. ( -6, 4 ). ( -1, 4 ) E. ( 5, 4 ) B. ( 6, 4) D. ( 1, 4 )
Learning Outcomes Sebaran Kontinu Nilai Harapan dan Ragam Beberapa Sebaran Kontinu. Peubah Acak Kontinu. Julio Adisantoso.
 Beberapa 27 April 2014 Beberapa Learning Outcome Outline Mahasiswa dapat mengerti dan menentukan peubah acak diskret Mahasiswa dapat memahami dan menghitung nilai harapan Mahasiswa dapat memahami dan menghitung
Beberapa 27 April 2014 Beberapa Learning Outcome Outline Mahasiswa dapat mengerti dan menentukan peubah acak diskret Mahasiswa dapat memahami dan menghitung nilai harapan Mahasiswa dapat memahami dan menghitung
Outline. Bagian 0: Motivasi. Bagian 1: Optimasi Taklinier Dasar dasar Teorema Karush Kuhn Tucker. Bagian 2: Sequential Quadratic Programming
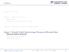 Outline Bagian 0: Motivasi Bagian 1: Optimasi Taklinier Dasar dasar Teorema Karush Kuhn Tucker Bagian 2: Sequential Quadratic Programming Bagian 3: Masalah Kendali Optimal dengan Persamaan Di erensial
Outline Bagian 0: Motivasi Bagian 1: Optimasi Taklinier Dasar dasar Teorema Karush Kuhn Tucker Bagian 2: Sequential Quadratic Programming Bagian 3: Masalah Kendali Optimal dengan Persamaan Di erensial
K A B U P A T E N B A D U N G
 L A P O R A N K I N E R J A I N S T A N S I P E M E R I N T A H ( L K j I P ) D I N A S P A R I W I S A T A K A B U P A T E N B A D U N G 2 0 1 4 K A T A P E N G A N T A R O m S w a s t y a s t u P u j
L A P O R A N K I N E R J A I N S T A N S I P E M E R I N T A H ( L K j I P ) D I N A S P A R I W I S A T A K A B U P A T E N B A D U N G 2 0 1 4 K A T A P E N G A N T A R O m S w a s t y a s t u P u j
MODUL RESPONSI MAM 4222 KALKULUS IV
 MODUL RESPONSI MAM 4222 KALKULUS IV Mata Kuliah Wajib 2 sks untuk mahasiswa Program Studi Matematika Oleh Dr. WURYANSARI MUHARINI KUSUMAWINAHYU, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS
MODUL RESPONSI MAM 4222 KALKULUS IV Mata Kuliah Wajib 2 sks untuk mahasiswa Program Studi Matematika Oleh Dr. WURYANSARI MUHARINI KUSUMAWINAHYU, M.Si. PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS
DASAR-DASAR TEORI PELUANG
 DASAR-DASAR TEORI PELUANG Herry P. Suryawan 1 Ruang Peluang Definisi 1.1 Diberikan himpunan tak kosong Ω. Aljabar-σ (σ-algebra pada Ω adalah koleksi subhimpunan A dari Ω dengan sifat (i, Ω A (ii jika A
DASAR-DASAR TEORI PELUANG Herry P. Suryawan 1 Ruang Peluang Definisi 1.1 Diberikan himpunan tak kosong Ω. Aljabar-σ (σ-algebra pada Ω adalah koleksi subhimpunan A dari Ω dengan sifat (i, Ω A (ii jika A
BAB VI KESIMPULAN DAN SARAN
 70 BAB VI KESIMPULAN DAN SARAN 6.1 Kesimpulan Setelah dilakukan pengamatan dan hasil pengolahan data, maka dapat disimpulkan beberapa hal sebagai berikut: 1. Outlet Biru Yogyakarta memiliki luas lahan
70 BAB VI KESIMPULAN DAN SARAN 6.1 Kesimpulan Setelah dilakukan pengamatan dan hasil pengolahan data, maka dapat disimpulkan beberapa hal sebagai berikut: 1. Outlet Biru Yogyakarta memiliki luas lahan
Kontrol Optimum. Syarat Transversalitas, Current-valued Hamiltonian. Toni Bakhtiar. Departemen Matematika IPB. Februari 2014
 Kontrol Optimum Syarat Transversalitas, Current-valued Hamiltonian Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 37 Outline Syarat
Kontrol Optimum Syarat Transversalitas, Current-valued Hamiltonian Toni Bakhtiar Departemen Matematika IPB Februari 2014 tbakhtiar@ipb.ac.id (IPB) MAT332 Kontrol Optimum Februari 2014 1 / 37 Outline Syarat
Pengantar Proses Stokastik
 Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia Peluang Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu.
Bab 1: Dasar-Dasar Probabilitas Statistika FMIPA Universitas Islam Indonesia Peluang Percobaan adalah kegiatan yang menghasilkan keluaran/hasil yang mungkin secara acak. Contoh: pelemparan sebuah dadu.
4 E 6? E 2988*e8. e * +es $ st. ,5 ^ Sl El. E $' Cg3ss il? fa E d-.$.el. o g *l= E ie titsl. B"HF-A x 5 HC 9. H ; sef. f I F E.
 P G c e cl & 11 3 il il & ] u ) ] 4.' \l 1 1 \ { e i \ f l C,) 1 l ( (,) q { \'D c1 Tl 8 g *l l?). ( x \ fi Y &Ē. 38 \l l S e ili,5 ^ Sl l 3 R f.$.l ie i $' Cg3 il?.;x \l e * +e$ 4 6? 2988*e8 ; ci cci+b..2
P G c e cl & 11 3 il il & ] u ) ] 4.' \l 1 1 \ { e i \ f l C,) 1 l ( (,) q { \'D c1 Tl 8 g *l l?). ( x \ fi Y &Ē. 38 \l l S e ili,5 ^ Sl l 3 R f.$.l ie i $' Cg3 il?.;x \l e * +e$ 4 6? 2988*e8 ; ci cci+b..2
Perhitungan Penetapan Kadar Susut Pengeringan. No Kadar (%) Rata-rata kadar (%) Syarat
 Lampiran 1 Perhitungan Penetapan Kadar Susut Pengeringan No Kadar (%) Rata-rata kadar (%) Syarat 1. 2. 3. 8,9 9,3 9,0 9,07 < 10 % Lampiran 2 Perhitungan Penetapan Kadar Abu Serbuk Daun Saga (Abrus precatorius
Lampiran 1 Perhitungan Penetapan Kadar Susut Pengeringan No Kadar (%) Rata-rata kadar (%) Syarat 1. 2. 3. 8,9 9,3 9,0 9,07 < 10 % Lampiran 2 Perhitungan Penetapan Kadar Abu Serbuk Daun Saga (Abrus precatorius
KUANTOR KHUSUS (Minggu ke-8)
 KUANTOR KHUSUS (Minggu ke-8) 1 4 Kuantor Jenis Lain Terdapatlah satu dan hanya satu x yang mempunyai sifat P. ( x)(p(x) ( y)(p(y) = y = x)) Terdapat x yang memenuhi sifat p dan untuk setiap y yang memenuhi
KUANTOR KHUSUS (Minggu ke-8) 1 4 Kuantor Jenis Lain Terdapatlah satu dan hanya satu x yang mempunyai sifat P. ( x)(p(x) ( y)(p(y) = y = x)) Terdapat x yang memenuhi sifat p dan untuk setiap y yang memenuhi
BAB IV HASIL DAN PEMBAHASAN
 24 BAB IV HASIL DAN PEMBAHASAN 4.1 Analisis Optimalisasi Waktu dan Biaya Usaha yang dilakukan dalam mempercepat waktu pelaksanaan proyek yakni dengan menambah sumber daya (biaya), penambahan ini berupa
24 BAB IV HASIL DAN PEMBAHASAN 4.1 Analisis Optimalisasi Waktu dan Biaya Usaha yang dilakukan dalam mempercepat waktu pelaksanaan proyek yakni dengan menambah sumber daya (biaya), penambahan ini berupa
P R O G R A M K ER J A T A H U N A N TIM P EN G G ER A K P K K D E SA P R IN G G O W IR A W A N TA H U N 2011
 P R O G R A M K ER J A T A H U N A N TIM P EN G G ER A K P K K D E SA P R IN G G O W IR A W A N TA H U N 2011 P O K JA IV NO B ID G PR O GR A M T U JU SA SA R K EG IATA N D A K ET 1 2 3 4 5 6 7 8 1 K E
P R O G R A M K ER J A T A H U N A N TIM P EN G G ER A K P K K D E SA P R IN G G O W IR A W A N TA H U N 2011 P O K JA IV NO B ID G PR O GR A M T U JU SA SA R K EG IATA N D A K ET 1 2 3 4 5 6 7 8 1 K E
STRUKTUR ALJABAR: RING
 STRUKTUR ALJABAR: RING BAHAN AJAR Oleh: Rippi Maya Program Studi Magister Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI - Bandung 2016 1 Pada grup telah dipelajari
STRUKTUR ALJABAR: RING BAHAN AJAR Oleh: Rippi Maya Program Studi Magister Pendidikan Matematika Sekolah Tinggi Keguruan dan Ilmu Pendidikan (STKIP) SILIWANGI - Bandung 2016 1 Pada grup telah dipelajari
KALKULUS MULTIVARIABEL II
 Definisi KALKULUS MULTIVARIABEL II (Minggu ke-7) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Definisi 1 Definisi 2 ontoh Soal Definisi Integral Garis Fungsi f K R 2 R di Sepanjang Kurva
Definisi KALKULUS MULTIVARIABEL II (Minggu ke-7) Andradi Jurusan Matematika FMIPA UGM Yogyakarta, Indonesia Definisi 1 Definisi 2 ontoh Soal Definisi Integral Garis Fungsi f K R 2 R di Sepanjang Kurva
TRANSFORMASI. Suatu transfornmasi pada bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga.
 1 TRANSFORMASI Suatu transfornmasi pada bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga. Sebuah fungsi yang bijektif adalah sebuah fungsi yang bersifat: 1.
1 TRANSFORMASI Suatu transfornmasi pada bidang V adalah suatu fungsi yang bijektif dengan daerah asalnya V dan daerah nilainya V juga. Sebuah fungsi yang bijektif adalah sebuah fungsi yang bersifat: 1.
Modifikasi Playfair Cipher dengan Pembalikan Pesan
 Modifikasi Playfair Cipher dengan Pembalikan Pesan Desfrianta Salmon Barus (13508107) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
Modifikasi Playfair Cipher dengan Pembalikan Pesan Desfrianta Salmon Barus (13508107) Program Studi Teknik Informatika Sekolah Teknik Elektro dan Informatika Institut Teknologi Bandung, Jl. Ganesha 10
Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc
 KALKULUS III Teorema Integral Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 INTEGRAL GARIS Integral Garis pada Fungsi Skalar Definisi : Jika f didefinisikan pada kurva diberikan secara parametrik
KALKULUS III Teorema Integral Dosen Pengampu : Puji Andayani, S.Si, M.Si, M.Sc 1 INTEGRAL GARIS Integral Garis pada Fungsi Skalar Definisi : Jika f didefinisikan pada kurva diberikan secara parametrik
UNIVERSITI SAINS MALAYSIA. Peperiksaan Semester Pertama Sidang 1991/92. Ok tober/november Kalkulus dan Aliabar Linear
 UNIVERSITI SAINS MALAYSIA Peperiksaan Semester Pertama Sidang 99/9 Ok tober/november 99 MAK 0 Kalkulus dan Aliabar Linear Masa : jam] Arahan: Soalan I dan II mesti dijawab di dalam kertas komputer OMR
UNIVERSITI SAINS MALAYSIA Peperiksaan Semester Pertama Sidang 99/9 Ok tober/november 99 MAK 0 Kalkulus dan Aliabar Linear Masa : jam] Arahan: Soalan I dan II mesti dijawab di dalam kertas komputer OMR
PDP linear orde 2 Agus Yodi Gunawan
 PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
PDP linear orde 2 Agus Yodi Gunawan Pada bagian ini akan dipelajari tiga jenis persamaan diferensial parsial (PDP) linear orde dua yang biasa dijumpai pada masalah-masalah dunia nyata, yaitu persamaan
STATISTIK PERTEMUAN VI
 STATISTIK PERTEMUAN VI 1. TEORI PENDUKUNG 1.1 Pendahuluan 1. Variabel acak 1.3 Distribusi variabel acak diskrit 1.4 Distribusi variabel acak kontinu 1.5 Distribusi multivariat 1.1 Pendahuluan Definisi
STATISTIK PERTEMUAN VI 1. TEORI PENDUKUNG 1.1 Pendahuluan 1. Variabel acak 1.3 Distribusi variabel acak diskrit 1.4 Distribusi variabel acak kontinu 1.5 Distribusi multivariat 1.1 Pendahuluan Definisi
menentukan bentuk pengendali yang indeks perfomansinya adalah norm H 2.
 BAB II Teori Kontrol H 4 BAB II Teori Kontrol H Bab ini akan membahas teori kontrol H yang tujuannya adalah menentukan bentuk pengendali yang indeks perfomansinya adalah norm H Untuk itu pertama-tama akan
BAB II Teori Kontrol H 4 BAB II Teori Kontrol H Bab ini akan membahas teori kontrol H yang tujuannya adalah menentukan bentuk pengendali yang indeks perfomansinya adalah norm H Untuk itu pertama-tama akan
Prestasi itu diraih bukan didapat!!! SOLUSI SOAL
 SELEKSI OLIMPIADE TINGKAT PROVINSI 013 TIM OLIMPIADE MATEMATIKA INDONESIA 014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi 013
SELEKSI OLIMPIADE TINGKAT PROVINSI 013 TIM OLIMPIADE MATEMATIKA INDONESIA 014 Prestasi itu diraih bukan didapat!!! SOLUSI SOAL BAGIAN PERTAMA Disusun oleh : Solusi Olimpiade Matematika Tk Provinsi 013
Fourier Analysis & Its Applications in PDEs - Part II
 Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
Fourier Analysis & Its Applications in PDEs Hendra Gunawan http://personal.fmipa.itb.ac.id/hgunawan/ Analysis and Geometry Group Bandung Institute of Technology Bandung, INDONESIA WIDE 2010 5-6 August
KEPUTUSAI[ 2. Undang-Undang Nomor 12 Tahun 2012 tentang Pendidikan Tinggi (LN No. 158 Tahun 2012, Tambahan LN No" 5336 Tahun 2Ol2);
 KTR RST, TKOOG PK TGG URSTS RGG KUTS PRK KUT KmuC UiJl, uly - Suby 0115 Tl, (031) 5911451,. (031) 595741 wbit : htt://uuyl ui..t -m : f @ ui,c,i KPUTUS[ K KUTS PRK KUT URSTS,RflGG m : 18 /U3.1"1lKPlO7
KTR RST, TKOOG PK TGG URSTS RGG KUTS PRK KUT KmuC UiJl, uly - Suby 0115 Tl, (031) 5911451,. (031) 595741 wbit : htt://uuyl ui..t -m : f @ ui,c,i KPUTUS[ K KUTS PRK KUT URSTS,RflGG m : 18 /U3.1"1lKPlO7
HUBUNGAN DAERAH DEDEKIND DENGAN GELANGGANG HNP
 HUBUNGAN DAERAH DEDEKIND DENGAN GELANGGANG HNP TEDUH WULANDARI Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor Jl. Meranti, Kampus IPB Darmaga, Bogor 16680,
HUBUNGAN DAERAH DEDEKIND DENGAN GELANGGANG HNP TEDUH WULANDARI Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor Jl. Meranti, Kampus IPB Darmaga, Bogor 16680,
BAB II TINJAUAN PUSTAKA
 7 BAB II TINJAUAN PUSTAKA Dalam bab ini akan dibahas beberapa poin tentang sistem dinamik, kestabilan sistem dinamik, serta konsep bifurkasi. A. Sistem Dinamik Secara umum Sistem dinamik didefinisikan
7 BAB II TINJAUAN PUSTAKA Dalam bab ini akan dibahas beberapa poin tentang sistem dinamik, kestabilan sistem dinamik, serta konsep bifurkasi. A. Sistem Dinamik Secara umum Sistem dinamik didefinisikan
KUBUS DAN BALOK. Kata-Kata Kunci: unsur-unsur kubus dan balok jaring-jaring kubus dan balok luas permukaan kubus dan balok volume kubus dan balok
 8 KUBUS DAN BALOK Perhatikan benda-benda di sekitar kita. Dalam kehidupan sehari-hari kita sering memanfaatkan benda-benda seperti gambar di samping, misalnya kipas angin, video cd, dan kardus bekas mainan.
8 KUBUS DAN BALOK Perhatikan benda-benda di sekitar kita. Dalam kehidupan sehari-hari kita sering memanfaatkan benda-benda seperti gambar di samping, misalnya kipas angin, video cd, dan kardus bekas mainan.
SMP / MTs Mata Pelajaran : Matematika
 Kunci Jawaban Latihan Soal Ujian Nasional 010 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika 1. Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari
Kunci Jawaban Latihan Soal Ujian Nasional 010 Sekolah Menengah Pertama / Madrasah Tsanawiyah SMP / MTs Mata Pelajaran : Matematika 1. Jawab: b Untuk menentukan hasil dari suatu akar telebih dahulu cari
Relasi, Fungsi, dan Transformasi
 Modul 1 Relasi, Fungsi, dan Transformasi Drs. Ame Rasmedi S. Dr. Darhim, M.Si. M PENDAHULUAN odul ini merupakan modul pertama pada mata kuliah Geometri Transformasi. Modul ini akan membahas pengertian
Modul 1 Relasi, Fungsi, dan Transformasi Drs. Ame Rasmedi S. Dr. Darhim, M.Si. M PENDAHULUAN odul ini merupakan modul pertama pada mata kuliah Geometri Transformasi. Modul ini akan membahas pengertian
SUATU$STUDI:$SOLUSI$MASALAH$NILAI$AWAL$$DENGAN$ METODE$PEMBAGI$BEDA$
 LAPORAN$HASIL$PENELITIAN$ $ NO:$III/LPPM/212-9/1-P$ SUATU$STUDI:$SOLUSI$MASALAH$NILAI$AWAL$$DENGAN$ METODE$PEMBAGI$BEDA$ $ MariaAnestasia IwanSugiarto LEMBAGAPENELITIANDANPENGABDIANKEPADAMASYARAKAT UNIVERSITASKATOLIKPARAHYANGAN
LAPORAN$HASIL$PENELITIAN$ $ NO:$III/LPPM/212-9/1-P$ SUATU$STUDI:$SOLUSI$MASALAH$NILAI$AWAL$$DENGAN$ METODE$PEMBAGI$BEDA$ $ MariaAnestasia IwanSugiarto LEMBAGAPENELITIANDANPENGABDIANKEPADAMASYARAKAT UNIVERSITASKATOLIKPARAHYANGAN
Denih Handayani Pembahasan :
 www.m4th-lab.net Denih Handayani www.m4th-lab.net Pembahasan : 8 59 5 4 8 59 5 4 81 1 864 1 = 5 (8 ) 1 5(9 ) 1 8 = 8 59 5 4 8 59 1 4 = 8 5 59 5 4 ( 1 4 ) = 8 5 59 6 4 = 8 1 ( ) = 8 = 7 8 Ingat! ( + 7)(
www.m4th-lab.net Denih Handayani www.m4th-lab.net Pembahasan : 8 59 5 4 8 59 5 4 81 1 864 1 = 5 (8 ) 1 5(9 ) 1 8 = 8 59 5 4 8 59 1 4 = 8 5 59 5 4 ( 1 4 ) = 8 5 59 6 4 = 8 1 ( ) = 8 = 7 8 Ingat! ( + 7)(
1.3 Segitiga-segitiga yang Kongruen
 1.3 Segitiga-segitiga yang Kongruen Apa yang akan kamu pelajari? B A Syarat Dua Bangun Datar Kongruen Mengenali dua bangun datar yang kongruen a- tau tak kongruen, dengan menyebut syaratnya. Menentukan
1.3 Segitiga-segitiga yang Kongruen Apa yang akan kamu pelajari? B A Syarat Dua Bangun Datar Kongruen Mengenali dua bangun datar yang kongruen a- tau tak kongruen, dengan menyebut syaratnya. Menentukan
